Abstract
I analyze the role of infinite idealizations used in the renormalization group (RG hereafter) method in explaining universality across microscopically different physical systems in critical phenomena. I argue that despite the reference to infinite limit systems such as systems with infinite correlation lengths during the RG process, the key to explaining universality in critical phenomena need not involve infinite limit systems. I develop my argument by introducing what I regard as the explanatorily relevant property in RG explanations: linearization* property; I then motivate and prove a proposition about the linearization* property in support of my view. As a result, infinite limit systems in RG explanations are dispensable.









Similar content being viewed by others
Notes
There are examples of universality that do not concern critical phase transitions, for instance when we utilize the same equation to calculate the periods of pendulums made of different materials (see Batterman (2001) for more details). This paper only concerns universal behaviors near critical phase transitions.
Two notes are in order. First, as will become clear in later sections, the RG methods are arguably the best because they explain universality by showing that the microscopic details that differentiate systems are irrelevant and they provide a sophisticated way of calculating the critical exponents. Second, later in the paper I will identify another less noted use of infinity in the RG method: the RG iterations limit (see Palacios (2019) for further discussions). For our current purposes, the use of thermodynamic limits already points to the core tension with respect to the role of infinite idealizations.
There is a separate debate about whether RG explanations, regardless of whether it involves infinite idealizations, fit into any of the above listed accounts of explanations. Many maintain that RG explanations constitute a special kind of non-causal explanations, though they disagree as to exactly what kind they are (see, for instance, Batterman (2000); Batterman and Rice (2014); Reutlinger (2014); Khalifa et al. (2020)). Note also that some accounts of explanations allow for fictional explanans (Bokulich 2008, 2012).
The relevant concepts such as “flow,” “fixed point,” and “RG trajectories” will be introduced in Sect. 3.2.
While Shech (2018) intends his distinction to extend to other scientific accounts such as understanding, representation, and prediction, I focus on explanation here.
In this paper I do not go into details about whether RG methods, regardless of the use of infinite limit systems, provide an explanation for universality, and exactly what account of explanation it is. For a cautious reader who does not agree that RG methods provide an explanation for universality at all, she is encouraged to read my claim in the following way: if infinite limit systems provide an explanation of universality in RG methods, then we have reasons to think that large but finite systems do as well.
Norton (2012) also considers a third situation where there is no limit system, but since we are already in the context of infinite limit systems, I suppress that part of the discussion.
One might worry that there are situations where a case (a) holds for some property, but the infinite limit system might still provide some “cognitive or epistemic goods” that are important or essential to the explanation. I am fairly sympathetic to this worry, and I think in these situations, there would be some other property of infinite limit system that provides these “cognitive or epistemic goods,” with respect to which a case (b) holds (i.e. the corresponding limiting property does not provide these goods). As I will suggest, in these situations, we would then want to examine whether this new property is explanatorily relevant, and whether these “cognitive or epistemic goods” can be equivalently provided by other properties of finite systems.
See Sklar (2000, pp. 61–71) for a discussion of “controllability” in the context of thermodynamics and limiting systems. Others have introduced similar distinctions as (un)controllability, such as “harmless and pernicious idealizations” in Earman (2008, p. 402) and “pathological/non-pathological idealizations” in Shech (2015).
This is related to, but different from, Baron (2016)’s notion of “explanatory load-carrying” in the following way. When the statement “infinite limit systems have property \({\mathcal {P}}\)” carries explanatory load (i.e. had a system not have \({\mathcal {P}}\), then some features of the phenomana we want to explain would have been otherwise), then the property in case (b) is central to the scientific explanation in my sense. However, the converse is not true, as I explain in the next paragraph. \({\mathcal {P}}\) could be central to the explanation without the statement “infinite limit systems have \({\mathcal {P}}\)” carrying explanatory load. This is because another property of finite systems could provide the same explanatory function. I stick to my way of presentation since I want to highlight later in the paper the equivalent explanatory functions that different properties serve.
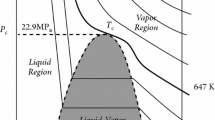
Note that this is in the direction from liquid to vapor. Phenomenologically speaking, when the volume of the system expands, we observe air bubbles coming out.
Here, we make the use of the fact that the overall mass of the system remains unchanged.
There is sometimes another related dependency question, namely why the categorization of universality classes only depends on fundamental symmetries and dimensions, that some scholars such as Batterman and Rice also take the RG method to explain (Batterman and Rice 2014; Batterman 2019). However, whether and how the RG method answers the dependency question is less clear. Those who claim that the RG method answers the dependency question nonetheless agree that the answer is a derivative, or a by-product, of how the universality class is delimited (Batterman and Rice 2014, p. 363). I believe that to the extent that infinite limit systems are concerned, if an explanation of the stability question can be provided using finite systems, then an explanation of the dependency question can also be provided using finite systems.
It is important to note that the two limits do not commute. See Palacios (2019) for further discussions.
Note that the argument that phase transitions require the thermodynamics limit, though very widely accepted, is not a rigorous theorem; there are efforts to develop a theory of phase transitions for finite systems (see Butterfield (2011, pp. 1124–25)).
For instance, the lattice spacing in an Ising model.
For instance, the coupling constants in an Ising model.
It is important to note here that in the space of Hamiltonians, the unrenormalized Hamiltonians, i.e. the Hamiltonians that we start with, represent actual physical systems in an already idealized manner. The Hamiltonians on the RG trajectories are successively coarser representations of the physical systems.
The asterisk is introduced to distinguish linearization* from ordinary linearization of the RG transformation. Linearization* specifically refers to linearization in the vicinity of the nontrivial fixed point such that we can retrieve reliable critical exponents.
We regard each RG transformation, \(R_b\), as an element of a semi-group. By definition of a semi-group, there is an associative group operation on elements: \(R_{bb'}=R_bR_{b'}\). Each element does not necessarily have an inverse. The semi-group property of RG transformations explains (in a folk usage of the word) the name “group” in Renormalization Group.
This also explains why the Hamiltonians starting off the basin of attraction move further and further away from the basin of attraction. The relation \(\xi \sim |t|^{-v}\) entails that the original systems with finite correlation length moves further and further away from the critical point.
Domain of attraction mentioned in the Batterman quote above is equivalent to the basin of attraction.
Of course we can linearize at the nontrivial fixed point, the result will just be trivial. What I claim is the impossibility to perform linearization*, with an asterisk, at the point. Linearization* entails that the results should give us meaningful information about the critical exponents of the universality class that the fixed point delimits. In this sense, linearization* on the RG transformation of a fixed point is impossible.
To be fair, I have not encountered any discussions in the literature suggesting that this situation is in fact possible, and it might well be the case that this requirement would turn out to be equivalent to the prima facie stronger requirement that I define next. However, I still consider this possibility to preemptively rule out potential counterexamples.
As an example of this, Yin (2011) constructs a Banach space from the interaction terms of an Ising model.
Or whether we can do away with the norms and introduce a metric on the space.
Mainwood (2006) and Butterfield (2011) have previously used finite-size crossover to support dispensabilism. Finite-size crossover describes a situation where, for a system of finite size, if its correlation length is small compared to the size of the system, but very large compared to minimum length scale, the system flows towards a fixed point associated with the infinite system. However, when the correlation length is comparable to the size of the finite system, then the flow crosses over to some other fixed point (Mainwood 2006, p. 244; Butterfield (2011), pp. 1131–32). This phenomenon lends support to my main argument. As the correlation length grows large, i.e. as we get closer to the critical phase transition, as long as we have a finite system whose size is still large compared to the correlation length, finite-size crossover tells us that its RG trajectory will flow towards the (right) fixed point (until it is driven away).
Such a Hamiltonian necessarily exists according to Haller and Kennedy (1996).
Note that this condition is possibly stronger than Yin (2011)’s result shows, in that we start in “the other direction”–from a bound on the renormalized Hamiltonian.
The point is also not entirely fixed, though its variation after RG transformation would be small.
For instance, what Hamiltonian addition means can look very different depending on the mathematical structures specified.
Although in theory \([R_b]_{ij}\) is real but not necessarily symmetric, in practice \([R_b]_{ij}\) is often diagonalizable with real eigenvalues. The treatment of non-symmetric matrix admits minor modifications, which I will not mention in the present paper. See (Goldenfeld 1992) for detailed discussion.
Here, \(t'=\frac{T'-T^*}{T^*}\).
Note that the structure of the proof can be schematized as \(\forall x \exists y \forall z (A)\Rightarrow \forall x \forall z \exists y (A)\).
Note that because of the semi-group property, the \(R_b^{m+i}\) surface is the same surface as the \(R_{b^{m+i}}\) surface, with the same norm.
References
Baron, S. (2016). The explanatory dispensability of idealizations. Synthese, 193(2), 365–386.
Batterman, R. W. (2000). Multiple realizability and universality. The British Journal for the Philosophy of Science, 51(1), 115–145.
Batterman, R. W. (2001). The devil in the details: Asymptotic reasoning in explanation, reduction, and emergence. Oxford: Oxford University Press.
Batterman, R. W. (2005). Critical phenomena and breaking drops: Infinite idealizations in physics. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 36(2), 225–244.
Batterman, R. W. (2015). Autonomy and scales. Why more is different (pp. 115–135). New York: Springer.
Batterman, R. W. (2017). Philosophical implications of kadanoff’s work on the renormalization group. Journal of Statistical Physics, 167(3–4), 559–574.
Batterman, R. W. (2018). Autonomy of theories: An explanatory problem. Noûs, 52(4), 858–873.
Batterman, R. W. (2019). Universality and RG explanations. Perspectives on Science, 27(1), 26–47.
Batterman, R. W., & Rice, C. C. (2014). Minimal model explanations. Philosophy of Science, 81(3), 349–376.
Bokulich, A. (2008). Reexamining the quantum-classical relation: Beyond reductionism and pluralism. Cambridge: Cambridge University Press.
Bokulich, A. (2012). Distinguishing explanatory from nonexplanatory fictions. Philosophy of Science, 79(5), 725–737.
Butterfield, J. (2011). Less is different: Emergence and reduction reconciled. Foundations of Physics, 41(6), 1065–1135.
Callender, C. (2001). Taking thermodynamics too seriously. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 32(4), 539–553.
Cardy, J. (1996). Scaling and renormalization in statistical physics (Vol. 5). Cambridge: Cambridge University Press.
Craver, C. F. (2006). When mechanistic models explain. Synthese, 153(3), 355–376.
Earman, J. (2008). Superselection rules for philosophers. Erkenntnis, 69(3), 377–414.
Fletcher, S. C., Palacios, P., Ruetsche, L., & Shech, E. (2019). Infinite idealizations in science: An introduction. Synthese, 196(5), 1657–1669.
Goldenfeld, N. (1992). Lectures on phase transitions and the renormalization group. (Frontiers in physics; Vol. 85). Westview Press.
Haller, K., & Kennedy, T. (1996). Absence of renormalization group pathologies near the critical temperature. Two examples. Journal of Statistical Physics, 85(5), 607–637.
Hempel, C. G., & Oppenheim, P. (1948). Studies in the logic of explanation. Philosophy of Science, 15(2), 135–175.
Kadanoff, L. (1971). Critical behavior, universality and scaling in critical phenomena.
Kadanoff, L. P. (2000). Statistical physics: Statics, dynamics and renormalization. Singapore: World Scientific Publishing Co Inc.
Kadanoff, L. P. (2010). Theories of matter: Infinities and renormalization. arXiv preprint arXiv:1002.2985.
Khalifa, K., Doble, G., & Millson, J. (2020). Counterfactuals and explanatory pluralism. The British Journal for the Philosophy of Science, 71(4), 1439–1460.
Mainwood, P. (2006). Is More Different? Emergent Properties in Physics. Ph. D. thesis, University of Oxford.
Morrison, M. (2015). Why is more different? Why more is different (pp. 91–114). New York: Springer.
Norton, J. D. (2012). Approximation and idealization: Why the difference matters. Philosophy of Science, 79(2), 207–232.
Palacios, P. (2019). Phase transitions: A challenge for intertheoretic reduction? Philosophy of Science, 86(4), 612–640.
Palacios, P., & Valente, G. (2021). The paradox of infinite limits: A realist response. Contemporary scientific realism. Oxford: Oxford University Press.
Reutlinger, A. (2014). Why is there universal macrobehavior? Renormalization group explanation as noncausal explanation. Philosophy of Science, 81(5), 1157–1170.
Shech, E. (2013). What is the paradox of phase transitions? Philosophy of Science, 80(5), 1170–1181.
Shech, E. (2015). Two approaches to fractional statistics in the quantum hall effect: Idealizations and the curious case of the anyon. Foundations of Physics, 45(9), 1063–1100.
Shech, E. (2018). Infinite idealizations in physics. Philosophy Compass, 13(9), e12514.
Simons, B. (1997). Phase transitions and collective phenomena. Lecture Notes, available at http://www.tcm.phy.cam.ac.uk/~bds10/phase.html
Sklar, L. (2000). Theory and truth: Philosophical critique within foundational science. Oxford: Oxford University Press.
Strevens, M. (2008). Depth: An account of scientific explanation. Cambridge: Harvard University Press.
Wilson, K. G. (1983). The renormalization group and critical phenomena. Reviews of Modern Physics, 55, 583–600.
Wilson, K. G., & Kogut, J. (1974). The renormalization group and the $\epsilon $ expansion. Physics Reports, 12(2), 75–199.
Woodward, J. (2005). Making things happen: A theory of causal explanation. Oxford: Oxford University Press.
Yin, M. (2011). Renormalization group transformations near the critical point: Some rigorous results. Journal of Mathematical Physics, 52(11), 113507.
Acknowledgements
I’m extremely grateful to Ben Feintzeig, Kareem Khalifa, John Norton, Patricia Palacios, Laura Ruetsche, Jim Weatherall, and two anonymous reviewers for their invaluable comments on previous drafts. Thanks to Sorin Bangu, Bob Batterman, Liam Kofi Bright, and Kade Cicchella, audience members at the Foundations of Physics 2018 Conference in Utrecht, audience members at the MCMP, and members of the Philosophy of Physics Research Group at UC Irvine for helpful discussions on the topic. I’m grateful to David for his years of companionship and support. This paper was made possible in part through the support of grant #61048 from the John Templeton Foundation. The opinions expressed in this publication are those of the author and do not necessarily reflect the views of the John Templeton Foundation.
Funding
(Information that explains whether and by whom the research was supported) John Templeton Foundation Grant #61048
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
(Include appropriate disclosures) The authors that they have declare no conflict of interest.
Appendices
Appendix A: The linearization* process
Through the linearization* process, we accomplish two main feats: first, we categorize the eigenvectors of the RG transformation matrix into relevant, irrelevant, and marginal eigenvectors, and define a basin of attraction spanned by the irrelevant eigenvectors in which all Hamiltonians flow to the nontrivial fixed point; second, we retrieve the critical exponents that characterize the universality class associated with the nontrivial fixed point. In this appendix, I illustrate how the two main feats are achieved through the linearization* process in detail. Note that this explication should be read in a heuristic way, since discussions about the exact mathematical structures of the space of Hamiltonians are still underway.Footnote 34
Following Goldenfeld (1992) and Simons (1997) , we start the linearization* process by taking \(S=S^*+\delta S\), a point in the vicinity of the nontrivial fixed point. We then linearize the RG transformation on S,
For \(S_i\), the i-th parameter of the Hamiltonian, we have
We assume that \([R_b]_{ij}\) is a real-valued symmetric matrix.Footnote 35 The semi-group property of \(R_b\) gives us the relation
where \(O_i\) is an eigenvector of \(R_b\), \(R_{b'}\), and \(R_{bb'}\), and \(\lambda _i(b)\), \(\lambda _i(b')\), and \(\lambda _i(bb')\) are the respective eigenvalues. Now, we differentiate Eq. 1 with respect to \(b'\),
We can solve Eq. 2 for \(\lambda _i(b)\) with the initial condition \(\lambda _i(1)=1\), and obtain
with \(y_i\) independent of b.
We can expand \(\delta S\) in terms of the eigenvectors of \(R_b\),
Therefore,
We then distinguish the following three cases based on the values of \(y_i\):
-
1.
\(y_i>0\). In this case, \(g'^i\) grows after RG transformations.
-
2.
\(y_i<0\). In this case, \(g'^i\) shrinks after RG transformations.
-
3.
\(y_i=0\). In this case, \(g'^i\) does not change after RG transformations.
The importance of this categorization is that after iterations of RG transformations, the components of \(\delta S\) along directions \(O_i\) for which case 1 holds are the only relevant components to drive the Hamiltonian away from the non-trivial fixed point. The components of \(\delta S\) in other directions either shrink to 0, driving the Hamiltonian towards the nontrivial fixed point (as in case 2), or stay the same (as in case 3). Because of this, we give the corresponding eigenvalues \(\lambda _i (b)\) and eigenvectors \(O_i\) the following names:
-
1.
\(\lambda _i (b)\) and \(O_i\) are relevant eigenvalues/eigenvectors if \(y_i>0\).
-
2.
\(\lambda _i (b)\) and \(O_i\) are irrelevant eigenvalues/eigenvectors if \(y_i<0\).
-
3.
\(\lambda _i (b)\) and \(O_i\) are marginal eigenvalues/eigenvectors if \(y_i=0\).
The irrelevant eigenvectors span the basin of attraction. Because \(g^i\) would shrink to 0 after iterations of RG transformations if \(O_i\) is an irrelevant eigenvector, we know that Hamiltonians that start in the basin of attraction would eventually flow to the nontrivial fixed point. Hamiltonians that start off the basin of attraction would eventually drive away from the basin of attraction towards a trivial fixed point by dint of relevant eigenvalues.
Through the linearization* process, we can also retrieve the critical exponents. To illustrate that, let’s consider a simple system with only one parameter, which can be taken to be the temperature, and consider the critical exponent v in \(\xi \sim t^{-v}\). Other critical exponents and for more complex systems can be similarly calculated.
For this simple system, we have \(T'=R_b(T)\) and at the critical temperature \(T^*\), \(T^*=R_b(T^*)\). \(T=0\) and \(T=\infty \) are the two trivial fixed points. Linearizing in the vicinity of the fixed point, we have
where Eq. 5 is from Eq. 3. We define the reduced temperature
then together with Eqs. 4 and 5 we have
Footnote 36 Iterating the RG transformation n times, we have
Now we consider how the correlation length transforms after n RG transformations. Because \(\xi '=\frac{\xi }{b}\) after one transformations, after n RG transformations we have
We can choose b arbitrary so that it satisfies
with u being an arbitrary positive number much larger than unity. Equations 6 and 7 together give us
Because u is much larger than unity, \(\xi (u)\) is the correlation length for temperatures well above the critical temperature, where fluctuations are small, we can use standard approximation methods to estimate its value. Therefore, if we compare Eq. 8 with the power relation between the correlation length and reduced temperature \(\xi \sim |t|^{-v}\), we can read off
Finally, we know from Eqs. 4 and 5 that
So it suffices to know \(R_b\), or a good approximation of it, in order to calculate \(\lambda _t(b)\), \(y_t\), and hence v, a critical exponent.
Appendix B: Proofs of propositions
Proposition 1
Proof
Suppose that a system \({\mathcal {S}}\) is in the universality class delimited by a nontrivial fixed point \(S^*\). Given an arbitrary linearization*-adequate neighborhood, from Definition 2 we know that there exists \(m\in {\mathbb {N}}\) such that for any arbitrary natural number n, there is a Hamiltonian S with \(S\not \in BoA\) such that for all Hamiltonians \(S'\) with \(0<\Vert S'-S_c\Vert \le \Vert S-S_c\Vert \) and \(S' \not \in BoA\), we have \(R^{m+i}_{b}(S)\in B_\epsilon (S^*)\) for all \(0\le i<n\) and \(i\in {\mathbb {N}}\). Now fix an arbitrary natural number n, we have a Hamiltonian S with \(S\not \in BoA\) such that for all Hamiltonians \(S'\) with \(0<\Vert S'-S_c\Vert \le \Vert S-S_c\Vert \) and \(S'\not \in BoA\), \(R^{m+i}_{b}(S)\in B_\epsilon (S^*)\) for all \(0\le i<n\) and \(i\in {\mathbb {N}}\). That is to say, all \(S'\) exhibits the linearization* property.Footnote 37\(\square \)
Proposition 2
Proof
Suppose that Conditions 1, 2, 3, and 4 all hold for a physical system \({\mathcal {S}}\).
\(\Longrightarrow \):
Suppose further that \(R_b^n(S_c)\rightarrow S^*\) as \(n\rightarrow \infty \).
Choose an arbitrary linearization*-adequate neighborhood \(B_\epsilon (S_c)\). From Condition 3, there exists an open set V in the basin of attraction such that (1) \(S^*\in V\), and (2) for all surfaces \(R_b^n\) such that \(R_b^n\cap V\ne \emptyset \) and for all \(P\in (R_b^n\cap V)\), there exists \(r\in {\mathbb {R}}^+\) such that \(Q\in B_\epsilon (S^*)\) for all \(Q\in R_b^n\), \(Q\not \in BoA\), and \(\Vert Q-P\Vert _b^n<r\).
Because \(R_b^n(S_c)\rightarrow S^*\) as \(n\rightarrow \infty \), we can find \(m\in {\mathbb {N}}\) such that for all \(m'>m\), we have \(R_b^{m'}(S_c)\in V\). Now choose an arbitrary natural number n. We have \(R_b^{m+i}(S_c)\in V\) for all \(0\le i<n\).
For each \(i\in {\mathbb {N}}\) with \(0\le i<n\), since \(R_b^{m+i}(S_c)\in (R_b^{m+i}\cap V)\), we have some \(r_i>0\) such that for all points \(Q'\) with \(Q'\in R_b^{m+i}\), \(Q'\not \in BoA\), and \(\Vert Q'-R_b^{m+i}(S_c)\Vert _b^{m+i}<r_i\), we have \(Q'\in B_\epsilon (S^*)\). From Condition 1, we know that there is a point \(S^i\) with \(S^i\not \in BoA\) on the original unrenormalized surface, such that
By the semi-group property of the RG transformation, \(R_bR_{b'}(P)=R_{bb'}(P)\) for all P in the space of Hamiltonians, Equation 9 is equivalent to
Footnote 38 from which we have \(R_b^{m+i}(S^i)\in B_\epsilon (S^*)\).
Now, let S be an unrenormalized point with \(S\not \in BoA\) such that \(0<\Vert S-S_c\Vert \le \Vert S^i-S_c\Vert \) for all \(i<n\). It follows from Condition 2 that
for all \(0\le i<n\). By the semi-group property of the RG transformation, Eq. 11 is equivalent to
for all \(0\le i<n\). Therefore, \(R_b^{m+i}(S)\in B_\epsilon (S^*)\).
Similarly, from Condition 2, we have, for all \(S'\) with \(S'\not \in BoA\) such that \(0<\Vert S'-S_c\Vert \le \Vert S-S_c\Vert \),
for all \(0\le i<n\). By the semi-group property of the RG transformation,
for all \(0\le i<n\). Therefore, \(R_b^{m+i}(S')\in B_\epsilon (S^*)\) for all \(S'\) with \(0<\Vert S'-S_c\Vert \le \Vert S-S_c\Vert \) and \(S'\not \in BoA\). The system \({\mathcal {S}}\) is in the universality class delimited by \(S^*\).
\(\Longleftarrow \):
Suppose further that \({\mathcal {S}}\) is in the universality class delimited by \(S^*\) under Definition 2.
Given an arbitrary open set V in the basin of attraction such that \(S^*\in V\). By Condition 4, we have a linearization*-adequate neighborhood \(B_\epsilon (S^*)\) such that \((\partial B_\epsilon (S^*)\cap BoA) \subseteq V\).
Because \({\mathcal {S}}\) is in the universality class delimited by \(S^*\) under Definition 2, there exists \(m\in {\mathbb {N}}\) such that for any arbitrary \(n\in {\mathbb {N}}\), there exists S with \(S\not \in BoA\) on the unrenormalized surface such that for all \(S'\) with \(0<\Vert S'-S_c\Vert <\Vert S-S_c\Vert \) and \(S'\not \in BoA\) we have \(R_b^{m+i}(S')\in B_\epsilon (S^*)\) for all \(0\le i<n\) and \(i\in {\mathbb {N}}\).
I will first show that \(R_b^{m'}(S_c)\in \partial B_\epsilon (S^*)\) for all \(m'>m\). To do so, we choose any arbitrary \(m'>m\) and any arbitrary neighborhood \(N(R_b^{m'}(S_c), r)=\{Q|\ \Vert R_b^{m'}(S_c)-Q\Vert _b^{m'}<r\}\) on the \(R_b^{m'}\) surface. We want to show that \(N(R_b^{m'}(S_c), r)\) contains at least one point in \(B_\epsilon (S^*)\), and at least one point not in \(B_\epsilon (S^*)\). The latter part is immediately satisfied, since \(R_b^{m'}(S_c)\in N(R_b^{m'}(S_c), r)\) and \(R_b^{m'}(S_c) \not \in B_\epsilon (S^*)\) because it is in the basin of attraction. We’re left to show that \(N(R_b^{m'}(S_c), r)\) contains at least one point in \(B_\epsilon (S^*)\).
From Condition 1, we have a point \(S''\) with \(S''\not \in BoA\) on the unrenormalized surface such that \(0<\Vert R_{b^{m'}}(S'')-R_{b^{m'}}(S_c)\Vert _{b^{m'}}^1<r\). By the semi-group property of the RG transformations, we have \(\Vert R_b^{m'}(S'')-R_b^{m'}(S_c)\Vert _b^{m'}<r\). This means that \(R_b^{m'}(S'')\in N(R_b^{m'}(S_c), r)\).
Now choose any \(n>(m'-m)\), we know that there exists S with \(S\not \in BoA\) on the unrenormalized surface such that for all \(S'\) with \(0<\Vert S'-S_c\Vert <\Vert S-S_c\Vert \) and \(S'\not \in BoA\) we have \(R_b^{m+i}(S')\in B_\epsilon (S^*)\) for all \(0\le i<n\) and \(i\in {\mathbb {N}}\), and in particular, \(R_b^{m'}(S')\in B_\epsilon (S^*)\).
If \(\Vert S''-S_c\Vert <\Vert S-S_c\Vert \), then from the above discussion, we have \(R_b^{m'}(S'')\in B_\epsilon (S^*)\).
If \(\Vert S''-S_c\Vert \ge \Vert S-S_c\Vert \), then for all \(S'\) with \(0<\Vert S'-S_c\Vert <\Vert S-S_c\Vert \le \Vert S''-S_c\Vert \), we have \(\Vert R_{b^{m'}}(S')-R_{b^{m'}}(S_c)\Vert _{b^{m'}}^1<\Vert R_{b^{m'}}(S'') -R_{b^{m'}}(S_c)\Vert _{b^{m'}}^1<r\), by Condition 2. By the semi-group property of the RG transformations, we have \(\Vert R_b^{m'}(S')-R_b^{m'}(S_c)\Vert _b^{m'}<r\). Therefore, \(R_b^{m'}(S')\in B_\epsilon (S^*)\) and \(R_b^{m'}(S')\in N(R_b^{m'}(S_c), r)\).
In both cases above, \(N(R_b^{m'}(S_c), r)\) contains at least one point in \(B_\epsilon (S^*)\). Therefore, \(R_b^{m'}(S_c)\in \partial B_\epsilon (S^*)\).
It is easy to show that \(R_b^{m'}(S_c)\) is in the basin of attraction, because \(S_c\) represents the system at its critical point. Therefore, \(R_b^{m'}(S_c)\in (\partial B_\epsilon (S^*)\cap BoA)\subseteq V\) for all \(m'>m\). Because V is arbitrary, we have \(R_b^n(S_c)\rightarrow S^*\) as \(n\rightarrow \infty \). \(\square \)
Appendix C Glossary of technical terms
-
Space of Hamiltonians: the space of “Hamiltonians” strictly speaking is a misnomer. In fact, it’s the space of coupling constants that serve as parameters in Hamiltonians of some generic form (see, e.g. Palacios (2019))). Every point in the space of Hamiltonians represent a set of values for the coupling constants, and the set of values then correspond to a Hamiltonian.
-
\({\mathcal {S}}\): this refers to physical systems such as the water-steam system. The system \({\mathcal {S}}\) can be represented by points on the unrenormalized surface.
-
\(S, S', S''\): these refer to points on the unrenormalized surface that represent the physical system \({\mathcal {S}}\).
-
\(R_b^n(S)\): this refers to a point on the space of Hamiltonians which is the result of the n-th iteration of the RG transformation of length b applied to the point S.
-
The \(R_b^n\) surface: this refers to a surface in the space of Hamiltonians that is the co-domain of \(R_b^n(S)\), for all S on the unrenormalized surface.
-
\(S^*\): this is a non-trivial fixed point.
-
\(S_c\): this is the Hamiltonian on the unrenormalized surface that represents the system \({\mathcal {S}}\) at its critical point.
-
\(P, Q, Q'\): these are points in the space of Hamiltonians, not necessarily representing any system.
-
Basin of Attraction (BoA): the basin of attraction is a surface in the space of Hamiltonians that is spanned by the irrelevant parameters. \(S^*\) and \(S_c\) are both in the basin of attraction. Among other things, the correlation length for points on the basin of attraction is infinite.
-
\(B_\epsilon (S^*)\): this is the linearization*-adequate neighborhood around the nontrivial fixed point \(S^*\).
Rights and permissions
About this article
Cite this article
Wu, J. Explaining universality: infinite limit systems in the renormalization group method. Synthese 199, 14897–14930 (2021). https://doi.org/10.1007/s11229-021-03448-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-021-03448-2