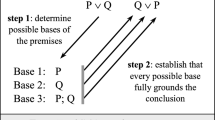
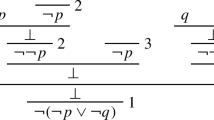Abstract
Most of the logics of grounding that have so far been proposed contain grounding axioms, or grounding rules, for the connectives of conjunction, disjunction and negation, but little attention has been dedicated to the implication connective. The present paper aims at repairing this situation by proposing adequate grounding principles for relevant implication. Because of the interaction between negation and implication, new grounding principles concerning negation will also arise.




Similar content being viewed by others
Notes
From now on, we use the term following from in Anderson and Belnap (1975)’s sense. B follows from A, C if there is a deduction of B from A, C which actually uses A, C (and A, C alone).
Even if our approach is developed in classical logic, the derivations we use for negative formulas are clearly relevant.
We work with multisets of formulas rather than with sets of formulas because we need to take into account the number of occurrences of each formula of M.
Note that \(\lnot ^{0}E\) is just E. Also we keep the term converse for continuity with Poggiolesi’s work. However, one should not confuse \(*\) with an idempotent operator.
For the rigorous definition of subformula in a grounding framework see Poggiolesi (2016b).
Note that when the multiset M is composed of only one formula, then positive and negative derivability amounts to an equivalence relation. This is typically the case of the two formulas A and \(\lnot \lnot A\), which although equivalent, are such that A completely and immediately grounds \(\lnot \lnot A\) and not viceversa. While other accounts of grounding (e.g. Fine 2012a, b) take this asymmetry as primitive, Definition 2.8 explains why A grounds \(\lnot \lnot A\) and not viceversa: because only in one case the g-complexity increases from the grounds to the conclusion.
This notion corresponds to a derivation from M to A with control indexes (namely M and A have the same set of indexes) in the natural deduction calculus for R, see Dunn and Restall (2002).
Differently from worlds of Kripke semantics, worlds of the relevant approach can be either inconsistent or incomplete. This is due to fact that formulas as \(p\wedge \lnot p\rightarrow q\) or \(p\rightarrow q\vee \lnot q\) are not wanted to be proved to be valid. And for that matter, we need words to be able to satisfy both p and \(\lnot p\), or to not satisfy neither q nor \(\lnot q\).
Note that g-complexity does not respect logical equivalence, since the g-complexity of p, p is not the same as the g-complexity of \(p\wedge p\). This fact is further developed in the diversified syntax introduced in Francez (2018).
Note that in the last five items of Definition 3.9, the natural number in the S-element corresponding to the g-complexity of C is 0.
For each proof of positive and negative derivability of this and the next section, it is straightforward to check that they are proofs of entailment in the sense of (Anderson and Belnap 1975, p. 277), that is that they correspond to derivations with control indexes in the natural deduction calculus for R, or that is that stars may be prefixed to the steps of the proofs, satisfying the conditions set up by Anderson and Belnap. Not to burden the presentation, we omit to prefix formulas with stars.
It is classically derivable but in the derivation weakening is used.
It is classically derivable but in the derivation weakening is used.
We still use follow in Anderson and Belnap (1975)’s sense. A contradiction follows from \(M, A\rightarrow B\) if there is a deduction of the contradiction from \(M, A\rightarrow B\) which actually uses \(M, A\rightarrow B\) (and \(M, A\rightarrow B\) alone).
We omit here all the details that we have developed for cases 7–10, since they are quite similar to them. The interested reader can straightforwardly reconstruct them on her own.
References
Anderson, A. R., & Belnap, N. (1975). Entailement. The logic of relevance and necessity. Princeton: Princeton University Press.
Betti, A. (2010). Explanation in metaphysics and Bolzano’s theory of ground and consequence. Logique et Analyse, 211, 281–316.
Correia, F. (2010). Grounding and truth-functions. Logique et Analyse, 53(211), 251–79.
Correia, F. (2014). Logical grounds. Review of Symbolic Logic, 7(1), 31–59.
Correia, F. (2016). On the logic of factual equivalence. Review of Symbolic Logic, 9, 103–122.
de Rosset, L. (2013). What is weak ground? Essays in Philosophy, 14(1), 7–18.
Doŝen, K. (1993). A historical introduction to substructural logics. In P. Schroeder-Heister & K. Doŝen (Eds.), Substructural logics (pp. 1–30). Oxford: Oxford University Press.
Dunn, M. (1970). Algebraic completeness for r-mingle and its extensions. Journal of Symbolic Logic, 25, 1–13.
Dunn, M., & Restall, G. (2002). Relevance logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (pp. 291–309). Amsterdam: Kluwer Academic Publishers.
Fine, K. (1974). Models for entailment. Journal of Philosophical Logic, 3, 347–372.
Fine, K. (2012a). Guide to ground. In F. Correia & B. Schnieder (Eds.), Metaphysical grounding (pp. 37–80). Cambridge: Cambridge University Press.
Fine, K. (2012b). The pure logic of ground. Review of Symbolic Logic, 25(1), 1–25.
Francez, N. (2018). Diversification of object-languages for propositional logics. Journal of Logic, Language and Information, 27, 193–203.
Francez, N. (2019). Relevant connexive logics. Logic and Logical Philosophy, 30, 1–18.
Jago, M. (2019). Truth-maker semantics for relevant logic. Journal of Philosophical Logic, 1–26, forthcoming.
Korbmacher, J. (2017). Axiomatic theories of partial ground i. The base theory. Journal of Philosophical Logic, 47, 161–191.
Krämer, S. (2013). A simpler puzzle of ground. Thought, 2(2), 85–89.
Mares, E. (2014). Relevance logic. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/spr2014/entries/logic-relevance/.
Poggiolesi, F. (2016a). A critical overview of the most recent logics of grounding. In F. Boccuni & A. Sereni (Eds.), Objectivity, realism and proof. Boston: Boston Studies in the Philosophy and History of Science.
Poggiolesi, F. (2016b). On defining the notion of complete and immediate formal grounding. Synthese, 193, 3147–3167.
Poggiolesi, F. (2018). On constructing a logic for the notion of complete and immediate formal grounding. Synthese, 195, 1231–1254.
Poggiolesi, F. (2020a). Bolzano, the appropriate relevant logic and grounding rules for implication. In S. Roski & B. Schnieder (Eds.), Bolzano and grounding. Oxford: Oxford University Press.
Poggiolesi, F. (2020b). Les conditionnels. In F. Poggiolesi & P. Wagner (Eds.), Précis de philosophie de la logique. Paris: Edition de la Sorbonne.
Roski, S. (2017). Bolzano’s conception of grounding. Jena: Klostermann Verlag.
Routley, R., & Meyer, R. K. (1973). Semantics of entailment. In H. Leblanc (Ed.), Truth syntax and modality. Amsterdam: North Holland.
Rumberg, A. (2013). Bolzano’s theory of grounding against the background of normal proofs. Review of Symbolic Logic, 6(3), 424–459.
Schaffer, J. (2009). On what grounds what. In D. Chalmers, D. Manley, & R. Wasserman (Eds.), Metametaphysics: New essays on the foundations of ontology (pp. 291–309). Oxford: Oxford University Press.
Schnieder, B. (2011). A logic for because. The Review of Symbolic Logic, 4(03), 445–465.
Troelstra, A. S., & Schwichtenberg, H. (1996). Basic proof theory. Cambridge: Cambridge University Press.
Urquhart, A. (1972). Semantics for relevant logics. Journal of Symbolic Logic, 37, 159–169.
Acknowledgements
We would like to express our gratitude to Nissim Francez and Brian Hill who both contributed to improve the paper with deep, interesting and rigorous remarks. We would like to thank the IBS PROJECT (ANR-18-CE27-0012-01) for the support in this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Poggiolesi, F. Grounding principles for (relevant) implication. Synthese 198, 7351–7376 (2021). https://doi.org/10.1007/s11229-019-02523-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02523-z