Skip to main content
SpringerLink
Log in

Vibrodiagnostics of the Presence of Surface Symmetrical Cracks in Beams of Rectangular and Round Cross-Sections by the Characteristics of Their Nonlinear Longitudinal Vibrations

  • Published:
Strength of Materials Aims and scope

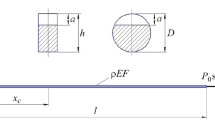
This work is devoted to the determination of vibrodiagnostic indicators of the presence of symmetric and annular breathing cracks in cantilever beams at their nonlinear longitudinal vibrations. The results of determining the vibrodiagnostic indicators of the presence of cracks, namely, the relative change in the fundamental frequency of longitudinal vibration and the ratio of the amplitudes of the dominant harmonics at the fundamental and superharmonic resonances for different depths and locations of cracks, are presented. To carry out computational studies, various computational models were developed, namely, with concentrated and distributed parameters, beam and volumetric finite element (FE) models, and methods for their research. The use of the model with concentrated parameters consists of the analytical determination of the nonlinearity parameter of the system, which takes into account the change in the stiffness of the system in the presence of damage and is determined by changing the potential deformation energy of the beam due to the opening of the crack during oscillations. The determination of vibrodiagnostic indicators of the presence of a crack using a model with distributed parameters is carried out by solving the differential equation of forced longitudinal vibrations of the second order, where the crack is represented as a section of the beam with a reduced cross-sectional area. The numerical analysis of vibrations of the objects of study with a breathing crack is carried out using the developed beam and volumetric FE models. In the beam FE model, the breathing crack is modeled by a finite element with variable stiffness, and in the volumetric model, it is represented as a mathematical section with the setting of contact interaction conditions for its banks. The main dependences of vibrodiagnostic indicators of the presence of cracks on their parameters are obtained analytically using a model with concentrated parameters and numerically using a beam FE model. To confirm the reliability of the obtained dependences, their individual values are compared with the data obtained for the volumetric FE model, which obviously describes the stress–strain state in the vicinity of the crack most accurately among the proposed models but at the same time requires more computational resources. The obtained numerical dependences of the ratio of the amplitudes of the dominant harmonics of displacements at the main resonance from the place of vibration registration are characterized by fractures in the vicinity of the crack and therefore can be used to determine the location of the crack. According to the results of the analysis of the obtained dependences, it was found that it is practically impossible to determine the location of the crack in this case, since the results obtained for the relative location of the crack in the range from 0.1 to 0.5 are close in values, and the dependences of the vibrodiagnostic indicator on the place of registration of vibrations at superharmonic resonance are uniform and have no fractures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.

Similar content being viewed by others

References

  1. H. Ma, J. Zeng, Z. Lang, et al., “Analysis of the dynamic characteristics of a slant-cracked cantilever beam,” Mech Syst Signal Process, 75, 261-279 (2016).

    Article  Google Scholar 

  2. V. V. Matveev , O. E. Boginich, E. A. Sinenko, and A. P. Yakovlev “On vibrodiagnostics of the presence of a closing edge crack in a beam with amplitude-dependent damping capacity under superharmonic resonance,” Strength Mater, 47, No. 5, 653-661 (2015).

    Article  Google Scholar 

  3. V. V. Matveev and E. A. Onishchenko, “Analysis of vibrodiagnostic parameters of the presence of a breathing surface crack of different configurations in a round bar,” Strength Mater, 49, No 6, 739-750 (2017).

    Article  Google Scholar 

  4. H. Long, Y. L. Liu, and K. F. Liu, “Nonlinear vibration analysis of a beam with a breathing crack,” Appl Sci, 9, 1-17 (2019).

    Article  Google Scholar 

  5. K. R. Collins, R. H. Plaut, and J. Wauer, “Free and forced longitudinal vibrations of a cantilevered bar with a crack,” ASME J Vib Acoust, 114, No. 2, 171-177 (1992).

    Article  Google Scholar 

  6. T. G. Chondros, A. D. Dimarogonas, and J. Yao, “Longitudinal vibration of a bar with a breathing crack,” Eng Fract Mech, 61, 503-518 (1998).

    Article  Google Scholar 

  7. F. B. Sayyad and B. Kumar, “Approximate analytical method for damage detection in beam,” Int J Damage Mech, 21, No. 7, 1064-1075 (2012).

    Article  Google Scholar 

  8. D. Broda, L. Pieczonka, V. Hiwarkar, et al., “Crack as modulator, detector and amplifier in structural health monitoring,” J Sound Vib, 381, 206-219 (2016).

    Article  Google Scholar 

  9. V. R. Hiwarkar, V. I. Babitsky, and V. V. Silberschmidt, “Crack as modulator, detector and amplifier in structural health monitoring,” J Sound Vib, 331, No 15, 3587-3598 (2012).

    Article  Google Scholar 

  10. V. V. Matveev, E. A. Onishchenko, and O. E. Boginich, “Vibration-based diagnostics of transverse surface cracks in beams of different cross section under longitudinal vibrations,” Strength Mater, 50, No. 4, 540-556 (2018).

    Article  Google Scholar 

  11. A. K. Darpe, K. Gupta, and A. Chawla, “Coupled bending, longitudinal and torsional vibrations of a cracked rotor,” J Sound Vib, 269, Nos. 1-2, 33-60 (2004).

    Article  Google Scholar 

  12. G. I. Giannopoulos, S. K. Georgantzinos , and N. K. Anifantis, “Coupled vibration response of a shaft with a breathing crack,” J Sound Vib, 336, 191-206 (2015).

    Article  Google Scholar 

  13. S. El Arem, “On the mechanics of beams and shafts with cracks: A standard and generic approach,” Eur J Mech-A/Solid, 85, 104088 (2021).

  14. Y. Murakami (Ed.), Handbook on Stress Intensity Factors [Russian translation], in 2 volumes, Vol. 1, Mir, Moscow (1990).

  15. R. Ruitolo and C. Surace, “Natural frequencies of a bar with multiple cracks,” J Sound Vib, 272, 301-316 (2004).

    Article  Google Scholar 

  16. S. P. Timoshenko, D. H. Young, and W. Weaver, Vibration Problems in Engineering, Wiley, Chichester (1974).

    Google Scholar 

  17. A. K. Chopra, Dynamics of Structures: Theory and Applications to Earthquake Engineering, Prentice Hall Inc. (2011).

Download references

Author information

Authors and Affiliations

  1. Pisarenko Institute of Problems of Strength, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    V. V. Matveev, E. O. Onishchenko, O. L. Derkach & O. E. Boginich

Authors
  1. V. V. Matveev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. O. Onishchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. O. L. Derkach
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. O. E. Boginich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. O. Onishchenko.

Additional information

Translated from Problemy Mitsnosti, No. 5, pp. 28 – 48, September – October, 2022.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Matveev, V.V., Onishchenko, E.O., Derkach, O.L. et al. Vibrodiagnostics of the Presence of Surface Symmetrical Cracks in Beams of Rectangular and Round Cross-Sections by the Characteristics of Their Nonlinear Longitudinal Vibrations. Strength Mater 54, 785–801 (2022). https://doi.org/10.1007/s11223-022-00455-7

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11223-022-00455-7

Keywords

Search

Navigation