Skip to main content
SpringerLink
Log in

The Influence of Inelastic Resistance on Vibrations of an Elastic Body with a Closing Crack under the Main and Subharmonic Resonances

  • Scientific and Technical Section
  • Published:
Strength of Materials Aims and scope

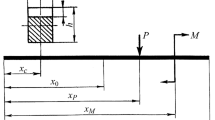
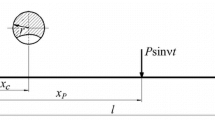
The paper presents some findings of analytical and numerical investigations aimed at determining the influence of inelastic resistance on vibrodiagnostic parameters indicating the presence of damage, such as a breathing crack, in an elastic body under the main and subharmonic resonances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. S. L. Tsyfansky and V. I. Beresnevich, “Detection of fatigue cracks in flexible geometrically non-linear bars by vibration monitoring,” J. Sound Vibration, 213, No. 1, 159–168 (1998).

    Article  Google Scholar 

  2. S. L. Tsyfansky and V. I. Beresnevich, “Non-linear vibration method for detection of fatigue cracks in aircraft wings,” J. Sound Vibration, 236, No. 1, 49–60 (2000).

    Article  Google Scholar 

  3. J. C. Ji and C. H. Hansen, “On the approximate solution of a piecewise nonlinear oscillator under super-harmonic resonance,” J. Sound Vibration, 283, No. 1-2, 467–474 (2005).

    Article  Google Scholar 

  4. A. P. Bovsunovskii, C. Surace, and O. A. Bovsunovskii, “The effect of damping and force application point on the non-linear dynamic behavior of a cracked beam at sub- and superresonance vibrations,” Strength Mater., 38, No. 5, 492–497 (2006).

    Article  Google Scholar 

  5. Z. K. Peng, Z. Q. Lang, and S. A. Billings, “Crack detection using nonlinear output frequency response functions,” J. Sound Vibration, 301, No. 3-5, 777–788 (2007).

    Article  Google Scholar 

  6. Animesh Chatterjee, “Structural damage assessment in a cantilever beam with a breathing crack using higher order frequency response functions,” J. Sound Vibration, 329, No. 16, 3325–3334 (2010).

    Article  Google Scholar 

  7. A. P. Bovsunovskii and O. A. Bovsunovskii, “Application of nonlinear resonances for the diagnostics of closing cracks in rodlike elements,” Strength Mater., 42, No. 3, 331–343 (2010).

    Article  Google Scholar 

  8. Ugo Andreaus and Paolo Baragatti, “Cracked beam identification by numerically analyzing the nonlinear behaviour of the harmonically forced response,” J. Sound Vibration, 330, 721–742 (2011).

    Article  Google Scholar 

  9. V. V. Matveev and O. E. Boginich, “Approximate determination of vibrodiagnostic parameter of nonlinearity for an elastic body due to the presence of a breathing crack at a subharmonic resonance,” Strength Mater., 44, No. 3, 250–258 (2012).

    Article  Google Scholar 

  10. G. S. Pisarenko, Energy Dissipation in Mechanical Vibration [in Russian], AN UkrSSR, Kiev (1962).

    Google Scholar 

  11. A. P. Bovsunovsky, “Shape of the mechanical hysteresis loop for metallic materials under harmonic stresses below the endurance limit. Part II. Experimental procedure and results,” Strength Mater., 29, No. 3, 298–307 (1997).

    Article  Google Scholar 

  12. V. V. Matveev, Damping of Vibration of Deformable Bodies [in Russian], Naukova Dumka, Kiev (1985).

    Google Scholar 

  13. V. V. Matveev, A. P. Yakovlev, and I. M. Vasinyuk, “On determining the damping rate of vibrations of nonlinear systems of the hysteresis type from the resonance curve,” Soviet Appl. Mech., 6, No. 1, 81–84 (1970).

    Article  Google Scholar 

  14. V. V. Matveev and A. P. Yakovlev, “Determination of the decrement of the vibrations of a nonlinear system of the hysteresis type from the width of the resonance peak of the amplitude–frequency characteristic,” Strength Mater., 8, No. 9, 1090–1092 (1976).

    Article  Google Scholar 

  15. V. V. Matveev, O. E. Boginich, and A. P. Yakovlev, “Approximate analytical method for determining the vibration-diagnostic parameter indicating the presence of a crack in a distributed-parameter elastic system at super- and subharmonic resonances,” Strength Mater., 42, No. 5, 528–543 (2010).

    Article  Google Scholar 

  16. V. V. Matveev, O. E. Boginich, and A. P. Yakovlev, “Approximate methods for and results of determination of vibrodiagnostic parameters indicating the presence of a crack in rod-like elements at super- and subharmonic resonances,” in: V. T. Troshchenko (Ed.), Strength of Materials and Structural Elements [in Russian], Proc. Int. Sci. Conf. “Strength of Materials and Structural Elements” (Kiev, Sept. 28–30, 2010), Pisarenko Institute of Problems of Strength of the National Academy of Sciences of Ukraine, Kiev (2011), pp. 59–77.

  17. A. E. Mudrov, Numerical Methods for PC Software in Basic, Fortran, and Pascal [in Russian], MP Rasko, Tomsk (1991).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Pisarenko Institute of Problems of Strength, National Academy of Sciences of Ukraine, Kiev, Ukraine

    V. V. Matveev & O. E. Boginich

Authors
  1. V. V. Matveev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. E. Boginich
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Problemy Prochnosti, No. 1, pp. 5 – 24, January – February, 2014.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Matveev, V.V., Boginich, O.E. The Influence of Inelastic Resistance on Vibrations of an Elastic Body with a Closing Crack under the Main and Subharmonic Resonances. Strength Mater 46, 1–17 (2014). https://doi.org/10.1007/s11223-014-9511-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11223-014-9511-4

Keywords

Search

Navigation