Construction of two-level integration schemes for the equations of plasticity in the theory of deformation along the paths of small curvature

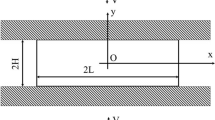
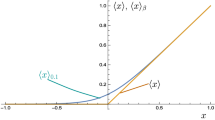
The construction of a set of two-level integration ω-schemes for the equations of the flow theory of plasticity, describing anisothermic loading processes along the deformation paths of small curvature, is described. In this case, a stress-strain state is dependent on thermomechanical loading history, and inelastic deformation should be followed over the whole examined time interval in step solving the boundary problem. Basic concepts of the phenomenological model are built upon the Prandtl– Reuss equations of plasticity and the Huber–Mises yield condition. The loading process is divided into several time steps. The equations of plasticity are integrated in a loading step. The general procedure of transformations to construct a set of two-level integration ω-schemes for the equations of plasticity is proposed. The conditions for the agreement between the considered equations of plasticity and the principle of work irreversibility with plastic strain increments and Drucker’s hardening postulate are formulated. As an example, illustrating the properties of these equations, the deformation problem is solved for a thin-walled round pipe subject to axial tension and torsional moment. Results of solving the model problem, obtained with different two-level integration schemes, are presented. Practical recommendations as to the choice of the parameter ω are given.