1 Introduction

The linear mixed model is a broadly used statistical model for analyzing clustered or longitudinal data. When data analysts use these models, they often face two practical problems: (a) the true model for explaining the response variable is unknown and (b) the model assumptions, especially the Gaussian assumptions of the error terms, are violated.

As the true model is unknown, data analysts find suitable/optimal models for explaining the dependent variable by using variable selection procedures. One popular approach in this context is the Akaike information criterion (AIC) introduced by Akaike (1973). For linear mixed models, there are different versions of AIC (Müller et al. 2013). They can be divided into two groups: marginal types of AIC (mAIC) and conditional types of AIC (cAIC). The mAIC is the common AIC for linear mixed models which uses marginal density and is one of the most widely used selection criteria (Müller et al. 2013). However, the mAIC is only appropriate when the model parameters are fixed (Burnham and Anderson 2010) and the use of mAIC as selection criterion is problematic for linear mixed models (Han 2013). Vaida and Blanchard (2005) introduced the cAIC as a more proper selection criterion for linear mixed models. cAIC uses the conditional density in contrast to mAIC. Vaida and Blanchard (2005) derive cAIC in case that the (scaled) covariance matrix of random effects is known and recommend to use a plug-in estimator for the covariance matrix of the random effects in practice. Liang et al. (2008) derive a more general cAIC that accounts for the estimation of the covariance matrix of the random effects. However, their conditional AIC can be computationally demanding in situations with large sample sizes and many potential variables (Greven and Kneib 2010).

Linear mixed models regularly rely on parametric assumptions such as normality for the random effects and the error terms. These assumptions may be violated in many applications, for instance, with skewed variables like consumption or income. One possible way to tackle this issue is to use robust mixed models. Such models are robust in various aspects, including the violation of the Gaussian assumptions. They allow more flexible distributions (Verbeke and Lesaffre 1997; Zhang and Davidian 2001; Sinha and Rao 2009) or apply a Bayesian framework (Rosa et al. 2003; Lachos et al. 2009). Jiang (2019) gives an overview of further models which deal with this problem. Another way to solve this problem is to apply fixed logarithmic or data-driven transformations for the dependent variable. The latter transformations are generally based on an adaptive transformation parameter \(\lambda \) that depends on the particular shape of the data. Among different data-driven transformations, the Box-Cox transformation (Box and Cox 1964) is widely used, as it includes various power transformations and the logarithmic transformation as a special case. Gurka et al. (2006) extend the use of the Box-Cox transformation to linear mixed models. They apply the residual maximum likelihood (REML) approach to estimate the transformation parameter \(\lambda \) from the data based on linear mixed model with fixed auxiliary variables.

However, the optimal data-driven transformation depends on the fixed model and the optimal model depends on the selected data-driven transformation. In particular, to select the optimal data-driven transformation parameter \(\lambda \) by the REML approach, the linear mixed model should be fixed; and to perform a variable selection based on the cAIC, the dependent variable should be fixed using an appropriate (data-driven) transformation parameter \(\lambda \). A first naive approach which is typically used in applications would be to perform the transformation and variable selection in a specific order. First, find an appropriate working model on the original/untransformed scale and keep this fixed when selecting the optimal data-driven transformation parameter. However, this may not offer the best way to the variable selection as the selected variables are not optimal on the transformed scale. In this paper, we aim to find the optimal model and the optimal transformation parameter simultaneously. This would allow for enjoying the advantages of both data-driven transformations and the optimal model for the transformed data.

Hoeting and Ibrahim (1998) and Hoeting et al. (2002) discuss methods for transformation and variable selection based on posterior probabilities in linear models. They focus on change-point transformations to transform the predictors of the linear model. Bunke et al. (1999) discuss the selection of the optimal transformation and the optimal model based on cross validation for the nonlinear model. To the best of our knowledge, none of the existing literature provides a joint solution when variable selection based on the cAIC and estimation of the data-driven transformation parameter are simultaneously applied to linear mixed models. From a theoretical perspective, we present an approach to concurrently choose the optimal linear model and the optimal transformation parameter. Since the cAIC is scale dependent, we can not directly compare different models with differently transformed response variables. Therefore, we adjust the cAIC using the Jacobian of the corresponding data-driven transformation such that different model candidates with differently transformed response variables can be compared. Although the paper focuses on the Box-Cox transformation as a particular data-driven transformation, the proposed approach is applicable to data-driven transformations in general. From a computational perspective, we provide a step-wise selection approach based on the proposed adjusted cAIC.

The structure of the paper is as follows: In Sect. 2 we provide an overview of linear mixed models and the cAIC. In Sect. 3, we derive the Jacobian adjusted cAIC for transformed linear mixed models and introduce the step-wise selection approach. In Sect. 4, we examine the performance of the proposed selection approach by using model-based simulations. In Sect. 5, the proposed selection approach is applied to data from Guerrero in Mexico for estimating poverty and inequality indicators at municipal level. Finally, we discuss our results and further directions of research in Sect. 6.

2 Variable selection using conditional AIC for linear mixed models

In this section we briefly introduce the existing variable selection methods for linear mixed models. In Sect. 2.1, we present a general notation of linear mixed models and in Sect. 2.2, we introduce and compare the cAIC by Vaida and Blanchard (2005) and Liang et al. (2008).

2.1 The linear mixed model

Assume there is a finite population divided into D clusters. Let \(y_i\) be a vector of the response variable for the i-th cluster for \(i=1,\cdots , D\), which is modeled with a linear mixed model

$$\begin{aligned} y_i=X_i\beta +Z_iu_i+\varepsilon _i. \end{aligned}$$

\(N_i\) is the cluster size of the i-th cluster, \(X_i\) and \(Z_i\) are known \(N_i\times p\) and \(N_i\times q\) design matrices for the fixed and random effects, \(\beta \) includes p fixed effects, \(u_i\) is a vector of q random effects, and \(\varepsilon _i\) is a vector of errors in the i-th cluster. \(u_i\) and \(\varepsilon _i\) are assumed to be independent and normally distributed

$$\begin{aligned} u_i\sim {\mathcal {N}}(0,G),~&~ \varepsilon _i \sim {\mathcal {N}}(0,\sigma ^2I_{N_i}), \end{aligned}$$

with \(I_{N_i}\), the \(N_i\times N_i\) identity matrix. G is the \(q\times q\) covariance matrix of random effects in the i-th cluster and depends on a set of variance components \(\eta \). Let \(N=\sum _{i=1}^D N_i\) be the population size and \(\theta =(\beta ,\sigma , \eta )\) be the vector of parameters in the model. The model is described for the population as follows

$$\begin{aligned} y=X\beta +Zu+\varepsilon , \end{aligned}$$
(1)

where \(X=(X_1^T,\cdots , X_D^T)^T\) is a \(N\times p\) matrix, \(Z=\text {diag}(Z_1,\cdots ,Z_D)\) is \(N\times r\) block-diagonal matrix with \(r=D\cdot q\), \(u=(u_1^T,\cdots ,u_D^T)^T\) and \(\varepsilon =(\varepsilon _1^T,\cdots ,\varepsilon _D^T)^T\). \(\varepsilon \) and u are independent and normally distributed with \(E(\varepsilon )=E(u)=0\), \(Var(\varepsilon )=\sigma ^2I_N\) and \(Var(u)=G_0\), where \(G_0=diag_D(G)\) is block-diagonal matrix with D blocks of G on the diagonal. As \(u\sim {\mathcal {N}}(0,G_0)\) and \( \varepsilon \sim {\mathcal {N}}(0,\sigma ^2I_N)\), the covariance matrix of y is given by

$$\begin{aligned} Cov(y)=V=\sigma ^2I_N+ZG_0Z^T. \end{aligned}$$

2.2 Conditional Akaike information criterion for linear mixed models

Assume there are P possible explanatory variables in the data. Since the number of all possible combinations of P variables is \(M=2^P\), there are M possible model candidates which can be fitted to the data. In order to find the optimal model among them, the variable selection should be performed based on an appropriate selection criterion. In this study, we focus on the variable selection based on the cAIC for linear mixed models. While this study focuses on the cAIC, the mAIC is briefly explained first to provide a better understanding of the cAIC.

The mAIC is derived from the Kullback-Leibler (K-L) divergence between the density of the true model and the density of a candidate model (Akaike 1973). Assume that the true model has the same form as Eq. (1) with true parameters. The vector of true parameters is denoted by \(\theta _0=(\beta _0,\sigma _0,\eta _0)\). Let \(f(\cdot )\) be the density function of the true generating model and \(g(\cdot \vert \theta )\) be the density of the approximating model with model parameters \(\theta \) for fitting the data. If the true distribution f belongs to the class of model candidates and \(\theta =\theta _0\) then \(g(\cdot \vert \theta _0)=f(\cdot )\). The mAIC measures the K-L divergence between \(f(\cdot )\) and \(g(\cdot \vert \theta )\).

The idea behind the cAIC derivation is the same as for the mAIC. While the mAIC measures the K-L divergence between two marginal densities, cAIC measures the K-L divergence between the true conditional density and the conditional density of a model candidate. The true conditional density is denoted by \(f(\cdot \vert u_0)\) with the true random effects (\(u_0\)) and the conditional density of a model candidate is denoted by \(g(\cdot \vert \theta , u)\). Let \(y^*\) be generated from the true conditional density and y be the observed data, also from the true conditional density. They are independent conditional on random effects, which means that \(y^*\) and y share the random effects and only differ in error terms (i.e., \(y^*=X\beta + Zu + \varepsilon ^*\) and \(y=X\beta + Zu + \varepsilon \) with \(\varepsilon ^*\sim N(0,\sigma ^2I_N)\) and \(\varepsilon \sim N(0,\sigma ^2I_N)\)). The K-L divergence between \(f(y^*\vert u_0)\) and \(g(y^*\vert \theta , u)\) with respect to \(f(y^*\vert u_0)\) is defined by

$$\begin{aligned} I[(\theta _0,u_0),(\theta , u)]=&E_{f(y^*\vert u_0)}\bigg [\log \frac{f(y^*\vert u_0)}{g(y^*\vert \theta , u)}\bigg ]\\ =&E_{f(y^*\vert u_0)}[\log f(y^*\vert u_0)]\\&-E_{f(y^*\vert u_0)}[\log g(y^*\vert \theta , u)]. \end{aligned}$$

The discrepancy between the conditional generating model and the conditional approximation model is given by

$$\begin{aligned} d[(\theta _0,u_0),(\theta , u)]=E_{f(y^*\vert u_0)} [-2\log g(y^*\vert \theta , u)]. \end{aligned}$$

By using the given definition of the discrepancy, the K-L divergence can be written as follows

$$\begin{aligned} 2I[(\theta _0,u_0),(\theta , u)]=&2E_{f(y^*\vert u_0)}[\log f(y^*\vert u_0)]\\&+d[(\theta _0,u_0),(\theta , u)]. \end{aligned}$$

Since \(2E_{f(y^*\vert u_0)}[\log f(y^*\vert u_0)]\) does not depend on \(\theta \) and u from the approximating model, the ranking of candidate models based on \(d[(\theta _0,u_0),(\theta , u)]\) is equivalent to the ranking of candidates based on \(2I[(\theta _0,u_0),(\theta , u)]\). Therefore, the fitted candidate models can be evaluated by using the discrepancy with \({{\hat{\theta }}}\) and \({{\hat{u}}}\),

$$\begin{aligned} d[(\theta _0,u_0),(\theta , u)]=d[(\theta _0,u_0),(\theta , u)] \vert _{\theta ={{\hat{\theta }}}, u={{\hat{u}}}}, \end{aligned}$$

where \({{\hat{\theta }}}\) includes the estimates of model parameters (i.e. \({{\hat{\theta }}}=({{\hat{\beta }}},~{{\hat{\sigma }}},~{{\hat{\eta }}})\)) and \({{\hat{u}}}=E(u\vert {{\hat{\theta }}},~y)\) contains the predicted random effects based on the empirical Bayes estimation. Hence, the selection problem based on K-L divergence can be solved by comparing \(d[(\theta _0,u_0),(\theta , u)] \vert _{\theta ={{\hat{\theta }}}, u={{\hat{u}}}}\) values of the candidate models. As the model parameters and random effects are estimated based on observed data, the expected estimated discrepancy should be used as the selection criterion (Burnham and Anderson 2010). This is also often denoted as conditional Akaike Information (cAI) (Vaida and Blanchard 2005; Liang et al. 2008; Han 2013)

$$\begin{aligned} cAI =&E_{f(y, u)}E_{f(y^*\vert u)}[-2\log g(y^*\vert {{\hat{\theta }}},{{\hat{u}}})]. \end{aligned}$$

\(-\log g(y\vert {{\hat{\theta }}}, {{\hat{u}}})\) is a biased estimator of \(E_{f(y, u)}E_{f(y^*\vert u)}[-\log g(y^*\vert {{\hat{\theta }}}, {{\hat{u}}})]\). As a consequence, the cAIC consists of the conditional log-likelihood and the bias correction term K

$$\begin{aligned} cAIC = -2\log g(y\vert {{\hat{\theta }}}, {{\hat{u}}})+2K, \end{aligned}$$

where

$$\begin{aligned} \log g(y\vert {{\hat{\theta }}},{{\hat{u}}})=-\frac{N}{2}\log (2\pi {\hat{\sigma }}^2)-\frac{1}{2{\hat{\sigma }}^2}(y-{{\hat{y}}})^T(y-{{\hat{y}}}), \end{aligned}$$

and \({\hat{y}}\) is the fitted vector \({\hat{y}}=X{{\hat{\beta }}}+Z{\hat{u}}\).

Vaida and Blanchard (2005) derive two different bias correction terms under different assumptions. When \(\sigma ^2\) and \(G_0\) are assumed to be known, the K equals \(\rho \), which is the effective degrees of freedom (Hodges and Sargent 2001)

$$\begin{aligned} K_a=&\rho =tr\Bigg [\bigg ( \begin{matrix} X^TX &{} X^TZ\\ Z^TX &{} Z^TZ+\sigma ^{-2}G_0 \end{matrix} \bigg )^{-1} \bigg ( \begin{matrix} X^TX &{} X^TZ \\ Z^TX &{} Z^TZ \end{matrix} \bigg ) \Bigg ]. \end{aligned}$$

When it is assumed that \(\sigma ^2\) is unknown and \(\sigma ^{-2}G_0\) is known, K is calculated by

$$\begin{aligned} K_{MLE}=&\frac{N(N-p-1)}{(N-p)(N-p-2)}(\rho +1)\nonumber \\&+\frac{N(p+1)}{(N-p)(N-p-2)}. \end{aligned}$$
(2)

The detailed derivation of \(K_a\) and \(K_{MLE}\) can be found in Vaida and Blanchard (2005).

Vaida and Blanchard (2005) derive the cAIC under the assumption that \(G_0\), the covariance matrix of the random effects, or \(\sigma ^{-2}G_0\), the scaled covariance matrix of the random effects, are known. However, in practice they are usually unknown. In the case of the unknown random effects covariance matrix, Vaida and Blanchard (2005) suggest to use \(K_{MLE}\) for the cAIC with the estimated \(\sigma ^{-2}G_0\), since the derivation of the bias correction term for the case of unknown \(\sigma ^{-2}G_0\) is analytically complicated and the effect of estimation can be asymptotically ignored.

Liang et al. (2008) propose a general cAIC for known \(\sigma ^2\), regardless of whether the covariance of random effects are known or unknown. Under these assumptions, Liang et al. (2008) derive the bias correction term using the first derivatives of \({{\hat{y}}}\) subject to y. In their technical report, they also derive an additional bias correction term for cAIC assuming more realistically that neither \(\sigma ^2\) nor the covariance of random effects are known.

In practice, the true value of \(\sigma ^2\) and the true \(G_0\) are usually unknown. Therefore, it seems reasonable to use the cAIC of Liang et al. (2008). However, Liang et al. (2008) show in the simulation part that their bias correction term is close to \(K_a\) and it is also shown in their technical report that the bias correction term under more realistic assumptions is close to \(K_{MLE}\). Moreover, Greven and Kneib (2010) point out that the use of cAIC by Liang et al. (2008) as a selection criterion poses severe computational difficulties, since the calculation of the bias correction term of Liang et al. (2008) requires at least N additional model fits to calculate derivatives. If there are M different model candidates, at least \(N \times M\) model fits are required to calculate cAIC derived by Liang et al. (2008), which is hard to implement for large N and M. As a result, this study focuses on the cAIC of Vaida and Blanchard (2005), and in particular on the cAIC with \(K_{MLE}\) that allows for unknown \(\sigma ^2\). The optimal model is the model which has the minimum value of cAIC among all M model candidates.

3 Variable selection for linear mixed models with transformations

In this section, we propose a step-wise variable selection approach for linear mixed models which allows comparing model candidates with differently transformed response variables. First, we give a general notation of linear mixed models with the Box-Cox transformation. Although the paper focuses on the Box-Cox transformation as a particular transformation, the proposed approach is applicable to data-driven transformations in general. In Sect. 3.2, we derive the Jacobian adjusted cAIC based on cAIC by Vaida and Blanchard (2005), which can compare model candidates with differently transformed data. In Sect. 3.3, we introduce a bootstrap method to estimate the bias correction term for Jacobian adjusted cAIC. From a computational perspective, we suggest to use step-wise selection with adjusted cAIC in Sect. 3.4

3.1 Linear mixed models with transformations

Assume that the original y variable is non-normal and there exists a transformation parameter of the Box-Cox transformation for which the transformed data follows the Gaussian assumption. The one-to-one Box-Cox transformation (Box and Cox 1964) of y is defined by

$$\begin{aligned} T_\lambda (y_{ij}) = {\left\{ \begin{array}{ll} \frac{(y_{ij}+s)^\lambda -1}{\lambda } &{} \text {if } \lambda \ne 0, \\ \log (y_{ij}+s)&{}\text {if } \lambda = 0, \end{array}\right. } \nonumber \\ i=1,...,D\text { and }j=1,...,N_i, \end{aligned}$$
(3)

where \(\lambda \) denotes the transformation parameter which has to be estimated and s denotes the shift parameter \(s=\vert \min (y)\vert +1\) only when \(\min (y) <0\). Let \({\widetilde{y}}\) be the vector of transformed y. Then, \({\widetilde{y}}\) is modeled as

$$\begin{aligned} T_\lambda (y)=&{\widetilde{y}}=X\beta + Zu+\varepsilon \end{aligned}$$
(4)

with \(u\sim {\mathcal {N}}(0,G_0)\) and \( \varepsilon \sim {\mathcal {N}}(0,\sigma ^2I_N)\). The covariance matrix of the transformed y is

$$\begin{aligned} Cov({\widetilde{y}})&=V=\sigma ^2I_N+ZG_0Z^T. \end{aligned}$$

Gurka et al. (2006) use the REML approach to estimate \(\lambda \), as the REML approach is recommended when the focus is the estimation of variance components (Verbeke and Molenberghs 2000). Moreover, Rojas-Perilla et al. (2020) compare the REML estimator of \(\lambda \) with other estimators and show that the REML approach has a smaller variability than alternative estimators. Accordingly, the optimal \(\lambda \) is estimated in this study with the REML approach. The optimal \(\lambda \) maximizes the residual log-likelihood function of a given model. However, the estimated optimal \(\lambda \) is only optimal for the given model. This means that each model candidate has its own optimal \(\lambda \). As we do not know which model candidate is the optimal and which \(\lambda \) is the optimal for the corresponding model, we should select the model and the \(\lambda \) concurrently.

To simultaneously select the best model based on cAIC and obtain the optimal \(\lambda \), we estimate it for each potential model in a first step. With P possible x variables there are \(M=2^P\) model candidates. The m-th model is defined by

$$\begin{aligned} T_{\lambda _m}(y)=&{\widetilde{y}}^{~(m)}=X^{(m)}\beta +Zu+\varepsilon , \nonumber \\ ~&m=1,...,M, \end{aligned}$$
(5)

where \(X^{(m)}\) is the design matrix of the m-th model and \(\lambda _m\) is the optimal transformation parameter for the m-th model. Based on the model in Eq. (5) the optimal transformation parameter is estimated using the REML approach and \({\hat{\lambda }}_m\) denotes the estimated optimal transformation parameter for the m-th model. Further details about the estimation of \(\lambda _m\) using the REML approach are explained in Gurka et al. (2006). In the second step, all model candidates with their own \({\hat{\lambda }}_m\) should be compared. However, AIC-type criteria cannot compare models with differently transformed target variable (Burnham and Anderson 2010). Therefore, an adjustment with the Jacobian to the cAIC should be performed first such that these M different models can be compared.

3.2 Jacobian adjusted cAIC for linear mixed models

Assume that \(f(\cdot \vert u_0)\) is the true conditional density function with the true model parameters \(\theta _0\) and the true random effects \(u_0\), while \(g(\cdot \vert \theta , u)\) denotes the conditional density of an approximating model. Let \({\widetilde{y}}^*=X\beta +Zu+\varepsilon ^*\) be a realization from the true conditional density function with \(\varepsilon ^*\sim N(0,\sigma ^2)\). Then, the cAI for the transformed model is given by

$$\begin{aligned} cAI=&E_{f({\widetilde{y}}, u)}E_{f({\widetilde{y}}^*\vert u)}[-2\log g({\widetilde{y}}^*\vert {{\hat{\theta }}},{{\hat{u}}})], \end{aligned}$$

where \({{\hat{\theta }}}\) is the vector of estimated model parameters and \({{\hat{u}}}\) is the vector of predicted random effects. \(-\log g({\widetilde{y}}\vert {{\hat{\theta }}}, {{\hat{u}}})\) is a biased estimator of \(E_{f({\widetilde{y}}, u)}E_{f({\widetilde{y}}^*\vert u)}[-\log g({\widetilde{y}}^*\vert {{\hat{\theta }}},{{\hat{u}}})]=0.5\cdot cAI\). The bias is obtained by

$$\begin{aligned} bias = E_{f({\widetilde{y}}, u)}[-\log g({\widetilde{y}}\vert {{\hat{\theta }}}, {{\hat{u}}})]-0.5\cdot cAI. \end{aligned}$$

To obtain an unbiased estimator of \(0.5\cdot cAI\), the bias correction term (BC) should be added as follows

$$\begin{aligned} BC =&-E_{f({\widetilde{y}}, u)}[-\log g({\widetilde{y}}\vert {{\hat{\theta }}}, {{\hat{u}}})]+0.5\cdot cAI\nonumber \\ =&E_{f({\widetilde{y}}, u)}[\log g({\widetilde{y}}\vert {{\hat{\theta }}},{{\hat{u}}})]\nonumber \\&-E_{f({\widetilde{y}}, u)}E_{f({\widetilde{y}}^*\vert u)}[ \log g({\widetilde{y}}^*\vert {{\hat{\theta }}},{{\hat{u}}})] \nonumber \\ =&E\bigg [\frac{1}{2\sigma ^2}[({\widetilde{y}}^*-\widehat{{\widetilde{y}}})^T({\widetilde{y}}^*-\widehat{{\widetilde{y}}})-({\widetilde{y}}-\widehat{{\widetilde{y}}})^T({\widetilde{y}}-\widehat{{\widetilde{y}}})]\bigg ], \end{aligned}$$
(6)

where \(\widehat{{\widetilde{y}}}=X{{\hat{\beta }}}+Z{\hat{u}}\).

Under the assumption that \(\sigma ^2\) is unknown, the BC in Eq. (6) can be replaced by \(K_{MLE}\) from Eq. (2). Consequently, the cAIC for the transformed model is given by

$$\begin{aligned} cAIC=&-2\log g({\widetilde{y}}\vert {{\hat{\theta }}}, {{\hat{u}}})+2K_{MLE}, \end{aligned}$$
(7)

where

$$\begin{aligned} \log g({\widetilde{y}}\vert {{\hat{\theta }}},{{\hat{u}}})=-\frac{N}{2}\log (2\pi {{{\hat{\sigma }}}}^2)-\frac{1}{2{{{\hat{\sigma }}}}^2}({\widetilde{y}}-\widehat{{\widetilde{y}}})^T({\widetilde{y}}-\widehat{{\widetilde{y}}}). \end{aligned}$$

However, this cAIC of the transformed model cannot be used to compare differently transformed model candidates. The cAIC measures the K-L distance between the true conditional density and a conditional density of a model candidate. In the case of linear mixed models without a transformation, the optimal model can be chosen using the cAIC by Vaida and Blanchard (2005), since all model candidates have the same response variable y. The model with the smallest distance (i.e., the smallest cAIC) is the optimal model among all candidates. However, for linear mixed models with a transformation we estimate for each model candidate its own optimal transformation parameter. As the transformation parameter differs from model to model, the transformed y differs too. Consequently, the response variables of the model candidates are no longer the same (i.e., \({\widetilde{y}}^{(1)}\ne {\widetilde{y}}^{(2)} \ne \cdots \ne {\widetilde{y}}^{(M)}\)). Therefore, the cAIC in Eq. (7) of a model candidate is in fact not the distance of the model from the true density of y, but the distance from the true density of \({\widetilde{y}}\). As \({\widetilde{y}}\) differs from candidate to candidate and cAIC is scale dependent, the model candidates cannot be compared with the cAIC. To allow for comparing model candidates using the cAIC, it needs to be adjusted, so that the adjusted cAIC of a model candidate measures the divergence of the model from the true density of y. Akaike (1978) shows that this adjustment can be done by adding the Jacobian of the transformation to the AIC value of time series models.

The Jacobian adjusted cAIC denoted by JcAIC is derived from the K-L divergence between the true conditional density and the model conditional density of the original y, and not of the transformed y. To define the K-L divergence between the true and a candidate model of y, the true and model conditional densities of y should be defined. As we know the conditional densities of the transformed y, the conditional densities of y can be derived by multiplying the Jacobian of the transformation. Let \(h(y\vert u_0)\) be the true conditional density of y and \(l(y\vert \theta , u)\) the conditional model density, which are defined with the Jacobian of the Box-Cox transformation \(J(\lambda ,y)\) as

$$\begin{aligned} h(y\vert u_0)=&f({\widetilde{y}}\vert u_0)\cdot J(\lambda , y), \nonumber \\ l(y\vert \theta , u) =&g({\widetilde{y}}\vert \theta , u)\cdot J(\lambda ,y), \end{aligned}$$
(8)

where

$$\begin{aligned} J(\lambda , y)=\bigg \vert \frac{\partial {\widetilde{y}}}{\partial y}\bigg \vert =&\prod _{i=1}^{D}\prod _{j=1}^{N_i} \frac{\partial {\widetilde{y}}_{ij}}{\partial y_{ij}}=\prod _{i=1}^{D}\prod _{j=1}^{N_i} (y_{ij}+s)^{\lambda -1}. \end{aligned}$$
(9)

Let \(y^*\) be a realization of the true conditional density \(h(y\vert u)\) and \({\widetilde{y}}^*\) be the vector of transformed \(y^*\). Then, the K-L divergence between conditional densities of \(y^*\) becomes

$$\begin{aligned} I[(\theta _0,u_0),(\theta , u)]=&E_{h(y^*\vert u)} \bigg [\log \frac{h(y^*\vert \theta _0, u_0)}{l(y^*\vert \theta , u)}\bigg ]\\ =&E_{h(y^*\vert u)}[\log h(y^*\vert \theta _0, u_0)] \\&- E_{h({y}^*\vert u)}[\log l(y^*\vert \theta , u)]. \end{aligned}$$

The discrepancy is defined by \(d[(\theta _0,u_0),(\theta ,u)]=E_{h(y^*\vert u)} [-2\log l(y^*\vert \theta , u)]\). Therefore, the K-L divergence can be formulated using discrepancies as follows

$$\begin{aligned} 2I[(\theta _0,u_0),(\theta ,u)]=&2E_{h(y^*\vert u)}[\log h(y^*\vert \theta _0, u_0)]\\&+d[(\theta _0,u_0),(\theta ,u)]. \end{aligned}$$

The ranking of \(d[(\theta _0, u_0), (\theta , u)]\) is equivalent to the ranking of \(2I[(\theta _0,u_0),(\theta ,u)]\), since the first term \(2E_{h(y^*\vert u)}[\log h(y^*\vert \theta _0, u_0)]\) is constant for all model candidates. The Jacobian adjusted cAI (JcAI) is

$$\begin{aligned} JcAI=&E_{h(y, u)}E_{h(y^*\vert u)}[-2\log l(y^*\vert {{\hat{\theta }}},{{\hat{u}}})]. \end{aligned}$$

\(-\log (l(y\vert {{\hat{\theta }}}, {{\hat{u}}}))\) is a biased estimator of \(0.5\cdot JcAI\). To obtain an unbiased estimator of \(0.5\cdot JcAI\), the bias should be corrected by the following bias correction term (BC):

$$\begin{aligned} BC=&-\left( E_{h(y, u)}[-\log (l(y\vert {{\hat{\theta }}}, {{\hat{u}}}))]-0.5\cdot JcAI\right) \\ =&E_{h(y, u)}[\log (l(y\vert {{\hat{\theta }}}, {{\hat{u}}}))]\\&-E_{h(y, u)}E_{h(y^*\vert u)}[\log (l(y^*\vert {{\hat{\theta }}},{{\hat{u}}}))]. \end{aligned}$$

\(l(y\vert {{\hat{\theta }}}, {{\hat{u}}})\) is defined as in Eq. (8). Then, \(l(y^*\vert {{\hat{\theta }}},{{\hat{u}}})\) can be defined by \(g({\widetilde{y}}^*\vert {{\hat{\theta }}}, {{\hat{u}}})\cdot J({{\hat{\lambda }}},y^*)\) using the same relation as in Eq. (8). By inserting these terms into the BC, we get

$$\begin{aligned} BC =&E_{h(y, u)}[\log (g(\widetilde{y}\vert \hat{\theta }, \hat{u})\cdot J(\hat{\lambda },y))]\nonumber \\&-E_{h(y, u)}E_{h(y^*\vert u)}[\log (g(\widetilde{y}^*\vert \hat{\theta }, \hat{u})\cdot J(\hat{\lambda },y^*))]\nonumber \\ =E\bigg [&-\frac{N}{2}\log (2\pi \hat{\sigma }^2)-\frac{1}{2\hat{\sigma }^{2}}(\widetilde{y}-\widehat{\widetilde{y}})^T(\widetilde{y}-\widehat{\widetilde{y}})\nonumber \\&+\log (J(\hat{\lambda }, y))\bigg ]\nonumber \\ -E&\bigg [-\frac{N}{2}\log (2\pi \hat{\sigma }^2)-\frac{1}{2\hat{\sigma }^{2}}(\widetilde{y}^*-\widehat{\widetilde{y}})^T(\widetilde{y}^*-\widehat{\widetilde{y}})\nonumber \\&+\log (J(\hat{\lambda }, y^*))\bigg ]. \end{aligned}$$
(10)

The Jacobian term of y is defined in Eq. (9) and the Jacobian term for \(y^{*}\) is given by \(\prod _{i=1}^{D}\prod _{j=1}^{N_i} (y_{ij}^{*}+s)^{\lambda -1}\) leading to

$$\begin{aligned} BC=E\bigg [&-\frac{N}{2}\log (2\pi \hat{\sigma }^2)-\frac{1}{2\hat{\sigma }^2}(\widetilde{y}-\widehat{\widetilde{y}})^T(\widetilde{y}-\widehat{\widetilde{y}})\nonumber \\&+(\hat{\lambda }-1)\sum _{i=1}^{D}\sum _{j=1}^{N_i} \log (y_{ij}+s))\bigg ]\nonumber \\ -E&\bigg [-\frac{N}{2}\log (2\pi \hat{\sigma }^2)-\frac{1}{2\hat{\sigma }^2}(\widetilde{y}^*-\widehat{\widetilde{y}})^T(\widetilde{y}^*-\widehat{\widetilde{y}})\nonumber \\&+(\hat{\lambda }-1)\sum _{i=1}^{D}\sum _{j=1}^{N_i} \log (y_{ij}^*+s)\bigg ]. \end{aligned}$$
(11)

3.3 Estimation of the bias correction

We propose a parametric bootstrap - following the ideas of Donohue et al. (2011) and Rojas-Perilla et al. (2020) - to estimate the BC for the JcAIC. The bootstrap captures not only the uncertainty due to the estimation of the model parameters but also the additional uncertainty due to the estimation of the transformation parameter \(\lambda \) (Rojas-Perilla et al. 2020). In addition, we use a resampling approach because the bootstrap variants of AIC are comparable with analytic approximations of the AIC (Donohue et al. 2011) and perform better than analytic approximations in terms of the model choice (Shang and Cavanaugh 2008; Marhuenda et al. 2014).

The BC in Eq. (11) consists of two expectation terms. Each expectation term is estimated by averaging the values over the B bootstrap replicates. The steps of the proposed bootstrap are as follows:

  1. 1.

    Estimate the optimal \(\lambda \) defined as \(\hat{\lambda }\) using REML for the model candidate and transform the y to the \(\widetilde{y}\) with the estimated \(\hat{\lambda }\).

  2. 2.

    Fit the model in Eq. (4) to obtain estimates of model parameters \(\hat{\theta }\).

  3. 3.

    Generate \(u^{(b)}\sim \mathcal {N}(0, \hat{G}_0)\) and \(\varepsilon ^{(b)}\sim \mathcal {N}(0, \hat{\sigma }^2)\) and create a bootstrap \(\widetilde{y}\) using \(\widetilde{y}^{(b)}=X\hat{\beta }+Zu^{(b)}+\varepsilon ^{(b)}\).

  4. 4.

    Refit the model with the bootstrap sample \(\widetilde{y}^{(b)}\) and obtain the bootstrap estimates of the model parameters \(\hat{\theta }^{(b)}\) and \(\hat{u}^{(b)}\).

  5. 5.

    Calculate the second expectation term of the BC for each bootstrap using \(\hat{\theta }^{(b)}\) and \(\hat{u}^{(b)}\). The unobserved (true) \(\widetilde{y}^*\) and \(y^*\) are replaced by \(\widetilde{y}\) and y respectively. Note that \(\widetilde{y}\) and y are treated as realizations from the true transformed/untransformed density with corresponding \(\hat{\lambda }\).

  6. 6.

    Back-transform \(\widetilde{y}^{(b)}\) using \(\hat{\lambda }\) to obtain \(y^{(b)}\) on the original scale. Re-estimate \(\hat{\lambda }^{(b)}\) based on \(y^{(b)}\) and re-transform the \(y^{(b)}\) using \(\hat{\lambda }^{(b)}\). The re-transformed bootstrap \(y^{(b)}\) is denoted by \(\widetilde{y}^{(\hat{\lambda }^{(b)}, (b))}\).

  7. 7.

    Refit the model with the bootstrap sample \(\widetilde{y}^{(\hat{\lambda }^{(b)}, (b))}\) and obtain the bootstrap estimates of the model parameters \(\hat{\theta }^{(\hat{\lambda }^{(b)}, (b))}\) and \(\hat{u}^{(\hat{\lambda }^{(b)}, (b))}\). Note that the estimates depend on the re-estimated transformation parameter indicated by the superscript \(\hat{\lambda }^{(b)}\).

  8. 8.

    Calculate the first expectation term of the BC for each bootstrap using \(\hat{\theta }^{(\hat{\lambda }^{(b)}, (b))}\), \(\hat{u}^{(\hat{\lambda }^{(b)}, (b))}\), \(\hat{\lambda }^{(b)}\), \(\widetilde{y}^{(\hat{\lambda }^{(b)}, (b))}\) and \({y}^{(b)}\).

The bootstrap estimate of the BC is then obtained by

$$\begin{aligned} \small BC=&\frac{1}{B}\sum _{b=1}^{B}\Bigg [-\frac{N}{2}log\big (2\pi \hat{\sigma }^{2(\hat{\lambda }^{(b)}, (b))}\big )-\frac{1}{2\hat{\sigma }^{2(\hat{\lambda }^{(b)}, (b))}}\cdot \nonumber \\&\bigg (\widetilde{y}^{(\hat{\lambda }^{(b)}, (b))}-X\hat{\beta }^{(\hat{\lambda }^{(b)}, (b))}-Z\hat{u}^{(\hat{\lambda }^{(b)}, (b))}\bigg )^T\nonumber \\&\bigg (\widetilde{y}^{(\hat{\lambda }^{(b)}, (b))}-X\hat{\beta }^{(\hat{\lambda }^{(b)}, (b))}-Z\hat{u}^{(\hat{\lambda }^{(b)}, (b))}\bigg )\nonumber \\&+\big (\hat{\lambda }^{(b)}-1\big )\sum _{i=1}^{D}\sum _{j=1}^{N_i} \log \big ({y}^{(b)}_{ij}+s\big )\Bigg ]\nonumber \\&-\frac{1}{B}\sum _{b=1}^{B}\Bigg [-\frac{N}{2}log\big (2\pi \hat{\sigma }^{2(b)}\big )-\frac{1}{2\hat{\sigma }^{2(b)}}\cdot \nonumber \\&\bigg (\widetilde{y}-X\hat{\beta }^{(b)}-Z\hat{u}^{(b)}\bigg )^T\bigg (\widetilde{y}-X\hat{\beta }^{(b)}-Z\hat{u}^{(b)}\bigg )\nonumber \\&+\big (\hat{\lambda }-1\big )\sum _{i=1}^{D}\sum _{j=1}^{N_i} \log \big (y_{ij}+s\big )\Bigg ]. \end{aligned}$$
(12)

Then, the JcAIC is estimated by

$$\begin{aligned} JcAIC=&-2\log (l(y\vert \hat{\theta }, \hat{u}))+2BC\nonumber \\ =&\! -2 \log (g(\widetilde{y}\vert \hat{\theta }, \hat{u}))\!-\!2\log (J(\hat{\lambda }, y))\!+\!2BC \end{aligned}$$
(13)

with BC defined in Eq. (12).

The JcAIC is the measure of the K-L divergence of a model candidate from the true model on the original y scale. Therefore, model candidates can be compared with JcAIC despite of their different response variable. A model with the minimum JcAIC is the optimal model with the corresponding optimal transformation parameter.

Using the derived JcAIC for the Box-Cox transformation, we will compare model candidates whose response variables are Box-Cox transformed with different transformation parameters. However, JcAIC can be also derived for other types of transformations, such as a logarithmic or dual-power transformation (Yang 2006). The JcAIC always measures the divergence of a candidate model from the true model on the original y scale independent of how the response variable of the model is transformed. Therefore, the JcAIC can compare not only model candidates that use the same transformation with different transformation parameters, but also the models with different types of transformations.

Table 1 Overview of data settings, \(i=1,...,d,\quad j =1,..., N_i\)
Full size table

3.4 Simultaneous selection of optimal transformation and model formula

As a consequence of the previous sections, we propose the following algorithm to simultaneously select the optimal \(\lambda \) of a Box-Cox transformation and the optimal model among several model candidates. As explained above, considering all possible theoretical M model candidates is often not feasible in practice due to the computational burden. Therefore, the usual step-wise algorithms can be applied where the algorithm stops, if no further improvement can be achieved. In the following, we have chosen backward elimination as the exemplary model selection direction. The exchange to forward or the extension to forward-backward are possible without any difficulties and were done for the simulation experiment in Sect. 4 and the application in Sect. 5.

  1. (1)

    Start with the full model including all P possible x-variables in the data. For the start, the full model is set as the optimal model. Estimate \({\hat{\lambda }}\) based on the full model to initiate the backward model selection.

  2. (2)

    For each step \(s=1,..., S\):

    1. (i)

      Consider all possible model candidates which exclude an explanatory variable from the previous optimal model.

    2. (ii)

      Estimate \({\hat{\lambda }}\) based on the reduced model formulas and transformed y values \({\tilde{y}} = T_{{\hat{\lambda }}}(y)\) for each model candidate. Calculate the JcAIC value from Eq. (13) with the estimated \({\hat{\lambda }}\) for each candidate.

    3. (iii)

      Compare all JcAIC values. The model with the smallest JcAIC value is chosen as the new optimal model for the step.

  3. (3)

    Compare the JcAIC value of the new optimal model in step s with the JcAIC value of the previous optimal model in step \(s-1\). If the JcAIC value of the new optimal model is smaller than the previous one, step 2) is repeated until there is no further improvement in terms of JcAIC values.

4 Model-based simulation experiment

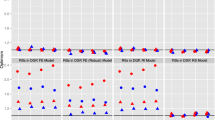
To support our theoretical findings and the proposed framework from the previous section we conduct simulation studies, which include several settings. The aim of the study is to show that under known data settings with a given transformation and model formula, the presented simultaneous algorithm for optimal model and transformation selection depicts the true model for a linear mixed model. The settings include four scenarios: Normal (1), Normal (2), Log and Box-Cox, each with three explanatory variables. The scenarios are oriented to the simulation study of Rojas-Perilla et al. (2020). The distributions of the explanatory variables are chosen to be representative of both, numeric and categorical variables coded as dummies. The first scenario with normally-distributed random effects and error terms (Normal (1)) has an explanatory power of around 40%, and the second (Normal (2)) has an explanatory power of 85%, as well as the Log and Box-Cox scenario. The exact definition of the data settings is given in Table 1. In each simulation run (Monte Carlo replication), the explanatory variables, random intercepts and error terms are generated by drawing from the corresponding distributions. Thus, a new pseudo population is created in each simulation run. A total of 500 Monte Carlo replications are generated for each setting. Each of the finite populations consists of \(N = 10,000\) units evenly divided into \(D=50\) clusters. Within each cluster, a simple random sample is drawn. The cluster-specific sample sizes range from 0 to 29, so that the total sample size sums up to \(n=565\). The distribution of \(y_{ij}\) of one population is shown in the Appendix in Table 9 and Fig. 4.

Table 2 Summary statistics of JcAIC over 500 Monte Carlo replications
Full size table

In addition to the explanatory variables \(x_{1,ij}\), \(x_{2,ij}\) and \(x_{3,ij}\), the random intercepts \(u_i\) and the error terms \(e_{ij}\), an additional variable \(z_{ij} \sim N(1, 0.1^2)\) is generated in each Monte Carlo replications, which is used to estimate the linear mixed model (but not included in the true data generating mechanism):

$$\begin{aligned}&T_{\lambda }(y_{ij}) = {\widetilde{y}}_{ij} = \nonumber \\&\beta _0+\beta _1 x_{1,ij} + \beta _2 x_{2,ij} + \beta _3 x_{3,ij} + \beta _4 z_{ij} + u_i + e_{ij}, \end{aligned}$$
(14)

where T denotes the Box-Cox transformation defined in Eq. (3). In each simulation run, the model selection is performed with four approaches, where the dependent variable y is on different scales:

  • on the original scale (no transformation), so that \(T_{\lambda }(y_{ij}) = y_{ij}\) (denoted by Original),

  • on the log scale, so that \(T_{\lambda }(y_{ij}) = log(y_{ij}{+s})\) (\(\lambda = 0\)) (denoted by Log),

  • on the Box-Cox scale, so that \(T(y_{ij})=\frac{(y_{ij}{+s})^{\lambda }-1}{\lambda }\) for \(\lambda \in [-2, 2]\) and \(\lambda \ne 0\); \(log(y_i)\) for \(\lambda = 0\) (denoted by Box-Cox Opt),

where s denotes the shift parameter \(s=\vert \min (y)\vert +1\) only when \(\min (y)\) is a negative number. A naive approach which is typically used in applications is

  • to perform the model selection on the original scale and afterwards estimate the optimal \(\lambda \) for a Box-Cox transformation (denoted by Box-Cox Naive).

In the Box-Cox Opt approach the optimal model and the optimal transformation parameter \(\lambda \) are determined simultaneously as described in Sect. 3.4. For each setting, the linear mixed model from (14) and a null model without covariates are estimated. The model selection is than performed with a step-wise algorithm using backward and forward directions based on the cAIC or JcAIC. For the Original approach (which operates on the untransformed scale), the cAIC is calculated and the JcAIC in Eq. (13) is calculated for the other approaches (which operate on the transformed scale). They can be directly compared, as cAIC equals the JcAIC for the Original approach. As analytic approximations of the AIC can exhibit negative bias for small sample sizes (Marhuenda et al. 2014), we also use bootstrap versions to estimate the bias correction in the JcAIC/cAIC when a log transformation or no transformation is used. This ensures a fair comparison in the simulation experiment with the estimated JcAIC for a Box-Cox transformation. The bootstrap algorithms to estimate the cAIC for the Original and the JcAIC for the Log approach are described in the Appendix. The bootstrap algorithms were executed with \(B=200\) replications. In the following, we always refer to JcAIC, as in the case of no transformation the cAIC equals the JcAIC.

There are three points of interest in the simulation: First, choice of the correct approach for the model selection, second, choice of the transformation parameter and third, choice of the correct transformation and correct model specification. To begin with, we want to evaluate whether the model with the correct approach based on the JcAIC is chosen in agreement with the data setting. For this, we look at the calculated JcAIC values and in relation to this, we also check whether in the case of the Box-Cox transformation the correct associated \(\lambda \) is estimated. Then, we focus on the proportion of simulation runs where the correct transformation is selected and the proportion of correctly specified model formula.

Table 3 Summary statistics of optimal transformation parameter \({\hat{\lambda }}\) over 500 Monte Carlo replications
Full size table

The parameter \(\lambda \) of the Box-Cox transformation is estimated with the REML algorithm and the simulation is implemented in the statistical programming language R (R Core Team 2021). For each combination of data settings and approaches the calculated JcAIC are compared and the model with the minimal JcAIC is chosen as optimal. Table 2 contains summary statistics of the JcAIC values over the 500 Monte Carlo replications. We observe that in the Normal (1) and Normal (2) data settings, the calculated JcAIC values of the model with no transformation (Original), the Box-Cox transformation (Box-Cox Opt), and the Box-Cox Naive approach are very close. Often, the calculated JcAIC values for Box-Cox Opt and Box-Cox Naive are identical. This makes sense considering the corresponding estimated \(\lambda \)s in Table 3, which are very close to one for both approaches and the resulting distribution close to normality. The deviations of the estimated parameters from one can be explained by the finite population sample from the normal distribution. Looking at the Log data setting we see that the distributions of the JcAIC values using the Log and the Box-Cox Opt approach are very close to each other. Again this makes sense as the estimated \(\lambda \)s (see Table 3) are close to zero, which results in a log transformation of the data. The JcAIC values of the Box-Cox Naive approach are slightly higher. In the case of the Box-Cox data setting, the JcAIC values of the Box-Cox Opt approach are the smallest, followed by the Box-Cox Naive approach. Again, the corresponding estimated \(\lambda \)s match the true \(\lambda \) of \(-0.5\) in this case. The values of the Log and Original approach are considerably higher, which is reasonable given the underlying distribution of the data in this setting. In each setting, the magnitudes and ordering of the values correspond to the underlying distributions of the data and thus to our expectations.

Table 4 Proportions [%] of approaches and formulas selected as optimal
Full size table

Table 4 shows the proportions of selected optimal approaches/ transformations and model formulas. For each data setting, the model with the transformation underlying in the data-generating process is selected mostly as optimal, i.e., has the smallest JcAIC values. In the two Normal data settings the calculated JcAIC are in around 64% and 69% the smallest, when no transformation is used (Original), therefore it is chosen as optimal. This corresponds to the underlying data generating process. In the other cases, Box-Cox Opt and Box-Cox Naive are chosen as optimal with identical JcAIC values and also very similar estimated \(\lambda \)’s, when looking at Table 3. This makes sense due to the underlying normal distribution. For normal data, it should make no difference whether the optimal model formula without a transformation is chosen first and then an optimal \(\lambda \) close to one is estimated, or whether the model formula and transformation parameter are chosen simultaneously, as in the Box-Cox Opt approach. In the Log setting in 71% out of the 500 samples (simulation runs) the true underlying transformation (Log) is chosen as optimal. While in mostly the rest of the samples, the Box-Cox Opt approach with optimal \({\hat{\lambda }}\) near zero, which corresponds to a log transformation, outperforms the Box-Cox Naive approach. In 5.8% JcAIC values are identical for both Box-Cox approaches. The advantage of the Box-Cox Opt approach is further illustrated in the Box-Cox data setting, where this approach is outperforming the other approaches in 83.6% of cases. Looking at the second part of Table 4, it can be seen that in settings with high explanatory power (Normal (2), Log, Box-Cox), the correct model formula (\(x_1 + x_2 + x_3\)) is selected in over 85% of the simulation runs. However, in the Normal (1) setting with lower explanatory power in 60.8% of the samples the correct model formula is selected. This result seems justifiable since, if the explanatory power of the underlying true model is lower, it is more difficult to identify the true underlying relationship. The results emphasize that the presented approach allows for the selection of the optimal transformation parameter for the Box-Cox transformation and detects the true transformation. In addition, it enables the selection of the correct model formula, whereby the degree depends on the explanatory power of the underlying model.

5 Case study: poverty and inequality in municipalities of Guerrero

In this section, the proposed selection approach is applied to data from the state Guerrero in Mexico for estimating poverty and inequality indicators at municipal level. To provide reliable estimates of these indicators at the municipal level, it is necessary to use small area estimation. In order to demonstrate the proposed selection approach, we use a particular small area method - the empirical best predictor (EBP) by Molina and Rao (2010) - which is based on a linear mixed model. In Sect. 5.1, we provide a brief overview of the small area estimation and the EBP. In Sect. 5.2, we describe the data and the problem of simultaneously finding the optimal (linear mixed) model and the transformation parameter. We apply our proposed selection approach and two naive approaches and present the results of the indicators in Sect. 5.3.

5.1 Small area estimation and the empirical best predictor

Many surveys are designed to study total populations. For a sample of the total population, direct estimators, for instance the Horvitz-Thompson estimator (Horvitz and Thompson 1952) can provide reliable estimates due to enough observations/units in the sample. However, direct estimation methods are appropriate only with a sufficient sample size for every domain/area of interest, which is often not the case on a disaggregated regional level. Furthermore, estimators cannot be calculated for domains with no sample data (i.e., out of sample domains) or estimators have too large standard errors for domains with only few sample data (Rao and Molina 2015). When direct estimation cannot provide adequate precision for a domain of interest because of insufficient data, the domain is defined as small and is called small area/small domain (Rao and Molina 2015; Tzavidis et al. 2018). One way to improve direct estimates is by small area estimation. Small area methods aim to improve the efficiency of the estimation by combining sample data with data from the census/register based on a model (Rao and Yu 1994; Jiang and Lahiri 2006). The census/register contains auxiliary variables that may be correlated with the dependent variable and may be used to improve the direct estimates. This is a more complex task as it depends on model building and diagnostics. The model building may include the use of transformation, the selection of the covariates or non-normal error terms.

Since there is no proper survey data which can produce reliable direct estimates of poverty and inequality indicators at municipal level in Guerrero, we use the EBP approach. The approach uses the nested error linear regression model by Battese et al. (1988). This model is a special linear mixed model which includes only random (area specific) intercepts. In the following, we briefly introduce the EBP. Further details are available in Molina and Rao (2010) and Rojas-Perilla et al. (2020).

Assume a finite population of size N divided into D domains. \(N_i\) denotes the size of the i-th domain for \(i=1,\cdots ,D\). Let y be the target welfare variable (e.g. income) and \(y_{ij}\) is the welfare measure of j-th unit in i-th domain where \(j=1,\cdots ,N_i\). The sample data does not include all N units in the population but only a part of the population. The sample has a size of n and this sample can also be divided into D domains. \(n_i\) denotes the sample size of the i-th domain and it results in \(n=\sum _{i=1}^{D} n_i\). Then, the nested error linear regression model is given by

$$\begin{aligned} y_{ij}=&x_{ij}^T\beta +u_i+\varepsilon _{ij}, \end{aligned}$$
(15)
$$\begin{aligned} u_i\overset{iid}{\sim } {\mathcal {N}}(0,\sigma _u^2),&~\varepsilon _{ij}\overset{iid}{\sim }{\mathcal {N}}(0,\sigma _\varepsilon ^2), \nonumber \end{aligned}$$

where \(u_i\) denotes the area random effects and \(\varepsilon _{ij}\) denotes the error term. Let \(\theta =(\beta ,\sigma _u,\sigma _\varepsilon )\) be a vector of model parameters. The EBP approach is shortly outlined as follows:

  1. 1.

    Fit the model using the sample data to obtain \(\hat{\theta }=(\hat{\beta }, \hat{\sigma }_u^2, \hat{\sigma }_\varepsilon ^2)\) and \(\hat{u}_i\).

  2. 2.

    For \(l=1,...,L\), generate

    $$\begin{aligned} \tilde{\epsilon }_{ij}^{(l)}\sim \mathcal {N}(0,\hat{\sigma }_\varepsilon ^2),&~\tilde{u}_i^{(l)}\sim \mathcal {N}(0,\hat{\sigma }_u^2(1-\hat{\gamma }_i)) \end{aligned}$$

    for in sample domains,

    $$\begin{aligned} \tilde{\epsilon }_{ij}^{(l)}\sim \mathcal {N}(0,\hat{\sigma }_\varepsilon ^2),&~\tilde{u}_i^{(l)}\sim \mathcal {N}(0,\hat{\sigma }_u^2) \end{aligned}$$

    for out of sample domains, using \(\hat{\theta }\) with \(\hat{\gamma }=\frac{\hat{\sigma }_u^2}{\hat{\sigma }_u^2+\hat{\sigma }_\varepsilon ^2/n_i}\).

  3. 3.

    Obtain L pseudo-populations by plugging in the explanatory variables in the auxiliary data (i.e. \(x_{ij}\)) with \(\hat{\beta }\), \(\hat{u}_i\), \(\tilde{u}_i\) and \(\tilde{\varepsilon }_{ij}\) obtained in previous steps into the following model

    $$\begin{aligned} y_{ij}^{(l)}=&x_{ij}^T\hat{\beta }+\hat{u}_i + \tilde{u}_i^{(l)}+\tilde{\varepsilon }_{ij}^{(l)}, l=1,...,L \end{aligned}$$

    for in sample domains,

    $$\begin{aligned} y_{ij}^{(l)}=&x_{ij}^T\hat{\beta }+ \tilde{u}_i^{(l)}+\tilde{\varepsilon }_{ij}^{(l)}, l=1,...,L \end{aligned}$$

    for out of sample domains.

  4. 4.

    Calculate the poverty or inequality indicator for each domain and pseudo population \(I_i^{(l)},~ i=1,...,D\) and \(l=1,...,L\).

  5. 5.

    Take the mean over the L Monte Carlo runs to estimate the EBP of the indicator

    $$\begin{aligned} \hat{I}_i^{EBP}=\frac{1}{L}\sum _{l=1}^{L}I_i^{(l)}. \end{aligned}$$

The EBP with data-driven transformed y is obtained similarly to the described EBP above. The detailed estimation of the EBP with data-driven transformations and corresponding uncertainty measures based on MSE of the EBP are further explained in Rojas-Perilla et al. (2020).

Table 5 Number of households per domain in survey and census data
Full size table
Fig. 1
figure 1

Distribution of the total household per capita income in MXN (ictpc)

Full size image

5.2 Data and problem

This study uses survey data from the 2010 Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH - National Survey of Household Income and Expenditure) as sample data. This survey is performed every two years by the Instituto Nacional de Estadística y Geografía (INEGI - The National Institute of Statistics and Geography) and contains socio-demographic information of households, which are also the units of data. INEGI also performs the national population and housing census every ten years. As auxiliary data, the census 2010 data is used for the further application.

Guerrero is located in Southwestern Mexico and borders the Pacific ocean. The state is divided into 81 municipalities. 40 municipalities are in the survey data and 41 municipalities are not in the sample. Table 5 shows a summary of the number of households per domain in the survey and census data. 1801 households are observed in the sample and on average there are 45 observations per domain. The survey and census data contain a large number of socio-demographic variables. The total household per capita income in MXN (i.e., ictpc) is used as the measurement of welfare. As we used the linear mixed model in Eq. (15) to explain ictpc, the Gaussian assumptions of random effects and errors are required. However, the histogram of ictpc in Fig. 1 shows that the distribution of ictpc is very right skewed. Therefore, we apply the Box-Cox transformation to the target variable ictpc, such that the violation can be corrected/reduced. For the Box-Cox transformation the optimal transformation parameter \(\lambda \) should be found.

In the survey data there are 34 possible explanatory variables after excluding variables which are highly/perfectly correlated with other variables. We do not know which variables should be included to optimally explain the response variable, therefore, a variable selection should be performed. Consequently, we have two problems to solve: obtaining the optimal transformation parameter \(\lambda \) and finding the optimal model. To solve these problems simultaneously, the optimal transformation parameters are estimated by the REML approach for each model candidate and all model candidates with their own transformed data are compared with the JcAIC introduced in Sect. 3. There are 34 possible explanatory variables in the data, therefore, we theoretically have \(2^{34}\) model candidates. However, fitting these models is unfeasible because of the computational intensity. Instead, a step-wise variable selection proposed in Sect. 3.4 is applied to find the optimal model. With the chosen optimal model the EBP of poverty and inequality indicators are estimated.

To evaluate the EBP based on our optimal model, we apply two naive approaches which are typically used in applications. The first one takes the simple logarithmic transformation to avoid the problem of finding the optimal transformation and performs variable selection based on cAIC on the log-scale. The second specification performs the variable selection initially on the original y scale to find the optimal model. Afterwards, the optimal transformation parameter is chosen based on the optimal model for the original y. Consequently, we have three different EBP estimates: Box-Cox Opt denotes the EBP based on our selection method based on the JcAIC as described in Sect. 3, Log denotes the first alternative EBP approach and Box-Cox Naive denotes the second alternative EBP approach. These three EBP estimates are compared to show that the use of our proposed selection approach based on the JcAIC can improve the predictive power and reduce the uncertainty of the poverty and inequality estimates.

Table 6 Chosen variables and optimal transformation parameters
Full size table

5.3 Results

First, the chosen variables for the optimal model and the optimal transformation parameters of each approach are compared. Table 6 shows the chosen variables of each approach and the estimated transformation parameter for models with the Box-Cox transformation. We can see that the results of variable selection can be strongly affected by the response variable. The Box-Cox Opt approach performs the variable selection on Box-Cox transformed y and Log performs the variable selection on logarithmic transformed y. For these two approaches, a transformation is used to correct the violation of the Gaussian assumptions and then the optimal model is chosen with transformed y. As a result, the chosen variables for the model of Box-Cox Opt and Log are very similar. In the meantime, the model of Box-Cox Naive choose the variables on the original y despite the violation of the Gaussian assumptions in the error terms. As a result, Box-Cox Naive has different variables in the model in comparison to the other models. Interestingly, optimal transformation parameters for Box-Cox Opt and for Box-Cox Naive only differ slightly even though they have many different variables in the models.

Second, in order to compare the predictive power of each model, marginal \(R^2\) and conditional \(R^2\) (Nakagawa and Schielzeth 2013) are calculated and summarized in Table 7. The marginal \(R^2\) measures the proportion of variance explained by fixed effects and the conditional \(R^2\) provides the proportion of variance explained by both the fixed and random effects. It is shown that the models with the Box-Cox transformation (i.e., Box-Cox Opt and Box-Cox Naive) have the higher predictive power than the model with the logarithmic transformation (i.e., Log). When we compare Box-Cox Opt and Box-Cox Naive, we can see that the Box-Cox Opt, whose model is optimal for transformed y, has a higher marginal and conditional \(R^2\) than Box-Cox Naive, whose model is optimal for the original y scale.

Table 7 \(R^2\) of models used for each approach
Full size table
Table 8 Skewness, kurtosis and p-value of Shapiro-Wilk test for the household and municipal level residuals
Full size table

Since the linear mixed model relies on Gaussian assumptions and we decided to use a transformation to correct the violation of the Gaussian assumptions, each approach should be examined concerning whether the violation is corrected. For the examination, the skewness, kurtosis of residuals, and p-value of the Shapiro-Wilk normality test (Shapiro and Wilk 1965) on residuals are calculated (Table 8). We observe that the logarithmic transformation performs worse than the Box-Cox transformations. For further details we provide quantile-quantile (Q-Q) plots of residuals from the three approaches in Fig. 5 in the Appendix. The household level residuals are clearly closer to the normal distribution with transformations. The Box-Cox transformation corrects the violation in household level residuals rather well, however, the residuals slightly deviate in the tails. From the models with the Box-Cox transformation we can at least observe that the municipal level residuals are very close to the normal distribution.

Finally, we want to assess if the improvement in the predictive power of the model due to the proposed simultaneous selection of the transformation and the covariates (Box-Cox Opt) translates to more precise small area estimates compared to the two alternative approaches (Log and Box-Cox Naive). Therefore, we estimate the mean income, head count ratio (HCR) (Foster et al. 1984), and Gini coefficient (Gini 1912) for the municipalities in Guerrero. To compare the efficiency of these three different approaches, the root mean squared error (RMSE) of the municipal indicators is estimated by a bootstrap (Rojas-Perilla et al. 2020). The RMSE values are visualized in Fig. 2. Figure 2 shows that the Box-Cox Opt is the most efficient approach, since for all three indicators it has the smallest estimated RMSE. When the naive approaches are compared, we cannot say which approach is more efficient because for some indicators Log has the smaller RMSE and for other indicators Box-Cox Naive has the smaller RMSE. It seems that the model and transformation selection is especially important for parameters associated with the tails of the distribution.

Fig. 2
figure 2

RMSE of EBP estimates for mean income, HCR and Gini

Full size image

Figure 3 shows EBP estimates of mean income, HCR, and Gini of municipalities in Guerrero based on Box-Cox Opt approach. The southwestern part of Guerrero, which resembles the coastline (Costa Grande region and Acapulco), features a tourism industry which contributes to the municipalities having a higher mean income. Furthermore, along a north-south axis between Chilpancingo in the south and Taxco in the north, numerous industries are concentrated. These industries focus on the production of handcrafted items using local resources. This also contributes to a higher income in these municipalities. Consequently, the HCR and Gini coefficient in these municipalities are lower than the others. This means, that the people in these municipalities earn more money than in other municipalities and the wealth is more equally distributed compared to other municipalities. On the other hand, the eastern part of Guerrero is suffering from higher levels of poverty and inequality. Municipalities in the region are covered with mountains and when compared to all other regions of Guerrero, these municipalities exhibit the highest number of indigenous people living there.

Fig. 3
figure 3

EBP estimates for mean income, HCR and Gini based on Box-Cox Opt approach

Full size image

6 Conclusions and future research directions

The main purpose of this study was to find a solution to two practical problems in the context of linear mixed models: (a) the true model for explaining the response variable is unknown and (b) the model assumptions, especially the Gaussian assumptions of the error terms, are violated. Since these problems commonly appear together, we provide a solution to find the optimal model and the optimal transformation simultaneously. We focus on one of the most commonly used transformations, the Box-Cox transformation. Since the cAIC is scale dependent, we provide an adjusted cAIC by using the Jacobian of the transformation such that different models with differently compared transformed response variables can be compared. As a large number of possible explanatory variables increases computational costs, we propose an optimal simultaneous selection approach based on Jacobian adjusted cAIC (JcAIC), which is also feasible for a large number of variables. Our model-based simulation studies show that the proposed selection approach chooses the true model with a transformation parameter close to the true value in most cases and performs better compared to naive selection approaches. The proposed simultaneous selection approach can be used in many different areas of research. As an example, we provide a case study where we apply the selection approach for estimating poverty and inequality indicators at municipal level in Mexico. We observe that the model selected by the proposed simultaneous approach has a higher predictive power than other approaches. The improvements in terms of predictive power and model building translate to more precise small area estimates of the poverty and inequality indicators.

Further research should be shifted towards alternative variable selection criteria. For instance, Bunke et al. (1999) show that the cross validation selection criterion can simultaneously select the optimal parametric model and the optimal transformation parameter of the Box-Cox transformation for nonlinear regression models. Furthermore, Fang (2011) proves that the cAIC is asymptotically equivalent to the leave-one-observation-out cross validation for linear mixed models. Therefore, deriving the cross validation selection criterion for the linear mixed model and comparing the results with the JcAIC might be a promising avenue for further research. The selection based on cross validation criterion may improve the quality of the prediction. Moreover, it is also possible to derive the JcAIC for other transformations which require the estimation of the transformation parameter. The use of JcAIC as a selection criterion between different transformations with different optimal models is also a potential research direction. However, it should be noted that the use of our proposed approach is less useful when the point of interest is to interpret the effect of the chosen explanatory variables on the original scaled data. Gurka et al. (2006) introduce a bias corrected beta coefficient for linear mixed models under the Box-Cox transformation which produces a more precise interpretation of the beta coefficients. However, the interpretation does only hold for the transformed response variable. On the original scaled response, it is not clear how strong the effects of the explanatory variables are. To enable interpreting the effects of explanatory variables on the original data, further research is needed for general regression models with the Box-Cox transformed response variable.