Changepoint detection in non-exchangeable data

Abstract

Changepoint models typically assume the data within each segment are independent and identically distributed conditional on some parameters that change across segments. This construction may be inadequate when data are subject to local correlation patterns, often resulting in many more changepoints fitted than preferable. This article proposes a Bayesian changepoint model that relaxes the assumption of exchangeability within segments. The proposed model supposes data within a segment are m-dependent for some unknown $m \geqslant 0$ that may vary between segments, resulting in a model suitable for detecting clear discontinuities in data that are subject to different local temporal correlations. The approach is suited to both continuous and discrete data. A novel reversible jump Markov chain Monte Carlo algorithm is proposed to sample from the model; in particular, a detailed analysis of the parameter space is exploited to build proposals for the orders of dependence. Two applications demonstrate the benefits of the proposed model: computer network monitoring via change detection in count data, and segmentation of financial time series.

1 Introduction

Standard changepoint models rely on partitioning the passage of time into segments, and fitting relatively simple models within each segment. In particular, the data within each segment are often assumed to be independent and identically distributed conditional on some segment specific parameter (Green 1995; Fearnhead 2006; Fryzlewicz 2014). This construction assumes the data within each segment are exchangeable, rendering the order in which the data are observed irrelevant when calculating their joint likelihood (Bernardo and Smith 1993). There are many examples of applications where this assumption is suitable; see for example Olshen et al. (2004), Fryzlewicz (2014) and Fearnhead and Rigaill (2019) for the detection of changes in the mean or variance of time series.

Fig. 1

Counts of computer network events each second between 10:00 and 10:20 on day 22 of the data collection period. Vertical lines indicate estimated changepoints for the proposed changepoint model (middle panel) and for the standard changepoint model (Fearnhead 2006) (bottom panel). Numbers in red indicate the maximum a posteriori (MAP) order of dependence m for each segment for the moving-sum model

However, for some applications it can be reductive to assume data are exchangeable within segments. For illustration purposes, we consider an application of changepoint detection in computer network monitoring. A cyber-attack typically changes the behaviour of the target network. Therefore, to detect the presence of a network intrusion, it might be informative to monitor for changes in the volumes of different types of traffic passing through a network over time. Yet, cyber data are often subject to population drifts, seasonal variations and other temporal trends that are unlikely to be evidence for cyber-attacks. As a result, traditional changepoint detection methods, which assume the data are exchangeable within segments, will fail to capture temporal dynamics and consequently fit many more changepoints than necessary. For example, consider the second-by-second counts of network events recorded on the Los Alamos National Laboratory enterprise network (Turcotte et al. 2017) that are displayed in Fig. 1; the data will be presented in more detail in Sect. 7.1. The vertical lines in the bottom plot indicate the maximum a posteriori (MAP) changepoints obtained with the standard changepoint model described in Fearnhead (2006), which assumes data are exchangeable within segments. No labels are available to indicate the optimal segmentation for these data, but we argue that more changepoints are fitted than would be preferable for network monitoring. It is desirable for abrupt changes, such as the ones observed near the 420th and 880th s, to be detected because they correspond to behavioural changes of the network that are sufficiently drastic that cyber-analysts may want to investigate whether they correspond to malicious activities. However, changes due to small fluctuations, such as the ones between the 100th and 380th s, may not be relevant to cyber-analysts because they result from local temporal dynamics in traffic volumes that are not suggestive of behavioural changes of the network. There are various possible causes for such small fluctuations, including data transfer mechanisms in networks. For example, when large data are transferred across a network, they are often divided up into batches following protocols that involve routing and queueing steps, which may lead to temporal correlations in traffic volumes. Hence, a changepoint model to detect clear discontinuities in the presence of non-exchangeable data is needed. Moreover, since temporal dynamics for cyber data may change when a clear discontinuity occurs, it would not be satisfactory to assume the dependence structure of the data is the same for each segment. For example, an attack may involve reconnaissance techniques such as port scanning that could change temporal dynamics in traffic volumes.

Existing models to detect clear discontinuities in the presence of non-exchangeable data typically assume the dependence structure is identical for each segment (Albert and Chib 1993; Sparks et al. 2011; Wyse et al 2011; Chakar et al. 2017; Romano et al. 2021; Cho and Fryzlewicz 2021). In particular, it is often assumed the data within each segment are Markov conditional on some segment parameter. Moreover, changepoint models for dependent data are often designed for a specific marginal distribution, for example the normal distribution (Chakar et al. 2017; Romano et al. 2021; Cho and Fryzlewicz 2021), the negative binomial distribution (Sparks et al. 2011; Yu et al. 2013) or the Poisson distribution (Weiß 2011; Franke et al. 2012).

This article extends a standard changepoint model (Fearnhead 2006), relaxing the assumption that data are exchangeable within segments. The proposed changepoint model, named the moving-sum changepoint model, supposes a segment model that is related to a model for m-dependent, stationary data discussed in Joe (1996); a sequence $x_1, x_2, \ldots$ is m-dependent if $(x_{t+m+1}, x_{t+m+2}, \ldots )$ is unconditionally independent of $(x_1, x_2, \ldots , x_t)$ for all $t \geqslant 1$. Within each segment, our model assumes the data are m-dependent and identically distributed conditional on some parameter $\theta$, where both $\theta$ and $m \geqslant 0$ are unknown and change from one segment to the next. Whilst $\theta$ denotes a parameter of the marginal distribution of the data such as the mean or the variance, m corresponds to the level of dependency within the segment. To maintain tractability, the marginal distribution of the observed data is assumed to belong to the class of convolution-closed infinitely divisible distributions, which includes, for example, the normal, negative binomial and Poisson distributions. Therefore, the moving-sum changepoint model is suitable for various settings where it is of interest to detect clear discontinuities in the presence of non-exchangeable data. For example, consider the MAP changepoints obtained with the moving-sum model for the counts of network events displayed in the middle panel of Fig. 1. In comparison with the standard changepoint model, the moving-sum changepoint model captures temporal dynamics of the network behaviour, resulting in a segmentation of the data that is more adapted to network monitoring.

A common approach to sampling changepoints for a time series is that of Green (1995), using a reversible jump Markov chain Monte Carlo (MCMC) algorithm to explore the state space of changepoints. At each iteration of the algorithm, one of the following move types is proposed: sample a segment parameter, propose a new changepoint, or delete or shift an existing changepoint to a new position. This article proposes a sampling strategy within that framework to sample from the moving-sum changepoint model. In particular, our approach exploits an analysis of the constraints of the parameter space; for example, for non-negative data such as count data, the constraints of the parameter space depend on the observed data, and this must be understood to build proposals for segment specific dependency levels.

The remainder of the article is organised as follows. Section 2 introduces a novel changepoint model for non-exchangeable data. Section 3 gives an approach for deriving the likelihood of the data conditional on proposed changepoints, characterising the segment model in terms of a stochastic difference equation with an unknown initial condition. Section 4 provides a detailed analysis of the constraints to the parameter space, along with asymptotic results on the behaviour of segment parameters. A reversible jump MCMC sampling strategy is given in Sect. 5. Section 6 presents results demonstrating the benefits of the proposed changepoint model, via a comparison with the standard model (Fearnhead 2006), PELT (Killick et al. 2012), DeCAFS (Romano et al. 2021) and WCMgSA (Cho and Fryzlewicz 2021). Section 7 considers two applications of changepoint detection showing the benefits of the proposed changepoint model: computer network monitoring via change detection in count data, and detection of breaks in daily prices of a stock. Section 8 concludes.

2 Moving-sum changepoint model

This section introduces the moving-sum model, which is used as a segment model to define a novel changepoint model for non-exchangeable data.

2.1 Moving-sum model

A moving-sum model assumes that observed data $x_1, \ldots , x_n$ satisfy

$$\begin{aligned} x_t \overset{}{=} \sum _{i=0}^{m}y_{t-i}, \end{aligned}$$

(1)

for $t=1, \ldots , n$, where $y_{-(m-1)}, \ldots , y_n$ are $m+n$ iid latent random variables with common parametric density $f_m( \cdot \, | \, \theta )$ for some unknown parameters $\theta \in \Theta$ and $m \geqslant 0$. If $m=0$, the construction in (1) implies that, for all $t=1, \ldots , n$,

$$\begin{aligned} x_t \overset{\text {iid}}{\sim } f_0( \cdot \, | \, \theta ), \end{aligned}$$

(2)

and, consequently, is equivalent to exchangeability in the data. Yet, if $m>0$, the sequence of observed data (1) is m-dependent and therefore non-exchangeable.

Definition 1

(m-dependence) For $m \geqslant 0$, the sequence $x_1, x_2, \ldots$ is $\, m$-dependent if $(x_{t+m+1}, x_{t+m+2}, \ldots )$ is unconditionally independent of $(x_1, x_2, \ldots , x_t)$ for all $t \geqslant 1$. Note that if a sequence is m-dependent, then it is also Markov of order m.

For all t, $x_t$ in (1) is the sum of $m+1$ latent random variables, leading to m-dependence. Noting this duality, for simplicity of presentation in the following discussion we use the notational convention

$$\begin{aligned} {\bar{m}} = m+1. \end{aligned}$$

It will be helpful to identify a class of distributions for which the construction in (1) gives rise to a tractable marginal distribution of the observed data. Recall the distribution of a random variable x is infinitely divisible if, for all $m \geqslant 0$, there exists a sequence of iid random variables $y_0, \ldots , y_m$ such that $\sum _{i=0}^{m}y_i$ has the same distribution as x. For all infinitely divisible marginal distributions F for $x_t$ (1), there exists a distribution $F_m$ for the latent random variables for all m, and $F_m$ is known if F is closed under convolution. In this article, it will be assumed that the marginal distribution of $x_t$ is an infinitely divisible distribution that is closed under convolution, so that the corresponding density $f_m( \cdot \, | \, \theta )$ of the iid latent variables is available for all m.

We consider in detail three instances of the moving-sum segment model based on such distributions, one for continuous data with unbounded domain given in Example 1, one for continuous data with bounded domain given in Example 2, and one for discrete data with bounded domain given in Example 3, which we will refer back to throughout the article for illustration. Conjugate priors for $\theta$ are given for each example.

Example 1

(Normal distribution) Suppose that $f_m( \cdot \, | \, \theta )$ corresponds to density of the normal distribution with mean $\mu / {\bar{m}}$ and variance $\sigma ^2 / {\bar{m}}$, for some $\theta = ( \mu , \sigma )$ where $\mu \in {\mathbb {R}}$ and $\sigma >0$. It follows that $(x_t)$ is marginally $N(\mu , \sigma ^2)$ with m-dependence. Moreover, a priori $\sigma ^{-2} \sim \text {Gamma}(\alpha , \beta )$, for some $\alpha >0$ and $\beta >0$, and $\mu \sim N(\mu _0, \sigma ^2 / \lambda )$ for some $\mu _0 \in {\mathbb {R}}$ and $\lambda > 0$.

Fig. 2

Data generated from the moving-sum changepoint model for negative binomial data given in Example 3 with three changepoints ($\tau _1$, $\tau _2$ and $\tau _3$) indicated by thick grey lines. The black dashed lines indicate the positions of the MAP changepoints obtained by fitting the standard changepoint model (2) to the data

Example 2

(Gamma distribution) Suppose that $f_m( \cdot \, | \, \theta )$ corresponds to density of the gamma distribution with shape parameter $\lambda /{\bar{m}}$ and rate $\theta$, where $\lambda >0$ and $\theta >0$. It follows that $(x_t)$ is marginally $\Gamma (\lambda , \theta )$ with m-dependence. The prior for $\theta$ is assumed to be $\Gamma (\alpha , \beta )$ for some $\alpha >0$ and $\beta >0$.

Example 3

(Negative binomial distribution) Suppose that $f_m( \cdot \, | \, \theta )$ corresponds to density of the negative binomial distribution with number of failures $r / {\bar{m}}$ and success probability $\theta \in [0, 1]$, for some fixed $r>0$. It follows that $(x_t)$ is marginally $NB(r, \theta )$ with m-dependence. Moreover, a priori $\theta \sim \text {Beta}(\alpha , \beta )$, for some $\alpha >0$ and $\beta >0$.

Other examples of such distributions include the Poisson, Cauchy and chi-squared distributions.

2.2 Bayesian changepoint analysis with moving-sums

Suppose we observe real-valued discrete time data $x_{1:T} = (x_{1}, \ldots , x_{T})$. The changepoint model assumes $k \geqslant 0$ changepoints with ordered positions $\tau _{1:k} = (\tau _1, \ldots , \tau _k)$, such that $1 \equiv \tau _{0}< \tau _{1}< \cdots< \tau _{k} < \tau _{k+1} \equiv T+1$, which partition the passage of time into $k + 1$ independent segments. The changepoints are assumed to follow a Bernoulli process, implying a joint prior probability mass function

$$\begin{aligned} \pi ( k, \tau _{1:k} ) = p^{k}(1-p)^{T-1-k}, \end{aligned}$$

for some $0<p<1$ that characterises the expected number of changepoints.

For the moving-sum changepoint model, within each segment j, the data $x_{\tau _{ j-1}}, \ldots , x_{\tau _{j}-1}$ are assumed to follow the moving-sum model (1) conditional on some unknown dependency level $m_j\geqslant 0$ and parameter $\theta _j\in \Theta$, which both change from one segment to the next. Dependency levels $m_1, \ldots , m_{k+1}$ and segment parameters $\theta _1, \ldots , \theta _{k+1}$ are assumed to be independent. For all j, it is assumed a priori that $m_j$ is drawn from a geometric distribution with parameter $0< \rho <1$, so that

$$\begin{aligned} \pi (m_j) = \rho (1-\rho )^{m_j}, \end{aligned}$$

meaning that for each segment the order of dependence may be increased or decreased at a fixed cost. Moreover, motivated by computational considerations, the prior for $\theta _j$ is chosen to be conjugate for $f_0$. For notational simplicity, we denote by $\pi$ the density of the prior distribution of both $m_j$ and $\theta _j$.

2.3 Simulation from the model

Figure 2 displays data generated from the moving-sum changepoint model, given a fixed sequence of changepoints, for negative binomial data given in Example 3 with $r = 200$, $\alpha = 20$ and $\beta = 10$. It is apparent that the changepoints correspond to changes in both the dependence structure and the mean of the data. In particular, we note that for larger values of $m_j$, the data tend to be smoother in the corresponding segment. For segments with $m_j>0$, it is reductive to judge the data to be exchangeable since there are clear temporal dynamics.

The bottom panel of Fig. 2 displays the positions of the MAP changepoints obtained by fitting the standard changepoint model for exchangeable data given in (2) to the simulated data using Metropolis-Hastings sampling of the changepoints as described in Denison et al. (2002). Within segments where the data are not exchangeable, the standard model cannot capture the temporal dynamics and therefore the data are inferred to be more segmented than preferable.

3 Conditional likelihood for the moving-sum changepoint model

Since changepoints split the data into independent segments, the joint posterior density of changepoints is tractable, up to a normalising constant, if the conditional likelihood of data within each segment can be computed. This section discusses the computation of the conditional likelihood of some data $x_1, \ldots , x_n$ observed within a single segment, assuming the moving-sum model defined in Sect. 2.1 for some $m \geqslant 0$ and $\theta$.

3.1 Relationship between the observed data and the latent variables

This section gives insights on the relationship between the observed data and the latent variables, which is exploited to compute the conditional likelihood of the observed data within a generic segment in Sect. 3.2. We show that, for the latent m-dependence framework (1), there are m free latent variables subject to some constraints, and then all further latent variables are implied by the observed data sequence. Some of the notation introduced in this section will be useful in the remainder of the article.

Consider the backward difference operator $\triangledown$ and the forward difference operator $\vartriangle \,$ defined such that, for all t,

$$\begin{aligned} \triangledown x_t&= x_t - x_{t-1}, \nonumber \\ \vartriangle x_t&= x_t - x_{t+1} = - \triangledown x_{t+1} . \end{aligned}$$

(3)

The equation given in (1) may be equivalently expressed as

$$\begin{aligned} y_t = y_{t-{\bar{m}}} + \triangledown x_t , \end{aligned}$$

(4)

for $t=2, \ldots , n$, and $y_1 = x_1 - (y_{-m+1} + \cdots + y_{0})$. Iterating the expression in (4) shows that, given the initial m latent random variables $y_{-m+1}, \ldots , y_{0}$, there is a one-to-one relationship between the finite differences of $x_{1:n}$ (3) and the remaining latent variables $y_{1:n}$. Let the first m latent variables be $\gamma _{1:m}= (\gamma _1, \ldots , \gamma _m)$, with

$$\begin{aligned} \gamma _{r} = y_{-m+r} \end{aligned}$$

for $r = 1, \ldots , m$. Explicitly, for all $t=1, \ldots , n$, letting r be the remainder and q the quotient of the Euclidean division of $t-1$ by ${\bar{m}}$ such that $t=q{\bar{m}}+r+1$, we have

(5)

where $x_0 \equiv 0$ and

(6)

The role played by $\gamma _{1:m}$ is akin to the role played by the unknown initial conditions of a stochastic difference equation.

The choice to condition on the first m latent random variables is arbitrary; given any sequence of m consecutive latent random variables, there is a one-to-one relationship between the other latent variables and the observed data. The following definition gives a transformation that may be used to obtain $\gamma _{1:m}$ from any m consecutive latent random variables, so that it is sufficient to consider conditioning on the first m latent variables in all subsequent discussion. The transformation is also useful in the later sections of the article, where, for example, we need to obtain the initial latent variables when some data are added to, or removed from, an edge of a segment.

Definition 2

Let $x_1, \ldots , x_n$ be data observed within a segment, assuming the model (1) for some $m \geqslant 0$. Let $S[y_{t}, \ldots , y_{t+m-1} ] = (y_{t+1}, \ldots , y_{t+m} )$ denote the ‘shift’ map, where $y_{t+m} = x_{t+m} - \sum _{i=0}^{m-1} y_{t+i}$, for all suitable t. Clearly, S is iterable and invertible, and for all sequences of m consecutive latent random variables $y_{(-m+1+u):u}$, with $0 \leqslant u \leqslant n$, $S^{-u}[y_{(-m+1+u):u}] = y_{(-m+1):0} = \gamma _{1:m}$.

3.2 Conditional likelihood of the data within a segment

Given m and $\gamma _{1:m}$, (5) provides a one-to-one deterministic mapping between $x_{1:n}$ and $y_{1:n}$ with unit Jacobian. Hence, if we treat the sequence $\gamma _{1:m}$ as an additional unknown segment parameter, whose elements are independent and identically distributed with density $f_m(\cdot \, |\, \theta )$, then the conditional likelihood of the observed data within a segment is

$$\begin{aligned} L(x_{1:n} \, | \,\theta , m, \gamma _{1:m})&= L(y_{1:n} \, | \, \theta , m, \gamma _{1:m}) \nonumber \\&= \prod _{i=1}^{n} f_m(y_i | \theta ). \end{aligned}$$

(7)

Thus, using the notation introduced in Sect. 2.2, but ignoring the subscripts corresponding to the indices of segments, the unknown segment parameters are $(\theta , m , \gamma _{1:m})$, with prior density $\pi (\theta ) \pi (m) \pi (\gamma _{1:m} \, | \theta , m)$ where $\pi (\gamma _{1:m} \, | \theta , m) = \prod _{r=1}^{m} f_m(\gamma _{r} \, | \, \theta )$.

Recall it is assumed that the prior for $\theta$ is chosen to be conjugate for $f_m(\cdot \, |\, \theta )$ conditional on m. Consequently, the joint likelihood of the data and the initial latent variables conditional on m can be derived by invoking Bayes’ theorem,

$$\begin{aligned}{} & {} L(x_{1:n}, \gamma _{1:m} \, | \, m) \nonumber \\{} & {} \quad = \int L(y_{1:n} \, | \, \theta , m, \gamma _{1:m} ) \pi (\gamma _{1:m} \, | \, \theta , m) \pi (\theta ) d \theta . \end{aligned}$$

(8)

Let ${\mathcal {F}}$ denote the support of $f_m(\cdot \, |\, \theta )$ and, given m, $x_{1:n}$ and (5), let

$$\begin{aligned} {\mathcal {Y}}_m&\equiv {\mathcal {Y}}_m(x_{1:n}) \nonumber \\&= \{ \gamma _{1:m} \in {\mathcal {F}}^m ; y_t \in {\mathcal {F}} \text { for all } t=1, \ldots , n \}. \end{aligned}$$

(9)

${\mathcal {Y}}_{m}$ is the set of sequences $\gamma _{1:m}$ such that the joint conditional probability density (8) is non-zero. As stated in Remark 1, it is not guaranteed that, for all m, ${\mathcal {Y}}_m$ will be non-empty. An expression for (8) is given below for the three examplar segment models introduced in Sect. 2.1.

Remark 1

(Set ${\mathcal {Y}}_m$) Note that in the case of $m=0$, where the sequence $x_{1:n}$ is assumed to be exchangeable, then $\gamma _{1:m}$ is the empty sequence, and the expression in (7) is always well defined. Now, if $m>0$, two cases need to be considered separately. If ${\mathcal {F}}$ is unbounded, for all m and sequence $x_{1:n}$, the set ${\mathcal {Y}}_m$ is ${\mathcal {F}}^{m}$. However, if ${\mathcal {F}}$ is bounded then ${\mathcal {Y}}_m$ is a proper subset of ${\mathcal {F}}^{m}$ and is not necessarily non-empty for all $m>0$ and $x_{1:n}$. For example, if ${\mathcal {F}}$ is bounded below by 0, for any non-negative sequence $x_{1:n}$ with $x_2 > x_1 + x_3$, the set ${\mathcal {Y}}_m$ is empty for all $m>0$.

Example 1

(Normal distribution) Given parameters $( m , \gamma _{1:m})$ and a known hyperparameters $\lambda , \alpha , \beta >0$, it follows that

$$\begin{aligned} L(x_{1:n}, \gamma _{1:m} \, | \, m)&= \left( \frac{ {\bar{m}} }{ 2 \pi } \right) ^{( n+m)/2} \left( \frac{ \lambda }{ \lambda ^\prime } \right) ^{1/2} \frac{\beta ^{ \alpha } }{\Gamma ( \alpha ) } \frac{ \Gamma ( \alpha ^\prime ) }{ (\beta ^{\prime })^{\alpha ^\prime } } , \end{aligned}$$

where $\lambda ^\prime = \frac{(n + m + {\bar{m}} \lambda )}{ {\bar{m}} }$, $\alpha ^\prime = \frac{ ( n+m) }{2} + \alpha$ and $\beta ^\prime = \beta + \frac{ {\bar{m}} }{2} (\sum _{t=-m+1}^n y_t^2) + \frac{ \lambda }{2} \mu _0^2 - \frac{ (\lambda \mu _0 + \sum _{t=-m+1}^n y_t )^2 }{ 2 \lambda ^\prime }$.

Example 2

(Gamma distribution) Given parameters $( m , \gamma _{1:m})$ and known hyperparameters $\lambda , \alpha , \beta >0$, it follows that

where $\lambda _{m} = \lambda /{\bar{m}}$, and .

Example 3

(Negative binomial distribution) Given parameters $( m , \gamma _{1:m})$ and known hyperparameters $r, \alpha , \beta >0$, it follows that

where $r_{m} = r/{\bar{m}}$ and .

Fig. 3

Cartoons of the set ${\mathcal {Y}}_m$ for $m=1,2,3$ with ${\mathcal {F}}$ assumed to be continuous

The segment parameters $(m, \gamma _{1:m})$ cannot be marginalised, and consequently to sample from the posterior distribution of the changepoints, we need to sample $(m, \gamma _{1:m})$ for each segment. Different challenges arise when attempting to do so: the dimension of the segment parameter space is unknown; as first hinted in Remark 1, the parameter space depends on the observed data when the support of $f_m(\cdot \, |\, \theta )$ is bounded. Hence, in order to develop a sampling strategy that is computationally realistic, it is necessary to characterise the parameter space we are seeking to navigate.

4 Analysis of the latent parameter space

In Sect. 3.2 we defined ${\mathcal {Y}}_{m}$ to be set of sequences $\gamma _{1:m}$ such that the joint conditional probability density of $\gamma _{1:m}$ and $x_{1:n}$ is non-zero within a generic segment. We now define

$$\begin{aligned} {\mathcal {M}} \equiv {\mathcal {M}}(x_{1:n}) = \{ m \in {\mathbb {N}}_{0} ; \, {\mathcal {Y}}_{m} \ne \emptyset \} \end{aligned}$$

to be the set of $m \geqslant 0$ for which ${\mathcal {Y}}_{m}$ is non-empty. In other words, given some observed data $x_1, \ldots , x_n$ within a generic segment, ${\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ provide the values of m and $\gamma _{1:m}$ for which the segment model (1) is valid.

As stated in Remark 1, it is always possible to assume the sequence $x_{1:n}$ to be exchangeable, and hence $0\in {\mathcal {M}}$. If ${\mathcal {F}}$, the support of $f_m(\cdot \, |\, \theta )$, is unbounded, such as in Example 1, then ${\mathcal {M}} = {\mathbb {N}}_{0}$, and ${\mathcal {Y}}_{m}$ is ${\mathcal {F}}^{m}$ for all $m>0$. However, if ${\mathcal {F}}$ is bounded, such as in Examples 2, 3, then both ${\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ depend on the observed data $x_{1:n}$, and ${\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ are proper subsets of ${\mathbb {N}}_{0}$ and ${\mathcal {F}}^{m}$, respectively. Infinitely divisible distributions with support bounded from below and from above have zero variance (Steutel 1975), and therefore we only consider the case where ${\mathcal {F}}$ is bounded below but not above, without loss of generality.

Section 4.1 explicitly states the relationship between the observed data $x_{1:n}$ and the sets ${\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ for $m\in {\mathcal {M}}$ when ${\mathcal {F}}$ is bounded below. Section 4.2 and Sect. 4.3 provides results on the structure of the constrained parameter space that are used in Sect. 5 to design a sampling strategy for the model parameters. Section 4.4 discusses the asymptotic behaviour of the parameter space as the number of observations increase; in particular, for the segment parameters $\gamma _{1:m}$, which may be considered to be the unknown initial conditions of a process governed by a difference equation as argued in Sect. 3.1, it is shown that, asymptotically, the uncertainty on the initial conditions vanishes.

4.1 Characterisation of the parameter space in terms of the observed data

Suppose that ${\mathcal {F}}$ is unbounded above but bounded below by a constant, which can be set to 0 without loss of generality. It follows that, given a sequence $x_{1:n}$ and some $m>0$, the set ${\mathcal {Y}}_{m}$ consists of those $\gamma _{1:m} \in {\mathcal {F}}^{m}$ such that $y_{t} \geqslant 0$ for all $t=1, \ldots , n$. According to (5) and (6), defining

$$\begin{aligned} \begin{array}{l} U^{m} \equiv U^{m}(x_{1:n}) = \min \{ x_1 , \ldots , \sum _{q = 0 }^{\kappa _{{\bar{m}}}} x_{q{\bar{m}}+1} \}, \\ L_r^{m} \equiv L_{r}^{m}(x_{1:n}) = \max \{ 0, \vartriangle x_{r} , \ldots , \sum _{q = 0 }^{\kappa _{r}} \vartriangle x_{q{\bar{m}}+r} \}, \end{array} \end{aligned}$$

(10)

where $x_0 \equiv 0$ and $\kappa _r = \kappa _r(n)$ is the largest $q \in {\mathbb {N}}_{0}$ such that $q{\bar{m}}+r+1 \leqslant n$ for all r, then

$$\begin{aligned} {\mathcal {Y}}_{m} = \mathbb {Y}[U^{m}, L^{m}_{1:m}], \end{aligned}$$

(11)

where

It will be useful both in the remainder of this section and in Sect. 5 to characterise ${\mathcal {Y}}_{m}$ (9) in terms of $\mathbb {Y}$ (11). Moreover, for $m\geqslant 0$, $m\in {\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ is non-empty if and only if

$$\begin{aligned} D^m \equiv D^{m}(x_{1:n}) = U^{m} - \sum _r L_{r}^{m} \geqslant 0. \end{aligned}$$

(12)

Example 4 gives expanded expressions of the bounds of ${\mathcal {Y}}_{m}$ for a small sequence of observed data.

Example 4

(Bounds of ${\mathcal {Y}}_{m}$) Let $x_1, \ldots , x_{7}$ be count data. If $m=1$ (${\bar{m}}=2$), then

$$\begin{aligned} \left\{ \begin{array}{l} U^{1} = \min \{ x_1, x_1 + (x_3 - x_2), x_1 + (x_3 - x_2) + (x_5 - x_4), \\ \quad \quad \quad x_1 + (x_3 - x_2) + (x_5 - x_4) + (x_7-x_6) \} \\ L_1^{1} = \max \{ 0, (x_1 - x_2 ), (x_1 - x_2 ) + (x_3 - x_4 ), \\ \quad \quad \quad (x_1 - x_2 ) + (x_3 - x_4 ) + (x_5 - x_6 ) \}, \end{array} \right. \end{aligned}$$

whilst if $m=3$ (${\bar{m}}=4$), then

$$\begin{aligned} \left\{ \begin{array}{l} \, U^{3} \, = \min \{ x_1, x_1 + (x_5 - x_4) \} \\ L_1^{3} = \max \{ 0, (x_1- x_2), (x_1- x_2) + (x_5 -x_6) \}\\ L_2^{3} = \max \{ 0, (x_2- x_3), (x_2- x_3) + (x_6-x_7) \} \\ L_3^{3} = \max \{ 0, (x_3- x_4) \}. \end{array} \right. \end{aligned}$$

Fig. 4

Cartoon representation of the mapping of $\gamma _{1:m} \in {\mathcal {Y}}_m$ to $\gamma _{1:{m^\prime }}^{\prime } = J_{m^\prime }(\gamma _{1:m}) \in {\mathcal {Y}}_{m^\prime }$ with $m=5$ and $m^\prime =2$

Figure 3 displays cartoon representations of ${\mathcal {Y}}_{m}$ for $m=1,2$ and 3. For all $m>0$, if non-empty, ${\mathcal {Y}}_{m}$ is a convex polyhedron in ${\mathcal {F}}^{m}$, whose vertices are determined by the bounds $U^{m}$ and $L^{m}_{1:m}$, and whose size only depends on m and $D^{m}$ for all m.

Given a sequence of observed data $x_{1:n}$ within a segment, it was shown in (11) that the sets ${\mathcal {M}}$ and ${\mathcal {Y}}_{m}$ may be expressed in terms of the first observation $\triangledown x_1 =x_1 - x_0 = x_1$ and all of the subsequent the finite differences of the data. Essentially, for all m, the larger the finite differences, or jumps, are relative to $x_1$, the smaller ${\mathcal {Y}}_m$ becomes unless the jumps happen to exhibit negative ${\bar{m}}$-lagged autocorrelations. In particular, if the observed data $x_{1:n}$ consist of a succession of gradual drifts, whose directions flip every ${\bar{m}}$ time points, then ${\mathcal {Y}}_m$ is large with respect to $x_1$. Furthermore, in order to stress that the size of the jumps must be considered relative to $x_1$, we note that for all sequences $x_{1:n}$ such that ${\mathcal {Y}}_m$ is non empty for some m, and for all constant $\mu$, $D^{m}( x_{1:n} + \mu ) = D^{m}( x_{1:n} )+ \mu$, where $x_{1:n} + \mu$ denotes the sequence $(x_{t} + \mu )_{t=1}^{n}$.

4.2 Adding and removing data

To develop a sampling strategy for the latent variables, it is important to determine how ${\mathcal {M}}$ and ${\mathcal {Y}}_m$, $m\in {\mathcal {M}}$, may change when data are added to, or removed from, an edge of a segment. Proposition 1 guarantees that, for all sequences of data, if there exist segment parameters $\gamma _{1:m}$ for some m, then we can obtain valid parameters of the same dimension for all sequences of data that could be obtained by removing data from the beginning or the end of the original sequence.

Proposition 1

Let $x_{1:n}$ be observed data and $1 \leqslant s \leqslant t \leqslant n$. Then ${\mathcal {M}}(x_{1:n}) \subseteq {\mathcal {M}}(x_{s:t})$, and $S^{s-1}[{\mathcal {Y}}_{m}(x_{1:n})]\subseteq {\mathcal {Y}}_{m}(x_{s:t})$ for all $m\in {\mathcal {M}}(x_{1:n})$, where the shift map S is defined in Definition 2. In particular, if $s=1$ we have ${\mathcal {Y}}_{m}(x_{1:n})\subseteq {\mathcal {Y}}_{m}(x_{1:t})$.

Proof

Suppose $\gamma _{1:m} = y_{(-m+1):0} \in {\mathcal {Y}}_{m}(x_{1:n})$ for some $m \in {\mathcal {M}}(x_{1:n})$. Let $y_{1:n}$ denote the latent variables obtained from $\gamma _{1:m}$ and $x_{1:n}$ via (5). By definition of the shift map, the latent variables obtained from $S^{s-1}[y_{(-m+1):0}] = y_{(-m+s):(s-1)}$ and $x_{s:t}$ via (5) are equal to $y_{s:t}$. Hence $S^{s-1}[y_{(-m+1):0}] \in {\mathcal {Y}}_{m}(x_{s:t})$, and therefore $m \in {\mathcal {M}}(x_{s:t})$. $\square$

However, if some data are added to the beginning or the end of a sequence of data for which we currently have valid parameters $\gamma _{1:m}$ for some m, then it is not guaranteed that $m \in {\mathcal {M}}$ for the extended sequence of data. For example, it follows directly from (10) that, as more data are added to the end of a segment, for all m, $U^{m}$ may only decrease and $L^{r}_m$ may only increase for all r, and therefore ${\mathcal {Y}}_{m} = \mathbb {Y}[U^{m}, L^{m}_{1:m}]$ may only shrink.

4.3 Different ranges of dependence

Given a segment of data, there is a non-negligible computational cost in verifying via (12) that some integer m belongs to the corresponding set ${\mathcal {M}}$. Hence, it is instructive to determine whether knowing that some m belongs to ${\mathcal {M}}$ can inform whether some $m^\prime \ne m$ is also an element of ${\mathcal {M}}$.

Suppose $m \in {\mathcal {M}}$ and $0 \leqslant m^\prime \leqslant m$ such that ${\bar{m}}^{\prime }$ divides ${\bar{m}}$ (written ${\bar{m}}^{\prime } \, | \, {\bar{m}}$), meaning ${\bar{m}} = \ell {\bar{m}}^{\prime }$ for some $\ell >0$. Then define a mapping

$$\begin{aligned} J_{m^\prime }(\gamma _{1:m}) = \left( \sum _{j=0}^{\ell -1} \gamma _{j{\bar{m}}^\prime +1}, \ldots , \sum _{j=0}^{\ell -1} \gamma _{j{\bar{m}}^\prime +m^{\prime }} \right) \end{aligned}$$

for aggregating the latent variables. Figure 4 displays a cartoon representation of the mapping. This mapping is required for the following proposition.

Proposition 2

For all $m \in {\mathcal {M}}$, $\gamma _{1:m} \in {\mathcal {Y}}_m$ and $m^\prime < m$ such that ${\bar{m}}^\prime \, | \, {\bar{m}}$,

• (i) $m^{\prime } \in {\mathcal {M}}$ and $J_{m^{\prime }}(\gamma _{1:m}) \in {\mathcal {Y}}_{m^{\prime }}$.

• (ii) $J_{m^{\prime }}({\mathcal {Y}}_m ) = \mathbb {Y}[{\tilde{U}} , J_{m^{\prime }}(L^{m}_{1:m} )] \subset \mathbb {Y}[U^{{ m^{\prime }}}, L^{ m^{\prime } }_{1:m^{\prime }}] = {\mathcal {Y}}_{m^{\prime }}$, where ${\tilde{U}} = U^{m}- \sum _{j=1}^{\ell -1} L^{m}_{j{\bar{m}}^\prime }$.

Proof

See Appendix A.1. $\square$

To provide some intuition for Proposition 2, it is helpful to consider the bounds given in Example 4, noting that $3+1 = 2(1+1)$ and that the finite differences appearing in $L^{3}_1$ and $L^{3}_3$ for $m=3$ coincide with the finite differences in $L^{1}_1$ for $m=1$.

Proposition 2 says that for all $m \in {\mathcal {M}}$ it follows immediately that ${\mathcal {D}}(m) \subset {\mathcal {M}}$, where

$$\begin{aligned} {\mathcal {D}}(m) = \{ m^\prime \in {\mathbb {N}}_{0}; \, {\bar{m}}^\prime \mid {\bar{m}} \} \end{aligned}$$

(13)

consists of the integers $m^\prime$ such that ${\bar{m}}^\prime$ divides ${\bar{m}}$.

4.4 Asymptotic properties of the parameter space

In Sect. 4.2 it was shown that the parameter space may only shrink as more data are observed within a segment. Proposition 3 sheds further light upon the asymptotic properties of ${\mathcal {M}}$ and ${\mathcal {Y}}_m$ for all m.

Proposition 3

For $m \in {\mathbb {N}}_{0}$, suppose a sequence of latent variables $y_{-m+1}, \ldots , y_{n}$, and a sequence of observed data $x_{1}, \ldots , x_n$ are generated from model (1), assuming some density $f_m(\cdot \, |\, \theta )$ with support ${\mathbb {N}}_{0}$ or ${\mathbb {R}}^{+}$. As $n \rightarrow \infty$, for all $m^\prime >0$,

for all $r=1, \ldots , m^\prime$, with $\gamma ^{\prime }_{1:m^\prime } = J_{m^\prime }(\gamma _{1:m})$, and thus, almost surely, ${\mathcal {M}}(x_{1:n})$ converges to ${\mathcal {D}}(m)$ (13) and, for all $m^\prime \in {\mathcal {D}}(m)$, ${\mathcal {Y}}_{m^\prime }(x_{1:n}) = \mathbb {Y}[U^{m^\prime }, L^{m^\prime }_{1:m^\prime }]$ converges to $\{ \gamma ^{\prime }_{1:m^\prime } \}$.

Proof

See Appendix A.2. $\square$

Proposition 3 tells us that if some data are generated from model (1) for some $m>0$ and some initial latent variables $\gamma _{1:m}$, then almost surely, as the number of observations tends to infinity, ${\mathcal {M}}$ converges to ${\mathcal {D}}(m)$ and ${\mathcal {Y}}_{m^\prime }$ converges to a set containing a unique sequence, namely the transformation of $\gamma _{1:m}$ by $J_{m^\prime }$, for all $m^\prime \in {\mathcal {D}}(m)$. We note that the result shows that both the structure in ${\mathcal {M}}$ and the transformation identified in Proposition 2 are fundamental, and increasingly important as the length of a changepoint segment increases.

Within the changepoint detection framework, it is appealing that, the more data are observed within a segment, the more information the parameter space gives us about the nature of the dependence within the segment, so that a changepoint may be forced immediately upon observing some data generated from a different dependency structure.

Recall that in Sect. 3.1 it was argued that the segment parameters $\gamma _{1:m}$ may be considered as the unknown initial conditions of a process governed by a difference equation. From this point of view, Proposition 3 says that, asymptotically, the uncertainty on the initial conditions vanishes.

Fig. 5

The colours indicate the proportion of simulations for which $m^\prime \in {\mathcal {M}}$, denoted $Q( m^\prime \in {\mathcal {M}} \, | \, n, m, \theta )$, based on 50 simulations from the moving-sum segment model for negative binomial data given in Example 3 for $m=0, \ldots , 30$, $n=200, 400, 800$ and $\theta = 0.4, 0.8$

An experiment was performed to illustrate Proposition 3. For six different parameter configurations corresponding to different fixed values of n and $\theta$, and for all m in $\{ 0, \ldots , 30 \}$, we performed 50 simulations from the moving-sum segment model for negative binomial data given in Example 3 with $r=300$. For all $m^\prime \in \{ 0, \ldots , 30 \}$ we computed the proportion of simulations for which $m^\prime \in {\mathcal {M}}$, denoted $Q( m^\prime \in {\mathcal {M}} \, | \, n, m, \theta )$. Figure 5 displays the results of the experiment. As expected from Proposition 3, for all parameter choices it is apparent that $m^\prime \in {\mathcal {M}}$ with estimated probability 1 for all $m^\prime \in {\mathcal {D}}(m)$, and that $Q( m^\prime \in {\mathcal {M}} \, | \, n, m, \theta )$ tends to decrease as n increases for all $m^\prime \notin {\mathcal {D}}(m)$. Moreover, three other trends are worth mentioning. First, $Q( m^\prime \in {\mathcal {M}} \, | \, n, m, \theta )$ tends to increase as m increases for all $m^\prime \notin {\mathcal {D}}(m)$ given n and $\theta$. Second, it tends to be more likely for $m^\prime _1$ to be in ${\mathcal {M}}$ than for $m^\prime _2$ to be in ${\mathcal {M}}$ for all $m^\prime _1, m^\prime _2 \notin {\mathcal {D}}(m)$ such that $m^\prime _1 < m^\prime _2$. Third, one may observe that $Q( m^\prime \in {\mathcal {M}} \, | \, n, m, \theta )$ tends to increase as $\theta$ increases for all $m^\prime \notin {\mathcal {D}}(m)$ given all m and n.

5 Markov chain Monte Carlo changepoint inference

For the Bayesian changepoint model given in Sect. 2.2, the reversible jump Markov chain Monte Carlo (MCMC) algorithm (Green 1995), which is a Metropolis-Hastings algorithm suitable for target distributions of varying dimension, may be used to sample from the posterior distribution of the positions of an unknown number of changepoints. Four types of moves are considered to explore the support of the target distribution: shift of a randomly selected changepoint; change of a randomly chosen segment parameter; birth of a new changepoint chosen uniformly over the time period; and death of a randomly selected changepoint.

In this section, within the framework given in Green (1995), we propose a strategy to sample from the posterior distribution of changepoints when the moving-sum model defined in Sect. 2 is assumed for each segment. To address the challenges that the dimensions of the segment parameters are unknown and that the segment parameter space depends on the observed data within each segment, we exploit the analysis of the segment parameter space in Sect. 4.

5.1 Description of the sampler

Suppose that the latest particle of the sample chain consists of k changepoints, whose positions are $\tau _{1:k}$, and $(k+1)$ segment parameters. For segment j, recall from Sect. 3.2 that we assume the latent variable density parameter $\theta _{j}$ may be marginalised, and thus the segment parameters consist of the order of dependence $m_{j}$ and the initial latent variables $\gamma _{ j,:} \equiv \gamma _{ j,1:m_j} = (\gamma _{j,1}, \ldots , \gamma _{j,m_j})$. To explore the support of the target distribution, we propose the next element of the chain via one of the following moves.

5.1.1 Shift move

The shift move proposes to modify the position of one randomly chosen changepoint. The index j is uniformly chosen from $\{1, \ldots , k \}$, and a new position $\tau _j^{\prime }$ is uniformly sampled from $\{\tau _{j-1}+1, \ldots , \tau _{j+1}-1 \}$. The parameters $m_j$, $m_{j+1}$ and $\gamma _{j,:}$ are not modified and we replace $\gamma _{j+1,:}$ by $\gamma _{j+1,:}^{\prime } = S^{u}(\gamma _{j+1,:})$, with $u = \tau _j^{\prime } - \tau _j$.

As noted in Sect. 4.2, when the support of $f_m(\cdot \, |\, \theta )$ is bounded, the move may be rejected because the updated latent variables are unvalid: If the length of the j-th segment is reduced by the shift move, i.e. $\tau _j^{\prime } - \tau _j$ is negative, then it is guaranteed that $\gamma _{j,:}$ remains a valid sequence of initial latent variables but not that $\gamma _{j+1,:}^{\prime }$ is valid for the extended $(j+1)$-th segment; one the other hand, if $\tau _j^{\prime } - \tau _j$ is positive then the sequence $\gamma _{j+1,:}^{\prime }$ is valid but it must be checked that $\gamma _{j,:}$ is valid for the extended j-th segment.

5.1.2 Sampling a segment parameter

A segment j is uniformly chosen amongst the $k+1$ segments, and the corresponding segment parameters are changed: Either sample the initial latent variables conditional on the order of dependence that is left unchanged; or the order of dependence is sampled and thus the initial latent variables must be adapted. Here, the focus is on one segment only, and therefore we temporarily drop the segment index j from the notation as in Sect. 4, and the data observed within the segment are denoted by $x_1, \ldots , x_n$, where $n = \tau _j - \tau _{j-1}$.

5.1.3 An approximation to the posterior distribution of $\theta$

First, we consider an approximation to the posterior distribution of $\theta$ that will be useful to build proposals for m and $\gamma _{1:m}$. In the absence of knowledge on m and $\gamma _{1:m}$, motivated by computational considerations, it is interesting to consider the posterior distribution of $\theta$ conditional on $m=0$. When the data are assumed to be exchangeable, by conjugacy of the prior for $\theta$, the posterior distribution of $\theta$ is tractable,

$$\begin{aligned} {\hat{\pi }}( \theta \, | \, x_{1:n} ) = \pi (\theta \, | \, m=0, x_{1:n} ). \end{aligned}$$

Based on this approximation, a natural estimator for $\theta$ is

$$\begin{aligned} {\hat{\theta }} = \text {arg max}_{\theta } \, {\hat{\pi }}( \theta \, | \, x_{1:n} ). \end{aligned}$$

5.1.4 Updating $\gamma _{1:m}$ conditional on m

The move consists in proposing $\gamma _{1:m}^\prime$ conditional on m and $\gamma _{1:m}$. Recall from Sect. 4.1 that, conditional on the observed data, the support of the initial latent variables is ${\mathcal {Y}}_m$, and note that $\gamma _{1:m} \in {\mathcal {Y}}_m$ if and only if, for all $r=1, \ldots , m$, $\gamma _r \in {\mathcal {Y}}_m^r$ where

$$\begin{aligned} {\mathcal {Y}}_m^r = \left\{ \gamma _r \in {\mathcal {F}} \, | \, L^{m}_{r} \leqslant \gamma _r \leqslant U^{m} - \sum _{i \ne r} \gamma _{i} \right\} , \end{aligned}$$

if ${\mathcal {F}}$ is bounded and ${\mathcal {Y}}_m^r = {\mathcal {F}}$ if ${\mathcal {F}}$ is unbounded.

We consider two distinct scenarios based on the nature of the latent variables. If the latent variables are discrete valued, then $\gamma _{1:m}^\prime$ are proposed via Gibbs sampling. It follows from the discussion in Sect. 3.2 that, for all $r=1, \ldots , m$, the full conditional distribution of $\gamma _r$ is

$$\begin{aligned} \pi ( \gamma _r | x_{1:n}, \gamma _{-r}, m) \propto L( x_{1:n}, \gamma _{1:m} | m) \mathbb {1}_{ {\mathcal {Y}}_m^{r} }( \gamma _r), \end{aligned}$$

where $\gamma _{-r} = (\gamma _{1}, \ldots ,\gamma _{r-1}, \gamma _{r+1}, \ldots , \gamma _{m})$. If the domain of the latent variables is continuous, then Gibbs sampling is not possible in general; instead, for all $r=1, \ldots , m$, sample $\gamma _r^\prime$ from the distribution with step function density

$$\begin{aligned} q(\gamma _r | x_{1:n}, \gamma _{-r}, m) \propto \sum _{i=1}^N L( \gamma _{1:m}, y_{1:n} | m) \mathbb {1}_{[\gamma ^{(i)}, \gamma ^{(i+1)})}( \gamma _r), \end{aligned}$$

(14)

where $\gamma ^{(1)}< \cdots < \gamma ^{(N)}$ form an equally spaced grid on the largest interval ${\mathcal {Y}}_m^{r*} \subseteq {\mathcal {Y}}_m^r$ satisfying

$$\begin{aligned} \int _{ y_r \in {\mathcal {Y}}_m^{r*}} f_m(\gamma _r \, | \, {\hat{\theta }}) \text {d} \gamma _{r} \leqslant \eta . \end{aligned}$$

The greater $N>1$ and $0< \eta < 1$, the more accurate the step function approximation of the full conditional distribution of $\gamma _r^\prime$ in (14). The tuning parameters N and $\eta$ can be chosen via pilot runs investigating the trade-off between precision and computational cost.

5.1.5 Updating m and $\gamma _{1:m}$

When m is replaced by some $m^{\prime }$, it is necessary that $m^{\prime } \in {\mathcal {M}}$ for the move to have a positive probability of being accepted, and we must propose some revised initial latent variables $\gamma ^{\prime }_{1:m^{\prime }}$.

To sample $m^{\prime }$, whose full conditional distribution is not tractable in general, we consider a proposal distribution that relies on the following observations: the joint likelihood of the jumps $( \nabla x_t)$ defined in (3) is not tractable in general due the dependence of the jumps; yet, the jumps are identically distributed with mean $E[ \nabla x_t ] = 0$ and variance $V[ \nabla x_t ] = 2 g(\theta , m)$ for some function g that depends on the marginal distribution of the latent variables $f_m(\cdot \, |\, \theta )$; and therefore the approximation of the likelihood of the jumps

$$\begin{aligned} {\hat{L}}( \nabla x_{1:n} | {\hat{\theta }}, m) = \prod _{t} \phi \left( \nabla x_t | 0, 2 g({\hat{\theta }}, m) \right) , \end{aligned}$$

where $\phi (.| \mu , \sigma ^2)$ is the density function of the normal distribution with mean $\mu$ and variance $\sigma ^2$, is tractable and depends on m. The proposed order of dependence $m^\prime$ is sampled from the distribution with probability mass function

$$\begin{aligned} q(m^\prime | \nabla x_{1:n} ) \propto {\hat{L}}( \nabla x_{1:n} | {\hat{\theta }}, m^\prime ) \pi (m^\prime ) \mathbb {1}_{ {\mathcal {M}} }( m^\prime ) . \end{aligned}$$

Then, according to Sect. 5.1.2, $\gamma _{1:m^{\prime }}^\prime$ is proposed conditional on $m^\prime$ and $\gamma _{1:m^\prime }^{*}$, where

$$\begin{aligned} \gamma _{1:m}^{*} = \text {arg max}_{ \, \gamma _{1:m^\prime }^{*} \in {\mathcal {Y}}_{m^\prime } } \prod _{r} f_{m^\prime } \left( \gamma _r^{*} | {\hat{\theta }} \right) \end{aligned}$$

is an estimator of the initial latent variables in ${\mathcal {Y}}_{m^\prime }$ that can be derived efficiently but does not take into account the dependence of the data.

5.1.6 Death and birth moves

If a death move is proposed, an index j of one element of $\tau _{1:k}$ is uniformly chosen, and the corresponding changepoint is removed, resulting in $k^{\prime } = k-1$ changepoints with positions $\tau _{1:k^{\prime }}^{\prime } = \left( \tau _{1},\ldots , \tau _{j-1}, \tau _{j+1}, \ldots , \tau _{k} \right)$. The parameters corresponding to the segments that are not impacted by the move are re-indexed but kept unchanged, and it is natural to propose the parameters for the j-th segment resulting from $\tau _{1:k^{\prime }}^{\prime }$, namely $( m^{\prime }_j, \gamma _{j,:}^{\prime } )$, based on the parameters of either the original j-th or $(j+1)$-th segment. Specifically, let i be either the index j or $j+1$ with probability proportional to the length of the segment with index i, and then set $m_j^{\prime }$ to $m_i$, and $\gamma _{j,:}^{\prime }$ to $S^{(\tau _j - \tau _i)}(\gamma _{i,:})$. Note that the death move may then be seen as the extension of one of the segments on either side of the deleted changepoint.

The above death move may be reversed by the following birth move. Draw $\tau _j^{\prime }$ uniformly from $\{2, \ldots , T\} \setminus \tau _{1:k}$, and obtain $\tau _{1:k^{\prime }}^{\prime }$ by inserting $\tau _j^{\prime }$ into $\tau _{1:k}$ at the j-th position, resulting in $k^{\prime } = k + 1$ changepoints. Let i be either the index j or $j+1$ with probability proportional to $\tau _{i}^\prime - \tau _{i-1}^\prime$. Set $m_i^{\prime }$ to $m_j$ and $\gamma _{i,:}^{\prime }$ to $S^{(\tau _i^{\prime } - \tau _j^{\prime })}(\gamma _{j,:} )$, and finally propose the segment parameters of the new segment using the approach given in Sect. 5.1.2.

5.2 Sampler initialisation

To speed-up the convergence of the sampler for the moving-sum changepoint model, the sample chain is initialised as follows: the changepoint parameters are set to be the changepoint estimates corresponding to the standard changepoint model; and, for each segment, the order of dependence is set to 0. Hence, the sampler begins with a sensible positioning of the changepoints obtained at a limited computational cost.

5.3 Parameter estimation

To give an account of the posterior distribution of changepoints, following Green (1995), it is natural to consider the posterior marginal distribution of the number of changepoints k, the posterior distribution of the changepoint positions $\tau _{1:k}$ conditional on k, and the posterior distribution of the orders of dependence $m_{1:k+1}$ conditional on $(k, \tau _{1:k})$. However, for some applications such as cyber security where timely investigations rely on succinct representations of the most probable changepoints, it will also be of interest to report a point estimate $({\hat{k}}, {\hat{\tau }}_{1:{\hat{k}}}, {\hat{m}}_{1:{\hat{k}}+1})$ for the parameters $(k, \tau _{1:k}, m_{1:k+1})$. In this article, the point estimate $({\hat{k}}, {\hat{\tau }}_{1:{\hat{k}}}, {\hat{m}}_{1:{\hat{k}}+1})$ is defined as follows: ${\hat{k}}$ is the MAP number of changepoints; ${\hat{\tau }}_{1:{\hat{k}}}$ are the MAP changepoint positions of dimension ${\hat{k}}$; and ${\hat{m}}_{1:{\hat{k}}+1}$ are the MAP orders of dependence conditional on MAP changepoint parameters $({\hat{k}}, {\hat{\tau }}_{1:{\hat{k}}})$.

5.4 Validating the estimated orders of dependence

Appendix C details an importance sampling approach to estimating the posterior distribution of the order of dependence within a segment. Conditional on MAP changepoint parameters obtained via MCMC, it can be used to validate the MAP orders of dependence.

6 Simulation study

This section describes a simulation study that demonstrates the benefits of the moving-sum changepoint model in comparison to changepoint models that assume the data are exchangeable within segments, namely the standard Bayesian changepoint model (2) and PELT (Killick et al. 2012), and models that detect abrupt mean changes in normal data subject to local fluctuations and autocorrelated noise, namely DeCAFS (Romano et al. 2021) and WCMgSa (Cho and Fryzlewicz 2021).

6.1 Synthetic data

Different scenarios were assumed to sample time series of length $T \in \{1200, 3200, 5200, 7200, 9200 \}$ from the moving-sum changepoint model with segment model defined in Example 1: within each segment, the data are m-dependent and marginally normally distributed with mean $\mu$ and variance $\sigma ^2$ for some segment specific parameters m, $\mu$ and $\sigma ^2$. Different scenarios were considered for the number of changepoints $k\in \{0, 1, 3, 5, 7, 9\}$, and changepoint positions $\tau _{1:k}$ were specified such that, for all $j=1, \ldots , k$, $\tau _j = \lfloor jT/(k+1)\rfloor + u_j$ for some $u_j$ drawn uniformly from $\{- \lfloor T/(2k+2) \rfloor , \ldots , \lfloor T/(2k+2) \rfloor \}$, so that segment lengths may be uneven. The orders of dependence for each segment were sampled independently from $\text {Geometric}(\nu )$ for some $0 \leqslant \upsilon \leqslant 1$; let ${\bar{\upsilon }} = (1-\upsilon )/\upsilon$ denote the expected order of dependence for each segment. The segment mean parameters are set such that, for all $j=1, \ldots , k+1$, $\mu _j = \mu$ if j is odd and $-\mu$ otherwise, for some $\mu \in {\mathbb {R}}$. The segment parameters $\sigma ^{-2}_1, \ldots , \sigma ^{-2}_{k+1}$ were sampled independently from $\text {Gamma}(\alpha _0, 100)$ for some $\alpha _0>0$. A grid of parameters such that $\upsilon \in \{1, 0.33, 0.2, 0.1, 0.06\}$, $\mu \in \{0.5, 1, 2, 4, 8\}$ and $\alpha _0 \in \{1, 5, 10, 25, 50, 75\}$ was considered for the experiments. For each scenario, 10 simulations were performed.

6.2 Model comparison

For each simulation, different models were used to infer changepoint estimates from the data: the moving-sum changepoint model assuming different hyperparameters, the standard changepoint model (2), DeCAFS, PELT with different penalties, and WCMgSA.

For the moving-sum changepoint model, the data within segments are assumed to follow the model given in Example 1 with $\alpha = \alpha _0$, $\beta = 100$ and $\lambda = 0.05 \beta / \alpha$; and the prior for the orders of dependence is assumed to be $\text {Geometric}(\rho )$ for $\rho \in \{0.01, 0.1, 0.5\}$. Ten independent sample chains of size 20000, after a burn-in of size 10000, were obtained via the MCMC algorithm described in Sect. 5 with tuning parameters $N=100$ and $\eta =0.99$ for the proposal of the initial latent variables (14). Changepoint estimates obtained from each independent sample chain, as described in Sect. 5.3, will be compared to assess the convergence of the sampler. Moreover, for the standard Bayesian changepoint model, changepoint estimates are obtained as for the moving-sum changepoint model with the only difference that, for each segment, we fix the order of dependence $m=0$, ensuring the data are assumed to be exchangeable. For PELT, we used the default implementation in the R package changepoint (Killick and Eckley 2014) with the MBIC penalty rescaled by a constant $\phi \in \{0.5, 1, 1.5\}$; as the penalty increases, more evidence is required from the data to flag changepoints. Finally, for DeCAFS and WCMgSA, changepoints were estimated with the default implementations described in Romano et al. (2021) and in Cho and Fryzlewicz (2021), respectively.

To compare changepoint estimations, we use the F1 score. A changepoint $\tau$ is said to be detected if there is an estimated changepoint ${\hat{\tau }}$ such that $|\tau - {\hat{\tau }}| \leqslant \epsilon$ for some error tolerance of size $\epsilon = 5$. Given some changepoints, the F1 score of the changepoint estimates is

$$\begin{aligned} F1 = \frac{2 P R}{ P + R} \in [0, 1], \end{aligned}$$

where R and P denote the recall, the proportion of simulated changes that are detected, and the precision, the proportion of detected changes that are correct, respectively. The greater the F1 score, the better the estimation. To compare the three changepoint models of interest, for each simulation the F1 score was computed for each estimation of the simulated changepoints $(k, \tau _{1:k})$.

6.3 Sampler convergence

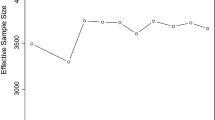
Recall from Sect. 6.1 that ten independent sample chains for the moving-sum changepoint model were obtained via the proposed MCMC algorithm for each time series analysed. Figure 6 displays the variance of the MAP number of changepoints obtained for the moving-sum model computed using the first M elements of the sample chains for a collection of scenarios; results are similar for other scenarios. As M increases, the variances tend to 0, suggesting the samplers converge; a burn-in of size 10000 seems adapted to all scenarios considered. The rate of convergence tends to decrease with the number of observations T and with the expected order of dependence ${\bar{v}}$ for each segment, but tends to increase with the number of changepoints k.

Moreover, to illustrate the benefits of the sampler initialisation proposed in Sect. 5.2 we assess the convergence of the sampler for one randomly selected simulation with $k=7$. Following Sect. 5.2, the ten independent sample chains for the moving-sum changepoint model were initialised with the changepoint estimates corresponding to the standard changepoint model. For comparison purposes only, twenty extra independent sample chains, initialised with randomly selected changepoint parameters such that $0 \leqslant k \leqslant 20$, were computed for the moving-sum model, as described in Sect. 6.2. Figure 7 displays the thirty independent sample chains for the number of changepoints k. All sample chains converge to the same number of changepoints, namely $k=7$, and the ten sample chains corresponding to our proposed initialisation, indicated in blue, converge faster, illustrating the benefits of our proposed sampling strategy.

Fig. 6

Variance of the MAP number of changepoints for the moving-sum model computed using the first M elements of sample chains obtained via the proposed MCMC algorithm for varying number of observations T, number of changepoints k and expected order of dependence ${\bar{\upsilon }}$ for each segment

Fig. 7

Thirty independent sample chains for the number of changepoints, obtained via the MCMC algorithm for the moving-sum changepoint model, for one selected time series with $k=7$. In blue: ten sample chains initialised with the proposed initialisation strategy. In grey: twenty sample chains initialised with randomly selected changepoint parameters such that $0 \leqslant k \leqslant 20$

Fig. 8

Average runtime in seconds per iteration for the MCMC algorithm for the moving-sum changepoint model for varying number of observations T, number of changepoints k and expected order of dependence ${\bar{\upsilon }}$ for each segment

Fig. 9

Average F1 scores of changepoint estimates for the changepoint models of interest (STD for the standard changepoint model (2); MV$\rho$ for the moving-sum changepoint model with hyperparameter $\rho$ for orders of dependence; PELT$\phi$ for PELT with MBIC penalty scaled by $\phi$; WCM for WCMgSa; and DeCAFS) for a collection of scenarios considered in the study

6.4 Runtime

The moving-sum changepoint model is computationally more demanding than the standard changepoint model due to the need to propose orders of dependence and initial latent variables. For our Python implementations, which could be optimised, the runtime is on average 8 times greater for the moving-sum model than for the standard changepoint model, but this could greatly vary for different implementations. Here it is of interest to demonstrate how runtimes are affected by different model parameters. Figure 8 displays the average runtime of an iteration of the MCMC algorithm for a collection of scenarios for the moving-sum changepoint model. The runtime increases linearly with the number of observations T and with the expected order of dependence ${\bar{v}}$ for each segment, but does not tend to increase with the number of changepoints k. Hence, settings with large segments where the order of dependence is high may be computationally demanding.

6.5 Results

Figure 9 displays the average F1 score of the changepoint models of interest for different scenarios considered in the study. The corresponding average precisions and recalls are displayed in Figs. 11, 12. For each scenario, the moving-sum model outperforms the other changepoint models of interest. Similar results for each $\rho$ demonstrate the model is robust to the choice of $\rho$. Results show that a decrease in performance can be observed when $\mu$ is low, that is when the magnitude of mean changes is small; when $\sigma _0$ is low, meaning the variance of the data is large; and when $\upsilon$ is low, that is when the mean and variance of orders of dependence is high.

The standard changepoint model and PELT assume data are exchangeable within segments, and consequently their segmentations of the simulated data are not satisfactory. In particular, F1 scores decrease as the orders of dependence increase because more changepoints are fitted than necessary. For PELT, as the penalty increases, F1 scores tend to increase because more evidence is required from the data to flag changepoints. For the standard changepoint model, F1 scores are satisfactory when $\upsilon =1$, that is when simulated data are exchangeable within segments.

The performances of DeCAFS and WCMgSA, which admit data may not be exchangeable within segments, tend to be relatively good when $k=0$, but they tend to deteriorate as the number of segments increases. In particular, for $k>0$, F1 scores decrease as $\upsilon$ or $\sigma _0$ decrease, because DeCAFS and WCMgSA assume that the dependence structure of the data is the same for each segment and that the mean of the data, but not their variance, change from one segment to the next.

Results demonstrate the moving-sum changepoint model may capture various temporal dynamics of m-dependent data within segments that challenge the other changepoint models considered in the simulation study.

Fig. 10

Daily prices of the stock SBRY.L from $20^{\text {th}}$ February 2006 to $16^{\text {th}}$ November 2010. Vertical lines indicate estimated changepoints for three models: moving-sum, standard and DeCAFS changepoint models. Numbers in red indicate the MAP order of dependence m for each segment for the moving-sum changepoint model

7 Applications

Two applications are considered to demonstrate the benefits of the proposed changepoint model for non-exchangeable data: computer network monitoring via change detection in count data, and detection of breaks in daily prices of a stock.

For each application, the moving-sum changepoint model is compared with the standard changepoint model for exchangeable data within segments (2). For each model, changepoint estimates from five independent samples of size $50 \, 000$ were obtained via the MCMC algorithm proposed in Sect. 5, with a burn-in of $10 \, 000$ iterations; changepoint estimates were identical for all independent chains, suggesting the sampler converged. Moreover, since DeCAFS is not suitable for count data (Romano et al. 2021), the moving-sum model is compared with DeCAFS for the daily stock prices only.

7.1 Change detection in enterprise-wide computer network traffic

A cyber attack typically changes the behaviour of the target network. Therefore, to detect the presence of a network intrusion, it can be informative to monitor for changes in computer network traffic.

Turcotte et al. (2017) presents a data set summarising 90 days of network events collected from the Los Alamos National Laboratory enterprise network, which is available online at http://lanl.ma.ic.ac.uk/data/2017/. Each recorded network event gives the start time and the duration of a transfer of packets from a network device to another. In addition, a destination port is associated to each network event, which describes the purpose of the transfer of packets: for example, web, email, remote login or file transfer. For the purpose of this article, events that do not correspond to the 100 most recurrent destination ports in the data were discarded, thereby restricting the analysis to the most common network activities.

It can be informative to monitor for temporal changes in counts of network events. For demonstration purposes, we consider the data $x_{1}, \ldots , x_{T}$ where, for all t, $x_t$ denotes the number of network events that are in progress across the network during the t-th second between 10:00 and 10:20 on day 22 of the data collection period. The data are displayed in Fig. 1. It is of interest to detect temporal changes in the distribution of $x_{1}, \ldots , x_{T}$.

Two models are used to estimate changepoints for the network data: the moving-sum and the standard changepoint model. For each changepoint model, the segment model for negative binomial data defined in Example 3 is assumed with $\alpha =3$, $\beta =1$ and $r=3000$. For each segment, $m \sim \text {Geometric}(0.1)$ for the moving-sum model, and $m=0$ for the standard changepoint model.

Figure 1 displays the changepoint estimates for each model, and the MAP segment orders of dependence for the moving-sum changepoint model. No labels are available to indicate the optimal segmentation for these data, but we argue that the moving-sum model gives a more suitable segmentation of the data than the standard changepoint model. Both changepoint models detect clear discontinuities, such as the ones observed near the 420th and 880th s, that correspond to behavioural changes of the network that are sufficiently drastic that cyber-analysts may want to investigate whether they correspond to malicious activities. However, local temporal correlations and small fluctuations, such as the ones between the 100th and 380th s, and the one between the 500th and 550th s, which is characterised by a small decrease quickly followed by a symmetric increase in the mean, give rise to changepoints for the standard model but not the moving-sum changepoint model. Such local temporal correlations and small fluctuations may be caused by normal temporal dynamics of the network behaviour that are less of interest to cyber-analysts, for example standard transfers of large data across networks that involve dividing the data into batches, routing and queueing steps, which may lead to temporal correlations in traffic volumes. Hence, the proposed changepoint model results in a segmentation of the data that is more adapted to network monitoring.

7.2 Change detection in financial time series

For economists and investors, it can be of interest to detect changepoints in financial time series, such as daily prices of a stock. Changes can be monitored to assess the impact of economic policies, or can indicate shifts in market behaviours. It is often reductive to assume the data are exchangeable within segments.

For demonstration purposes, this article considers the price of the stock Sainsbury plc (SBRY.L). For all t, let $x_t$ be the closing price of the stock SBRY.L at the t-th day between $20{\text {th}}$ February 2006 to $16{\text {th}}$ November 2010. The data $x_1, \ldots , x_{T}$, which are available online at finance.yahoo.com, are displayed in Fig. 10. The stock data are subject to changes that may be associated with takeover bids and the 2008 financial crisis: on 2nd February 2007 major private equity groups reveal they are considering a bid for Sainsbury plc; on 5th November 2007 takeover bids are abandoned in the wake of the global credit crunch; November 2008 ends a period of major uncertainty in financial markets; in August 2009 major decisions to develop the business are announced, including acquisitions of new shops and important increase in workforce; and, on 7th July 2010 a possible takeover bid is announced by Qatari investors.

Three models are considered for the data: the moving-sum changepoint model, the standard changepoint model, and DeCAFS using an inflated BIC beta penalty as suggested in Romano et al. (2021). For the moving-sum and the standard changepoint models, the segment model for normal data defined in Example 1 is assumed with $\alpha =7$, $\beta =1$, $\mu _0=350$ and $\lambda =1$. For each segment, $m \sim \text {Geometric}(0.1)$ for the moving-sum model, and $m=0$ for the standard changepoint model.

Figure 10 displays the changepoint estimates for each model of interest. All models detect changes associated with takeover bids on 2nd February 2007 and 5th November 2007. In contrast with the standard changepoint model, the moving-sum changepoint model captures temporal dynamics of the stock price, and therefore market trends are not unnecessarily segmented. For example, smooth drifts of the stock price, such as the ones before 2nd February 2007 and between 5th November 2007 and 26th November 2008, give rise to multiple changepoints for the standard model but not for the moving-sum model. Moreover, the proposed model detects changes in the mean as well as changes in the level of dependency of the data, so that it detects both shifts in price levels and changes in the temporal dynamics of prices, which are both of interest to financial analysts. In contrast with DeCAFS, the moving-sum changepoint model detects the change associated with the takeover bid on 7th July 2017, and perhaps less importantly, the change in August 2009 associated with business developments after the financial crisis. The estimated orders of dependence for the moving-sum model vary greatly across segments, suggesting prices have been subject to distinct market dynamics. In particular, the order of dependence decreases drastically in November 2008, marking the end of strong market dynamics associated with the 2008 financial crisis, and it increases again in July 2017 as the announcement of a takeover bid leads to increased market activity. MAP orders of dependence obtained via MCMC were validated with the method proposed in Sect. 5.4 conditional on MAP changepoint parameters obtained via MCMC: estimates are identical for each segment except for the second one where the importance sampling approach gives 39 instead of 38.

8 Discussion

Standard changepoint models, which typically assume data are exchangeable within each segment, may be inadequate when data are subject to local temporal dynamics, often resulting in many more changepoints being fitted than is preferable. This article proposes a novel changepoint model that relaxes the assumption of exchangeable data within segments, reducing the excess fitting of changepoints.

The proposed model supposes that within each segment the data are m-dependent and identically distributed conditional on some parameter $\theta$, where both $\theta$ and $m \geqslant 0$ are unknown and vary between segments. The proposed model is suitable for count data, which is rarely the case for changepoint models robust to non-exchangeable data. The benefits of the model are demonstrated on both synthetic and real data.

Future work could consider a model extension relaxing the assumption that both m and $\theta$ change at each changepoint; changepoint parameters could be augmented with indicator vectors specifying for each changepoint if only m, only $\theta$ or both m and $\theta$ change. The MCMC algorithm would need to be adapted to sample indicator vectors alongside changepoint parameters.

Other future work could also consider building alternative segment models that are robust to other possible dependence structures within segments.

Appendices

Appendix

Proofs

1.1 Proof of Proposition 2

• (1) For all n and for all reals $z_1, z_2, \ldots , z_n$,

  $$\begin{aligned} \min \{ z_1, \ldots , z_n \} = -\max \{ -z_1, \ldots , -z_n \}, \end{aligned}$$

  and therefore $U^{m} = x_1 - L^{m}_{m+1}$ for all m by definition (10). Moreover, for all $\ell$ and for all reals $(z_{ij})$,

  $$\begin{aligned}{} & {} \sum _{i = 1}^{\ell } \max \{0, z_{i1}, z_{i2}, z_{i3}, \ldots \} \\{} & {} \quad \geqslant \max \left\{ 0, z_{11}, z_{11} + z_{21}, z_{11} + z_{21} + z_{31}, \ldots , \sum _j \sum _{i=1}^{\ell } z_{ij} \right\} , \end{aligned}$$

  and therefore, with $\ell$ such that $m+1 = \ell (m^{\prime }+1)$ and using the notations introduced in (10), for all $r=1, \ldots , m^{\prime }+1$,

  $$\begin{aligned}{} & {} \sum _{j=0}^{\ell -1} L^{m}_{j(m^{\prime }+1)+r} \\{} & {} \quad = \sum _{j=0}^{\ell -1} \max \left\{ 0, \vartriangle x_{j(m^{\prime }+1)+r} , \ldots \sum _{q = 0 }^{\kappa _{j{\bar{m}}^{\prime }+r}} \vartriangle x_{(q\ell +j)(m^{\prime }+1)+r} \right\} \\{} & {} \quad \geqslant L^{m^{\prime }}_r. \end{aligned}$$

  As a result, for all $\gamma _{1:m}$ such that $U^{m} \geqslant \sum _r \gamma _r$ and $\gamma _r \geqslant L^{m}_r$ for all $r=1, \ldots , m$, that is $\gamma _{1:m} \in {\mathcal {Y}}_m$, it follows that

  $$\begin{aligned} U^{m^{\prime }} = x_1 - L^{m^{\prime }}_{m^{\prime }+1}&\geqslant x_1 - \sum _{j=0}^{\ell -1} L^{m}_{j(m^{\prime }+1) + (m^{\prime }+1)} \\&= U^{m} - \sum _{j=0}^{\ell -2} L^{m}_{(j+1)(m^{\prime }+1)} \\&\geqslant \left( \sum _{r=1}^{m} \gamma _r \right) - \sum _{j=0}^{\ell -2} \gamma _{(j+1)(m^{\prime }+1)} \\&= \sum _{r=1}^{m^{\prime }} \gamma ^{\prime }_r \end{aligned}$$

  and $\gamma ^{\prime }_r \geqslant \sum _j L^{m}_{j(m^{\prime }+1) + r} \geqslant L^{m^{\prime }}_r$ for all $r= 1, \ldots , m^{\prime }$, that is $\gamma ^{\prime }_{1:m^{\prime }} \in {\mathcal {Y}}_{m^{\prime }}$.

• (2) Follows from (1).

• (3) It is immediate from the definition of $J_{m^{\prime }}$ that the transformation between $\gamma _{1:m}$ and $( \gamma ^{\prime }_{1:m^{\prime }}, \gamma _{(m^{\prime }+1):m} )$ is one-to-one and its Jacobian is equal to 1. Now, for all $\gamma ^{\prime }_{1:m^{\prime }} \in J_{m^{\prime }}({\mathcal {Y}}_m)$, it is of interest to characterise the set of $\gamma _{(m^{\prime }+1):m}$ such that $(\gamma _{1:m^{\prime }}, \gamma _{(m^{\prime }+1):m}) \in {\mathcal {Y}}_m$, with

  $$\begin{aligned} \gamma _r = \gamma ^{\prime }_r -\sum _{j=1}^{\ell -1} \gamma _{j(m^{\prime }+1)+r} \end{aligned}$$

  for all $r=1, \ldots , m^{\prime }$. Recall that ${\mathcal {Y}}_m = \mathbb {Y}[U^{m}, L^{m}_{1:m}]$, where $\mathbb {Y}$ is defined in (11), and observe that

  $$\begin{aligned} \gamma ^{\prime }_r - L^{m}_r \geqslant \gamma ^{\prime }_r - \gamma _r = \sum _{j=1}^{\ell -1} \gamma _{j(m^{\prime }+1)+r} \end{aligned}$$

  for all $r=1, \ldots , m^{\prime }$. As a result, the set of interest consists of the $\gamma _{(m^{\prime }+1):m}$ such that

  $$\begin{aligned} \left( \gamma _{j(m^{\prime }+1) + r} \right) _{j>0} \in \mathbb {Y}\left[ \gamma ^{\prime }_r - L^{m}_r, \, ( L^{m}_{j(m^{\prime }+1) + r} )_{j>0} \right] \end{aligned}$$

  for all $r=1, \ldots , m^{\prime }$ and

  $$\begin{aligned} \left( \gamma _{j(m^{\prime }+1)} \right) _{j>1} \in \mathbb {Y} \left[ U^{m} - \sum _r \gamma ^{\prime }_r, \, (L^{m}_{j(m^{\prime }+1)})_{j>1} \right] . \end{aligned}$$

1.2 Proof of Proposition 3

Note that (3) and (4) imply that $\vartriangle x_t = - \triangledown ^{(m+1)} y_{t+1}$ for all t. Hence, by definition of the bounds in (10), for all n,

$$\begin{aligned}{} & {} L^{m^{\prime }}_r(x_{1:n}) \nonumber \\ {}{} & {} \quad = \max \left\{ 0, -\triangledown ^{(m+1)} y_{r+1} , \ldots , - \sum \limits _{q = 0 }^{\kappa _{r}(n)} \triangledown ^{(m+1)} y_{q(m^{\prime }+1)+r+1} \right\} ,\nonumber \\ \end{aligned}$$

(15)

with $\kappa _r(n)$ defined to be the largest $q\in {\mathbb {N}}_{0}$ such that $q(m^{\prime }+1)+r+1 \leqslant n$, for all r.

If $m^{\prime }\in {\mathcal {D}}(m)$, that is there is some $\ell >0$ such that $m+1 = \ell (m^{\prime }+1)$, then for all q,

$$\begin{aligned} \triangledown ^{(m+1)} y_{q(m^{\prime }+1)+r+1} = y_{q(m^{\prime }+1)+r+1} - y_{ (q-\ell )(m^{\prime }+1)+r+1}, \end{aligned}$$

and we note that $q(m^{\prime }+1) + r + 1= (q + \ell - \ell )(m^{\prime }+1) + r + 1$. Therefore

$$\begin{aligned} L^{m^{\prime }}_r(x_{1:n})&= \left( \sum _{q=0}^{\ell -1} y_{(q-\ell )(m^{\prime }+1) + r + 1} \right) - B_n = \gamma ^{\prime }_r - B_n, \end{aligned}$$

where

$$\begin{aligned} B_n= \min \left\{ \sum _{q=j-\ell }^{j-1} y_{q(m^{\prime }+1) + r + 1} , \quad j = 0, \ldots , \kappa _r(n) \right\} \end{aligned}$$

is a random variable that converges almost surely to 0, since it is non-increasing and converges in probability to the infimum of the support of $f_m(\, \cdot \, | \theta )$ which is 0. Hence $L^{m^{\prime }}_r(x_{1:n})$ converges almost surely to $\gamma ^{\prime }_r$.

However if $m^{\prime }\notin {\mathcal {D}}(m)$ then for all $q_1, q_2 \in \{0, \ldots , \kappa _r(n) \}$, we have that $q_1(m^{\prime }+1)+r+1 = q_2(m^{\prime }+1)+r+1$ if and only if $q_1 = q_2$, so that no cancellations occur in (15). Hence $L^{m^{\prime }}_r(x_{1:n})$, which is non-decreasing, converges almost surely to the supremum of the support of $f_m(\, \cdot \, | \theta )$ which is $\infty$.

Finally, the results on the upper bound then follow from the observation that

$$\begin{aligned} U^{m^{\prime }}(x_{1:n})= & {} x_1 - L^{m^{\prime }}_{m^{\prime }+1}(x_{1:n}) \\= & {} \left( \sum _{r=1}^{m^{\prime }} \gamma ^{\prime }_r \right) + \left( \sum _{q=0}^{\ell -1} y_{(q-\ell + 1)(m^{\prime }+1) + 1} \right) \\{} & {} - L^{m^{\prime }}_{m^{\prime }+1}(x_{1:n}). \end{aligned}$$

Fig. 11

Average precisions of changepoint estimates for the changepoint models of interest (STD for the standard changepoint model (2); MV$\rho$ for the moving-sum changepoint model with hyperparameter $\rho$ for orders of dependence; PELT$\phi$ for PELT with MBIC penalty scaled by $\phi$; WCM for WCMgSa; and DeCAFS) for a collection of scenarios considered in the study

Fig. 12

Average recalls of changepoint estimates for the changepoint models of interest (STD for the standard changepoint model (2); MV$\rho$ for the moving-sum changepoint model with hyperparameter $\rho$ for orders of dependence; PELT$\phi$ for PELT with MBIC penalty scaled by $\phi$; WCM for WCMgSa; and DeCAFS) for a collection of scenarios considered in the study

Simulation study

Figures 11, 12 display the average precisions and recalls of the changepoint estimations that correspond to the F1 scores displayed in Fig. 9, which are discussed in Sect. 6.5.

Order of dependence estimation

The sampling algorithm proposed in Sect. 5 can be used to estimate changepoint parameters as well as orders of dependence within segments. This section proposes an approach to estimate the posterior distribution of the order of dependence within a segment, which may be used to validate MCMC based estimations of orders of dependence conditional on MAP changepoint parameters.

Let $x_1, \ldots , x_n$ be some data observed within a single segment, assuming the moving-sum model defined in Sect. 2.1 for some $m \geqslant 0$ and $\theta$. The posterior density of m, $\pi (m| x_{1:m}) \propto \pi (m) I_m {\textbf{1}}_{{\mathcal {M}}}(m)$, where

$$\begin{aligned} I_m = \int _{ \gamma _{1:m} \in {\mathcal {Y}}_m } L(x_{1:n}, \gamma _{1:m} \mid m) \text {d} \gamma _{1:m} \end{aligned}$$

is not tractable in general. However, an importance sampling estimate of $I_m$ can be computed for each m, as described below, to obtain an approximation to the posterior density of m. Given N samples $\gamma _{1:m}^{(1)}, \ldots , \gamma _{1:m}^{(N)}$ from the distribution with density

$$\begin{aligned} q(\gamma _{1:m}) = \prod _{\ell =1}^m f_m( \gamma _\ell \mid {\hat{\theta }}), \end{aligned}$$

where ${\hat{\theta }}$ is the MAP estimate of $\theta$, which is tractable by conjugacy of $\theta$,

$$\begin{aligned} {\hat{I}}_m = \frac{1}{N}\sum _{i=1}^N \frac{ L \left( x_{1:n}, \gamma _{1:m}^{(i)} \mid m \right) }{q \left( \gamma _{1:m}^{(i)} \right) } \end{aligned}$$

is an estimator of $I_m$ that converges almost surely to $I_m$ as N tends to infinity. The posterior density of m can be estimated by the density

$$\begin{aligned} {\hat{\pi }}(m| x_{1:m}) \propto \pi (m) {\hat{I}}_m {\textbf{1}}_{{\mathcal {M}}}(m). \end{aligned}$$