Hierarchical sparse Cholesky decomposition with applications to high-dimensional spatio-temporal filtering

Abstract

Spatial statistics often involves Cholesky decomposition of covariance matrices. To ensure scalability to high dimensions, several recent approximations have assumed a sparse Cholesky factor of the precision matrix. We propose a hierarchical Vecchia approximation, whose conditional-independence assumptions imply sparsity in the Cholesky factors of both the precision and the covariance matrix. This remarkable property is crucial for applications to high-dimensional spatiotemporal filtering. We present a fast and simple algorithm to compute our hierarchical Vecchia approximation, and we provide extensions to nonlinear data assimilation with non-Gaussian data based on the Laplace approximation. In several numerical comparisons, including a filtering analysis of satellite data, our methods strongly outperformed alternative approaches.

1 Introduction

Symmetric positive-definite matrices arise in spatial statistics, Gaussian-process inference, and spatiotemporal filtering, with a wealth of application areas, including geoscience (e.g., Cressie 1993; Banerjee et al. 2004), machine learning (e.g., Rasmussen and Williams 2006), data assimilation (e.g., Nychka and Anderson 2010; Katzfuss et al. 2016), and the analysis of computer experiments (e.g., Sacks et al. 1989; Kennedy and O’Hagan 2001). Inference in these areas typically relies on Cholesky decomposition of the positive-definite matrices. However, this operation scales cubically in the dimension of the matrix, and it is thus computationally infeasible for many modern problems and applications, which are increasingly high-dimensional.

Countless approaches have been proposed to address these computational challenges. Heaton et al. (2019) provide a recent review from a spatial-statistics perspective, and Liu et al. (2020) review approaches in machine learning. In high-dimensional filtering, proposed solutions include low-dimensional approximations (e.g., Verlaan and Heemink 1995; Pham et al. 1998; Wikle and Cressie 1999; Katzfuss and Cressie 2011), spectral methods (e.g., Wikle and Cressie 1999; Sigrist et al. 2015), and hierarchical approaches (e.g., Johannesson et al. 2003; Li et al. 2014; Saibaba et al. 2015; Jurek and Katzfuss 2021). Operational data assimilation often relies on ensemble Kalman filters (e.g., Evensen 1994; Burgers et al. 1998; Anderson 2001; Evensen 2007; Katzfuss et al. 2016, 2020d), which represent distributions by samples or ensembles.

Perhaps the most promising approximations for spatial data and Gaussian processes implicitly or explicitly rely on sparse Cholesky factors. The assumption of ordered conditional independence in the popular Vecchia approximation (Vecchia 1988) and its extensions (e.g., Stein et al. 2004; Datta et al. 2016; Guinness 2018; Katzfuss and Guinness 2021; Katzfuss et al. 2020a, b; Schäfer et al. 2021a) implies sparsity in the Cholesky factor of the precision matrix. Schäfer et al. (2021b) use an incomplete Cholesky decomposition to construct a sparse approximate Cholesky factor of the covariance matrix. However, these methods are not generally applicable to spatiotemporal filtering, because the assumed sparsity is not preserved under filtering operations.

Here, we relate the sparsity of the Cholesky factors of the covariance matrix and the precision matrix to specific assumptions regarding ordered conditional independence. We show that these assumptions are simultaneously satisfied for a particular Gaussian-process approximation that we call hierarchical Vecchia (HV), which is a special case of the general Vecchia approximation (Katzfuss and Guinness 2021) based on hierarchical domain partitioning (e.g., Katzfuss 2017; Katzfuss and Gong 2020). We show that the HV approximation can be computed using a simple and fast incomplete Cholesky decomposition.

Due to its remarkable property of implying a sparse Cholesky factor whose inverse has equivalent sparsity structure, HV is well suited for extensions to spatiotemporal filtering; this is in contrast to other Vecchia approximations and other spatial approximations relying on sparsity. We provide a scalable HV-based filter for linear Gaussian spatiotemporal state-space models, which is related to the multi-resolution filter of Jurek and Katzfuss (2021). Further, by combining HV with a Laplace approximation (cf. Zilber and Katzfuss 2021), our method can be used for the analysis of non-Gaussian data. Finally, by combining the methods with the extended Kalman filter (e.g., Grewal and Andrews 1993, Ch. 5), we obtain fast filters for high-dimensional, nonlinear, and non-Gaussian spatiotemporal models. For a given formulation of HV, the computational cost of all of our algorithms scales linearly in the state dimension, assuming sufficiently sparse temporal evolution.

This paper makes several important contributions. First, it succinctly summarizes and proves conditional-independence conditions that ensure that particular elements of the Cholesky factor and its inverse vanish; while some of these conditions have been known before, we present them in a unified framework and provide precise proofs. Second, we describe a new version of the Vecchia approximation and demonstrate that it satisfies all of the conditional-independence conditions. Third, we show how the HV approximation can be easily computed using an incomplete Cholesky decomposition (IC0). Fourth, we present how IC0 can be used to create an approximate Kalman filter. Finally, we describe how all these developments can be combined in a filtering algorithm. Using the Laplace approximation and the extended Kalman filter, our method is applicable to a broad class of state-space models with convex likelihoods and to nonlinear evolution models that can be linearized.

The remainder of this document is organized as follows. In Sect. 2, we specify the relationship between ordered conditional independence and sparse (inverse) Cholesky factors. Then, we build up increasingly complex and general methods, culminating in nonlinear and non-Gaussian spatiotemporal filters: In Sect. 3, we introduce the HV approximation for a linear Gaussian spatial field at a single time point; in Sect. 4, we extend this to non-Gaussian data; and in Sect. 5, we consider the general spatiotemporal filtering case, including nonlinear evolution. Section 6 contains numerical comparisons to existing approaches. Section 7 presents a filtering analysis of satellite data. Section 8 concludes. Appendices A–B contain proofs and further details. Sections S1–S6 in the Supplementary Material provide additional information, including on a particle filter for inference on unknown parameters in the model, an application to a nonlinear Lorenz model, and comparisons with the ensemble Kalman filter. Code implementing our methods and numerical comparisons is available at https://github.com/katzfuss-group/vecchiaFilter.

2 Sparsity of Cholesky factors

We begin by specifying the connections between ordered conditional independence and sparsity of the Cholesky factor of the covariance and precision matrix.

Remark 1

Let $\mathbf {w}$ be a normal random vector with variance–covariance matrix $\mathbf {K}$.

• 1. Let $\mathbf {L}= {{\,\mathrm{chol}\,}}(\mathbf {K})$ be the lower-triangular Cholesky factor of the covariance matrix $\mathbf {K}$. For $i>j$:

  $$\begin{aligned} \mathbf {L}_{i,j}=0 \iff w_i \perp w_j \, | \, \mathbf {w}_{1:j-1} \end{aligned}$$

• 2. Let $\mathbf {U}= {{\,\mathrm{rchol}\,}}(\mathbf {K}^{-1}) = \mathbf {P}{{\,\mathrm{chol}\,}}( \mathbf {P}\mathbf {K}^{-1}\mathbf {P})\,\mathbf {P}$ be the Cholesky factor of the precision matrix under reverse ordering, where $\mathbf {P}$ is the reverse-ordering permutation matrix. Then $\mathbf {U}$ is upper-triangular, and for $i>j$:

  $$\begin{aligned} \mathbf {U}_{j,i}=0 \iff w_i \perp w_j \, | \, \mathbf {w}_{1:j-1},\mathbf {w}_{j+1:i-1} \end{aligned}$$

The connection between ordered conditional independence and the Cholesky factor of the precision matrix is well known (e.g., Rue and Held 2010); Part 2 of our remark states this connection under reverse ordering (e.g., Katzfuss and Guinness 2021, Prop. 3.3). In Part 1, we consider the lesser-known relationship between ordered conditional independence and sparsity of the Cholesky factor of the covariance matrix, which was recently discussed in Schäfer et al.(2021b, Sect. 1.4.2). For completeness, we provide a proof of Remark 1 in “Appendix B”.

Remark 1 is crucial for our later developments and proofs. In Sect. 3, we specify the HV approximation of Gaussian processes that satisfies both types of conditional independence in Remark 1; the resulting sparsity of the Cholesky factor and its inverse allows extensions to spatiotemporal filtering in Sect. 5.

3 HV approximation for large Gaussian spatial data

Consider a Gaussian process $x(\cdot )$ and a vector $\mathbf {x}= (x_1, \ldots , x_n)^\top$ representing $x(\cdot )$ evaluated on a grid $\mathcal {S}= \{\mathbf {s}_1,\ldots ,\mathbf {s}_n \}$ with $\mathbf {s}_i \in \mathcal {D}\subset \mathbb {R}^d$ and $x_i = x(\mathbf {s}_i)$ for $\mathbf {s}_i \in \mathcal {D}$, $i=1,\ldots ,n$. We assume the following model:

$$\begin{aligned} y_{i} \,|\, \mathbf {x}&{\mathop {\sim }\limits ^{ind}} \mathcal {N}(x_i,\tau _i^2),\quad i \in \mathcal {I}, \end{aligned}$$

(1)

$$\begin{aligned} \mathbf {x}&\sim \mathcal {N}_n(\varvec{\mu },\varvec{\Sigma }), \end{aligned}$$

(2)

where $\mathcal {N}$ and $\mathcal {N}_n$ denote, respectively, a univariate and multivariate normal distribution, $\mathcal {I}\subset \{1,\ldots ,n\}$ are the indices of grid points at which observations are available, and $\mathbf {y}$ is the data vector consisting of these observations $\{y_{i}: i \in \mathcal {I}\}$. Note that we can equivalently express (1) using matrix notation as $\mathbf {y}\,|\, \mathbf {x}\sim \mathcal {N}(\mathbf {H}\mathbf {x},\mathbf {R})$, where $\mathbf {H}$ is obtained by selecting only the rows with indices $i \in \mathcal {I}$ from an identity matrix, and $\mathbf {R}$ is a diagonal matrix with entries $\{\tau _i^2: i \in \mathcal {I}\}$. While (1) assumes conditional independence of each observation, we discuss in Section S1 how this assumption can be relaxed.

Our interest is in computing the posterior distribution of $\mathbf {x}$ given $\mathbf {y}$, which requires inverting or decomposing an $n \times n$ matrix at a cost of $\mathcal {O}(n^3)$ if $|\mathcal {I}| = \mathcal {O}(n)$. This is computationally infeasible for large n.

3.1 The HV approximation

We now describe the HV approximation with unique sparsity and computational properties, which enable fast computation for spatial models as in (1)–(2) and also allow extensions to spatiotemporal filtering as explained later.

Assume that the elements of the vector $\mathbf {x}$ are hierarchically partitioned into sets $\mathcal {X}^m$, for $m=0, \ldots M$, where for $m>1$ we have $\mathcal {X}^m = \bigcup _{j_1=1}^{J_1} \cdots \bigcup _{j_m=1}^{J_m} \mathcal {X}_{j_1,\ldots ,j_m}$, and $\mathcal {X}_{j_1,\ldots ,j_m}$ is a set consisting of $|\mathcal {X}_{j_1,\ldots ,j_m}|$ elements of $\mathbf {x}$, such that there is no overlap between any two sets, $\mathcal {X}_{j_1,\ldots ,j_m}\cap \mathcal {X}_{i_1,\ldots ,i_l}= \emptyset$ for $({j_1,\ldots ,j_m}) \ne ({i_1,\ldots ,i_l})$. Note that this also means that the sets $\mathcal {X}^m$ and $\mathcal {X}^l$ are disjoint for $m \ne l$. Define $\mathcal {X}^{0:m} = \bigcup _{k=0}^m \mathcal {X}^k$. We assume that $\mathbf {x}$ is ordered according to $\mathcal {X}^{0:M}$, in the sense that if $i>j$, then $x_i \in \mathcal {X}^{m_1}$ and $x_j \in \mathcal {X}^{m_2}$ with $m_1 \ge m_2$. We also say that if $m>l$, then elements of $\mathcal {X}^m$ are at a higher level than elements of $\mathcal {X}^l$. As a toy example with $n=6$, the vector $\mathbf {x}= (x_1,\ldots ,x_6)$ might be partitioned with $M=1$, $J_1 = 2$, as $\mathcal {X}^{0:1} = \mathcal {X}^0 \cup \mathcal {X}^1$, $\mathcal {X}^0 = \mathcal {X}= \{x_1,x_2\}$, and $\mathcal {X}^1 = \mathcal {X}_{1,1} \cup \mathcal {X}_{1,2}$, where $\mathcal {X}_{1,1}=\{x_3,x_4\}$, and $\mathcal {X}_{1,2} = \{x_5,x_6\}$. Another toy example is illustrated in Fig. 1.

Fig. 1

Toy example with $n=35$ of the HV approximation in (3) with $M=2$ and $J_1=J_2=2$; the color for each set $\mathcal {X}_{j_1,\ldots ,j_m}$ is consistent across (a)–(c). a Partitioning of the spatial domain $\mathcal {D}$ and the locations $\mathcal {S}$; for level $m=0,1,2$, locations of $\mathcal {X}^{0:m}$ (solid dots) and locations of points at higher levels ($\circ$). b DAG illustrating the conditional-dependence structure, with bigger arrows for connections between vertices at neighboring levels of the hierarchy, to emphasize the tree structure. c Corresponding sparsity pattern of $\mathbf {U}$ (see Proposition 1), with groups of columns/rows corresponding to different levels separated by pink lines, and groups of columns/rows corresponding to different $\mathcal {X}_{j_1,\ldots ,j_m}$ at the same level separated by blue lines. (Color figure online)

The exact distribution of $\mathbf {x}\sim \mathcal {N}_n(\varvec{\mu },\varvec{\Sigma })$ can be written as

$$\begin{aligned} \textstyle p(\mathbf {x})= & {} \prod _{m=0}^M \prod _{j_1,\ldots ,j_m}\\&p\left( \mathcal {X}_{j_1,\ldots ,j_m}|\mathcal {X}^{0:m-1},\mathcal {X}_{{j_1,\ldots ,j_{m-1}},1:j_m-1}\right) , \end{aligned}$$

where the conditioning set of $\mathcal {X}_{j_1,\ldots ,j_m}$ consists of all sets $\mathcal {X}^{0:m-1}$ at lower levels, plus those at the same level that are previous in lexicographic ordering. The idea of Vecchia (1988) was to remove many of these variables in the conditioning set, which for geostatistical applications often incurs only small approximation error due to the so-called screening effect (e.g., Stein 2002, 2011).

Here we consider the HV approximation of the form

$$\begin{aligned} \textstyle \hat{p}(\mathbf {x}) = \prod _{m=0}^M \prod _{j_1,\ldots ,j_m}p(\mathcal {X}_{j_1,\ldots ,j_m}|\mathcal {A}_{j_1,\ldots ,j_m}), \end{aligned}$$

(3)

where $\mathcal {A}_{j_1,\ldots ,j_m}= \mathcal {X}\cup \mathcal {X}_{j_1} \cup \cdots \cup \mathcal {X}_{{j_1,\ldots ,j_{m-1}}}$. We call $\mathcal {A}_{j_1,\ldots ,j_m}$ the set of ancestors of $\mathcal {X}_{j_1,\ldots ,j_m}$. For example, the set of ancestors of $\mathcal {X}_{2,1,2}$ is $\mathcal {A}_{2,1,2} = \mathcal {X}\cup \mathcal {X}_2 \cup \mathcal {X}_{2,1}$. Thus, $\mathcal {A}_{j_1,\ldots ,j_m}= \mathcal {A}_{j_1,\ldots ,j_{m-1}}\cup \mathcal {X}_{j_1,\ldots ,j_{m-1}}$, and the ancestor sets are nested: $\mathcal {A}_{j_1,\ldots ,j_{m-1}}\subset \mathcal {A}_{j_1,\ldots ,j_m}$. We can equivalently write (3) in terms of individual variables as

$$\begin{aligned} \textstyle \hat{p}(\mathbf {x}) = \prod _{i=1}^n p(x_i|\,\mathcal {C}_i), \end{aligned}$$

(4)

where $\mathcal {C}_i = \mathcal {A}_{j_1,\ldots ,j_m}\cup \{x_k \in \mathcal {X}_{j_1,\ldots ,j_m}\! : \, k<i \}$ for $x_i \in \mathcal {X}_{j_1,\ldots ,j_m}$. The choice of the $\mathcal {C}_i$ involves a trade-off: generally, the larger the $\mathcal {C}_i$, the higher the computational cost (see Proposition 4), but the smaller the approximation error; HV is exact when all $\mathcal {C}_i = \{x_1,\ldots ,x_{i-1}\}$.

Vecchia approximations and their conditional-independence assumptions are closely connected to directed acyclic graphs (DAGs; Datta et al. 2016; Katzfuss and Guinness 2021). Summarizing briefly, as illustrated in Fig. 1b, we associate a vertex with each set $\mathcal {X}_{j_1,\ldots ,j_m}$, and we draw an arrow from the vertex corresponding to $\mathcal {X}_{{i_1,\ldots ,i_l}}$ to the vertex corresponding to $\mathcal {X}_{j_1,\ldots ,j_m}$ if and only if $\mathcal {X}_{{i_1,\ldots ,i_l}}$ is in the conditioning set of $\mathcal {X}_{j_1,\ldots ,j_m}$ (i.e., $\mathcal {X}_{{i_1,\ldots ,i_l}} \subset \mathcal {A}_{j_1,\ldots ,j_m}$). DAGs corresponding to HV approximations always have a tree structure, due to the nested ancestor sets. Necessary terminology and notation from graph theory is reviewed in Appendix A.

In practice, as illustrated in Fig. 1a, we partition the spatial field $\mathbf {x}$ into the hierarchical set $\mathcal {X}^{0:M}$ based on a recursive partitioning of the spatial domain $\mathcal {D}$ into $J_1$ regions $\mathcal {D}_{1},\ldots ,\mathcal {D}_{J_1}$, each of which is again split into $J_2$ regions, and so forth, up to level M (Katzfuss 2017): $\mathcal {D}_{j_1,\ldots ,j_{m-1}}= \bigcup _{j_m=1}^{J_m} \mathcal {D}_{j_1,\ldots ,j_m}$, $m=1,\ldots ,M$. We then set each $\mathcal {X}_{j_1,\ldots ,j_m}$ to be a subset of the variables in $\mathbf {x}$ whose location is in $\mathcal {D}_{j_1,\ldots ,j_m}$: $\mathcal {X}_{j_1,\ldots ,j_m}\subset \{x_i: \mathbf {s}_i \in \mathcal {D}_{j_1,\ldots ,j_m}\}$. This implies that the ancestors $\mathcal {A}_{j_1,\ldots ,j_m}$ of each set $\mathcal {X}_{j_1,\ldots ,j_m}$ consist of the variables associated with regions at lower levels $m=0,\ldots ,m-1$ that contain $\mathcal {D}_{j_1,\ldots ,j_m}$. Specifically, for all our numerical examples, we set $J_1=\cdots =J_M=2$, and we select each $\mathcal {X}_{j_1,\ldots ,j_m}$ corresponding to the first $|\mathcal {X}_{j_1,\ldots ,j_m}|$ locations in a maximum-distance ordering (Guinness 2018; Schäfer et al. 2021b) of $\mathcal {S}$ that are contained in $\mathcal {D}_{j_1,\ldots ,j_m}$ but are not already in $\mathcal {A}_{j_1,\ldots ,j_m}$.

The HV approximation (3) is closely related to the multi-resolution approximation (MRA; Katzfuss 2017; Katzfuss and Gong 2020), as noted in Katzfuss and Guinness (2021, Sect. 2.5); specifically, while HV makes conditional-independence assumptions that result in an approximate covariance matrix ${\hat{\varvec{\Sigma }}}$ of $\mathbf {x}$ with a sparse Cholesky factor (see Proposition 1), the MRA relies on a basis-function representation of a spatial process that results in a sparse nontriangular matrix square root. However, the approximate covariance matrices ${\hat{\varvec{\Sigma }}}$ implied by both HV and MRA are hierarchical off-diagonal low-rank (HODLR) matrices (e.g., Hackbusch 2015; Ambikasaran et al. 2016; Saibaba et al. 2015; Geoga et al. 2020), as was noted for the MRA in Jurek and Katzfuss (2021). The definition, exposition, and details based on conditional independence and sparse Cholesky factors provided here enable our later proofs, simple incomplete-Cholesky-based computation, and extensions to non-Gaussian data and to nonlinear space–time filtering.

3.2 Sparsity of the HV approximation

For all Vecchia approximations, the assumed conditional independence implies a sparse Cholesky factor of the precision matrix (e.g., Datta et al. 2016; Katzfuss and Guinness 2021, Prop. 3.3). The conditional-independence assumption made in our HV approximation also implies a sparse Cholesky factor of the covariance matrix, which is in contrast to many other formulations of the Vecchia approximation. Let $\mathcal {N}(\mathbf {x}|\varvec{\mu }, \varvec{\Sigma })$ denote the density of a normal distribution with mean $\varvec{\mu }$ and covariance matrix $\varvec{\Sigma }$ evaluated at $\mathbf {x}$.

Proposition 1

For the HV approximation in (3), we have ${\hat{p}}(\mathbf {x}) = \mathcal {N}_n(\mathbf {x}|\varvec{\mu },{\hat{\varvec{\Sigma }}})$. Define $\mathbf {L}= {{\,\mathrm{chol}\,}}({\hat{\varvec{\Sigma }}})$ and $\mathbf {U}= {{\,\mathrm{rchol}\,}}({\hat{\varvec{\Sigma }}}^{-1}) = \mathbf {P}{{\,\mathrm{chol}\,}}( \mathbf {P}{\hat{\varvec{\Sigma }}}^{-1}\mathbf {P})\,\mathbf {P}$, where $\mathbf {P}$ is the reverse-ordering permutation matrix.

• 1. For $i\ne j$:

  • (a) $\mathbf {L}_{i,j} = 0$ unless $x_j \in \mathcal {C}_i$

  • (b) $\mathbf {U}_{j,i} = 0$ unless $x_j \in \mathcal {C}_i$

• 2. $\mathbf {U}= \mathbf {L}^{-\top }$

The proof relies on Remark 1. All proofs can be found in “Appendix B”. Proposition 1 says that the Cholesky factors of the covariance and precision matrix implied by a HV approximation are both sparse, and $\mathbf {U}$ has the same sparsity pattern as $\mathbf {L}^{\top }$. An example of this pattern is shown in Fig. 1c. Furthermore, because $\mathbf {L}= \mathbf {U}^{-\top }$, we can quickly compute one of these factors given the other, as described in Sect. 3.3 (see the proof of Proposition 4).

For other Vecchia approximations, the sparsity of the prior Cholesky factor $\mathbf {U}$ for $\mathbf {x}$ does not necessarily imply the same sparsity for the Cholesky factor of the posterior precision matrix of $\mathbf {x}$ given $\mathbf {y}$, and in fact there can be substantial fill-in (Katzfuss and Guinness 2021). However, this is not the case for the particular case of HV, for which the posterior sparsity is exactly the same as the prior sparsity:

Proposition 2

Assume that $\mathbf {x}$ has the distribution ${\hat{p}}(\mathbf {x})$ given by the HV approximation in (3). Let ${\widetilde{\varvec{\Sigma }}} = {{\,\mathrm{Var}\,}}(\mathbf {x}|\mathbf {y})$ be the posterior covariance matrix of $\mathbf {x}$ given data $y_{i} \,|\, \mathbf {x}{\mathop {\sim }\limits ^{ind}} \mathcal {N}(x_i,\tau _i^2)$, $i \in \mathcal {I}\subset \{1,\ldots ,n\}$, as in (1). Then:

• 1. ${\widetilde{\mathbf {U}}} = {{\,\mathrm{rchol}\,}}({\widetilde{\varvec{\Sigma }}}^{-1})$ has the same sparsity pattern as $\mathbf {U}= {{\,\mathrm{rchol}\,}}({\hat{\varvec{\Sigma }}}^{-1})$.

• 2. ${\widetilde{\mathbf {L}}} = {{\,\mathrm{chol}\,}}({\widetilde{\varvec{\Sigma }}})$ has the same sparsity pattern as $\mathbf {L}= {{\,\mathrm{chol}\,}}({\hat{\varvec{\Sigma }}})$.

3.3 Fast computation using incomplete Cholesky factorization

For notational and computational convenience, we assume now that each conditioning set $\mathcal {C}_i$ consists of at most $N$ elements of $\mathbf {x}$. For example, this can be achieved by setting $|\mathcal {X}_{j_1,\ldots ,j_m}|\le r$ with $r = N/(M+1)$. Then $\mathbf {U}$ can be computed using general expressions for the Vecchia approximation in $\mathcal {O}(nN^3)$ time (e.g., Katzfuss and Guinness 2021). Inference using the related multi-resolution decomposition (Katzfuss 2017; Katzfuss and Gong 2020; Jurek and Katzfuss 2021) can be carried out in $\mathcal {O}(nN^2)$ time, but these algorithms are fairly involved.

Instead, we show here how HV inference can be carried out in $\mathcal {O}(nN^2)$ time using standard sparse-matrix algorithms, including the incomplete Cholesky factorization, based on at most $nN$ entries of $\varvec{\Sigma }$. Our algorithm, which is based on ideas in Schäfer et al. (2021b), is much simpler than multi-resolution decompositions.

The incomplete Cholesky factorization (e.g., Golub and Van Loan 2012), denoted by ${{\,\mathrm{\text {ichol}}\,}}(\mathbf {A}, \mathbf {S})$ and given in Algorithm 1, is identical to the standard Cholesky factorization of the matrix $\mathbf {A}$, except that we skip all operations that involve elements that are not in the sparsity pattern represented by the zero-one matrix $\mathbf {S}$. It is important to note that to compute $\mathbf {L}={{\,\mathrm{\text {ichol}}\,}}(\mathbf {A}, \mathbf {S})$ for a large dense matrix $\mathbf {A}$, we do not actually need to form or access the entire $\mathbf {A}$; instead, to reduce memory usage and computational cost, we simply compute $\mathbf {L}={{\,\mathrm{\text {ichol}}\,}}(\mathbf {A}\circ \mathbf {S}, \mathbf {S})$ based on the sparse matrix $\mathbf {A}\circ \mathbf {S}$, where $\circ$ denotes element-wise multiplication. Thus, while we write expressions like $\mathbf {L}={{\,\mathrm{\text {ichol}}\,}}(\mathbf {A}, \mathbf {S})$ for notational simplicity below, this should always be read as $\mathbf {L}={{\,\mathrm{\text {ichol}}\,}}(\mathbf {A}\circ \mathbf {S}, \mathbf {S})$.

For our HV approximation in (3), we henceforth set $\mathbf {S}$ to be a sparse lower-triangular matrix with $\mathbf {S}_{i,j}=1$ if $x_j \in \mathcal {C}_i$ or if $i=j$, and 0 otherwise. Thus, the sparsity pattern of $\mathbf {S}$ is the same as that of $\mathbf {L}$, and its transpose is that of $\mathbf {U}$ shown in Fig. 1c.

Proposition 3

Assuming (3), denote ${{\,\mathrm{Var}\,}}(\mathbf {x}) = {\hat{\varvec{\Sigma }}}$ and $\mathbf {L}= {{\,\mathrm{chol}\,}}({\hat{\varvec{\Sigma }}})$. Then, $\mathbf {L}= {{\,\mathrm{\text {ichol}}\,}}(\varvec{\Sigma }, \mathbf {S})$.

Hence, the Cholesky factor of the covariance matrix ${\hat{\varvec{\Sigma }}}$ implied by the HV approximation can be computed using the incomplete Cholesky algorithm based on the (at most) nN entries of the exact covariance $\varvec{\Sigma }$ indicated by $\mathbf {S}$. Using this result, we propose Algorithm 2 for posterior inference on $\mathbf {x}$ given $\mathbf {y}$.

By combining the incomplete Cholesky factorization with the results in Propositions 1 and 2 (saying that all involved Cholesky factors are sparse), we can perform fast posterior inference:

Proposition 4

Algorithm 2 can be carried out in $\mathcal {O}(nN^2)$ time and $\mathcal {O}(nN)$ space, assuming that $|\mathcal {C}_i| \le N$ for all $i=1,\ldots ,n$.

3.4 Approximation accuracy

Formal error quantification for the HV approximation is a matter of ongoing research. Numerical simulations suggest that it can be almost as accurate (adjusting for its lower computational complexity) as the state-of-the-art general Vecchia approximation in many settings (Katzfuss et al. 2020a, Fig. S3). Generally, the quality of the approximation increases with the conditioning set size $N$ and with the strength of the screening effect in the process to be approximated. For an approximately low-rank covariance matrix, only a small number of levels M will be necessary to capture it accurately, while greater local variations might require a greater M. In our numerical experiments, we rely on the default strategy implemented in the GPvecchia package (Katzfuss et al. 2020c), which we have found to produce good results. A drawback of the HV approximation is that its hierarchical conditional-independence assumptions can result in visual artifacts or edge effects along partition boundaries; some examples and a discussion of this issue are provided in Section S5. For situations in which these edge effects are of major concern, it may be useful to use a larger N (and hence sacrifice some computational speed), to manually place the conditioning points at low levels near partition boundaries (e.g., Katzfuss 2017, Sect. 2.5), or to forgo the HV approximation in favor of a different (Vecchia) approximation for purely spatial problems. However, for spatiotemporal filtering, we are not aware of any other spatial approximation method which will ensure that the Cholesky factor of the filtering precision matrix will preserve its sparsity pattern when filtering across time points. This key advantage of our approach ensures scalability of the HV filter discussed in Sect. 5. Using the HV approximation in a filtering setting has the added benefit that the boundary artifacts in the filtering mean field tend to fade or even disappear within a few time steps (see Sect. S5). This is because dependence between neighboring points is captured not only by the spatial covariance function, but also by the temporal evolution operator, which is particularly helpful in the case of diffusion or transport evolution models.

4 Extensions to non-Gaussian spatial data using the Laplace approximation

Now consider the model

$$\begin{aligned} y_{i} \,|\, \mathbf {x}&{\mathop {\sim }\limits ^{ind}} g_i(y_{i} | x_{i}),\quad i \in \mathcal {I}, \end{aligned}$$

(5)

$$\begin{aligned} \mathbf {x}&\sim \mathcal {N}_n(\varvec{\mu },\varvec{\Sigma }), \end{aligned}$$

(6)

where $g_i$ is a distribution from an exponential family, and we slightly abuse notation by using $g_i(y_i|x_i)$ to denote both the distribution and its density. Using the HV approximation in (3)–(4) for $\mathbf {x}$, the implied posterior can be written as:

$$\begin{aligned} \hat{p}(\mathbf {x}|\mathbf {y}) = \frac{p(\mathbf {y}|\mathbf {x}) \hat{p}(\mathbf {x})}{\int p(\mathbf {y}|\mathbf {x}) \hat{p}(\mathbf {x}) d\mathbf {x}} = \frac{(\prod _{i \in \mathcal {I}} g_i(y_i|x_i)) \hat{p}(\mathbf {x})}{\int (\prod _{i \in \mathcal {I}} g_i(y_i|x_i)) \hat{p}(\mathbf {x}) d\mathbf {x}}.\nonumber \\ \end{aligned}$$

(7)

Unlike in the Gaussian case as in (1), the integral in the denominator cannot generally be evaluated in closed form, and Markov Chain Monte Carlo methods are often used to numerically approximate the posterior. Instead, Zilber and Katzfuss (2021) proposed a much faster method that combines a general Vecchia approximation with the Laplace approximation (e.g., Tierney and Kadane 1986; Rasmussen and Williams 2006, Sect. 3.4). The Laplace approximation is based on a Gaussian approximation of the posterior, obtained by carrying out a second-order Taylor expansion of the posterior log-density around its mode. Although the mode cannot generally be obtained in closed form, it can be computed straightforwardly using a Newton–Raphson procedure, because $\log \hat{p}(\mathbf {x}|\mathbf {y}) = \log p(\mathbf {y}|\mathbf {x}) + \log \hat{p}(\mathbf {x}) + c$ is a sum of two concave functions and hence also concave (as a function of $\mathbf {x}$, under appropriate parametrization of the $g_i$).

While each Newton–Raphson update requires the computation and decomposition of the $n \times n$ Hessian matrix, the update can be carried out quickly by making use of the sparsity implied by the Vecchia approximation. To do so, we follow Zilber and Katzfuss (2021) in exploiting the fact that the Newton–Raphson update is equivalent to computing the conditional mean of $\mathbf {x}$ given pseudo-data. Specifically, at the $\ell$th iteration of the algorithm, given the current state value $\mathbf {x}^{(\ell )}$, let us define

$$\begin{aligned} \mathbf {u}^{(\ell )}= & {} \big [ u^{(\ell )}_i \big ]_{i \in \mathcal {I}},\nonumber \\&\text {where} \quad u^{(\ell )}_i = \frac{\partial }{\partial x} \log g_i(y_i|x)\big \vert _{x=x^{(\ell )}_i}, \end{aligned}$$

(8)

and

$$\begin{aligned} \mathbf {D}^{(\ell )}= & {} {{\,\mathrm{diag}\,}}\big (\{d_i^{(\ell )}: i \in \mathcal {I}\}\big ), \nonumber \\&\text {where} \quad d_i^{(\ell )} = -\big (\frac{\partial ^2}{\partial x^2} \log g_i(y_i|x)\big )^{-1}\big \vert _{x=x^{(\ell )}_i}. \end{aligned}$$

(9)

Then, we compute the next iteration’s state value $\mathbf {x}^{(\ell +1)} = \mathbb {E}(\mathbf {x}|\mathbf {t}^{(\ell )})$ as the conditional mean of $\mathbf {x}$ given pseudo-data $\mathbf {t}^{(\ell )} = \mathbf {x}^{(\ell )} + \mathbf {D}^{(\ell )} \mathbf {u}^{(\ell )}$ assuming Gaussian noise, $t^{(\ell )}_i | \mathbf {x}{\mathop {\sim }\limits ^{ind.}} \mathcal {N}(x_i,d_i^{(\ell )})$, $i \in \mathcal {I}$. Zilber and Katzfuss (2021) recommend computing the conditional mean $\mathbb {E}(\mathbf {x}|\mathbf {t}^{(\ell )})$ based on a general Vecchia prediction approach proposed in Katzfuss et al. (2020a). Here, we instead compute the posterior mean using Algorithm 2 based on the HV method described in Sect. 3, due to its sparsity-preserving properties. In contrast to the approach recommended in Zilber and Katzfuss (2021), our algorithm is guaranteed to converge, because it is equivalent to Newton–Raphson optimization of the log of the posterior density in (7), which is concave. Once the algorithm converges to the posterior mode ${\widetilde{\varvec{\mu }}}$, we obtain a Gaussian HV-Laplace approximation of the posterior as

$$\begin{aligned} \hat{p}_L(\mathbf {x}|\mathbf {y}) = \mathcal {N}_n(\mathbf {x}|{\widetilde{\varvec{\mu }}},{\widetilde{\mathbf {L}}}{\widetilde{\mathbf {L}}}^\top ), \end{aligned}$$

where ${\widetilde{\mathbf {L}}}$ is the Cholesky factor of the negative Hessian of the log-posterior at ${\widetilde{\varvec{\mu }}}$. Our approach is described in Algorithm 3. The main computational expense for each iteration of the for loop is carrying out Algorithm 2, and so each iteration requires only $\mathcal {O}(nN^2)$ time.

In the Gaussian case, when $g_i(y_i | x_i) = \mathcal {N}(y_i|a_i x_i,\tau _i^2)$ for some $a_i \in \mathbb {R}$, it can be shown using straightforward calculations that the pseudo-data $t_i = y_i/a_i$ and pseudo-variances $d_i = \tau _i^2$ do not depend on $\mathbf {x}$, and so Algorithm 3 converges in a single iteration. If, in addition, $a_i=1$ for all $i=1,\ldots ,n$, then (5) becomes equivalent to (1), and Algorithm 3 simplifies to Algorithm 2.

For non-Gaussian data, our HVL algorithm shares the limitations of the Laplace approximation. In particular, it approximates the mean of the filtering distribution with its mode, which can result in significant errors for highly non-Gaussian settings. Furthermore, because the variance estimate is based on the curvature of the likelihood at the mode, it is prone to underestimating the true uncertainty. Nickisch and Rasmussen (2008) provide further details and a comprehensive comparison of several methods of approximating non-Gaussian likelihoods. Notwithstanding these known limitations, empirical studies (e.g., Bonat and Ribeiro Jr 2016; Zilber and Katzfuss 2021) have shown that Laplace-type approximations can be effectively applied to environmental data sets and can strongly outperform sampling-based approaches such as Markov chain Monte Carlo.

5 Fast filters for spatiotemporal models

5.1 Linear evolution

We now turn to a spatiotemporal state-space model (SSM), which adds a temporal evolution model to the spatial model (5) considered in Sect. 4. For now, assume that the evolution is linear. Starting with an initial distribution $\mathbf {x}_0 \sim \mathcal {N}_{n}(\varvec{\mu }_{0|0},\varvec{\Sigma }_{0|0})$, we consider the following SSM for discrete time $t=1,2,\ldots$:

$$\begin{aligned} y_{ti} \,|\, \mathbf {x}_t&{\mathop {\sim }\limits ^{ind}} g_{ti}(y_{ti} | x_{ti}), \quad i \in \mathcal {I}_t \end{aligned}$$

(10)

$$\begin{aligned} \mathbf {x}_t \,|\, \mathbf {x}_{t-1}&\sim \mathcal {N}_n(\mathbf {E}_t\mathbf {x}_{t-1},\mathbf {Q}_t), \end{aligned}$$

(11)

where $\mathbf {y}_{t}$ is the data vector consisting of $n_t \le n$ observations $\{y_{ti}: i \in \mathcal {I}_t\}$, $\mathcal {I}_t \subset \{1,\ldots ,n\}$ contains the observation indices at time t, $g_{ti}$ is a distribution from the exponential family, $\mathbf {x}_t = (x_1,\ldots ,x_n)^\top$ is the latent spatial field of interest at time t observed at a spatial grid $\mathcal {S}$, and $\mathbf {E}_t$ is a sparse $n \times n$ evolution matrix. Note that we allow for different observation locations at each time point, which is helpful in many remote-sensing applications where observations are often missing (e.g., due to changing cloud cover). The methods we propose are suitable for any type of $\mathbf {Q}_t$ matrices; due to its hierarchical structure, HV is able to successfully capture both long-range dependence (which corresponds to low-rank structures in $\mathbf {Q}_t$) as well as finer, local variations.

At time t, our goal is to obtain or approximate the filtering distribution $p(\mathbf {x}_t|\mathbf {y}_{1:t})$ of $\mathbf {x}_t$ given data $\mathbf {y}_{1:t}$ up to the current time t. This task, also referred to as data assimilation or on-line inference, is commonly encountered in many fields of science whenever one is interested in quantifying the uncertainty in the current state or in obtaining forecasts into the future. If the observation equations $g_{ti}$ are all Gaussian, the filtering distribution can be derived using the Kalman filter (Kalman 1960) for small to moderate n. At each time t, the Kalman filter consists of a forecast step that computes $p(\mathbf {x}_t|\mathbf {y}_{1:t-1})$, and an update step which then obtains $p(\mathbf {x}_t|\mathbf {y}_{1:t})$. For linear Gaussian SSMs, both of these distributions are multivariate normal.

Our Kalman–Vecchia–Laplace (KVL) filter extends the Kalman filter to high-dimensional SSMs (i.e., large n) with non-Gaussian data, as in (10)–(11). Its update step is very similar to the inference problem in Sect. 4, and hence, it essentially consists of the HVL in Algorithm 3. We complement this update with a forecast step, in which the moment estimates are propagated forward using the temporal evolution model. This forecast step is exact, and so the KVL approximation error is solely due to the HVL approximation at each update step.

The KVL filter is given in Algorithm 4. In Line 4, $\mathbf {L}_{t|t-1;i,:}$ denotes the ith row of $\mathbf {L}_{t|t-1}$. The KVL filter scales well with the state dimension n. The evolution matrix $\mathbf {E}_t$, which is often derived using a forward finite difference scheme and thus has only a few nonzero elements in each row, can be quickly multiplied with $\mathbf {L}_{t-1|t-1}$ in Line 3, as the latter is sparse (see Sect. 3.3). The $\mathcal {O}(nN)$ necessary entries of $\varvec{\Sigma }_{t|t-1}$ in Line 4 can also be calculated quickly due to the sparsity of $\mathbf {L}_{t|t-1;i,:}$. The low computational cost of the HVL algorithm has already been discussed in Sect. 4. Thus, assuming sufficiently sparse $\mathbf {E}_t$, the KVL filter scales approximately as $\mathcal {O}(nN^2)$ per iteration. In the case of Gaussian data (i.e., all $g_{ti}$ in (10) are Gaussian), our KVL filter will produce similar filtering distributions as the more complicated multi-resolution filter of Jurek and Katzfuss (2021).

5.2 An extended filter for nonlinear evolution

Finally, we consider a nonlinear and non-Gaussian model, which extends (10)–(11) by allowing nonlinear evolution operators, $\mathcal {E}_t: \mathbb {R}^n \rightarrow \mathbb {R}^n$. This results in the model

$$\begin{aligned} y_{ti} \,|\, \mathbf {x}_t&{\mathop {\sim }\limits ^{ind}} g_{ti}(y_{ti} | x_{ti}), \quad i \in \mathcal {I}_t \end{aligned}$$

(12)

$$\begin{aligned} \mathbf {x}_t \,|\, \mathbf {x}_{t-1}&\sim \mathcal {N}_n(\mathcal {E}_t(\mathbf {x}_{t-1}),\mathbf {Q}_t). \end{aligned}$$

(13)

Due to the nonlinearity of the evolution operator $\mathcal {E}_t$, the KVL filter in Algorithm 4 is not directly applicable anymore. However, similar inference is still possible as long as the evolution is not too far from linear. Approximating the evolution as linear is generally reasonable if the time steps are short, or if the measurements are highly informative. In this case, we propose the extended Kalman–Vecchia–Laplace filter (EKVL) in Algorithm 5, which approximates the extended Kalman filter (e.g., Grewal and Andrews 1993, Ch. 5) and extends it to non-Gaussian data using the Vecchia–Laplace approach. For the forecast step, EKVL computes the forecast mean as $\varvec{\mu }_{t|t-1} = \mathcal {E}_t(\varvec{\mu }_{t-1|t-1})$. The forecast covariance matrix $\varvec{\Sigma }_{t|t-1}$ is obtained as before, after approximating the evolution using the Jacobian as $\mathbf {E}_t = \frac{\partial \mathcal {E}_t(\mathbf {y}_{t-1})}{\partial \mathbf {y}_{t-1}} \big |_{\mathbf {y}_{t-1} = \varvec{\mu }_{t-1|t-1} }$. Errors in the forecast covariance matrix due to this linear approximation can be captured in the model-error covariance, $\mathbf {Q}_t$. If the Jacobian matrix cannot be computed, it is sometimes possible to build a statistical emulator (e.g., Kaufman et al. 2011) instead, which approximates the true evolution operator.

Once $\varvec{\mu }_{t|t-1}$ and $\varvec{\Sigma }_{t|t-1}$ have been obtained, the update step of the EKVL proceeds exactly as in the KVL filter by approximating the forecast distribution as Gaussian.

Similarly to Algorithm 4, EKVL scales very well with the dimension of $\mathbf {x}$, the only difference being the additional operation of calculating the Jacobian in Line 3, whose cost is problem dependent. Only those entries of $\mathbf {E}_t$ need to be calculated that are multiplied with nonzero entries of $\mathbf {L}_{t-1|t-1}$, whose sparsity structure is known ahead of time.

Our approach, which is based on linearizing the evolution operator, is not without its limits. Approximating $\mathcal {E}_t$ with $\mathbf {E}_t$ may be inaccurate for highly nonlinear models, because the forecast distribution of $\mathcal {E}(\mathbf {x}_{t-1})$ is assumed to be normal (which is generally not true if $\mathcal {E}_t$ is not linear) and because the covariance matrix of $\mathcal {E}_t(\mathbf {x}_{t-1})$ is approximated as $\mathbf {E}_t \varvec{\Sigma }_{t|t} \mathbf {E}_t^T$. A potential application of our method should consider these sources of error in addition to those discussed in Sect. 3.4 and at the end of Sect. 4. However, exact inference for high-dimensional nonlinear models is not possible in general, and all existing methods suffer from limitations in this challenging setting. Section S3 in the Supplement shows a successful application of Algorithm 5 to a nonlinear Lorenz model.

6 Numerical comparison

6.1 Methods and criteria

We considered and compared the following methods:

Hierarchical Vecchia (HV): Our methods as described in this paper.

Low rank (LR): A special case of HV with $M=1$, in which the diagonal and the first N columns of $\mathbf {S}$ are nonzero, and all other entries are zero. This results in a matrix approximation ${\hat{\varvec{\Sigma }}}$ that is of rank $N$ plus diagonal, known as the modified predictive process (Banerjee et al. 2008; Finley et al. 2009) in spatial statistics. LR has the same computational complexity as HV.

Dense Laplace (DL): A further special case of HV with $M=0$, in which $\mathbf {S}$ is a fully dense matrix of ones. Thus, there is no error due to the Vecchia approximation, and so in the non-Gaussian spatial-only setting, this is equivalent to a Gaussian Laplace approximation. DL will generally be more accurate than HV and low-rank, but it scales as $\mathcal {O}(n^3)$ and is thus not feasible for high dimension n.

For each scenario below, we simulated observations using (12), taking $g_{t,i}$ to be each of four exponential family distributions: Gaussian, $\mathcal {N}(x,\tau ^2)$; logistic Bernoulli, $\mathcal {B}(1/(1+e^{-x}))$; Poisson, $\mathcal {P}(e^x)$; and gamma, $\mathcal {G}(a, ae^{-x})$, with shape parameter $a=2$. For most scenarios, we assumed a moderate state dimension n, so that DL remained feasible; a large n was considered in Sect. 6.4. In the case of non-Gaussian observations, we used $\epsilon = 10^{-5}$ in Algorithm 3.

The main metric to compare HV and LR was the difference in KL divergence between their posterior or filtering distributions and those generated by DL; as the exact distributions were not known here, we approximated the divergence by the difference in joint log scores (dLS; e.g., Gneiting and Katzfuss 2014) calculated at each time point for the joint posterior or filtering distribution of the entire field and averaged over several simulations. We also calculated the relative root mean square prediction error (RRMSPE), defined as the root mean square prediction error of HV and LR, respectively, divided by the root mean square prediction error of DL; the error is calculated with respect to the true simulated latent field. For both criteria, lower values are better. In each simulation scenario, the scores were averaged over a sufficiently large number of repetitions to achieve stable averages.

For comparisons over a range of conditioning-set sizes $N$, we supplied a set of desired sizes to the GPvecchia package, upon which our method implementation is based. For a desired size, GPvecchia automatically determines a suitable partitioning scheme (and hence a suitable N) for the grid $\mathcal {S}$, such that $N$ is equal to or slightly below the desired value. We generated the HV approximation using this approach and then used the resulting $N$ value for both LR and DL, to ensure a fair comparison.

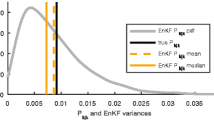
Large-scale spatiotemporal filtering is also often achieved using the ensemble Kalman filter (EnKF) and its extensions. As the EnKF is a substantially different approach that does not neatly fit into our framework here, we conducted a separate comparison between HV and EnKF in Section S4 in the Supplementary Materials; the results strongly favored the HV filter.

6.2 Spatial-only data

In our first scenario, we considered spatial-only data according to (5)–(6) on a grid $\mathcal {S}$ of size $n=34 \times 34 = 1{,}156$ on the unit square, $\mathcal {D}= [0,1]^2$. We set $\varvec{\mu }= \mathbf {0}$ and $\varvec{\Sigma }_{i,j} = \exp (-\Vert \mathbf {s}_i - \mathbf {s}_j\Vert /0.15)$. For the Gaussian likelihood, we assumed variance $\tau ^2 = 0.2$.

The comparison scores averaged over 100 simulations for the posteriors obtained using Algorithm 3 are shown as a function of $N$ in Fig. 2. HV (Algorithm 2) was much more accurate than LR for each value of $N$.

Fig. 2

Approximation accuracy for the posterior distribution $\mathbf {x}|\mathbf {y}$ for spatial data (see Sect. 6.2)

6.3 Linear temporal evolution

Next, similar to Jurek and Katzfuss (2021), we considered a linear spatiotemporal advection–diffusion process $x(\mathbf {s}, t)$ whose evolution is governed by the partial differential equation,

$$\begin{aligned} \frac{\partial x}{\partial t} = \alpha \left( \frac{ \partial ^2 x }{ \partial ^2 s_x } + \frac{ \partial ^2 x }{ \partial ^2 s_y } \right) + \beta \left( \frac{ \partial x}{\partial s_x} + \frac{\partial x}{\partial s_y} \right) + \nu (\mathbf {s}, t), \end{aligned}$$

where $\mathbf {s}= (s_x, s_y) \in \mathcal {D}=[0,1]^2$ and $t \in [0, T]$. We set the diffusion parameter $\alpha = 4 \times 10^{-5}$ and advection parameter $\beta = 10^{-2}$. The error $\nu (\mathbf {s}, t)$ was a zero-mean stationary Gaussian process with exponential covariance function with range $\lambda = 0.15$, independent across time.

The spatial domain $\mathcal {D}$ was discretized on a grid of size $n=34 \times 34 = 1{,}156$ using centered finite differences, and we considered discrete time points $t=1,\ldots ,T$ with $T=20$. After this discretization, our model was of the form (10)–(11), where $\varvec{\Sigma }_{0|0}=\mathbf {Q}_1=\cdots =\mathbf {Q}_T$ with (i, j)th entry $\exp (-\Vert \mathbf {s}_i - \mathbf {s}_j\Vert /\lambda )$, and $\mathbf {E}_t$ was a sparse matrix with nonzero entries corresponding to interactions between neighboring grid points to the right, left, top, and bottom. See the supplementary material of Jurek and Katzfuss (2021) for details.

At each time t, we generated $n_t = n/10$ observations with indices $\mathcal {I}_t$ sampled randomly from $\{1,\ldots ,n\}$. For the Gaussian case, we assumed variance $\tau ^2=0.25$. We used conditioning sets of size at most $N=41$ for both HV and LR; specifically, for HV, we used $J=2$ partitions at $M=7$ levels, with set sizes $|\mathcal {X}_{j_1,\ldots ,j_m}|$ of 5, 5, 5, 5, 6, 6, 6, respectively, for $m=0,1,\ldots ,M-1$, and $|\mathcal {X}_{j_1,\ldots ,j_M}| \le 3$.

Figure 3 compares the scores for the filtering distributions $\mathbf {x}_t | \mathbf {y}_{1:t}$ obtained using Algorithm 4, averaged over 80 simulations. Again, HV was much more accurate than LR. Importantly, while the accuracy of HV was relatively stable over time, LR became less accurate over time, with the approximation error accumulating.

Fig. 3

Accuracy of filtering distributions $\mathbf {x}_t | \mathbf {y}_{1:t}$ for the advection–diffusion model in Sect. 6.3

6.4 Simulations using a very large n

We repeated the advection–diffusion experiment from Sect. 6.3 on a high-resolution grid of size $n=300 \times 300 = 90{,}000$, with $n_t=9{,}000$ observations corresponding to 10% of the grid points. In order to avoid numerical artifacts related to the finite differencing scheme, we reduced the advection and diffusion coefficients to $\alpha = 10^{-7}$ and $\beta =10^{-3}$, respectively. We set $N=44$, $M=14$, $J=2$, and $|\mathcal {X}_{j_1,\ldots ,j_m}| = 3$ for $m=0,1,\ldots ,M-1$, and $|\mathcal {X}_{j_1,\ldots ,j_M}| \le 2$. DL was too computationally expensive due to the high dimension n, and so we simply compared HV and LR based on the root mean square prediction error (RMSPE) between the true state and their respective filtering means, averaged over 10 simulations.

As shown in Fig. 4, HV was again much more accurate than LR. Comparing to Fig. 3, we see that the relative improvement in HV to LR increased even further; taking the Gaussian case as an example, the ratio of the RMSPE for HV and LR was around 1.2 in the small-n setting and greater than 2 in the large-n setting.

Fig. 4

Root mean square prediction error (RMSPE) for the filtering mean in the high-dimensional advection–diffusion model with $n=90{,}000$ in Sect. 6.4

7 Filtering analysis of satellite data

We also applied the filtering method described in Algorithm 5 to measurements of total precipitable water vapor (TPW) acquired by the Microwave Integrated Retrieval System (MIRS) instrument mounted on NASA’s Geostationary Operational Environmental Satellite (GOES). This data set was previously analyzed in Katzfuss and Hammerling (2017). We used 11 consecutive sets of observations collected over a period of 40 h in January 2011 on a grid of size $263 \times 263 = 69{,}169$ over the continental United States, with each cell covering a square of size $16 \times 16$km. In order to avoid specifying boundary conditions for the diffusion model below, we restricted the area of interest to a smaller grid of size $n = 247 \times 247 = 61{,}009$. Observations at selected time points are shown in Fig. 5.

Fig. 5

Total precipitable water measurements (first row), and complete filtering maps made using an HV filter and a LR filter (second and third row, respectively). While HV introduced some artifacts at $t=1$, they became less pronounced at later time points. HV preserved important details that were lost when using LR

We assumed that over the period in which data were collected the dynamics of the TPW can be reasonably approximated by a diffusion process x. More formally, and similar to Sect. 6.3, we assumed that

$$\begin{aligned} \frac{\partial x}{\partial t} = \alpha \left( \frac{ \partial ^2 x }{ \partial ^2 s_x } + \frac{ \partial ^2 x }{ \partial ^2 s_y } \right) + \nu (\mathbf {s}, t), \end{aligned}$$

(14)

where $\nu (\mathbf {s}, t)$ is a zero-mean stationary Gaussian process with Matérn covariance function with smoothness 1.5, range $\lambda$ and marginal variance $\sigma ^2$, independent across time. Exploratory analysis showed that TPW changed slowly between consecutive time points, and so we set $\alpha = 0.99$. We discretized (14) using centered finite differences with 4 internal steps, which resulted in a model of the form (11). Within this context $\mathbf {x}_t$ represents the values of the process in the middle of each grid cell and $\varvec{\Sigma }_{0|0} = \frac{1}{1 - \alpha ^2}\mathbf {Q}_1 = \frac{1}{1 - \alpha ^2}\mathbf {Q}_2 = \cdots = \frac{1}{1 - \alpha ^2}\mathbf {Q}_{11}$, with $\varvec{\Sigma }_{0|0}$ obtained by evaluating the covariance function of $\nu$ over the centers of grid cells.

Following Katzfuss and Hammerling (2017), we assumed independent and additive measurement error for each time t and grid cell i, such that $y_{ti} \sim \mathcal {N}(x_{ti}, \tau ^2)$ with $\tau = 4.5$. At each time point, we held out randomly selected 10% of all observations, which we later used to assess the performance of our method. Covariance function parameters were chosen using a procedure described in Section S6, resulting in the values $\lambda =2.09$ and $\sigma ^2=0.3376$. We then used Algorithm 5 to obtain the filtering distribution of $\mathbf {x}_t$ at all time points. We applied two approximation methods: the HV filter and the LR filter, which are described in Sect. 6.1. We used the same size of the conditioning set, $N=78$, for both methods, which ensures comparable computation time; for HV, we set $J=4$, $M=7$, and $|\mathcal {X}_{j_1,\ldots ,j_m}|$ equal to 25, 15, 15, 5, 5, 5, 3, 3, respectively, for $m = 0, 1, \ldots , M$. The computational cost of the DL method is prohibitive for a data set as big as ours.

We compared the performance of the two filters by calculating the root mean squared prediction error (RMSPE) between the filtering means in $\varvec{\mu }_{t|t}$ obtained with either method and the true observed values, both only at the held-out test locations. Figure 6 shows the values of RMSPE at all time points. We conclude that the HV filter significantly outperformed the LR filter due to its ability to capture much more fine scale detail. Plots of data and filtering results at selected time points are shown in Fig. 5 and are representative of full results. We show the plots of the point-wise standard errors in Section S6 in the Supplement.

Fig. 6

Root mean square prediction error (RMSPE) for the HV (red) and LR (blue) filters versus the 11 time points in the satellite-data application. (Color figure online)

8 Conclusions

We specified the relationship between ordered conditional independence and sparse (inverse) Cholesky factors. Next, we described the HV approximation and showed that it exhibits equivalent sparsity in the Cholesky factors of both its precision and covariance matrices. Due to this remarkable property, the approximation is suitable for high-dimensional spatiotemporal filtering. The HV approximation can be computed using a simple and fast incomplete Cholesky decomposition. Further, by combining the approach with a Laplace approximation and the extended Kalman filter, we obtained scalable filters for non-Gaussian and nonlinear spatiotemporal state-space models.

Our methods can also be directly applied to spatiotemporal point patterns modeled using log-Gaussian Cox processes, which can be viewed as Poisson data after discretization of the spatial domain, resulting in accurate Vecchia–Laplace-type approximations (Zilber and Katzfuss 2021). We plan on investigating an extension of our methods to retrospective smoothing over a fixed time period. Another interesting extension would be to combine our methodology with the unscented Kalman filter (Julier and Uhlmann 1997) for strongly nonlinear evolution. Finally, while we focused our attention on spatiotemporal data, our work can be extended to other applications, as long as a sensible hierarchical partitioning of the state vector can be obtained as in Sect. 3.1.

Code implementing our methods and reproducing our numerical experiments is available at https://github.com/katzfuss-group/vecchiaFilter.

Appendices

Appendix A: Glossary of graph theory terms

We briefly review here some graph terminology necessary for our exposition and proofs, following Lauritzen (1996).

If $a \rightarrow b$ then we say that a is a parent of b and, conversely, that b is a child of a. Moreover, if there is a sequence of distinct vertices $h_1, \ldots , h_k$ such that $h_i \rightarrow h_{i+1}$ or $h_i \leftarrow h_{i+1}$ for all $i<k$, then we say that $h_1, \ldots , h_k$ is a path. If all arrows point to the right, we say that $h_k$ is a descendant of $h_i$ for $i<k$, while each $h_i$ is an ancestor of $h_k$.

A moral graph is an undirected graph obtained from a DAG by first finding the pairs of parents of a common child that are not connected, adding an edge between them, and then by removing the directionality of all edges. If no edges need to be added to a DAG to make it moral, we call it a perfect graph.

Let $G=(V,E)$ be a directed graph with vertices V and edges E. If $V_1$ is a subset of V, then the ancestral set of $V_1$, denoted $\text {An}(V_1)$, is the smallest subset of V that contains $V_1$ and such that for each $v \in \text {An}(V_1)$ all ancestors of v are also in $\text {An}(V_1)$.

Finally, consider three disjoint sets of vertices A, B, C in an undirected graph. We say that C separates A and B if, for every pair of vertices $a \in A$ and $b \in B$, every path connecting a and b passes through C.

Appendix B: Proofs

Proof (of Remark 1)

• 1. This proof is based on Schäfer et al. (2021b, Sect. 3.2). Split $\mathbf {w}= (w_1,\ldots ,w_n)^\top$ into two vectors, $\mathbf {u}=\mathbf {w}_{1:j-1}$ and $\mathbf {v}=\mathbf {w}_{j:n}$. Then,

  $$\begin{aligned} \mathbf {L}= & {} \mathbf {K}^{\frac{1}{2}} = \text {chol}\left( \begin{array}{cc} \mathbf {K}_{uu} &{} \mathbf {K}_{uv} \\ \mathbf {K}_{vu} &{} \mathbf {K}_{vv} \end{array}\right) \\= & {} \text {chol}\left( \left( \begin{array}{cc} \mathbf {I}&{} \mathbf {0}\\ \mathbf {K}_{vu}\mathbf {K}_{uu}^{-1} &{} \mathbf {I}\end{array}\right) \left( \begin{array}{cc} \mathbf {K}_{uu} &{} \mathbf {0}\\ \mathbf {0}&{} \mathbf {K}_{vv} - \mathbf {K}_{vu}\mathbf {K}_{uu}^{-1}\mathbf {K}_{uv} \end{array}\right) \right. \\&\left. \left( \begin{array}{cc} \mathbf {I}&{} \mathbf {K}_{uu}^{-1}\mathbf {K}_{uv} \\ \mathbf {0}&{} \mathbf {I}\end{array}\right) \right) \\= & {} \left( \begin{array}{cc} \mathbf {K}_{uu}^\frac{1}{2} &{} \mathbf {0}\\ \mathbf {K}_{vu}\mathbf {K}_{uu}^{-\frac{1}{2}} &{} \left( \mathbf {K}_{vv} - \mathbf {K}_{vu}\mathbf {K}^{-1}_{uu} \mathbf {K}_{vu}\right) ^\frac{1}{2}\end{array}\right) . \end{aligned}$$

  Note that $\mathbf {L}_{i,j}$ is the $(i-j+1)$th element in the first column of $\left( \mathbf {K}_{vv} - \mathbf {K}_{vu}\mathbf {K}^{-1}_{uu} \mathbf {K}_{vu}\right) ^\frac{1}{2}$, which is the Cholesky factor of ${{\,\mathrm{Var}\,}}(\mathbf {v}|\mathbf {u}) = \mathbf {K}_{vv} - \mathbf {K}_{vu}\mathbf {K}^{-1}_{uu} \mathbf {K}_{vu}$. Careful examination of the Cholesky factorization of a generic matrix $\mathbf {A}$, which is described in Algorithm 1 when setting $s_{i,j}=0$ for all (i, j), shows that the computations applied to the first column of $\mathbf {A}$ are fairly simple. In particular, this implies that

  $$\begin{aligned} \mathbf {L}_{i,j} = \big ({{\,\mathrm{chol}\,}}({{\,\mathrm{Var}\,}}(\mathbf {v}|\mathbf {u}))\big )_{i-j+1,1} = \frac{{{\,\mathrm{Cov}\,}}(w_i,w_j|\mathbf {w}_{1:j-1})}{\sqrt{{{\,\mathrm{Var}\,}}(w_j|\mathbf {w}_{1:j-1})}}, \end{aligned}$$

  because $w_j = \mathbf {v}_1$ and $w_i = \mathbf {v}_{i-j+1}$. Thus, $\mathbf {L}_{i,j}=0 \iff {{\,\mathrm{Cov}\,}}(w_i,w_j|\mathbf {w}_{1:j-1})=0 \iff w_i \perp w_j \, | \, \mathbf {w}_{1:j-1}$ because $\mathbf {w}$ was assumed to be jointly normal.

• 2. Theorem 12.5 in Rue and Held (2010) implies that for a Cholesky factor $\breve{\mathbf {U}}$ of a precision matrix $\mathbf {P}\mathbf {K}^{-1}\mathbf {P}$ of a normal random vector $\breve{\mathbf {w}} = \mathbf {P}\mathbf {w}$, we have $\breve{\mathbf {U}}_{i,j}=0 \iff \breve{w}_i \perp \breve{w}_j \,|\, \{\breve{\mathbf {w}}_{j+1:i-1}, \breve{\mathbf {w}}_{i+1:n}\}$. Equivalently, because $\mathbf {U}= \mathbf {P}\breve{\mathbf {U}}\mathbf {P}$, we conclude that $\mathbf {U}_{j,i}=0 \iff w_i \perp w_j \,|\, \{\mathbf {w}_{1:j-1}, \mathbf {w}_{j+1:i}\}$.$\square$

Proof (of Proposition 1)

The fact that ${\hat{p}}(\mathbf {x})$ is jointly normal holds for any Vecchia approximation (e.g., Datta et al. 2016; Katzfuss and Guinness 2021, Prop. 1). By straightforward extension of the proof of Katzfuss and Guinness (2021, Prop. 1) to the case with nonzero mean $\varvec{\mu }$, it can be shown that the Vecchia approximation does not modify the mean (only the covariance matrix). Hence, we can write ${\hat{p}}(\mathbf {x}) = \mathcal {N}_n(\mathbf {x}|\varvec{\mu },{\hat{\varvec{\Sigma }}})$.

• 1. First, note that $\mathbf {L}$ and $\mathbf {U}$ are lower- and upper-triangular matrices, respectively. Hence, we assume in the following that $j < i$ but $x_j \not \in \mathcal {C}_i$ and then show the appropriate conditional-independence results.

  • (a) By Remark 1, we only need to show that $x_i \perp x_j | \mathbf {x}_{1:j-1}$. Let G be the graph corresponding to factorization (3) and denote by $G_{\text {An}(A)}^m$ the moral graph of the ancestral set of A. By Corollary 3.23 in Lauritzen (1996), it is enough to show that $\left\{ x_1, \ldots , x_{j-1}\right\}$ separates $x_i$ and $x_j$ in $G_{An\left( \left\{ x_1, \ldots , x_j, x_i\right\} \right) }^m$. In the rest of the proof we label each vertex by its index, to simplify notation. We make three observations which can be easily verified. [1] $\text {An}\left( \left\{ 1, \ldots , j, i\right\} \right) \subset \left\{ 1, \ldots , i\right\}$; [2] Given the ordering of variables described in Sect. 3.1, if $k \rightarrow l$ then $k<l$; [3] G is a perfect graph, so $G_{An\left( \left\{ 1, \ldots , j, i\right\} \right) }^m$ is a subgraph of G after all edges are turned into undirected ones. We now prove Proposition 1.1.a by contradiction. Assume that $\left\{ x_1, \ldots , x_{j-1}\right\}$ does not separate $x_i$ and $x_j$, which means that there exists a path $(h_1, \ldots , h_k)$ in $\left\{ x_1, \ldots , x_i\right\}$ connecting $x_i$ and $x_j$ such that $h_k \in \text {An}(\left\{ 1, \ldots , j, i\right\} )$ and $j+1 \le h_k \le i-1$. There are four cases we need to consider and we show that each one of them leads to a contradiction. First, assume that the last edge in the path is $h_k \rightarrow j$. This violates observation [2]. Second, assume that the first edge is $i \leftarrow h_1$. But because of [1] we know that $h_1<i$, and by [2] we get a contradiction again. Third, let the path be of the form $i \rightarrow h_1 \leftarrow \cdots \leftarrow h_k \leftarrow j$ (i.e., all edges are of the form $h_r \leftarrow h_{r+1}$). However, this would mean that $\mathcal {X}_{j_1,\ldots ,j_\ell }\subset \mathcal {A}_{i_1,\ldots ,i_m}$, for $x_i\in \mathcal {X}_{i_1,\ldots ,i_m}$ and $x_j\in \mathcal {X}_{j_1,\ldots ,j_\ell }$. This implies that $j \in \mathcal {C}_i$, which in turn contradicts the assumption of the proposition. Finally, the only possibility we have not excluded yet is a path such that $i\leftarrow h_1 \cdots h_k \leftarrow j$ with some edges of the form $h_r \rightarrow h_{r+1}$. Consider the largest r for which this is true. Then by [3] there has to exist an edge $h_r \leftarrow h_p$ where $h_p \in \{h_{r+2}, \ldots , h_k, j\}$. But this means that j is an ancestor of $h_r$ so the path can be reduced to $i \rightarrow h_1, \ldots h_r \rightarrow j$. We continue in this way for each edge “$\leftarrow$” which reduces this path to case 3 and leads to a contradiction. Thus we showed that all paths in $G_{An\left( \left\{ 1, \ldots , j, i\right\} \right) }^m$ connecting i and j necessarily have been contained in $\left\{ 1, \ldots , j-1\right\}$, which proves Proposition 1.1.a.

  • (b) Like in part (a), we note that by Remark 1 it is enough to show that $x_i \perp x_j | \mathbf {x}_{1:j-1, j+1:i-1}$. Therefore, proceeding in a way similar to the previous case, we need to show that $\{1, \ldots , j-1, j+1, \ldots , i\}$ separates i and j in $G_{An\left( \left\{ 1, \ldots , i\right\} \right) }^m$. However, notice that it can be easily verified that $\text {An}(\{1, \ldots , i\}) \subset \{1, \ldots , i\})$, which means that $\text {An}(\{1, \ldots , i\}) = \{1, \ldots , i\})$. Moreover, observe that the subgraph of G generated by $\text {An}(\{1, \ldots , i\})$ is already moral, which means that if two vertices did not have a connecting edge in the original DAG, they also do not share an edge in $G^m_{1, \ldots , i}$. Thus i and j are separated by $\{1, \ldots , j-1, j+1, \ldots , i-1\}$ in $G^m_{1, \ldots , i}$, which by Corollary 3.23 in Lauritzen (1996) proves part (b).

• 2. Let $\mathbf {P}$ be the reverse-ordering permutation matrix. Let $\mathbf {B}= {{\,\mathrm{chol}\,}}(\mathbf {P}\hat{\varvec{\Sigma }}^{-1}\mathbf {P})$. Then $\mathbf {U}= \mathbf {P}\mathbf {B}\mathbf {P}$. By the definition of $\mathbf {B}$, we know that $\mathbf {B}\mathbf {B}^\top = \mathbf {P}\hat{\varvec{\Sigma }}^{-1}\mathbf {P}$, and consequently $\mathbf {P}\mathbf {B}\mathbf {B}^\top \mathbf {P}= \hat{\varvec{\Sigma }}^{-1}$. Therefore, $\hat{\varvec{\Sigma }} = \left( \mathbf {P}\mathbf {B}\mathbf {B}'\mathbf {P}\right) ^{-1}$. However, we have $\mathbf {P}\mathbf {P}= \mathbf {I}$ and $\mathbf {P}= \mathbf {P}^\top$, and hence $\hat{\varvec{\Sigma }} = \left( (\mathbf {P}\mathbf {B}\mathbf {P})(\mathbf {P}\mathbf {B}^\top \mathbf {P})\right) ^{-1}$. So we conclude that $\hat{\varvec{\Sigma }} = (\mathbf {U}\mathbf {U}^\top )^{-1} = (\mathbf {U}^\top )^{-1}\mathbf {U}^{-1} = (\mathbf {U}^{-1})^\top \mathbf {U}^{-1}$ and $(\mathbf {U}^{-1})^\top = \mathbf {L}$, or alternatively $\mathbf {L}^{-\top } = \mathbf {U}$.$\square$

Proof (of Proposition 2)

• 1. We observe that HV satisfies the sparse general Vecchia requirement specified in Katzfuss and Guinness (2021, Sect. 4), because the nested ancestor sets imply that $\mathcal {C}_j \subset \mathcal {C}_i$ for all $j<i$ with $i,j \in \mathcal {C}_k$. Hence, reasoning presented in Katzfuss and Guinness (2021, Proof of Prop. 6) allows us to conclude that $\widetilde{\mathbf {U}}_{j,i}= 0$ if $\mathbf {U}_{j,i}= 0$.

• 2. As the observations in $\mathbf {y}$ are conditionally independent given $\mathbf {x}$, we have

  $$\begin{aligned}&\hat{p}(\mathbf {x}|\mathbf {y}) \propto \hat{p}(\mathbf {x}) p(\mathbf {y}|\mathbf {x})\nonumber \\&\quad = \big ( \prod _{i=1}^n p(x_i|\mathcal {C}_i) \big ) \big ( \prod _{i \in \mathcal {I}} p(y_i|x_i) \big ), \end{aligned}$$

  (15)

  Let G be the graph representing factorization (3), and let $\tilde{G}$ be the DAG corresponding to (15). We order vertices in $\tilde{G}$ such that vertices corresponding to $\mathbf {y}$ have numbers $n+1, n+2, \ldots , n+|\mathcal {I}|$. For easier notation we also define $\tilde{\mathcal {I}} = \{i+n : i\in \mathcal {I}\}$. Similar to the proof of Proposition 1.1, we suppress the names of variables and use the numbers of vertices instead (i.e., we refer to the vertex $x_k$ as k and $y_j$ as $n+j$). Using this notation, and following the proof of Proposition 1, it is enough to show that $\{1, \ldots , j-1\} \cup \tilde{\mathcal {I}}$ separate i and j in $\tilde{\mathcal {G}}^m$, where $\tilde{\mathcal {G}} := G_{\text {An}(\{1, \ldots , j, i\} \cup \tilde{\mathcal {I}})}$. We first show that $1, \ldots , j-1$ separate i and j in G. Assume the opposite that there exists a path $(h_1, \ldots , h_k)$ in $\{j+1, \ldots , i-1, i+1, \ldots , n\}$ connecting $x_i$ and $x_j$. Let us start with two observations. First, note that the last arrow has to go toward j (i.e., $h_k \rightarrow j$), because $h_k>j$. Second, let $p_0 = \max \{p < k: h_p \rightarrow h_{p+1}\}$, the index of the last vertex with an arrow pointing toward j that is not $h_k$. If $p_0$ exists, then $(h_1, \ldots , h_{p_0})$ is also a path connecting i and j. This is because $h_{p_0}$ and j are parents of $h_{p_0+1}$, and so $h_{p_0} \rightarrow j$, because G is perfect and $h_p > j$. Now notice that a path $(h_1)$ (i.e., one consisting of a single vertex) cannot exist, because we would either have $i \rightarrow h_1 \rightarrow j$ or $i \leftarrow h_1 \leftarrow j$. The first case implies that $i \rightarrow j$, because in G a node is a direct parent of all its descendants. Similarly in the second case, because G is perfect and $j<i$, we also have that $i \leftarrow j$. In either case the assumption $j \not \in \mathcal {C}_i$ is violated. Now consider the general case of a path $(h_1, \ldots , h_k)$ and recall that by observation 1 also $h_k \leftarrow j$. But then the path $(h_1)$ also exists because by 3 all descendants are also direct children of their ancestors. As shown in the previous paragraph, we thus have a contradiction. Finally, consider the remaining case such that $p_0 = \max \{p:h_p \rightarrow h_{p+1}\}$ exists. But then $(h_1, \ldots , h_{p_0})$ is also a path connecting i and j. If all arrows in this reduced paths are to the left, we already showed it produces a contradiction. If not, we can again find $\max \{p: h_p \rightarrow h_{p+1}\}$ and continue the reduction until all arrows are in the same direction, which leads to a contradiction again. Thus we show that i and j are separated by $\{1, \ldots , j-1\}$ in G. This implies that they are separated by this set in every subgraph of G that contains vertices $\{1, \ldots , j, i\}$ and in particular in $\mathcal {G} := G_{An(\{1, \ldots , j-1\} \cup \{j\}\cup \{i\}\cup \tilde{\mathcal {I}})}$. Recall that we showed in Proposition 1 that G is perfect, which means that $\mathcal {G} = \mathcal {G}^m$. Next, for a directed graph $\mathcal {F} = (V, E)$ define the operation of adding a child as extending $\mathcal {F}$ to $\tilde{\mathcal {F}} = \left( V \cup \{w\}, E \cup \{v \rightarrow w\}\right)$ where $v \in V$. In other words, we add one vertex and one edge such that one of the old vertices is a parent and the new vertex is a child. Note that a perfect graph with an added child is still perfect. Moreover, because the new vertex is connected to only a single existing one, adding a child does not create any new connections between the old vertices. It follows that if C separates A and B in $\mathcal {F}$, then $C \cup \{w\}$ does so in $\bar{\mathcal {F}}$ as well. Finally, notice that $\tilde{\mathcal {G}}$, the graph we are ultimately interested in, can be obtained from $\mathcal {G}$ using a series of child additions. Because these operations preserve separation even after adding the child to the separating set, we conclude that i and j are separated by $\{1, \ldots , j-1\} \cup \tilde{\mathcal {I}}$ in $\tilde{\mathcal {G}}$. Moreover, because $\mathcal {G}$ was perfect and because graph perfection is preserved under child addition, we have that $\tilde{\mathcal {G}} = \tilde{\mathcal {G}}^m$.$\square$

Remark 2

Assuming the joint distribution $\hat{p}(\mathbf {x})$ as in (4), we have $\hat{p}(x_i, x_j)=p(x_i, x_j)$ if $x_j \in \mathcal {C}_i$; that is, the marginal bivariate distribution of a pair of variables is exact if one of the variables is in the conditioning set of the other.

Proof

First, consider the case where $x_i, x_j \in \mathcal {X}_{j_1,\ldots ,j_m}$. Then note that $\hat{p}(\mathcal {X}_{j_1,\ldots ,j_m}) = \int \hat{p}(\mathbf {x}) d\mathbf {x}_{-\mathcal {X}_{j_1,\ldots ,j_m}}$. Furthermore, notice that given the decomposition (3) and combining appropriate terms we can write

$$\begin{aligned} \hat{p}(\mathbf {x})= & {} p\left( \mathcal {X}_{j_1,\ldots ,j_m}|\mathcal {A}_{j_1,\ldots ,j_m}\right) p\left( \mathcal {A}_{j_1,\ldots ,j_m}\right) \\&p\left( \mathbf {x}_{-\left\{ \mathcal {X}_{j_1,\ldots ,j_m}\cup \mathcal {A}_{j_1,\ldots ,j_m}\right\} }\right) . \end{aligned}$$

Using these two observations, we conclude that

$$\begin{aligned}&\hat{p}(\mathcal {X}_{j_1,\ldots ,j_m}) = \int \hat{p}(\mathbf {x}) d\mathbf {x}_{-\mathcal {X}_{j_1,\ldots ,j_m}} \\&\quad = \int \prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_m}|\mathcal {A}_{j_1,\ldots ,j_m}) d(\mathcal {X}, \mathcal {X}_{j_1}, \\&\quad \quad \ldots , \mathcal {X}_{j_1,\ldots ,j_{m-1}}) = p(\mathcal {X}_{j_1,\ldots ,j_m}), \end{aligned}$$

which proves that $\hat{p}(x_i, x_j)=p(x_i, x_j)$ if $x_i, x_j \in \mathcal {X}_{j_1,\ldots ,j_m}$.

Now let $x_i \in \mathcal {X}_{j_1,\ldots ,j_m}$ and $x_j \in \mathcal {X}_{j_1,\ldots ,j_\ell }$ with $\ell < m$, because $x_j \in \mathcal {C}_i$ implies that $j<i$. Then,

$$\begin{aligned}&\hat{p}(\mathcal {X}_{j_1,\ldots ,j_m}, \mathcal {X}_{j_1,\ldots ,j_\ell }) \\&\quad =\int \hat{p}(\mathbf {x}) d\mathbf {x}_{-\{\mathcal {X}_{j_1,\ldots ,j_m}\cup \mathcal {X}_{j_1,\ldots ,j_\ell }\}} \\&\quad = \int \prod _{k=0}^M \prod _{j_1,\ldots ,j_k}p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}) d\mathbf {x}_{-\{\mathcal {X}_{j_1,\ldots ,j_m}\cup \mathcal {X}_{j_1,\ldots ,j_\ell }\}} \\&\quad = \int \prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}) d(A_{j_1,\ldots ,j_\ell }\cup \mathcal {X}_{j_1,\ldots ,j_{\ell +1}}\cup \\&\qquad \cdots \cup \mathcal {X}_{j_1,\ldots ,j_{m-1}}). \end{aligned}$$

The second equality uses (3), the definition of $\hat{p}$; the last equation is obtained by integrating out $\mathcal {X}^{0:M}\setminus \bigcup _{k=0}^m \mathcal {X}_{j_1,\ldots ,j_k}$. Note that $\mathcal {A}_{j_1,\ldots ,j_m}= \mathcal {A}_{j_1,\ldots ,j_\ell }\cup \bigcup _{k=\ell }^{m-1} \mathcal {X}_{j_1,\ldots ,j_k}$. Therefore, by Bayes law, for any $k>\ell$:

$$\begin{aligned} p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k})= & {} p\left( \mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_\ell }\cup (\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })\right) \\= & {} \frac{p\left( \mathcal {A}_{j_1,\ldots ,j_\ell }| \mathcal {X}_{j_1,\ldots ,j_k}\cup (\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })\right) p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })}{p(\mathcal {A}_{j_1,\ldots ,j_\ell }|\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })} \\= & {} \frac{p(\mathcal {A}_{j_1,\ldots ,j_\ell }|\mathcal {A}_{j_1,\ldots ,j_{k+1}}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })}{p(\mathcal {A}_{j_1,\ldots ,j_\ell }|\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell })} = (*) \end{aligned}$$

The last equality holds because $\mathcal {X}_{j_1,\ldots ,j_m}\cup \mathcal {A}_{j_1,\ldots ,j_m}= \mathcal {A}_{j_1,\ldots ,j_{m+1}}$. As a consequence

$$\begin{aligned}&\prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}) \\&\quad = \prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_k}|\mathcal {A}_{j_1,\ldots ,j_k}\setminus \mathcal {A}_{j_1,\ldots ,j_\ell }) p(\mathcal {A}_{j_1,\ldots ,j_\ell }) \\&\quad = \prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_k}|\bigcup _{s=k-1}^\ell \mathcal {X}_{j_1,\ldots ,j_s}) p(\mathcal {A}_{j_1,\ldots ,j_\ell }) \end{aligned}$$

and

$$\begin{aligned} (*)&= \int \prod _{k=0}^m p(\mathcal {X}_{j_1,\ldots ,j_m}|\mathcal {A}_{j_1,\ldots ,j_m}) p(\mathcal {A}_{j_1,\ldots ,j_\ell })\\&\quad d(\mathcal {A}_{j_1,\ldots ,j_\ell }\cup \mathcal {X}_{j_1,\ldots ,j_{\ell +1}}\cup \cdots , \cup \mathcal {X}_{j_1,\ldots ,j_{m-1}}) \\&= \int p(\mathcal {X}_{j_1,\ldots ,j_m}, \mathcal {X}_{j_1,\ldots ,j_{m-1}}, \ldots , \mathcal {X}_{j_1,\ldots ,j_\ell }, \mathcal {A}_{j_1,\ldots ,j_\ell })\\&\quad d(\mathcal {A}_{j_1,\ldots ,j_\ell }\cup \mathcal {X}_{j_1,\ldots ,j_{\ell +1}}\cup \cdots , \cup \mathcal {X}_{j_1,\ldots ,j_{m-1}}) \\&= p(\mathcal {X}_{j_1,\ldots ,j_m}, \mathcal {X}_{j_1,\ldots ,j_\ell }) \end{aligned}$$

This means that $\hat{p}(\mathcal {X}_{j_1,\ldots ,j_m}, \mathcal {X}_{j_1,\ldots ,j_\ell }) =$ $p(\mathcal {X}_{j_1,\ldots ,j_m}, \mathcal {X}_{j_1,\ldots ,j_\ell })$, or that the marginal distribution of $\mathcal {X}_{j_1,\ldots ,j_m}$ and $\mathcal {X}_{j_1,\ldots ,j_\ell }$ in (3) is the same as in the true distribution p. Because p is Gaussian, it follows that $\hat{p}(x_i, x_j) = p(x_i, x_j).$ This ends the proof. $\square$

Proof (of Proposition 3)

We use $l^\text {inc}_{i,j}$, $l_{i,j}$, $\sigma _{i,j}$, $\hat{\sigma }_{i,j}$ to denote the (i, j)th elements of $\mathbf {L}^\text {inc} = {{\,\mathrm{\text {ichol}}\,}}(\varvec{\Sigma }, \mathbf {S})$, $\mathbf {L}= {{\,\mathrm{chol}\,}}({\hat{\varvec{\Sigma }}})$, $\varvec{\Sigma }$, $\hat{\varvec{\Sigma }}$, respectively. It can be seen easily in Algorithm 1 that ${{\,\mathrm{chol}\,}}(\varvec{\Sigma })={{\,\mathrm{\text {ichol}}\,}}(\varvec{\Sigma }, \mathbf {S}^{\varvec{1}})$, where $\mathbf {S}^{\varvec{1}}_{i,j} = 1$ for $i\ge j$ and 0 otherwise.

We prove that $l^\text {inc}_{i,j}=l_{i,j}$ by induction over the elements of the Cholesky factor, following the order in which they are computed. First, we observe that $l^\text {inc}_{1,1}=l_{1,1}$. Next, consider the computation of the (i, j)th entry, assuming that we have $l^\text {inc}_{k,q}=l_{k,q}$ for all previously computed entries. According to Algorithm 1, we have

$$\begin{aligned} l_{i,j}= & {} \frac{1}{l_{j,j}} \big ( \hat{\sigma }_{i,j} - \sum _{k=1}^{j-1}l_{i,k}l_{j,k} \big ), \nonumber \\ l^{inc}_{i,j}= & {} \frac{s_{i,j}}{l_{j,j}} \big ( \sigma _{i,j} - \sum _{k=1}^{j-1}l_{i,k}l_{j,k} \big ). \end{aligned}$$

(16)

Now, if $s_{i,j}=1 \iff x_j \in \mathcal {C}_i$, then Remark 2 tells us that $\sigma _{i,j} = \hat{\sigma }_{i,j}$, and hence $l_{i,j} = l^\text {inc}_{i,j}$. If $s_{i,j}=0 \iff x_j \not \in \mathcal {C}_i$, then $l^\text {inc}_{i,j}=0$, and also $l_{i,j}=0$ by Proposition 1.1(a). This completes the proof via induction. $\square$

Remark 3

Let $\mathbf {x}$ have density $\hat{p}(\mathbf {x})$ as in (3), and let each conditioning set $\mathcal {C}_i$ have size at most N. Then $\varvec{\Lambda }$, the precision matrix of $\mathbf {x}$, has $\mathcal {O}(nN)$ nonzero elements. Moreover, the columns of $\mathbf {U}= {{\,\mathrm{rchol}\,}}(\varvec{\Lambda })$ and the rows of $\mathbf {L}= {{\,\mathrm{chol}\,}}(\varvec{\Lambda }^{-1})$ each have at most $N$ nonzero elements.

Proof

Because the precision matrix is symmetric, it is enough to show that there are only $\mathcal {O}(nN)$ nonzero elements $\varvec{\Lambda }_{i,j}$ in the upper triangle (i.e., with $i<j$). Let $x_i \not \in \mathcal {C}_j$. This means that $x_i \not \rightarrow x_j$ and because by (3) all edges go from a lower index to a higher index, $x_i$ and $x_j$ are not connected. Moreover, because $\mathcal {A}_{j_1,\ldots ,j_m}\supset \mathcal {A}_{j_1,\ldots ,j_{m-1}}$ there is also no $x_k$ with $k>\max (i,j)$ such that $x_i \rightarrow x_k$ and $x_j \rightarrow x_k$. Thus, using Proposition 3.2 in Katzfuss and Guinness (2021) we conclude that $\varvec{\Lambda }_{i,j}=0$ for $x_i \not \in \mathcal {C}_j$. This means that each row i has at most $|\mathcal {C}_i|\le N$ nonzero elements, and the entire lower triangle has $\mathcal {O}(nN)$ nonzero values.

Proposition 1 implies that the ith column of $\mathbf {U}$ has at most as many nonzero entries as there elements in the conditioning set $\mathcal {C}_i$, which we assumed to be of size at most $N$. Similarly, the ith row of $\mathbf {L}$ has at most as many nonzero entries as the number of elements in the conditioning set $\mathcal {C}_i$. $\square$

Remark 4

Let $\mathbf {A}$ be an $n \times n$ lower triangular matrix with at most $N<n$ nonzero elements in each row at known locations. Letting $a_{ij}$ and $\tilde{a}_{ij}$ be the (i, j)th element of $\mathbf {A}$ and $\mathbf {A}^{-1}$, respectively, assume that $\tilde{a}_{i,j}=0$ if $a_{i,j}=0$. Then, the cost of calculating $\mathbf {A}^{-1}$ from $\mathbf {A}$ is $\mathcal {O}(nN^2)$.

Proof

Notice that calculating $\tilde{\mathbf {a}}_k$, the kth column of $\mathbf {A}^{-1}$, is equivalent to solving a linear system of the form

$$\begin{aligned} \left[ \begin{array}{ccccc} a_{11} &{} 0 &{} 0 &{} \cdots &{} 0 \\ a_{21} &{} a_{22} &{} 0 &{} \cdots &{} 0 \\ a_{31} &{} a_{32} &{} a_{33} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ a_{n1} &{} a_{n2} &{} a_{n3} &{} \cdots &{} a_{nn} \end{array}\right] \left[ \begin{array}{c} \tilde{a}_{1k} \\ \tilde{a}_{2k} \\ \tilde{a}_{3k} \\ \vdots \\ \tilde{a}_{nk} \end{array}\right] =e_k, \end{aligned}$$

(17)

where $e_{ik} = 1$ if $k=i$ and 0 otherwise. Using forward substitution, the ith element of $\tilde{\mathbf {a}}_k$ can be calculated as $\tilde{a}_{ik} = \frac{1}{a_{kk}}\left( e_{ik} - \sum _{j=1}^{i-1}a_{ij}\tilde{a}_{jk}\right)$. This requires $\mathcal {O}(N)$ time, because our assumptions imply that there are at most N nonzero terms under the summation. Moreover, we also assumed that $\tilde{\mathbf {a}}_k$ has at most $N$ nonzero elements at known locations, and so we only need to calculate those. Thus computing $\tilde{\mathbf {a}}_k$ has $\mathcal {O}(N^2)$ time complexity. As there are n columns to calculate, this ends the proof. $\square$

Proof (of Proposition 4)

Starting with the ichol() procedure in Line 1, obtaining each nonzero element $l_{i,j}$ requires calculating the outer product of previously computed segments of rows i and j. Because Remark 3 implies that each row of $\mathbf {L}$ has at most $N$ nonzero elements, obtaining $l_{i,j}$ is $\mathcal {O}(N)$. Remark 3 also shows that for each i, there are at most $N$ nonzero elements $s_{i,j}=1$, which implies that each row of the incomplete Cholesky factor can be calculated in $\mathcal {O}(N^2)$. Finally, because the matrix to be decomposed has n rows, the overall cost of the algorithm is $\mathcal {O}(nN^2)$. In Line 2, because $\mathbf {L}^{-1} = \mathbf {U}^\top$, Proposition 1 tells us exactly which elements of $\mathbf {L}^{-1}$ need to be calculated (i.e., are nonzero) and that there are only $N$ of them (Remark 3). Using Remark 4, this means that computing $\mathbf {L}^{-1}$ can be accomplished in $\mathcal {O}(nN^2)$ time. Analogous reasoning and Proposition 2 allow us to conclude that computing $\widetilde{\mathbf {L}}$ in Line 5 has the same complexity. The cost of Line 3 is dominated by taking the outer product of $\mathbf {U}$, because $\mathbf {H}$ and $\mathbf {R}$ are assumed to have only one nonzero element in each row. However, $\mathbf {U}\mathbf {U}^\top$ is by definition equal to the precision matrix of $\mathbf {x}$ under (3). Therefore, by Remark 3 there are at most $\mathcal {O}(nN)$ elements to calculate and each requires multiplication of two rows with at most N nonzero elements. This means that this step can be accomplished in $\mathcal {O}(nN^2)$ time. The most expensive operation in Line 4 is taking the Cholesky factor. However, its cost proportional to the square of the number of nonzero elements in each column (e.g., Toledo 2021, Thm. 2.2), which by Remark 3 we know to be $N$. As there are n columns, this step requires $\mathcal {O}(nN^2)$ time. Finally, the most expensive operation in Line 6 is the multiplication of a vector by matrix ${\widetilde{\mathbf {L}}}$. By Proposition 2, $\widetilde{\mathbf {L}}$ has the same number of nonzero elements per row as $\mathbf {L}$, which is at most $N$ by Remark 3. Thus, multiplication of $\widetilde{\mathbf {L}}$ and any dense vector can be performed in $\mathcal {O}(nN)$ time. To conclude, each line of Algorithm 2 can be computed in at most $\mathcal {O}(nN^2)$ time, and so the total time complexity of the algorithm is also $\mathcal {O}(nN^2)$.

Regarding memory complexity, notice that by Remarks 3 and 1, matrices $\mathbf {L}$, $\mathbf {U}$, $\widetilde{\mathbf {L}}$, $\widetilde{\mathbf {U}}$, and $\varvec{\Lambda }$ have $\mathcal {O}(nN)$ nonzero elements, and (1) implies that matrices $\mathbf {H}$ and $\mathbf {R}$ have at most n entries. Further, the incomplete Cholesky decomposition in Line 1 requires only those elements of $\varvec{\Sigma }$ that correspond to the nonzero elements of $\mathbf {S}$. Because $\mathbf {S}$ has at most $N$ nonzero elements in each row by construction, each of the matrices that are decomposed can be stored using $\mathcal {O}(nN)$ memory, and so the memory requirement for Algorithm 2 is $\mathcal {O}(nN)$. $\square$