1 Introduction

The problem of inferring unknown parameters associated with the solution of (partial) differential equations (PDEs) is referred to as an inverse problem. In such a context, when the forward problem is well posed, the inverse problem is often ill-posed and challenging to solve, even numerically. The area has a long history and a large literature (see e.g. Engl et al. (1996); Tikhonov and Glasko (1964)) yet the intersection with statistics is still comparatively small, particularly considering the significant overlap, in terms of methods, algorithms as well as objectives. If one adopts a Bayesian approach to solution of the inverse problem, then the object of interest is a posterior distribution and, in particular, expectations with respect to this distribution (Franklin 1970; Stuart 2010). While this provides an elegant solution and quantified uncertainty via well-defined target distribution, it is more computationally challenging to solve than its deterministic counterpart. Here, we assume solution of the Bayesian inverse problem (BIP) requires computationally intensive Monte Carlo methods for accurate estimation. We furthermore assume that the statistical model can only be defined up to some unknown parameters.

Consider a BIP with unknown \(u\in {\mathsf {X}}\) and data \(y \in {\mathsf {Y}}\), related through a PDE, and assume that there is an unknown parameter \(\theta \in \Theta \subseteq {\mathbb {R}}^{d_{\theta }}\) in the sense that one could consider the posterior density

$$\begin{aligned} p(u, \theta | y) \propto p(y | u, \theta ) p(u|\theta )p(\theta ) \end{aligned}$$

where \(p(y | u, \theta )\) is the conditional likelihood function of \(Y|(u,\theta )\), \(p(u|\theta )\) is the prior on the unknown u, for a given \(\theta \), and p is some prior density for \(\theta \). Due to the strong correlation of the unknown u with respect to the parameter \(\theta \), such posterior distributions can be highly complex and very challenging to sample from, even using quite advanced Markov chain Monte Carlo (MCMC) algorithms. In this article, the unknown u is treated as a nuisance parameter and the goal is to maximize the marginal likelihood of the parameters

$$\begin{aligned} p_{\theta }(y) = \int _{\mathsf {X}} p_{\theta }(y|u) p_{\theta }(u)du \end{aligned}$$

where we have dropped the conditioning on \(\theta \) and used subscripts instead, as is classical in the literature (e.g. Cappé et al. (2005)) and du is a sigma-finite measure on some measurable space \(({\mathsf {X}},{\mathcal {X}})\). Maximum likelihood estimation based upon the marginal likelihood appears in a wide variety of modelling contexts (e.g. Gland and Mevel (1997)), and the resulting estimators often have desirable mathematical properties, e.g. Cappé et al. (2005) in the context of hidden Markov models. In our given scenario, one is left with a finite-dimensional optimization problem, albeit with an objective function that is not available analytically. This intractability arises from two sources:

  • first, for a given \((u,\theta )\) only a discretization of the likelihood \(p_{\theta }(y|u)\) can be evaluated;

  • second, the discretized marginal likelihood is a high-dimensional integral which itself must be approximated.

Moreover, the associated gradient of the log-likelihood is not available, which may be of interest in optimization algorithms. In the following, we will suppress the notation for fixed observation y and present the method generally. In particular, we use the notation \(\gamma _\theta (u) = p_{\theta }(y | u) p_{\theta }(u)\). We will set \(Z_\theta = p_{\theta }(y)\) and \(\eta _{\theta }(du) = [\gamma _{\theta }(u)/Z_{\theta }]du\)

In this article, we present a new scheme to provide finite variance estimates of the gradient of the log-likelihood that are unbiased. To be precise, let \(E_{\theta } = \nabla _\theta \log ( Z_\theta )\) denote the gradient of the log-likelihood with no discretization bias. The proposed method provides an estimator \({\hat{E}}_{\theta }\) such that \({\mathbb {E}}[{\hat{E}}_{\theta }]=E_{\theta }\), where \({\mathbb {E}}\) is the expectation with respect to the randomization induced by our numerical approach. Moreover, the estimator \({\hat{E}}_{\theta }\) is constructed so that one only needs access to finite resolution (discretized) approximations of the BIP. This scheme is of interest for several reasons:

  1. 1.

    Unbiased estimates of gradients help to facilitate stochastic gradient algorithms;

  2. 2.

    The method is easy to parallelize;

  3. 3.

    The method helps to provide a benchmark for other computations.

In terms of the first point, it is often simpler to verify the validity of stochastic gradient algorithms when the estimate of the noisy functional is unbiased e.g. Benveniste et al. (1990). While this is not always needed (see Tadic and Doucet (2018) for a special case, which does not apply in our context), it at least provides the user a peace of mind when implementing optimization schemes. The second point relates to efficiency of implementation relative to competing methods. Indeed the method delivers independent and identically distributed (i.i.d.) unbiased estimators of expectations with respect to the posterior, which are therefore “embarrassingly parallel” to simulate. Synchronization is only required to average these in order to construct the final estimator. This is a scalar operation, so is unlikely to impact the strong scaling with reasonably complex models and existing (super)computer architectures. The practical limitations in terms of memory will be investigated in a future publication. The third point simply states that one can check the precision of biased methodology. We now explain the approach in a little more detail.

The method that we use is based upon a technique developed in Jasra et al. (2020). In that article, the authors consider the filtering of a class of diffusion processes, which have to be discretized. The authors develop a method which allows one to approximate the filtering distribution, unbiasedly and without any discretization error. The methodology that is used in Jasra et al. (2020) is a double randomization scheme based upon the approaches in McLeish (2011); Rhee and Glynn (2015). The work in McLeish (2011); Rhee and Glynn (2015) provides a methodology to turn a sequence of convergent estimators into an unbiased estimator, using judicious randomization across the level of discretization. It is determined for the problem of interest in Jasra et al. (2020) that an additional randomization is required in order to derive efficient estimators, that is, estimators that are competitive with the existing state-of-the-art methods in the literature. In this article, we follow the basic approach that is used in Jasra et al. (2020), except that one cannot use the same estimation methodology for the current problem. An approach is introduced in Beskos et al. (2017b) which enables application of the related deterministic multilevel Monte Carlo identity (Vihola 2018) to a sequential Monte Carlo (SMC) sampler Del Moral (2013, 2004) for inference in the present context. In this article, we consider such a strategy to allow the application of the approach in Jasra et al. (2020) to unbiasedly estimate the gradient of the log-likelihood for BIPs. The method of Beskos et al. (2017b) is one of the most efficient techniques that could be used for estimation of the gradient of the log-likelihood for BIPs. However, this method is subject to discretization bias. In other words, suppose \(E_{\theta }^l\) is the gradient of the log-likelihood with a choice of discretization bias level, e.g. \(2^{-l}\). The original method would produce an estimate \({\hat{E}}_{\theta }^l\) for which \({\mathbb {E}}[{\hat{E}}_{\theta }^l] \ne E_{\theta }^l\). On the other hand, under assumptions, it is proved that the new method introduced here can produce an estimate \(E_{\theta }\) with finite variance and without bias, i.e. \({\mathbb {E}}[{\hat{E}}_{\theta }] = E_{\theta }^\infty \). We also show that the cost to achieve a given variance is very similar to the multilevel SMC (MLSMC) approach of Beskos et al. (2017b), with high probability. This is confirmed in numerical simulations. We furthermore numerically investigate the utility of our new estimator in the context of stochastic gradient algorithms, where it is shown that a huge improvement in efficiency is possible.

Our approach is one of the first which can in general provide unbiased and finite variance estimators of the gradient of the log-likelihood for BIPs. A possible alternative would be the approach of Agapiou et al. (2018); however, the methodology in that article is not as general as is presented here. In more detail, the work presented in Agapiou et al. (2018) considers unbiased estimation of expectations associated with particular classes of BIP, namely ones with either uniform or Gaussian priors. The article uses the randomization schemes of McLeish (2011); Rhee and Glynn (2015) along with particular coupled Markov chain simulation schemes. In the case of uniform priors, the methodology is based upon a global minorization condition, which is not reasonable in that case, but not if the priors (when truncated to finite dimension) lie on a non-compact state space. In the case of Gaussian priors, the approach is based upon a synchronous coupling of a type of Metropolis–Hastings algorithm. Such couplings require strong assumptions and may not always mix well. We do not constrain our BIP to uniform or Gaussian priors, and in principle, one does not need a particularly restrictive set of assumptions to apply our methodology. Certain hypotheses are made in order to ensure our proofs are reasonably concise, but these can be relaxed. See Del Moral et al. (2017) for an example.

This article is structured as follows. In Sect. 2, we explain the generic problem to which our approach is applicable. In particular, a concrete example in the context of Bayesian inverse problems is described. In Sect. 3, we present our methodology and the proposed estimator. In Sect. 4, we show that our proposed estimator is unbiased and of finite variance and we consider the cost to obtain the estimate. In Sect. 5, several numerical examples are presented to investigate performance of the estimator in practice, including the efficiency of the estimator when used in the relevant context of a stochastic gradient algorithm for parameter estimation. In “Appendix A”, the proofs of some of our theoretical results can be found.

2 Problem setting

2.1 Generic problem

Let \(({\mathsf {X}},{\mathcal {X}})\) be a measurable space, and define a probability measure on it as

$$\begin{aligned} \eta _{\theta }(du) = \frac{\gamma _{\theta }(u)du}{\int _{{\mathsf {X}}}\gamma _{\theta }(u)du} \end{aligned}$$

where \(\theta \in \Theta \subseteq {\mathbb {R}}^{d_{\theta }}\), \(\gamma :\Theta \times {\mathsf {X}}\rightarrow {\mathbb {R}}_+\) and recall du is a sigma-finite measure on \(({\mathsf {X}},{\mathcal {X}})\). We are interested in computing

$$\begin{aligned}&\nabla _{\theta }\log \Big (\int _{{\mathsf {X}}}\gamma _{\theta }(u)du\Big )\\&\quad = \frac{1}{\int _{{\mathsf {X}}}\gamma _{\theta }(u)du}\nabla _{\theta }\Big (\int _{{\mathsf {X}}}\gamma _{\theta }(u)du\Big )\\&\quad = \frac{1}{\int _{{\mathsf {X}}}\gamma _{\theta }(u)du}\int _{{\mathsf {X}}}\frac{\nabla _{\theta }\{\gamma _{\theta }(u)\}}{\gamma _{\theta }(u)}\gamma _{\theta }(u)du \\&\quad = \int _{{\mathsf {X}}}\frac{\nabla _{\theta }\{\gamma _{\theta }(u)\}}{\gamma _{\theta }(u)}\eta _{\theta }(du) \\&\quad = \int _{{\mathsf {X}}}\nabla _{\theta }\log \Big (\gamma _{\theta }(u)\Big ) \eta _{\theta }(du) \\&\quad = \int _{{\mathsf {X}}}\varphi _{\theta }(u) \eta _{\theta }(du) \, , \end{aligned}$$

where we have defined \(\varphi _{\theta }(u) = \nabla _{\theta }\log \Big (\gamma _{\theta }(u)\Big )\) and we are assuming it is legitimate to interchange differentiation and integration in the second line. From here on, we will use the following shorthand notation for a measure \(\mu \) on \(({\mathsf {X}},{\mathcal {X}})\) and a measurable \(\mu -\)integrable \(\varphi :{\mathsf {X}}\rightarrow {\mathbb {R}}^d\)

$$\begin{aligned} \mu (\varphi ):=\int _{{\mathsf {X}}}\varphi (x)\mu (dx) \, , \end{aligned}$$

which should be understood as a column vector of integrals.

In practice, we assume that we must work with an approximation of \(\varphi _{\theta }(u)\) and \(\eta _{\theta }(du)\). Let \(l\in {\mathbb {N}}_0\), and set

$$\begin{aligned} \eta _{\theta }^l(du) = \frac{\gamma _{\theta }^l(u)du}{\int _{{\mathsf {X}}}\gamma _{\theta }^l(u)du} \end{aligned}$$

where \(\gamma ^l:\Theta \times {\mathsf {X}}\rightarrow {\mathbb {R}}_+\). We are now interested in computing

$$\begin{aligned}&\nabla _{\theta }\log \Big (\int _{{\mathsf {X}}}\gamma _{\theta }^l(u)du\Big ) \\&\quad = \int _{{\mathsf {X}}}\nabla _{\theta }\log \Big (\gamma _{\theta }^l(u)\Big ) \eta _{\theta }^l(du) \\&\quad = \int _{{\mathsf {X}}}\varphi _{\theta }^l(u) \eta _{\theta }^l(du). \end{aligned}$$

It is assumed explicitly that \(\forall \theta \in \Theta \)

$$\begin{aligned} \lim _{l\rightarrow +\infty }\eta _{\theta }^l(\varphi _{\theta }^l) = \eta _{\theta }(\varphi _{\theta }). \end{aligned}$$

2.2 Example of problem

We will focus on the following particular problem as an example. Let \(D\subset {\mathbb {R}}^d\) with \(\partial D\in C^1\) convex and \(f\in L^2(D)\). Consider the following PDE on D:

$$\begin{aligned}&-\nabla \cdot ({\hat{u}}^s(u)\nabla v) =f,\quad \text { on } D, \end{aligned}$$
(1)
$$\begin{aligned}&\quad v= 0, \quad \text { on } \partial D \, . \end{aligned}$$
(2)

Two examples of diffusion coefficients will be considered

$$\begin{aligned} {\hat{u}}^s(x; u) = {\left\{ \begin{array}{ll} {\bar{u}} + \sum _{k=1}^K u_k\sigma _k\phi _k(x) \, , \quad s=1 \, ,\\ \sum _{k=1}^K \exp (u_k) \phi _k(x) \, , \quad ~ s=2 \, . \end{array}\right. } \end{aligned}$$
(3)

For any \(s \in \{1,2\}\), we define \(u=\{u_k\}_{k=1}^K\), and the state space will be \({\mathsf {X}}=\prod _{k=1}^K[-1,1]\). Let \(v(\cdot ;u)\) denote the weak solution of (1) for parameter value u. If \(s=1\), the prior is given by \(u_k \sim U[-1,1]\) (the uniform distribution on \([-1,1]\)) i.i.d. for \(k=1,\dots , K\). If \(s=2\), the prior is given by the truncated normal \(u \sim \mathbf{1}_{u \in {\mathsf {X}}} N(0, \Sigma _\theta )\), where \(N(0,\Sigma _\theta )\) denotes the normal random variable with mean 0 and covariance matrix \(\Sigma _\theta \), and \(\mathbf{1}_{{\mathsf {X}}}\) is the indicator function on the set \({\mathsf {X}}\). In this case, the prior depends on some parameters \(\theta \in \Theta \) through \(\Sigma _\theta \). The covariance matrix \(\Sigma _\theta \) is defined element-wise by \(\Sigma _{\theta ,ij} = \theta _1 \exp ( -\theta _2 \Vert x_i - x_j\Vert ^2 )\). The notation \(\Vert \cdot \Vert \) is always used for the \(L^2-\)norm, either the Euclidean norm of the appropriate dimension or the \(L^2(D)\) norm. The corresponding inner products will be denoted \(\langle \cdot , \cdot \rangle \). The following will be assumed.

(H1):

If \(s=1\), then \(\phi _k \in C(D)\), \(\Vert \phi _k\Vert _\infty \le 1\), and there is a \(u_*>0\) such that \({\bar{u}} > \sum _{k=1}^K\sigma _k + u_*\). If \(s=2\) then \(\phi _k\) are piecewise multilinear nodal basis functions as described in Sect. 2.2.1, such that \({{\hat{u}}}^s(u)\) interpolates between the coefficients \(\exp (u_k)\).

Note that under Assumption (H1), \({{\hat{u}}}^s(u) > \min \{u_*,\exp (-1)\}\) uniformly in u for any \(s \in \{1,2\}\). Hence, there is a well-defined (weak) solution \(v(\cdot ;u)\) which is bounded in uniformly in u in \(L^\infty (D)\) and \(L^2(D)\) and its gradient is also bounded uniformly in u in \(L^2(D)\)Ciarlet (2002); Dashti and Stuart (2011). Define the following vector-valued function

$$\begin{aligned} {\mathcal {G}}(u) = [\langle g_1, v(\cdot ;u)\rangle ,\dots ,\langle g_m, v(\cdot ;u)\rangle ]^{\intercal }, \end{aligned}$$

where \(g_i \in L^2(D)\) for \(i=1,\dots ,m\). We note that pointwise evaluation is also permissible since \(u \in L^\infty (D)\), i.e. \(g_i\) can be Dirac delta functions; however, for simplicity we restrict the presentation to \(L^2(D)\). It is assumed that the data take the form

$$\begin{aligned} y = {\mathcal {G}}(u) + \xi ,\quad \xi \sim N(0,\theta _3^{-1}\cdot {\varvec{I}}_m),\quad \xi \perp u \, , \end{aligned}$$

where \(\perp \) denotes independence. The un-normalized density of u for fixed \(\theta \) is then given by the following (if \(s=1\) then \(d_\theta =1\) and we use the notation \(\theta =\theta _3\))

$$\begin{aligned} \gamma _{\theta ,s}(u) = {\left\{ \begin{array}{ll} \theta ^{m/2}\exp \Big (-\frac{\theta }{2}\Vert {\mathcal {G}}(u) - y\Vert ^2\Big ) {{{\mathbf {1}}}}_{\mathbf {u \in {\mathsf {X}}}} \, , \quad s=1 \, ,\\ \theta _3^{m/2}\exp \Big (-\frac{\theta _3}{2}\Vert {\mathcal {G}}(u) - y\Vert ^2\Big ) \exp \left( -\frac{1}{2}\Vert \Sigma _\theta ^{-1/2}u \Vert ^2 \right) {{{\mathbf {1}}}}_{\mathbf {u \in {\mathsf {X}}}} \, , \qquad s=2 \, . \end{array}\right. } \end{aligned}$$
(4)

The normalized density is given by

$$\begin{aligned} \eta _{\theta ,s}(u) = \frac{\gamma _{\theta ,s}(u)}{Z_{\theta ,s}} \, , \end{aligned}$$

where \(Z_{\theta ,s} = {\int _{{\mathsf {X}}}\gamma _{\theta ,s}(u)du}\), and the quantity of interest is defined for \(u \in {\mathsf {X}}\) as

$$\begin{aligned} \varphi _{\theta ,s}(u) := \nabla _{\theta }\log \Big (\gamma _{\theta ,s}(u)\Big ) = {\left\{ \begin{array}{ll} \frac{m}{2\theta } - \frac{1}{2}\Vert {\mathcal {G}}(u) - y\Vert ^2 \, , ~~~\qquad s=1 \, ,\\ \begin{pmatrix} \frac{1}{2} u^{\intercal } \Sigma _\theta ^{-1} \frac{\partial \Sigma _\theta }{\partial \theta _1} \Sigma _\theta ^{-1} u \\ \frac{1}{2} u^{\intercal } \Sigma _\theta ^{-1} \frac{\partial \Sigma _\theta }{\partial \theta _2} \Sigma _\theta ^{-1} u \\ \frac{m}{2\theta _3} - \frac{1}{2}\Vert {\mathcal {G}}(u) - y\Vert ^2 \\ \end{pmatrix} \, , \qquad \qquad s=2 \, . \end{array}\right. } \end{aligned}$$
(5)

Henceforth, the notation s will be suppressed except when it is necessary to refer to the above explicit example. The method presented is very general and applicable to essentially any problem of the form presented in Sect. 2.1, as long as it satisfies appropriate assumptions which will be provided below.

2.2.1 Numerical approximation

The finite element method (FEM) is utilized for solution of (2) with piecewise multilinear nodal basis functions. For \(s=1\), we will let \(d=1\) and \(D=[0,1]\), while for \(s=2\) we will let \(d=2\) and \(D=[0,1]^2\). For brevity, we will completely present only the case \(s=1\). For the case \(s=d=2\), the product of such piecewise linear functions described below is used to generate a bilinear approximation on \([0,1]^2\). The reader is referred to Section 5.3 of Beskos et al. (2017a) for details. We note the approach is easily generalized following standard FEM literature Brenner and Scott (2007). As mentioned above, the notation for s is suppressed here.

The PDE problem at resolution level l is solved using FEM with piecewise linear shape functions on a uniform mesh of width \(h_l=2^{-l}\), for \(l\ge 0\). Thus, on the lth level the finite element basis functions are \(\{\psi _i^l\}_{i=1}^{2^l-1}\) defined as (for \(x_i = i\cdot 2^{-l}\)):

$$\begin{aligned} \psi _i^l(x) = \left\{ \begin{array}{ll} (1/h_l)[x-(x_i-h_l)] &{} \text {if}~x\in [x_i-h_l,x_i], \\ (1/h_l)[x_i+h_l-x] &{} \text {if}~x\in [x_i,x_i+h_l] \, . \end{array}\right. \end{aligned}$$

To solve the PDE, \(v^l(x)=\sum _{i=1}^{2^l-1}v_i^l\psi _i^l(x)\) is plugged into (1) and projected onto each basis element:

$$\begin{aligned} -\Big \langle \nabla \cdot \Big ({\hat{u}}\nabla \sum _{i=1}^{2^l-1}v_i^l \psi _i^l \Big ),\psi _j^l \Big \rangle = \langle f, \psi _j^l \rangle , \end{aligned}$$

resulting in the following linear system:

$$\begin{aligned} {\varvec{A}}^l(u){\varvec{v}}^l = {\varvec{f}}^l, \end{aligned}$$

where we introduce the matrix \({\varvec{A}}^l(u)\) with entries \(A_{ij}^l(u) = \langle {\hat{u}}\nabla \psi _i^l,\nabla \psi _j^l \rangle \), and vectors \({\varvec{v}}^l, {\varvec{f}}^l\) with entries \(v_i^l=\langle v, \psi _i^l\rangle \) and \(f_i^l=\langle f, \psi _i^l\rangle \), respectively.

Define \({\mathcal {G}}^l(u) = [\langle g_1, v^l(\cdot ;u)\rangle ,\dots ,\langle g_m, v^l(\cdot ;u)\rangle ]^{\intercal }\). Denote the corresponding approximated un-normalized density by

$$\begin{aligned}&\gamma _{\theta }^l(u) = \theta ^{m/2}\exp \Big \{-\frac{\theta }{2}\Vert {\mathcal {G}}^l(u) - y\Vert ^2\Big \} {{{\mathbf {1}}}}_{\mathbf {u \in {\mathsf {X}}}} \, , \end{aligned}$$
(6)

and the approximated normalized density by

$$\begin{aligned} \eta _{\theta }^l(u) = \frac{\gamma _{\theta }^l(u)}{Z_\theta ^l} \, , \end{aligned}$$

where \(Z_\theta ^l = {\int _{{\mathsf {X}}}\gamma _{\theta }^l(u)du}\). We further define

$$\begin{aligned}&\varphi ^l_\theta (u) := \nabla _{\theta }\log \Big (\gamma _{\theta }^l(u)\Big )\nonumber \\&\quad = \frac{m}{2\theta } - \frac{1}{2}\Vert {\mathcal {G}}^l(u) - y\Vert ^2 \, . \end{aligned}$$
(7)

Recall from (5) that in the case \(s=2\) only \(\partial \log \Big (\gamma _{\theta }^l(u)\Big ) /\partial \theta _3\) depends upon l, and is given as above.

It is well known that under assumption (H1) \(v^l(u)\) converges to v(u) as \(l \rightarrow \infty \) in \(L^2(D)\) (as does its gradient), uniformly in u (Brenner and Scott 2007; Ciarlet 2002). Furthermore, continuity ensures \(\gamma _{\theta }^l(u)\) converges to \(\gamma _{\theta }(u)\) and \(\varphi ^l_\theta (u)\) converges to \(\varphi _\theta (u)\) uniformly in u as well. See also Beskos et al. (2017a, 2017b) and Sect. 4 for further details.

3 Methodology for unbiased estimation

We now describe our methodology for computing an unbiased estimate of \(\eta _{\theta }(\varphi _{\theta })\). For simplicity of exposition, we will suppose that for \(i\in \{1,\dots ,d_{\theta }\}\), \((\varphi _\theta (u))_i\in {\mathcal {B}}_b({\mathsf {X}})\), where \((x)_i\) denotes the \(i^{th}\) element of a vector and \({\mathcal {B}}_b({\mathsf {X}})\) are the collection of bounded, measurable and real-valued functions on \({\mathsf {X}}\). This constraint is not needed for the numerical implementation of the method, but shall reduce most of the technical exposition to follow. As remarked in Introduction, the basic approach follows that in Jasra et al. (2020) with some notable differences. We now detail how the approach will work.

3.1 Methodology in Jasra et al. (2020)

The underlying approach of Jasra et al. (2020) is a type of double randomization scheme. The first step is to use the single-term estimator as developed in Rhee and Glynn (2015). Suppose one wants to estimate \(\eta _{\theta }(\varphi _{\theta })\), but, only has access to a methodology that can approximate \(\eta _{\theta }^l(\varphi _{\theta }^l)\) for each fixed \(l\in {\mathbb {N}}_0\). Let \({\mathbb {P}}_L(l)\) be a positive probability mass function on \({\mathbb {N}}_0\) and suppose that one can construct a sequence of random variables \((\Xi _{\theta }^l)_{l\ge 0}\) such that

$$\begin{aligned}&{\mathbb {E}}[\Xi _{\theta }^0] = \eta _{\theta }^0(\varphi _{\theta }^0) \end{aligned}$$
(8)
$$\begin{aligned}&\quad {\mathbb {E}}[\Xi _{\theta }^l] = \eta _{\theta }^l(\varphi _{\theta }^l) - \eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1})\quad \quad l\in {\mathbb {N}} \end{aligned}$$
(9)

and that

$$\begin{aligned} \sum _{l\in {\mathbb {N}}_0}\frac{1}{{\mathbb {P}}_L(l)}{\mathbb {E}}[\Vert \Xi _{\theta }^l\Vert ^2] < +\infty \, . \end{aligned}$$
(10)

Now if one draws \(L\sim {\mathbb {P}}_L(\cdot )\), then \(\Xi _{\theta }^L/{\mathbb {P}}_{L}(L)\) is an unbiased and finite variance estimator of \(\eta _{\theta }(\varphi _{\theta })\). It should be noted that (8)-(9) are not necessary conditions, but are sufficient to ensure the unbiasedness of the estimator.

In the context of interest, it can be challenging to obtain a sequence of random variables which can possess the properties (8)-(10). We will detail one possible approach at a high level and then explain in detail how one can actually construct a simulation method to achieve this high-level description.

3.2 High-level approach

The objective of this section is to highlight the generic procedure that is used in Jasra et al. (2020) for producing estimates that satisfy (8)–(9). The basic idea is to use another application of randomization to construct such unbiased estimators from a consistent sequence of estimators. In particular, consider a given increasing sequence \((N_p)_{p\in {\mathbb {N}}_0}\) with \(N_p\in {\mathbb {N}}\) for each \(p\in {\mathbb {N}}_0\), \(1\le N_0< N_1< \cdots \) and \(\lim _{p\rightarrow \infty }N_p=\infty \). Then, we suppose that one can construct \(N_p\)-sample Monte Carlo (type) estimators \(\xi _\theta ^{l,p}\) for \(l\in {\mathbb {N}}_0\), such that almost surely the following consistency results hold

$$\begin{aligned} \lim _{p\rightarrow \infty }\xi _\theta ^{0,p}= & {} \eta _{\theta }^{0}(\varphi _{\theta }^0) \, , \end{aligned}$$
(11)
$$\begin{aligned} \lim _{p\rightarrow \infty } \xi _\theta ^{l,p}= & {} \eta _{\theta }^{l}(\varphi _{\theta }^l)-\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1}) \, , \quad \quad l\in {\mathbb {N}} \, . \end{aligned}$$
(12)

For a given \((l,p,p')\in {\mathbb {N}}_0^3\), \(p\ne p'\) we do not require \(\xi _\theta ^{l,p}\) and \(\xi _\theta ^{l,p'}\) to be independent, nor do we require unbiasedness of the individual estimators as in

$$\begin{aligned} {\mathbb {E}}[\xi _\theta ^{0,p}]= & {} \eta _{\theta }^{0}(\varphi _{\theta }^0) \, , \\ {\mathbb {E}}[\xi _\theta ^{l,p}]= & {} \eta _{\theta }^{l}(\varphi _{\theta }^l)-\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1}) \, , \quad \quad l\in {\mathbb {N}} \, . \end{aligned}$$

Now set

$$\begin{aligned} \Xi _{\theta }^{0,0}:= & {} \xi _\theta ^{0,0} \, ,\\ \Xi _{\theta }^{0,p}:= & {} \xi _\theta ^{0,p} - \xi _\theta ^{0,p-1} \, , \quad \quad p\in {\mathbb {N}} \, . \end{aligned}$$

For \(l\in {\mathbb {N}}\) given, set

$$\begin{aligned} \Xi _{\theta }^{l,0}:= & {} \xi _\theta ^{l,0} \, , \\ \Xi _{\theta }^{l,p}:= & {} \xi _\theta ^{l,p} - \xi _\theta ^{l,p-1} \, , \quad \quad p\in {\mathbb {N}} \, . \end{aligned}$$

Let \({\mathbb {P}}_P(p)\), \(p\in {\mathbb {N}}_0\), be a positive probability mass function with \(\overline{{\mathbb {P}}}_P(p)=\sum _{q=p}^{\infty }{\mathbb {P}}_P(q)\). Now if

$$\begin{aligned}&\sum _{p\in {\mathbb {N}}_0}\frac{1}{\overline{{\mathbb {P}}}_P(p)} {\mathbb {E}}[\Vert \xi _\theta ^{l,p} -\eta _{\theta }^0(\varphi _{\theta }^0)\Vert ^2] < +\infty \, , \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{p\in {\mathbb {N}}_0}\frac{1}{\overline{{\mathbb {P}}}_P(p)}{\mathbb {E}}[\Vert \xi _\theta ^{l,p} - \{\eta _{\theta }^{l}(\varphi _{\theta }^l) - \eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1})\} \Vert ^2] < +\infty \, ,\nonumber \\&\qquad \qquad l\in {\mathbb {N}} \end{aligned}$$
(14)

and \(P\sim {\mathbb {P}}_P(\cdot )\), then

$$\begin{aligned} \Xi _{\theta }^l = \sum _{p=0}^P \frac{1}{\overline{{\mathbb {P}}}_P(p)} \Xi _{\theta }^{l,p} \end{aligned}$$
(15)

will allow \((\Xi _{\theta }^l)_{l\in {\mathbb {N}}_0}\) to satisfy (8)-(9), where expectations are understood to be with respect to \({\mathbb {P}}_P\) yet P is suppressed in the notation. Moreover, \((\Xi _{\theta }^l)_{l\in {\mathbb {N}}_0}\) will have finite variances. This result follows as we are simply using the coupled sum estimator as in Rhee and Glynn (2015) and using (Vihola 2018, Theorem 5), for instance, to verify the conditions required.

3.3 Details of the approach

We will now describe how to obtain the sequence \((\Xi _{\theta }^{l,p})_{p\in {\mathbb {N}}_0}\) for \(l\in {\mathbb {N}}_0\) fixed.

3.3.1 MLSMC method of Beskos et al. (2017b)

To introduce our approach, we first consider the MLSMC method in Beskos et al. (2017b) which will form the basis for our estimation procedure. The approach in Beskos et al. (2017b) allows one to consistently estimate quantities such as \(\eta _{\theta }^l(\varphi )\), \(\varphi \in {\mathcal {B}}_b({\mathsf {X}})\) and to estimate differences \(\eta _{\theta }^l(\varphi )-\eta _{\theta }^{l-1}(\varphi )\), \(l\in {\mathbb {N}}\), in a manner which will be suited to our objectives. The algorithm is simply a type of SMC sampler Del Moral et al. (2006) which generates a collection of samples, sequentially, to approximate \(\eta _{\theta }^0\) then \(\eta _{\theta }^1\) and so on.

The following notations will be used to accurately describe the method in Beskos et al. (2017b). Define for \(l\in {\mathbb {N}}_0\)

$$\begin{aligned} G_{\theta }^l(u) = \frac{\gamma _{\theta }^{l+1}(u)}{\gamma _{\theta }^{l}(u)}. \end{aligned}$$

Note that \(\eta _{\theta }^{l-1}(G_{\theta }^{l-1}) = \frac{1}{Z_{\theta }^{l-1}}\int _{{\mathsf {X}}}\gamma _{\theta }^l(u)du=Z_{\theta }^l/Z_{\theta }^{l-1}\), where we recall that \(Z_{\theta }^l= \int _{{\mathsf {X}}}\gamma _{\theta }^l(u)du\). For \(l\in {\mathbb {N}}\), \(M_{\theta }^l\) is a \(\eta _{\theta }^l\)-invariant Markov kernel; that is, for any \(\varphi \in {\mathcal {B}}_b({\mathsf {X}})\)

$$\begin{aligned} \eta _{\theta }^l(\varphi ) = \int _{{\mathsf {X}}}\Big (\int _{{\mathsf {X}}}\varphi (u') M_{\theta }^l(u,du')\Big )\eta _{\theta }^l(du). \end{aligned}$$
(16)

Define for \(\mu \in {\mathcal {P}}({\mathsf {X}})\) (the collection of probability measures on \(({\mathsf {X}},{\mathcal {X}})\)), \(l\in {\mathbb {N}}\)

$$\begin{aligned} \Phi _{\theta }^l(\mu )(du') := \frac{1}{\mu (G_{\theta }^{l-1})} \int _{{\mathsf {X}}}G_{\theta }^{l-1}(u)M_{\theta }^l(u,du') \mu (du) \, . \end{aligned}$$
(17)

Noting that

$$\begin{aligned}&\eta _{\theta }^l(\varphi ) = \frac{\eta _{\theta }^{l-1}(G_{\theta }^{l-1}\varphi )}{\eta _{\theta }^{l-1}(G_{\theta }^{l-1})}\nonumber \\&\quad = \frac{Z_\theta ^{l-1}}{Z_\theta ^l}\eta _{\theta }^{l-1}(G_{\theta }^{l-1}\varphi ) \quad = \frac{1}{Z_\theta ^l} \int _{{\mathsf {X}}} ( \gamma _\theta ^l(u) \varphi (u) ) du \, , \end{aligned}$$
(18)

equations (16) and (17) lead to the recursion

$$\begin{aligned}&\eta _{\theta }^l(\varphi ) = \frac{\eta _{\theta }^{l-1}(G_{\theta }^{l-1}\varphi )}{\eta _{\theta }^{l-1}(G_{\theta }^{l-1})}\nonumber \\&\quad = \frac{1}{\eta _{\theta }^{l-1}(G_{\theta }^{l-1})} \int _{{\mathsf {X}}} G_{\theta }^{l-1}(u)\nonumber \\&\quad \Big ( \int _{{\mathsf {X}}}\varphi (u') M_{\theta }^l(u,du') \Big ) \eta _{\theta }^{l-1}(du) \nonumber \\&\quad = \Phi _{\theta }^l(\eta _{\theta }^{l-1})(\varphi ) \, . \end{aligned}$$
(19)

The significance of this recursion is that it allows one to turn a simulation from \(\eta _{\theta }^{l-1}\) into one from \(\eta _{\theta }^{l}\). This is important in a sequential context, where we will replace \(\eta _{\theta }^{l-1}\) with approximations, but still use this given recursion.

Algorithm 1 A Multilevel Sequential Monte Carlo Sampler with a fixed number of samples \(N\in {\mathbb {N}}\) and a given level \(l\in {\mathbb {N}}_0\).

1. Initialization: For \(i\in \{1,\dots ,N\}\) sample \(U_0^{i}\) from \(\eta _\theta ^0\). If \(l=0\) stop; otherwise set \(s=1\) and go to step 2.

2. Resampling and Sampling: For \(i\in \{1,\dots ,N\}\) sample \(U_s^{i}\) from \(\Phi _{\theta }^s(\eta _{\theta }^{s-1,N})\). This consists of sampling \(a_s^i\in \{1,\dots ,N\}\) with probability mass function

         \({\mathsf {P}}_\theta ^N(a_s^i=j) = \frac{G_{\theta }^{s-1}(u_{s-1}^j)}{\sum _{k=1}^N G_{\theta }^{s-1}(u_{s-1}^k)} \, ,\)

and then sampling \(U_s^i\) from \(M_{\theta }^s(u_{s-1}^{a_s^i},\cdot )\). If \(s=l\) stop; otherwise set \(s=s+1\) and return to the start of 2.

Consider \(N\in {\mathbb {N}}\), and slightly modify the MLSMC algorithm used in Beskos et al. (2017b) to keep the number of samples across levels fixed, up to some given level \(l\in {\mathbb {N}}\). Details are given in Algorithm 1. This algorithm yields samples distributed according to the following joint law

$$\begin{aligned}&{\mathsf {P}}_\theta ^N\big (d(u_0^{1:N},\dots ,u_l^{1:N})\big ) \nonumber \\&\quad = \Big (\prod _{i=1}^{N} \eta _{\theta }^{0}(du_0^i)\Big )\nonumber \\&\quad \Big (\prod _{s=1}^l \prod _{i=1}^{N} \Phi _{\theta }^s(\eta _{\theta }^{s-1,N})(du_s^i) \Big ) \, , \end{aligned}$$
(20)

where \(\eta _{\theta }^{s-1,N}(du)=\frac{1}{N}\sum _{i=1}^{N}\delta _{u_{s-1}^i}(du)\) for \(s\in {\mathbb {N}}\). The intuition of the algorithm can be understood by considering (19). For instance, if one observes \(\Phi _{\theta }^1(\eta _{\theta }^{0,N})(du_1^i)\), we know that \(\eta _{\theta }^{0,N}\) will converge to \(\eta _{\theta }^{0}\) as N grows, so we might expect that \(u_1^i\) might be approximately sampled according to \(\eta _{\theta }^1\). If this logic applies recursively, then one can approximate \(\eta _{\theta }^2\) and so on. One can compute an estimate of \(\eta _{\theta }^0(\varphi _{\theta }^0)\) as

$$\begin{aligned}&\eta _{\theta }^{0,N}(\varphi _{\theta }^0)\\&\quad :=\frac{1}{N}\sum _{i=1}^N \varphi _{\theta }^0(u_0^i) \, . \end{aligned}$$

Following from (18), for \(l\in {\mathbb {N}}\), one can estimate \(\eta _{\theta }^l(\varphi _{\theta }^l)-\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1})\) with

$$\begin{aligned}&\frac{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N}(\varphi _{\theta }^{l-1}) \\&\quad = \frac{\frac{1}{N}\sum _{i=1}^N G_{\theta }^{l-1}(u_{l-1}^i)\varphi _{\theta }^{l}(u_{l-1}^i)}{\frac{1}{N}\sum _{i=1}^N G_{\theta }^{l-1}(u_{l-1}^i)} \\&\quad - \frac{1}{N}\sum _{i=1}^N \varphi _{\theta }^{l-1}(u_{l-1}^i) \, . \end{aligned}$$

The reason for using the samples generated at level \(l-1\) to estimate \(\eta _{\theta }^l(\varphi _{\theta }^l)\) as well as \(\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1})\) is to construct estimators which satisfy conditions such as (10). Standard results (for instance in Del Moral (2013)) allow one to prove that almost surely

$$\begin{aligned}&\lim _{N\rightarrow \infty } \eta _{\theta }^{0,N}(\varphi _{\theta }^0)\\&\quad = \eta _{\theta }^{0}(\varphi _{\theta }^0) \\&\lim _{N\rightarrow \infty } \left( \frac{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1})}\right. \\&\quad \left. - \eta _{\theta }^{l-1,N}(\varphi _{\theta }^{l-1}) \right) \\&\quad =\eta _{\theta }^l(\varphi _{\theta }^l)-\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1}) \, ,\quad \quad l\in {\mathbb {N}} \, . \end{aligned}$$

Note that in general one has

$$\begin{aligned}&{\mathsf {E}}_\theta ^N\bigg [\Big (\frac{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N}(\varphi _{\theta }^{l-1}) \Big )\bigg ] \\&\quad \ne \eta _{\theta }^l(\varphi _{\theta }^l)-\eta _{\theta }^{l-1}(\varphi _{\theta }^{l-1}) \, ,\quad \quad l\in {\mathbb {N}} \, , \end{aligned}$$

where \({\mathsf {E}}_\theta ^N\) is an expectation associated with the probability in (20).

3.3.2 Approach for constructing \((\Xi _{\theta }^{l,p})_{p\in {\mathbb {N}}_0}\)

In order to calculate our approximation, we will consider the following approach, which was also used in Jasra et al. (2020). Given any \((l,P)\in {\mathbb {N}}_0^2\), we will run Algorithm 2 in order to obtain \((\Xi _{\theta }^{l,p})_{p\in \{0,1,\dots ,P\}}\).

Algorithm 2 Approach to construct \((\Xi _{\theta }^{l,p})_{p\in \{0,1,\dots ,P\}}\) for \((l,P)\in {\mathbb {N}}_0^2\) given.

1. Sample: Run Algorithm 1 independently with \(N_p-N_{p-1}\) samples for \(p\in \{0,1,\dots ,P\}\), up to level \((l-1)\vee 0\), where we define for convenience \(N_{-1}:=0\).

2. Estimate: construct \(\Xi _{\theta }^{l,p}\) as in equation (23), for \(p\in \{0,1,\dots ,P\}\).

The joint probability law of the samples simulated according to Algorithm 2 is

$$\begin{aligned}&{\mathbb {P}}_{\theta }\big (d(u_0^{1:N_p},\dots ,u_{(l-1)\vee 0}^{1:N_p})\big )\nonumber \\&\quad = \prod _{p=0}^P {\mathsf {P}}_\theta ^{N_p-N_{p-1}}\nonumber \\&\quad \big ((u_0^{N_{p-1}+1:N_p},\dots ,u_{(l-1)\vee 0}^{N_{p-1}+1:N_p})\big ) \, , \end{aligned}$$
(21)

where \(N_{-1}=0\) and \({\mathsf {P}}_\theta ^{N_p-N_{p-1}}\) is as defined in (20). For \((l,P)\in {\mathbb {N}}_0^2\) given, consider running Algorithm 2. Then for any \(s\in \{0,1,\dots ,(l-1)\vee 0\}\) and any \(p \in \{0,\dots , P\}\), we can construct the following empirical probability measure on \(({\mathsf {X}},{\mathcal {X}})\)

$$\begin{aligned} \eta _\theta ^{s,N_{0:p}}(du_s) := \sum _{q=0}^p \Big (\frac{N_q-N_{q-1}}{N_p}\Big )\eta _\theta ^{s,N_q-N_{q-1}}(du_s) \, . \end{aligned}$$
(22)

Note the recursion

$$\begin{aligned}&\eta _\theta ^{s,N_{0:p}}(du_s) = \Big (\frac{N_p-N_{p-1}}{N_p}\Big )\eta _\theta ^{s,N_p-N_{p-1}}(du_s)\\&\quad + \frac{N_{p-1}}{N_p}\eta _\theta ^{s,N_{0:p-1}}(du_s) \, . \end{aligned}$$

Now define

$$\begin{aligned} \Xi _{\theta }^{l,p} := \left\{ \begin{array}{ll} \eta _{\theta }^{0,N_{0:p}}(\varphi _{\theta }^0) - \eta _{\theta }^{0,N_{0:p-1}}(\varphi _{\theta }^0) &{} \text {if}~l=0 \\ \frac{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N_{0:p}}(\varphi _{\theta }^{l-1}) - \Big (\frac{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N_{0:p-1}}(\varphi _{\theta }^{l-1})\Big ) &{} \text {otherwise} \, , \end{array}\right. \end{aligned}$$
(23)

where \(\eta _{\theta }^{0,N_{0:-1}}(\varphi _{\theta }^0):=0\), and

$$\begin{aligned}&\frac{\eta _{\theta }^{l-1,N_{0:-1}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:-1}}(G_{\theta }^{l-1})}\\&\quad - \eta _{\theta }^{l-1,N_{0:-1}}(\varphi _{\theta }^{l-1}) := 0 \, . \end{aligned}$$

For convenience in the next section, the conditions (13)-(14) translated to the notations used in this section are

$$\begin{aligned}&\sum _{p\in {\mathbb {N}}_0}\frac{1}{\overline{{\mathbb {P}}}_P(p)}{\mathbb {E}}_{\theta }\nonumber \\&\quad [\Vert [\eta _\theta ^{0,N_{0:p}}-\eta _\theta ^{0}](\varphi _\theta ^{0})\Vert ^2] < +\infty \end{aligned}$$
(24)
$$\begin{aligned}&\quad \sum _{p\in {\mathbb {N}}_0}\frac{1}{\overline{{\mathbb {P}}}_P(p)} {\mathbb {E}}_{\theta }\Big [\Big \Vert \frac{ \eta _\theta ^{l-1,N_{0:p}}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1,N_{0:p}}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1,N_{0:p}}(\varphi _\theta ^{l-1}) \nonumber \\&\qquad - \Big ( \frac{ \eta _\theta ^{l-1}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1}(\varphi _\theta ^{l-1}) \Big ) \Big \Vert ^2\Big ]\nonumber \\&\quad < +\infty , \,\, l\in {\mathbb {N}} \, , \end{aligned}$$
(25)

where \({\mathbb {E}}_{\theta }\) is used to denote expectation associated with the probability \({\mathbb {P}}_{\theta }\) in (21).

3.4 Method

Algorithm 3 Method for Unbiasedly Estimating \(\eta _{\theta }(\varphi _{\theta })\).

For \(i=1,\dots , M\):

1. Generate \(L_i\sim {\mathbb {P}}_L\) and \(P_i\sim {\mathbb {P}}_P\).

2. Run Algorithm 2 with \(l=L_i\) and \(P=P_i\).

3.Compute:

\(\Xi _{\theta }^{L_i} = \sum _{p=0}^{P_i} \frac{1}{\overline{{\mathbb {P}}}_P(p)}\Xi _{\theta }^{L_i,p}\)

      where \(\Xi _{\theta }^{L_i,p}\) is given in (23).

Return the estimate:

\(\widehat{\eta _{\theta }(\varphi _{\theta })} := \frac{1}{M}\sum _{i=1}^M \frac{1}{{\mathbb {P}}_L(L_i)}\Xi _{\theta }^{L^i}\) .         (26)

The new method is now presented in Algorithm 3. The estimate of \(\eta _{\theta }(\varphi _{\theta })\) is given by (26). In Sect. 4, we will prove that it is both unbiased and of finite variance, as well as investigating the cost of computing the estimate. Indeed one has a finite variance unbiased estimator even if \(M=1\), and in the numerical examples, it will be shown that such an estimator can be useful in some contexts. However, the variance of such estimator may be rather large. Therefore, in the interest of accuracy one will typically want to adjust M to achieve suitable variance.

There are several points of practical interest to be made at this stage (the first two were noted already in Jasra et al. (2020)). First, the loop over the number of independent samples i in Algorithm 3 can be easily parallelized. Second, one does not need to make L and P independent; this is only assumed for simplicity of presentation, but is not required. Third, the current method uses only the level \(l-1\) marginal of (21). All the samples for \(s=\in \{0,\dots , l-2\}\) and associated empirical measures (22) are discarded and only the level \(l-1\) empirical measure is utilized. This differs from Beskos et al. (2017b) where all the lower-level empirical measures are used. It is possible these samples could be utilized to improve the accuracy of the method, but it is not necessary and so is not investigated further here. The potential efficiency of the double randomization scheme, as well as a discussion of the overall efficiency of the approach, is given in (Jasra et al. 2020, Section 2.5).

4 Theoretical results

Our main objective is to show that \((\Xi _\theta ^l)_{l\in {\mathbb {N}}_0}\) as defined in (15) with \((\Xi _\theta ^{l,p})_{p\in {\mathbb {N}}_0}\) as in (23) will satisfy (8)-(10). To that end, one must first show that \((\Xi _\theta ^{l,p})_{p\in {\mathbb {N}}_0}\) satisfy (24)-(25) which certainly verifies (8)-(9) and then one must establish that (10) holds. We make the following assumptions.

  1. (A1)

    For each \(\theta \in \Theta \), there exist \(0<{\underline{C}}<\overline{C}<+\infty \) such that

    $$\begin{aligned} \sup _{l\ge 0} \sup _{u\in {\mathsf {X}}} G_{\theta }^l (u)\le & {} \overline{C}\\ \inf _{l\ge 0} \inf _{u\in {\mathsf {X}}} G_{\theta }^l (u)\ge & {} {\underline{C}}. \end{aligned}$$
  2. (A2)

    For each \(\theta \in \Theta \), , there exist a \(\rho \in (0,1)\) such that for any \(l\ge 1\), \((u,v)\in {\mathsf {X}}^2\), \(A\in {\mathcal {X}}\)

    $$\begin{aligned} \int _A M_{\theta }^l(u,du') \ge \rho \int _A M_{\theta }^l(v,dv'). \end{aligned}$$
  3. (A3)

    For each \(\theta \in \Theta \), there exists a \({\widetilde{C}}<+\infty \) such that for each \(i\in \{1,\dots ,d_{\theta }\}\)

    $$\begin{aligned} \sup _{l\ge 0} \sup _{u\in {\mathsf {X}}} |(\varphi _{\theta }^l(u))_i| \le {\widetilde{C}}. \end{aligned}$$

For \(\varphi \in {\mathcal {B}}_b({\mathsf {X}})\), we set \(\Vert \varphi \Vert _{\infty }=\sup _{u\in {\mathsf {X}}}|\varphi (u)|\). To simplify our notations, we will set for \(l\in {\mathbb {N}}\)

$$\begin{aligned} \Vert {\varphi }_\theta ^{l}-{\varphi }_\theta ^{l-1}\Vert _{\infty }^2 = \max _{i\in \{1,\dots ,d_{\theta }\}}\Big \{\Vert (\varphi _\theta ^{l})_i-(\varphi _\theta ^{l-1})_i\Vert _{\infty }^2\Big \}. \end{aligned}$$

We begin with the following result, which is associated with verifying that (24)-(25) can hold.

Proposition 4.1

Assume (A1-3). Then for any \(\theta \in \Theta \) there exists a \(C<+\infty \) such that for any \(p\in {\mathbb {N}}_0\), \(1\le N_0<N_1<\cdots<N_p<+\infty \):

$$\begin{aligned} {\mathbb {E}}_{\theta }[\Vert [\eta _\theta ^{0,N_{0:p}}-\eta _\theta ^{0}](\varphi _\theta ^{0})\Vert ^2] \le \frac{C}{N_p}\Big (1+\frac{p^2}{N_p}\Big ). \end{aligned}$$

In addition, for any \((l,p)\in {\mathbb {N}}\times {\mathbb {N}}_0\), \(1\le N_0<N_1<\cdots<N_p<+\infty \):

$$\begin{aligned}&{\mathbb {E}}_{\theta }\Bigg [\Bigg \Vert \frac{ \eta _\theta ^{l-1,N_{0:p}}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1,N_{0:p}}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1,N_{0:p}}(\varphi _\theta ^{l-1}) \nonumber \\&\quad - \Big ( \frac{ \eta _\theta ^{l-1}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1}(\varphi _\theta ^{l-1}) \Big ) \Bigg \Vert ^2\Bigg ] \\&\quad \le \frac{C}{N_p}\Big (1+\frac{p^2}{N_p}\Big )\Big (\Vert {\varphi }_\theta ^{l}-{\varphi }_\theta ^{l-1}\Vert _{\infty }^2+\Big \Vert G_{\theta }^{l-1}\frac{Z_\theta ^{l-1}}{Z_\theta ^{l}}-1\Big \Vert _{\infty }^2\Big ). \end{aligned}$$

Proof

The first result follows by Lemma A.2 in appendix and the second from Lemma A.4 also in appendix. \(\square \)

Remark 4.1

To show that (24)-(25) can hold, one can set, for instance \(N_p=2^p\) and \({\mathbb {P}}_P(p)\propto 2^{-p}(p+1)\log _2(p+2)^2\). See, for example, Jasra et al. (2020) and Rhee and Glynn (2015).

To continue our discussion, to complete our proof, we must know something about the quantity

$$\begin{aligned} \Vert {\varphi }_\theta ^{l}-{\varphi }_\theta ^{l-1}\Vert _{\infty }^2+ \Big \Vert G_{\theta }^{l-1}\frac{Z_\theta ^{l-1}}{Z_\theta ^{l}}-1\Big \Vert _{\infty }^2 \end{aligned}$$

in terms of a possible decay as a function of l. To that end, we shall assume that this term is \({\mathcal {O}}(h_l^{\beta })\) for some \(\beta >0\). This assumption can be verified for the example in Sect. 2.2. Recall from Sect. 2.2 that \(h_l=2^{-l}\).

Proposition 4.2

Assume (H1). Then there are \(C > 0\) and \(\beta >0\), depending on f and \(u_*\), such that for all \(u\in {\mathsf {X}}\)

$$\begin{aligned}&\Vert v^l(\cdot ;u) \Vert , \Vert v(\cdot ;u) \Vert <C \, , \qquad \Vert v^l(\cdot ;u) - v(\cdot ;u) \Vert ^2 \le C h_l^\beta \, ,\nonumber \\ \end{aligned}$$
(27)

where the norm is \(L^2(D)\). Given a function \(F : {\mathbb {N}} \times {\mathsf {X}} \rightarrow \mathbb {R}^n\), suppose that there is a \(C'>0\) which does not depend on (l, u) such that for all \(i=1,\dots , n\)

$$\begin{aligned} | F_i(l,u) - F_i(\infty ,u) | \le C' \Vert v^l(\cdot ; u) - v(\cdot ; u) \Vert \, , \end{aligned}$$
(28)

where the norm is \(L^2(D)\), and \(F(\infty , \cdot ) := \lim _{l\rightarrow \infty } F(l,\cdot )\). Then there is another \(C>0\) which does not depend on (l, u) such that

$$\begin{aligned} \max _{i\in \{1,\dots ,n\}} \Big \{ \sup _{u\in {\mathsf {X}}} | F_i(l,u) - F_i(l-1,u) |^2 \Big \} \le C h_l^\beta \, . \end{aligned}$$
(29)

Proof

This is a slight generalization of the results of Beskos et al. (2017b), Sect. 4. In particular, Eqs. 18, 21, 22 and 23 of Beskos et al. (2017b) provide (27). Plugging (27) into (28) immediately implies that there is a \(C>0\) independent of l such that \(\sup _{u\in {\mathsf {X}}} |F_i(l,u) - F_i(\infty ,u)|^2 \le C h_l^\beta \) for all \(i=1,\dots , n\). The triangle inequality implies

$$\begin{aligned}&| F_i(l,u) - F_i(l-1,u) |^2 \le 2 (| F_i(l,u) - F_i(\infty ,u) |^2\\&\quad + | F_i(l-1,u) - F_i(\infty ,u) |^2) \, . \end{aligned}$$

Since \(h_{l-1} = 2 h_l\), combining the results at levels l and \(l-1\) gives the result. \(\square \)

This proposition simply states that if a vector-valued function has the continuity property (28) with respect to the solution of (2), then the quantity on the left-hand side of (29) inherits the same rate of convergence.

Note that \(G_{\theta }^{l-1}\frac{Z_\theta ^{l-1}}{Z_\theta ^{l}} = \frac{G_{\theta }^{l-1}}{\eta _\theta ^{l-1}(G_{\theta }^{l-1})}\) and \(G_\theta ^{\infty }=1\). So

$$\begin{aligned}&\Vert G_{\theta }^{l-1}\frac{Z_\theta ^{l-1}}{Z_\theta ^{l}}-1\Vert _\infty \\&\quad = \left\| \frac{1}{\eta _\theta ^{l-1}(G_{\theta }^{l-1})} \left( (G_{\theta }^{l-1}-1) +\eta _\theta ^{l-1}(1-G_{\theta }^{l-1}) \right) \right\| _\infty \\&\quad \le \left\| \frac{2}{\eta _\theta ^{l-1}(G_{\theta }^{l-1})} \right\| _\infty \Vert G_{\theta }^{l-1}-1\Vert _\infty \, . \end{aligned}$$

A slight generalization of Prop. 4.1 of Beskos et al. (2017b) to include \(\beta \), together with Proposition 4.2 imply assumption (A1) and that there is a \(C>0\) such that

$$\begin{aligned} \Big \Vert G_{\theta }^{l-1}\frac{Z_\theta ^{l-1}}{Z_\theta ^{l}}-1\Big \Vert _{\infty }^2 \le C h_l^\beta \, . \end{aligned}$$

Now defining \(F(l,u) := {\varphi }_\theta ^{l}(u)\) and \(F(\infty ,u) = {\varphi }_\theta (u)\), as in (7) and (5) for \(s=1\), then it is easy to show that Proposition 4.2 ensures

$$\begin{aligned} \Vert {\varphi }_\theta ^{l}-{\varphi }_\theta ^{l-1}\Vert _{\infty }^2 \le C h_l^\beta \, . \end{aligned}$$

In particular, notice that \(n=d_\theta =1\) and

$$\begin{aligned}&{\varphi }_\theta ^{l}-{\varphi }_\theta \nonumber \\&\quad = \frac{1}{2} \left( \Vert \mathcal {G}(u) - y \Vert ^2 - \Vert \mathcal {G}^l(u) - y \Vert ^2 \right) \nonumber \\&\quad = \frac{1}{2} \left( \Vert \mathcal {G}(u)\Vert ^2 - \Vert \mathcal {G}^l(u)\Vert ^2 + \langle y , \mathcal {G}^{l}(u) - \mathcal {G}(u)\rangle \right) \nonumber \\&\quad \le \frac{1}{2} ( \Vert \mathcal {G}(u)\Vert + \Vert \mathcal {G}^l(u)\Vert + \Vert y\Vert ) \Vert \mathcal {G}^{l}(u) - \mathcal {G}(u)\Vert \, , \end{aligned}$$
(30)

where the scalar identity \((a+b)(a-b)=a^2-b^2\) is used along with Cauchy–Schwartz twice in going from the second to the third line (the norms and inner product are all Euclidean on \(\mathbb {R}^m\)). Now using Cauchy–Schwartz again m times

$$\begin{aligned}&\Vert \mathcal {G}^{l}(u) - \mathcal {G}(u)\Vert = \left( \sum _{i=1}^m \langle g_i , v^l(\cdot ;u) - v(\cdot ;u) \rangle ^2 \right) ^{1/2}\\&\quad \le \left( \sum _{i=1}^m \Vert g_i\Vert ^2\right) ^{1/2} \Vert v^l(\cdot ;u) - v(\cdot ;u) \Vert \, . \end{aligned}$$

It should not cause confusion that the norms and inner products to the right of the first equal sign are on \(L^2(D)\). Assumption (A3) then follows straightforwardly from (27). As mentioned in Sect. 2.2.1, (7), for the case \(s=2\) only \(({\varphi }_\theta ^{l})_3\) depends explicitly on l, and it is given as above. For \(i=1,2\), we have \(({\varphi }_\theta ^{l})_i=({\varphi }_\theta ^{l-1})_i\).

Theorem 1

Assume (A1-3). Then there exist choices of \({\mathbb {P}}_L,{\mathbb {P}}_P\) and \((N_p)_{p\in {\mathbb {N}}_0}\), \(1\le N_0<N_1<\cdots \) so that \((\Xi _\theta ^l)_{l\in {\mathbb {N}}_0}\) as defined in (15) with \((\Xi _\theta ^{l,p})_{p\in {\mathbb {N}}_0}\) as in (23) will satisfy (8)-(10). That is, (26) is an unbiased and finite variance estimator of \(\eta _{\theta }(\varphi _{\theta })\).

Proof

Throughout the proof, C is a finite constant that will not depend on l or p and whose value will change upon each appearance. Given the commentary above, we need only show that (10) can hold for some given choices of \({\mathbb {P}}_L,{\mathbb {P}}_P\) and \((N_p)_{p\in {\mathbb {N}}_0}\). Note that in the context of (10) \(\Xi _{\theta }^l\) is as (15) and in the case of (15) \(\Xi _{\theta }^{l,p}\) is as (23). We have that, by direct computation and the Cauchy–Schwarz inequality

$$\begin{aligned}&\sum _{l\in {\mathbb {N}}_0}\frac{1}{{\mathbb {P}}_L(l)}{\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^l\Vert ^2] \nonumber \\&\quad \le \sum _{(l,p)\in {\mathbb {N}}_0^2}\frac{{\mathbb {P}}_P(p)}{{\mathbb {P}}_L(l)}\Big \{ \sum _{s=0}^p \frac{{\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert ^2]}{\overline{{\mathbb {P}}}_P(s)^2} \nonumber \\&\quad + 2\sum _{0\le s <q\le p} \frac{{\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert \Vert \Xi _{\theta }^{l,q}\Vert ]}{\overline{{\mathbb {P}}}_P(s)\overline{{\mathbb {P}}}_P(q)} \Big \}. \end{aligned}$$
(31)

The strategy is now to control the terms \({\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert ^2]\) and \({\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert \Vert \Xi _{\theta }^{l,q}\Vert ]\), which can then allow one to find choices of \({\mathbb {P}}_L,{\mathbb {P}}_P\) and \((N_p)_{p\in {\mathbb {N}}_0}\) to ensure that the R.H.S. of (31) is finite. Now recalling (23) and noting that for \(p\in {\mathbb {N}}\)

$$\begin{aligned}&\eta _{\theta }^{0,N_{0:p}}(\varphi _{\theta }^0) - \eta _{\theta }^{0,N_{0:p-1}}(\varphi _{\theta }^0)\\&\quad = \eta _{\theta }^{0,N_{0:p}}(\varphi _{\theta }^0) - \eta _{\theta }^{0}(\varphi _{\theta }^0) \\&\quad \quad - \{\eta _{\theta }^{0,N_{0:p-1}}(\varphi _{\theta }^0)-\eta _{\theta }^{0}(\varphi _{\theta }^0)\} \end{aligned}$$

and that for \(p\in {\mathbb {N}}\)

$$\begin{aligned}&\frac{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1})}\\&\quad - \eta _{\theta }^{l-1,N_{0:p}}(\varphi _{\theta }^{l-1})\\&\quad - \left( \frac{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N_{0:p-1}}(\varphi _{\theta }^{l-1})\right) \\&= \frac{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p}}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N_{0:p}}(\varphi _{\theta }^{l-1}) \\&\quad -\Big (\frac{ \eta _\theta ^{l-1}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1}(\varphi _\theta ^{l-1}) \Big ) \\&\quad -\Big \{ \Big (\frac{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1}\varphi _{\theta }^l)}{\eta _{\theta }^{l-1,N_{0:p-1}}(G_{\theta }^{l-1})} - \eta _{\theta }^{l-1,N_{0:p-1}}(\varphi _{\theta }^{l-1})\Big )\\&\quad - \Big ( \frac{ \eta _\theta ^{l-1}(G_{\theta }^{l-1}\varphi _\theta ^{l}) }{\eta _\theta ^{l-1}(G_{\theta }^{l-1})}- \eta _\theta ^{l-1}(\varphi _\theta ^{l-1}) \Big ) \Big \} \end{aligned}$$

by Proposition 4.1 that for \((l,s)\in {\mathbb {N}}_0^2\)

$$\begin{aligned} {\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert ^2] \le \frac{Ch_l^{\beta }}{N_s}\Big (1+\frac{s^2}{N_s}\Big ). \end{aligned}$$
(32)

Also, by using Cauchy–Schwarz, \((l,p,q)\in {\mathbb {N}}_0\times {\mathbb {N}}^2\)

$$\begin{aligned} {\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert \Vert \Xi _{\theta }^{l,q}\Vert ] \le \frac{Ch_l^{\beta }}{N_s^{1/2}N_q^{1/2}}\Big (1+\frac{s^2}{N_s}\Big )^{1/2}\Big (1+\frac{q^2}{N_q}\Big )^{1/2}.\nonumber \\ \end{aligned}$$
(33)

Then using the bounds (32)-(33) in (31) gives the upper bound (noting that the case \(s=0=q\) the terms \({\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert ^2]\) and \({\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^{l,s}\Vert \Vert \Xi _{\theta }^{l,q}\Vert ]\) are \({\mathcal {O}}(1)\) so one can find a C such that the following upper bound holds)

$$\begin{aligned}&\sum _{l\in {\mathbb {N}}_0}\frac{1}{{\mathbb {P}}_L(l)}{\mathbb {E}}_{\theta }[\Vert \Xi _{\theta }^l\Vert ^2] \\&\quad \le C\sum _{(l,p)\in {\mathbb {N}}_0^2}\frac{{\mathbb {P}}_P(p)h_l^{\beta }}{{\mathbb {P}}_L(l)}\Bigg \{ \sum _{s=0}^p \frac{\Big (1+\frac{s^2}{N_s}\Big )}{N_s\overline{{\mathbb {P}}}_P(s)^2} +\\&\quad \sum _{0\le s <q\le p} \frac{\Big (1+\frac{s^2}{N_s}\Big )^{1/2}\Big (1+\frac{q^2}{N_q}\Big )^{1/2}}{N_s^{1/2}N_q^{1/2}\overline{{\mathbb {P}}}_P(p)\overline{{\mathbb {P}}}_P(q)} \Bigg \}. \end{aligned}$$

Now if one chooses, for instance \(N_p=2^p\) and \({\mathbb {P}}_P(p)\propto 2^{-p}(p+1)\log _2(p+2)^2\) and \({\mathbb {P}}_L(l)\propto h_l^{\alpha \beta }\) for any \(\alpha \in (0,1)\) then (10) is satisfied, and hence, the proof is completed. \(\square \)

In most cases of practical interest, it is not possible to choose \({\mathbb {P}}_L,{\mathbb {P}}_P\) and \((N_p)_{p\in {\mathbb {N}}_0}\) so that (26) is an unbiased and finite variance estimator, as well as having finite expected cost. Suppose, in the case of Sect. 2.2, the cost to evaluate \(G_{\theta }^l\) is \({\mathcal {O}}(h_l^{-1})\) and \(\beta =1\). Then, just as in Jasra et al. (2020), if we choose \({\mathbb {P}}_L(l)\propto 2^{-l}(l+1)\log _2(l+2)^2\), \(N_p=2^p\), and \({\mathbb {P}}_P(p)\propto 2^{-p}(p+1)\log _2(p+2)^2\), then to achieve a variance of \({\mathcal {O}}(\epsilon ^2)\) (for \(\epsilon >0\) arbitrary) the cost is \({\mathcal {O}}(\epsilon ^{-2}|\log (\epsilon )|^{2+\delta })\) for any \(\delta >0\), with high probability. For the MLSMC method in Beskos et al. (2017b), the cost to obtain a mean square error of \({\mathcal {O}}(\epsilon ^2)\) is \({\mathcal {O}}(\epsilon ^{-2}\log (\epsilon )^2)\), which is a mild reduction in cost. However, we note that this discussion is constrained to the case of a single processor. The unbiased method is straightforwardly parallelized.

5 Numerical results

First we will consider a toy example where we can analytically calculate the marginal likelihood and investigate the performance of the resulting estimator in comparison with the estimator obtained using the original MLSMC method of Beskos et al. (2017b) (not presented here). Subsequently we will consider the examples from Sect. 2.2. Finally, for all examples we will explore the potential applicability of our estimators within the context of parameter optimization using the stochastic gradient descent (SGD) method.

The forward model is the same for all problems, and the right-hand side \(f \in L^2(D)\) is always smooth. Hence, the anticipated rate of convergence is the same, and is estimated as \(\beta =4\), just as in Beskos et al. (2017b). The cost is \({\mathcal {O}}(h_l^{-\gamma })\) in general for the problem in Sect. 2.2, where \(\gamma \) will depend upon the dimension d of the PDE (2) and the linear solver used for the forward problem. We redefine \(h_l = 2^{-3-l}\) for all problems, so that the coarsest resolution is \(h_0=2^{-3}\). The optimal probability distribution for levels is given by \(\mathbb {P}_L(l) \propto 2^{-l (\beta +\gamma )/2}\) Rhee and Glynn 2015. For the toy problem and the \(d=1\) example, we have \(\gamma =1\) and \(\mathbb {P}_L(l) \propto 2^{-2.5 l}\). For the more complex \(d=2\) example, we have \(\gamma =2+\epsilon \), for \(\epsilon >0\). We choose \(\epsilon =0.5\) in simulations so we can explicitly calculate \(\mathbb {P}_L(l) \propto 2^{- 3.25l}\). Both examples are in the so-called canonical regime (\(\beta >\gamma \), see (Rhee and Glynn 2015, Section 4) for details), and therefore, we allow unbounded L, i.e. \(L_{\mathrm{max}}=\infty \) in the terminology of Jasra et al. (2020). The reason for this is basically that the sum (10) and the corresponding cost series both converge, if the cost is deterministic and \({\mathcal {O}}(h_l^{-\gamma })\) as a function of \(h_l\). However, in this case the cost depends upon the randomized estimator of the series in p. Since the rate of convergence is borderline in the p direction, \(\beta _p=\gamma _p=1\), as in Jasra et al. (2020) we impose a maximum \(P_{\mathrm{max}}\) on P. This is necessary to prevent the possibility of the algorithm getting stuck with an extremely expensive sample. It is discussed further in that work. In particular, we choose \(N_p=2^{p+3}\) and

$$\begin{aligned} {\mathbb {P}}_P(p) \propto {\mathbb {I}}(0\le p\le P_{\mathrm{max}}) \left\{ \begin{array}{ll} 2^{-p+4} &{} \text {if}~p<4, \\ 2^{-p}\cdot p \cdot \log _2(p)^2 &{} \text {otherwise} \, . \end{array}\right. \end{aligned}$$

The piecewise definition of \({\mathbb {P}}_P\) ensures that it has the correct asymptotic behaviour, but is also monotonically decreasing. Note that in this regime, i.e. strongly canonical convergence in L, or large \(\beta >\gamma \), the MLSMC method easily achieves the optimal complexity \({\mathcal {O}}(\epsilon ^{-2})\). However, since the convergence rate in P is necessarily subcanonical, our method therefore suffers from a logarithmic penalty, i.e. \({\mathcal {O}}(\epsilon ^{-2}\log (\epsilon )^{2+\delta })\), for any \(\delta >0\). This cannot be observed in the simulations though. Empirically we observe that we can set \(P_{\mathrm{max}}\) rather small, which is perhaps afforded by the very fast convergence in the L direction. This may be why we cannot see the theoretically predicted log penalty in the simulations.

5.1 Toy example

We first consider an example where the marginal likelihood is analytically calculable. Let \(d=1\) and \(D=[0,1]\) and consider the following DE on D:

$$\begin{aligned} \nabla ^2 v&= u,\quad \text { on } D, \\ v&= 0, \quad \text { on } \partial D \, . \end{aligned}$$

The solution of this DE is \(v(x;u)=\frac{u}{2}(x^2-x)\). Define the observation operator as

$$\begin{aligned} {\mathcal {G}}(u)=[v(x_1;u),v(x_2;u), \dots , v(x_m;u)]^{\intercal }\triangleq Gu \, . \end{aligned}$$

We note that pointwise observations are indeed defined thanks to the regularity of the right-hand side \(u \in L^2(D)\). Suppose the observation takes the form \(y = {\mathcal {G}}(u) + \xi , ~\xi \sim N(0,\theta ^{-1}\cdot {\varvec{I}}_m), ~\xi \perp u\), and \(\log (\theta )\) follows a normal prior distribution with mean 0 and variance 1. The explicit solution of the log-likelihood and its gradient are given in “Appendix B”.

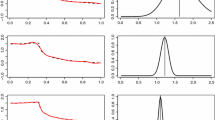
First, the performance of the unbiased algorithm for a single gradient estimation is verified. The data are generated with \(\theta ^*=2\), \(m=50\), and observation operator \({\mathcal {G}}(u)=[p(x_1;u),p(x_2;u),\) \(\dots , v(x_m;u)]^{\intercal }\) with \(x_i = i/(m+1)\). The true value of the derivative of the log-likelihood at \(\theta ^*\) is calculated using the analytical solution given in “Appendix B”. For each L, the MLSMC estimator is realized 50 times and the MSE is reported. Similarly, the MSE of unbiased algorithm is calculated based on 50 realizations as M increases. The results are presented in the left panel of Fig. 1. The cost reported in the plot is proportional to the sum of the cost per forward solve at level l (tridiagonal linear system), \(h_l^{-1}\), multiplied by the total number of samples at level l. The effect of the truncation at \(P_{\mathrm{max}}\) is not observed here, even for very small MSE. We observe that the rate of convergence is the same as MLSMC (the canonical 1/cost rate), and our estimator suffers a slightly higher constant. We note that this is for a single processor and does not account for the (embarrassing) parrallelizability of our algorithm over the M individual estimators – indeed, as mentioned several times already, each estimator is i.i.d. and so each can be in principle computed on a separate processor with 0 communication between them until the individual estimators are combined in (26) to produce the final estimator.

Fig. 1
figure 1

Single estimator asymptotic complexity in terms of MSE vs cost for (i) the unbiased algorithm with different choices of \(P_{\mathrm{max}}\) and (ii) MLSMC. Left: Toy example, single estimator. Middle: Example of Sect. 2.2 with \(s=d=1\) Right: Example of Sect. 2.2 with \(s=d=2\)

Full size image

5.2 Examples of Sect. 2.2

We now consider the example from Sect. 2.2, for both cases of the potential defined in (3).

5.2.1 Case \(s=1\)

For the case \(s=1\) in (3), we let \(d=1\), \(D=[0,1]\), \(f(x)=100x\). For the prior specification of u, we set \(K=2, {\bar{u}}=0.15\), and for \(k=1,2\), we let \(\sigma _k=(2/5)4^{-k}, \phi _k(x)=\sin (k\pi x)\) if k is odd and \(\phi _k(x)=\cos (k\pi x)\) if k is even. The observation operator is \({\mathcal {G}}(u)=[p(0.25;u),p(0.75;u)]^{\intercal }\), and the parameter in observation noise covariance is taken to be \(\theta =0.3\). We note again that pointwise observations are defined thanks to the regularity of the right-hand side \(f \in L^2(D)\). Again, \(\theta \) will follow the same log-normal distribution, and this will be included in the definition of \(\gamma _\theta (u)\), as above, in other words, with respect to (5) the target for \(s=1\) here will be replaced with \(\gamma _\theta (u) \leftarrow \gamma _\theta (u)\theta ^{-1}\exp (-(\log (\theta ))^2/2)\).

Here, we do not have an analytical solution, so the true value of the target was first estimated with the MLSMC algorithm with \(L=12.\) This sampler was realized 50 times and the average of the estimator is taken as the ground truth. Now for each L, the MLSMC estimator is realized 50 times and the MSE is reported. Similarly, the MSE of unbiased algorithm is calculated based on 50 realizations as M increases. The results are presented in the middle panel of Fig. 1. The cost in the plot is proportional to the sum of the cost per forward solve at level l (tridiagonal linear system), \(h_l^{-1}\), multiplied by the total number of samples at level l. In this case, the bias from truncation at \(P_{\mathrm{max}}\) is observed, but only for very small MSE. Again, the comparison shows that our method achieves approximately the same canonical rate, and again, we iterate that this comparison does not leverage the parrallelizability of our method.

5.2.2 Case \(s=2\)

For the case \(s=2\) in (3), we let \(d=2\), \(D=[0,1]^2\), and \(f(x)=\sum _{i=1}^4 a_i \exp (-\frac{1}{2}\Vert x - m_i\Vert ^2)\), where \(m_i \in \{(0.3,0.3), (0.3,0.7), (0.7,0.3), (0.7,0.7)\}\) and \(a_i \in \{2,-3,-2,3\}\), respectively. In this case, \(\phi _i\) are piecewise bilinear finite elements of the type described in Sect. 2.2.1 between nodes \(x_i\) on a mesh in \([0,1]^2\) with a fixed \(l^*=2\), for \(i=1,\dots , K=(2^{l^*}-1)^2\), such that \({\hat{u}}(x)\) is itself piecewise bilinear. Observations of the potential function v are collected at 25 measurement points, evenly spaced within \([0.2,0.6]^2\) (boundaries included). Again pointwise observations are defined even for \(d=2\) due to the regularity of the right-hand side \(f \in L^2(D)\). The observation precision \(\theta ^*_3=2.64\) is chosen such that a prescribed signal-to-noise ratio (SNR) \(\max _{x\in D}{|v(x)|}\theta _3^*=10\), where \(v^*\) is the truth solution at which the observations are collected. The values of the other parameters are given by \(\theta _1^*=3\) and \(\theta _2^*=5\) Now the priors on \(\theta _1\) and \(\theta _2\) are taken as Gamma distributions with mean and variance 1, and the prior on \(\theta _3\) is again log-normal as above. This will be included in the definition of \(\gamma _\theta (u)\), as above, in other words, with respect to (5) the target for \(s=2\) here will be replaced with \(\gamma _\theta (u) \leftarrow \gamma _\theta (u)\theta _3^{-1}\exp (-(\log (\theta _3))^2/2-\theta _1-\theta _2)\).

Again we do not have an analytical solution here, so the true value of the target was first estimated with the MLSMC algorithm with \(L=8\). This sampler was again realized 50 times and the average of the estimator is taken as the ground truth. Now for each L, the MLSMC estimator is realized 50 times and the MSE is reported. Similarly, the MSE of unbiased algorithm is calculated based on 50 realizations. The results are presented in the right panel of Fig. 1. The forward model inversion is done by the conjugate gradient method with the number of iteration steps proportional to level l, and we find the cost is given by \(\gamma =2\) with a log penalty. The cost in the plot is proportional to the sum of the cost per forward solve at level l multiplied by the total number of samples at level l. The MSE in the plot is the summation of three individual MSE. (We multiply the MSEs of the estimators of \(\theta _1\) and \(\theta _2\) by a constant so the scale is consistent with the MSE of the estimator of \(\theta _3\).) Here, we observe that the curves of our unbiased algorithm are more wiggly than the cures when \(s=d=1\), presumably due to complexity of the model.

5.3 Application to stochastic gradient descent

In this section, we investigate the potential to use our unbiased estimators within the SGD method. The objective here is to find the maximum a posteriori (MAP) estimator of \(\theta \) by minimizing \(-\log p_\theta (y) = -\log (\int \gamma _{\theta }(u)du)\). Our estimator given in equation (26) provides an unbiased estimator \(\widehat{\eta _{\theta }(\varphi _{\theta })}\) of \(\nabla _\theta \log p_\theta (y)\), for any choice of \(M\ge 1\). In other words \(\mathbb {E}\widehat{\eta _{\theta }(\varphi _{\theta })} = \nabla _\theta \log p(y,\theta )\). We will see that it is most efficient to choose \(M=1\). To ensure the output of the SGD algorithm satisfies \(\theta >0\), we let \(\theta =\exp (\xi )\) and optimize \(\xi \). The details are given in Algorithm 4.

Algorithm 4 SGD using new unbiased estimator.

1. Initialize \(\xi _1\) and choose a sequence \(\{\alpha _k\}_{k=1}^\infty \) and a value \(M\in {\mathbb {N}}\).

2. For \(k=1,\dots , K\) (or until convergence criterion is met)

   -    Compute \(\widehat{\eta _{\theta }(\varphi _{e^{\xi _k}})}\) using (26)

      -    Update \(\xi _{k+1} = \xi _k - \alpha _k \widehat{\eta _{\theta }(\varphi _{e^{\xi _k}})} \exp (\xi _k)\).

3. Return \(\theta _{K+1}=\exp (\xi _{K+1})\).

As above, it makes sense to first explore the toy model with analytical solution, as described in Sect. 5.1. The MAP estimate is first computed using gradient descent. The MSE is then calculated based on 50 realizations, and the cost in the plot is again proportional to the sum of the cost per forward solve at level l (tridiagonal linear system), \(h_l^{-1}\), multiplied by the total number of samples at level l.

Fig. 2
figure 2

Toy example, SGD. MSE vs cost for (left) \(\alpha _k=0.025/k\) and \(\alpha _k=0.1/k\) for a range of sample sizes M, (middle) \(\alpha _k=\alpha _1/k\) and a range of \(\alpha _1\), and (right) some examples of constant \(\alpha \). \(P_{\mathrm{max}}=0\) is fixed

Full size image
Fig. 3
figure 3

Toy example, SGD. Left panel: MSE vs cost for \(M=1\) fixed and \(\alpha _k=0.1/k\), and various choices of \(P_{\mathrm{max}}\). Right panel: MSE vs cost for \(\alpha _k=0.1/k\), and unbiased estimator with \(P_{\mathrm{max}}=0\) and \(M=1\) in comparison with MLSMC estimator with different choices of L

Full size image

There is a well-developed literature on SGD methods. The choice of nuisance parameter \(\alpha _k\), or “learning rate” as it is referred to in the machine learning literature, is still an active topic of investigation (Kushner and Yin 2003; Gower et al. 2019). It is well known that convergence to a local optimum is achieved for unbiased gradients when \(\alpha _k \propto k^{-a}\), for \(a \in (1/2,1]\) (Kushner and Yin 2003; Gower et al. 2019), but beyond that we are not aware of a general rule. Furthermore, in our case we are able to control the variance of the gradient, via the number M of individual estimators which are averaged in (26). Our experiments revealed that the method is quite sensitive to the choice of these nuisance parameters. So, despite that it is not the focus of the present work and a general or theoretical treatment is outside of scope, we present the results of several experiments for the analytical model, which have guided our choices and can be useful for practitioners and guide future investigation. In the left panel of Fig. 2, we explore the performance of the unbiased estimator with different choices of \(\alpha _k = \alpha _1/k\), \(\alpha _1\in \{0.1,0.025\}\), and different choices of the number of samples M used to construct \(\widehat{\eta _{\theta }(\varphi _{e^{\xi _k}})}\) using (26) in step 2 of Algorithm 4. The two takeaways from this experiment are that (1) it is more efficient to take fewer samples M (in particular \(M=1\)), and (2) it is more efficient to choose a larger constant \(\alpha _1 = 0.1\). In particular, the dynamics of the algorithm experiences a phase transition as one varies the constant \(\alpha _1\). A large enough value provides gradient descent type exponential convergence \({\mathcal {O}}(e^{-\mathrm cost})\), while a value which is too small yields Monte Carlo (MC) type \({\mathcal {O}}(1/\mathrm{cost})\). It is notable that the exponential convergence eventually gives way to MC type convergence, and that the point where this occurs increases proportionally to the additional constant in cost incurred with larger sample size M, so that the error curves for different values of M eventually intersect. A similar phenomenon has been documented in the recent literature on SGD Gower et al. (2019).

Natural questions are then whether there is a limit to how large one can choose \(\alpha _1\) and at which value precisely the phase transition occurs. These questions are partially answered by the experiments presented in the middle panel of Fig. 2, where we see that \(\alpha _1\) should not be chosen larger than 0.2 and the phase transition happens in between 0.025 and 0.05. The right panel of Fig. 2 illustrates the benefits and drawbacks of using a constant \(\alpha \). In particular, the algorithm may converge more quickly at first, but plateaus when it reaches the induced bias.

In the left panel of Fig. 3, we explore various choices of \(P_{\mathrm{max}}\), for \(M=1\) fixed and \(\alpha _1=0.1\). It is apparent that it is preferable to choose a smaller value of \(P_{\mathrm{max}}\). We note, however, that there will be an induced bias, which will be larger for smaller \(P_{\mathrm{max}}\). However, for this particular problem we do not even observe that bias over the range of MSE and cost considered.

Fig. 4
figure 4

Examples of Sect. 2.2, SGD. MSE vs cost for unbiased estimator with \(P_{\mathrm{max}}=0\) and \(M=1\) in comparison with MLSMC estimator with different choices of L. Left: \(s=d=1\) and \(\alpha _k=0.5/k\). Right: \(s=d=2\) and \(\alpha _k=0.1/k\)

Full size image

As a last experiment with the toy example, we compare the convergence of SGD using our unbiased algorithm with \(P_{\mathrm{max}}=0\), \(M=1\), and \(\alpha _1=0.1\) to the analogous algorithm where an MLSMC estimator with various L (single gradient estimator MSE \(\propto 2^{-\beta L}\)) replaces the unbiased estimator in step 2 of Algorithm 4. Similar behaviour was observed for MLSMC relative to different choices of \(\alpha _k\) as compared to the unbiased estimator. The results are shown in the right panel of Fig. 3. Here, it is clear that over a wide range of MSE the unbiased estimator provides a significantly more efficient alternative to the MLSMC estimator.

Next, we consider the same last experiment except with the examples of Sect. 2.2. The results are presented in Fig. 4. Again, over a wide range of MSE the unbiased estimator provides a significantly more efficient alternative to the MLSMC estimator, although it is less conspicuous for the \(s=2\) case (right) than when \(s=1\) (left). Here, one can already observe the induced \(P_{\mathrm{max}}=0\) bias for the unbiased estimator around \(2^{-20}\) (\(s=1\)) and \(2^{-19}\) (\(s=2\)). Adjusting the various tuning parameters resulted in similar behaviour as was observed in the earlier experiments with the toy example. These results are not presented.