Learning causal structure from mixed data with missing values using Gaussian copula models

Abstract

We consider the problem of causal structure learning from data with missing values, assumed to be drawn from a Gaussian copula model. First, we extend the ‘Rank PC’ algorithm, designed for Gaussian copula models with purely continuous data (so-called nonparanormal models), to incomplete data by applying rank correlation to pairwise complete observations and replacing the sample size with an effective sample size in the conditional independence tests to account for the information loss from missing values. When the data are missing completely at random (MCAR), we provide an error bound on the accuracy of ‘Rank PC’ and show its high-dimensional consistency. However, when the data are missing at random (MAR), ‘Rank PC’ fails dramatically. Therefore, we propose a Gibbs sampling procedure to draw correlation matrix samples from mixed data that still works correctly under MAR. These samples are translated into an average correlation matrix and an effective sample size, resulting in the ‘Copula PC’ algorithm for incomplete data. Simulation study shows that: (1) ‘Copula PC’ estimates a more accurate correlation matrix and causal structure than ‘Rank PC’ under MCAR and, even more so, under MAR and (2) the usage of the effective sample size significantly improves the performance of ‘Rank PC’ and ‘Copula PC.’ We illustrate our methods on two real-world datasets: riboflavin production data and chronic fatigue syndrome data.

1 Introduction

Causal structure learning (Pearl and Verma 1992; Pearl 2009), or causal discovery, aims to learn underlying directed acyclic graphs (DAG), in which the vertices denote random variables and the edges represent causal relations among the variables. It is a useful tool for multivariate analysis and has been widely studied in the past decade (Spirtes et al. 2000; Colombo et al. 2012; Chen et al. 2013; Harris and Drton 2013; Peters et al. 2014; Budhathoki and Vreeken 2016). Constraint-based methods, e.g., the PC (named by its two inventors, Peter and Clark) algorithm and the FCI algorithm (Spirtes et al. 2000), have attracted extensive attention and generated many recent improvements (Colombo et al. 2012; Claassen et al. 2013; Harris and Drton 2013; Cui et al. 2016), yielding better search strategies and interpretability. Since all these algorithms share the adjacency search of the PC algorithm as a common first step, any improvements to PC can be directly transferred to the others. Therefore, we focus our analysis on the PC algorithm in this paper.

The adjacency search of the PC algorithm starts with a completely connected undirected graph and then iteratively removes the edges according to conditional independence decisions. For testing the conditional independence, the PC algorithm requires the correlation matrix and the sample size as input. The sample size is necessary: The higher the sample size, the more reliable the estimated correlation matrix, and the more easily the null hypothesis of conditional independence gets rejected [see Eq. (1)]. When applied to Gaussian data, the standard PC algorithm estimates the correlation matrix based on Pearson correlations between variables. Harris and Drton (2013) extended the PC algorithm to nonparanormal models, i.e., Gaussian copula models with purely continuous marginal distributions, by replacing the Pearson correlations with rank-based correlations. Cui et al. (2016) further extended the PC algorithm to mixed discrete and continuous data assumed to be drawn from a Gaussian copula model. However, all these approaches were based on the assumption that the data are fully observed.

In practice, all branches of experimental science are plagued by data with missing values (Little and Rubin 1987; Poleto et al. 2011), e.g., failure of sensors or dropouts of subjects in a longitudinal study. Tables 1 and 2 give two real-world examples from the Quality in Acute Stroke Care (QASC) study (Middleton et al. 2011) and the Longitudinal Study of American Youth (LSAY) (Baraldi and Enders 2010), respectively, providing a summary of part of the variables therein. Because of its pervasive nature, some methodologists have described missing data as ‘one of the most important statistical and design problems in research’ (Baraldi and Enders 2010). In this paper, we target to generalize the PC algorithm to settings where the data are still assumed to be drawn from a Gaussian copula model, but with some missing values. For this, we need to estimate the underlying correlation matrix and the ‘effective sample size’ from incomplete data. The notion ‘effective sample size,’ typically smaller than or equal to the sample size, was proposed in Cui et al. (2016) to account for the information loss incurred by discrete variables. In this paper, we use it to account for the information loss incurred by missing values, acting as if the estimated correlations on incomplete data are in fact estimated from a smaller size of equivalent complete data.

Table 1 Summary of partial variables in the QASC

Table 2 Summary of partial variables in the LSAY

A variety of methods have been developed for estimating correlation matrices from Gaussian (Städler and Bühlmann 2012; Kolar and Xing 2012; Lounici 2014) or conditional Gaussian (Didelez and Pigeot 1998) data with missing values in the context of undirected graphical models. In nonparanormal cases, Wang et al. (2014) proposed to apply rank correlation to pairwise complete observations for estimating the correlation matrix, which is then plugged into existing procedures for inferring the underlying graphical structure. The convergence rate of this rank-based correlation estimator has been derived in the presence of missing values. In this paper, we transfer this idea to causal structure learning, where this estimator is used for the correlation matrix and the number of pairwise complete observations is taken as the effective sample size. This extends the ‘Rank PC’ algorithm to incomplete data. We carry over the error bound of ‘Rank PC’ to nonparanormal data with missing values as well.

Although we will provide theoretical guarantees of the ‘Rank PC’ algorithm for incomplete data, these only apply to nonparanormal data under missingness completely at random (MCAR), which is a pretty strong assumption (Rubin 1976). By contrast, we prefer an approach that is valid for both nonparanormal and mixed data under a less restrictive assumption, missingness at random (MAR) (Rubin 1976; Schafer and Graham 2002). To this end, we propose a Gibbs sampling procedure to draw correlation matrix samples from the posterior distribution given mixed continuous and discrete data with missing values. Then, following the idea of the ‘Copula PC’ algorithm (Cui et al. 2016), these Gibbs samples are translated into an average correlation matrix and an effective sample size, which are input to the standard PC algorithm for causal discovery. The difference is that now the effective sample size accounts for information loss incurred by both missing values and discrete variables.

An earlier version of this article was published at the IEEE International Conference on Data Mining (ICDM) 2017 (Cui et al. 2017). This version is significantly expanded with new theoretical and experimental results.

The rest of this paper is organized as follows. Section 2 reviews necessary background knowledge. Sections 3 and 4 present the ‘Rank PC’ algorithm and the ‘Copula PC’ algorithm for incomplete data, respectively, while Sect. 5 introduces alternative approaches. Section 6 compares ‘Rank PC,’ ‘Copula PC’ with alternative approaches, and evaluates the justification of the usage of the effective sample size in causal discovery on simulated data, whereas Sect. 7 provides an illustration on two real-world datasets. Section 8 concludes this paper and gives potential extensions.

2 Preliminaries

In this section, we review some background about missing values, Gaussian copula and causal discovery.

2.1 Missingness mechanism

Following Rubin (1976), let $\varvec{Y} = (y_{ij}) \in \mathbb {R}^{n \times p}$ be a data matrix with the rows representing independent samples and $\varvec{R} = (r_{ij}) \in \{0,1\}^{n \times p}$ be a matrix of indicators, where $r_{ij} = 1$ if $y_{ij}$ was observed and $r_{ij} = 0$ otherwise. $\varvec{Y}$ consists of two parts, $\varvec{Y}_{\mathrm{obs}}$ and $\varvec{Y}_{\mathrm{miss}}$, where $\varvec{Y}_{\mathrm{obs}}$ contains the observed elements in $\varvec{Y}$ and $\varvec{Y}_{\mathrm{miss}}$ the missing elements. When the missingness does not depend on the observed values, i.e., $P(\varvec{R}|\varvec{Y}, \theta ) = P(\varvec{R}|\theta )$ with $\theta$ denoting unknown parameters, the data are said to be missing completely at random (MCAR), which is a special case of a more realistic assumption called missing at random (MAR). MAR allows the dependency between missingness and observed values, i.e., $P(\varvec{R}|\varvec{Y}, \theta ) = P(\varvec{R}|\varvec{Y}_{\mathrm{obs}},\theta )$. For example, all people in a group are required to take a blood pressure test at time point 1, while only those whose values at time point 1 lie in the abnormal range need to take the test at time point 2. This results in some missing values at time point 2 that are MAR. A third missingness mechanism is called missing not at random (MNAR), which states that the missingness may be dependent on missing values, namely, $P(\varvec{R}|\varvec{Y}, \theta ) = P(\varvec{R}|\varvec{Y}_{\mathrm{obs}},\theta )$ no longer holds. For instance, all the people in the example above are required to take the test at time point 2, but the doctor only records those lying in the abnormal range, leaving others missing.

2.2 Gaussian copula model

Definition 1

(Gaussian copula model) Consider a latent random vector $\varvec{Z}=(Z_1,\ldots ,Z_p)^T$ and an observed random vector $\varvec{Y}=(Y_1,\ldots ,Y_p)^T$, satisfying conditions

$$\begin{aligned}&\varvec{Z} \sim \mathscr {N}(0,C), \\&Y_j = F_j^{-1}\big [\varPhi (Z_j)\big ], \forall j = 1,\ldots ,p, \end{aligned}$$

where C denotes the correlation matrix of $\varvec{Z}$, $\varPhi (\cdot )$ is the standard normal cumulative distribution function, and ${F_{j}}^{-1}(t) = \inf \{ y{:}\,F_{j}(y) \ge t\}$ is the pseudo-inverse of a cumulative distribution function $F_j(\cdot )$. Then this model is called a Gaussian copula model with correlation matrix C and univariate margins $F_j(\cdot )$.

This model provides an elegant way to conduct multivariate data analysis for two reasons. First, it raises the theoretical framework in which multivariate associations can be modeled separately from the univariate distributions of the observed variables (Nelsen 2007). This is very important in practice, because in many studies people are generally concerned with statistical associations among the variables but not necessarily the scale on which the variables are measured (Hoff 2007). Second, the use of copulas is advocated to model multivariate distributions involving diverse types of variables, say binary, ordinal and continuous (Dobra et al. 2011). A variable $Y_j$ that takes a finite number of ordinal values $\{1,\, 2,\, \ldots ,\, c\}$ with $c \ge 2$ is incorporated into our model by introducing a latent Gaussian variable $Z_j$, which complies with the well-known standard assumption for an ordinal variable (Muthén 1984), i.e.,

$$\begin{aligned} Y_j = m,~\text{ if }\quad ~\tau _{m-1}< Z_j < \tau _m, \end{aligned}$$

where $m \in \{1,\, 2,\, \ldots ,\, c\}$ and $\tau$ is the threshold $(-\,\infty =\tau _0< \tau _1< \tau _2< \cdots < \tau _c = +\infty )$.

Because of these two advantages, recent years have seen wide usage of this model in a variety of research fields, e.g., factor analysis (Murray et al. 2013; Gruhl et al. 2013), undirected graphical modeling (Dobra et al. 2011; Liu et al. 2012; Fan et al. 2017) and causal structure learning (Harris and Drton 2013; Cui et al. 2016). As an example, Dobra et al. (2011) makes use of a Gaussian copula-based graphical model to determine the conditional independence relationships in the National Long Term Care Survey functional disability data, which contain 6 binary variables measuring activities of daily living and another 10 binary variables for instrumental activities of daily living. See Dobra et al. (2011) for a detailed description of this example.

Fig. 1

Gaussian copula model

Note that an underlying assumption behind the copula model is that the dependencies among observed variables are due to the interactions among their corresponding latents, in the sense that observed variables do not interact directly but via their latents, as shown in Fig. 1. From a causal prospective, the whole model consists of two parts: the (underlying) causal structure over latent variables and the causal relations from latents to their corresponding observed variables, i.e., $Z_j \rightarrow Y_j, \, \forall j$. Our goal in this paper is to infer the causal structure among latent variables from observations. The implicit assumption is that possible interventions act on the latent variables, not on the observations themselves, much along the lines of Chapter 10 in Spirtes et al. (2000).

2.3 Causal discovery

A graphical model is a graph ${G} = (V,E)$, where the vertices $(X_i{:}\,X_i \in {V})$ denote random variables and the edges E represent dependence structure among the variables. A graph is directed if it just contains directed edges and undirected if all edges are undirected. A graph that contains both directed and undirected edges is called a partially directed graph. Graphs without directed cycles (e.g., $X_i\rightarrow X_j \rightarrow X_i$) are acyclic. We refer to a graph as a directed acyclic graph (DAG) if it is both directed and acyclic. If there is a directed edge $X_i \rightarrow X_j$, we say that $X_i$ is a parent of $X_j$.

A probability distribution over a random vector $\varvec{X}$ with $X_i \in V$ is said to be Markov w.r.t. a DAG ${G} = (V,E)$, if $\varvec{X}$ satisfies the causal Markov condition: Each variable in G is independent of its nondescendants given its parents, which is also implied by so-called d-separation (Pearl 2009). A distribution is faithful w.r.t. a DAG if there are no conditional independencies in the distribution that are not encoded via d-separation. If a distribution is both Markov and faithful w.r.t. a DAG G, the DAG is called a perfect map of the distribution.

Several DAGs may, via d-separation, correspond to the same set of conditional independencies. The set of such DAGs is called a Markov equivalence class, which can be represented by a completed partially directed acyclic graph (CPDAG) (Chickering 2002a). Arcs in a CPDAG imply a cause–effect relationship between pairs of variables since the same arc appears in all members of the CPDAG. An undirected edge $X_i-X_j$ in a CPDAG indicates that some of its members contain an arc $X_i\rightarrow X_j$ while others contain an arc $X_j\rightarrow X_i$.

Problem formulation Assume that the underlying DAG ${G} = ({V},{E})$ is a perfect map of the distribution over $\varvec{X}$ with $X_i \in {V}$. Causal discovery aims to learn the Markov equivalence class of the DAG G from observations.

2.4 PC algorithms

The PC algorithm (Spirtes et al. 2000), a reference algorithm for causal discovery, consists of two stages: adjacency search and orientation. Starting with a fully connected undirected graph, the adjacency search iteratively removes the edges according to conditional independence decisions, yielding the skeleton and separation sets. The orientation first directs the unshielded triples according to the separation sets and then directs as many of the remaining undirected edges as possible by applying the orientation rules repeatedly.

A key part of the procedure is to test conditional independence. When a random vector $\varvec{X}\sim \mathscr {N}(0,C)$, the PC algorithm considers the so-called partial correlation, denoted by $\rho _{uv|S}$, which can be estimated through the correlation matrix C (Anderson 2003). Specifically, given observations of $\varvec{X}$ and significance level $\alpha$, classical decision theory yields

(1)

where $u \ne v$, $S\subseteq \{1,\ldots ,p\}\backslash \{u,v\}$. Hence, the PC algorithm requires the sample correlation matrix $\hat{C}$ (to estimate $\rho _{uv|S}$) and the sample size n as input. High-dimensional consistency of the PC algorithm for Gaussian data is shown under some mild assumptions on the sparsity of the true underlying structure (Kalisch and Bühlmann 2007).

Harris and Drton (2013) use rank correlations, typically Spearman’s $\rho$ and Kendall’s $\tau$, to replace the Pearson correlations for estimating the correlation matrix, which extends the PC algorithm to the broader class of Gaussian copula models but limited to continuous margins, also called nonparanormal models. High-dimensional consistency of the resulting ‘Rank PC’ algorithm has also been proved.

Cui et al. (2016) further extend the PC algorithm to the Gaussian copula models with any mixture of discrete and continuous margins. They first apply a Gibbs sampler on rank-based data to draw correlation matrix samples. These are then translated into an average correlation matrix and an effective sample size, which are input to the standard PC algorithm for causal discovery.

However, when the data are not fully observed, estimators for correlation matrices in the current PC algorithms fail; therefore, our first challenge is to estimate the underlying correlation matrix efficiently from incomplete data. A second challenge concerns the information loss induced by missing values. Specifically, the estimated correlation matrix based on incomplete data is less reliable than on fully observed data. Thus, still using the sample size (n) in the tests of conditional independence, i.e., Eq. (1), can lead to underestimation of the p values, which consequently incurs many incorrect edges in the output graph of the PC algorithm. For this, we propose to estimate an effective sample size (denoted by $\hat{n}$) to replace the sample size in conditional independence tests to account for the reduced reliability incurred by missing values.

3 Rank PC algorithm for data with missing values

In this section, we first introduce the basic procedure of the ‘Rank PC’ algorithm for incomplete data and then derive the convergence rate of the rank-based correlation estimator as well as the probability error bound of ‘Rank PC’ in the presence of missing values.

3.1 Basic procedure

Our procedure consists of three steps: (1) estimate rank correlations based on pairwise complete observations; (2) estimate the underlying correlation matrix and the effective sample size; and (3) plug these into the standard PC algorithm for causal discovery. All analysis in this section is based on nonparanormal data under MCAR.

Since the two typical rank correlations, Kendall’s $\tau$ and Spearman’s $\rho$, are similar in our analysis, we focus our attention on Kendall’s $\tau$ in this paper. Given the data matrix $\varvec{Y}$ and indicator matrix $\varvec{R}$, we compute the Kendall’s $\tau$ between $Y_j$ and $Y_k$ on samples which have observed values for both the two variables, i.e.,

$$\begin{aligned} \hat{\tau }_{jk} = \dfrac{2}{\hat{n}_{jk}(\hat{n}_{jk}-1)} \sum _{1 \le i<i'\le n} r_{ij} r_{ik} r_{i'j} r_{i'k} K(y_i,y_{i'}), \end{aligned}$$

(2)

where $K(y_i,y_{i'}) = \mathrm{sign}\,((y_{ij}-y_{i'j})(y_{ik}-y_{i'k}))$ and $\hat{n}_{jk} = \sum _{i=1}^n r_{ij} r_{ik}$, which is the number of pairwise complete observations for variables $Y_j$ and $Y_k$.

Then, we estimate the underlying correlation matrix. For nonparanormal data, the following lemma connects the Kendall’s $\tau$ to the underlying Pearson correlation.

Proposition 1

(refer to Kendall 1948; Kruskal 1958) Assuming $\varvec{X}$ follows a nonparanormal distribution with correlation matrix C, we have $C_{jk} = \sin \bigg (\dfrac{\pi }{2} \tau _{jk}\bigg )$.

Motivated by this proposition, we consider the estimator $\hat{S}^{\tau } = (\hat{S}^{\tau }_{jk})$ for the underlying correlation matrix:

$$\begin{aligned} \hat{S}^{\tau }_{jk} = \sin \left( \dfrac{\pi }{2} \hat{\tau }_{jk}\right) . \end{aligned}$$

When translating the number of pairwise complete observations $\hat{n}_{jk}$ [see Eq. (2)] into an effective sample size to be used in the conditional independence tests of the PC algorithm, we compare two schemes.

Scheme 1

We take the average over all the $\hat{n}_{jk}$’s, i.e.,

$$\begin{aligned} \hat{n} = \dfrac{2}{p(p-1)}\sum _{1\le j < k \le p} \hat{n}_{jk}. \end{aligned}$$

We refer to this estimator $\hat{n}$ as the global effective sample size (GESS). In this scheme, all the conditional independence tests share the same effective sample size.

Scheme 2

We give a different effective sample size to different conditional independence tests, since each test relies on a local structure involving only part of the variables. In this case, we rewrite the conditional independence testing criteria to

(3)

where $\hat{n}_{uv|S}$ is defined as

$$\begin{aligned} \hat{n}_{uv|S} = \frac{2}{q(q-1)} \sum _{ \begin{array}{c} j, k \in \{u, v, S\} \\ j < k \end{array}} \hat{n}_{jk}, \end{aligned}$$

with $q = 2+|S|$. We refer to $\hat{n}_{uv|S}$ as the local effective sample size (LESS).

In the last step, we take the estimated correlation matrix $\hat{S}^{\tau }$ and the global (or local) effective sample size as input to the standard PC algorithm for causal discovery.

3.2 Theoretical analysis

3.2.1 Convergence rate of estimator $\hat{S}^{\tau }$

When all values in $\varvec{Y} \in \mathbb {R}^{n \times p}$ are missing with probability $\delta$, i.e., $\forall i,j$$P(r_{ij} = 0) = \delta$, Wang et al. (2014) prove the convergence rate of $\hat{S}^{\tau }$, shown in Theorem 1.

Theorem 1

For any $n \ge 1$, any $m > 0$, and any $0< \varepsilon < 1$, with probability at least $\big (1-\dfrac{1}{p^m}\big )\big (1-\exp (-(\varepsilon ^2(1-\delta )^2 n/2 - 2\log p))\big )$, we have

$$\begin{aligned} \sup _{jk} \big \vert \hat{S}^{\tau }_{jk} - C_{jk} \big \vert \le \dfrac{\pi }{1-\delta } \sqrt{\dfrac{m+2}{1-\varepsilon }} \sqrt{\dfrac{\log p}{n}}. \end{aligned}$$

3.2.2 Error bound of rank PC for incomplete data

Since $\hat{\tau }_{jk}$ is unbiased, i.e., $\mathrm{E}\,[\hat{\tau }_{jk}] = \tau _{jk}$, we have

$$\begin{aligned}&P\left( \vert \hat{S}^{\tau }_{jk} - C_{jk} \vert> t \right) \nonumber \\&= P\left( \bigg \vert \sin \left( \dfrac{\pi }{2}\hat{\tau }_{jk}\right) - \sin \left( \dfrac{\pi }{2}\tau _{jk}\right) \bigg \vert> t \right) \nonumber \\&\le P\left( |\hat{\tau }_{jk} - \tau _{jk}| > \dfrac{2}{\pi } t\right) \nonumber \\&\le 2\exp \left( -\dfrac{2 \lfloor n_{jk}/2 \rfloor t^2}{\pi ^2}\right) \nonumber \\&\le 2\exp \left( -\dfrac{n' t^2}{\pi ^2}\right) , \end{aligned}$$

(4)

where the second inequality follows from the Hoeffding bound for one-sample U-statistics (Hoeffding 1963), $\lfloor n_{jk}/2 \rfloor$ is the largest integer contained in $n_{jk}/2$, and $n' = \min \{2 \lfloor n_{jk}/2 \rfloor {:}\,\forall j,k\}$.

Building upon the result in Eq. (4), we will now derive the error bound of Rank PC for incomplete data following the same line of reasoning as in Harris and Drton (2013).

For a DAG $G = (V, E)$ and a correlation matrix C, let

$$\begin{aligned} c_{\min }(C) := \min \left\{ \vert \rho _{uv|S}\vert {:}\, \rho _{uv|S} \ne 0 \right\} \end{aligned}$$

be the minimal nonzero absolute partial correlation, and $\lambda _{\min }(C)$ be the minimal eigenvalue. Then for any integer $q \ge 2$, let

$$\begin{aligned} c_{\min }(C,q):= & {} \min \left\{ c_{\min }(C_{I,I}){:}\,I \subseteq V, |I| \le q\right\} , ~\text{ and }~ \\ \lambda _{\min }(C,q):= & {} \min \left\{ \lambda _{\min }(C_{I,I}){:}\,I \subseteq V, |I| \le q\right\} \end{aligned}$$

be the minimal nonzero absolute partial correlation and eigenvalue, respectively, of any principal submatrix of order at most q.

Theorem 2

(Error Bound of Rank PC under MCAR) Let $\varvec{y_1},\ldots ,\varvec{y_n}$ be independent samples with some MCAR missing values drawn from a nonparanormal distribution with correlation matrix C that is faithful to a DAG G with p nodes. For $q:= \deg (G) + 2$ with $\deg (G)$ the degree of G, let $c:= c_{\min }(C,q)$ and $\lambda :=\lambda _{\min }(C,q)$. If $n'>q$, then there exists a threshold $\gamma \in [0,1]$ for which

$$\begin{aligned} P(\hat{M}_{\gamma }(G) \ne M(G)) \le p^2 \exp \left( -\dfrac{\lambda ^4 n' c^2}{36 \pi ^2 q^2}\right) , \end{aligned}$$

(5)

where $\hat{M}_{\gamma }(G)$ and M(G) are the estimated and true Markov equivalence class, respectively, and $n'$ is from Eq. (4).

The proof of Theorem 2 directly follows from the proof of Theorem 8 in Harris and Drton (2013). From the probability error bound in Theorem 2, one could deduce the high-dimensional consistency of the Rank PC algorithm under MCAR. For a large enough n (thus a large enough $n'$), the left-handed term in Eq. (5) goes to zero under some conditions that govern the growth rate of c, $\lambda$, q, p, and $n'$. See Corollary 9 in Harris and Drton (2013) for more details.

4 Copula PC algorithm for data with missing values

In this section, we extend the ‘Copula PC’ algorithm to incomplete data. It includes three steps: (1) apply a Gibbs sampler to draw correlation matrix samples from the posterior distribution given data with missing values (Sect. 4.1); (2) use these samples to estimate the underlying correlation matrix (Sect. 4.2) and the effective sample size (Sect. 4.3); and (3) plug the estimated correlation matrix and effective sample size into the standard PC algorithm for causal discovery. All analysis in this section is under the MAR assumption, unless explicitly stated otherwise.

4.1 Gibbs sampling for data with missing values

We choose $\varSigma$ from an inverse Wishart distribution, denoted by ${\mathscr {W}}^{-1}(\varSigma ;\varPsi ,\nu )$, and write

$$\begin{aligned} P(C) = {\mathscr {PW}}^{-1}(C;\varPsi ,\nu ), \end{aligned}$$

where $C = (C_{jk})$ with $C_{jk} = \varSigma _{jk} / \sqrt{\varSigma _{jj}\varSigma _{kk}}$. Then this distribution on correlation matrix C is called a projected inverse Wishart distribution with scale matrix $\varPsi$ and degrees of freedom $\nu$ (Cui et al. 2016). In Bayesian inference, this distribution is the conjugate prior of correlation matrices for Gaussian models. Specifically, when we choose the prior $P(C) = {\mathscr {PW}}^{-1}(C;\varPsi _0,\nu _0)$, the posterior given data $\varvec{Z} = (\varvec{z_1},\ldots ,\varvec{z_n})^T$ reads

$$\begin{aligned} P(C|\varvec{Z}) = {\mathscr {PW}}^{-1}(C;\varPsi _0 + \varvec{Z}^T\varvec{Z},\nu _0 + n). \end{aligned}$$

(6)

For Gaussian copula models with missing values, we cannot observe the random vector $\varvec{Z}$ directly (refer to Definition 1), but an idea is to first obtain the Gaussian pseudo-data from the observed data (i.e., $\varvec{Y}$) and then do inference for C. We use a Gibbs sampling procedure to implement this idea.

Let $\varvec{Z} = (z_{ij}) \in \mathbb {R}^{n \times p}$ be the Gaussian pseudo-data implied by $\varvec{Y}$; thus, $\varvec{Z}$ has two parts as well, $\varvec{Z}_{\mathrm{obs}}$ and $\varvec{Z}_{\mathrm{miss}}$. As initialization of our Gibbs sampling procedure, we propose to obtain the Gaussian pseudo-data of nonmissing values $\varvec{Z}_{\mathrm{obs}}$. For this, we substitute the empirical cumulative distribution function based on nonmissing data $\varvec{Y}_{\mathrm{obs}}$:

$$\begin{aligned} z_{ij} = \varPhi ^{-1}\left[ \dfrac{\sum _{d=1}^{n} r_{dj} mathbb {1}(y_{dj} < y_{ij})}{\sum _{d=1}^{n} r_{dj}+1}\right] ,~\text{ if }\quad r_{ij} = 1, \end{aligned}$$

(7)

where $mathbb {1}(\cdot )$ is the indicator function.

For nonparanormal data with missing values completely at random, each marginal distribution of $\varvec{Z}_{\mathrm{obs}}$ can approximately represent the underlying true distribution. Then we iterate the following two steps to impute missing values (step 1) and draw correlation matrix samples from the posterior (step 2):

• 1. $\varvec{Z}_{\mathrm{miss}} \sim P(\varvec{Z}_{\mathrm{miss}}|\varvec{Z}_{\mathrm{obs}},C)$;

• 2. $C \sim P(C|\varvec{Z}_{\mathrm{obs}},\varvec{Z}_{\mathrm{miss}})$.

This procedure generates a Markov chain that has its stationary distribution equal to $P(C|\varvec{Y})$, which can be easily implemented via the Gibbs scheme in Algorithm 1.

However, for mixed data under MAR, the initialization shown in Eq. (7) is no longer sufficient for two reasons: (1) tied observations may occur, making the ranks no longer well defined, and (2) the missing values in one variable may depend on the values of others. These differentiate the obtained marginal distributions from the underlying true distributions. Hence, we need an additional strategy to obtain $\varvec{Z}_{\mathrm{obs}}$ to leverage the sampling scheme in Algorithm 1.

For this, we borrow the idea of the so-called extended rank likelihood (Hoff 2007), derived as follows. Since the transformation $Y_j = F_j^{-1}[\varPhi (Z_j)]$ is nondecreasing, observing $\varvec{y}_j = (y_{1,j},\ldots ,y_{n,j})^T$ implies a partial ordering on $\varvec{z}_j = (z_{1,j},\ldots ,z_{n,j})^T$, i.e., $\varvec{z}_j$ must lie in

$$\begin{aligned} D(\varvec{y}_j) = \left\{ \varvec{z}_j \in \mathbb {R}^n{:}\,y_{i,j}< y_{k,j} \Rightarrow z_{i,j} < z_{k,j}\right\} . \end{aligned}$$

Therefore, observing $\varvec{Y}$ suggests that $\varvec{Z}$ must be in

$$\begin{aligned} D(\varvec{Y}) = \left\{ \varvec{Z} \in \mathbb {R}^{n \times p}{:}\,\varvec{z}_j \in D(\varvec{y}_j), \forall j = 1,\ldots ,p\right\} . \end{aligned}$$

Taking the occurrence of this event as the data, one can compute the following likelihood

$$\begin{aligned} P(\varvec{Z} \in D(\varvec{Y})|C,F_1,\ldots ,F_p)&= \int _{D(\varvec{Y})} p(\varvec{Z}|C)d\varvec{Z} \\&= P(\varvec{Z} \in D(\varvec{Y})|C), \end{aligned}$$

which is independent of the margins $F_j$. Then inference for C proceeds by iterating the following two steps:

• 1. $\varvec{Z} \sim P(\varvec{Z}|\varvec{Z} \in D(\varvec{Y}),C)$;

• 2. $C \sim P(C|\varvec{Z})$.

The strong posterior consistency for C under the extended rank likelihood has been proved in Murray et al. (2013). We now use this method to obtain $\varvec{Z}_{\mathrm{obs}}$ from $\varvec{Y}_{\mathrm{obs}}$ and embed it into our procedure in Algorithm 1, resulting in the Gibbs sampler in Algorithm 2. Note that line 16 in Algorithm 2 needs to relocate the data such that the mean of each coordinate of $\varvec{Z}$ is zero. This is necessary for the algorithm to be sound because the mean may shift when missing values depend on the observed data (MAR). For clarity, we list step 1 and step 2 separately in Algorithm 2, but the actual implementation takes these together to avoid repeated computation of lines 3 and 4. This Gibbs sampler can be implemented using the function sbgcop.mcmc in the R package sbgcop (Hoff 2010), where the equivalent of line 16 in Algorithm 2 should be added to guarantee that the procedure also works under MAR.¹

4.2 Estimating the underlying correlation matrix

By iterating the steps in Algorithm 1 (or 2), we can draw samples of the correlation matrix, denoted by $\{C^{(1)},\ldots , C^{(m)}\}$. The mean over all the samples is a natural estimate of the underlying correlation matrix $\hat{C}$, i.e.,

$$\begin{aligned} \hat{C} = \frac{1}{m} \sum _{i=1}^m C^{(i)}. \end{aligned}$$

(8)

We refer to the estimator in Eq. (8) as the copula estimator for the correlation matrix.

Since Kendall’s $\tau$ is a U-statistic and can be treated as the sum of a set of bounded variables ($K(y_i,y_{i'})$ in Eq. (2) is bounded by the interval [− 1, 1]), Hoeffding’s inequalities can be used to prove its convergence rate, as we did in Sect. 3.2. Such analysis of the copula estimator, on the other hand, is much more complicated (see Hoff 2007; Hoff et al. 2014 for recent achievements). Nevertheless, intuitively, one would expect the Gibbs sampler to yield better convergence rates than Kendall’s $\tau$, in particular in the case of missing values, because it more efficiently makes use of all available data instead of restricting itself to independent estimation of the individual elements of the correlation matrix based on pairwise complete observations. We will check this empirically in Sect. 6.2.2.

4.3 Estimating the effective sample size

While it is straightforward to estimate the effective sample size for the pairwise deletion method (the one we used in Sect. 3), a different strategy in the current case is needed.

The projected inverse Wishart distribution has a property that is summarized in Theorem 3 (see Cui et al. 2016 for the proof), showing the relationship between the mean, variance and degrees of freedom.

Theorem 3

Consider a p-dimensional random matrix C. If $P(C) = {\mathscr {PW}}^{-1}(C;\varPsi ,\nu )$, we have

$$\begin{aligned} \mathrm{Var}\,[C_{jk}] \approx {(1 - (\mathrm{E}\,[C_{jk}] )^2)^2 \over \nu }, \end{aligned}$$

for each off-diagonal element $C_{jk}$ and large $\nu \,(\gg p)$.

In Eq. (6), since generally $\nu _0 \ll n$, the posterior degrees of freedom $\nu _0 + n \approx n$. From Theorem 3, the variance of each estimated correlation by our copula estimator for an n-size fully observed and continuous dataset is

$$\begin{aligned} \mathrm{Var}\,[C_{jk}] \approx {(1 - (\mathrm{E}\,[C_{jk}] )^2)^2 \over n}, \forall j\ne k. \end{aligned}$$

However, this does not hold any longer when the observational dataset of size n is mixed and contains some missing values. Specifically, there will be some additional variance (or reduced information) in the correlation matrix samples incurred by missing values and ties in discrete variables.

Definition 2

(Effective sample size) The effective sample size for a population quantity (pairwise correlation here) is a number $\hat{n}$, with the property that a mixed dataset of size n with missing values contains the same information (thus variance) as a fully observed and continuous dataset of size $\hat{n}$.

According to Definition (2), the effective sample size for the correlation $C_{jk}$ (denoted by $\hat{n}_{jk}$ for clarity since it can vary for different combinations of j and k) reads

$$\begin{aligned} \hat{n}_{jk} = \dfrac{\left( 1 - (\mathrm{E}\,_n[C_{jk}] )^2\right) ^2}{\mathrm{Var}\,_n[C_{jk}]}, \forall j\ne k, \end{aligned}$$

where $\mathrm{E}\,_n[C_{jk}]$ and $\mathrm{Var}\,_n[C_{jk}]$ denote, respectively, the mean and variance estimated through the correlation matrix samples drawn from a mixed dataset of size $\hat{n}$ with missing values.

When applying the effective sample size to conditional independence tests, we also compare the two different schemes discussed in Sect. 3.1: the same effective sample size for all conditional independence tests or a separate local effective sample size for each test.

4.4 Consistency of Copula PC algorithm

Theorem 4

(Consistency of Copula PC under MCAR) Let $\varvec{y_1},\ldots ,\varvec{y_n}$ be independent samples with some missing values drawn from a Gaussian copula model with correlation matrix C and univariate margins $F_j$. Suppose (1) C is faithful to a DAG G; (2) the data are missing completely at random. Then

$$\begin{aligned} \lim _{n \rightarrow \infty } P(\hat{M}_{\gamma }(G) = M(G)) = 1, \end{aligned}$$

where $\hat{M}_{\gamma }(G)$ and M(G) are the estimated and true Markov equivalence class, respectively.

The proof of Theorem 4 follows two separate steps: Gibbs sampling to estimate the correct underlying correlation matrix and the PC algorithm to reach the correct causal structure. The first step directly follows from the proof of Theorem 1 in Murray et al. (2013), with the additional observation that the estimation of ordinary and polychoric/polyserial correlations from pairwise complete data is still consistent under MCAR. The second step has been proved in Kalisch and Bühlmann (2007). While it is straightforward to prove the consistency of our Gibbs sampling procedure under MCAR, a theoretical proof that it is still consistent under MAR is much more difficult. Hence, we will empirically show in Sect. 6.2.1 that our procedure still works favorably while the rank-based estimator fails under MAR.

5 Alternative approach

In this section, we describe some alternative approaches for handling missing values and for causal discovery with mixed data.

5.1 Listwise deletion

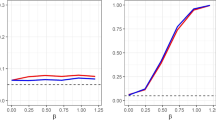
A simple widely used approach for missing values is the so-called listwise deletion (LD), also known as case deletion or complete case analysis. It excludes all records with missing information, so the analyses are restricted to cases that have complete data. This approach is consistent under MCAR and can produce a complete dataset, which in turn allows for the use of standard analysis techniques. However, the drawbacks of this approach are numerous. For example, it dramatically reduces the total sample size, particularly for datasets with a large proportion of missing data or many variables. Suppose that we have p variables and let $\delta _j$ denote the proportion of missing values in the jth variable. We randomly draw $\delta _j$ from a uniform distribution with mean $\beta$, e.g.,

$$\begin{aligned} \delta _j \sim \mathscr {U}\left( 0,\, 2\times \beta \right) , \forall j = 1,\ldots ,p. \end{aligned}$$

(9)

Then, the expected percentage of complete cases under MCAR in such a dataset reads:

$$\begin{aligned} \mathrm{E}\,\left[ \prod _{j=1}^p (1-\delta _j)\right]&= \prod _{j=1}^{p}\mathrm{E}\,(1-\delta _j) \\&= \prod _{j=1}^{p} (1-\beta ) = (1-\beta )^p. \end{aligned}$$

Figure 2 shows the relationship between the percentage of complete cases and the number of variables for different expected proportions of missing values ($\beta$). We can see that the percentage of complete cases decreases dramatically with the increase in variables, which becomes more serious for a bigger $\beta$. Therefore, our conjecture is that a causal discovery algorithm with listwise deletion for handling missing values would output a very sparse or even empty graph, especially when the underlying graph has many vertices and the data contains many missing values. We will check this conjecture in Sects. 6 and 7.

Fig. 2

Percentage of complete cases against the number of variables for different proportions of missing values

5.2 Imputation methods

Instead of discarding the entire record with missing information, a potentially more efficient method is to replace the missing items with plausible values and proceed with the desired analysis. A common procedure is called mean substitution (MS), in which missing values are replaced with the average of observed values for that variable. MS keeps the mean of that variable but ignores the variance. Another option in wide use is called hot deck (HD), in which the missing items are randomly drawn from the observed values of that variable. HD keeps the whole distribution of the variable, but incurs distortions of the covariance with other variables. In what follows, we use a simple example to illustrate how MS and HD influence correlations between variables, since the correlations are parameters of interest in causal discovery.

Without loss of generality, we consider a zero-mean (we can always relocate the mean of a distribution to be zero subject to an unchanged correlation) bivariate distribution (X, Y) with correlation $\rho$, i.e.,

$$\begin{aligned} \rho = \dfrac{\mathrm{E}\,[XY] }{\sqrt{\mathrm{E}\,[X^2] \mathrm{E}\,[Y^2]}}. \end{aligned}$$

Let $(X_1, Y_1), \ldots , (X_n, Y_n)$ be independent samples drawn from the population distribution, where X is fully observed while Y contains MCAR missing values with proportion $\delta$. Under MS, since all the imputed values are zeros in large sample limit, the covariance for such data reads $(1-\delta ) \, \mathrm{E}\,[XY]$ and the variance of Y is $(1-\delta ) \, \mathrm{E}\,[Y^2]$. Thus, the correlation in this case reads:

$$\begin{aligned} \rho _\mathrm{{MS}} = \dfrac{(1-\delta ) \, \mathrm{E}\,[XY]}{\sqrt{\mathrm{E}\,[X^2] \, (1-\delta ) \, \mathrm{E}\,[Y^2]}} = \sqrt{1-\delta } \, \rho . \end{aligned}$$

Under HD, the covariance is also $(1-\delta ) \, \mathrm{E}\,[XY]$ since (independent draws). The variance of each univariate margin remains the same as the population value. Thus, the correlation for HD reads:

$$\begin{aligned} \rho _\mathrm{HD} = \dfrac{(1-\delta ) \, \mathrm{E}\,[XY]}{\sqrt{ \mathrm{E}\,[X^2] \mathrm{E}\,[Y^2]}} = (1-\delta ) \rho . \end{aligned}$$

We see that both MS and HD tend to diminish the correlation especially for a large proportion of missing values although they keep the same sample size as the original data, and they are not consistent for estimating correlations even under MCAR. A simulation study regarding the behavior of correlation estimators with different missing value strategies is provided in Sect. 6.2.1.

There are other procedures for imputation, like maximum likelihood and multiple imputation (Schafer and Graham 2002), but they usually assume multivariate normality that is obviously violated in our case. Therefore, we do not consider these approaches in our analysis.

5.3 Hetcor PC algorithm

In terms of causal discovery for mixed data, we consider the ‘Hetcor PC’ algorithm (HPC) as an alternative to ‘Rank PC’ (RPC). HPC replaces the rank correlation in RPC with the so-called Hetcor (Fox 2007) correlation which tests Pearson correlation between continuous variables, polyserial correlation between continuous and ordinal variables, as well as polychoric correlation between ordinal variables. Non-Gaussian continuous components can be turned into Gaussian components via the nonparanormal transformation in Eq. (7). Note that the nonparanormal transformation is strictly increasing with no need to be smooth or even continuous. For more details, see Definition 2 in Harris and Drton (2013).

6 Simulation study

In this section, we compare the proposed methods with alternative approaches through simulation studies. Section 6.1 introduces the simulation setup. Sections 6.2 and 6.3 evaluate the performance of these approaches in correlation estimation and in causal discovery, respectively.

6.1 Simulation setup

We choose two well-known DAGs from the Bayesian network repository² for evaluating our approaches:

• Asia network (Lauritzen and Spiegelhalter 1988): this network contains 8 nodes, 5 arcs and 3 undirected edges in its Markov equivalence class. It describes the effect of visiting Asia and smoking behavior on the probability of contracting tuberculosis, cancer or bronchitis. The Asia network is depicted in Fig. 3.

• Alarm network (Beinlich et al. 1989): this network contains 37 nodes, 46 arcs and 4 undirected edges in the CPDAG of the equivalence class. It was originally designed to help interpret monitoring data to alert anesthesiologists to various situations in the operating room. The Alarm network is depicted in Fig. 4.

Fig. 3

Asia network

Fig. 4

Alarm network

Given a DAG, we simulate normally distributed samples that are faithful to the DAG, following the procedure of Kalisch and Bühlmann (2007): (1) obtain a lower triangle adjacency matrix A to represent the DAG where ones and zeros denote directed edges and absence of edges, respectively; (2) change the ones to be random weights in the interval $\left[ 0.1,1\right]$. Then, the samples of a random vector $\varvec{Z}$ are drawn through

$$\begin{aligned} Z_j = \sum _{i < j} A_{ji} Z_i + \varepsilon _j, \end{aligned}$$

with $\varepsilon _j \sim \mathscr {N}(0,1)$. The data generated in this way follow a multivariate Gaussian distribution with mean zero and covariance matrix $\varSigma = (\mathbb {I} - A)^{-1} (\mathbb {I} - A)^{-T}$, where $\mathbb {I}$ is the identity matrix. In the last step, we scale the data such that each coordinate follows a standard normal distribution, to simulate the random vector $\varvec{Z}$ in Definition 1. The implementation of this process and the standard PC algorithm is based on the R package pcalg (Kalisch et al. 2010).

Missing values with a certain proportion $\delta _j$ in a variable (the jth variable) are created following the procedure in Kolar and Xing (2012):

• Under MCAR, $\forall i,j$, $z_{i,j}$ is missing if $r_{i,j}=0$ where $r_{i,j} \sim \mathrm{Bern}(1-\delta _j)$.

• Under MAR, for $j = 1,\ldots ,\lfloor p/2 \rfloor$, $i = 1,\ldots ,n$: $z_{i,2*j}$ is missing if $z_{i,2*j-1} < \varPhi ^{-1}(\delta _j)$.

Motivated by the two real-world datasets shown in Tables 1 and 2, we give a different missing rate to different variables. Specifically, we randomly draw $\delta _j$ from a uniform distribution as shown in Eq. (9).

For recovering the causal structure, we consider the conservative PC (Ramsey et al. 2012) as our standard algorithm, in which the significance level is set to $\alpha = 0.01$. For the Gibbs sampling step, we abandon the first 500 samples (burn-in) and save the next 500 for estimating the underlying correlation matrix and the effective sample size.

6.2 Evaluating correlation estimators

Section 6.2.1 illustrates how different missing value strategies behave in correlation estimation. Section 6.2.2 aims to empirically show that the copula estimator has a better convergence rate than the estimator based on Kendall’s $\tau$ whose convergence rate was shown theoretically.

6.2.1 Consistency

We now empirically check the behavior of correlation estimators with different strategies for handling missing values through a simple example. We consider a zero-mean bivariate normal distribution with a population correlation $\rho$, in which the first coordinate is fully observed (no missing values). Under MCAR, we randomly set 50% of values in the second coordinate to be missing. Under MAR, the second coordinate is forced to be missing provided that the observations of the first is negative (thus also 50% missing values). A first strategy for missing data is the listwise deletion that reduces to pairwise deletion in bivariate cases; thus, it is equivalent to the method proposed in Sect. 3, denoted by ‘Tau.’ Another two alternative approaches are based on the mean substitution and hot deck, denoted by ‘MS’ and ‘HD,’ respectively, for simplicity. A fourth method involved is our copula correlation estimator, denoted by ‘Cop.’

Fig. 5

True correlations (dotted horizontal line) and the correlations learned by methods based on mean substitution (MS), hot deck (HD), pairwise deletion (Tau) and the copula estimator (Cop) for different sample sizes, showing the mean over 100 experiments with error bars representing one standard deviation, under a MCAR and b MAR

Figure 5 shows the results obtained by the four approaches under (a) MCAR and (b) MAR, providing the mean over 100 experiments with error bars representing one standard deviation for different sample sizes $n \in \{100, \, 500,\, 1000\}$ and different population correlations $\rho \in \{0,\, 0.3,\, 0.6,\, 0.9\}$, where the dotted horizontal lines denote the true correlations. Under MCAR, we see that estimates of ‘Tau’ and ‘Cop’ are consistently around the true values, which confirms our theoretical results in Sects. 3 and 4. By contrast, MS and HD report clearly biased results when the true $\rho$ is not zero (more serious for HD), which is identical to the analysis in Sect. 5.2. Under MAR, the most encouraging result is that our copula estimator can still consistently estimate the correlations while ‘Tau’ fails and MS as well as HD performs even worse than MCAR cases. This compensates the theoretical analysis in Sect. 4.4. When $\rho = 0$, ‘Tau’ goes back to be unbiased because MAR reduces to MCAR in this case.

Fig. 6

Supremum (left panel) and correlation matrix distance (right panel) between estimated and true correlation matrices for different sample sizes under a MCAR and b MAR, with triangles for the rank-based estimator and circles for the copula estimator, showing the mean over 100 experiments

6.2.2 Convergence rate

While we have shown the convergence rate of the estimator based on Kendall’s $\tau$ in Theorem 1, it is difficult to analyze the copula estimator theoretically. Therefore, we empirically compare the convergence rate of the two estimators to get an insight into the finite-sample behavior of the copula estimator. We first randomly generate a $p = 20$-dimensional correlation matrix, under which normally distributed samples are drawn. Then, we fill in some missing values to these samples, to which we apply the two correlation estimators to learn the correlation matrix. The supremum (SUP) and correlation matrix distance (CMD) (Herdin et al. 2005) are used to measure the distance between learned and true correlation matrices:

$$\begin{aligned} \text{ SUP } = \sup _{jk} |\hat{C}_{jk} - C_{jk}|, \text{ and } \text{ CMD } = 1 - \dfrac{\mathrm{tr}(\hat{C}C)}{\Vert \hat{C}\Vert _f \Vert C \Vert _f}, \end{aligned}$$

where $\mathrm{tr}(\cdot )$ is matrix trace and $\Vert \cdot \Vert _f$ is the Frobenius norm.

Figure 6 shows the convergence property of the two estimators for different sample sizes under (a) MCAR and (b) MAR when the expected percentage of missing values $\beta = 0.25$, providing the mean of SUP and CMD over 100 experiments, where ‘Tau’ and ‘Cop’ denote the estimator based on Kendall’s $\tau$ and the copula estimator, respectively. We see that the copula estimator reports a smaller SUP and CMD for all sample sizes, showing better convergence than the rank-based estimator under both MCAR and MAR. Figure 7 provides the results over different proportions of missing values when the sample size $n = 1000$, for the same experimental setting as in Fig. 6. It suggests that the copula estimator substantially outperforms the rank-based estimator: The more the missing values, the bigger the advantage. More extensive experiments (not shown) done for different numbers of variables reveal a similar picture. To conclude, the copula correlation estimator is at least bounded by the error bound of the Kendall’s $\tau$-based estimator that is shown in Theorem 1.

Fig. 7

Supremum (left panel) and correlation matrix distance (right panel) for different proportions of missing values under a MCAR and b MAR, where ‘beta’ denotes the expected proportion of missing values, i.e., the $\beta$ shown in Eq. (9)

6.3 Causal discovery on benchmark DAGs

In this subsection, we evaluate the ‘Rank PC’ (RPC) and ‘Copula PC’ (CoPC), and assess the justification of the usage of the effective sample size in causal discovery on the two benchmark DAGs: the Asia network and the Alarm network. A first alternative is the listwise deletion-based approach, in which we first perform listwise deletion and then apply the standard PC algorithm for causal discovery, denoted by ‘PC $+$ LD.’ A second alternative considers the mean substitution-based approach, denoted by ‘PC $+$ MS.’ We do not incorporate the hot deck-based approach because, from the previous analysis (Sects. 5.2, 6.2.1), we know that MS is better than HD in correlation estimation and they share the same sample size; thus, MS should naturally outperform HD in causal discovery.

Three metrics are used to evaluate the algorithms: the true positive rate (TPR) and the false positive rate (FPR), which are defined as

$$\begin{aligned} \text{ TPR } = \dfrac{\text{ TP }}{|\varvec{E}|} \text{ and } \text{ FPR } = \dfrac{\text{ FP }}{p(p-1)/2 - |\varvec{E}|} \end{aligned}$$

with $|\varvec{E}|$ the number of edges in the true skeleton, as well as the structural Hamming distance (SHD), counting the number of edge insertions, deletions, and flips in order to transfer the estimated CPDAG into the correct CPDAG (Tsamardinos et al. 2006). The TPR and FPR evaluate the estimated skeleton while SHD is an overall measure for evaluating the estimated CPDAG. A higher TPR, a lower FPR and a smaller SHD imply better performance. We consider different proportions of missing values $\beta \in \{0.1,\, 0.2,\, 0.3\}$, and different sample sizes $n \in \{100,\, 500,\, 1000\}$ for the Asia network and $n \in \{500,\, 1000,\, 2000\}$ for the Alarm network.

Fig. 8

Performance of causal discovery algorithms on nonparanormal data generated by the Asia network under a MCAR and b MAR, showing the mean of TPR, FPR and SHD over 100 experiments with $95\%$ confidence interval, where ‘PC $+$ LD’ and ‘PC $+$ MS’ denote the standard PC algorithm with listwise deletion and mean substitution, ‘RPC $+$ SS’ denotes the Rank PC with the sample size, ‘RPC $+$ GESS’ denotes the Rank PC with the global effective sample size, etc. The three rows in each subfigure represent the results when the sample sizes are 100, 500, 1000, respectively

Fig. 9

Performance of causal discovery algorithms on nonparanormal data generated by the Alarm network under a MCAR and b MAR. The three rows in each subfigure represent the results when the sample sizes are 500, 1000, 2000, respectively

Figure 8 shows the results on nonparanormal data generated by the Asia network under (a) MCAR and (b) MAR, providing the mean of TPR, FPR and SHD over 100 experiments and error bars representing the 95% confidence interval, where SS, GESS and LESS represent the original sample size, global effective sample size and local effective sample size, respectively. Thus, ‘RPC $+$ SS’ denotes the Rank PC with the sample size, ‘RPC $+$ GESS’ denotes the Rank PC with the global effective sample size, etc. Figure 8 shows that, compared to other approaches, ‘PC $+$ LD’ deteriorates dramatically w.r.t. TPR as the percentage of missing values increases regardless of the sample sizes and missingness types. This is due to the sharp decrease in the number of complete cases in the listwise deletion method, as shown in Fig. 2. ‘PC $+$ MS,’ on the other hand, scales well w.r.t. TPR, but reports a very bad result w.r.t. FPR for large sample sizes. Our analysis is that the sample size used in ‘PC $+$ MS,’ usually much larger than the number of complete cases used in ‘PC $+$ LD,’ makes the conditional independence tests rejected more easily and thus incurs more edges in the resulting graph. Therefore, both ‘PC $+$ LD’ and ‘PC $+$ MS’ give a bad overall performance especially for a larger sample size. By contrast, RPC and CoPC can be seen to be relatively robust to the increase in missing values, where the group of CoPC (with SS, GESS or LESS) shows an advantage over the group of RPC.

The results for the Alarm network on nonparanormal data are shown in Fig. 9, for the same experiments as in Fig. 8. We do not consider ‘PC $+$ LD’ here, because there are only very few complete records left ($2\%$ even when $\beta =0.1$). Figure 9 shows that RPC and CoPC substantially outperform ‘PC $+$ MS,’ as expected. In terms of the comparison of Rank PC and Copula PC, we have that both approaches are indistinguishable under MCAR w.r.t SHD: RPC is slightly better for small sample sizes with many missing values while CoPC shows a small advantage over RPC for larger sample sizes. However, CoPC significantly outperforms RPC w.r.t. all the three metrics under MAR, which becomes even more prominent for larger sample sizes. This is mainly because the Gibbs sampler in CoPC still works quite well in correlation estimation while RPC gives a biased estimate under MAR, as shown in Fig. 5.

Next, we analyze whether the effective sample size improves causal discovery. Although a decrease in TPR appears for both CoPC and RPC when SS is replaced with GESS or LESS, we see a bigger improvement in FPR. Thus, w.r.t. the overall metric SHD, the PC algorithms with GESS and LESS perform substantially better than with SS. Also, we notice that LESS can yield more accurate results than GESS: indistinguishable TPR, but better FPR and SHD. Overall, we conclude that: (1) compared to the sample size, the usage of an effective sample size (both GESS and LESS) significantly reduces the number of false positives, which thus leads to a better CPDAG; (2) the local effective sample size is a better choice in the conditional independence tests. More experiments (not shown) done for networks with more variables indicate that: The more the variables, the bigger the advantage of LESS over GESS and SS.

Apart from the experiments on the two known DAGs, we also evaluate the algorithms on randomly simulated DAGs and mixed data. These results that are given in “Appendix” confirm the above conclusions.

7 Application to real-world data

In this section, we illustrate our approaches on two real-world datasets: riboflavin production data and chronic fatigue syndrome data. The first contains no missing values while the second contains only a few. The reason why we choose such two datasets is not because datasets with many missing values are not popular, but because we can take the result on the (almost) complete dataset as a baseline to be used for evaluating our approaches on the datasets with some manually added missing values.

7.1 Riboflavin production data

Our first application to real-world data considers the dataset of riboflavin production by Bacillus subtilis, which is publicly available in the R package hdi (Dezeure et al. 2015). It contains 71 continuously measured observations of 4088 predictors (gene expressions) and a one-dimensional response. For the ease of reproduction, we choose the 10 genes with largest empirical variance as our experimental data, denoted by riboflavinV10,³ as done in Bühlmann et al. (2014). The resulting graph on all the 71 available observations by the conservative version of ‘Rank PC’ or ‘Copula PC’ with significance level 0.05 is shown in Fig. 10, which we take as the ‘pseudo-ground truth’ to be used for evaluating resulting graphs of the algorithms on data with missing values. The algorithms do not orient any edges, mainly because the number of observations is very small and we use the conservative version of the standard PC algorithm. Then, we manually fill in a specific proportion of missing values (measured by $\beta$) to riboflavinV10 following the procedure in Sect. 6.1 and run our algorithms on the resulting incomplete data. The number of ‘missing edges’ (edges that appear in the true skeleton but not in the learned one) and ‘extra edges’ (edges that appear in the learned skeleton but not in the true one) are used to evaluate the skeleton, while SHD evaluates the learned CPDAG.

Fig. 10

Graph based on all available observations on riboflavinV10 dataset

Table 3 Results obtained by various causal discovery algorithms on the riboflavinV10 dataset with different proportions of missing values ($\beta$), showing the mean of missing edges, extra edges and SHD over 50 repeated experiments with an indication of the number of perfect solutions (the corresponding metric is 0) over these trials

Table 3 shows the mean of ‘missing edges,’ ‘extra edges’ and SHD over 50 experiments with an indication of the number of perfect solutions (‘missing edges’ $=$ 0, ‘extra edges’ $=$ 0, SHD $=$ 0) over these trials, for different proportions of added missing values. ‘PC $+$ LD’ for $\beta = 0.2$ and 0.3 under MCAR leaves only a few complete records and hence fails. It still works under MAR, on the other hand, because here only even-indexed variables contain missing values (see Sect. 6.1). Table 3 shows that, despite a good performance of ‘PC $+$ LD’ in incurring extra edges, it leads to more missing edges at the same time especially for a larger proportion of missing values, which thus yields a worse SHD than other approaches. Second, MS shows a better performance than LD for handling missing values in causal discovery, which is because the usage of original sample size (much larger than the number of complete records) obtains a better balance between ‘missing edges’ and ‘extra edges.’ Most importantly, CoPC substantially outperforms RPC and ‘PC $+$ MS’ w.r.t. all the metrics regardless of the proportions of missing values, which becomes more significant under MAR. In addition, we do not see clear difference between ‘CoPC $+$ SS,’ ‘CoPC $+$ GESS’ and ‘CoPC $+$ LESS,’ which is mainly because the small sample size (only 71 available observations) and small number of variables (only 10) make SS, GESS and LESS almost indistinguishable.

7.2 Chronic fatigue syndrome data

In this subsection, we consider a dataset about chronic fatigue syndrome (CFS) of 183 subjects (Heins et al. 2013), which originally comes from a longitudinal study with five time slices. In this paper, we focus only on one time slice representing the subjects after the first treatment as done in Rahmadi et al. (2017), resulting in a subset of the original data, denoted by CFS1. This dataset contains 6 ordinal variables: (1) fatigue severity assessed with the subscale fatigue severity of the checklist individual strength, denoted by ‘fatigue’; (2) the sense of control over fatigue assessed with the self-efficacy scale, denoted by ‘control’; (3) focusing on symptoms measured with the illness management questionnaire, denoted by ‘focusing’; (4) the objective activity of the patient measured using an actometer, denoted by ‘oActivity’; (5) the subject’s perceived activity measured with the subscale activity of the checklist individual strength, denoted by ‘pActivity’; and (6) physical functioning measured with subscale physical functioning of the medical outcomes survey, denoted by ‘functioning.’ For a detailed description of the questionnaires, the actometer and other information, we refer the readers to Heins et al. (2013).

In CFS1, there are only a few missing values: 2 in ‘fatigue,’ 2 in ‘control,’ 2 in ‘focusing,’ 21 in ‘oActivity,’ 2 in ‘pActivity’ and 2 in ‘functioning.’ We run the conservative version of ‘Hetcor PC’ and ‘Copula PC’ with significance level 0.05 on CFS1. Due to the small number of missing values, both HPC and CoPC output the same structure shown in Fig. 11a, regardless of using SS, GESS or LESS. We take this structure as the ‘pseudo-ground truth.’ Then, we manually add more missing values to CFS1 as follows: (1) set ‘oActivity’ to be missing when ‘pActivity’ is smaller than the 37th smallest observation (that is, since $20\% \times 183 = 36.6$, we add about $20\%$ missing values to ‘oActivity’ depending on ‘pActivity’); (2) set ‘fatigue’ to be missing provided that ‘functioning’ is smaller than the 37th smallest observation; and (3) set ‘control’ to be missing given ‘focusing’ under the same condition. We refer to the resulting dataset as CFS1_0. The datasets CSF1 and CSF1_0, as well as the code are publicly available.⁴

Fig. 11

Resulting graphs on the chronic fatigue syndrome dataset: a graph based on all available data; b–f graphs learned by different approaches after manually adding some missing values, where ‘HPC $+$ GESS’ and ‘HPC $+$ LESS’ output the same structure shown in e while CoPCs with SS, GESS and LESS output the same structure shown in f. a Pseudo-ground truth, b PC $+$ LD, c PC $+$ MS, d HPC $+$ SS, e HPC $+$ GESS (or LESS), f CoPC $+$ SS (or GESS, LESS)

The learned graphs of running the causal discovery approaches on CFS1_0 are shown in Fig. 11 from (b) to (f), in which ‘HPC $+$ GESS’ and ‘HPC $+$ LESS’ output the same structure shown in (e) while CoPCs with SS, GESS and LESS output the same structure shown in (f). Compared to the ‘pseudo-ground truth,’ ‘PC $+$ LD’ reports the absence of three edges, in correspondence with what we hypothesized in Sect. 5 and the empirical results in Sect. 6. ‘PC $+$ MS’ gives a very bad result: four missing edges and two extra edges. ‘HPC $+$ SS’ indicates one missing edge, two extra edges and some extra orientations while ‘HPC $+$ GESS or LESS’ suggests two missing edges and one extra edge. By contrast, it is very encouraging that the Copula PC algorithm only implies one missing edge, showing better performance than the other approaches.

8 Conclusion and future work

In this paper, we extended the ‘Rank PC’ algorithm to incomplete data by applying rank correlations to pairwise complete observations and taking the number of pairwise complete observations as an effective sample size. Despite theoretical guarantees, this naive approach has several limitations. First, it only works for continuous data. Second, MCAR is a strong assumption that is quite difficult to justify. Departures from MCAR may lead to a biased analysis and a possibly distorted conclusion. Third, it is hard to compute standard errors or other measures of uncertainty since parameters are estimated from different sets of units. See Schafer and Graham (2002) for more information about the limitations of pairwise complete case analysis.

To solve these limitations, we proposed a novel Bayesian approach, in which a Gibbs sampler is designed to draw correlation matrix samples from the posterior distribution given incomplete data. These are then translated into the underlying correlation matrix and the effective sample size for causal discovery. One highlight of this approach is that it works for mixed data under MAR, a less restrictive assumption, and even if MAR fails, Bayesian methods like ours can still show strong robustness (Schafer and Graham 2002). Another highlight is that the approach uses an elegant way to carry over the additional uncertainty from missing values to conditional independence tests. From the experiments, the Gibbs sampler used in our approach showed good scalability over the network size, in the sense that the burn-in period (number of iterations before convergence) hardly grows as the number of variables increases. In addition, one could plug in some available optimizations of this step (Kalaitzis and Silva 2013) to reduce the time complexity.

For both ‘Rank PC’ and ‘Copula PC,’ we proposed to replace the sample size with an effective sample size in the tests for conditional independence when that data contains missing values, which significantly improves the performance of the PC algorithm. In particular, a local effective sample size for each conditional independence test makes much sense in particular when some variables contain more missing values than others. While we considered the PC algorithm for estimating the underlying causal structure, the idea of using the (local) effective sample size can be applied to other standard algorithms like FCI (Spirtes et al. 2000), in particular for handling potential confounders and selection bias, GES (Chickering 2002b), or their state-of-the-art variants (Claassen et al. 2013; Triantafillou and Tsamardinos 2015; Magliacane et al. 2016).

Although our interest in this paper is in causal structure estimation, the proposed technique for handling missing values in Sect. 4.1 can serve as a general tool for other tasks, e.g., factor analysis (Murray et al. 2013; Gruhl et al. 2013) and undirected graphical models (Dobra et al. 2011; Fan et al. 2017). Our method can not only give a quite good estimate for the underlying correlation matrix under MAR, but also provide an uncertainty measure for this estimate, which is especially important in analyses based on incomplete data.

Fig. 12

Performance of causal discovery algorithms on nonparanormal data generated by randomly simulated DAGs under a MCAR and b MAR, showing the mean of TPR, FPR and SHD over 100 experiments with $95\%$ confidence interval. The three rows in each subfigure represent the results when the sample sizes are 500, 1000, 2000, respectively

Fig. 13

Performance of causal discovery algorithms on mixed data generated by randomly simulated DAGs under a MCAR and b MAR. The three rows in each subfigure represent the results when the sample sizes are 500, 1000, 2000, respectively

While the extended rank likelihood (the basis of our Gibbs sampler) is justifiable for ordinal and continuous variables, it cannot meaningfully handle numeric values for nominal variables (categorical variables without ordering). To include such nominal variables in our copula model, we may consider a multinomial probit model. The main idea is to relate a nominal variable to a vector of latent variables that can be thought of as the unnormalized probabilities of choosing each of the categories, as done in Wang et al. (2017). Also, we consider extending our work to MNAR cases, which can be done under some additional assumptions, e.g., that none of the missingness indicators causally affect each other in the underlying causal graph (Strobl et al. 2017).

Appendix: Evaluation on simulated DAGs

In Sect. 6, we showed the experimental results on two well-known benchmark networks. In order to test our algorithms on more networks, we randomly simulate DAGs following the procedure of Kalisch and Bühlmann (2007) that is implemented via the function randomDAG in the R package pcalg (Kalisch et al. 2010). We restrict the number of variables to $p=20$ and set the sparseness parameter in generating DAGs to $s = 2/(p-1)$, such that the average neighbors of each node is two (Kalisch and Bühlmann 2007). For each experiment, we obtain a random DAG that is used to generate nonparanormal data, on which we evaluate our algorithms. The mean of TPR, FPR and SHD over 100 experiments with $95\%$ confidence interval are shown in Fig. 12.

In order to evaluate the performance of Copula PC on mixed data, we generate data as follows: (1) generate Gaussian data and fill in some missing values (as we did before); (2) discretize $25\%$ variables (randomly chosen) into binary; (3) discretize another $25\%$ into ordinal variables with 5 levels. Then, we run the Hetcor PC algorithm and the Copula PC algorithm on such mixed data, which yields the results shown in Fig. 13.

The results in Figs. 12 and 13 confirm our conclusions: (1) both Rank PC and Copula PC substantially outperform a simple data interpolation-based method ‘PC $+$ MS’; (2) the Copula PC algorithm shows a significant advantage over the Rank (Hetcor) PC algorithm under MAR; (3) the PC algorithm with the local effective sample size performs better than with the global effective sample size, which in turn outperforms the one with the original sample size.