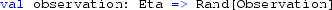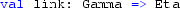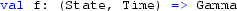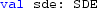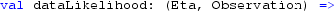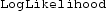Composable models for online Bayesian analysis of streaming data

Abstract

Data is rapidly increasing in volume and velocity and the Internet of Things (IoT) is one important source of this data. The IoT is a collection of connected devices (things) which are constantly recording data from their surroundings using on-board sensors. These devices can record and stream data to the cloud at a very high rate, leading to high storage and analysis costs. In order to ameliorate these costs, the data is modelled as a stream and analysed online to learn about the underlying process, perform interpolation and smoothing and make forecasts and predictions. Conventional state space modelling tools assume the observations occur on a fixed regular time grid. However, many sensors change their sampling frequency, sometimes adaptively, or get interrupted and re-started out of sync with the previous sampling grid, or just generate event data at irregular times. It is therefore desirable to model the system as a partially and irregularly observed Markov process which evolves in continuous time. Both the process and the observation model are potentially non-linear. Particle filters therefore represent the simplest approach to online analysis. A functional Scala library of composable continuous time Markov process models has been developed in order to model the wide variety of data captured in the IoT.

1 Introduction

Observations across sensor networks are highly heterogeneous, such as weather and temperature, counts of cars and bikes or tweets from Twitter. Dynamic linear models (DLMs) are often applied to modelling time series data. They are discrete time, latent variable models which can be applied to a wide variety of problems, provided the data is Normally distributed and the model is linear. The Kalman filter is an analytical solution to find the distribution of the latent variables of a DLM, which can be used to perform forecasting (Kalman 1960). The closed form solution can be found in the case of a linear-Gaussian model because of special properties of the Gaussian distribution; the sum of two Gaussian distributions is a Gaussian distribution and a linear translation of a Gaussian distribution is still Gaussian with predictable mean and variance. However, data arising from sensor networks is highly heterogeneous and in order to model this data, non-linear models with a wide variety of observation models are needed.

In order to model non-linear systems, the extended (EKF) and later unscented Kalman filter (UKF) have been developed (Julier and Uhlmann 1997). The extended Kalman filter linearises at the current time step, by calculating the Jacobian of the transition and observation functions at the given time and using these in the Kalman filter equations. The extended Kalman filter becomes unstable when applied to highly non-linear problems, so the unscented transform was introduced.

Particle filters can determine the state space of a non-linear, non-Gaussian latent variable model, with minimal modification between models. The unscented Kalman Filter is more computationally efficient than the simulation based particle filter and can be more accurate when models are near-linear (Bellotto and Hu 2007). However, particle filters allow more flexibility of model choice and as such are considered when performing inference for the models presented in this paper. As the number of particles in the particle filter is increased, the estimation error tends to zero, the same is not true of the UKF, since a limited number of sigma points are used (Simon 2006). So with access to more computing power, the particle filter is preferred for accurate inference.

Gordon et al. (1993) developed the theory of the bootstrap particle filter and compared the performance of the new filter to the Extended Kalman Filter (EKF). They found the performance of the bootstrap filter to be greatly superior to the EKF using a highly non-linear model. A target tracking model was also considered, where the bootstrap filter again outperforms the EKF.

Partially observed Markov processes (POMP) (Ionides et al. 2006) are a type of state space model. For a review of state space modelling and filtering see Doucet et al. (2001). In a POMP model, the evolution of the latent state is governed by a continuous-time Markov process which allows modelling of irregularly spaced observations in a natural way. The observations are conditionally independent given the current value of the state.

POMP models are flexible in the choice of state and observation distributions, hence they can be used to model a wide variety of processes, such as counts, proportions or strictly positive time varying data. For a full Bayesian analysis of a POMP model, the full-joint posterior distribution of the parameters and the latent state can be determined using the Particle Marginal Metropolis Hastings algorithm (PMMH) (Andrieu et al. 2010). PMMH is an off-line algorithm which requires a batch of observations to determine the parameters. On-line filtering and forecasting can be carried out using a particle filter with pre-determined static parameters, and occasional re-training of the model can be carried out as required. On-line learning of model parameters is an active research area. On-line parameter learning can be used for the composable models considered in this paper, but this is not the main focus (Carvalho et al. 2010; Vieira and Wilkinson 2016). Here we illustrate our approach in the context of on-line state estimation.

It is useful to reuse and combine existing models when exploring new data and building more complex models. The POMP models considered in this paper can be composed together to create new models. A software package has been written in Scala (Odersky et al. 2004) which allows users to build and compose models and perform inference using the composable particle filter and the PMMH algorithm.¹ On-line filtering and forecasting of streaming data is facilitated using Akka Streams² for Scala. Akka streams can be used to process unbounded streams of data with bounded resources, hence on-line filtering can be applied to large, live streams of data from application endpoints, databases and files.

There are other software packages for performing inference on POMP models: LibBi (Murray 2015) implements inference for general state-space models using particle Markov chain Monte Carlo methods and sequential Monte Carlo (SMC). It is optimised for parallel hardware and utilises CUDA (a parallel programming platform by NVIDIA) for GPU (Graphics Processing Unit) programming. There is also an R (R Core Team 2015) package, POMP (King et al. 2015) which implements Frequentist and Bayesian methods of parameter inference for POMP models. Biips (Todeschini et al. 2017) is a probabilistic programming language written in C++ for SMC and particle MCMC using a similar input language to BUGS (Lunn et al. 2000). However, none of these packages support on-line filtering of live streaming data, or model composition.

A Hidden Markov Model (HMM) is a type of state space model with discrete time and discrete state. Factorial HMMs (Ghahramani and Jordan 1997) have a distributed state, which can reduce the complexity of approximate parameter inference when the discrete state space is large. As mentioned by Ghahramani and Jordan, if the model structure is known to consist of loosely coupled states, then the models can be combined from constituent parts. This is similar in spirit to the composable POMP models considered in this paper, however here the state is continuous and evolves in continuous time.

The composable POMP models presented in this paper have been developed to analyse data in the Urban Observatory (James et al. 2014), a grid of sensors deployed around the city of Newcastle Upon Tyne, UK. In order to demonstrate the utility of this class of composable POMP models, there is a real world example presented in Sect. 5. The example consists of irregularly observed (aggregated) Traffic Flow Data collected from the North East Combined Authority Transport Open Data (NECA 2016).

Section 2 introduces POMP models as a means to model a wide variety of time series data. Section 3 describes the composition operator for POMP models, to enable complex models to be developed by combining simple models. Section 4.1 presents the bootstrap particle filter and how it can be applied to estimate the latent state of a composed model. Futher, the composed particle filter can be used to calculate an estimate of the marginal likelihood of the observations given a set of parameters. Section 4.2 outlines the Particle Marginal Metropolis Hastings algorithm, which can be used to calculate the full joint posterior of the parameters and latent state of a POMP model.

2 Partially observed Markov processes

Streaming data arrives frequently and discretely as an observation, y, and a timestamp, t. In order to describe this time series data, a parametric probabilistic model is proposed:

$$\begin{aligned}&Y(t_i)|\eta (t_i) \sim \pi (y(t_i) | \eta (t_i), \theta ), \nonumber \\&\eta (t_i)|\mathbf{x }(t_i) = g(F_{t_i}^T \mathbf{x }(t_i)), \nonumber \\&\mathbf{X }(t_i)|\mathbf{x }(t_{i-1}) \sim p(\mathbf{x }(t_i)|\mathbf{x }(t_{i-1}), \theta ), \nonumber \\&\mathbf{x }(t_0) \sim p(\mathbf{x }(t_0) | \theta ). \end{aligned}$$

(1)

$Y(t_i) \in {\mathbb {R}}$ is a scalar observation from the observation distribution, $\pi (y(t_i)|\eta (t_i), \theta )$. $\mathbf{X }(t_i)$ is the (possibly multidimensional) unobserved state of the process. The state is Markovian and is governed by the transition kernel $p(\mathbf{x }(t_i)|\mathbf{x }(t_{i-1}), \theta )$ that we assume realisations can be generated from, but in general may not represent a tractable distribution, in the sense that we do not assume that we can evaluate the transition kernel pointwise. The prior distribution on the state is given by $p(\mathbf{x }(t_0) | \theta )$. $F_t$ is a time dependent vector, the application results in $\gamma (t) = F_t^T \mathbf{x }(t)$, where $\gamma (t) \in {\mathbb {R}}$. The function g is a link-function allowing a non-linear transformation as required by the observation distribution. For example, the link-function for a Poisson distribution is $g(x) = \exp \{x\}$, since the rate of a Poisson distribution is required to be positive. $\theta$ represents the static parameters of the model, some observation distributions have scale parameters, Markov transition kernels require parameters and the initial state, $\mathbf{x }(t_0)$, requires parameters.

In order to specify the model, the observation distribution $\pi (\cdot )$, the state evolution kernel $p(\cdot )$, the linking function $g(\cdot )$, and the linear transformation vector $F_t^T$ are assumed known and arent learned from the data. The parameters of the observation distribution and state evolution kernel are learned from the data. Models with different specifications for the same data can be assesed using model selection techniques (Wasserman 2000).

The model is expressed as a directed graph in Fig. 1. Although the latent state evolves continuously, it is indicated only when there is a corresponding observation of the process.

Fig. 1

Representation of a POMP model as a directed acyclic graph (DAG)

2.1 Observation model

There is a need for flexible observation distributions to model the variety of data recorded by large heterogeneous sensor networks. The Scaled Exponential family models can be used for the observation model, which includes, Poisson, Bernoulli and the Gaussian distribution among others.

Following the notation of West and Harrison (1997), the exponential family of dynamic models are parameterised by $x(t_i)$, V and three known functions $b(Y(t_i), V)$, $S(Y(t_i))$, $a(x(t_i))$, the density, $p(Y(t_i)|x(t_i), V)$ is given by:

$$\begin{aligned} b(Y(t_i), V) \exp \left\{ \frac{S(Y(t_i))x(t_i) -a(x(t_i))}{V} \right\} , \end{aligned}$$

(2)

$x(t_i)$ is called the natural parameter of the distribution, $V > 0$ is the scale parameter, $S(Y(t_i))$ is the sufficient statistic, $b(Y(t_i), V)$ is the base measure and $a(x(t_i))$ is known as the log-partition. The model class is then a generalisation of dynamic generalised linear models (DGML) (West and Harrison 1997).

An extension to the POMP model class is also considered, the Log-Gaussian Cox-Process, for modelling time-to-event data. It should be noted that additional extensions to non-exponential family observation models are possible with the methods for filtering and inference presented in Sect. 4, but are not considered here.

2.2 Modelling seasonal data

Many natural phenomena feature predictable periodic changes in the rate of their process. For instance, when monitoring urban traffic, traffic flow is higher around 9am and 5pm as commuters make their way to and from the city. In order to model a periodic process, a time-dependent linear transformation vector is used:

$$\begin{aligned} F_{t_i} = \begin{pmatrix} \cos (\omega t_i) \\ \sin (\omega t_i) \\ \vdots \\ \cos (\omega h t_i) \\ \sin (\omega h t_i) \end{pmatrix}, \end{aligned}$$

where $\omega = \frac{2\pi }{P}$ is the frequency, P represents the period of the seasonality and h represents the number of harmonics required. The phase and amplitude of the waves are controlled by the value of the latent state, if the hth harmonic at time $t_i$ is given by:

$$\begin{aligned} S_h = \begin{pmatrix} \cos (\omega h t_i) \\ \sin (\omega h t_i) \end{pmatrix} \cdot \begin{pmatrix} x_1(t_i) \\ x_2(t_i) \end{pmatrix}, \end{aligned}$$

the phase of the wave is $\varphi = \arctan (-x_2(t_i)/x_1(t_i))$ and the amplitude is, $A = \sqrt{x_2(t_i)^2 + x_1(t_i)^2}$. The first multiplicand of $S_h$ is a component representing the hth harmonic of $F_t$. The observation model can be any appropriate distribution. The full specification of the seasonal POMP model is given by (1) with an identity link-function, $g(x) = x$. The latent state of the seasonal model is 2h-dimensional.

In DLMs seasonality is commonly represented using block diagonal matrices to transform the state, the blocks contain rotation matrices which are time homogeneous (West and Harrison 1997). This is not feasible with continuous-time models where observations can arrive irregularly. In order to apply the block diagonal matrix to irregularly spaced data, a small discretised time-grid would have to be determined before the data arrived and each observation would be assumed to arrive at a time on this grid. This is more computationally intensive than using a time-dependent vector transformation as proposed above, since the model must be simulated forward at each step of the discretised time-grid which may not have a corresponding observation.

Figure 2 shows a simulation from a Normal seasonal model, with a latent state evolution governed by Brownian Motion as introduced in Sect. 2.4.

Fig. 2

(Top) Simulated values from a seasonal model with Normal observations, $V = 1.0$, observed discretely at integer time points, (Middle) Transformed State, mean of the Normal Observations, (Bottom) Generalised Brownian Motion latent state with $\mu = 0.1$, $\sigma = 0.3$ with the initial state drawn from ${\mathscr {N}}(0.0, 1.0)$

2.3 Time to event data: the Log-Gaussian Cox-Process

The Log-Gaussian Cox-Process (LGCP) is an inhomogeneous Poisson process whose rate is driven by a log-Gaussian process. In an inhomogeneous Poisson process the hazard, $\lambda (t)$, varies in time according to a log-Gaussian process, for an inhomogeneous Poisson process, the total number of events in the interval $(t_0,t_n]$ is distributed as:

$$\begin{aligned} N(t_n) \sim \text {Poisson}\left( \int _{t_0}^{t_n} \lambda (s) ds\right) , \end{aligned}$$

where the the cumulative hazard can be written as $\varLambda (t_n) = \int _{t_0}^{t_n} \lambda (s) ds$. The cumulative distribution function of the Log-Gaussian Cox-Process is $1 - \exp \{-\varLambda (t_n)\}.$ The conditional density is then,

$$\begin{aligned} \pi (t_n|\lambda (t_n), \varLambda (t_n)) = \lambda (t_n)\exp \{-\varLambda (t_n)\}, \end{aligned}$$

The general form of the LGCP POMP model is given by,

$$\begin{aligned}&t_i|\lambda (t_i) \sim \pi (t|\lambda (t_i), \varLambda (t_i)), \\&\begin{pmatrix}\lambda (t_i) \\ \text {d}\varLambda (t_i) \end{pmatrix} = \begin{pmatrix} \exp \{x(t_i)\} \\ \lambda (t_i) \text {d}t \end{pmatrix}, \\&X(t_i)|x(t_{i-1}) \sim p(x(t_i)|x(t_{i-1}), \theta ), \\&x(t_0) \sim p(x(t_0)|\theta ). \end{aligned}$$

where $p(x(t_i)|x(t_{i-1}), \theta )$ is the transition kernel of a continuous time Gaussian Markov process. Figure 3 shows a simulation from the Log-Gaussian Cox-Process, using an approximate simulation algorithm presented in “Appendix A.2”.

Fig. 3

(Top) Simulated event times from the Log-Gaussian Cox-Process, (Middle) The unobserved hazard, (Bottom) The unobserved state evolving according to the Ornstein–Uhlenbeck Process with mean $\theta = 0.1$, speed $\alpha = 0.4$ and volatility $\sigma = 0.5$, the initial state is sampled from ${\mathscr {N}}(2.0, 1.0)$

2.4 The latent state: diffusion processes

The latent state evolves according to a continuous time Markov process. Any Markov process can be used to represent the state; however in this paper, the focus is on Itô diffusion processes. Diffusion processes are represented by solutions to stochastic differential equations (SDE), (see Oksendal (2013) for a detailed treatment). The continuous-time evolution of the latent space is governed by a time homogeneous SDE of the form,

$$\begin{aligned} \text {d}\mathbf{X }(t) = \mu (\mathbf{X }(t)) \text {d}t + \sigma (\mathbf{X }(t)) \text {d}\mathbf{W }(t). \end{aligned}$$

(3)

Generally, $\mathbf{X } \in {\mathbb {R}}^n$ and $\mu (\cdot ): {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ is referred to as the drift coefficient, $\sigma (\cdot ): {\mathbb {R}}^n \rightarrow {\mathbb {R}}^{n\times m}$ is the diffusion coefficient and $\mathbf{W }(t)$ is an $m \times 1$ Wiener Process. The Wiener process is sometimes referred to as Brownian motion and written $\mathbf{B }(t)$.

If an SDE doesn’t have an analytic solution, it can be simulated approximately using the Euler–Maruyama approximation or higher-order schemes suh as the Milstein method (Kloeden and Platen 1992). The Euler–Maruyama approximation gives an approximate solution to an SDE, as a Markov chain. Start with a general SDE for a diffusion process as in Eq. 3.

The interval of interest, $[t_0,t_M]$ is partitioned into N even sized sub-intervals, of size $\Delta t = \frac{t_M - t_0}{N}$. A value is defined for $\mathbf{X }_0$, the initial value of the Markov chain, then for $i = 1,\dots ,N$

$$\begin{aligned} \mathbf{X }_{i} = \mathbf{X }_{i-1} + \mu (\mathbf{X }_{i-1})\Delta t + \sigma (\mathbf{X }_{i-1})\Delta \mathbf{W }_{i-1}, \end{aligned}$$

(4)

where $\Delta \mathbf{W }_n \sim \text {MVN}(\mathbf{0 }, I_m \Delta t)$, are independent and identically distributed Multivariate Normal random variables with mean zero and variance $I_m \Delta t$, where $I_m$ is the m-dimensional identity matrix. The approximate transition density for any diffusion process, for sufficiently small $\Delta t$, can then by written as:

$$\begin{aligned} \begin{aligned} \mathbf{X }_i|\mathbf{X }_{i-1}&\sim {\text {MVN}}\left( \mathbf{X }_{i-1}+ \mu (\mathbf{X }_{i-1})\Delta t, \right. \\&\left. \quad \Delta t \sigma (\mathbf{X }_{i-1}) \sigma (\mathbf{X }_{i-1})^T \right) . \end{aligned} \end{aligned}$$

Equation 4 is the Euler–Maruyama discretisation. The transition to the next state only depends on the current value, hence the Euler–Maruyama approximation scheme for stochastic differential equations is a Markov Process. Analytic solutions of diffusion processes are also Markovian, necessarily.

3 Composing models

In order to model more real-world data, it is convenient to compose simple model components to form a more complex model, representative of the real-world measurements. Consider the traffic data example presented in Sect. 5, the data consists of readings of passenger car units, which are positive integer values representing the size of a vehicle. The observation model is chosen to be the Negative Binomial distribution. The traffic data displays daily and weekly seasonal cycles, so the transformed latent state, $\eta (t)$ must vary periodically with time. In order to account for the two periods of seasonality with a Poisson observation model, a seasonal-Poisson model with drift is formed by the composition of a Poisson model with a one-dimensional latent state and two seasonal models. One seasonal model has a weekly period and the other has a daily period.

The composable POMP model can be thought of as a partially observed (uncoupled) multivariate SDE, however model specification has been simplified using model composition.

Consider a POMP model, with its associated functions, distributions and latent state indexed by j, where $j = \{1, 2, \dots , \text {Model Number}\}$. Where $\theta ^{(j)}$ represents the the parameters of the jth model:

$$\begin{aligned}&Y(t_i)|\eta ^{(j)}(t_i) \sim \pi _j(y(t_i) | \eta ^{(j)}(t_i), \theta ^{(j)}), \nonumber \\&\eta ^{(j)}(t_i)|\mathbf{x }^{(j)}(t_i) = g_j( F^{(j)T}_{t_i} \mathbf{x }^{(j)}(t_i)), \nonumber \\&\mathbf{X }^{(j)}(t_i)|\mathbf{x }^{(j)}(t_{i-1}) \sim p_j(\mathbf{x }^{(j)}(t_i)|\mathbf{x }^{(j)}(t_{i-1}), \theta ^{(j)}), \nonumber \\&\mathbf{x }^{(j)}(t_0) \sim p_j(\mathbf{X }^{(j)}(t_0) | \theta ^{(j)}). \end{aligned}$$

(5)

Now define the composition of model ${\mathscr {M}}_1$ and ${\mathscr {M}}_2$ as ${\mathscr {M}}_3 = {\mathscr {M}}_1 \star {\mathscr {M}}_2$. By convention, the observation model will be that of the left-hand model, ${\mathscr {M}}_1$ and the observation model of the right-hand model will be discarded. As such, the non-linear linking-function must be that of the left-hand model, $g_1: {\mathbb {R}} \rightarrow {\mathbb {R}}$. The linking-function ensures the state is correctly transformed into the parameter space of the observation distribution.

In order to compose the latent state, the initial state vectors are concatenated:

$$\begin{aligned} \mathbf{X }^{(3)}(t_o) \sim \begin{pmatrix} p(\mathbf{x }^{(1)}(t_0) | \theta ^{(1)}) \\ p(\mathbf{x }^{(2)}(t_0) | \theta ^{(2)}) \end{pmatrix}. \end{aligned}$$

The composed model’s transition function for the state is given by:

$$\begin{aligned} p_3(\mathbf{x }(t_i) | \mathbf{x }(t_{i-1}), \theta ) = \begin{pmatrix} p_1(\mathbf{x }^{(1)}(t_i) | \mathbf{x }^{(1)}(t_{i-1}), \theta ^{(1)}) \\ p_2(\mathbf{x }^{(2)}(t_i) | \mathbf{x }^{(2)}(t_{i-1}), \theta ^{(2)}) \end{pmatrix}. \end{aligned}$$

The linear deterministic transformation-vectors, $F^{(j)}(t)$, $j = \{1,2\}$, are vertically concatenated:

$$\begin{aligned} F^{(3)}(t) = \begin{bmatrix} F^{(1)}(t) \\ F^{(2)}(t) \end{bmatrix}. \end{aligned}$$

The vector dot-product with the composed latent state is then computed, such that: $F^{(3)T}_t \mathbf{x }(t) \equiv F^{(1)T}_t \mathbf{x }^{(1)}(t) + F^{(2)T}_t \mathbf{x }^{(2)}(t)$. The dot product, $\gamma (t) = F_t^T \mathbf{x }(t)$ results in a one-dimensional state, $\gamma (t) \in {\mathbb {R}}$. The full composed model, ${\mathscr {M}}_3$ can then be expressed as follows:

$$\begin{aligned}&Y(t_i)|\eta (t_i) \sim \pi _1(y(t_i) | \eta (t_i)), \\&\eta (t_i)|\mathbf{x }(t_i) = g_1(F^{(3)T}_{t_i} \mathbf{x }(t_i)) \\&\mathbf{X }(t_i) | \mathbf{x }(t_{i-1}) \sim \begin{pmatrix} p_1(\mathbf{x }^{(1)}(t_i) | \mathbf{x }^{(1)}(t_{i-1}), \theta ^{(1)}) \\ p_2(\mathbf{x }^{(2)}(t_i) | \mathbf{x }^{(2)}(t_{i-1}), \theta ^{(2)}) \end{pmatrix}, \\&\mathbf{X }(t_0) \sim \begin{pmatrix} p(\mathbf{x }^{(1)}(t_0) | \theta ^{(1)}) \\ p(\mathbf{x }^{(2)}(t_0) | \theta ^{(2)}) \end{pmatrix}. \end{aligned}$$

The POMP models, along with the closed, associative binary composition operator, form a semigroup. In order to compose three or more models the binary operator is applied pairwise, remembering that it is not commutative:

$$\begin{aligned} {\mathscr {M}}_5&= ({\mathscr {M}}_1 \star {\mathscr {M}}_2) \star {\mathscr {M}}_4, \nonumber \\&= {\mathscr {M}}_3 \star {\mathscr {M}}_4, \nonumber \\&= {\mathscr {M}}_1 \star ({\mathscr {M}}_2 \star {\mathscr {M}}_4). \end{aligned}$$

(6)

In the first line of Eq. 6, we compose ${\mathscr {M}}_1$ and ${\mathscr {M}}_2$ to form ${\mathscr {M}}_3$ as in the example above, then we proceed to compose ${\mathscr {M}}_3$ and ${\mathscr {M}}_4$ to form ${\mathscr {M}}_5$.

The semigroup structure exhibited by the composable model class is the most basic of algebraic properties, but it is nevertheless very powerful. In particular, it allows the creation of very large, complex models from simpler components in a recursive, hierarchical fashion. Many functional programming languages provide support for datatypes with semigroup structure, and provide convenient syntax for composition. Further details on composing models in Scala are presented in “Appendix A.3”. Figure 4 shows a directed acyclic graph of a composed model.

Fig. 4

A directed acyclic graph representing the composition of two models, the latent state is represented as separate, and advancing according to each model components transition kernel: $p_i$

3.1 Example: A seasonal-poisson model

To illustrate model composition, consider a Poisson model with a seasonally-varying time-dependent rate parameter, $\lambda (t)$. This model is the composition of two models, a single Poisson model, ${\mathscr {M}}_1$, and a single seasonal model, ${\mathscr {M}}_2$, to make ${\mathscr {M}}_3 = {\mathscr {M}}_1 \star {\mathscr {M}}_2$. This model could represent the flow of traffic through a city, as in the example in Sect. 5.

The Poisson model, ${\mathscr {M}}_1$, has a 1-dimensional latent state, which evolves according to generalised Brownian motion. The linking function is the exponential function, $g(x) = \exp (x)$, and the linear transformation vector is one, $F^{(1)}_{t_i} = 1$. The Poisson model is given by:

$$\begin{aligned}&N(t_i) \sim Poisson (\lambda (t_i)), \\&\lambda (t_i) | x(t_i) = \exp \{ x(t_i) \}, \\&\text {d}X(t_i) = \mu ^{(1)} \text {d}t + \sigma \text {d}W^{(1)}(t_i). \end{aligned}$$

The latent state of the seasonal model, ${\mathscr {M}}_2$, has a dimension of 2h, where h represents the number of harmonics. Generalised Brownian motion is used to represent the time evolution of the 2h-dimensional latent state, hence the drift coefficient $\varvec{\mu }^{(2)}$ is $2h \times 1$ vector and the diffusion coefficient, $\varSigma$, is a $2h \times 2h$ diagonal matrix. The standard seasonal model has the Normal distribution as the observation distribution, and the linking function is the identity function:

$$\begin{aligned}&N(t_i)|\eta (t_i) \sim {\mathscr {N}}(\eta (t_i), \sigma ^2), \\&\eta (t_i)|\mathbf{x }(t_i) = F_{t_i}^{(2)T} \mathbf{x }(t_i), \\&\text {d}\mathbf{X }(t_i) = \pmb {\mu }^{(2)} \text {d}t + \varSigma \text {d}\mathbf{W }^{(2)}(t_i) \end{aligned}$$

The vector $F^{(2)}_{t_i}$ is a $2h \times 1$ vector of fourier components:

$$\begin{aligned} F^{(2)}_{t_i} = \begin{pmatrix} \cos \omega t \\ \sin \omega t \\ \cos 2\omega t \\ \sin 2\omega t \\ \vdots \\ \cos h\omega t \\ \sin h\omega t \\ \end{pmatrix}, \end{aligned}$$

(7)

$\omega = 2\pi /P$ is the frequency and P is the period of the seasonality. In order to model a daily seasonality, $P = 24$, if the observation timestamps are in hour units.

In the composed model, the observation model of ${\mathscr {M}}_1$ is chosen, in this case the Poisson distribution. This necessitates the left-hand linking function ($g(x) = \exp (x)$) since the rate parameter of the Poisson distribution is greater than zero, $\lambda (t) > 0$. The full composed model can be expressed as:

$$\begin{aligned}&N(t_i) | \lambda (t_i) \sim Poisson (\lambda (t_i)), \\&\lambda (t_i) | \mathbf{x }(t) = \exp \{F_{t_i}^{(3)T} \mathbf{x }(t_i)\}, \\&\text {d}\mathbf{X }(t_i) = \pmb {\mu }\text {d}t + \begin{pmatrix} \sigma &{} 0 \\ 0 &{} \varSigma \end{pmatrix}\text {d}\mathbf{W }(t_i). \end{aligned}$$

The system state is $n = 2h + 1$ dimensional, hence the drift coefficient $\pmb {\mu }$ is an $n \times 1$ dimensional vector and the diffusion coefficient is an $n \times n$ diagonal matrix. The Weiner processes, $W^{(1)}$ and $\mathbf{W }^{(2)}$ advance independently. The linear transformation vector $F^{(3)}_{t_i}$ is a time-dependent, $n \times 1$ vector, which is the concatenation of the two $F^{(j)}_{t_i}, j = 1,2$, vectors:

$$\begin{aligned} F^{(3)}_{t_i} = \begin{pmatrix} 1 \\ \cos \omega t \\ \sin \omega t \\ \vdots \\ \cos h\omega t \\ \sin h\omega t \\ \end{pmatrix}. \end{aligned}$$

(8)

3.1.1 Seasonal Poisson composed model in Scala

Define a Poisson model with a representing the solution to a Markov process and the models associated parameters.

Each model, including the Poisson model is parameterised by the latent-state, allowing flexibility in the choice of latent state. The contains the parameters for the diffusion process representing the latent state (including the parameters of the initial state), the in the first argument corresponds to a scale parameter required by some observation distributions (not required for the Poisson model). Now define a single seasonal model:

The seasonal model has a Gaussian observation distribution, in order to use the seasonal model by itself the observation noise (standard deviation) for the Gaussian observation model must be specified in the scale parameter (currently set as None). The infix notation is available on the unparameterised model and the parameters because both define a semigroup and hence have a binary function (described in detail in the “Appendix A.3”). To compose the parameters and model:

The can be simulated from, it can be fit to observed data using the PMMH algorithm, and a particle filter and can used for on-line filtering as described in Sect. 4.

4 Statistical inference

Consider a POMP model of the form in Eq. 1, observed at discrete times, $\{t_1, t_2, \ldots ,t_M\}$. The joint distribution of all the random variables in the model can be written as:

$$\begin{aligned}&p(\mathbf{x }(t_{0:M}), y(t_{1:M}), \theta ) \\&\quad = p(\mathbf{x }(t_{0:M}), \theta )\pi (y(t_{1:M}) | g(F^T_{t_{0:M}} \mathbf{x }(t_{0:M})), \theta ) \\&\quad = p(\theta ) p(\mathbf{x }(t_0)|\theta ) \Bigg [\prod _{i=1}^M p(\mathbf{x }(t_{i})|\mathbf{x }(t_{i-1}), \theta ) \\&\qquad \pi (y(t_i) | \eta (t_i), \theta )\Bigg ]. \end{aligned}$$

Since the latent state is a Markov process and the observations $y(t_{1:M})$ are conditionally independent given the latent state, the joint distribution can be written as the product of the distribution over the parameters, $p(\theta )$, the initial distribution of the latent state $p(\mathbf{x }(t_0)|\theta )$, the transition density, $p(\mathbf{x }(t_{i})|\mathbf{x }(t_{i-1}), \theta )$ and the conditional density for the observations $\pi (y(t_i) | \eta (t_i), \theta )$.

In general the full-joint posterior distribution of the parameters and state is analytically intractable. The particle marginal Metropolis–Hastings algorithm, presented in Sect. 4.2, can be used to determine the joint-posterior of the parameters and state, $p(\mathbf{x }(t_{0:M}), \theta | y(t_{1:M}))$. The PMMH utilises the pseudo-marginal likelihood estimated using the composable particle filter presented in Sect. 4.1

4.1 On-line state estimation using the composable particle filter

The bootstrap particle filter (Gordon et al. 1993) can be used to estimate the latent state of a POMP model. The latent state is a Markov process with an associated transition kernel $\mathbf{X }(t_i)|\mathbf{x }(t_{i-1}) \sim p(\mathbf{x }(t_i)|\mathbf{x }(t_{i-1}))$, from which realisations can be sampled. The transition kernel can be any continuous time Markov process, but in this paper only diffusion processes represented by SDEs are considered. The transition kernel can either be an exact solution of an SDE or simulated on a fine grid using the Euler–Maruyama method, presented in Sect. 2.4. The process is observed through an observation model $Y(t_i)|\eta (t_i) \sim \pi (y(t_i) | \eta (t_i))$.

The bootstrap particle filter is used to estimate the unobserved system state by approximating the filtering distribution, $p(\mathbf{x }(t_i)| y(t_{1:i}))$. The algorithm to determine an empirical approximation of the latent state at each observation time is presented below:

• 1. Initialise: Simulate N particles from the initial distribution of the latent state, $\mathbf{x }(t_0)^{(k)} \sim p(\mathbf{x }(t_0))$, and set $i = 1$

• 2. Advance the particle cloud to the time of the next observation, $\mathbf{x }(t_i)^{(k)} \sim p(\mathbf{x }(t_i)^{(k)}|\mathbf{x }(t_{i-1})^{(k)})$, $k = 1,2,\dots ,N$

• 3. Transform each particle appropriately as required by the observation model, $\eta (t_i)^{(k)} = g(F^T_{t_i} \mathbf{x }(t_i)^{(k)})$

• 4. Calculate the weight of each particle, using the conditional density of the observation given the particle value: $w^*(t_i)^{(k)} = \pi (y(t_i)|\eta (t_i)^{(k)})$

• 5. Normalise the weights, $w(t_i)^{(k)} = \frac{w^*(t_i)^{(k)}}{\sum _{j=1}^N w^*(t_i)^{(j)}}$. The particles and associated normalised weights form a weighted sample from the filtering distribution $p(\mathbf{x }(t_i)| y$ $(t_{1:i}))$, $\{\mathbf{x }(t_i)^{(k)}, w(t_i)^{(k)} | k = 1,\dots ,N \}$

• 6. Resample the state, by sampling with replacement N times from a Multinomial distribution with each category representing a particle and the probability of choosing a particle represented by the associated weights, $w(t_i)^{(k)}$. This gives an approximate random sample from $p(\mathbf{x }(t_i)| y(t_{1:i}))$

• 7. Return the random samples from the filtering distribution $p(\mathbf{x }(t_i)| y(t_{1:i})).$ If $i < M$ set $i = i + 1$ and go to step 2, else stop.

The average of the un-normalised weights at each time point gives an estimate of the marginal likelihood of the current data point given the data observed so far:

$$\begin{aligned} {\hat{p}}(y(t_i)|y(t_{1:i-1})) = \frac{1}{N}\sum _{j=1}^N w^*(t_i)^j. \end{aligned}$$

The estimate of the likelihood of the full path is given by:

$$\begin{aligned} {\hat{p}}(y(t_{1:M})) = {\hat{p}}(y(t_1))\prod _{i=2}^M {\hat{p}}(y(t_i)|y(t_{1:i-1})). \end{aligned}$$

The estimated marginal likelihood is consistent, meaning that as the number of particles are increased, $N \rightarrow \infty$, then the estimate converges in probability to the true value. The estimate is also unbiased, meaning that the expectation of the estimate is equal to the true value, ${\mathbb {E}}({\hat{p}}_{\theta ^*}(y(t_{1:M}))) = p_{\theta ^*}(y(t_{1:M}))$ where the expectation is taken over all the random variables generated in the particle filter; see Del Moral (2004) for a proof. This marginal likelihood is used in the PMMH algorithm discussed in Sect. 4.2.

In practice, the bootstrap particle filter can be easily parallelised, advancing the state and calculating the likelihood are naturally parallel. Multinomial resampling (as described above) requires communication between multiple threads of execution, in order to sum the value of the weights. Other resampling schemes, such as stratified and systematic resampling are more amenable to parallelisation. For a comparison of resampling schemes used in the particle filter see Murray et al. (2016).

4.1.1 Implementation (fold and scan)

The composable models and inference algorithms described in this paper have been implemented in Scala, a functional, object-oriented language which runs on the Java Virtual Machine (JVM). This means that the code can be deployed without change across different operating systems and on servers in the cloud which have the JVM installed. Observations arrive as a stream: a stream can be thought of as a lazy list. A list can be represented recursively as a pair, with the first element a single value at the head of the list and the second element another list (called the tail), this is called a cons list. A lazy list, or stream, is also a pair, where the first element is a computed value and the second element is a thunk (an unevaluated computation). The stream is homogeneous in its type, meaning there can be streams of integers, or streams of strings, but not a list containing both integers and strings. A stream can be forced to evaluate its contents, for instance when performing a side effect such as printing to the screen or writing to a file. In practice, when considering live streaming data, the function in the second element of the pair might be one which polls a web service for the next observation. The approach taken in this paper is similar to Beckman ’s series of papers on Kalman folding, implementing the Kalman filter on streams in the Wolfram language (Beckman 2016).

is a function which operates on a recursive datatype, such as list or stream. The function signature of is given by:

is used to apply a function to elements of a data structure ( is a data structure) pairwise in order to calculate an aggregated result. The function takes two arguments, the first of which is of type (a placeholder for any type) and the second is of type , the same as the elements of the Stream (whatever that may be). The first application of , is to the first element of the stream and (the so called zero of the fold). The result is then passed to the next application of , along with the second element of the stream.

For instance, consider adding values in a list using foldLeft:

The first application of will add the zero element, 0, to the first element in the list (from the left): . Then the next element of the list and the previously evaluation of is passed to the next evaluation of : . This is repeated until the list is exhausted and the value returned is 15. In this way, the list is summed without mutating state in the program. Also note that if = and the function is associative, the fold can be computed in parallel via a binary tree reduction.

In the application of the particle filter there is an internal state which propagates as the stream of data arrives. The internal state includes the particle cloud, the time of the most recent observation and the log-likelihood. The function in can be implemented as a single step of the particle filter. An illustrative implementation of , called is implemented in the code block Listing 1. Firstly a is defined containing abstract implementations of three important functions in the particle filter, which will be implemented when applying the particle filter in practice. and are implemented in each model and can be specified in a concrete class for a specific particle filter implementation. The function is not model specific, and Multinomial resampling is typically employed.

Consider the implementation of a single step of the composable particle filter: Firstly, calculate the time difference between subsequent observations . The time difference is used in the function to advance the state. The new weights are calculated, given a new observation, using the function. The states are resampled to get an approximate unweighted random sample from $p(\mathbf{x }(t_i)|y(t_{1:i}))$. The higher-order function , with the signature:

is used to apply a function to the inner type of the collection, a , in this case . Each Particle is advanced independently by applying the function to each particle using . Each particle weight is calculated independently using and . In practice, the log-likelihood is computed to avoid arithmetic underflow from multiplying many small values. The value of the log-likelihood, $\log {\hat{p}}_\theta (y(t_{1:M}))$, is updated by adding the log of the mean of the unnormalised-weights to the previous value. Note that the log-sum-exp trick (Murphy 2012) should be used when updating the value of the log likelihood in line 11:

This rescaling of the weights ensures that large numbers aren’t exponentiated, hence preventing overflow. It also ensures that not all weights will underflow. The largest weight is rescaled to $\exp (0) = 1$, but since

$$\begin{aligned} \log \sum _{i=1}^N \exp (w_i) = a + \log \sum _{i=1}^N \exp (w_i - a), \end{aligned}$$

the value of the log-likelhood should remain the same.

In order to calculate the log-likelihood (a single value) of a path, the function is used:

the value is implemented by sampling 1000 times (equivalent to 1000 particles) from the initial state distribution of the model. The initial time is 0.0 and the initial value of the log-likelihood is set to zero. The log-likelihood is extracted by appending on the call to .

A closely related function to is which will return an aggregated stream of reduced values using a provided function, the signature is:

In order to understand , consider the application of to a stream of natural numbers:

then an infinite stream containing the cumulative sum will be returned, . The following code block runs a particle filter on a stream of data, where filterStep, initState and data are the same as supplied above in Listing 2.

this code accumulates the particle cloud (states and associated weights) and the running log-likelihood into a stream, using the function .

4.1.2 Filtering for the Log-Gaussian Cox-Process

When considering observations from the LGCP, the filtering needs to be performed slightly differently. The likelihood for the LGCP is given by:

$$\begin{aligned} \pi (t_n | \lambda (t_n), \varLambda (t_n)) = \lambda (t_n) \exp (-\varLambda (t_n)), \end{aligned}$$

the likelihood depends on the instantaneous hazard, $\lambda (t_n)$ and the cumulative hazard, $\varLambda (t_n) = \int _{t_0}^{t_n} \lambda (s) ds$. The log-likelihood is calculated to avoid arithmetic underflow and to simplify calculations, the log-likelihood is given by; $\ell = \log (\lambda (t)) - \varLambda (t)$. The state must be augmented to include the cumulative hazard, $\varLambda (t)$ in addition to $\lambda (t)$. In practice the value of $\varLambda (t)$ is calculated approximately, using numerical integration.

4.2 Parameter estimation

The emphasis of this paper is on on-line learning for the dynamic latent-state of the composable models, however to perform on-line filtering, the static parameters of the model must be determined. The PMMH provides an offline method of parameter inference in situations where an unbiased estimate of the likelihood can be determined using a particle filter. On-line parameter inference can be performed for the composable models considered in this paper but is not considered here Vieira and Wilkinson (2016).

The Particle Marginal Metropolis–Hastings algorithm (PMMH) (Andrieu et al. 2010) is an offline Markov chain Monte Carlo (MCMC) algorithm which targets the full joint posterior $p(\mathbf{x }(t_{0:M}), \theta | y(t_{1:M}))$ of a POMP model. The parameters of a POMP mdoel as in Eq. 1 include the measurement noise in the observation distribution, the parameters of the Markov transition kernel for the system state and the parameters of the initial state distribution. The data, y(t), is observed discretely. In order to simulate a Markov chain which targets the full posterior, $p(\mathbf{x }(t_{0:M}), \theta | y(t_{1:M}))$, firstly a new set of parameters $\theta ^*$ is proposed from a proposal distribution $q(\theta ^*|\theta )$. Then the bootstrap particle filter (see Sect. 4.1), is run over all of the observed data up to time $t_M$ using the newly proposed $\theta ^*$. The output of running the filter with the new set of parameters is used to estimate the marginal likelihood, ${\hat{p}}_{\theta ^*}(y) = {\hat{p}}_{\theta ^*}(y(t_i))\prod _{i=2}^n {\hat{p}}_{\theta ^*}(y(t_i)|y(t_{1:i-1}))$ and to sample a new proposed system state, $x^*$ from the conditional distribution $p(x^* | \theta ^*, y)$. The pair $(\theta ^*, x^*)$ is accepted with probability $\text {min}(1, A)$. A is given by:

$$\begin{aligned} A = \frac{p(\theta ^*){\hat{p}}_{\theta ^*}(y) q(\theta |\theta ^*)}{p(\theta ){\hat{p}}_{\theta }(y)q(\theta ^*|\theta )}, \end{aligned}$$

(9)

where the distribution $p(\theta )$ represents the prior distribution over the parameters. It is shown in Andrieu et al. (2010) that this algorithm has as its target the exact posterior $p(\theta , x|y)$, regardless of the number of particles in the filter used to estimate the marginal likelihood. If the only interest is in sampling the parameters, $\theta$, then this reduces to the parameter posterior $p(\theta | y)$ as in Andrieu and Roberts (2009).

The Metropolis–Hastings ratio can be simplified in the case of a symmetric proposal distribution. For a symmetric proposal distribution $q(\theta ^*|\theta ) = q(\theta |\theta ^*)$. Commonly, the proposal is chosen to be a Normal distribution centered at the previously selected parameter, and this is known as a random walk proposal, $q(\theta ^*|\theta ) = {\mathscr {N}}(\theta , \sigma )$, where $\sigma$ is a parameter controlling the step size of the random walk. If a flat prior distribution is chosen, then the ratio in Eq. 9 can be simplified further to:

$$\begin{aligned} A = \frac{{\hat{p}}_{\theta ^*}(y)}{{\hat{p}}_{\theta }(y)}. \end{aligned}$$

The full-joint posterior distribution is explored by performing many iterations of the PMMH algorithm, discarding burn-in iterations and possibly thinning the iterations to get less correlated samples from the posterior distribution.

4.2.1 Implementation (MCMC as a stream)

The Particle Marginal Metropolis–Hastings algorithm must be applied to a batch of data. Window functions, such as , can be applied to a stream of data to aggregate observations into a batch. accepts an integer, n, and groups each observation into another (finite) stream of size n.

The PMMH algorithm can then be applied to the aggregated group using . Iterations from the PMMH algorithm are naturally implemented as a stream. In the Scala standard library there is a method for producing infinite streams from an initial seed:

, applies the function to the starting value, then passes on the result to the next evaluation of . is an anamorphism, it is the categorical dual to the catamorphism which are generalisations of  (Meijer et al. 1991). For example, to create an infinite stream of natural numbers:

Iterations of an MCMC algorithm can be generated using , by starting with an initial value of the required state (at a minimum the likelihood and the initial set of parameters) and applying the Metropolis–Hastings update at each iteration. Inside of each application of , a new value of the parameters is proposed, the marginal likelihood is calculated using the new parameters (using the bootstrap particle filter) and the Metropolis–Hastings update is applied.

An example of a single step in the PMMH algorithm using the Metropolis Kernel can be seen in Listing 3. Three important functions are given abstract implementations in the trait, , and . The represents the (symmetric) proposal distribution, is a monadic distribution which can be sampled from by calling the method . is a particle filter, with the observed data and number of particles fixed, which outputs an estimate of the log-likelihood for a given value of the parameters. represents the prior distribution over the parameters. These three functions will be implemented in a concrete class extending the trait and correspond to specific implementation of the PMMH algorithm.

The implementation of the Monad, representing a distribution, is from the Breeze³ numerical and statistical programming library for Scala. is used to preserve referential transparency of the function. Referential transparency is an important concept in functional programming, whereby a function evaluated twice with the same set of parameters should return the same result. This is achieved in practice by using immutable data structures and deferring side-effects (which are not referentially transparent) until the end of the program. Pseudo random number generators make writing pure functions difficult. returns a distribution over represented by the monad, the function can be used to transform values inside of the distribution . In the function , the parameters are perturbed by the function but the parameters are not drawn from the distribution, instead a construction called a comprehension is used to perform calculations inside of the monad. The comprehension is alternative syntax for chains of and .

In order to use the function , an with the following signature is required:

The Breeze library provides a function called, which produces an infinite sequence of dependent draws from a Markov Chain given a transition kernel:

are drawn from the prior distribution and the initial value of the log-likelihood is chosen to be very small so the first iteration of the PMMH is accepted.

Keeping the state of the PMMH algorithm inside of the monad until the program is run and results are required, preserves referential transparency until the main method of the program, which is expected to have side effects, such as printing to the screen, writing to a file or database or generating pseudo-random numbers. The particle filter in Listing 1 can also be written using this monadic style. This is presented in “Appendix A.4”.

Built in stream operations can be used to discard burn-in iterations and thin the iterations to reduce auto-correlation between samples. The stream can be written to a file or database at each iteration, so the PMMH algorithm implemented as a stream uses constant memory as the chain size increases.

5 Example: Traffic monitoring

The Urban Observatory (James et al. 2014) has many sensors for monitoring traffic, sourced from data provided by the North East Combined Authority (NECA 2016). Traffic cameras provide information on traffic flow, average speed and congestion. The example considers traffic flow, which is provided in passenger car units at approximately 5 minute intervals. Passenger car units represents the size of a vehicle, with larger values representing larger vehicles. In the data provided by the NECA, the values are all integers.

Sensor N05171T is the sensor considered in this analysis, it is located on Hollinside Road near the Metro Centre in Gateshead. Figure 5 (top) shows readings from the first three weeks of January. There are two strong trends appearing, a daily trend where most traffic is observed to be during the day and a weekly trend where most traffic is on the weekend with an exception for the bank holiday on Monday 2nd January.

Fig. 5

(Top) Measurements of passenger car units from sensor N05171T for the first three weeks of January 2017, (Bottom) Passenger car units for the second week of January 2017

The time difference between observations is typically five minutes or multiples of five minutes, however on the 9th January there is a time gap of 356 seconds. This means all of the following observations are out of sync with observations made before the 9th January as shown in Table 1. This is not problematic for the class of composable models presented in this paper, as these models have a continuous time latent state, but this would cause difficulties for a discrete time analysis.

In Fig. 5 (bottom), starting Wed 11th January the measurements are received at sporadic intervals, again this poses no problems for the class of models considered in this paper, and is typical of sensor data.

The timestamp is translated to an hourly scale, ie. five minutes is represented as $5/60 \approx 0.083$. A sensible choice of observation model is the Poisson distribution. However it was found that the Poisson model is not a good fit for this data, the data is overdispersed, meaning the sample variance of the count data is greater than the sample mean. The Negative Binomial distribution is commonly used for overdispersed count data, and is chosen as the observation model. The data shows a clear daily seasonal trend, and a slightly less pronounced weekly trend. A sensible model is therefore a composition of a Negative Binomial model and two seasonal models, one with daily seasonality, the other with weekly seasonality.

$$\begin{aligned}&Y(t_i) | \eta (t_i) \sim \text {NegBin}(\eta (t_i), \phi ), \\&\eta (t_i) | \mathbf{x }(t_i) = \exp \{ F_{t_i}^T \mathbf{x }(t_i) \}, \\&\mathbf{X }(t) | (\mathbf{X }(t_{i-1}) = \mathbf{x }(t_{i-1})) \sim p(\mathbf{X }(t_i) | \mathbf{x }(t_{i-1}), \theta ), \\&\mathbf{X }(t_0) | \theta \sim \text {MVN}(\mathbf{m }_0 | \mathbf{C }_0). \end{aligned}$$

Table 1 Five readings from sensor N05171T, with varying time difference ($\Delta t$)

The Negative Binomial model is the leftmost model in the composition, ${\mathscr {M}}_1$ and has a scalar latent state which evolves according to Brownian motion. This will account for drift in the observed data not modelled by the seasonal components. $\eta (t)$ is the mean of the Negative Binomial which is positive, therefore the link function is the log-link. The parameter $\phi$ is the size parameter which controls the overdispersion of the data. The probability mass function for the Negative Binomial distribution with mean $\eta (t_i)$ and size $\phi$ is:

$$\begin{aligned} {\text {NegBin}}(y(t_i) | \eta (t_i), \phi )&\sim \begin{pmatrix} y(t_i) + \phi - 1 \\ y(t_i) \end{pmatrix} \left( \frac{\eta (t_i)}{\eta (t_i) + \phi } \right) ^{y(t_i)} \\&\quad \left( \frac{\phi }{\eta (t_i) + \phi } \right) ^{\phi }. \end{aligned}$$

The mean is $\eta (t_i)$ and the variance is $\eta (t_i) + \eta (t_i)^2 / \phi$, so $\eta (t_i)^2 / \phi$ represents the additional variance above that of the Poisson distribution.

The second model in the composition is a daily seasonal model, ${\mathscr {M}}_2$. The daily seasonal model is chosen to have four harmonics, and period, $P = 24$, which means the frequency is $\omega = \frac{2\pi }{24}$, the vector $F_{t}$ is:

$$\begin{aligned} F_t = \begin{pmatrix} \sin (\omega t) \\ \cos (\omega t) \\ \vdots \\ \sin (4\omega t) \\ \cos (4\omega t) \\ \end{pmatrix}. \end{aligned}$$

The daily seasonal model is chosen to have an Ornstein–Uhlenbeck latent state with a non-zero mean, $\theta$:

$$\begin{aligned} \text {d}\mathbf{X }_t = \alpha \mathbf {1}_8 ({\theta }\mathbf {1}_8-\mathbf{X }_t)\text {d}t + \sigma I_8, \text {d}\mathbf{W }_t \end{aligned}$$

The rate, $\alpha$, mean $\theta$ and variance $\sigma$ were chosen to be the same for each state component. $\mathbf {1}_n$ is a vector of ones of dimension n and $I_n$ is the identity matrix of dimension n.

The weekly seasonal model, ${\mathscr {M}}_3$ is the same as the daily seasonal model, but with the period of the seasonality, $P = 24 \times 7$ and the number of harmonics, $h = 2$, hence the latent state is 4-dimensional. The fully composed model is given by ${\mathscr {M}} = {\mathscr {M}}_1 \star {\mathscr {M}}_2 \star {\mathscr {M}}_3$.

5.1 Tuning the PMMH

The PMMH (as described in Sect. 4.2) is used to determine the joint posterior distribution of the parameters and latent state, $p(x, \theta | y(t))$, given the training data. The likelihood in the particle Metropolis Hastings algorithm is estimated using the bootstrap particle filter. The accuracy of the estimated marginal likelihood can be improved by increasing the number of particles in the filter, however this results in more computational time required for each MCMC iteration.

The PMMH algorithm requires the particle filter to run once per iteration (re-using the likelihood estimate from the previous iteration) and hence deciding on the optimum number of particles is a non-trivial task. Several pilot runs with different numbers of particles are performed to ensure the variance of the log of the likelihood estimate is close to one (Doucet et al. 2015). This is difficult to achieve as the variance of the estimate can vary at different parameter values, not only with the number of particles. From several pilot runs at different values of the parameters, it was decided that 500 particles provided the best compromise between accuracy and computational time.

5.2 Parameter estimates

In order to estimate the value of the parameters, 500 particles were used in the particle filter estimating the value of the marginal likelihood ${\hat{p}}_\theta (y(t_{1:M}))$, 100,000 iterations of the PMMH algorithm were taken with 10,000 iterations discarded as burn-in. The prior distributions on the parameters were chosen to be weakly informative. The initial state of the local-level model follows a Gaussian distribution, the prior on the each seasonal model initial state is a Multivariate Normal distribution with diagonal covariance matrices, $C_0^{(i)}I_{2h_i}$ where i is the model number and $h_i$ is the number of harmonics in model i. The prior distributions for the parameters of the initial state distributions were chosen to be the same for each model component: $m_0^{(i)}$, $C_0^{(i)}$, $i = 1,2,3$, where i represents the model number:

$$\begin{aligned} m_0^{(i)}&\sim {\mathscr {N}}(0.5, 3.0), \\ C_0^{(i)}&\sim \text {Gamma}(2.0, 0.4), \end{aligned}$$

the mean of the initial state was chosen to have a Gaussian prior, and the standard deviation a Gamma prior. The Gamma distribution is parameterised by shape, $\alpha$ and rate $\beta$ so that the expectation is $\alpha /\beta$ and the variance is $\alpha /\beta ^2$. Next, the diffusion parameter of the Brownian motion controlling the evolution of the latent state in the Negative Binomial model component:

$$\begin{aligned} \sigma \sim {\text {Gamma}}(0.01, 0.1). \end{aligned}$$

The size parameter, $\phi$, of the Negative Binomial observation distribution which controls the overdispersion is chosen to have a Gamma prior:

$$\begin{aligned} \phi \sim {\text {Gamma}}(1.0, 0.3). \end{aligned}$$

The Ornstein–Uhlenbeck process controls the evolution of the latent state of the daily and weekly model components, the parameters of the OU process in model components 2 and 3 were given the following prior distributions:

$$\begin{aligned} \theta _j^{(i)}&\sim {\mathscr {N}}(0.5, 3.0), \\ \alpha ^{(i)}&\sim {\text {Gamma}}(0.1, 0.3), \\ \sigma ^{(i)}&\sim {\text {Gamma}}(2.0, 0.4). \end{aligned}$$

The parameters are indeved by their model number, i, for $i = \{2,3\}$, additionally the mean $\theta _j^{(i)}$ is indexed by j as there is a different value for each harmonic in the model. The mean of the Ornstein–Uhlenbeck process, $\theta ^{(i)}$ is assigned a Gaussian prior, and the positive parameters, $\alpha ^{(i)}$ and $\sigma ^{(i)}$ are given Gamma Priors.

A sample from the parameter prior distribution is used to initialise the PMMH algorithm. The mean of the parameters and associated 95% posterior intervals are presented in Table 2. The mean value of the size parameter, $\phi$ in the Negative Binomial observation distribution was 3.23.

Table 2 Posterior mean and 95% posterior intervals for the parameters in the Negative Binomial Traffic Model

5.3 On-line filtering

The joint posterior of the state and parameters, $p(x, \theta | y)$ can be used to perform filtering and forecasting on-line. The data used for on-line filtering is the last week of January, these observations have not been considered when estimating the posterior distribution. In order to take into account uncertainty in the posterior distribution, a pair $(x^*, \theta ^*)$ is sampled from the posterior distribution and used to initialise 100 particle filters each with 1000 particles. In order to get a precise representation of the filtering distribution, many more particles can be used than in the PMMH algorithm. Once an approximation to the filtering distribution is determined at time t, it is then advanced to the time of the next expected measurement ($t+ 5$ min in this case) and the associated observation is simulated for each particle, giving a predictive distribution for the observations which can be summarised.

Figure 6 shows the actual measurements on 25 and 26th January and the associated one-step forecast mean with 90% prediction intervals. It is clear that the variance of the one-step-predictive distribution is larger when the expected value of passenger car units is larger.

Fig. 6

On-Line filtering with mean of the one-step forecast and 90% prediction intervals

6 Conclusion

Composable Markov process models are a flexible class of models which can be used to model a variety of real world data. The class of composable models together with the composition operator form a semigroup, making it easy to build complex models by combining simple models components. The use of the particle filter for simulation based inference allows for a flexible choice of observation model and SDE governing the latent state. Further, by using a continuous time Markov process to represent the latent state, the requirement to simulate the state on a regular grid is relaxed. If there is an exact solution to the Markov process, then the latent state can be simulated forward to the next time of interest using the time increment and the previous realisation of the state. This allows for faster computation when using real world data and is important since many sensors sample at an adaptive rate, or consumption must be slowed down due to limited computing resources for inference and forecasting.

Incoming observations are represented as streams, which can represent live observations from a webservice or other source. This allows for flexible and scalable analysis. The composable model framework can be easily tested on simulated data and the same code deployed for real world applications. The particle filter is implemented as a functional , a higher-order function allowing recursive data structures (such as the cons-list or cons-stream) to be reduced pairwise without side-effecting. The PMMH algorithm is expressed as a stream using, , defined in the Breeze numerical library for Scala. These functions are often called unfold operations and start with a seed value and first apply a function to the seed, the each subsequent value to create an infinite stream of values which can be manipulated using built-in stream processing functions. In the accompanying software for this paper, the streams are implemented using Akka Streams, this allows for easy implementation of parallel chains, online monitoring and constant-time memory usage, when used with asynchronous-IO.

The Scala implementation is typically faster than dynamic langauges such as R and Python, but slightly slower than C or C++. Algorithms such as the particle filter can be written in a functional way, using higher order functions ( , etc.) which allows one implementation of the algorithm to be parametric over different collection types. This simplifies development and testing, since the algorithm can be tested and debugged using sequential collections and deployed in production using parallel collections, or distributed collections, for example RDDs (Resilient Distributed Datasets) in Apache Spark (Zaharia et al. 2010). The traffic sensors, such as the one considered in the example in Sect. 5 are placed in close proximity to each other, hence they have correlated observations. The models presented in this paper currently consider observations at each station independently, but sharing information between sensors could mean more accurate inference. There is also a potential to determine faulty sensors, which do not record similar readings to those in its neighbourhood.

In some cases, results are needed quickly and accuracy is not of paramount concern. In this case, approximate inference could be performed using the Extended Kalman Filter and Unscented Kalman Filter introduced in Sect. 1 or by reducing the number of particles used in the particle filter.

Unusual events in the sensor network (for instance the presence of a major event on traffic and pollution) can cause estimated parameters from past events to be ineffective to forecast future observations of the process. In this case it may be useful to have time varying parameters and estimate the parameters on-line.

A Appendix

1.1 A.1 Simulating exponential family models

In order to perform forecasting and interpolation, a method must be developed to forward simulate from POMP models. After determining the parameters for the model, as in Sect. 4.2, forward simulation of the model beyond observed values can be used to predict future observations along with the uncertainty of the predictions. In the case of the traffic data in Sect. 5, forecasting can help with route planning and diversions. Similarly, simulating at periods of interest without real world observations is used to interpolate missing data.

In order to forward simulate from a POMP model, the following steps are required:

• 1. Set $i = 1$ and generate a list of times to observe the process, $t_0, t_1 , \dots , t_M$

• 2. Initialise the state space at time $t_0$, by drawing from the initial distribution, $\mathbf{x }(t_0) \sim p(\mathbf{x }(t_0) | \theta )$

• 3. Calculate $\delta t = t_i - t_{i-1}$ and advance the state according to the Markov transition kernel $\mathbf{x }(t_i) \sim p(\mathbf{x }(t_i) | \mathbf{x }(t_{i-1}), \theta )$

• 4. Apply the linear-deterministic transformation to the state, $\gamma (t_i) = F^T_{t_i}\mathbf{x }(t_i)$

• 5. Transform the state into the parameter space of the observation distribution using the non-linear link-function, $\eta (t_i) = g(\gamma (t_i))$

• 6. Sample once from the observation distribution, $y(t_i) \sim \pi (y(t_i) | \eta (t_i), \theta )$, if $i \ge n$ return sampled values, else set $i = i + 1$ and go to step 3

Forward simulation can also be useful to generate synthetic data to test inferential algorithms.

1.2 A.2 Simulating the Log-Gaussian Cox-Process

As explained in Sect. 1, simulating from POMP models is important for forecasting and interpolation. The steps uses to simulate from the LGCP are as follows, suppose the interval to be simulated on is [0, T] and the last even occurred at time $t_0$:

• 1. Simulate the log-Gaussian process, $\lambda (t)$ on a fine grid on the interval [0, T]

• 2. $U_\lambda = \max \limits _{t \in [0,T]} \lambda (t)$

• 3. Set $i = 1$

• 4. Sample $t \sim Exp(U_\lambda )$

• 5. Set $t_i = t_{i-1} + t$

• 6. If $t_i > T$ stop

• 7. Sample $u \sim U[0,1]$

• 8. If $u \le \lambda (t_i)/U_\lambda$ then accept $t_i$ as a new event time

• 9. Set $i = i + 1$, go to 4.

1.3 A.3 Computing with composed models

The models are programmed using Scala, a language which runs on the JVM (Java Virtual Machine) and has good support for functional and concurrent programming (Chiusano and Bjarnason 2014).

To define a model in the Scala language, the following must be provided:

• 1. A stochastic observation function:

  

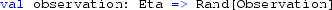
• 2. A deterministic, non-linear linking function:

  

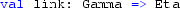
• 3. A deterministic linear transformation function:

  

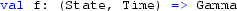
• 4. A stochastic differential equation representing the latent state:

  

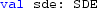
• 5. A likelihood function:

  

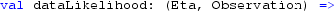
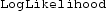
is a function from the transformed latent state $\eta (t)$ to a distribution over the observations, $\pi (y(t)|\eta (t))$. The distribution, can be sampled from by calling the method . is an implementation of a probability monad from the Scala library Breeze.⁴

Probabilistic programming with monads has been developed in the literature (Ścibior et al. 2015). Haskell (a general purpose functional programming language) is used to build a representation of a distribution as a Generalized algebraic datatype and implement several inference methods.

The linking function ensures the value of $\eta (t)$ is appropriate for the observation distribution. The function is used to perform a linear transformation of the latent state. The latent state is represented by an object, contains , a function from and to the next and which returns a distribution over states, which can be sampled from.

1.3.1 A.3.1 A binary operation for composing models

In order to compose models, define an associative binary operation called which combines two models at a time. accepts two un-parameterised models, (parameterisation is described in Sect. 1) and and returns a third model representing the composition of the two models. Along with the operator, the models form a semigroup, since the operation is associative and closed.

Further, an identity model, e, can be defined such that for any model ${\mathscr {M}}_a$, $e \star {\mathscr {M}}_a = {\mathscr {M}}_a = {\mathscr {M}}_a \star e$. Un-parameterised models now form a monoid.

In order to define the operation, firstly consider combining the latent state of two models: A binary tree is used in order to represent the latent state of a model, this is depicted in Figure 7. For a single model, the latent space is a . In order to represent the state of two models, the state of each model is combined into a with the left and right branch corresponding to the latent state of each model in the composition of two. A binary tree is defined in Scala as:

and both extend the trait, when a function accepts a parameter of type it can be either a or a . Pattern matching is used in order to decompose the tree and perform functions on the values contained in the leaf nodes. The value is a placeholder value, stating that the values at the of the can be anything. In the case of the state tree, it is represented as a . The state tree is defined as a type alias .

Fig. 7

State Space as a Binary Tree, this composed model state consists of the combined states of three models

Consider advancing the state space of a combined model, by drawing from the transition kernel conditional on the current state using the . Each model in the combined model has a corresponding state and , each model’s must act on the corresponding state. To advance the state of a composed model of two, the left-hand (correspondingly right-hand) model’s is applied to the left-hand (right-hand) model’s state space.

The application of the vector $F_t$ is performed using the function . For two models, this function expects a , which can be decomposed using pattern matching:

The observation distribution is taken to be that of the left-hand model, , hence the linking function must also be that of the left-hand model .

In order to simulate from a model or initialise a particle filter, there must be an initial distribution for the state, this is given by the function. Adding two models will result in a for the initial state:

1.3.2 A.3.2 Parameterising the model

The parameters of a model given in Eq. 1, are that of the Markov transition for the state space, $p(\mathbf{x }(t_i)|\mathbf{x }(t_{i-1}), \theta )$, the parameters of the initial system state $\mathbf{x }(t_0) \sim p(\mathbf{x }(t_0) | \theta )$ and any additional parameters for the observation distribution. An un-parameterised model is a function from , which can then be supplied with appropriate parameters to form a .

When composing two models, a set of parameters for each model must be combined into a new set of parameters for the new model. As with the state-space, it is natural to model the parameters of a composed model as a binary tree. A single model is parameterised by a . When composing two models, the two s will be combined into a single . ’s have a left and a right branch, which can either be another or a . Parameters must be combined in the same order as models are combined, combining parameters is not commutative.

Cats ⁵ is a library which extends the functional programming capabilities in Scala by providing typeclasses commonly used in functional programming. In order to combine parameter trees, an instance of the Monoid typeclass is defined, a monoid is a set with an associative, closed operation and an which is an identity element with respect to the operator. Listing 1 explains how to define a new monoid for the binary .

Upon defining a typeclass with the operator, cats provides an associative infix operator, , which is an alias for .

This is equivalent to constructing the parameters as nested s:

A composed model of two, has a containing two s. The Parameters of the composed model will be a containing two s. In order to advance the state pattern matching is used to decompose both the parameters and the state simultaneously:

Similar methods are used to parameterise the observation distribution, the likelihood function and the initial state distribution.

As mentioned in Sect. 3, the models form a semigroup. Once a semigroup is defined for the unparameterised models,the infix notation, , is available to use.

1.4 A.4 Monadic particle filter

The implementation of the bootstrap particle filter in Sect. 4.1.1 was not a referentially transparent function, to regain referential transparency, a monadic style can be adopted as in the implementation of the PMMH in Sect. 4.2.1. The problem functions are , and , these functions are not referentially transparent by design, they are pseudo random functions. They can be re-written as:

where the return types clearly state that they return a distribution over the and can be sampled from by calling the method. The particle filter step can then be re-written as:

Each step of the filter returns a , and the function on line 4 has been replaced by the function . The signature for is:

The traverse function is defined for collections, such as and and allows a function with an effect, , to be applied to the elements in the collection and return the collection wrapped in the effect, . is given the type bound applicative which is more general than a monad, and all monads are applicatives, so the monad is also an applicative. Therefore, applying the function to a collection of particles using ’ , returns a .

To calculate the pseudo-marginal log-likelihood of a path, there is a more general fold function (provided in the Cats library) which allows reduction using a monadic function:

and means a function to calculate the pseudo-marginal likelihood can be written as: