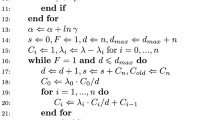A comparison of efficient approximations for a weighted sum of chi-squared random variables

Abstract

In many applications, the cumulative distribution function (cdf) $F_{Q_N}$ of a positively weighted sum of N i.i.d. chi-squared random variables $Q_N$ is required. Although there is no known closed-form solution for $F_{Q_N}$, there are many good approximations. When computational efficiency is not an issue, Imhof’s method provides a good solution. However, when both the accuracy of the approximation and the speed of its computation are a concern, there is no clear preferred choice. Previous comparisons between approximate methods could be considered insufficient. Furthermore, in streaming data applications where the computation needs to be both sequential and efficient, only a few of the available methods may be suitable. Streaming data problems are becoming ubiquitous and provide the motivation for this paper. We develop a framework to enable a much more extensive comparison between approximate methods for computing the cdf of weighted sums of an arbitrary random variable. Utilising this framework, a new and comprehensive analysis of four efficient approximate methods for computing $F_{Q_N}$ is performed. This analysis procedure is much more thorough and statistically valid than previous approaches described in the literature. A surprising result of this analysis is that the accuracy of these approximate methods increases with N.

1 Introduction

The cumulative distribution function (cdf) $F_{Q_N}$ of a positively weighted sum of i.i.d. $\chi ^{2}_{1}$ random variables $Q_N$,

$$\begin{aligned} Q_N = \sum _{i=1}^N d_i W_i^2, \qquad d_i > 0, \qquad W_i \sim N(0, 1), \end{aligned}$$

(1)

has no known closed-form solution. An approximation of $F_{Q_N}$ is used in goodness-of-fit tests (Moore and Spruill 1975) and various other applications (Zhang and Chen 2007; Jayasuriya 1996; Bentler and Xie 2000). Our particular interest is change detection in streaming data (Bodenham 2014). In offline situations where computational resources are not an issue, Imhof’s method (Imhof 1961), which inverts the characteristic function numerically, should be the preferred choice. It can be considered exact (Solomon and Stephens 1977; Johnson et al. 2002) since it provides error bounds and can be used to compute $F_{Q_N}(x)$, for some quantile value x, to within a desired precision. Similar numerical methods such as Farebrother’s method (Farebrother 1984) could also be used, but some (Sheil and O’Muircheartaigh 1977; Davis 1977; Davies 1980) lack the precision-bounding feature of Imhof’s method. However, Imhof’s method and Farebrother’s method are both iterative, which affects their speed of computation, as shown in Sect. 6.4. Besides being iterative, these methods all require the entire vector of coefficients $(d_1, \dots , d_N)$ to be stored in order to compute the approximate cdf. As described in Sect. 2, this may not be possible in a streaming data context.

Perhaps, the earliest approximate method, which has come to be known as the Satterthwaite–Welch method (Welch 1938; Satterthwaite 1946; Fairfield-Smith 1936), involved matching the first two moments of $Q_N$ with the first two moments of a Gamma distribution. See Box (1954, Sect. 3) for a discussion on the history of this method. The Hall–Buckley–Eagleson (Hall 1983; Buckley and Eagleson 1988) and Wood F (Wood 1989) methods match the first three moments of $Q_N$ to other distributions in a similar fashion. The Lindsay–Pilla–Basak method (Lindsay et al. 2000) matches the first 2n moments of $Q_N$ to a mixture distribution. These four moment-matching methods are described in Sect. 3 and are implemented in the R package momentchi2 (Bodenham 2015).

The method described in Solomon and Stephens (1977) takes the Satterthwaite–Welch method a step further by matching the first three moments of $Q_N$ to a random variable $aX^b$, where $X \sim \chi ^{2}_{1}$. It is accurate in both the upper and lower tails, but requires the solution of two simultaneous non-linear equations, perhaps via an iterative method. An interesting method using Laguerre polynomials is described in Castaño-Martínez and López-Blázquez (2005), but is also iterative and requires the setting of certain control parameters.

While the methods discussed here have superseded those published previously (e.g. Patnaik 1949; Jensen and Solomon 1972), a good review of older methods can be found in Johnson et al. (2002). Although not considered here, a review of the current state-of-the art for weighted sums of non-central chi-squared random variables can be found in Duchesne and Lafaye De Micheaux (2010), and methods for computing the cdf of a single non-central chi-squared random variable are described in Farebrother (1987), Ding (1992) and Penev and Raykov (2000). An earlier version of this work appeared in the unpublished PhD thesis of Bodenham (2014).

2 Approximations in a streaming data context

If we wished to simply compute a single evaluation of $F_{Q_N}$, for some vector of coefficients $\mathbf {d}= (d_1, d_2, \dots , d_N)$, then we have already described a plethora of methods from which to choose. Amongst these, since Imhof’s method is essentially exact it would probably be the preferred choice. There are, however, situations when Imhof’s method might not be suitable. For instance, one might wish to compute $F_{Q_N}(x)$, for $Q_N$ defined in Eq.  (1), and then soon afterwards compute $F_{Q_{N+1}}(x')$, where

$$\begin{aligned} Q_{N+1} = Q_N + d_{N+1} W_{N+1}^2. \end{aligned}$$

(2)

Imhof’s method requires the whole vector of weights $\mathbf {d}$ in order to compute $F_{Q_{N+1}}(x')$, but in a streaming data context (discussed in the next paragraph) N might be very large, and so storing the whole coefficient vector $(d_1, \dots , d_N, d_{N+1})$ would be undesirable. Finally, Imhof’s method is also iterative, since it runs until a specified precision is obtained. This is also unappealing, since iterative methods have the potential to be slow and computationally expensive. Given this construction, Imhof’s method is clearly not suitable for deployment.

Streaming data algorithms (e.g. Gama et al. 2010; Bodenham and Adams 2013) require methods that are both fast and only require a small, fixed number of parameters and data to be stored. Amongst the methods discussed above, the moment-matching methods of Satterthwaite–Welch, Hall–Buckley–Eagleson, Wood and Lindsay–Pilla–Basak are the only options that meet these criteria and are described in Sect. 3 below. The first three of these methods only require a single evaluation of a particular cdf and the storage of a fixed number of parameters that can be easily sequentially updated. The Lindsay–Pilla–Basak method is more computationally intensive, but has the potential to give more accurate results by matching higher-order moments. There are other approximate methods (e.g. Solomon and Stephens 1977) besides these four, but they all have shortcomings (e.g. require too much memory, too expensive to compute) that would render them unsuitable for streaming data applications.

Our motivating application for computing $F_{Q_N}$ is as part of a sequential change detector for the variance of a process; see Bodenham (2014, Chap. 8) for methodological background, and Ye et al. (2002) for an application in computer network security. Suppose we are interested in making inference on the sequence $z_1, z_2, \dots , z_N$ which are observations generated from random variables $Z_1, Z_2, \dots , Z_N$, and the weighted variance is defined as

$$\begin{aligned} V_{\mathbf {c}, N} = \sum _{i=1}^N c_i \left[ Z_i - \bar{Z}\right] ^2, \end{aligned}$$

(3)

where $\mathbf {c} = (c_1, c_2, \dots , c_N)$ are some weights, and $\bar{Z}$ is the (possibly weighted) mean of $Z_1, \dots , Z_N$. If the $Z_i$ are i.i.d normal, then it can be shown that $V_{\mathbf {c}, N}$ is distributed as some $Q_N$. This formulation is similar to the exponentially weighted moving variance described in MacGregor and Harris (1993). In a streaming data scenario, it would be infeasible to use a method such as Imhof’s which requires the storage of the whole vector $\mathbf {c}$, particularly when N becomes large. In sequential change detection, N increases until a change is detected. The size of the change would then depend on the application; in cybersecurity problems of interest to us, we expect N to be between 100 and 1000. Streaming data algorithms need to have low and fixed memory requirements and be computationally inexpensive.

3 Efficient approximate moment-matching methods

As the name suggests, these methods involve matching the moments of $Q_N$ to those of another distribution, and using that distribution’s cdf to approximate $F_{Q_N}$. In order to do this, the moments of $Q_N$ need to be computed. However, instead of computing the moments directly, it is easier to first compute the cumulants of $Q_N$ and then obtain the moments from the cumulants. In fact, the first three methods described below directly use the computed cumulants, and do not require computation of the moments.

3.1 Computing cumulants and moments

The cumulants of $Q_N$, a weighted sum of i.i.d. $\chi ^{2}_{1}$ random variables as in Eq. (1), are denoted by $\kappa _r(Q_N)$ and can be computed using the formula

$$\begin{aligned} \kappa _r(Q_N) = 2^{r-1}(r-1)! \sum _{i=1}^N (d_i)^r, \qquad r = 1, 2, \dots . \end{aligned}$$

(4)

where $\mathbf {d}= (d_1, d_2, \dots , d_N)$ are the weighting coefficients. This can easily be shown using the properties of cumulants and recalling that for a $\chi ^{2}_{1}$ random variable X, $\kappa _r(X) = 2^{r-1}(r-1)!$ [e.g. Box (1954)]. In a sequential context, when $Q_N$ becomes $Q_{N+1}$, the cumulants can be easily updated by

$$\begin{aligned} \kappa _r(Q_{N+1}) = \kappa _r(Q_N) + 2^{r-1}(r-1)! \cdot (d_{N+1})^r. \end{aligned}$$

(5)

For the remainder of this chapter, we shall only be concerned with $Q_N$, and so shall write $\kappa _r = \kappa _r(Q_N)$. The moments of $Q_N$, denoted $m_r = m_r(Q_N)$, can be computed from the cumulants using $m_1 = \kappa _1$ and

$$\begin{aligned} m_r = \kappa _r + \sum _{i=1}^{r-1} \left( {\begin{array}{c}r-1\\ i-1\end{array}}\right) \kappa _i m_{r-i}, \qquad r = 2, 3, \dots . \end{aligned}$$

(6)

Since the first three methods described below only require the first two or three cumulants of $Q_N$, these are explicitly provided here:

$$\begin{aligned} \kappa _1 = \sum _{i=1}^N d_i, \,\,\, \kappa _2 = 2\sum _{i=1}^N (d_i)^2, \,\,\, \kappa _3 = 8\sum _{i=1}^N (d_i)^3. \end{aligned}$$

(7)

3.2 Satterthwaite–Welch approximation

Equating the first two moments of $Q_N$ with a $\varGamma (\widehat{k}, \widehat{\theta })$ variable yields

$$\begin{aligned} \widehat{k}= \frac{1}{2} \kappa _1^2 / \kappa _2 , \qquad \widehat{\theta }= \kappa _2 / \kappa _1. \end{aligned}$$

(8)

If we use $F_{\varGamma (k, \theta )}$ to denote the cdf of a $\varGamma (k, \theta )$ distribution, then the Satterthwaite–Welch approximation uses $F_{\varGamma (\widehat{k}, \widehat{\theta })}$ to approximate $F_{Q_N}$. In the references [e.g. Box (1954)], the $\varGamma (k, \theta )$ distribution is often written as a scaled $\chi ^{2}_{1}$ distribution.

3.3 Hall–Buckley–Eagleson approximation

We provide a brief outline of the method which is fully described in Buckley and Eagleson (1988). First, $Q_N'$ is used to denote $Q_N$ normalised as in

$$\begin{aligned} Q'_N = \frac{Q_N - \text {E}[Q_N]}{\sqrt{\text {Var}[Q_N]}} = \kappa _2^{-1/2}(Q_N - \kappa _1). \end{aligned}$$

(9)

Second, if $\nu$ is defined as

$$\begin{aligned} \nu = 8 \kappa _2^3 / \kappa _3^2, \end{aligned}$$

(10)

and $X_{\nu } \sim \chi ^2_{\nu } \equiv \varGamma (\nu /2, 2)$, then it can be shown that $Q'_N$ and $(X_{\nu } - \nu )/\sqrt{2 \nu }$ have the same first three central moments. If $Y\sim Q_N$ and y is an observation of Y, the Hall–Buckley–Eagleson approximation of $F_{Q_N}(y)$ is obtained by

$$\begin{aligned} F_{\varGamma (\nu /2, 2)} \left( \sqrt{2 \nu } \cdot \left[ \kappa _2^{-1/2}(y - \kappa _1) \right] + \nu \right) . \end{aligned}$$

(11)

3.4 Wood F approximation

Wood’s F method (Wood 1989) matches the first three moments of $Q_N$ with another distribution that has a probability density function of the form

$$\begin{aligned} f(x | \alpha _1, \alpha _2, \beta )= \frac{ \beta ^{\alpha _{2}} x^{\alpha _1 - 1} (\beta + x)}{\text {B}(\alpha _1, \alpha _2) }, \end{aligned}$$

(12)

where

$$\begin{aligned} \text {B}(\alpha _1, \alpha _2) = \frac{\varGamma (\alpha _1)\varGamma (\alpha _2)}{\varGamma (\alpha _1+\alpha _2)} \end{aligned}$$

(13)

is the beta function. Although in Wood (1989) it is referred to as an F distribution, the density in Eq. (12) can be better described as that of a G3F or corrected F distribution (Pham-Gia and Duong 1989; Johnson et al. 1995). The parameters $\alpha _1, \alpha _2, \beta$ can be defined in terms of the cumulants $\kappa _1, \kappa _2, \kappa _3$ computed in Eq. (4) above (e.g. using Gröbner bases):

$$\begin{aligned}&r_1 = 4 \kappa _1\kappa _2^2 + \kappa _3\left( \kappa _2 - \kappa _1^2\right) , \qquad r_2 = \kappa _1 \kappa _3 - 2 \kappa _2^2 \nonumber \\&\alpha _1 = 2 \kappa _1 \left( \kappa _1 \kappa _3 + \kappa _1^2 \kappa _2 - \kappa _2^2 \right) {\big {/}}r_1 \nonumber \\&\alpha _2 = 3 + 2 \kappa _2 \left( \kappa _2 + \kappa _1^2 \right) {\big {/}}r_2 \nonumber \\&\beta = r_1 / r_2 \end{aligned}$$

(14)

It is noted in Wood (1989) that if X is distributed according to the density in Eq. (12), then

$$\begin{aligned} \frac{\alpha _2}{\alpha _1 \beta } X \sim F(2\alpha _1, 2\alpha _2), \end{aligned}$$

(15)

where $F(2\alpha _1, 2\alpha _2)$ is a standard F-distribution with parameters $2\alpha _1$ and $2\alpha _2$. Therefore, if $Y \sim Q_N$, and y is an observation of Y, the Wood F approximation of $F_{Q_N}(y)$ is obtained by

$$\begin{aligned} F_{F(2 \alpha _1, 2 \alpha _2)} \left( \frac{\alpha _2}{\alpha _1 \beta } y\right) . \end{aligned}$$

(16)

This approximation can be used as long as both ${r_1, r_2 > 0}$, which is guaranteed in many cases (Wood 1989). When either $r_1 = 0$ or $r_2 = 0$ (it is proved in Wood (1989) that neither can be negative), then Wood (1989) recommends using either the Satterthwaite–Welch approximation, or another two-moment approximation.

3.5 Lindsay–Pilla–Basak approximation

The method described in Lindsay et al. (2000) approximates $F_{Q_N}$ using $F_{\widetilde{Q}_N}$, a finite mixture of n Gamma cdfs $F_{\varGamma (k, \theta _i)}$,

$$\begin{aligned} F_{\widetilde{Q}_N} = \sum _{i=1}^{n} \pi _i F_{\varGamma (k, \theta _i)}, \end{aligned}$$

(17)

where each $\pi _i \ge 0$ and $\sum _i \pi _i=1$, and the $2n+1$ parameters $k, \theta _1, \theta _2, \dots , \theta _n,$ $\pi _1, \pi _2, \dots , \pi _n$ are to be determined. These parameters are computed by following a sequence of steps that make use of results concerning moment matrices (Uspensky 1937, Appendix II). The sequence in Lindsay et al. (2000) is complicated, so we extract the main steps here (without proofs). The first step is to compute the first 2n cumulants $\kappa _1, \kappa _2, \dots , \kappa _{2n}$ of $Q_N$ using Eq. (4), and then use the recursive formula in Eq. (6) to compute the first 2n moments $m_1, m_2, \dots , m_{2n}$ of $Q_N$. The second step is to define, for a variable $\alpha$, the functions $\delta _{r}(\alpha )$ as

$$\begin{aligned} \delta _{r}(\alpha ) = \frac{m_r}{ \prod _{i=1}^{r} \left( 1+ (i-1)\alpha \right) }, \,\,\,\, r=1,2, \dots , 2n, \end{aligned}$$

(18)

and $\delta _{0}(\alpha ) = 1$. These functions are then used to create the $(r+1)\times (r+1)$ pseudo-moment matrices $\Delta _{r}(\alpha )$, defined as

$$\begin{aligned} \Delta _{r}(\alpha ) = \left\{ \delta _{i+j}(\alpha ) \right\} _{\begin{array}{c} i=0,1,\dots r \\ j=0,1,\dots r \end{array}}, \qquad r=1, 2, \dots , n. \end{aligned}$$

(19)

For example,

$$\begin{aligned} \Delta _2(\alpha )&= \left( \begin{array}{ccc} \delta _0(\alpha ) &{}\quad \delta _1(\alpha ) &{}\quad \delta _2(\alpha ) \\ \delta _1(\alpha ) &{}\quad \delta _2(\alpha ) &{}\quad \delta _3(\alpha ) \\ \delta _2(\alpha ) &{}\quad \delta _3(\alpha ) &{}\quad \delta _4(\alpha ) \end{array} \right) \end{aligned}$$

(20)

$$\begin{aligned}&= \left( \begin{array}{ccc} 1 &{}\quad m_1 &{}\quad \frac{m_2}{(1+\alpha )} \\ m_1 &{}\quad \frac{m_2}{(1+\alpha )} &{}\quad \frac{m_3}{(1+\alpha )(1+2\alpha )} \\ \frac{m_2}{(1+\alpha )} &{}\quad \frac{m_3}{(1+\alpha )(1+2\alpha )} &{}\quad \frac{m_4}{(1+\alpha )(1+2\alpha )(1+3\alpha )} \end{array} \right) . \end{aligned}$$

(21)

The third step is to find certain roots $\widetilde{\lambda }_1, \widetilde{\lambda }_2, \dots \widetilde{\lambda }_n$ such that

$$\begin{aligned} \det \Delta _{r}(\widetilde{\lambda }_r) = 0, \qquad r = 1, 2, \dots , n. \end{aligned}$$

(22)

For $r=1$, there is a unique positive root ${\widetilde{\lambda }_1 = m_2/(m_1^2) - 1}$. For $r>1$, one can use a bisection method (e.g. Everitt 2012) to solve for the root $\widetilde{\lambda }_r \in [0, \widetilde{\lambda }_{r-1})$ of the equation $\det \Delta _{r}(\alpha ) = 0$. Eventually, $\widetilde{\lambda }_{n}$ is obtained. The fourth step is to define the matrix $M_{n}(\widetilde{\lambda }_n, t)$,

$$\begin{aligned} M_n(\widetilde{\lambda }_n, t) \!=\! \left( \begin{array}{ccccc} 1 &{}\quad \delta _1(\widetilde{\lambda }_n) &{}\quad \cdots &{}\quad \delta _{n-1}(\widetilde{\lambda }_n) &{}\quad 1 \\ \delta _1(\widetilde{\lambda }_n) &{}\quad \delta _2(\widetilde{\lambda }_n) &{}\quad \cdots &{}\quad \delta _{n}(\widetilde{\lambda }_n) &{}\quad t \\ \delta _2(\widetilde{\lambda }_n) &{}\quad \delta _3(\widetilde{\lambda }_n) &{}\quad \cdots &{}\quad \delta _{n+1}(\widetilde{\lambda }_n) &{}\quad t^2 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ \delta _n(\widetilde{\lambda }_n) &{}\quad \delta _{n+1}(\widetilde{\lambda }_n) &{}\quad \cdots &{}\quad \delta _{2n-1}(\widetilde{\lambda }_n)&{}\quad t^n \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(23)

Note that $M_n(\widetilde{\lambda }_n, t)$ is the same as $\Delta _{n}(\widetilde{\lambda }_n)$ but with the last column replaced by $(1 , t , \dots , t^n)'$. This matrix is used to compute the nth degree polynomial $S_n(\lambda , t)$, where

$$\begin{aligned} S_n(\lambda , t) = \det M_n(\widetilde{\lambda }_n, t) = \sum _{j=0}^n c_j t^j, \end{aligned}$$

(24)

for some $c_j \in \mathbb {R}$ and $j = 0, 1, \dots , n$. In order to obtain the value of the coefficient $c_j$, one can replace the last column of $M_n(\widetilde{\lambda }_n, t)$ (the powers of t), with the basis vector $e_{j+1}$ (the $(j+1)$th component equals one, all others are zero), and compute the determinant of this modified matrix. With the coefficients computed, the n roots of $S_n(\lambda , t)=0$, denoted $\mu _1, \mu _2, \dots , \mu _n$, can be found [the roots are real and distinct (Uspensky 1937, Appendix II.4)]. The fifth step is to use these roots $\mu _i$ to solve the system of linear equations

$$\begin{aligned} \left( \begin{array}{cccc} 1 &{}\quad 1 &{}\quad \cdots &{}\quad 1 \\ \mu _1 &{}\quad \mu _2 &{}\quad \cdots &{} \mu _n \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ \mu _1^{n-1} &{}\quad \mu _2^{n-1} &{}\quad \cdots &{}\quad \mu _n^{n-1} \end{array} \right) \left( \begin{array}{c} \pi _1 \\ \pi _2 \\ \vdots \\ \pi _n \end{array} \right) = \left( \begin{array}{c} 1 \\ \delta _1(\widetilde{\lambda }_n) \\ \vdots \\ \delta _{n-1}(\widetilde{\lambda }_n) \end{array} \right) \nonumber \\ \end{aligned}$$

(25)

to compute the mixture proportions $\pi _1, \pi _2, \dots , \pi _n$. Since the matrix on the left of Eq. (25) is a Vandermonde matrix, it is non-singular (Macon and Spitzbart 1958), and so this system of linear equations has a unique solution. Finally, we define $k = (\widetilde{\lambda }_n)^{-1}$ and $\theta _i = \widetilde{\lambda }_n \cdot \mu _i$, for $i = 1, 2, \dots , n$, and now can compute the approximate cdf $F_{\widetilde{Q}_N}$ in Eq. (17). Note that the Lindsay–Pilla–Basak method agrees with the Satterthwaite–Welch method for $n=1$.

It should be remarked that Robbins and Pitman (1949) also attempt to obtain an approximation using a method of mixtures, but by computing the characteristic function rather than using the method of moments.

3.6 Sequential implementation

As described in Sect. 2, one might wish to compute $F_{Q_N}(x)$ and then soon afterwards compute $F_{Q_{N+1}}(x')$, for $Q_{N+1}=Q_N + d_{N+1} W^2_{N+1}$. Note that x and $x'$ may be different values. This can be done easily and efficiently using one of the four moment-matching methods described above. When computing $F_{Q_N}(x)$, we store the cumulants $\kappa _{1}(Q_N)$, $\kappa _{2}(Q_N)$, ..., $\kappa _{\ell }(Q_N)$, where the value of $\ell$ depends on the method we are using (e.g. for Hall–Buckley–Eagleson, $\ell =3$). Now, one can simply use the new coefficient $d_{N+1}$ and Eq. (5) to update $\kappa _{r}(Q_N)$ to $\kappa _{r}(Q_{N+1})$, for $r=1, 2, \dots \ell$. These updated cumulants, together with $x'$, are all that is needed to compute $F_{Q_{N+1}}(x')$. Note that this method only requires the storage of the $\ell$ cumulants, regardless of the value of N, which makes this method suitable for a streaming data context.

4 Evaluation of approximate methods for computing $F_{Q_N}$ in the literature

In previous work on approximations for computing the cdf $F_{Q_N}$ of weighted sums of chi-squared random variables $Q_N$ (Imhof 1961; Solomon and Stephens 1977; Wood 1989; Lindsay et al. 2000; Castaño-Martínez and López-Blázquez 2005), it was common to estimate the performance of an approximate method by demonstrating its accuracy for a selected sample of M distributions $Q_{N, \mathbf {d}_1}, Q_{N, \mathbf {d}_2}, \dots , Q_{N, \mathbf {d}_M}$, where for $k = 1, 2, \dots , M$,

$$\begin{aligned} Q_{N, \mathbf {d}_k} = \sum _{i=1}^{N} d_{i, k} W_i^2, \qquad d_{i, k} > 0, \,\,\, W_i \sim \text {N}(0, 1), \end{aligned}$$

(26)

and $\mathbf {d}_k = (d_{1, k}, d_{2, k}, \dots , d_{N, k})$. Recall that the cdf of a random variable X is defined by

$$\begin{aligned} F_X(x) = \text {Pr}(X \le x). \end{aligned}$$

(27)

In this article, values x in the domain of the cdf $F_X$ will be called quantile values, and values $F_X(x)$ will be called probability values. For each $Q_{N, \mathbf {d}_k}$, the quantile values $x_{j,k}$ are found such that, for $k = 1, 2, \dots , M$,

$$\begin{aligned} F_{Q_{N, \mathbf {d}_k}}(x_{j, k}) = p_j, \qquad j=1, 2, \dots , L, \end{aligned}$$

(28)

for a specific set of probability values $p_j$. Then a table of errors $\epsilon _{j, k}$, where, for $k = 1, 2, \dots , M$,

$$\begin{aligned} \epsilon _{j, k} = | G(x_j) - F_{Q_{N, \mathbf {d}_k}}(x_j) |, \qquad j=1, 2, \dots , L, \end{aligned}$$

(29)

is presented for one or more approximate methods, where G is the cdf produced by the approximate method. According to the literature, the method with the smallest set of errors is then considered to be the best approximate method.

This may seem to be a reasonable approach, but the execution in previous works leaves something to be desired. In Imhof (1961), Solomon and Stephens (1977), Wood (1989), Lindsay et al. (2000), Castaño-Martínez and López-Blázquez (2005), each analysis only considers a selection of between $M=8$ and $M=18$ distributions $Q_N$ for a selected set of coefficients and number of terms. Results established for an approximation procedure based on the analysis of such a small selection should be viewed with caution. So, while previous works may have established the accuracy for the particular selections considered, those results cannot reasonably be assumed to hold for all possible $Q_N$. Moreover, previous works only considered $Q_N$ with fewer than $N=10$ terms, so it is natural to wonder how approximate methods perform for distributions $Q_N$ with significantly larger N. This is particularly relevant in the context of streaming data problems.

There is a possible explanation for why previous works only consider a limited selection of distributions $Q_N$ in their analyses. When these approximate methods were first considered in the 1950s and 1960s (e.g. Box 1954; Imhof 1961), calculating the probability values $p_j$ may have been difficult, especially with computing in its infancy. Therefore, only a limited table of results was produced. When later methods in the 1970s and 1980s (e.g. Solomon and Stephens 1977; Wood 1989) were developed, it would have been natural to use the performance analysis of earlier methods as the benchmark, and so a table of errors $\epsilon _{j, k}$ was again compiled for a small (in some cases the same) sample of distributions. Unfortunately, this method of evaluating performance has continued unchanged (e.g. Lindsay et al. 2000; Castaño-Martínez and López-Blázquez 2005), even though computers that are able to complete a much more thorough analysis are now readily available. In Sect. 5, we outline such an analysis, which will seem natural following the discussion in this section.

It should be mentioned that while we shall use Farebrother’s method in combination with a bisection procedure (e.g. Everitt 2012) to compute the exact quantile values [i.e. Eq. (28)] in Sect. 6, it was not indicated in previous works how the exact quantile values were obtained for performance calculations.

5 A new method for evaluating the performance of an approximate method for a cdf of a weighted sum of random variables

This section discusses the issue of evaluating the performance of approximation methods for the cdf of a weighted sum of random variables. This procedure is then used in Sect. 6 to analyse the performance of approximate methods for the cdf of a weighted sum of chi-squared random variables. In this section, $R_N$ is a weighted sum of i.i.d. unspecified random variables (not necessarily chi-squared as $Q_N$). It is assumed that a method exists for computing the true probability value $F_{R_N}(x)$ for quantile value x, to arbitrary accuracy. However, the method may be too computationally or memory intensive for routine application.

5.1 Performance of an approximate method for a particular distribution $R_{N, \mathbf d }$

Suppose a method provides approximate probability values $G(x)$ for a weighted sum of random variables $R_N$. Suppose further that we wish to determine how close G is to the true cdf $F_{R_N}$, for a particular distribution $R_{N, \mathbf {d}}$ with weights $\mathbf {d}= (d_1, d_2, \dots , d_N)$. For a set of probability values

$$\begin{aligned} \left\{ p_1, p_2, \dots , p_L \right\} , \end{aligned}$$

(30)

suppose that the “exact” quantile values

$$\begin{aligned} \left\{ x_1, x_2, \dots , x_L \right\} \end{aligned}$$

(31)

can be computed to an arbitrary precision, perhaps at a practically unacceptable computational cost, so that

$$\begin{aligned} | F_{R_N}(x_j) - p_j | < \xi , \qquad \xi \ll 1, \, \,\, j=1, 2, \dots , L. \end{aligned}$$

(32)

In this case, we shall say that the quantiles are accurate to precision $\xi$, when we mean that the true cdf will evaluate the quantile to within $\xi$ of the corresponding probability value. The errors of the approximate method G, denoted by $\epsilon _j$, are then defined as

$$\begin{aligned} \epsilon _j = | G(x_j) - F_{R_N}(x_j) |, \qquad j = 1,2, \dots , L. \end{aligned}$$

(33)

The smaller the $\epsilon _j$, the better that G approximates $F_{R_N}$ for the probability values $p_j$. By a simple application of the triangle inequality,

$$\begin{aligned} | G(x_j) - p_j | < \epsilon _j + \xi , \qquad j = 1,2, \dots , L, \end{aligned}$$

(34)

is obtained. Therefore, if the $x_j$ can be computed to ensure $\xi \ll \epsilon _j$ for all j, it is then only necessary to look at the values $| G(x_j) - p_j |$ to obtain a good approximation for $\epsilon _j$.

5.2 Estimating the accuracy of an approximate method for $R_N$, for a particular N

The first step to more comprehensively evaluating the performance of an approximate method for distributions with N terms is to randomly generate a large sample of M coefficient vectors $\mathbf {d}_k= (d_{1, k}, d_{2, k}, \dots , d_{N, k})$, where

$$\begin{aligned} d_{1, k}, d_{2, k}, \dots , d_{N, k} \sim D, \qquad k = 1, 2, \dots , M, \end{aligned}$$

(35)

for some distribution D, so that $F_{R_{N,\mathbf {d}_k}}$ is the cdf of

$$\begin{aligned} R_{N, \mathbf {d}_k} = \sum _{i=1}^{N} d_{i, k} Y_i , \qquad Y_i \sim Y, \,\, k = 1, 2, \dots , M, \end{aligned}$$

(36)

for some distribution Y. The next step is to select a wide range of probability values $\{ p_1, p_2, \dots , p_L \}$, and then to compute the quantile values

$$\begin{aligned} \{ x_{1,k}, x_{2,k}, \dots , x_{L,k} \}, \qquad k = 1, 2, \dots , M, \end{aligned}$$

(37)

so that for some precision $\xi$, with $\xi \ll 1$,

$$\begin{aligned} | F_{R_{N,\mathbf {d}_k}} (x_{j, k}) - p_j | < \xi , \qquad j=1, 2, \dots , L. \end{aligned}$$

(38)

Finally, the errors $\epsilon _{j, k}$ are computed as

$$\begin{aligned} \epsilon _{j, k} = | G(x_j) - F_{R_{N, \mathbf {d}_k}}(x_j)|, \end{aligned}$$

(39)

for $j=1, 2, \dots , L$ and $k = 1, 2, \dots , M$. The set of errors for probability value $p_j$ is defined as

$$\begin{aligned} E_j = \left\{ \epsilon _{j, k} | k = 1, 2, \dots , M \right\} , \qquad j = 1, 2, \dots , L. \end{aligned}$$

(40)

While it would now be easy to compute $\max E_j$ and declare this to be a reasonable upper bound for the error when computing $p_j$, provided that M is large, the following procedure is preferable because it establishes a probabilistic result. Define $\bar{\epsilon }_j$ to be the sample mean, $s^2_{\epsilon _j}$ the sample variance, and $q^2_{\epsilon _j}$ the scaled sample variance of $E_j$ by the equations:

$$\begin{aligned} \bar{\epsilon }_j&= \frac{1}{M} \sum _{k=1}^M \epsilon _{j, k}, \end{aligned}$$

(41)

$$\begin{aligned} s^2_{\epsilon _j}&= \frac{1}{M-1} \sum _{k=1}^M \left[ \epsilon _{j, k} - \bar{\epsilon }_j \right] ^2, \end{aligned}$$

(42)

$$\begin{aligned} q^2_{\epsilon _j}&= \left( \frac{M+1}{M} \right) s^2_{\epsilon _j}. \end{aligned}$$

(43)

Suppose that $\epsilon _{j}^{*}$ is the error for $F_{R_{N, \mathbf {d}^{*}}}$, with coefficient vector $\mathbf {d}^{*}$ generated as in Eq. (35). If we assume that the error values in $E_j$ are i.i.d. according to some distribution, then Chebyshev’s inequality with the sample mean and variance Saw et al. (1984) gives us, for any $\delta > 0$,

$$\begin{aligned} \Pr \left( |\epsilon _{j}^{*} - \bar{\epsilon }_j| > \delta q_{\epsilon _j} \right) \le \frac{1}{\delta ^2} + \frac{1}{M} \left( 1 - \frac{1}{\delta ^2} \right) . \end{aligned}$$

(44)

If we set the the right-hand side of Eq. (44) to be

$$\begin{aligned} \alpha _{\delta , M} = \frac{1}{\delta ^2} + \frac{1}{M} \left( 1 - \frac{1}{\delta ^2} \right) , \end{aligned}$$

(45)

then Eq. (44) implies

$$\begin{aligned}&\Pr \left( \epsilon _{j}^{*} > \bar{\epsilon }_j + \delta q_{\epsilon _j} \right) \le \alpha _{\delta , M}, \end{aligned}$$

(46)

$$\begin{aligned}&\Rightarrow \Pr \left( \epsilon _{j}^{*} \le \bar{\epsilon }_j + \delta q_{\epsilon _j} \right) > 1- \alpha _{\delta , M}. \end{aligned}$$

(47)

Then $\bar{\epsilon }_j + \delta q_{\epsilon _j}$ provides an upper bound for $100(1-\alpha _{\delta , M})\%$ of all possible errors obtained when computing $p_j$ using the approximate method. In other words, the probability that the error exceeds the upper bound is less than $\alpha _{\delta , M}$. For example, when $\delta =10$ and $M=10{,}000$ then $\alpha _{\delta , M} \approx 0.01$, or $\delta =32$ and $M=10{,}000$ gives $\alpha _{\delta , M} \approx 0.001$, and so then $\bar{\epsilon }_j + \delta q_{\epsilon _j}$ provides an upper bound for $99.9\%$ for all errors.

The same procedure could be followed to obtain a bound for the error of computing $p_j$ for every $p_j\in \left\{ p_1, p_2, \dots , p_L \right\}$, and so an estimate of the error for an approximate method of computing probability values for distributions $Q_N$ is obtained, for a particular N.

The assumption that the errors in $E_j$ are i.i.d. may seem restrictive, but in fact the errors need only be weakly exchangeable. Finally, although Saw et al. (1984) give a slightly sharper bound for the inequality in Eq.  (44), its expression is far more complicated and does not significantly change the bound for our purposes here.

6 Results

A simulation is performed by computing $M=10{,}000$ sets of coefficients $d_{i, k} \sim U(0, 1)$ for cases where $N=10, 20, 50, 100$, and then computing the quantile values $x_{j, k}$ corresponding to probability values $p_j \in P$, where

$$\begin{aligned}&P = P_L \cup P_M \cup P_U \nonumber \\&P_L = \left\{ 0.001, 0.05, 0.01 \right\} \nonumber \\&P_M = \left\{ 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 \right\} \nonumber \\&P_U = \left\{ 0.95, 0.99, 0.999 \right\} . \end{aligned}$$

(48)

For the purposes of discussion below, let us define the lower tail to be the probability values in $P_L$ and the upper tail to be probability values in $P_U$. Values in $P_M$ will be referred to as middle probability values. Assuming that the coefficients are sampled from U(0, 1) is not particularly restrictive; if a particular application uses coefficients that are known to be bounded, they can be rescaled to the range (0, 1). Farebrother’s method is used to ensure that the quantiles are accurate to $\xi =10^{-8}$ as in Eq. (38). Imhof’s method could also have been used, but the implementation of Farebrother’s method in the R package CompQuadForm (Lafaye de Micheaux 2011) appears to allow a greater precision to be specified. The analysis is then performed using $\delta =32$ to obtain an upper bound with confidence $\alpha _{\delta , M} \approx 0.001$ (see Eq. (45)). The accuracy of each of the four moment-matching methods in Sect. 3 is computed for all $p_j$, and the methods are compared side by side in Sect. 6.1. The Lindsay–Pilla–Basak method is computed for $n=4$ (that is for the first eight moments), and so will be abbreviated to LPB4. In Sect. 6.4, we then investigate the relative speeds of each method. Note that none of the sampled coefficient vectors $\mathbf {d}_{k}$ yielded degenerate cases (as mentioned in Sect. 3.4) for the Wood F approximation.

6.1 Accuracy

The accuracy of the Satterthwaite–Welch (SW), Hall–Buckley–Eagleson (HBE), Wood F (WF) and Lindsay–Pilla–Basak with $n=4$ (LPB4) approximate methods is shown in Figs. 1 and 2, for a wide selection of probability values and a range of values of N. The horizontal axes indicate the value of N, while the vertical axes show the number of digits of accuracy; the value shown is $-\log _{10}(\bar{\epsilon }_j + \delta q_{\epsilon _j})$ [see Eq.  (47)]. Figure 1 groups the values by method, while Fig. 2 groups the values by probability value.

Fig. 1

Error of Satterthwaite–Welch, Hall–Buckley–Eagleson, Wood F and Lindsay–Pilla–Basak approximations for varying number of terms N, grouped by method

Fig. 2

Error of Satterthwaite–Welch, Hall–Buckley–Eagleson, Wood F and Lindsay–Pilla–Basak approximations for varying number of terms N, grouped by probability value

s

Figure 1 illustrates several points. The first feature of interest is that the methods generally increase in accuracy as N increases. There are a couple of exceptions (e.g. $p_j=0.999$ for the LPB4), but any decrease is minor. This seems to suggest a trend which would continue for $N \ge 100$ (indeed, similar figures showing results for $N=200, 500$ and 1000 confirm this). Following this observation, if method A has number of digits of accuracy a for number of terms $N'$, we shall say that method A is accurate to a decimal places for $N \ge N'$. As far as we are aware, this observation that the accuracy of these approximate methods generally increases, as the value of N increases, has not been noted before and is not apparent or implied from the construction of the methods. As already mentioned, previous analyses only focused on distributions $Q_N$ for a limited range of N.

If the results shown in Fig. 1 for each individual method are now examined, it can be seen that SW is accurate in the upper and lower tails to at least two decimal places for $N \ge 100$. The HBE method is accurate to two decimal places for all $p_j$ for $N \ge 50$ and to three places for almost all values in the upper and lower tails for $N \ge 100$. The WF method is also accurate to two decimal places for $p_j$ for $N \ge 50$ and is accurate in the upper tail to three digits for $N \ge 50$. The LPB4 method is accurate to four decimal places for almost all probability values (only exceptions are a few middle probability values) for $N \ge 50$ and has close to five digits of accuracy for the upper and lower tails for $N \ge 100$. Note that Fig. 1 is meant to illustrate the general behaviour for each method across a range of probability values, as N increases. In the supplementary material, this figure has been split into three separate figures, displaying the upper, middle and lower probability values, for readers who may be interested in the behaviour for a particular probability value.

Figure 2 shows that over the different probability values, SW is the least accurate, while LPB4 is clearly the most accurate, and WF and HBE appear to be essentially matched, although for most probability values WF has a slightly better accuracy than HBE (one exception is for $p_j=0.975$ and $N=50$).

Note that if Imhof and Farebrother’s methods were included in Figs. 1 and 2, since they are essentially exact (they will iterate until the desired accuracy is achieved), the result would be horizontal lines at the level of the accuracy specified.

One reviewer raised the question of how these methods perform for very small probability values. An investigation into the accuracy of these methods for small probability values in the set $\{10^{-4}, 10^{-5}, \dots , 10^{-10} \}$ is included in the supplementary material, which shows that the Wood F and Lindsay–Pilla–Basak methods perform well for probability values in this range, but that the Hall–Buckley–Eagleson method should not be used in this case.

Another reviewer raised the question of how these methods perform for coefficients that are not U(0, 1)-distributed or are not i.i.d.. A section in the supplementary material shows similar performance to that in Fig. 1 for coefficients that are Beta(2, 5)-distributed, for coefficients that are sampled from a mixture of distributions, and for coefficients that are highly correlated. These results indicate that the actual distribution of the coefficients is not too important when considering the results in Fig. 1. Finally, other sections in the supplementary material show similar results for which the variables are $\chi ^2(\nu )$ for $\nu > 1$, rather than $\chi ^2(1)$, and that the accuracy of the methods increases when $N = 200, 500, 1000$.

6.2 Comparison to the normal approximation

Although the normal approximation is not considered to be as good as the four approximations considered above, it is interesting to investigate how it compares to SW, the simplest of the approximations above.

The normal approximation is computed in a similar manner to SW. Equating the first two moments of $Q_N$ with a $\text {N}(\widehat{\mu }, \widehat{\sigma }^2)$ variable yields

$$\begin{aligned} \widehat{\mu }= \kappa _1, \qquad \widehat{\sigma } = \sqrt{\kappa _2}, \end{aligned}$$

(49)

following the definition of the cumulants $\kappa _1$ and $\kappa _2$ in Sect. 3.1. Then $F_{\text {N}(\widehat{\mu }, \widehat{\sigma }^2)}$ is used to approximate $F_{Q_N}$. Figure 3 shows that SW appears to be one decimal place more accurate than the normal approximation. The only exception is for $p_j=0.999$, where the two methods appear to have similar accuracy. Even though both methods are two-moment approximations, and the computational complexity is virtually the same, SW’s use of a Gamma cdf provides a significant increase in accuracy over the normal approximation.

Fig. 3

Error of the Normal approximation, compared to the Satterthwaite–Welch approximation, grouped by method

6.3 Accuracy for small number of terms N

It is worth investigating the accuracy of these methods for the cases where $N \in \{2, 3, ..., 10\}$. The results of this investigation are shown in Fig. 4 and show that SW, HBE and WF will generally give between 0 and 2 digits of accuracy, while LPB4 generally gives at least 2 digits of accuracy. These results suggest that when $N < 10$, these methods should be used with caution. Note that for $N=2, 3$ there are choices of coefficient vector $\mathbf {d}_k$ which result in the LPB4 method not being able to provide an approximation [fails to find roots $\widetilde{\lambda }_r$ for Eq. (22)], so values for $N=2, 3$ for LPB4 are omitted.

Fig. 4

Error of Satterthwaite–Welch, Hall–Buckley–Eagleson, Wood F and Lindsay–Pilla–Basak approximations for a small number of terms N, grouped by method. Note that results are not provided for LPB4 for $N=2, 3$

If one were only interested in computing the cdf for a fixed, small N, then, as one of the reviewers has suggested, Imhof’s method should be used. However, if the number of terms N were increasing, as in a change detection scenario (see Sect. 2), it would be better to use one of the moment-matching methods for all N.

6.4 Speed of computation

Table 1 shows that while the SW, HBE and WF methods have similar speeds (of the same order), LPB4 is significantly slower. This could be due to the iterative methods needed in steps 3 and 4 of the algorithm (as described in Sect. 3.5) and the matrix algebra in several steps. Besides the matrix operations, the LPB method needs to employ root-finding algorithms (which can be very efficient, but are still iterative). For comparison purposes, the speeds of the normal approximation, Imhof’s method and Farebrother’s method have also been included. The normal approximation is slightly faster than SW, but is much less accurate. Surprisingly, Imhof’s method is faster than LPB4, but is still over 40 times slower than HBE. LPB4 is over 300 times slower than HBE. Farebrother’s method is significantly slower than any of the other methods, but it is unclear if this is due to a few problematic cases, or if this is a general property of the algorithm. However, the table shows its performance over 10,000 samples, which gives an indication of its average behaviour.

Table 1 The time taken (in seconds) for each method to compute $M=17 \times 10{,}000$ probability values for $Q_N$ with $N=100$, and the relative speed to HBE

The four algorithms (SW, HBE, WF and LPB) and the normal approximation were written in R, while Imhof’s method and Farebrother’s are implemented in C++ in the R package CompQuadForm (Lafaye de Micheaux 2011). Note that the implementation in C++, a compiled language, may explain why Imhof’s method is faster than LPB4. The speed test was done on an Apple iMac with an Intel Core i5 (3.2 GHz) processor (4 cores) and 8 GB of RAM.

7 Conclusion

While Imhof’s method is essentially exact, it is not suitable for a streaming data scenario, where it is necessary for algorithms to (a) not store all the coefficients of $Q_N$, and (b) have efficient computation. In such situations, moment-matching methods such as the four described in Sect. 3 may be very useful.

Choosing between these methods is not a simple matter of choosing the most accurate. One also needs to consider the speed of computation, and, to a lesser extent, the ease of implementation. While Figs. 1 and 2 show the Lindsay–Pilla–Basak method to be extremely accurate, it is also significantly slower to compute (see Table 1) and laborious to implement (Sect. 3.5). If it is not necessary to have four decimal places of accuracy, other methods could be used.

Of the remaining three methods, the Hall–Buckley–Eagleson method is perhaps the best alternative. It is one decimal place more accurate in the tails than the Satterthwaite–Welch method, yet is only marginally slower (see Sect. 6.1 and Table 1), and is essentially as accurate as the Wood F method, without needing to worry about degenerate cases (see Sects. 6.1 and 3.4). For this reason, the Hall–Buckley–Eagleson method is recommended for most practitioners.

This recommendation is based on the observation, revealed by Figs. 1 and 2 and not previously described in the literature, that the accuracy of the four moment-matching methods generally increases as the number of terms N increases.

However, as described in Sect. 6.1 and shown in the supplementary material, for very small probability values, either the Wood F or the Lindsay–Pilla–Basak method should be used.

Furthermore, Sect. 5 provides a new statistical framework for evaluating the accuracy of an approximate method for computing $F_{R_N}$, the cdf of a weighted sum of random variables $R_N$ (for any distribution).