Nonlinear Generation of Fluting Perturbations by Kink Mode in a Twisted Magnetic Tube

Abstract

We study the excitation of fluting perturbations in a magnetic tube by an initially imposed kink mode. We use the ideal magnetohydrodynamic (MHD) equations in the cold-plasma approximation. We also use the thin-tube approximation and scale the dependent and independent variables accordingly. Then we assume that the dimensionless amplitude of the kink mode is small and use it as an expansion parameter in the regular perturbation method. We obtain the expression for the tube boundary perturbation in the second-order approximation. This perturbation is a superposition of sausage and fluting perturbations.

1 Introduction

Transverse oscillations of coronal magnetic loops were first observed by the Transition Region and Coronal Explorer (TRACE) in 1998. These observations were reported by Aschwanden et al. (1999) and Nakariakov et al. (1999), and interpreted as fast kink standing waves in magnetic flux tubes. After this first observation, the kink oscillations of coronal magnetic tubes remain in the limelight of theoretical studies in solar physics. Initially, these oscillations were studied using the simplest model of a straight homogeneous magnetic flux tube (e.g. Ryutov and Ryutova, 1976; Edwin and Roberts, 1983). Later, more sophisticated models taking into account such effects as the plasma density variation along and across a tube and the presence of flows were developed (see, e.g. the review by Ruderman and Erdélyi, 2009; Nakariakov et al., 2021).

The majority of studies on coronal-loop kink oscillations were carried out using linear magnetohydrodynamics (MHD). Studies of nonlinear coronal loop kink oscillations are not numerous. Ruderman (1992) and Ruderman, Goossens, and Andries (2010) studied analytically nonlinear propagating kink waves, while Ruderman and Goossens (2014) analytically investigated nonlinear standing kink waves. There were also a few numerical studies of nonlinear kink oscillations (e.g. Terradas et al., 2008; Magyar, Van Doorselaere, and Marcu, 2015; Magyar and Van Doorselaere, 2016).

In a meeting of an international group led by G. Verth and R. Morton at the International Space Science Institute (ISSI) Terradas, Magyar, and Van Doorsselaere (2018) presented the results of a numerical study of nonlinear kink oscillations of a magnetic tube. In particular, they reported the appearance of fluting perturbation of the tube boundary excited by an initially imposed kink oscillation. The period of the fluting perturbation was equal to half the period of the kink oscillation, and its amplitude took its maximum at the centre of the magnetic tube. Some of the meeting participants insisted that the fluting perturbation must be the first harmonic of the first fluting mode. The amplitude of this harmonic is zero at the tube centre.

Ruderman, Goossens, and Andries (2010) and Ruderman and Goossens (2014) predicted the excitation of the fluting perturbation with the frequency equal to double the frequency of the kink mode. They also predicted that the amplitude of the fluting perturbation would be proportional to the amplitude of the kink mode squared. However, their results cannot be directly compared with those reported by Terradas, Magyar, and Van Doorsselaere (2018) because Ruderman, Goossens, and Andries (2010) studied propagating waves, and Ruderman and Goossens (2014) concentrated on the effect of nonlinearity on the kink oscillations of a magnetic tube strongly stratified in the longitudinal direction.

The results reported by Terradas, Magyar, and Van Doorsselaere (2018) motivated Ruderman (2017) to study the problem of the excitation of a fluting perturbation by an initially imposed kink mode. The results that he obtained coincide qualitatively with those reported by Terradas, Magyar, and Van Doorsselaere (2018). In particular, he obtained that the fundamental kink mode generates the first fluting mode with double the frequency and fundamental in the axial direction. In the interpretation of these results, an important role is played by the fact that the equilibrium used by both Terradas, Magyar, and Van Doorsselaere (2018) and Ruderman (2017) is mirror symmetric in the axial direction.

One particular property of magnetic flux tubes that can affect the kink waves is the magnetic twist. The effect of magnetic twist on standing kink oscillations in solar magnetic flux tubes was studied by Ruderman (2007), Karami and Bahari (2012), Terradas and Goossens (2012), and Ruderman and Terradas (2015). An important property of twist is that it destroys the mirror symmetry of the magnetic tube in the axial direction. Hence, we can expect that the excitation of fluting modes by kink oscillations in a twisted tube is qualitatively different from that in a straight tube. This article aims to study analytically the effect of magnetic twist on the excitation of fluting modes by kink oscillations. The article is organised as follows. In the next section, we formulate the problem and write down the governing equations and boundary conditions. In Section 3 we use the regular perturbation method to study the excitation of fluting perturbations in a twisted tube. Section 4 contains the summary of the results obtained and our conclusions.

2 Problem Formulation and Governing Equations

We use the cold-plasma approximation. The equilibrium density $[\rho _{0}]$ is given by

$$ \rho _{0} = \left \{ \textstyle\begin{array}{c@{\quad}c} \rho _{\mathrm{i}}, & r < R, \\ \rho _{\mathrm{e}}, & r > R,\end{array}\displaystyle \right . $$

(1)

where $\rho _{\mathrm{i}}$ and $\rho _{\mathrm{e}}$ are constant, and $\rho _{\mathrm{e}} < \rho _{\mathrm{i}}$. Outside the tube, the equilibrium magnetic field $[\boldsymbol{B}]$ is given by $\boldsymbol{B} = B_{0}\boldsymbol{e}_{z}$, where $\boldsymbol{e}_{z}$ is the unit vector in cylindrical coordinates $(r,\phi ,z)$ $z$-direction. Inside the tube, the equilibrium magnetic field is twisted. Hence, the azimuthal component of the equilibrium magnetic field is defined by

$$ B_{\phi }= \left \{ \textstyle\begin{array}{c@{\quad}c} Ar, & r < R, \\ 0, & r > R,\end{array}\displaystyle \right . $$

(2)

where $A$ is a constant. The equilibrium magnetic field satisfies the equation

$$ \frac{dB^{2}}{dr} = -\frac{2B_{\phi}^{2}}{r}. $$

(3)

It follows from Equations 2 and 3 and the condition that the magnetic-field magnitude must be continuous at the tube boundary that

$$ B^{2} = B_{0}^{2} + A^{2}(R^{2} - r^{2}). $$

(4)

The perturbations are governed by the ideal MHD equations

$$ \rho \left (\frac{\partial \boldsymbol{v}}{\partial t} + ( \boldsymbol{v}\cdot \nabla )\boldsymbol{v}\right ) = \frac{1}{\mu _{0}}[\nabla \times (\boldsymbol{B} + \boldsymbol{b})] \times (\boldsymbol{B} + \boldsymbol{b}) , $$

(5)

$$ \frac{\partial \boldsymbol{b}}{\partial t} = \nabla \times [ \boldsymbol{v}\times (\boldsymbol{B} + \boldsymbol{b})], \quad \nabla \cdot \boldsymbol{v} = 0, $$

(6)

where $\rho$ is the density, $\boldsymbol{v}$ is the plasma velocity, $\boldsymbol{b}$ is the magnetic-field perturbation, and $\mu _{0}$ is the magnetic permeability of free space. The perturbations must satisfy the frozen-in conditions at the tube footpoints,

$$ \boldsymbol{v}_{\perp }=0 \quad \text{at} \quad z = \pm L/2, $$

(7)

where $L$ is the tube length and $\boldsymbol{v}_{\perp }= \boldsymbol{v} - B^{-2} \boldsymbol{B}(\boldsymbol{v}\cdot \boldsymbol{B})$. We also impose the boundary conditions at the tube boundary,

$$ \boldsymbol{v}\cdot \boldsymbol{e}_{r} = \frac{\partial \eta}{\partial t} + \boldsymbol{v}\cdot \nabla \eta , \quad [\hspace{-0.5mm}[B^{2} + 2\boldsymbol{b}\cdot \boldsymbol{B} + |\boldsymbol{b}|^{2} ]\hspace{-0.5mm}]= 0 \quad \text{at} \quad r = R + \eta (t,\phi ,z), $$

(8)

where $\eta (t,\phi ,z)$ is the tube boundary perturbation, $\boldsymbol{e}_{r}$ is the unit vector in the radial direction, and the double brackets indicate the jump of a quantity across the tube boundary. For an arbitrary function $[f]$ this jump is defined as

$$ [\hspace{-0.5mm}[f ]\hspace{-0.5mm}]= \lim _{\varepsilon \to +0}[f(R + \eta + \varepsilon ) - f(R + \eta - \varepsilon )]. $$

Below we assume that the tube is thin: $R/L = \epsilon \ll 1$. In accordance with this assumption we introduce the stretching variable $Z = \epsilon z$. The characteristic Alfvénic time related to the tube radius is $R/V_{\mathrm{A}}$, where $V_{\mathrm{A}} = B(\mu _{0}\rho _{0})^{-1/2}$ is the Alfvén speed. It can be the Alfvén speed either inside or outside the tube, because we assume that the density ratio $[\rho _{\mathrm{i}}/\rho _{\mathrm{e}}]$ is not large, implying that the two Alfvén speeds are of the same order. On the other hand, the oscillation period is of the order of $L/V_{\mathrm{A}} = \epsilon ^{-1}R/V_{\mathrm{A}}$. This inspires us to introduce the “slow” time $T = \epsilon t$. Below we assume that the maximum tube axis displacement is of the order of $aR$, where $a \ll 1$. The quantity $a$ can be considered as the dimensionless amplitude of the tube’s kink oscillation. Later, we assume that, although $a$ is small, $a \gg \epsilon$. Finally, we assume that the twist is weak and write $B_{\phi }= \epsilon \widetilde{B}_{\phi}$ and $A = \epsilon \widetilde{A}$, where $\widetilde{B}_{\phi}$ is of the order of $B_{0}$ and $\widetilde{A}$ is of the order of $B_{0}/R$. Now it follows from Equation 4 that

$$ B = B_{0} + {\mathcal{O}}(\epsilon ^{2}), \quad B_{z} = B_{0} + {\mathcal{O}}( \epsilon ^{2}). $$

(9)

In accordance with the definition of $a$ we have $\eta /R = {\mathcal{O}}(a)$. We now obtain similar estimates for other variables. Although we use nonlinear equations, the nonlinear correction to the linear solution will be small. Then we can use the estimates for the order of magnitude of perturbation of various quantities obtained using the linear theory. It follows that the ratio of the radial and azimuthal components of the velocity to $V_{\mathrm{A}}$ is of the order of $\epsilon a$, and the same is true for the ratio of the radial and azimuthal components of the magnetic field perturbation to $B$. On the other hand, the ratio of the $z$-component of the velocity to $V_{\mathrm{A}}$, and the ratio of the $z$-component of the magnetic field perturbation to $B$ are both of the order of $\epsilon ^{2} a$. In accordance with these estimates, we introduce the scaled components of the velocity and magnetic-field perturbation and write

$$ \boldsymbol{v} = (\epsilon v_{r},\epsilon v_{\phi},\epsilon ^{2} v_{z}), \quad \boldsymbol{b} = (\epsilon b_{r},\epsilon b_{\phi}, \epsilon ^{2} b_{z}). $$

(10)

In addition, $\rho - \rho _{0} = {\mathcal{O}}(\epsilon ^{2} a)$. We now substitute these expressions in Equations 5 and 6 and write the equations obtained in components, keeping only the leading terms with respect to $\epsilon$. As a result we obtain

$$\begin{aligned} \frac{\partial v_{r}}{\partial T} +& v_{r} \frac{\partial v_{r}}{\partial r} + \frac{v_{\phi}}{r} \frac{\partial v_{r}}{\partial \phi} - \frac{v_{\phi}^{2}}{r} = - \frac{1}{\rho _{0}}\frac{\partial P}{\partial r} \\ +& \frac{1}{\mu _{0}\rho _{0}}\bigg(B_{0} \frac{\partial b_{r}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{r}}{\partial \phi} + b_{r} \frac{\partial b_{r}}{\partial r} + \frac{b_{\phi}}{r} \frac{\partial b_{r}}{\partial \phi} - \frac{2\widetilde{B}_{\phi }b_{\phi}}{r} - \frac{b_{\phi}^{2}}{r}\bigg) , \end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial v_{\phi}}{\partial T} +& v_{r} \frac{\partial v_{\phi}}{\partial r} + \frac{v_{\phi}}{r} \frac{\partial v_{\phi}}{\partial \phi} + \frac{v_{r} v_{\phi}}{r} = - \frac{1}{r\rho _{0}}\frac{\partial P}{\partial \phi} + \frac{1}{\mu _{0}\rho _{0}}\bigg(B_{0} \frac{\partial b_{\phi}}{\partial Z} \\ +& \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{\phi}}{\partial \phi} + b_{r} \frac{\partial b_{\phi}}{\partial r} + \frac{b_{\phi}}{r} \frac{\partial b_{\phi}}{\partial \phi} + \frac{2\widetilde{B}_{\phi }b_{r}}{r} + \frac{b_{r} b_{\phi}}{r}\bigg) , \end{aligned}$$

(12)

$$ \frac{\partial b_{r}}{\partial T} = B_{0} \frac{\partial v_{r}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{r}}{\partial \phi} + \frac{1}{r} \frac{\partial}{\partial \phi}(v_{r} b_{\phi }- v_{\phi }b_{r}), $$

(13)

$$ \frac{\partial b_{\phi}}{\partial T} = B_{0} \frac{\partial v_{\phi}}{\partial Z} - \frac{\partial}{\partial r}(v_{r} \widetilde{B}_{\phi }+ v_{r} b_{\phi }- v_{\phi }b_{r}), $$

(14)

$$ \frac{\partial (rv_{r})}{\partial r} + \frac{\partial v_{\phi}}{\partial \phi} = 0, $$

(15)

where

$$ P = \frac{1}{2\mu _{0}}\big(2\widetilde{B}_{\phi }b_{\phi }+ 2B_{0} b_{z} + b_{r}^{2} + b_{\phi}^{2}\big) $$

(16)

is the scaled perturbation of the total pressure. We note that although there is no equation for $P$, the system of Equations 11 – 15 is closed. The boundary conditions take the form

$$ v_{r} = v_{\phi }= 0 \quad \text{at} \quad Z = \pm R/2 , $$

(17)

$$ v_{r} = \frac{\partial \eta}{\partial T} + \frac{v_{\phi}}{r} \frac{\partial \eta}{\partial \phi}, \quad \text{at} \quad r = R + \eta , $$

(18)

$$ P_{\mathrm{i}} - \frac{\widetilde{A}^{2}}{2\mu _{0}}\left (2R\eta + \eta ^{2} \right ) = P_{\mathrm{e}} , \quad \text{at} \quad r = R + \eta , $$

(19)

where the indices “i” and “e” indicate that a quantity is calculated inside and outside the tube, respectively. When deriving Equations 17 and 19, we took into account that $\epsilon L = R$ and used Equations 4 and 9.

An important property of this system of equations is that it does not contain $v_{z}$. What is also worth noting is that the $z$-component of the mass conservation equation reduces to Equation 15, which shows that the motion is incompressible in the leading order approximation with respect to $\epsilon$. It is remarkable that although we use the linearised ideal MHD equations for cold plasmas, Equation 15 describes an incompressible motion. It would be the same even if we use the equations with finite plasma pressure. This is an intrinsic property of kink and fluting modes that the plasma motion is incompressible in the thin tube approximation. The contribution of compressibility in Equation 15 would be of the oder of $\epsilon ^{2}$. This contribution is neglected since we only keep the terms of the leading-order with respect to $\epsilon$.

The system of Equations 11 – 15 with the boundary conditions in Equations 17 – 19 is used in the next section to study the generation of fluting perturbations by a kink mode.

3 Generation of Fluting Perturbations

We use the regular perturbation method and look for the solution to the system of Equations 11 – 15 in the form of expansions with respect to the small dimensionless wave amplitude $a$. We use the power series expansion

$$ f = a f_{1} + a^{2} f_{2} + \cdots , $$

(20)

where $f$ is any of the dependent variables. We will specify $a$ later. We substitute the expansions of all dependent variables in Equations 11 – 15 and the boundary conditions in Equations 13 and 14, and collect the terms of the same order with respect to $a$.

3.1 The First-Order Approximation

In the first-order approximation we recover the results of the linear theory.

3.1.1 Equations and Boundary Conditions

We collect the terms of the order of $a$. As a result we obtain

$$ \frac{\partial v_{r1}}{\partial T} = \frac{1}{\mu _{0}\rho _{0}}\bigg(B_{0} \frac{\partial b_{r1}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{r1}}{\partial \phi} - \frac{2\widetilde{B}_{\phi }b_{\phi 1}}{r}\bigg) - \frac{1}{\rho _{0}} \frac{\partial P_{1}}{\partial r}, $$

(21)

$$ \frac{\partial v_{\phi 1}}{\partial T} = \frac{1}{\mu _{0}\rho _{0}} \bigg( B_{0}\frac{\partial b_{\phi 1}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{\phi 1}}{\partial \phi} + \frac{2\widetilde{B}_{\phi }b_{r1}}{r}\bigg) - \frac{1}{r\rho _{0}} \frac{\partial P_{1}}{\partial \phi}, $$

(22)

$$ \frac{\partial b_{r1}}{\partial T} = B_{0} \frac{\partial v_{r1}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{r1}}{\partial \phi}, $$

(23)

$$ \frac{\partial b_{\phi 1}}{\partial T} = B_{0} \frac{\partial v_{\phi 1}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{\phi 1}}{\partial \phi}, $$

(24)

$$ \frac{\partial (rv_{r1})}{\partial r} + \frac{\partial v_{\phi 1}}{\partial \phi} = 0 . $$

(25)

When deriving Equation 24 we used Equations 2 and 25. In this order approximation, the boundary conditions in Equations 17 – 19 reduce to

$$ v_{r1} = v_{\phi 1} = 0 \quad \text{at} \quad Z = \pm R/2 , $$

(26)

$$ v_{r1} = \frac{\partial \eta _{1}}{\partial T}, \quad P_{\mathrm{i1}} - \frac{\widetilde{A}^{2}}{\mu _{0}}R\eta _{1} = P_{\mathrm{e1}} \quad \text{at} \quad r = R . $$

(27)

Eliminating the magnetic-field perturbation, we transform Equations 21 and 22 into

$$\begin{aligned} \frac{\partial ^{2} v_{r1}}{\partial T^{2}} -& V_{\mathrm{A}}^{2} \frac{\partial ^{2} v_{r1}}{\partial Z^{2}} - \frac{2B_{0}\widetilde{B}_{\phi}}{r\mu _{0}\rho _{0}} \frac{\partial}{\partial Z} \bigg(\frac{\partial v_{r1}}{\partial \phi} - v_{\phi 1}\bigg) \\ -& \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}\rho _{0}}\bigg( \frac{\partial ^{2} v_{r1}}{\partial \phi ^{2}} - 2 \frac{\partial v_{\phi 1}}{\partial \phi}\bigg) = -\frac{1}{\rho _{0}} \frac{\partial ^{2} P_{1}}{\partial r\partial T}, \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial ^{2} v_{\phi 1}}{\partial T^{2}} -& V_{\mathrm{A}}^{2} \frac{\partial ^{2} v_{\phi 1}}{\partial Z^{2}} - \frac{2B_{0}\widetilde{B}_{\phi}}{r\mu _{0}\rho _{0}} \frac{\partial}{\partial Z}\bigg( \frac{\partial v_{\phi 1}}{\partial \phi} + v_{r1}\bigg) \\ -& \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}\rho _{0}} \frac{\partial}{\partial \phi}\bigg( \frac{\partial v_{\phi 1}}{\partial \phi} + 2v_{r1}\bigg) = - \frac{1}{r\rho _{0}} \frac{\partial ^{2} P_{1}}{\partial \phi \partial T}. \end{aligned}$$

(29)

3.1.2 Solutions to Equations of the First-Order Approximation

Now we differentiate Equation 28 with respect to $\phi$, multiply Equation 29 by $r$ and differentiate it with respect to $r$, and then subtract the second equation from the first one and use Equation 25. As a result we obtain

$$ \frac{\partial ^{2} F}{\partial T^{2}} - V_{\mathrm{A}}^{2} \frac{\partial ^{2} F}{\partial Z^{2}} - \frac{2B_{0}\widetilde{B}_{\phi}}{r\mu _{0}\rho _{0}} \frac{\partial ^{2} F}{\partial \phi \partial Z} - \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}\rho _{0}} \frac{\partial ^{2} F}{\partial \phi ^{2}} = 0, $$

(30)

where

$$ F = \frac{\partial v_{r1}}{\partial \phi} - \frac{\partial (rv_{\phi 1})}{\partial r} . $$

(31)

We assume that perturbations start at the initial time $t = 0$. It follows from Equation 26 that $F = 0$ at $Z = \pm R/2$. Taking this into account, we can expand $F$ in the Fourier series

$$ F = \sum _{m=-\infty}^{\infty}\sum _{n=1}^{\infty }e^{im\phi}\left (F_{mn}^{ \mathrm{c}}(T) \cos \frac{(2n-1)\pi Z}{R} + F_{mn}^{\mathrm{s}}(T)\sin \frac{2\pi nZ}{R}\right ), $$

(32)

where $m \neq 0$ in this expression. Substituting Equation 32 in Equation 30, we obtain, in particular, from the third term in this equation that

$$ \frac{m(2k-1)\pi}{R} F_{mn}^{\mathrm{c}}(T)\sin \frac{(2n-1)\pi Z}{R} = 0, \quad \frac{2m\pi n}{R} F_{mn}^{\mathrm{s}}(T)\cos \frac{2\pi nZ}{R} = 0. $$

(33)

This implies that $F_{mn}^{\mathrm{c}}(T) = F_{mn}^{\mathrm{s}}(T) = 0$, and consequently $F = 0$. Now we eliminate $v_{\phi 1}$ from equation $F = 0$ and Equation 25 to obtain

$$ \frac{\partial}{\partial r}r\frac{\partial (rv_{r1})}{\partial r} + \frac{\partial ^{2} v_{r1}}{\partial \phi ^{2}} = 0. $$

(34)

It is worth noting that this is an equation with separable variables. As a result, obtaining the solution to this equation is straightforward. We assume that at the initial time the loop displacement is zero, while the displacement velocity is finite. After that, the loop oscillates harmonically. In accordance with this we take $v_{r1}$ to be proportional to $\cos (\Omega T)$. Then we look for the solution to this equation in the form

$$ v_{r1} = f(r)\tilde{v}_{r1}(Z)\cos (\Omega T)\cos \phi . $$

(35)

Substituting this expression in Equation 34 yields

$$ \frac{d}{dr}r\frac{d(rf)}{\partial r} - f = 0. $$

(36)

Taking into account that $v_{r1}$ must be regular at $r = 0$ and decay as $r \to \infty$, and in accordance with the first boundary condition in Equation 27$v_{r1}$ must be continuous at $r = R$, we obtain

$$ f(r) = \left \{ \textstyle\begin{array}{c@{\quad}c} 1, & r < R, \\ (R/r)^{2}, & r > R.\end{array}\displaystyle \right . $$

(37)

Now, it follows from the first boundary condition in Equations 27 that

$$ \eta _{1} = \tilde{\eta}_{1}(Z)\sin (\Omega T)\cos \phi , \quad \tilde{\eta}_{1}(Z) = \Omega ^{-1}\tilde{v}_{r1}(Z) . $$

(38)

Using Equations 25, 35, and 38 yields

$$ v_{\phi 1} = g(r)\tilde{\eta}_{1}(Z)\Omega \cos (\Omega T)\sin \phi , $$

(39)

where

$$ g(r) = \left \{ \textstyle\begin{array}{c@{\quad}c} -1, & r < R, \\ (R/r)^{2}, & r > R. \end{array}\displaystyle \right . $$

(40)

Now, substituting Equations 35 and 39 in Equation 29, we obtain with the aid of Equation 38

$$ \frac{\partial ^{2} P_{1}}{\partial \phi \partial T} = r\rho _{0} \Omega \cos (\Omega T)\sin \phi \bigg[g(r)\bigg(\Omega ^{2}\tilde{ \eta}_{1} + V_{\mathrm{A}}^{2}\frac{d^{2}\tilde{\eta}_{1}}{dZ^{2}} \bigg) - \frac{\widetilde{B}_{\phi}^{2}\tilde{\eta}_{1}}{r^{2}\mu _{0}\rho _{0}} \bigg)\bigg] . $$

(41)

It follows from this equation that

$$ P_{1} = r\rho _{0}\sin (\Omega T)\cos \phi \bigg[ \frac{\widetilde{B}_{\phi}^{2}\tilde{\eta}_{1}}{r^{2}\mu _{0}\rho _{0}} - g(r)\bigg(\Omega ^{2}\tilde{\eta}_{1} + V_{ \mathrm{A}}^{2}\frac{d^{2}\tilde{\eta}_{1}}{dZ^{2}}\bigg)\bigg]. $$

(42)

Using Equations 38 and 42 we obtain from the second boundary condition in Equation 27

$$ \frac{d^{2}\tilde{\eta}_{1}}{dZ^{2}} + \frac{\Omega ^{2}}{C_{k}^{2}} \tilde{\eta}_{1} = 0, \quad C_{\mathrm{k}}^{2} = \frac{2B_{0}^{2}}{\mu _{0}(\rho _{i} + \rho _{e})}. $$

(43)

$C_{\mathrm{k}}$ is the phase speed of kink waves in the thin tube approximation. It is remarkable that in the thin tube approximation the phase speeds of all fluting modes are also equal to $C_{\mathrm{k}}$. Hence, in a thin tube, the kink mode and all fluting modes are in exact resonance. Solving this equation and using Equation 26 yields

$$ \tilde{\eta}_{1} = R\cos \frac{\pi Z}{R}, \quad \Omega = \frac{\pi C_{\mathrm{k}}}{R} , $$

(44)

where we now define $a$ as the maximum displacement of the tube axis to the tube radius. Using Equations 23, 24, 35, 38, 39, and 42, we obtain the expressions for all variables of the first-order approximation:

$$ \textstyle\begin{array}{c} \eta _{1} = R\sin (\Omega T)\cos \phi \cos (\pi Z/R), \\ v_{r1} = R\Omega f(r)\cos (\Omega T)\cos \phi \cos (\pi Z/R), \\ v_{\phi 1} = R\Omega g(r)\cos (\Omega T)\sin \phi \cos (\pi Z/R), \\ b_{r1} = -f(r)\sin (\Omega T)[\pi B_{0}\cos \phi \sin (\pi Z/R) + (R \widetilde{B}_{\phi}/r)\sin \phi \cos (\pi Z/R)], \\ b_{\phi 1} = -g(r)\sin (\Omega T)[\pi B_{0}\sin \phi \sin (\pi Z/R) - (R \widetilde{B}_{\phi}/r)\cos \phi \cos (\pi Z/R)], \\ \displaystyle P_{1} = rRf(r)\bigg(\Omega ^{2} \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{2} + \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}}\bigg)\sin (\Omega T) \cos \phi \cos (\pi Z/R). \end{array} $$

(45)

We introduce auxiliary Cartesian coordinates $x$ and $y$ related to the cylindrical coordinates by $x = r\cos \phi$ and $y = r\sin \phi$. Then we obtain that the $x$- and $y$-component of the velocity inside the tube are given by

$$ v_{x1} = v_{r1}\cos \phi - v_{\phi 1}\sin \phi = R\Omega f(r)\cos ( \Omega T)\cos (\pi Z/R), $$

(46)

$$ v_{y1} = v_{r1}\sin \phi + v_{\phi 1}\cos \phi = 0. $$

(47)

We see that Equation 45 describes an oscillation linearly polarised in the $x$-direction.

3.2 The Second-Order Approximation

In this section we aim to obtain the expression for the nonlinear correction to the tube boundary displacement $\eta _{2}$.

3.2.1 Equations and Boundary Conditions

We collect terms of the order of $a^{2}$ in Equations 7 – 11 and the boundary conditions Equations 13 and 14. This yields

$$\begin{aligned} \frac{\partial v_{r2}}{\partial T} +& \frac{1}{\rho}_{0} \frac{\partial P_{2}}{\partial r} - \frac{1}{\mu _{0}\rho _{0}}\bigg(B_{0} \frac{\partial b_{r2}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{r2}}{\partial \phi} - \frac{2\widetilde{B}_{\phi }b_{\phi 2}}{r}\bigg) = -v_{r1} \frac{\partial v_{r1}}{\partial r} \\ -& \frac{v_{\phi 1}}{r}\frac{\partial v_{r1}}{\partial \phi} + \frac{v_{\phi 1}^{2}}{r} + \frac{1}{\mu _{0}\rho _{0}}\bigg(b_{r1} \frac{\partial b_{r1}}{\partial r} + \frac{b_{\phi 1}}{r} \frac{\partial b_{r1}}{\partial \phi} - \frac{b_{\phi 1}^{2}}{r}\bigg) , \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial v_{\phi 2}}{\partial T} +& \frac{1}{\rho _{0} r} \frac{\partial P_{2}}{\partial \phi} - \frac{1}{\mu _{0}\rho _{0}} \bigg(B_{0}\frac{\partial b_{\phi 2}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{\phi 2}}{\partial \phi} + \frac{2\widetilde{B}_{\phi }b_{r2}}{r}\bigg) = -v_{r1} \frac{\partial v_{\phi 1}}{\partial r} \\ -& \frac{v_{\phi 1}}{r}\frac{\partial v_{\phi 1}}{\partial \phi} - \frac{v_{r1}v_{\phi 1}}{r} + \frac{1}{\mu _{0}\rho _{0}}\left (b_{r1} \frac{\partial b_{\phi 1}}{\partial r} + \frac{b_{\phi 1}}{r} \frac{\partial b_{\phi 1}}{\partial \phi} + \frac{b_{r1}b_{\phi 1}}{r} \right ) , \end{aligned}$$

(49)

$$ \frac{\partial b_{r2}}{\partial T} - B_{0} \frac{\partial v_{r2}}{\partial Z} - \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{r2}}{\partial \phi} = \frac{1}{r} \frac{\partial}{\partial \phi}(v_{r1} b_{\phi 1} - v_{\phi 1} b_{r1}), $$

(50)

$$ \frac{\partial b_{\phi 2}}{\partial T} - B_{0} \frac{\partial v_{\phi 2}}{\partial Z} - \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{\phi 2}}{\partial \phi} = - \frac{\partial}{\partial r}(v_{r1} b_{\phi 1} - v_{\phi 1} b_{r1}), $$

(51)

$$ \frac{\partial (rv_{r2})}{\partial r} + \frac{\partial v_{\phi 2}}{\partial \phi} = 0, $$

(52)

$$ v_{r2} = v_{\phi 2} = 0 \quad \text{at} \quad Z = \pm R/2 , $$

(53)

$$ v_{r2} - \frac{\partial \eta _{2}}{\partial T} = \frac{v_{\phi 1}}{R} \frac{\partial \eta _{1}}{\partial \phi} - \eta _{1} \frac{\partial v_{r1}}{\partial r} , \quad \text{at} \quad r = R , $$

(54)

$$ P_{\mathrm{i2}} - P_{\mathrm{e2}} - \frac{\widetilde{A}^{2}}{\mu _{0}}R\eta _{2} = \bigg(\frac{\partial P_{\mathrm{e1}}}{\partial r} - \frac{\partial P_{\mathrm{i1}}}{\partial r}\bigg)\eta _{1} + \frac{\widetilde{A}^{2}}{2\mu _{0}}\eta _{1}^{2}, \quad \text{at} \quad r = R . $$

(55)

Using Equations 44 and 45 we reduce Equations 48 – 51, 54, and 55 to

$$\begin{aligned} \frac{\partial v_{r2}}{\partial T} +& \frac{1}{\rho}_{0} \frac{\partial P_{2}}{\partial r} - \frac{1}{\mu _{0}\rho _{0}}\bigg(B_{0} \frac{\partial b_{r2}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r} \frac{\partial b_{r2}}{\partial \phi} - \frac{2\widetilde{B}_{\phi }b_{\phi 2}}{r}\bigg) = \frac{\pi ^{2} R^{2}[f(r) + g(r)]}{r^{3}} \\ \times & \big[C_{k}^{2}\cos ^{2}(\Omega T)\cos ^{2}(\pi Z/R) - V_{ \mathrm{A}}^{2}\sin ^{2}(\Omega T)\sin ^{2}(\pi Z/R)\big], \end{aligned}$$

(56)

$$ \frac{\partial v_{\phi 2}}{\partial T} + \frac{1}{\rho _{0} r} \frac{\partial P_{2}}{\partial \phi} - \frac{1}{\mu _{0}\rho _{0}} \bigg(B_{0}\frac{\partial b_{\phi 2}}{\partial Z} + \frac{\widetilde{B}_{\phi}}{r}\frac{\partial b_{\phi 2}}{\partial \phi} + \frac{2\widetilde{B}_{\phi }b_{r2}}{r}\bigg) = 0, $$

(57)

$$ \frac{\partial b_{r2}}{\partial T} - B_{0} \frac{\partial v_{r2}}{\partial Z} - \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{r2}}{\partial \phi} = 0, $$

(58)

$$ \frac{\partial b_{\phi 2}}{\partial T} - B_{0} \frac{\partial v_{\phi 2}}{\partial Z} - \frac{\widetilde{B}_{\phi}}{r} \frac{\partial v_{\phi 2}}{\partial \phi} = 0, $$

(59)

$$\begin{aligned} v_{r2} - \frac{\partial \eta _{2}}{\partial T} =& \frac{\Omega R}{4}\{f(r) + [f(r) + 2g(r)]\cos (2\phi )\} \\ \times & \sin (2\Omega T)\cos ^{2}(\pi Z/R) \quad \text{at} \quad r = R , \end{aligned}$$

(60)

$$\begin{aligned} P_{\mathrm{i2}} - P_{\mathrm{e2}} - \frac{\widetilde{A}^{2}}{\mu _{0}}R\eta _{2} =& -R^{2}\bigg(\Omega ^{2}(\rho _{\mathrm{i}} - \rho _{\mathrm{e}}) + \frac{\widetilde{A}^{2}}{2\mu _{0}}\bigg) \\ \times & \sin ^{2}(\Omega T)\cos ^{2}\phi \cos ^{2}(\pi Z/R), \quad \text{at} \quad r = R . \end{aligned}$$

(61)

Eliminating $b_{r2}$ and $b_{\phi 2}$ in Equations 56 – 59 yields

$$\begin{aligned} \frac{\partial ^{2} v_{r2}}{\partial T^{2}} +& \frac{1}{\rho _{0}} \frac{\partial ^{2} P_{2}}{\partial r\partial T} - V_{\mathrm{A}}^{2} \frac{\partial ^{2} v_{r2}}{\partial Z^{2}} - \frac{2B_{0}\widetilde{B}_{\phi}}{r\mu _{0}\rho _{0}} \frac{\partial}{\partial Z} \bigg(\frac{\partial v_{r2}}{\partial \phi} - v_{\phi 2}\bigg) \\ -& \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}\rho _{0}} \frac{\partial}{\partial \phi}\bigg( \frac{\partial v_{r2}}{\partial \phi} - 2v_{\phi 2}\bigg) = - \frac{\pi ^{2}\Omega R^{2}[f(r) + g(r)]}{r^{3}} \\ \times & \big[C_{\mathrm{k}}^{2}\cos ^{2}(\pi Z/R) + V_{\mathrm{A}}^{2}\sin ^{2}( \pi Z/R)\big]\sin (2\Omega T) , \end{aligned}$$

(62)

$$\begin{aligned} \frac{\partial ^{2} v_{\phi 2}}{\partial T^{2}} -& V_{\mathrm{A}}^{2} \frac{\partial ^{2} v_{\phi 2}}{\partial Z^{2}} - \frac{2B_{0}\widetilde{B}_{\phi}}{r\mu _{0}\rho _{0}} \frac{\partial}{\partial Z}\bigg( \frac{\partial v_{\phi 2}}{\partial \phi} + v_{r2}\bigg) \\ -& \frac{\widetilde{B}_{\phi}^{2}}{r^{2}\mu _{0}\rho _{0}} \frac{\partial}{\partial \phi}\bigg( \frac{\partial v_{\phi 2}}{\partial \phi} + 2v_{r2}\bigg) + \frac{1}{r\rho _{0}} \frac{\partial ^{2} P_{2}}{\partial \phi \partial T} = 0. \end{aligned}$$

(63)

3.2.2 Derivation of Governing Equation for Amplitudes of Kink and Fluting Modes

We eliminate $P_{2}$ from Equations 62 and 63. To do this, we differentiate Equation 62 with respect to $\phi$, then multiply Equation 63 by $r$ and differentiate the result with respect to $r$, and, finally, subtract the second equation from the first one. As a result, we obtain the same Equation 30, but with $F_{2}$ substituted for $F$, where $F_{2}$ is obtained from the expression for $F$ by substituting $v_{r2}$ and $v_{\phi 2}$ for $v_{r1}$ and $v_{\phi 1}$. Then, in the same way as in the previous subsection we show that $F_{2} = 0$. Using Equation 52 to eliminate $v_{\phi 1}$ from equation $F_{2} = 0$, we obtain

$$ \frac{\partial}{\partial r}r\frac{\partial (rv_{r2})}{\partial r} + \frac{\partial ^{2} v_{r2}}{\partial \phi ^{2}} = 0. $$

(64)

The general solution to this equation satisfying the condition that is regular at $r = 0$ and decay as $r \to \infty$ is

$$ v_{r2} = \left \{ \textstyle\begin{array}{c@{\quad}c} \displaystyle \sum _{m=1}^{\infty }(r/R)^{m-1}\big[a_{m}^{\mathrm{c}}(T,Z) \cos (m\phi ) + a_{m}^{\mathrm{s}}(T,Z)\sin (m\phi )\big], & r < R, \\ \displaystyle \sum _{m=1}^{\infty }(R/r)^{m+1}\big[q_{m}^{\mathrm{c}}(T,Z) \cos (m\phi ) + q_{m}^{\mathrm{s}}(T,Z)\sin (m\phi )\big], & r > R, \end{array}\displaystyle \right . $$

(65)

where $a_{m}^{\mathrm{c},\mathrm{s}}(T,Z)$ and $q_{m}^{\mathrm{c},\mathrm{s}}(T,Z)$ are arbitrary functions. It follows from Equation 60 that

$$ v_{r2}\big|_{r=R+0} - v_{r2}\big|_{r=R-0} = \Omega R\sin (2\Omega T) \cos (2\phi )\cos ^{2}(\pi Z/R), $$

(66)

where the subscripts $r=R-0$ and $r=R+0$ indicate that a quantity is calculated as $r$ tends to $R$ from the left and the right, respectively. It follows from Equations 65 and 66 that

$$ q_{2}^{\mathrm{s}}(T,Z) = a_{2}^{\mathrm{s}}(T,Z), \quad q_{m}^{\mathrm{c},\mathrm{s}}(T,Z) = a_{m}^{ \mathrm{c},\mathrm{s}}(T,Z), \quad m = 1,3,4,\dots , $$

(67)

$$ q_{2}^{\mathrm{c}}(T,Z) - a_{2}^{\mathrm{c}}(T,Z) = \Omega R\sin (2\Omega T) \cos ^{2}(\pi Z/R). $$

(68)

Using Equations 52 and 65, we obtain

$$ v_{\phi 2} = \left \{ \textstyle\begin{array}{c@{\quad}c} \displaystyle \sum _{m=1}^{\infty }(r/R)^{m-1}\big[a_{m}^{\mathrm{s}}(T,Z) \cos (m\phi ) - a_{m}^{\mathrm{c}}(T,Z)\sin (m\phi )\big], & r < R, \\ \displaystyle \sum _{m=1}^{\infty }(R/r)^{m+1}\big[q_{m}^{\mathrm{c}}(T,Z) \sin (m\phi ) - q_{m}^{\mathrm{s}}(T,Z)\cos (m\phi )\big], & r > R. \end{array}\displaystyle \right . $$

(69)

Substituting Equations 65 and 69 in Equation 63 and integrating the obtained equation with respect to $\phi$ yields

$$\begin{aligned} \frac{\partial P_{\mathrm{i2}}}{\partial T} =& \rho _{\mathrm{i}} R\sum _{m=1}^{ \infty }\bigg(\frac{r}{R}\bigg)^{m}\bigg[\bigg(-\frac{1}{m} \frac{\partial ^{2} a_{m}^{\mathrm{c}}}{\partial T^{2}} + \frac{V_{Ai}^{2}}{m}\frac{\partial ^{2} a_{m}^{\mathrm{c}}}{\partial Z^{2}} + \frac{2(m-1)\chi V_{Ai}^{2}}{mR} \frac{\partial a_{m}^{\mathrm{s}}}{\partial Z} \\ -& \frac{(m-2)\chi ^{2} V_{\mathrm{Ai}}^{2} a_{m}^{\mathrm{c}}}{R^{2}}\bigg) \cos (m\phi ) - \bigg(\frac{1}{m} \frac{\partial ^{2} a_{m}^{\mathrm{s}}}{\partial T^{2}} - \frac{V_{\mathrm{Ai}}^{2}}{m} \frac{\partial ^{2} a_{m}^{\mathrm{s}}}{\partial Z^{2}} \\ +& \frac{2(m-1)\chi V_{\mathrm{Ai}}^{2}}{mR} \frac{\partial a_{m}^{\mathrm{c}}}{\partial Z} + \frac{(m-2)\chi ^{2} V_{\mathrm{Ai}}^{2} a_{m}^{\mathrm{s}}}{R^{2}}\bigg)\sin (m \phi )\bigg] + \frac{\partial P_{\mathrm{i0}}}{\partial T}, \end{aligned}$$

(70)

$$\begin{aligned} \frac{\partial P_{\mathrm{e2}}}{\partial T} =& \rho _{\mathrm{e}} R\sum _{m=1}^{ \infty}\frac{1}{m} \bigg(\frac{R}{r}\bigg)^{m}\bigg[\bigg( \frac{\partial ^{2} q_{m}^{\mathrm{c}}}{\partial T^{2}} - V_{\mathrm{Ae}}^{2} \frac{\partial ^{2} q_{m}^{\mathrm{c}}}{\partial Z^{2}}\bigg)\cos (m\phi ) \\ +& \bigg(\frac{\partial ^{2} q_{m}^{\mathrm{s}}}{\partial T^{2}} - V_{ \mathrm{Ae}}^{2}\frac{\partial ^{2} q_{m}^{\mathrm{s}}}{\partial Z^{2}}\bigg) \sin (m\phi )\bigg] + \frac{\partial P_{\mathrm{e0}}}{\partial T}, \end{aligned}$$

(71)

where $P_{\mathrm{i0}}(r,T,Z)$ and $P_{\mathrm{e0}}(r,T,Z)$ are arbitrary functions, and

$$ \chi = \frac{R\widetilde{A}}{B_{0}}. $$

(72)

We note that the number of turns of a magnetic-field line inside the tube over the tube length is $\chi /2\pi$. Substituting Equations 70 and 71 in Equation 62, we can show that, in fact, $\partial P_{\mathrm{i0}}/\partial T$ is independent of $r$, and obtain the expression for $\partial P_{\mathrm{e0}}/\partial T$. However, we do not do this because these results are not used below.

Differentiating Equation 61 with respect to $T$ and using Equation 60, we obtain

$$\begin{aligned} \frac{\partial P_{\mathrm{i2}}}{\partial T} - \frac{\partial P_{\mathrm{e2}}}{\partial T} -& \frac{\chi ^{2}\rho _{0} V_{\mathrm{A}}^{2} v_{r\mathrm{i2}}}{R} = -\Omega \bigg[ \pi ^{2} C_{\mathrm{k}}^{2}(\rho _{\mathrm{i}} - \rho _{\mathrm{e}}) \cos ^{2}\phi + \frac{1}{2}\chi ^{2}\rho _{0} V_{\mathrm{A}}^{2}\bigg] \\ \times & \sin (2\Omega T)\cos ^{2}(\pi Z/R) \quad \text{at} \;\; r = R. \end{aligned}$$

(73)

We recall that $\rho _{\mathrm{i}}V_{\mathrm{Ai}}^{2} = \rho _{\mathrm{e}}V_{\mathrm{Ae}}^{2}$. Using Equations 65, 67, 68, 70, and 71, we obtain from Equation 73

$$ \frac{\partial P_{\mathrm{i0}}}{\partial T} - \frac{\partial P_{\mathrm{e0}}}{\partial T} = -\frac{\Omega}{2}\big[\pi ^{2} C_{ \mathrm{k}}^{2}(\rho _{\mathrm{i}} - \rho _{\mathrm{e}}) + \chi ^{2}\rho _{0} V_{ \mathrm{A}}^{2}\big]\sin (2\Omega T)\cos ^{2}(\pi Z/R), $$

(74)

$$ \frac{\partial ^{2} a_{m}^{\mathrm{c},\mathrm{s}}}{\partial T^{2}} - C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{m}^{\mathrm{c},\mathrm{s}}}{\partial Z^{2}} + \frac{(m-1)\chi C_{\mathrm{k}}^{2}}{R}\bigg(\frac{m\chi a_{m}^{\mathrm{c},\mathrm{s}}}{2R} \mp \frac{\partial a_{m}^{\mathrm{s},\mathrm{c}}}{\partial Z}\bigg) = 0, \;\; m = 1,3,4, \dots $$

(75)

$$\begin{aligned} \frac{\partial ^{2} a_{2}^{\mathrm{c}}}{\partial T^{2}} -& C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{2}^{\mathrm{c}}}{\partial Z^{2}} - \frac{\chi C_{\mathrm{k}}^{2}}{R}\bigg( \frac{\partial a_{2}^{\mathrm{s}}}{\partial Z} - \frac{\chi a_{2}^{\mathrm{c}}}{R}\bigg) \\ =& \frac{\pi ^{2}\Omega C_{\mathrm{k}}^{2}}{2R}\sin (2\Omega T) \bigg( \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \cos \frac{2\pi Z}{R}\bigg), \end{aligned}$$

(76)

$$ \frac{\partial ^{2} a_{2}^{\mathrm{s}}}{\partial T^{2}} - C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{2}^{\mathrm{s}}}{\partial Z^{2}} + \frac{\chi C_{\mathrm{k}}^{2}}{R}\bigg( \frac{\partial a_{2}^{\mathrm{c}}}{\partial Z} + \frac{\chi a_{2}^{\mathrm{s}}}{R}\bigg) = 0, $$

(77)

where the upper and lower signs in Equation 75 correspond to the superscripts “c” and “s”, respectively. Equations 74 – 77 must be supplemented with the boundary conditions

$$ a_{m}^{\mathrm{c},\mathrm{s}} = 0 \quad \text{at} \quad Z = \pm R/2. $$

(78)

3.2.3 Kink and Higher Fluting Modes

In this section we show that we can disregard the nonlinear correction to the kink mode while the higher fluting modes are not driven. First, we take $m = 1$ in Equation 75 to obtain

$$ \frac{\partial ^{2} a_{1}^{\mathrm{c},\mathrm{s}}}{\partial T^{2}} - C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{1}^{\mathrm{c},\mathrm{s}}}{\partial Z^{2}} = 0. $$

(79)

We look for the solution to this equation satisfying the boundary conditions in Equation 78, corresponding to the fundamental mode. As a result we obtain

$$ a_{1}^{\mathrm{c},\mathrm{s}} = \bar{a}_{1}^{\mathrm{c},\mathrm{s}}\sin (\Omega (T+T_{0}))\cos ( \pi Z/R), $$

(80)

where $\bar{a}_{1}^{\mathrm{c},\mathrm{s}}$ and $T_{0}$ are constants. This solution corresponds to the fundamental mode of kink oscillations, linearly polarised in the direction constituting the angle $\phi _{0} = \arctan (\bar{a}_{1}^{\mathrm{s}}/\bar{a}_{1}^{\mathrm{c}})$ with the $x$-axis. Then the superposition of the two linearly polarised oscillations, one with the amplitude proportional to $a$, and the other with the amplitude proportional to $a^{2}$, will be again a linearly polarised oscillation with the amplitude proportional to $a$. We impose the condition that the angle $\phi$ is measured from the direction of the oscillation polarisation and the amplitude of the radial velocity is exactly equal to $aR\Omega$. Then we obtain that $a_{1}^{\mathrm{c}} = a_{1}^{\mathrm{s}} = 0$.

Next, we take $m \geq 3$ in Equation 75. Multiplying this equation with the second superscript by i and adding to this equation with the first superscript yields

$$ \frac{\partial ^{2} a_{m}}{\partial T^{2}} - C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{m}}{\partial Z^{2}} + \frac{(m-1)\chi C_{\mathrm{k}}^{2}}{R}\bigg(\frac{m\chi a_{m}}{2R} + {\mathrm{i}} \frac{\partial a_{m}}{\partial Z}\bigg) = 0, $$

(81)

where $a_{m} = a_{m}^{\mathrm{c}} + {\mathrm{i}}a_{m}^{\mathrm{s}}$. We look for solutions to this equation proportional to $e^{-{\mathrm{i}}\varpi T}$. Then Equation 81 reduces to

$$ C_{\mathrm{k}}^{2}\frac{d^{2} a_{m}}{dZ^{2}} - \frac{{\mathrm{i}}(m-1)\chi C_{\mathrm{k}}^{2}}{R}\frac{da_{m}}{dZ} + \bigg( \varpi ^{2} - \frac{m(m-1)\chi ^{2} C_{\mathrm{k}}^{2}}{2R^{2}}\bigg)a_{m} = 0. $$

(82)

The solution to this equation must satisfy the boundary conditions

$$ a_{m} = 0 \quad \text{at} \quad Z = \pm R/2. $$

(83)

The solution to Equation 82 is

$$ a_{m} = e^{-{\mathrm{i}}\theta _{m} Z}\big(H_{+} e^{{\mathrm{i}}\kappa _{m} Z} + H_{-} e^{-{\mathrm{i}}\kappa _{m} Z}\big), $$

(84)

where $H_{+}$ and $H_{-}$ are constants, and

$$ \theta _{m} = -\frac{(m-1)\chi}{2R}, \quad \kappa _{m} = \sqrt{ \frac{\varpi ^{2}}{C_{\mathrm{k}}^{2}} - \frac{(m^{2} - 1)\chi ^{2}}{4R^{2}}}. $$

(85)

Substituting Equation 84 in the boundary conditions Equation 83 yields

$$ H_{+} e^{{\mathrm{i}}\kappa _{m} R/2} + H_{-} e^{-{\mathrm{i}}\kappa _{m} R/2}, \quad H_{+} e^{-{\mathrm{i}}\kappa _{m} R/2} + H_{-} e^{{\mathrm{i}}\kappa _{m} R/2} = 0. $$

(86)

This system of linear homogeneous algebraic equations with respect to $H_{+}$ and $H_{-}$ has non-trivial solutions only when its determinant is zero. This condition is written as $e^{2{\mathrm{i}}\kappa _{m} R} = 1$, which gives

$$ \varpi ^{2} = \frac{C_{\mathrm{k}}^{2}}{R^{2}}\left [\pi ^{2} n^{2} + \frac{\chi ^{2}(m^{2} - 1)}{4}\right ], $$

(87)

where $n = 1$ corresponds to the fundamental mode with respect to $Z$ and $n > 1$ to overtones. The expression for the frequency of the fundamental fluting modes given by Equation 87 with $n = 1$ was previously obtained by Ruderman (2007).

3.2.4 Driving the Sausage and First Fluting Mode

Finally, we consider the driving of the first fluting mode by the kink perturbation. We will see that simultaneously the sausage mode is also driven. We multiply Equation 77 by i, add the result to Equation 76, and introduce

$$ a_{2} = (a_{2}^{\mathrm{c}} + {\mathrm{i}}a_{2}^{\mathrm{s}})\exp (-{\mathrm{i}}\chi Z/2R) $$

(88)

to obtain

$$\begin{aligned} & \frac{\partial ^{2} a_{2}}{\partial T^{2}} - C_{\mathrm{k}}^{2} \frac{\partial ^{2} a_{2}}{\partial Z^{2}} + \frac{3\chi ^{2} C_{\mathrm{k}}^{2} a_{2}}{4R^{2}} \\ & \hphantom{xx} = \frac{\pi ^{3} C_{\mathrm{k}}^{3}}{2R^{2}}\sin (2\Omega T) \exp \bigg(\! \!-\frac{{\mathrm{i}}\chi Z}{2R}\bigg) \bigg( \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \cos \frac{2\pi Z}{R}\bigg). \hphantom{xxx} \end{aligned}$$

(89)

We assume that at $T = 0$ all variables of the second-order approximation are zero. In particular, this implies that $v_{r2} = 0$ at $T = 0$. It also follows from Equation 56 that $\partial v_{r2}/\partial T = 0$ at $T = 0$ for $r \leq R$ (but not for $r > R$). Then, using Equation 65 we obtain that $a_{2}$ must satisfy the initial conditions

$$ a_{2} = \frac{\partial a_{2}}{\partial T} = 0 \quad \text{at}\;\; T = 0. $$

(90)

We look for the solution to Equation 89 satisfying the boundary conditions in Equation 83 with $m = 2$ and the initial conditions Equation 90, as the sum of a particular solution and the solution to the homogeneous counterpart of Equation 89,

$$ a_{2} = a_{\mathrm{2p}} + a_{\mathrm{2h}} . $$

(91)

We look for a particular solution in the form $\tilde{a}_{\mathrm{2p}}(Z)\sin (2\Omega T)$. Then we obtain

$$\begin{aligned} \frac{{\mathrm{d}}^{2}\tilde{a}_{\mathrm{2p}}}{{\mathrm{d}}Z^{2}} +& \frac{16\pi ^{2} - 3\chi ^{2}}{4R^{2}}\tilde{a}_{\mathrm{2p}} \\ =& -\frac{\pi ^{3} C_{\mathrm{k}}}{2R^{2}}\exp \bigg(\!\!- \frac{{\mathrm{i}}\chi Z}{2R}\bigg) \bigg( \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \cos \frac{2\pi Z}{R}\bigg). \end{aligned}$$

(92)

The general solution to this equation is

$$\begin{aligned} \tilde{a}_{\mathrm{2p}} =& - \frac{\pi ^{3} C_{\mathrm{k}}}{2(4\pi ^{2} - \chi ^{2})} \exp \bigg(\!\!- \frac{{\mathrm{i}}\chi Z}{2R}\bigg)\bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}}\bigg(\cos \frac{2\pi Z}{R} \\ +& \frac{2\pi \/{\mathrm{i}}}{\chi}\sin \frac{2\pi Z}{R}\bigg)\bigg] + A_{1} \cos \frac{2\Lambda Z}{R} + A_{2}\sin \frac{2\Lambda Z}{R}, \end{aligned}$$

(93)

where $A_{1}$ and $A_{2}$ are arbitrary constants and

$$ \Lambda = \frac{1}{4}\sqrt{16\pi ^{2} - 3\chi ^{2}}. $$

(94)

Determining them from the condition that $\tilde{a}_{\mathrm{2p}} = 0$ at $r = \pm R/2$, we eventually arrive at

$$\begin{aligned} a_{\mathrm{2p}} =& - \frac{\pi ^{3} C_{\mathrm{k}}\sin (2\Omega T)}{4\pi ^{2} - \chi ^{2}} \bigg\{ \frac{1}{2} \exp \bigg(\!\!-\frac{{\mathrm{i}}\chi Z}{2R}\bigg)\bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}}\bigg(\cos \frac{2\pi Z}{R} \\ +& \frac{2\pi \/{\mathrm{i}}}{\chi}\sin \frac{2\pi Z}{R}\bigg)\bigg] - \frac{\cos (\chi /4)}{\cos \Lambda}\cos \frac{2\Lambda Z}{R} + \frac{{\mathrm{i}}\sin (\chi /4)}{\sin \Lambda} \sin \frac{2\Lambda Z}{R} \bigg\} . \end{aligned}$$

(95)

It follows from Equation 90, 91, and 95 that $a_{\mathrm{2h}}$ must satisfy the following initial conditions at $T = 0$:

$$ a_{\mathrm{2h}} = 0 , $$

(96)

$$\begin{aligned} \frac{\partial a_{\mathrm{2h}}}{\partial T} =& \frac{2\pi ^{4} C_{\mathrm{k}}^{2}}{R(4\pi ^{2} - \chi ^{2})} \bigg\{ \frac{1}{2}\exp \bigg(\!\!-\frac{{\mathrm{i}}\chi Z}{2R}\bigg)\bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} - \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}}\bigg(\cos \frac{2\pi Z}{R} \\ +& \frac{2\pi \/{\mathrm{i}}}{\chi}\sin \frac{2\pi Z}{R}\bigg)\bigg] - \frac{\cos (\chi /4)}{\cos \Lambda}\cos \frac{2\Lambda Z}{R} + \frac{{\mathrm{i}}\sin (\chi /4)}{\sin \Lambda} \sin \frac{2\Lambda Z}{R} \bigg\} . \end{aligned}$$

(97)

We look for the expression for $a_{\mathrm{2h}}$ in the form

$$ a_{\mathrm{2h}} = C_{\mathrm{k}}\sum _{n=1}^{\infty}\bigg(U_{n}^{\mathrm{c}}(T)\cos \frac{(2n-1)\pi Z}{R} + {\mathrm{i}}U_{n}^{\mathrm{s}}(T)\sin \frac{2\pi nZ}{R} \bigg). $$

(98)

Substituting this expression in the homogeneous counterpart of Equation 89 we obtain the system of equations

$$\begin{aligned} \frac{{\mathrm{d}}^{2} U_{n}^{\mathrm{c}}}{{\mathrm{d}}T^{2}} + (\lambda _{n}^{\mathrm{c}})^{2} U_{n}^{\mathrm{c}} = 0, \end{aligned}$$

(99)

$$\begin{aligned} \frac{{\mathrm{d}}^{2} U_{n}^{\mathrm{s}}}{{\mathrm{d}}T^{2}} + (\lambda _{n}^{\mathrm{s}})^{2} U_{n}^{\mathrm{s}} = 0, \end{aligned}$$

(100)

where

$$ \lambda _{n}^{\mathrm{c}} = \frac{C_{\mathrm{k}}}{2R}\sqrt{4\pi ^{2}(2n - 1)^{2} + 3\chi ^{2}}, \quad \lambda _{n}^{\mathrm{s}} = \frac{C_{\mathrm{k}}}{2R}\sqrt{16 \pi ^{2} n^{2}\ + 3\chi ^{2}}. $$

(101)

Using Equation 96, 97, and 120 – 123 from Appendix A, we obtain that $U_{n}^{\mathrm{c}}$ and $U_{n}^{\mathrm{s}}$ must satisfy the following initial conditions:

$$ U_{n}^{\mathrm{c}} = U_{n}^{\mathrm{s}} = 0, \quad \frac{{\mathrm{d}}U_{n}^{\mathrm{c}}}{{\mathrm{d}}T} = \frac{C_{\mathrm{k}} W_{n}^{\mathrm{c}}}{R}, \;\; \frac{{\mathrm{d}}U_{n}^{\mathrm{s}}}{{\mathrm{d}}T} = \frac{C_{\mathrm{k}} W_{n}^{\mathrm{s}}}{R} \;\; \text{at} \;\; T = 0, $$

(102)

where

$$\begin{aligned} W_{n}^{\mathrm{c}} =& \frac{16\pi ^{5} (-1)^{n+1}}{4\pi ^{2} - \chi ^{2}} \cos \frac{\chi}{4} \bigg[ \frac{(\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}})(2n - 1)}{(\rho _{\mathrm{i}} + \rho _{\mathrm{e}}) [4\pi ^{2}(2n-1)^{2} - \chi ^{2}]} \\ +& \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \bigg(\frac{n + 1}{4\pi ^{2}(2n+1)^{2} - \chi ^{2}} + \frac{n - 2}{4\pi ^{2}(2n-3)^{2} - \chi ^{2}}\bigg) \\ -& \frac{4(2n - 1)}{4\pi ^{2}(2n + 1)(2n - 3) + 3\chi ^{2}}\bigg], \end{aligned}$$

(103)

$$\begin{aligned} \hphantom{x} & \hspace{-8mm} W_{n}^{\mathrm{s}} = \frac{16\pi ^{5} (-1)^{n}}{4\pi ^{2} - \chi ^{2}}\sin \frac{\chi}{4}\bigg[ \frac{2n(\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}})}{(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})[16\pi ^{2} n^{2} - \chi ^{2}]} + \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{2(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} \\ \hphantom{x} & \hspace{-5mm} \times \bigg(\frac{2n + 3}{16\pi ^{2}(n+1)^{2} - \chi ^{2}} + \frac{2n - 3}{16\pi ^{2}(n-1)^{2} - \chi ^{2}}\bigg) - \frac{4n}{16\pi ^{2}(n^{2} - 1) + 3\chi ^{2}}\bigg]. \hphantom{xx} \end{aligned}$$

(104)

The solutions to Equations 99 and 100 satisfying the boundary conditions in Equation 102 are

$$ U_{n}^{\mathrm{c}} = \frac{W_{n}^{\mathrm{c}}}{\lambda _{n}^{\mathrm{c}}}\sin ( \lambda _{n}^{\mathrm{c}}T), \quad U_{n}^{\mathrm{s}} = \frac{W_{n}^{\mathrm{s}}}{\lambda _{n}^{\mathrm{s}}}\sin (\lambda _{n}^{\mathrm{s}}T). $$

(105)

Substituting these expressions in Equation 98, we obtain

$$ a_{\mathrm{2h}} = \frac{C_{\mathrm{k}}^{2}}{R}\sum _{n=1}^{\infty}\bigg( \frac{W_{n}^{\mathrm{c}}}{\lambda _{n}^{\mathrm{c}}}\sin (\lambda _{n}^{\mathrm{c}}T)\cos \frac{(2n-1)\pi Z}{R} + {\mathrm{i}} \frac{W_{n}^{\mathrm{s}}}{\lambda _{n}^{\mathrm{s}}}\sin (\lambda _{n}^{\mathrm{s}}T) \sin \frac{2\pi nZ}{R}\bigg). $$

(106)

The radial displacement of the tube boundary is $\eta$. To calculate $\eta _{2}$ we use Equation 60 with $r \to R - 0$ and Equation 65. Then recalling that only terms with $m = 2$ in Equation 65 are non-zero, we obtain

$$\begin{aligned} \frac{\partial \eta _{2}}{\partial T} =& a_{2}^{\mathrm{c}}(T,Z)\cos (2 \phi ) + a_{2}^{\mathrm{s}}(T,Z)\sin (2\phi ) \\ -& \frac{\Omega R}{4}[1 - \cos (2\phi )]\sin (2\Omega T)\cos ^{2}(\pi Z/R). \end{aligned}$$

(107)

Imposing the initial condition $\eta _{2} = 0$ at $T = 0$ and using Equations 91, 95, 98, 101, and 106, we obtain from this equation

$$ \eta _{2} = \eta _{21} + \eta _{22} + \eta _{23}, $$

(108)

where

$$ \eta _{21} = -\frac{R}{8}[1 - \cos (2\Omega T)]\cos ^{2}(\pi Z/R), $$

(109)

$$ \eta _{22} = \frac{R}{8}[1 - \cos (2\Omega T)][X(Z) \cos (2\phi ) + Y(Z) \sin (2\phi )], $$

(110)

$$\begin{aligned} \eta _{23} =& 4R\sum _{n=1}^{\infty}\bigg\{ \frac{W_{n}^{\mathrm{c}} [1 - \cos (\lambda _{n}^{\mathrm{c}}T)]}{4\pi ^{2}(2n - 1)^{2} + 3\chi ^{2}} \cos \bigg(2\phi - \frac{\chi Z}{2R}\bigg)\cos \frac{(2n-1)\pi Z}{R} \\ +& \frac{W_{n}^{\mathrm{s}}[1 - \cos (\lambda _{n}^{\mathrm{s}}T)]}{16\pi ^{2} n^{2} + 3\chi ^{2}} \sin \bigg(2\phi - \frac{\chi Z}{2R}\bigg)\sin \frac{2\pi nZ}{R}\bigg\} , \end{aligned}$$

(111)

and

$$\begin{aligned} X(Z) =& \cos ^{2}(\pi Z/R) + \frac{4\pi ^{2}}{4\pi ^{2} - \chi ^{2}} \bigg( \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{2(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})}\cos \frac{2\pi Z}{R} - \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{2(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} \\ +& \frac{\cos (\chi /4)}{\cos \Lambda}\cos \frac{\chi Z}{2R}\cos \frac{2\Lambda Z}{R} + \frac{\sin (\chi /4)}{\sin \Lambda}\sin \frac{\chi Z}{2R}\sin \frac{2\Lambda Z}{R}\bigg), \end{aligned}$$

(112)

$$\begin{aligned} Y(Z) =& \frac{4\pi ^{2}}{4\pi ^{2} - \chi ^{2}}\bigg( \frac{\pi (\rho _{\mathrm{i}} - \rho _{\mathrm{e}})}{\chi (\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} \sin \frac{2\pi Z}{R} \\ -& \frac{\sin (\chi /4)}{\sin \Lambda}\cos \frac{\chi Z}{2R}\sin \frac{2\Lambda Z}{R} + \frac{\cos (\chi /4)}{\cos \Lambda}\sin \frac{\chi Z}{2R}\cos \frac{2\Lambda Z}{R} \bigg). \end{aligned}$$

(113)

3.2.5 Properties of Driven Modes

The term $\eta _{21}$ in Equation 109 describes a sausage oscillation of the tube with double the frequency of the kink oscillation $2\Omega$. The term $\eta _{22}$ describes the first fluting mode, again oscillating with double the frequency of the kink oscillation $2\Omega$. Both oscillation modes are forced oscillations caused by nonlinear interaction with the kink oscillation. Finally, the term $\eta _{23}$ describes the sum of all modes that correspond to the first fluting mode and with the eigenfrequencies corresponding to various harmonics in the axial direction. The presence of this term is related to the initial conditions.

If we introduce any mechanism causing wave damping, then these modes would describe the transition from the initial state with only the kink mode to the state where there are forced oscillations with the frequency $2\Omega$. One possibility to have such a damping mechanism is to consider a more general model of a magnetic tube with the transitional layer between the dense core and the rarified surrounding plasma. Then wave damping would be caused by resonant absorption in this transitional layer. Of course if the kink mode is excited by an initial perturbation, it would also damp as well as the forced oscillations with the frequency $2\Omega$. The higher eigenoscillations described by terms in Equation 111 with sufficiently large $n$ would damp much faster than the kink oscillations. However, the damping time of the eigenoscillations described by terms in Equation 111 with small values of $n$ would be of the same order as the damping time of the kink oscillation. Hence, in this scenario, we would not arrive at the state with only the kink mode and forced oscillations with the frequency $2\Omega$.

However, we can consider another scenario. Tian et al. (2012) and Wang et al. (2012) reported observations of low-amplitude coronal loop kink oscillations that do not decay. Similar observations were later reported by Nisticò, Nakariakov, and Verwichte (2013), Nisticò, Anfinogentov, and Nakariakov (2014), Anfinogentov, Nakariakov, and Nisticò (2015), and Duckenfield et al. (2018) (see also the review by Nakariakov et al., 2021). If we now assume that a decayless kink oscillation started at $T = 0$ then after a transitional time, the modes with the eigenfrequencies $\lambda _{n}^{\mathrm{c}}$ and $\lambda _{n}^{\mathrm{s}}$ will decay, and the tube oscillations will be the superposition of this decayless kink oscillation with the frequency $\Omega$ and two forced oscillations with the frequency $2\Omega$, which will be the sausage mode described by $\eta _{21}$ in Equation 108, and the first fluting mode described by $\eta _{22}$.

It is instructive to consider the limit $\chi \to 0$ corresponding to an untwisted tube. We can see from Equation 109 that $\eta _{21}$ is independent of $\chi$. This implies that the forced sausage oscillations with the frequency $2\Omega$ are not affected by the twist. It follows from Equations 125 and 129 that both $\eta _{22}$ and $\eta _{23}$ have singularities at $\chi = 0$. However, $\eta _{22} + \eta _{23}$ is a regular function of $\chi$. Using Equation 125 and 129 in Appendix B, we obtain that

$$\begin{aligned} & \lim _{\chi \to 0}(\eta _{22} + \eta _{23}) = \frac{R}{8}\cos (2\phi )[1 - \cos (2\Omega T)] \bigg(\frac{4\pi Z}{3R}\sin \frac{2\pi Z}{R} \\ & \hphantom{xx} - \frac{2\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}}\cos ^{2}(\pi Z/R) \bigg) - \pi R\sum _{n=1}^{\infty }(-1)^{n} \frac{1 - \cos [(2n-1)\Omega T]}{(2n - 1)^{2}} \\ & \hphantom{xx} \times \bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{(2n-1) (\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} + \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}}\bigg(\frac{n + 1}{(2n+1)^{2}} + \frac{n - 2}{(2n-3)^{2}}\bigg) \\ & \hphantom{xx} -\, \frac{4(2n - 1)}{(2n + 1)(2n - 3)}\bigg]\cos \frac{(2n-1)\pi Z}{R} . \end{aligned}$$

(114)

Below we consider

$$ \tilde{\eta}_{22} = \eta _{22} + \frac{4RW_{1}^{\mathrm{s}}[1 - \cos (\lambda _{1}^{\mathrm{s}}T)]}{16\pi ^{2} + 3\chi ^{2}} \sin \bigg(2\phi - \frac{\chi Z}{2R}\bigg) \sin \frac{2\pi Z}{R} . $$

(115)

This quantity is also a regular function of $\chi$. When $\chi = 0$, it contains all terms describing the oscillation with the frequency $2\Omega$. We have

$$ \lim _{\chi \to 0}\tilde{\eta}_{22} = \frac{R}{4}\cos (2\phi )[1 - \cos (2 \Omega T)]G(Z), $$

(116)

where

$$ G(Z) = \frac{2\pi Z}{3R}\sin \frac{2\pi Z}{R} - \frac{1}{\zeta + 1}\cos ^{2}( \pi Z/R), $$

(117)

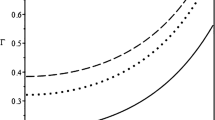
and $\zeta = \rho _{\mathrm{i}}/\rho _{\mathrm{e}}$. The graph of function $G(Z)$ is shown in Figure 1 for a few values of $\zeta$. Since $G(Z)$ is an even function, we only show the dependence of $G(Z)$ for $Z \in [0,R/2]$.

Figure 1

Dependence of $G$ on $Z$. The solid, dashed, and dash-dotted lines correspond to $\zeta = 3$, 5, and 10, respectively.

When $\chi \neq 0$ the flute oscillation with the frequency $2\Omega$ is described by $\eta _{22}$. Hence, below we investigate the properties of this quantity. We introduce the amplitude of flute oscillation $[Am(Z)]$ and its phase $[\Phi (Z)]$ defined by

$$ Am(Z) = \sqrt{X^{2}(Z) + Y^{2}(Z)}, \quad \Phi (Z) = \frac{1}{2}{\mathrm{arccot}} \frac{X(Z)}{Y(Z)}. $$

(118)

Then we can transform Equation 110 into

$$ \eta _{22} = \frac{R}{8}[1 - \cos (2\Omega T)]Am(Z)\cos [2(\phi - \Phi (Z))] $$

(119)

The graphs of $Am(Z)$ and $\Phi (z)$ are shown in Figures 2 and 3 for $\zeta = 3$ and various values of $\chi$. Since $X(Z)$ is an even function and $Y(Z)$ is an odd function, it follows that $Am(Z)$ is an even function. Hence, we only plot its graph for $Z \in [0, R/2]$. As for the phase, we can use the definition of $\Phi (Z)$ given by Equation 118 only for $Z \in [0,R/2]$, while for $Z \in [-R/2,0]$ we take $\Phi (Z) = -\Phi (-Z)$. Then $\Phi (Z)$ is an odd function and we only show the dependence of $\Phi$ on $Z$ for $Z \in [0, R/2]$. We see in Figure 2 that $Am(Z)$ takes maximum at approximately the middle of the interval $[0,R/2]$. The maximum value of $Am(Z)$ at $\chi = \pi /6$ is much higher than at larger values of $\chi$. This result is in agreement with the fact that $\eta _{22}$ is singular at $\chi = 0$.

Figure 2

Dependence of the amplitude $Am(Z)$ on $Z$. The solid, dashed, dotted, and dash-dotted lines correspond to $\chi = \pi /6$, $\pi /2$, $\pi$, and $3\pi /2$, respectively.

Figure 3

Dependence of phase $\Phi (Z)$ on $Z$. The solid, dashed, dotted, and dash-dotted lines correspond to $\chi = \pi /6$, $\pi /2$, $\pi$, and $3\pi /2$, respectively.

The tube boundary perturbed by the first fluting mode has an elliptic shape. In accordance with Figure 3, when we move from the middle of the tube corresponding to $Z = 0$ in the positive $Z$-direction the large and small axes of the ellipse rotate in the counter-clockwise direction. Since $\Phi (Z)$ is an odd function, these axes rotate in the clockwise direction when we move from the middle of the tube in the negative $Z$-direction.

4 Summary and Conclusions

In this article, we studied the excitation of the first fluting mode on a twisted magnetic tube by an imposed kink oscillation. We used the ideal MHD equations in the approximation of cold plasma, i.e. we neglected the plasma pressure in comparison with the magnetic pressure. We also used the thin tube approximation.

Next, we used the regular perturbation method with the dimensionless amplitude of the kink oscillation as a small parameter. The first-order approximation describes the kink oscillation. Ruderman (2017) investigated the excitation of the first fluting mode by a kink oscillation in a non-twisted tube. He imposed the condition that the solution is periodic in time. However, from the physical point of view, it is more convenient to consider the initial value problem. In accordance with this, we assumed that the kink oscillation starts at the initial time and then studied the evolution of the system. We found that the solution in the second-order approximation is proportional to the dimensionless amplitude of the kink mode squared. In this order approximation the perturbation of the tube boundary is described by the sum of three terms $[\eta _{21} + \eta _{22} + \eta _{23}]$. The first term $[\eta _{21}]$ describes a forced sausage oscillation with double the frequency of the kink oscillation $2\Omega$. We see that the kink oscillations can nonlinearly excite a sausage mode. Previously the same result was obtained by Ruderman (2017).

The second term $[\eta _{22}]$ describes the forced fluting oscillation again with the frequency $[2\Omega ]$. The third term $[\eta _{23}]$ describes the superposition of oscillations corresponding to the first fluting mode with the eigenfrequencies. In our analysis, we did not take into account any physical processes that can cause the damping of oscillation. The term $[\eta _{23}]$ is related to satisfying the initial conditions. If we add any damping mechanism, for example resonant damping related to a transitional layer at the tube boundary, then $[\eta _{23}]$ would decay. Of course, if the kink oscillation is launched at the initial time by a finite input of energy, it would also decay, and then $[\eta _{21}]$ and $[\eta _{22}]$ would also decay. However, if the kink oscillation is a decayless oscillation (e.g. Nisticò, Nakariakov, and Verwichte, 2013; Anfinogentov, Nakariakov, and Nisticò, 2015; Nakariakov et al., 2021) then, for large times, the oscillation of the tube boundary in the second-order approximation would be periodic with the period $2\Omega$. It would be described by the sum of the first and second terms in Equation 109.

An important property of $\eta _{22}$ is that it is singular at $\chi = 0$. This property is related to the fact that the first term in the expression for $\eta _{23}$ describes an oscillation with the frequency $2\Omega$, when $\chi = 0$. As a result, the oscillation described by this term does not damp even when wave damping is present and the kink oscillation is decayless. Hence, in an untwisted tube, the forced fluting oscillation with the frequency $2\Omega$ is described the sum of $\eta _{22}$ and the first term in the expression for $\eta _{23}$. They both have a singularity at $\chi = 0$, however their sum $[\tilde{\eta}_{22}]$ is regular.

Appendices

Appendix A: Useful Identities

In this section we present the identities obtained by expansions in the Fourier series. These identities are used in Section 3.2.4. They read

$$\begin{aligned} \exp \bigg(\!\!-\frac{{\mathrm{i}}\chi Z}{2R}\bigg) =& 16\pi \sum _{n=1}^{ \infty }(-1)^{n}\bigg( \frac{2n{\mathrm{i}}\sin (\chi /4)}{16\pi ^{2} n^{2} - \chi ^{2}} \sin \frac{2\pi nZ}{R} \\ -& \frac{(2n - 1)\cos (\chi /4)}{4\pi ^{2}(2n-1)^{2} - \chi ^{2}} \cos \frac{(2n-1)\pi Z}{R}\bigg) , \end{aligned}$$

(120)

$$\begin{aligned} & \exp \bigg(\!\!-\frac{{\mathrm{i}} \chi Z}{2R}\bigg)\cos \frac{2\pi Z}{R} = 8\pi \sum _{n=1}^{\infty }(-1)^{n}\bigg[\bigg( \frac{2n + 1}{4\pi ^{2}(2n + 1)^{2} - \chi ^{2}} \\ & \hphantom{xx} +\,\frac{2n - 3}{4\pi ^{2}(2n - 3)^{2} - \chi ^{2}}\bigg)\cos \frac{\chi}{4} \cos \frac{(2n-1)\pi Z}{R} \\ & \hphantom{xx} -\,2{\mathrm{i}}\bigg(\frac{n + 1}{16\pi ^{2}(n + 1)^{2} - \chi ^{2}} + \frac{n - 1}{16\pi ^{2}(n - 1)^{2} - \chi ^{2}}\bigg)\sin \frac{\chi}{4} \sin \frac{2\pi nZ}{R}\bigg], \hphantom{xxx} \end{aligned}$$

(121)

$$\begin{aligned} & \exp \bigg(\!\!-\frac{{\mathrm{i}} \chi Z}{2R}\bigg)\sin \frac{2\pi Z}{R} = 4\chi \sum _{n=1}^{\infty }(-1)^{n+1}\bigg[\bigg( \frac{{\mathrm{i}}}{4\pi ^{2}(2n + 1)^{2} - \chi ^{2}} \\ & \hphantom{xx} -\,\frac{{\mathrm{i}}}{4\pi ^{2}(2n - 3)^{2} - \chi ^{2}}\bigg)\cos \frac{\chi}{4} \cos \frac{(2n-1)\pi Z}{R} \\ & \hphantom{xx} +\,\bigg(\frac{1}{16\pi ^{2}(n + 1)^{2} - \chi ^{2}} - \frac{1}{16\pi ^{2}(n - 1)^{2} - \chi ^{2}}\bigg)\sin \frac{\chi}{4}\sin \frac{2\pi nZ}{R}\bigg], \hphantom{xxx} \end{aligned}$$

(122)

$$\begin{aligned} & \frac{\cos (\chi /4)}{\cos \Lambda}\cos \frac{2\Lambda Z}{R} - \frac{{\mathrm{i}}\sin (\chi /4)}{\sin \Lambda}\sin \frac{2\Lambda Z}{R} \\ & \hphantom{xx} = 16\pi \sum _{n=1}^{\infty }(-1)^{n} \bigg[ \frac{{\mathrm{i}}\/n\sin (\chi /4)}{16\pi ^{2}(n^{2} - 1) + 3\chi ^{2}} \sin \frac{2n\pi Z}{R} \\ & \hphantom{xx} -\, \frac{2(2n - 1)\cos (\chi /4)}{4\pi ^{2}(2n + 1)(2n - 3) + 3\chi ^{2}}\cos \frac{(2n-1)\pi Z}{R} \bigg] . \end{aligned}$$

(123)

Appendix B: Limit of Untwisted Tube ($\chi \to 0$)

In this section we consider the limit of the untwisted tube that corresponds to $\chi \to 0$. We can see that $[\eta _{21}]$ is independent of $[\chi ]$. Hence, the forced sausage oscillation of the tube is not affected by twist. Using the expansion

$$ \Lambda = \pi - \frac{3\chi ^{2}}{32\pi} + \mathcal{O}(\chi ^{4}), $$

(124)

valid for $|\chi | \ll 1$, we obtain from Equation 110

$$\begin{aligned} \eta _{22} =& \frac{R}{8}[1 - \cos (2\Omega T)]\bigg[\cos (2\phi ) \bigg(\frac{4\pi Z}{3R}\sin \frac{2\pi Z}{R} - \frac{2\rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \cos ^{2}(\pi Z/R) \bigg) \\ -& \frac{\pi (5\rho _{\mathrm{i}} + 11\rho _{\mathrm{e}})}{3\chi (\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} \sin (2\phi )\sin \frac{2\pi Z}{R}\bigg] + \mathcal{O}(\chi ). \end{aligned}$$

(125)

We also use the expressions

$$ \lambda _{n}^{\mathrm{c}} = \Omega (2n - 1) + \mathcal{O}(\chi ^{2}), \quad \lambda _{n}^{\mathrm{s}} = 2\Omega n + \mathcal{O}(\chi ^{2}), \quad n = 1,2,\dots , $$

(126)

$$\begin{aligned} W_{n}^{\mathrm{c}} =& \pi (-1)^{n+1}\bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{(2n-1)(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} + \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \bigg(\frac{n + 1}{(2n+1)^{2}} + \frac{n - 2}{(2n-3)^{2}}\bigg) \\ -& \frac{4(2n - 1)}{(2n + 1)(2n - 3)}\bigg] + \mathcal{O}(\chi ^{2}), \quad n = 1,2,\dots , \end{aligned}$$

(127)

$$ W_{1}^{\mathrm{s}} = \frac{\pi ^{3}(5\rho _{\mathrm{i}} + 11\rho _{\mathrm{e}})}{6\chi (\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} + \mathcal{O}(\chi ), \quad W_{n}^{ \mathrm{s}} = \mathcal{O}(\chi ), \quad n = 2,3,\dots $$

(128)

Using Equations 126 – 128, we obtain from Equation 111 that

$$\begin{aligned} \eta _{23} =& \frac{\pi R[1 - \cos (2\Omega T)](5\rho _{\mathrm{i}} + 11\rho _{\mathrm{e}})}{24\chi (\rho _{\mathrm{i}} + \rho _{\mathrm{e}})}\sin (2\phi )\sin \frac{2\pi Z}{R} \\ -& \pi R\cos (2\phi )\sum _{n=1}^{\infty }(-1)^{n} \frac{1 - \cos [(2n-1)\Omega T]}{(2n - 1)^{2}} \\ \times & \bigg[ \frac{\rho _{\mathrm{i}} + 3\rho _{\mathrm{e}}}{(2n-1)(\rho _{\mathrm{i}} + \rho _{\mathrm{e}})} + \frac{\rho _{\mathrm{i}} - \rho _{\mathrm{e}}}{\rho _{\mathrm{i}} + \rho _{\mathrm{e}}} \bigg(\frac{n + 1}{(2n+1)^{2}} + \frac{n - 2}{(2n-3)^{2}}\bigg) \\ -& \frac{4(2n - 1)}{(2n + 1)(2n - 3)}\bigg]\cos \frac{(2n-1)\pi Z}{R} + \mathcal{O}(\chi ). \end{aligned}$$

(129)