1 Introduction

The sunspot-group number [\(R_{\mathrm{G}}\)] was introduced by Hoyt, Schatten, and Nesme-Ribes (1994) and Hoyt and Schatten (1998). For after about 1900 it matches quite well the behaviour of sunspot numbers, such as Version 1 of the Wolf/Zürich/International sunspot number composite [\(R_{\text{ISNv1}}\): Clette et al. 2007], but is well known to be significantly lower for earlier years (e.g. Lockwood, Owens, and Barnard, 2014a; 2014b). This topical issue includes two articles detailing two new sunspot-group-number series that are intended to be homogeneous and of stable calibration. Svalgaard and Schatten (2016) have proposed the “backbone” sunspot-group series [\(R_{\text{BB}}\)], and Usoskin et al. (2016) proposed a group-number series that is here termed \(R_{\text{UEA}}\). Compared to the (suitably scaled) original \(R_{\mathrm{G}}\), both of these new group-number data series give higher values before 1900, but in the case of \(R_{\text{BB}}\), they are radically higher. The main differences between \(R_{\text{BB}}\) and \(R_{\text{UEA}}\) arise from the method used to calibrate the historic data. The backbone series passes the calibration from one dataset to an adjacent one using a relationship between the two (usually a regression fit for the period of overlap between the two). This is called “daisy-chaining”, and the problem with this method is that both systematic and random errors, compared to modern values, compound as one goes back in time. Furthermore, as discussed in Article 3 of this series (Lockwood et al. 2016c), there are problems and pitfalls with regression techniques in general, and there are particular concerns about the way that they were implemented by Svalgaard and Schatten (2016) in the generation of \(R_{\text{BB}}\) (specifically, the assumption that data from different observers are proportional to each other is not generally correct in either principle or practice). Usoskin et al. (2016) avoided all of these pitfalls, and the potential for error propagation inherent in daisy-chaining, by devising a method that calibrates all data against one standard dataset. Note that, in general, observed group-numbers from different observers vary non-linearly (Usoskin et al. 2016; Lockwood et al. 2016c).

In addition to these new group-number series, a new version of the Wolf/Zürich/International sunspot-number composite (ISN Version 2, \(R_{\text{ISNv2}}\)) has recently been issued by the Solar Influences Data Analysis Center (SIDC, the Solar Physics research department of the Royal Observatory of Belgium). Like \(R_{\text{BB}}\), this uses daisy-chaining of calibrations and, also like \(R_{\text{BB}}\), gives higher values for the eighteenth and nineteenth centuries (Clette et al. 2015). A less “root-and-branch” approach to correcting \(R_{\text{ISNv1}}\) was taken by Lockwood, Owens, and Barnard (2014a), who made simple corrections for errors to generate a “corrected” series [\(R_{\mathrm{C}}\)]. It should be noted that because \(R_{\mathrm{C}}\) makes corrections at only two dates in the series, other errors in \(R_{\text{ISNv1}}\), such as the recently revealed error in modern data that is due to the drift in the Locarno standard (Clette et al. 2015), are carried forward and not corrected.

This article concentrates on differences between these sunspot-number and sunspot-group-number data series in the twentieth century, specifically around 1946. Larger differences, inferred from geomagnetic-activity data, low-latitude auroral sightings, and cosmogenic isotope abundances in ice sheets, tree trunks, and meteorites, are found for earlier years, which are discussed in Article 2 (Lockwood et al. 2016b) and in the article by Asvestari et al. (2016). Changes around 1946 are of interest as there has been discussion about a putative inhomogeneity in the calibration of the original Zürich sunspot-number data series [\(R_{\text{ISNv1}}\)] that has been termed the “Waldmeier discontinuity”, as discussed in Article 1 (Lockwood et al. 2016a). This is thought to have been caused by the introduction of a weighting scheme for sunspot counts according to their size, a change in the procedure used to define a group, and, in particular, the “evolutionary” aspect of the new sunspot-group classification scheme (called the Zürich scheme) introduced by Waldmeier (Waldmeier 1947; Kiepenheuer 1953). This raises two important questions: i) What is this the correct quantification of this effect? ii) Which datasets employed the Zürich classification scheme and so would be subject to any such effect or may have been re-calibrated using the Zürich data? It is now agreed that \(R_{\text{ISNv1}}\) needs correcting for this effect, but it is unclear if, why, and how it influences other data series. Tests comparing against ionospheric data (Lockwood et al. 2016a), auroral sightings, and geomagnetic data (Lockwood et al. 2016b) all suggest that, somehow, an excessive or inappropriate allowance for the Waldmeier discontinuity has been introduced into \(R_{\text{BB}}\).

In the past, corrections to sunspot numbers have often been applied by taking ratios, which implicitly assumes that proportionality between the different data applies. This is often not the case (Lockwood et al. 2016c). A particular problem occurs when sunspot numbers are small because the errors in such ratios become highly asymmetric, and both the ratio and its error tend to infinity if the denominator approaches zero. Two ways of avoiding this (in its most extreme form) have been employed. The first is to consider ratios only when the denominator exceeds an arbitrarily chosen threshold (e.g. Svalgaard 2011), but this preferentially removes sunspot-minimum values, which do not always go to zero. The second way is to employ averages over one or more solar cycles so that the denominator remains large (outside grand minima): this matches long-term average values, but loses information about cycle amplitudes (because values at sunspot minimum do not always fall to zero). Consequently, Lockwood, Owens, and Barnard (2014a) devised two different procedures to test for discontinuities. The first fits the same polynomial form of a proxy or test dataset to two intervals, one before the putative error, one after it, and studies the probability of the difference in the mean fit residual for the “before” and “after” intervals. The second method looks at the effect of a full range of assumed discontinuities on the correlation between the data and the test data. Generally the methods provide similar answers, but uncertainties are lower for the fit-residual procedure, so that it is the more stringent test. We here make a number of improvements to the implementation of the Lockwood, Owens, and Barnard (2014a) methods.

In the original analysis of the Waldmeier discontinuity by Svalgaard (2011), it was assumed that the correction required was a single multiplicative (“inflation”) scaling factor [\(f_{\mathrm{R}}\)], such that before the discontinuity the data were adjusted by multiplying by \(f_{\mathrm{R}}\) (i.e. the corrected sunspot number is \(R' = f_{\mathrm{R}} R\)). This assumption was also used by Lockwood, Owens, and Barnard (2014a) and Lockwood et al. (2016a). In general, it is not clear what the functional form of the correction for the Waldmeier discontinuity should be and it will be different for different sunspot-number and group-number series, depending on how they were compiled. Svalgaard, Cagnotti, and Cortesi (2016) and Clette and Lefèvre (2016) have analysed the effect on Zürich sunspot numbers by applying both the pre-1946 and post-1946 procedures to modern data. The effects depend on timescale and, in general, are non-linear in \(R\). The effect on annual averages is not as clear as for daily or monthly means.

We here generalise the correction by allowing for a zero-level offset [\(\delta \)] and a nonlinear dependence (with an exponent [\(n\)] of \(R\)) as well as the scaling factor [\(f_{\mathrm{R}}\)]. The exponent \(n\) would be unity for a linear correction (i.e. the correction required is the same at all \(R\)): note that \(n\) could be either greater or smaller than unity. For a proportional correction \(n = 1\) and \(\delta = 0\). We apply the correction to the data before the putative discontinuity. Hence, the corrected \(R\) \([R ']\) for a discontinuity at a date [\(t = t_{\mathrm{d}}\)] is defined by

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} R ' = R& \mbox{for}\ t \geq t_{\mathrm{d}} \\ R ' = f_{\mathrm{R}} R^{\mathrm{n}} + \delta & \mbox{for}\ t < t_{\mathrm{d}}. \end{array}\displaystyle \end{aligned}$$
(1)

Lockwood, Owens, and Barnard (2014a) used all of the sunspot-group-number dataset from the Royal Observatory Greenwich/Royal Greenwich Observatory (hereafter “RGO”), which covers the years 1875 to 1976. The stability of the calibration of the earliest of these data (before 1885) has been questioned (Cliver and Ling 2016) and this may have influenced the derived correction (Clette and Lefèvre 2016). In the present article, as in Lockwood et al. (2016a), we avoid using any RGO data from before 1900.

In addition, Clette and Lefèvre (2016) make the valuable point that there are other factors that may have influenced the correction factor derived by Lockwood, Owens, and Barnard (2014a). The first is that other errors in the data series may be influencing the optimum correction for the Waldmeier discontinuity. The second is that the precise date of the discontinuity [\(t_{\mathrm{d}}\)] has an effect and is not known because Waldmeier’s documentation is not clear on when the changes were actually implemented. Clette and Lefèvre (2016) made use of the ratio of \(R/R_{\mathrm{G}}\) to define \(t_{\mathrm{d}}\), something that had been avoided by Lockwood, Owens, and Barnard (2014a) because the error in such ratios tends to infinity when \(R_{\mathrm{G}}\) tends to zero and \(R_{\mathrm{G}}\) has a minimum in 1944, just before the putative discontinuity: hence changes would naturally become more apparent as sunspots began to rise in the subsequent cycle. From the \(R/R_{ \mathrm{G}}\) ratio, Clette and Lefèvre (2016) placed the discontinuity in 1946 (whereas Lockwood, Owens, and Barnard 2014a and Lockwood et al. 2016a used 1945), although they noted that there is some documentary evidence that at least some of the new procedures that are thought to be the cause of the discontinuity were in use earlier than this date. Clette and Lefèvre (2016) analysed the effects of both the start date of the comparison and the assumed discontinuity date [\(t_{\mathrm{d}}\)] on the \(R_{\text{ISNv1}}\) correction. They reproduced the Lockwood, Owens, and Barnard (2014a) values when using the same dates; however, they found that the required correction could be larger if other dates were adopted. The analysis presented in this article makes improvements to the procedure of Lockwood, Owens, and Barnard (2014a) to remove these potential uncertainties.

2 Analysis

The analysis presented here employs five test data series and is applied to five tested sunspot reconstructions.

2.1 Tested Sunspot Data Series

We here test how five different sunspot-number or sunspot-group-number data series behave around 1946: these are summarised in Table 1 and compared in Figure 1.

Figure 1
figure 1

Comparison of the tested sunspot data series: (black) \(R_{\text{ISNv1}}\), (red) \(R_{\text{ISNv2}}\), (blue) \(R_{\text{BB}}\), (pink) \(R_{\text{UEA}}\), and (olive) \(R_{\mathrm{C}}\). To enable easy comparison, all have been scaled by linear regression to the RGO sunspot-group number [\(N_{\mathrm{G}}\)] over the interval 1921 – 1945. The top panel shows the regressed time series, and the bottom panel shows the differences between each regressed variation and the average of the five scaled tested series. The vertical dot–dashed line is the most likely time of the Waldmeier discontinuity (1946), and the vertical-dashed lines delineate the optimum “before” and “after” intervals found by the analysis.

Full size image
Table 1 Sunspot data series tested
Full size table

2.1.1 The Original Composite of the Wolf/Zürich/International Sunspot Number [\(R_{\text{ISNv1}}\)]

\(R_{\text{ISNv1}}\) is still available in the archive section of the SIDC website, but has not been updated since 01 July 2015. This is a composite of sunspot numbers, initially generated by Wolf and continued at the Zürich observatory until 1980 and then subsequently compiled by SIDC (until July 2015, when it was replaced by Version 2). This is the dataset that moved to the Zürich classification scheme and so will show all aspects of the Waldmeier discontinuity. As for all the tested data series, with the exception of that by Usoskin et al. (2016), the calibration is by daisy-chaining, i.e. the calibration is passed from one observer to the next (or previous) one by comparison of simultaneous data from both observers.

2.1.2 The New SIDC Composite of the Wolf/Zürich/International Sunspot Number [\(R_{\text{ISNv2}}\)]

\(R_{\text{ISNv2}}\) became SIDC’s default series on 01 July 2015. It corrects for a number of causes of long-term change in \(R_{\text{ISNv1}}\), including the Waldmeier discontinuity and the correction of a drift in the calibration of the main station (Locarno), which had varied by \({\pm}\,15~\%\) between 1987 and 2009 (Clette et al. 2015). Note that this no longer uses the traditional scaling factor of 0.6 employed in \(R_{\text{ISNv1}}\).

2.1.3 The New “Backbone” Group-Sunspot Number [\(R_{\mathrm{BB}}\)]

\(R_{\text{BB}}\) was proposed by Svalgaard and Schatten (2016). This group-number composite differs in its long-term variation from the Hoyt and Schatten (1998) group-number [\(R_{\mathrm{G}}\)] and dispenses with the scaling factor of 12.08 introduced by Hoyt, Schatten, and Nesme-Ribes (1994) and Hoyt and Schatten (1998) (to make means of \(R_{\mathrm{G}}\) and \(R_{\text{ISNv1}}\) the same in modern data). \(R_{\text{BB}}\) is the mean of the results of two different methods: taking such a mean has the problem that, although errors can be halved, any error in either method is propagated into the final result, something that can be avoided if a probabilistic combination technique is applied. The main method employed in the construction of \(R_{\text{BB}}\) involves daisy-chaining of compiled “backbone” data sequences using linear regression. The exception to this is the earliest join for which a different method is used: this is not within the interval studied here, however, and so this inhomogeneity in the series compilation is not a factor for this article. The assembly of the backbones assumes proportionality, and although their use reduces the number of linear regressions between backbones, it makes no difference to the number of observers through which the calibration is passed in the daisy-chaining. The second method involves taking the largest group number defined by any observer in each year and scaling this to a backbone series. That four such intervals are required implies the relationship of the highest value to the optimum values changes over time, and the calibration of this is again passed from one sequence to the previous one and hence this is also daisy-chaining. The daisy-chaining calibrations in \(R_{\text{BB}}\) assume not only linearity of the data between different observers, but also proportionality, which is not in principle correct and generated errors in the tests carried out by Lockwood et al. (2016c).

2.1.4 The “Corrected” Sunspot Number [\(R_{\mathrm{C}}\)]

\(R_{\mathrm{C}}\) was proposed by Lockwood, Owens, and Barnard (2014a) to provide a sensitivity analysis of the effect of different inputs to the modelling of open solar flux and streamer-belt width by Lockwood and Owens (2014). \(R_{\mathrm{C}}\) is based on \(R_{\text{ISNv1}}\) with the best estimate by Lockwood, Owens, and Barnard (2014a, 2014b) of the correction required for the Waldmeier discontinuity plus, for earlier times, the correction derived by Leussu, Usoskin, and Mursula (2013) using data by Schwabe, which applies to all data before 1848. The sequence was extended back to before the Maunder minimum using linearly regressed \(R_{\mathrm{G}}\) values. This series contains no correction for any other errors that have subsequently been revealed, such as the Locarno calibration error.

2.1.5 The Usoskin et al. Group-Number Composite [\(R_{\text{UEA}}\)]

The composite group-number series assembled at the University of Oulu by Usoskin et al. (2016) [\(R_{\text{UEA}}\)] directly calibrates all data to the number of groups [\(N_{\mathrm{G}}\)] defined by observers of the RGO for 1900 – 1976 from the photo-heliographic plates. Note that, like \(R_{\text{BB}}\), it does not employ the 12.08 scaling factor that was used in the generation of \(R_{\mathrm{G}}\). This series is unique in that it avoids using either daisy-chaining or regression techniques, and it makes no assumptions about linearity or proportionality between different datasets. For the test interval presented here (1920 – 1976), \(R_{\text{UEA}}\) and \(N_{\mathrm{G}}\) are identical. Note also that the original group-number by Hoyt and Schatten (1998) [\(R_{\mathrm{G}}\)] is also of the same in form as \(N_{ \mathrm{G}}\) over this interval (being \(12.08N_{\mathrm{G}}\) for the interval analysed here) and so tests of \(R_{\mathrm{G}}\) are not performed here as they would give identical answers to \(R_{\text{UEA}}\).

2.1.6 Summary of the Tested Data Series

The tested data series are summarised in Table 1. Figure 1a shows the five tested data series. Some are group numbers, while others are sunspot numbers, and they employ different scaling factors, as discussed above: hence, so that they can be compared in Figure 1, each has been regressed against the RGO sunspot-group number [\(N_{\mathrm{G}}\)] over the interval 1921 – 1945. The start date of this interval is chosen to be after any interval when there are some concerns over the calibration of the RGO data (Cliver and Ling 2016); the end date is just before the Waldmeier discontinuity (Svalgaard 2011; Clette and Lefèvre 2016). Figure 1a shows that before 1946 (the vertical dot–dashed line) all the series are either identical (other than the scaling factors) or very similar indeed. In fact, \(R_{\mathrm{C}}\) is, by its definition, identical to \(R_{\text{ISNv1}}\) between 1848 and 1945 the scaled \(R_{\text{ISNv2}}\) is found to also be virtually identical to \(R_{\text{ISNv1}}\) for the interval 1921 – 1946. After 1946 it can be seen that these scaled variations diverge. Because some of the differences are rather small in Figure 1a, Figure 1b shows the deviations of each from the mean of the five scaled sequences [\(\Delta [R_{\mathrm{G}}]_{\text{fit}}\)]. The Waldmeier discontinuity is clear in \(R_{\text{ISNv1}}\) because after 1946 there are high positive values of this deviation around each sunspot maximum. Both \(R_{\text{ISNv2}}\) and \(R_{\text{BB}}\) show similar variations, but of the opposite sense to those for \(R_{\text{ISNv1}}\); the variations for \(R_{\text{BB}}\) being larger than those for \(R_{\text{ISNv2}}\). These deviations for \(R_{\mathrm{C}}\) and \(R_{\text{UEA}}\) oscillate around zero.

Figure 2 analyses the regressions over 1921 – 1945 used to set all variations on the same scale in Figure 1a. The best-fit regression lines in the scatter plots shown in the left-hand panels of this plot do not pass through the origin, showing linear, but not proportional, dependencies between the tested sunspot numbers and the RGO group-number [\(N_{\mathrm{G}}\)]. Note that \(R_{\text{ISNv1}}\) and \(R_{\mathrm{C}}\) are identical over this regression interval, and therefore both are analysed in the top row of Figure 2. Note also that no plot is given for \(R_{\text{UEA}}\) as it equals \(N_{\mathrm{G}}\) for this regression interval.

Figure 2
figure 2

Analysis of the regressions between annual means [\(N_{\mathrm{G}}\)] of RGO group numbers and the independent tested sunspot data series over the interval 1921 – 1945, as used in Figure 1. The left-hand panel (parts a, c, and e) shows the scatter plots and the best-fit linear regression line, and the right-hand panel (parts b, d, and f) shows the corresponding quantile–quantile (Q – Q) plots in which the ordered standardised fit residuals [\(\mathrm{e}_{(\mathrm{i}|\mathrm{n})}/\sigma \)], where \(\sigma \) is their standard deviation, are plotted as a function of \({\mathrm{F}_{\mathrm{N}}}^{-1}(i-0.5/n)\), the quantiles of a standard normal distribution. (a) and (b) are for both \(R_{\text{ISNv1}}\) and \(R_{\mathrm{C}}\) (which are identical over the regression interval), (c) and (d) are for \(R_{\text{BB}}\), and (e) and (f) are for \(R_{\text{ISNv2}}\). No plots are given for \(R_{\text{UEA}}\) because over this interval it equals 12.08 \(N_{\mathrm{G}}\).

Full size image

Great care must be taken when using linear regressions. For example, errors caused by inadequate and/or inappropriate regression techniques were discussed by Lockwood et al. (2006) in relation to differences between reconstructions of the magnetic field in near-Earth space from geomagnetic-activity data. Nau (2016) has neatly summarised the problems: “If any of the assumptions is violated (i.e., if there are nonlinear relationships between dependent and independent variables or the errors exhibit correlation, heteroscedasticity, or non-normality), then the forecasts, confidence intervals, and scientific insights yielded by a regression model may be (at best) inefficient or (at worst) seriously biased or misleading.” In the context of sunspot numbers and sunspot-group numbers, Lockwood et al. (2016c) found that the most complex problems were associated with non-normal distributions of data errors (especially if linearity or proportionality was inappropriately assumed), which violate the assumptions made by most regression techniques: such errors should always be tested for before a correlation is used for any scientific inference or prediction (Lockwood et al., 2006, 2016c). A normal distribution of fit residuals can be readily tested for using a quantile–quantile (Q – Q) plot (e.g. Wilk and Gnanadesikan 1968). This is a graphical technique for determining whether two datasets come from populations with a common distribution; hence by making one of the datasets normally distributed, we can test the other to see if it also has a normal distribution. The left-hand panel of Figure 2 gives the corresponding Q – Q plots in which the ordered standardised fit residuals [\(\mathrm{e}_{(\mathrm{i}|\mathrm{n})}/\sigma \), where \(\sigma \) is their standard deviation] are plotted as a function of quantiles of a standard normal distribution [\(\mathrm{F}_{\mathrm{N}}^{-1}(i-0.5/n)\)]. To be a reliable and useable regression fit, the points in a Q – Q plot should form a straight line along the diagonal as this shows the errors in the fitted data form a Gaussian distribution, which is one of the assumptions of least-squares regression fitting. It can be seen that this condition is reasonably well met for \(R_{\text{ISNv1}}\) (and hence \(R_{\mathrm{C}}\)) and \(R_{\text{ISNv2}}\) (which are almost identical in form over the interval used) but not for \(R_{\text{BB}}\) (Figure 2d). Hence the error distribution for \(R_{\text{BB}}\) is not Gaussian. The form of Figure 2d suggests that the \(R_{\text{BB}}\) distribution has a different kurtosis (sharpness of peak) compared to \(N_{\mathrm{G}}\) and is asymmetric. This applies for all of the \(R_{\text{BB}}\) data series, but Figure 2 shows that it even applies for the interval of the regression shown here (1921 – 1945), over which \(R_{\text{BB}}\) and the other data series appear, at least visually, to be very similar (see Figure 1a). Hence Figure 2 stresses that although some linear regressions give valid Q – Q plots, others do not. In general, linear regression fits therefore cannot be relied upon and are used here in Figure 1 for illustrative purposes only in displaying the tested data series.

2.2 Test Data Series

We used five independent data series to test the various sunspot-number sequences that are summarised in Table 2 and compared in Figure 3.

Figure 3
figure 3

Comparison of the test data shown in the same format as Figure 1: (mauve) the RGO group-number [\(N_{\mathrm{G}}\)]; (green) the fitted RGO whole spot total area (corrected for foreshortening) [\(A _{\mathrm{G}}\)], (red) the fitted MWO group-number [\(N_{\text{MWO}}\)], (blue) the fitted MWO Ca K index [CaKi], (orange) the fitted Slough F2 layer critical frequency [foF2]. All series shown use a second-order polynomial fit to the RGO \(N_{\mathrm{G}}\)-data over 1921 – 1961. The vertical dot–dashed line is the most likely time of the Waldmeier discontinuity (1946), and the vertical dashed lines delineate the optimum “before” and “after” intervals found by the analysis.

Full size image
Table 2 Test data series used and the coefficients of the best-fit second-order polynomial fit of test series \(x\) to \(N_{ \mathrm{G}}\), given by \([N_{\mathrm{G}}]_{\mathrm{fit}} = ax^{2} + bx + c\).
Full size table

2.2.1 Total Spot Area from the Greenwich Photoheliographic Results [\(A_{\mathbf{G}}\)]

The total sunspot area was computed (corrected for limb foreshortening) [\(A_{\mathrm{G}}\)] from the RGO dataset (also called the Greenwich Photoheliographic Results: GPR) (Baumann and Solanki 2005; Willis et al. 2013a, 2013b). This dataset was compiled using white-light photographs (photoheliograms) of the Sun from a small network of observatories to produce a dataset of daily observations between 17 April 1874 and the end of 1976, thereby covering nine solar cycles. The observatories used were The Royal Observatory, Greenwich (until 02 May 1949); the Royal Greenwich Observatory, Herstmonceux (03 May 1949 – 21 December 1976); the Royal Observatory at the Cape of Good Hope, South Africa; the Dehra Dun Observatory, in the North–West Provinces (Uttar Pradesh) of India; the Kodaikanal Observatory, in southern India (Tamil Nadu); and the Royal Alfred Observatory in Mauritius. Any remaining data gaps were filled using photographs from many other solar observatories, including the Mount Wilson Observatory, the Harvard College Observatory, Melbourne Observatory, and the US Naval Observatory. The sunspot areas were measured from the photographs with the aid of a large position micrometer (see Willis et al. 2013a, 2013b and references therein). The \(A_{\mathrm{G}}\)-values are the total sunspot area (umbrae plus penumbrae) and have been corrected for the effect of foreshortening, which increases as sunspots are closer to the limb of the solar disc.

2.2.2 The number of sunspot groups from the Greenwich photoheliographic results [\(N_{\mathbf{G}}\)]

The number of groups [\(N_{\mathrm{G}}\)] was computed from the same RGO photographs as were used to generate \(A_{\mathrm{G}}\). The RGO data did not employ the Zürich group-classification scheme so that \(N_{\mathrm{G}}\) is not influenced by the Waldmeier discontinuity. It is well known that the RGO group-numbers show a drift relative to the Zürich sunspot numbers (e.g. Jakimcowa 1966). This is not necessarily a calibration error as there are a number of ways in which it could have arisen from real changes in solar activity. The most obvious is that there has been a drift in the ratio of the number of individual spots to the number of spot groups, which would influence \(N_{\mathrm{G}}\) and sunspot numbers differently. However, in addition, over the same interval there has been a drift in the lifetimes of spot groups, giving an increase in the number of recurrent groups (groups that are sufficiently long-lived to be seen for two or more traversals of the solar disc as seen from Earth) (Henwood, Chapman, and Willis 2010). This has the potential to have influenced group numbers derived using different classification schemes in different ways.

2.2.3 The Mount Wilson Ca K Index [CaKi]

Spectroheliograms in the ionized calcium K line Ca ii K (393.37 nm) were obtained between 1915 and 1985 using the 60-foot solar tower at Mount Wilson Observatory as part of their solar-monitoring programme. Calibration of these images is, however, not straightforward. A new and homogeneous index quantifying the area of plages and active network in the Ca ii K line has been derived from the digitization of almost 40,000 photographic solar images by Bertello, Ulrich, and Boyden (2010) (here referred to as the Ca K index: CaKi). Although these data are available up to 1985, there were changes to the calibration procedure employed with step-wedge exposures used from 09 October 1961. Because we wish to exclude effects by inhomogenities in the data caused by such changes, and because for the purposes of this article the later data are not required, we here only employ CaKi data from before this date. Note that the Ca K index has a pronounced non-linear variation with sunspot numbers (e.g. Foukal et al. 2009).

2.2.4 The Slough F2 Layer Critical Frequencies [foF2]

Ionospheric F2 region critical frequencies are observed at Slough [foF2]. As discussed in Article 1 (Lockwood et al. 2016a), the location of Slough means that the variation over each year is dominated by the plasma loss rate (and so by thermospheric composition), giving a dominant annual variation, as opposed to the semi-annual variation that dominates at some other stations (Scott and Stamper 2015), and a close variation with sunspot numbers. Additional effects, quantified by the area of white-light faculae, are small for the Slough data (Smith and King 1981), and Article 1 shows that the main effect of including them in quantifying the Waldmeier discontinuity is to increase noise levels. Hence in this article, Slough foF2 values are used without allowance for facular areas. In Article 1 (Lockwood et al. 2016a), nine dayside Universal Times (UTs) were identified for which the correlation of foF2 with sunspot numbers (after the Waldmeier discontinuity) exceeds 0.99 for all of the sunspot-data series tested. Rather than treat these as independent data series, we average the nine together in the present article.

2.2.5 The Mount Wilson Observatory (MWO) Sunspot-Group Number [\(N_{\text{MWO}}\)]

\(N_{\text{MWO}}\) has been compiled routinely from January 1917 onwards using the 150-foot solar tower telescope from sketches of the solar disc. These data did not use the Zürich group classification scheme, employing instead the scheme originally developed by Hale and co-workers (Hale et al. 1919). Thus \(N_{\text{MWO}}\) will not be influenced by the Waldmeier discontinuity. Because of different equipment and procedures, \(N_{\text{MWO}}\) does not vary linearly with \(N_{\mathrm{G}}\).

2.2.6 Summary of the Test Data Series

The test data series are shown in Figure 3 in the same format as Figure 1 and are summarised in Table 2. In Figure 3a each variation has been scaled to the variation of \(N_{\mathrm{G}}\) using regressions over the interval 1932 – 1961 (except foF2 for which data availability makes this interval 1933 – 1961). Because some proxies for solar activity, such as the CaKi index, do not vary linearly with sunspot numbers, the fits are made using a second-order polynomial. The coefficients for the derived second-order polynomial fits are given in Table 2. The analysis presented in this article was repeated for third-order polynomial fits and the results were essentially identical. The deviations from the mean of the five are shown in Figure 3b. Deviations are comparable to those in Figure 1 before 1945 (but are considerably smaller for after 1945). They are also random in nature in that they are generally largest in single years and of the same general character before 1945 as after. Differences are largest at the start of the interval shown in Figure 3. Figure 4 shows the regression scatter plots of these best polynomial fits and the corresponding \(\mathrm{Q}-\mathrm{Q}\) plots. It can be seen that the fit residuals for CaKi and foF2 are slightly non-Gaussian in the tails, but the bulk of the population follows a normal distribution. There is a slight deviation from a normal distribution of errors for \(A_{\mathrm{G}}\), but \(N_{\text{MWO}}\) gives an almost perfect normal distribution of errors. Hence all of the test series show a near Gaussian distribution of errors when compared to \(N_{\mathrm{G}}\). The scatter plots show that the polynomial fits remove non-linearity, and further tests on the residuals (see Lockwood et al. 2006) reveal that they show neither correlation nor heteroscedasticity. Because they pass all of these tests, the regressions between the fitted test series can be safely employed. In particular, the Q – Q plots shown in Figures 2 and 4 justify the use of the parametric (i.e. assuming a Gaussian distribution) \(t\)-test on the fit residuals described in the next section (and explains why non-parametric tests give very similar answers).

Figure 4
figure 4

Analysis of the regressions between annual means \(N_{\mathrm{G}}\) and the other four test series over the interval 1921 – 1961, as used in Figure 2. The left-hand panel (a, c, e, and g) shows the scatter plots and the best-fit linear regression, and the right-hand panel (b, d, f, and h) the corresponding quantile–quantile (Q – Q) plots in which the ordered standardised fit residuals, [\(\mathrm{e}_{(\mathrm{i}|\mathrm{n})}/\sigma \)], (where \(\sigma \) is their standard deviation) are plotted as a function of quantiles of a standard normal distribution, \({\mathrm{F}_{\mathrm{N}}}^{-1} (i-0.5/n)\). (a) and (b) are for the calcium K index [CaKi], (c) an (d) are for the mean dayside Slough F-layer critical frequency [foF2], (e) and (f) are for the MWO sunspot-group count [\(N_{\text{MWO}}\)], and (g) and (h) are for the total RGO sunspot area [\(A_{\mathrm{G}}\)].

Full size image

2.3 Analysis

Article 3 (Lockwood et al. 2016c) shows that it is important not to force linear regression fits between different sunspot-number sequences through the origin of the scatter plot. Doing so means that proportionality between the sequences is assumed and results in the inflation of solar-cycle amplitudes in data from a lower-acuity observer. Furthermore, Lockwood et al. (2016c) and Usoskin et al. (2016) showed that results from different observers often have a non-linear dependence. Most previous studies of the Waldmeier discontinuity (Svalgaard 2011; Lockwood, Owens, and Barnard 2014a; Lockwood et al. 2016a; Clette and Lefèvre 2016) implicitly made the assumption of proportionality because they assumed that correction for the Waldmeier discontinuity could be achieved using a single multiplicative factor. In this article, we do not make this assumption, instead we evaluate a correction for before the Waldmeier discontinuity from \(R\) to \(R '\) that is given by Equation (1). Adjusting the values before the putative Waldmeier discontinuity with the optimum \(f_{\mathrm{R}}\), \(n\), and \(\delta \) means that the sequence of older data is made consistent with the post-discontinuity data.

Clette and Lefèvre (2016) made the valuable point that the precise date of the Waldmeier discontinuity is not known, and this can influence the results if the “before” and “after” intervals used in the method of Lockwood, Owens, and Barnard (2014a) end and start, respectively, at an assumed date for the discontinuity. (This is because if that date were wrong, some dataset that is from before the discontinuity can be placed in the after interval, or vice versa). Here we remove this dependency by ending the “before” interval in 1943 and starting the “after” interval in 1949. Thus, the precise date or the waveform of discontinuity does not have an effect, provided the bulk of it is within the six-year interval around 1946, which is the most likely date defined by Clette and Lefèvre (2016). The length of the “before” and “after” intervals was varied until an optimum was achieved, as discussed below.

The procedure used was to first determine the exponent [\(n\)] and offset [\(\delta \)] required by Equation (1). Because these relate to the correction needed for a given tested sunspot-number series, the same values of \(n\) and \(\delta \) are used when testing against all five test series. These values were obtained using the Nelder–Mead search procedure to find the optimum combination of \(n\), \(\delta \), and \(f_{\mathrm{R}}\) that made \(R '\) correlate best with each of the test data series for the period between the start of the “before” interval and the end of the “after” interval. Because the test series are so similar (see Figure 3), they gave very similar optimum \(n\), \(\delta \), and \(f_{\mathrm{R}}\) values, and the values of \(n\) and \(\delta \) adopted here were those for the test series that gave the highest correlation (which was invariably for the RGO sunspot-group-number \([N_{\mathrm{G}}]\)). Having defined the optimum values of \(n\) and \(\delta \), the procedure used was to vary the factor \(f_{\mathrm{R}}\) between 0.5 and 1.3 (in steps of 0.001) to evaluate the mean fit residuals in the “before” and “after” intervals.

As in Lockwood, Owens, and Barnard (2014a), Welch’s \(t\)-test was used to evaluate the probability \(p\)-values of the difference between the mean fit residuals (between the tested and test series in question) for the “before” and “after” intervals being zero. This two-sample \(t\)-test is a parametric test (i.e. it assumes a Gaussian distribution) that compares two independent data samples (Welch 1947). Because it is not assumed that the two data samples are from populations with equal variances, the test statistic under the null hypothesis has an approximate Student’s \(t\)-distribution with a number of degrees of freedom given by Satterthwaite’s approximation (Satterthwaite 1946). The distributions of residuals were found to be close to Gaussian in most cases, and so application of non-parametric tests (specifically, the Mann–Whitney U (Wilcoxon) test of the medians and the Kolmogorov–Smirnov test of the overall distributions) gave very similar results. The overall pdf [\(p(f_{\mathrm{R}})\)] for the five test data series combined was obtained by taking the product of those for each individually:

$$ p_{0}(f_{\mathrm{R}}) = \bigl[p(f_{\mathrm{R}}) \bigr]_{\mathrm{N}_{\mathrm{G}}} \bigl[p(R)\bigr]_{\mathrm{A}_{\mathrm{G}}} \bigl[p(f_{\mathrm{R}}) \bigr]_{\mathrm{CaK}} \bigl[p(f_{ \mathrm{R}})\bigr]_{\mathrm{NMWO}}. $$
(2)

The peak value of \(p(f_{\mathrm{R}})\) is then defined [\(p_{\mathrm{m}}\)]. Note that \([p(f_{\mathrm{R}})]_{\text{foF2}}\) was not used for reasons discussed below. (However, including a term in \([p(f_{\mathrm{R}})]_{\text{foF2}}\) makes very little difference to the results).

Another valuable point made by Clette and Lefèvre (2016) is that if the “before” and “after” intervals are too long in duration, then other errors (such as the Locarno calibration error in the case of \(R_{\text{ISNv1}}\)) can enter into both the tested and test series and so influence the estimate of the discontinuity correction. On the other hand, if these intervals are too short, then the inter-annual variability that is due to “geophysical noise” in both the test and tested data will also degrade the final value. Hence an optimum compromise is needed. To reduce the number of variables, the “before” and “after” intervals were assigned the same duration [\(T\)]. The value of \(T\) was then varied between 1 year and 23 years (the latter using all the test data shown in Figure 3, except for the six-year interval around the putative Waldmeier discontinuity). As expected from the above, both the lowest and the highest values of \(T\) gave a low peak value of \(p_{\mathrm{m}}\), and hence broad distributions [\(p_{0}(f _{\mathrm{R}})\)]. The narrowest \(p_{0}(f_{\mathrm{R}})\)-distribution, giving the highest peak value [\(p_{\mathrm{m}}\)], was for \(T = 11\) years (approximately one full solar cycle). Hence we used a “before” interval of 1932 – 1943 and an “after” interval of 1949 – 1960, as this minimised the width of the overall probability distribution function obtained, and hence the uncertainties. This is the optimum compromise between having sufficient data points and minimising the potential to introduce other errors and discontinuities present in either data series.

The second, subsidiary, test used by Lockwood, Owens, and Barnard (2014a) and Lockwood et al. (2016a) employed the correlations [\(r\)] between \(R '\) and each of the test series over the whole interval (1932 – 1960). The peak in \(r\) will occur when the discontinuity introduced into \(R '\) most closely cancels that inherent in the data series \(R\): values of \(r\) will be lower for less-than-optimum combinations of \(f_{\mathrm{R}}, n\), and \(\delta \). The peaks of the correlograms (\(r\) against \(f_{\mathrm{R}}\) for the optimum \(\delta \) and \(n\)) were defined and for each \(f_{\mathrm{R}}\) the significance [\(S\)] of the difference between \(r\) and its peak value was quantified using the Fischer-Z transform by comparison against the AR1 noise model. These significance values were then combined into an overall variation for all five test series by multiplying the probabilities:

$$ S_{0}(f_{\mathrm{R}}) = 1-\bigl\{ \bigl(1-\bigl[S(f_{\mathrm{R}}) \bigr]_{\text{N}_{\text{G}}}\bigr) \bigl(1-\bigl[S(f_{\mathrm{R}})\bigr]_{\text{A}_{\text{G}}} \bigr) \bigl(1-\bigl[S(f_{\mathrm{R}})\bigr]_{\text{CaK}}\bigr) \bigl(1- \bigl[S(f_{\mathrm{R}})\bigr]_{\text{NMWO}}\bigr) \bigr\} . $$
(3)

Note that, as for \(p_{0}(f_{\mathrm{R}})\), the term \([S(f _{\mathrm{R}})]_{\text{foF2}}\) has been omitted in Equation (3) (but, again, its inclusion makes very little difference). Ideally, the minimum in \(S_{0}(f_{\mathrm{R}})\) would be at the same \(f_{ \mathrm{R}}\) as the peak in \(p(f_{\mathrm{R}})\). A minimum \(S_{ 0}(f_{\mathrm{R}})\) of zero would indicate perfect agreement between the results of this second test for all five test data series.

3 Results

3.1 Results for \(R_{\text{ISNv1}}\)

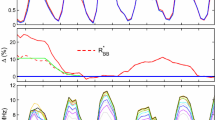
Figure 5 summarises the results of these tests for Version 1 of the SIDC Wolf/Zürich/International sunspot-number composite (i.e. \(R\) in Equation (1) is \(R_{\text{ISNv1}}\)). The figure is for the optimum values of \(\delta \) and \(n\), which are found to be 2.731 and 1.088, respectively. The various coloured lines in the top panel show the correlation coefficients between the adjusted \(R_{\text{ISNv1}}\) series [\({R_{\text{ISNv1}}}'\)] and the test series for annual means over the full internal (1932 – 1960) \([r]\) as a function of \(f_{\mathrm{R}}\) for this \(\delta \) and \(n\). The best correlation is for the number of spot groups from the RGO data [\(N_{\mathrm{G}}\)]. Peak correlation occurs at the same \(f_{\mathrm{R}}\) for [CaKi]fit (the polynomial-fitted Ca K index) and \([N_{\text{MWO}}]_{\mathrm{fit}}\) (the fitted Mount Wilson sunspot-group number). \([A_{\mathrm{G}}]_{\mathrm{fit}}\) is the fitted total spot area from the RGO data and peaks at a slightly lower \(f_{\mathrm{R}}\) and the peak for \([\text{foF2}]_{\mathrm{fit}}\) (the fitted average Slough F2 layer critical frequency) is at a yet lower \(f_{\mathrm{R}}\).

Figure 5
figure 5

Evaluation of the discontinuity around 1946 for Version 1 of the Wolf/Zürich/International sunspot number [\(R_{\text{ISNv1}}\)]. (a) The correlation \(r\) as a function of the factor \(f_{\mathrm{R}}\) of the adjusted sequence [\(R_{\text{ISNv1}'}\)] (generated using Equation (1) before 1946 where the tested parameter \(R\) is \(R_{\text{ISNv1}}\)) with (mauve) the RGO group-number [\(N_{\mathrm{G}}\)], (green) the corrected RGO total-spot area-number [\(A_{\mathrm{G}}\)], (blue) the Mount Wilson CaKi index, and (orange) the F2 layer critical frequency at Slough [foF2]. (b) The significance [\(S\)] of the differences between the peak \(r\) and the \(r\) at general \(f_{\mathrm{R}}\) (using the same colour scheme). The black line is the combination of the four \(S(f_{\mathrm{R}})\) variations using Equation (3). (c) The \(p\)-values of the difference in the mean residuals between the “before” (1932 – 1943) and “after” (1949 – 1960) intervals [\(p(f_{\mathrm{R}})\)], again using the same colour scheme. The black line is the combination of the four pdfs [\(p(f_{\mathrm{R}})\)] made using Equation (2). The vertical-dashed line marks the peak, and the grey area the range between the \(2\sigma \) points, of the combined \(p(f_{\mathrm{R}})\). The plot is for the optimum offset value [\(\delta \)] of 2.7309 and exponent [\(n\)] of 1.0884 (see Table 3).

Full size image

The middle panel of Figure 5 shows the statistical significances of the difference between the \(r\) at general \(f_{\mathrm{R}}\) and the peak value using the same colour scheme. The black line shows the overall significance \(S_{0}(f_{\mathrm{R}})\), given by Equation (3).

The bottom panel of Figure 5 shows the \(p\)-values of the differences in fit residuals between for the “before” and “after” intervals for the fits of the adjusted tested series \(R '\) and each test series, again using the same colour scheme. The black line shows the overall pdf [\(p _{0}(f_{\mathrm{R}})\)], as given by Equation (2). It can be seen that the minimum in the combined \(S_{0}(f_{\mathrm{R}})\) and the peak in the combined \(p_{0}(f_{\mathrm{R}})\) are at very similar \(f_{\mathrm{R}}\), which means that the two tests are in excellent agreement. The uncertainty in the optimum value for \(S_{0}(f_{\mathrm{R}})\) is much greater than that for \(p_{0}(f_{\mathrm{R}})\) (the distribution being much broader), and so \(p_{0}(f_{\mathrm{R}})\) provides the most stringent test for the optimum \(f_{\mathrm{R}}\)-value. The grey band marks the \(2\sigma\) points of the \(p_{0}(f_{\mathrm{R}})\) distribution. Note that the agreement of the \(f_{\mathrm{R}}\) of minimum \(S_{ 0}(f_{\mathrm{R}})\) and peak \(p_{0}(f_{\mathrm{R}})\) is less close for [foF2]fit. Thus the foF2 test series is the only one for which the two tests do not completely agree. This was found to be true for all of the tested sunspot series. For this reason, foF2 is left out of the computation of both \(p_{0}(f_{\mathrm{R}})\) and \(S_{0}(f_{\mathrm{R}})\) in Equations (2) and (3). The orange lines in Figure 4 (and subsequent figures) do, however, serve to show that this terrestrial proxy for solar activity gives results that are still (just) within the \(2\sigma \) uncertainty band derived from the four more direct solar indices. Indeed, all of the test data series give results within the \({\pm }\,2\sigma \) uncertainty. The optimum combination of \(f_{\mathrm{R}}\), \(n\), and \(\delta \) defined by Figure 5 is given for this tested series [\(R_{\text{ISNv1}}\)] in the top row of Table 3.

Table 3 Optimum values of the fitted values of \(\delta \), \(n\), and \(f_{\mathrm{R}}\) in Equation (1) for the five tested sunspot data series.
Full size table

The optimum correction for the Waldmeier discontinuity for \(R_{\text{ISNv1}}\) is

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} {R_{\text{ISNv1}}}' = R_{\text{ISNv1}}& \mbox{for}\ t \geq 1946.0 \\ {R_{\text{ISNv1}}}' = 0.7350 {R_{\text{ISNv1}}}^{1.0883} + 2.7308& \mbox{for}\ t < 1946.0. \end{array}\displaystyle \end{aligned}$$
(4)

Applying Equation (4) gives a mean \(\langle {R_{\text{ISNv1}}}'\rangle\) of 61.23 over the “before” interval, whereas \(\langle R_{\text{ISNv1}}\rangle \) is 54.53 over the same interval. Hence this test shows that \(R_{\text{ISNv1}}\) is 12.28 % too low in the “before” interval. This, like previous studies, confirms that the Waldmeier discontinuity is a real factor in \({R_{\text{ISNv1}}}'\). Using the \(2\sigma \) points for \(f_{\mathrm{R}}\), \(n\), and \(\delta \) yields an uncertainty in the 12.28 % error of \({\pm}\, 3.37~\%\) (the total uncertainty being dominated by that due to \(f_{\mathrm{R}}\)). The percent change is only slightly greater than the 11.9 % correction found in the studies by Lockwood, Owens, and Barnard (2014a) and Lockwood et al. (2016a), despite the several improvements and refinements to the method that have been made in the present. The optimum value is lower than the 15.8 % derived by Clette and Lefèvre (2016) for \(R_{\text{ISNv1}}\), which is close to, but just outside, the upper edge of the \(2\sigma \) uncertainty band found here. As in previous studies by Lockwood, Owens, and Barnard (2014a, 2014b, 2016a), the probability that the required change is the 20 % originally invoked by Svalgaard (2011) is essentially zero. However, notice that neither the zero-level offset nor the exponent is small: hence the Waldmeier discontinuity in \(R_{\text{ISNv1}}\) requires non-linear corrections and a proportional (i.e. multiplicative) one is not adequate.

3.2 Results for \(R_{\text{ISNv2}}\)

Figure 6 is the equivalent to Figure 5 for the new version of the SIDC Wolf/Zürich/International sunspot-number composite [\(R_{\text{ISNv2}}\)]. The behaviour is very similar to Figure 5, except that the peak of the pdf is at \(f_{\mathrm{R}} = 0.9967\) for \(\delta = 0.0001\) and \(n = 0.9967\) (see Table 3). Again, the level of agreement between the results for the different test series is exceptionally good. The optimum correction is

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} {R_{\text{ISNv2}}}' = R_{\text{ISNv2}}& \mbox{for}\ t \geq 1946.0 \\ {R_{\text{ISNv2}}}' = 0.9760 {R_{\text{ISNv2}}}^{0.9967} + 0.0001 & \mbox{for}\ t < 1946.0. \end{array}\displaystyle \end{aligned}$$
(5)
Figure 6
figure 6

Same as Figure 5 for Version 2 of the of the Wolf/Zürich/International sunspot number [\(R_{\text{ISNv2}}\)]. (a) The correlation [\(r\)] as a function of the factor \(f_{\mathrm{R}}\) of the adjusted sequence [\({R_{\text{ISNv2}}}'\)] (generated using Equation (1) before 1946 where the tested parameter \(R\) is \(R_{\text{ISNv2}}\)) with (mauve) the RGO group-number [\(N_{\mathrm{G}}\)], (green) the corrected RGO total-spot-area number [\(A_{\mathrm{G}}\)], (blue) the Mount Wilson CaKi index, and (orange) the F2 layer critical frequency at Slough [foF2]. (b) The significance [\(S\)] of the differences between the peak \(r\) and the \(r\) at general \(f_{\mathrm{R}}\) (using the same colour scheme). The black line is the combination of the four \(S(f_{\mathrm{R}})\) variations using Equation (3). (c) The \(p\)-values of the difference in the mean residuals between the “before” (1932 – 1943) and “after” (1949 – 1960) intervals [\(p(f_{\mathrm{R}})\)], again using the same colour scheme. The black line is the combination of the four pdfs [\(p(f_{\mathrm{R}})\)] made using Equation (2). The vertical-dashed line marks the peak, and the grey area the range between the \(2\sigma \) points, of the combined \(p(f_{\mathrm{R}})\). The plot is for the optimum offset value [\(\delta \)] of \(1.4938\times 10^{-4}\) and exponent [\(n\)] of 0.9967 (see Table 3).

Full size image

This test finds that \(R_{\text{ISNv2}}\) overestimates the mean for the “before” interval by \(3.80 \pm 2.91~\%\). Thus the Waldmeier discontinuity has been slightly overestimated in \(R_{\text{ISNv2}}\). Note that the ideal value of zero is (just) outside the \(2\sigma \) uncertainty for \(R_{\text{ISNv2}}\). The very small \(\delta \) and the closeness of \(n\) to unity mean that the correction needed is very close to being proportional. Hence the correction in \(R_{\text{ISNv2}}\), although slightly too large, has removed the non-linearity introduced by the changes made by Waldmeier.

3.3 Results for \(R_{\mathrm{C}}\)

Figure 7 is the equivalent to Figure 5 for the corrected Wolf/Zürich/International sunspot number composite proposed by Lockwood, Owens, and Barnard (2014a). The peak of the pdf is at \(f_{\mathrm{R}} = 0.6240\) for \(\delta = 3.4957\) and \(n = 1.0950\) (see Table 3). Again, the level of agreement between the results for the different test series is exceptionally good. The optimum correction is

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} {R_{\mathrm{C}}}' = R_{\mathrm{C}}& \mbox{for}\ t \geq 1946.0 \\ {R_{\mathrm{C}}}' = 0.6240 {R_{\mathrm{C}}}^{1.0950} + 3.4957 & \mbox{for}\ t < 1946.0. \end{array}\displaystyle \end{aligned}$$
(6)

This test finds that \(R_{\mathrm{C}}\) underestimates the mean for the “before” interval by \(0.44 \pm 3.01~\%\). Although this underestimate is zero to within the \(2\sigma \) uncertainty, the correction for the Waldmeier discontinuity in \(R_{\mathrm{C}}\) is nevertheless less satisfactory than that in \(R_{\text{ISNv2}}\). This is because, as for \(R_{\text{ISNv1,}}\) the value of \(n\) is not close to unity and therefore the non-linear behaviour introduced by the Waldmeier discontinuity has not been removed.

Figure 7
figure 7

Same as Figure 5 for the corrected Wolf/Zürich/International sunspot-number composite proposed by Lockwood, Owens, and Barnard (2015) \([R_{\mathrm{C}}]\). (a) The correlation [\(r\)] as a function of the factor \(f_{\mathrm{R}}\) of the adjusted sequence \([{R_{\mathrm{C}}}']\) (generated using Equation (1) before 1946 where the tested parameter \(R\) is \(R_{\mathrm{C}}\)) with (mauve) the RGO group number [\(N_{\mathrm{G}}\)], (green) the corrected RGO total-spot-area number [\(A_{\mathrm{G}}\)], (blue) the Mount Wilson CaKi index, and (orange) the F2 layer critical frequency at Slough [foF2]. (b) The significance [\(S\)] of the differences between the peak \(r\) and the \(r\) at general \(f_{\mathrm{R}}\) (using the same colour scheme). The black line is the combination of the four \(S(f_{\mathrm{R}})\) variations using Equation (3). (c) The \(p\)-values of the difference in the mean residuals between the “before” (1932 – 1943) and “after” (1949 – 1960) intervals [\(p(f_{\mathrm{R}})\)], again using the same colour scheme. The black line is the combination of the four pdfs [\(p(f_{\mathrm{R}})\)] made using Equation (2). The vertical-dashed line marks the peak, and the grey area the range between the \(2\sigma \) points, of the combined \(p(f_{\mathrm{R}})\). The plot is for the optimum offset value [\(\delta \)] of 3.4957 and exponent [\(n\)] of 1.0950 (see Table 3).

Full size image

3.4 Results for \(R_{\mathrm{BB}}\)

Figure 8 is the equivalent plot to Figure 5 for the new backbone sunspot-group-number composite proposed by Svalgaard and Schatten (2016) \([R_{\text{BB}}]\). The peak of the pdf is at \(f_{\mathrm{R}} = 0.7410\) for \(\delta = 0.3108\) and \(n = 1.0932\) (see Table 3). Again, the level of agreement between the results for the different test series is exceptionally good. The optimum correction is

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} {R_{\text{BB}}}' = R_{\text{BB}}& \mbox{for}\ t \geq 1946.0 \\ {R_{\text{BB}}}' = 0.7410 {R_{\text{BB}}}^{1.0932} + 0.3108& \mbox{for}\ t < 1946.0. \end{array}\displaystyle \end{aligned}$$
(7)

This test finds that \(R_{\text{BB}}\) overestimates the mean for the “before” interval by \(5.74\pm 2.25~\%\). In addition to this being significantly different from zero, the correction for the Waldmeier discontinuity is, as for \(R_{\mathrm{C}}\), less satisfactory than that in \(R_{\text{ISNv2}}\) because the value of \(n\) is not as close to unity and therefore any non-linear behaviour introduced by the Waldmeier discontinuity has not been removed.

Figure 8
figure 8

Same as Figure 5 for the new backbone sunspot-group-number composite proposed by Svalgaard and Schatten (2016) \([R_{\text{BB}}]\). (a) The correlation [\(r\)] as a function of the factor \(f_{\mathrm{R}}\) of the adjusted sequence [\({R_{\text{BB}}}'\)] (generated using Equation (1) before 1946 where the tested parameter \(R\) is \(R_{\text{BB}}\)) with (mauve) the RGO group-number [\(N_{\mathrm{G}}\)], (green) the corrected RGO total-spot-area number [\(A_{\mathrm{G}}\)], (blue) the Mount Wilson CaKi index, and (orange) the F2 layer critical frequency at Slough [foF2]. (b) The significance [\(S\)] of the differences between the peak \(r\) and the \(r\) at general \(f_{ \mathrm{R}}\) (using the same colour scheme). The black line is the combination of the four \(S(f_{\mathrm{R}})\) variations using Equation (3). (c) The \(p\)-values of the difference in the mean residuals between the “before” (1932 – 1943) and “after” (1949 – 1960) intervals [\(p(f_{\mathrm{R}})\)], again using the same colour scheme. The black line is the combination of the four pdfs [\(p(f_{\mathrm{R}})\)] made using Equation (2). The vertical-dashed line marks the peak, and the grey area the range between the \(2\sigma \) points, of the combined \(p(f_{\mathrm{R}})\). The plot is for the optimum offset value [\(\delta \)] of 0.3108 and exponent [\(n\)] of 1.0932 (see Table 3).

Full size image

3.5 Results for \(R_{\text{UEA}}\)

Figure 9 is the equivalent to Figure 5 for the new Usoskin et al. (2016) group-number reconstruction [\(R_{\mathit{UEA}}\)]. We would expect this to give \(f_{\mathrm{R}}\) very close to unity and \(\delta \) very close to zero because, for the interval studied in this article, \(R_{\text{UEA}} = N_{\mathrm{G}}\) and hence it is the same as one of the four test data sequences. However, the test is interesting as it shows the net effect of the other solar test sequences (the CaKi index, the RGO spot areas \(A_{\mathrm{G}}\), and the Mount Wilson group-numbers \(N_{\text{MWO}}\)) on the result is negligible and also shows the same behaviour for foF2 as the other tested sunspot series. The top panel of Figure 9 shows the unity peak \(r\) between \(R_{\text{UEA}}\) and \(N_{\text{G,}}\) but except for this, the behaviour for the other test series is very similar to that for the other tested series. In this case, the \(p_{0}(f_{\mathrm{R}})\) curve is essentially a \(\delta \)-function (the plot scale in Figure 9c is the same as for panels c of Figures 5 – 8, but the peak value of \(p_{0}(f _{\mathrm{R}}) [p_{\mathrm{m}}]\) is off-scale in this case as it is close to unity). To within four decimal places, values of \(n\) and \(f_{\mathrm{R}}\) are unity and \(\delta \) is zero. The change required in the “before” interval is \(0.005 \pm 0.048~\%\).

Figure 9
figure 9

Same as Figure 5 for the new Usoskin et al. (2015) group-number reconstruction [\(R_{\text{UEA}}\)]. (a) The correlation \(r\) as a function of the factor \(f_{\mathrm{R}}\) of the adjusted sequence [\({R_{\text{UEA}}}'\)] (generated using Equation (1) before 1946 where the tested parameter \(R\) is \(R_{\text{UEA}}\)) with (mauve) the RGO group number [\(N_{\mathrm{G}}\)], (green) the corrected RGO total spot area number [\(A_{\mathrm{G}}\)], (blue) the Mount Wilson CaKi index, and (orange) the F2 layer critical frequency at Slough [foF2]. (b) The significance [\(S\)] of the differences between the peak \(r\) and the \(r\) at general \(f_{\mathrm{R}}\) (using the same colour scheme). The black line is the combination of the four \(S(f_{\mathrm{R}})\) variations using Equation (3). (c) The \(p\)-values of the difference in the mean residuals between the “before” (1932 – 1943) and “after” (1949 – 1960) intervals [\(p(f_{\mathrm{R}})\)], again using the same colour scheme. The black line is the combination of the four pdfs [\(p(f_{\mathrm{R}})\)] made using Equation (2). The vertical-dashed line marks the peak, and the grey area the range between the \(2\sigma \) points, of the combined \(p(f_{\mathrm{R}})\). The plot is for the optimum offset value [\(\delta \)] of 0 and exponent [\(n\)] of 1 (see Table 3). Note that \([p(f_{\mathrm{R}})]_{\text{NG}}\) and hence \(p(f_{\mathrm{R}})\) are very close to \(\delta \)-functions in this case (they are not quite because the other test series are not quite identical in waveform to \(N_{\mathrm{G}}\)) and although part c uses the same \(p(f_{\mathrm{R}})\) scale as Figures 3 – 6, the peak \(p(f_{\mathrm{R}})\) value [\(p_{\mathrm{m}}\)] is close to unity.

Full size image

This test of \(R_{\text{UEA}}\) shows that the procedure works well, and that when presented with one dominant correlation the other test series, which give slightly different optimum \(f_{\mathrm{R}}\), do not degrade the result.

4 Conclusions

We have tested five sunspot data series around the putative Waldmeier discontinuity in sunspot numbers around 1945 using five diverse test datasets that are all completely independent of the Zürich sunspot number, which is the source of this discontinuity. The test data are the sunspot-group number from the RGO dataset [\(N_{\mathrm{G}}\)], the total sunspot area from the RGO dataset (corrected for foreshortening) [\(A _{\mathrm{G}}\)], the Mount Wilson Ca K index [CaKi], the Mount Wilson sunspot-group number [\(N_{\text{MWO}}\)], and the ionospheric F2 region critical frequency observed at Slough [foF2]. We have tested various sunspot data series in two ways, using the fit residuals and using the correlation coefficient. In all cases, the results of these two methods are remarkably consistent, but the uncertainties are lower for the fit residual method. The most persistent difference between the two methods occurs for the ionospheric foF2 data, which are here not included in overall tests but are nevertheless plotted to show that these terrestrial data still give results that are consistent with those for the solar test data to within the \(2\sigma \) uncertainties. The diversity of the derivations and sources of these test series means that the chances that all suffer from the same error around 1946 are negligible and comparison shows random data noise differences between them (Figure 3) and not systematic errors.

To summarise our results graphically, Figure 10 plots the variations of all of the tested series over the test period (which covers Solar Cycles 17, 18, and 19). The grey area is the mean of the five regressed test series, and in parts b – f, the blue line is the original tested series and the red line is the tested series after the relevant adjustment to the data before 1946, as derived in this article, has been made. Part a of Figure 10 compares the five test series.

Figure 10
figure 10

Summary of annual mean variations over the optimum test interval 1932 – 1961. (a) The fitted test series, using the same colour coding as previous figures. The grey-shaded area is the mean of the five test series and is repeated in all other parts of the figure. In panels b – f the blue lines show the original sunspot data series and the red lines the version corrected for before 1946 using the best fits derived in this article. Because the red lines are plotted second, they cover the blue lines where the two agree. The plots are for (b) \(R_{\text{ISNv1}}\), (c) \(R_{\text{BB}}\), (d) \(R_{\text{ISNv2}}\), (e) \(R_{\mathrm{C}}\), and (f) \(R_{\text{UEA}}\). Because this is a mixture of sunspot numbers and sunspot-group numbers, all series have been scaled to \(R_{\text{ISNv2}}\) for the interval 1946 – 1961.

Full size image

Figure 10b is for \(R_{\text{ISNv1}}\) and the Waldmeier discontinuity is clearly visible in the blue line as low values during Solar Cycle 17. The red line demonstrates how effective the correction is – and this is true for all of the tested series. Figure 10c is for \(R_{\text{BB}}\) and the blue line shows that values in Cycle 17 are persistently too high. It is not at all clear how this has occurred because \(R_{\text{BB}}\) was compiled from various observers, most of whom did not change practices in defining groups when such changes were made at Zürich. However, it appears that \(R_{\text{BB}}\) has somehow been adjusted to allow for the Waldmeier discontinuity, and this adjustment is either not warranted or excessive. Figure 10d shows \(R_{\text{ISNv2}}\), and the Waldmeier discontinuity is much reduced compared to \(R_{\text{ISNv1}}\). However, there appears to be a slight over-correction for the discontinuity, as values for Cycle 17 are slightly too high. This is consistent with the estimated inflation factors used to correct \(R_{\text{ISNv1}}\), which was 18 % (Clette and Lefèvre 2016), which is higher than the value for the mean of \(R_{\text{ISNv1}}\) over Cycle 17 of \(12.28 \pm 3.37~\%\) that was derived here. Figure 10d confirms the effects of the mean for \(R_{\text{ISNv2}}\) for Cycle 17 being too large by the \(3.80 \pm 2.91~\%\) that was derived in this article. Figure 10e shows the results for \(R_{\mathrm{C}}\) and, although a good match to the mean for Cycle 17 is obtained, the effects of the residual non-linearity can be seen with values at both sunspot minimum and sunspot maximum being slightly low in \(R_{\mathrm{C}}\). Figure 10f shows the effects of the mean for \(R_{\text{UEA}}\); because the tested series and one of the test series are the same here, the blue and red lines are essentially identical and both match the main test series very well.

Table 3 gives the optimum corrections needed for the five tested sunspot data series. Direct and careful allowance for this discontinuity has been made in Version 2 of the Wolf/Zürich/International sunspot number [\(R_{\text{ISNv2}}\)] but we here show that the correction applied is slightly too large but does remove the non-linearity inherent in \(R_{\text{ISNv1}}\). Note that because \(R_{\text{ISNv2}}\) is compiled by daisy-chaining of calibrations, this systematic error will be passed to all prior data. The correction used in the “backbone” sunspot-group series [\(R_{\text{BB}}\)] of Svalgaard and Schatten (2016) is also too large. A large part of this is likely to be the 7 % correction introduced by Svalgaard and Schatten to allow for the “evolutionary” aspect of Waldmeier’s classification scheme, but it is not at all obvious that this is required for the data used to compile \(R_{\text{BB}}\). The backbone series is the only one not to give usable Q – Q plots when regressed against other sunspot series. From the analysis presented in Article 3 (Lockwood et al. 2016c), some of the error probably has arisen from the use of linear inter-correlation of segments of annual mean data (when in general the relationship is non-linear) and because fits were unnecessarily forced through the origin, which tends to amplify solar-cycle amplitudes in fitted data. As for \(R_{\text{ISNv2}}\), \(R_{\text{BB}}\) uses daisy-chaining of calibrations, and this error will be passed to prior data and such errors will accumulate as one goes back in time.

The correction applied by Lockwood, Owens, and Barnard (2014a) to \(R_{\text{ISNv1}}\) to generate \(R_{\mathrm{C}}\) is designed to remove the Waldmeier discontinuity on average data series. These tests show that this is achieved, but that the non-linear variation with the test data, as also found for \(R_{\text{ISNv1}}\) has not been removed. In addition, \(R_{\mathrm{C}}\) only considered two known errors and others certainly exist; for example the modern values were not corrected for the drift in the Locarno calibration values (Clette et al. 2015).