Modeling Local BES Indicators by Copula-Based Bayesian Networks

Abstract

In Italy, the measure of the Equitable and Sustainable Well-being is provided by the Italian Institute of Statistics by means of a dashboard of basic and composite indicators. To investigate the dependence structure between the different domains of well-being, we propose the use of Non-Parametric Bayesian Networks based on the normal copula distribution, that allow to explore the conditional independence relationships between the composite indicators. The main advantage of the non-parametric models is that, as opposed to the parametric approach, they do not require any assumption on the marginal distributions of the variables. The proposed model is applied to the Equitable and Sustainable Well-being indicators measured at the provincial level and enriches the analysis of well-being by inspecting similarities and differences between Italian urban areas and territories.

1 Introduction

Before the 1990s, the Gross Domestic Product (GDP) has been the only indicator accepted as a valid measure of a country’s progress. Over the last decades, this approach has been largely criticized: the international debate on the measurement of citizens’ well-being has emphasized the multidimensional definition of well-being (Sen 1980, 1985) that can not be described by looking just at the economic production. Hence, the need to go beyond GDP, developing a set of indicators taking into account also the environmental and social aspects related to the quality of life.

In the final report of the European Commission for Measuring Economic Performance and Social Progress, known as “Stiglitz report” (Stiglitz et al. 2009), the Commission’s objective was clearly that of identifying new relevant indicators, different than GDP, accounting for all dimensions of well-being.

In Italy, in 2010, Istat (Italian Institute of Statistics) and Cnel (Italian Council for Economics and Labour) launched the “Equitable and Sustainable Well-being” (BES) project whose first report was published in March 2013 (Istat 2013). The main goal of the project was that of building a dashboard of indicators of well-being involving the two basic concepts of equity and sustainability (Burchi and Gnesi 2016). As pointed out by Giovannini and Rondinella (2012), the new approach had to consider the social and environmental aspects as important as the economic one. 134 basic indicators were identified, grouped in 12 domains: Health, Education and training, Work and life balance, Economic well-being, Social relationships, Politics and Institutions, Security, Subjective well-being, Landscape and cultural heritage, Environment, Innovation, research and creativity and Quality of services.

Starting from the 2015 BES Report (Istat 2015), also the composite indicators for each domain were computed, at a regional level and over the time. The series are available from 2010 allowing temporal and spatial comparisons.

To extend the analysis at the provincial level, in 2011, Istat launched two pilot projects named UrBes and Provinces’ BES: the former studies well-being in cities and other urban areas while the latter focuses on Italian Provinces and Metropolitan cities.

In 2015, the Provinces’ BES was listed in the National Statistical Programme as Statistical Information System (SIS) becoming a commitment of Cuspi (Coordination of statistical offices of Italian provinces) and Istat.

In the last edition, according to the BES framework, 56 basic indicators have been taken into account, grouped in 11 dimensions of well-being, the same proposed at the regional level with the exception of the Subjective well-being domain. At the local level, the composite indicators have not been provided, even if some recent interesting proposals could be found in Chelli et al. (2016), Mazziotta (2018), Davino et al. (2018) and Costa et al. (2019).

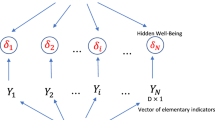
Therefore, to take into account the multidimensionality of well-being, this study focuses on modeling the dependence relationships between the different BES domains at NUTS-3 level.

To deal with the theoretical issue of modeling a very complex multivariate dependence structure, we propose the use of Non-Parametric Bayesian Networks (NPBNs), as introduced in literature by Hanea et al. (2006) and Kurowicka and Cooke (2006). Based on the pair-copula construction (PCC) and D-vines theory (Bedford and Cooke 2002; Joe 1996), NPBNs build the joint density using the joint normal copula without requiring any parametric assumption on the marginals, as opposed to the parametric models that work with Gaussian distributions. The main advantage consists in avoiding the bad common practice of variables’ discretization when the marginals are far from normal; more often, the discretizazion destroys the true underlying dependence structure.

The main goal of this work is to show BNs potentialities, working in a non-parametric setting by taking advantage of the mathematical framework provided by normal copula.

Based on our knowledge, the Non-Parametric BNs, in the context of BES framework, have not been applied yet; only two works recently applied the parametric BNs to national BES indicators (D’Urso and Vitale 2020; Onori and Jona Lasinio 2020).

The paper is organized as follows. In the Sect. 2 we provide a detailed description of the Non-Parametric Bayesian Networks, analyzing their mathematical properties and connections with the graphical models called vines. In Sect. 3, we describe the BES indicators used in the model, the adopted learning procedure and the main application results. The last section addresses some conclusions and open research problems.

2 Non Parametric Bayesian Networks

2.1 Basics on Bayesian Networks

Bayesian Networks (BNs) (Pearl 1988; Cowell et al. 1999) belong to the wider class of probabilistic graphical models. Properly, they are multivariate statistical models satisfying sets of (conditional) independence statements encoded in a Directed Acyclic graph (DAG).

Each node in the graph is matched with a random variable while the edges between the nodes represent probabilistic dependencies among the corresponding variables. The arrow from $X_{i}$ to $X_{j}$ means that $X_{j}$ is influenced by $X_{i}$: $X_{j}$ is said the child of $X_{i}$ that, in turn, is said the parent of $X_{j}$. The set of parents of $X_{j}$ in the graph G is denoted by $pa(X_{j})$.

The independence assumptions can be read off from the DAG looking at the pairs of nodes that are not directly connected to one another by a directed arc.

Furthermore, each node is associated with a conditional distribution given its parents and, according to the conditional independence statements entailed in the DAG, the joint distribution can be factorized as:

$$\begin{aligned} p(X_{1}\ldots X_{p})= \prod _{j=1}^{p} p(X_{j}|pa(X_{j})) \end{aligned}$$

(1)

Despite the broad fields of applicability and popularity, in the parametric setting, the most inference and structural learning methods work under the joint multinomial assumption for discrete data and under the joint normality for the continuous data. In the mixed case, it is possible to define discrete-continuous models for which the conditional Gaussian distribution is assumed with the constraint that continuous nodes can not have discrete children. Therefore, for discrete BNs, the marginal and conditional probability tables have to be specified for root and child nodes, respectively; for the mixed and continuous BNs, the influence of the parents on a child is translated in terms of partial regression coefficients when the child is regressed on the parents.

However in many real situations, the marginal distributions of the involved variables are far from Gaussian; therefore, their dependencies could not be adequately modeled by the Gaussian multivariate distribution.

The weakness of the Gaussian and discrete-Gaussian BNs is that the joint normality is a very strong assumption, rarely met in practice.

In search for flexible multivariate distributions, copula modeling has become very popular in many fields of applications and, recently, many papers also combine the theory of copulae and Bns. More popular is the class of Non-Parametric BNs (NPBNs) introduced in the following section and proposed in literature by Hanea et al. (2006) and Kurowicka and Cooke (2006).¹

2.2 Non-Parametric Bayesian Networks

The Non-Parametric continuous BNs are strictly related to the graphical models called vines and their properties. Therefore, in this section, the copula-vine approach to continuous BNs is described and analyzed in detail.

In the Non-Parametric Bayesian Networks, the nodes can represent either quantitative and (ordinal) qualitative variables whose dependence structure is modelled by copulae. The term “Non-Parametric” is justified by the fact that no distributional assumption on the marginals is required.

Properly, for continouous NPBNs, their nodes correspond to continuous variables with arbitrary invertible distribution functions while each arc is associated with a (conditional) rank correlation between parent and child assessed by means of the selected copula.

More specifically, Normal vines are invoked in order to realize the dependence structure specified via (conditional) rank correlations on the continuous BNs. Normal copula, as shown in detail later, inherits the important property, from normal distributions, that a zero partial correlation is equal to a zero conditional correlation that, in turn, implies conditional independence.

The link between copula vines and Bns could be more clear if we focus on BNs quantifications; in order to do it, one only needs to specify all one-dimensional marginal distributions and the (conditional) rank correlations associated to the arcs of the BN. To specifiy the joint distribution and to sample it, we need to translate the BN rank correlation specifications in rank correlations specifications suitable for a (normal) vine; then, by means of vine sampling procedure, one can sample the joint distribution of the original variables.

The other important feature related to the normal copula-vine approach, concerns the possibility to perform conditioning analytically. Dealing with a joint normal vine, in fact, any conditional distribution will also be normal with known mean and variance.

More specifically, let $X_{1}$ and $X_{2}$ be two continuous random variables, with invertible distribution functions $F_{1}$ and $F_{2}$ while $Y_{1}$ and $Y_{2}$ are the corresponding transformation to standard normal variables. The conditional distribution of $X_{1}|X_{2}$ is obtained directly applying $F_{1}^{-1}(\varPhi (Y_{1}|Y_{2}))$.

The next paragraphs describe in detail the vine-copula graphical models showing the strict relationship between vines and continuous BNs.

2.3 Pair Copula Construction and Regular Vines

Let F be a n-dimensional distribution function of the random vector $\mathbf {X}=(X_{1},\ldots X_{n})$ with univariate marginals $F_{1}\ldots F_{n}$.

A n-variate copula is a multivariate cumulative distribution function (cdf) $C:\left[ 0,1\right] ^{n} \rightarrow \left[ 0,1\right]$ with $n\in N$ and uniformly distributed marginals on the interval $\left[ 0,1\right]$, i. e. U(0, 1).

By Sklar (1959) theorem, we have that every cdf F with marginals $F_{1}\ldots F_{n}$ can be written as:

$$\begin{aligned} F(\mathbf {x})=C(F_{1}(x_{1}),\ldots ,F_{n}(x_{n})) \end{aligned}$$

(2)

for some appropriate n-dimensional copula C.

Therefore, the copula from Eq. 2 can be expressed as:

$$\begin{aligned} C(\mathbf {u})=F(F_{1}^{-1}(u_{1}),\ldots ,F_{n}^{-1}(u_{n})) \end{aligned}$$

(3)

where C is unique if $F_{1}\ldots F_{n}$ are continuous.

In other words, Sklar (1959) theorem states that the modeling of the marginal distributions can be adequately separated from the depedence modeling in terms of copula. Hence, a large number of variables can be handled without introducing any distributional assumption on the marginals.

As far as the joint density function f is concerned, if F is absolutely continuous with strictly increasing continuous marginals $F_{1}\ldots F_{n}$, through the chain rule decomposition, we have:

$$\begin{aligned} f(\mathbf {x})=c(F_{1}(x_{1})\ldots F_{n}(x_{n}))\prod _{i=1}^{n}f_{i}(x_{i}) \end{aligned}$$

(4)

where the copula density c is uniquely determined.

While for the bidimensional case there is an exaustive literature on bivariate copula families, their extension to multivariate case is not straightforward [for theoretical references to copulae we can refer to Joe (1997)]. Standard multivariate copulae, such as Gaussian or Student-t, lack in flexibility and accuracy in modeling the dependence structure in higher dimensions.

Inspired by the work of Joe (1996), Bedford and Cooke (2001, 2002) and Kurowicka and Cooke (2006) proposed a rich and flexible class of multivariate copulae based on bivariate (conditional) copulae (called pair copulae). This decomposition of the multivariate copulae into product of a bivariate ones is known in literature as pair-copula construction (PCC). Each pair-copula can be selected indipendently from the others allowing a great flexibility in dependence modeling.

Since in higher dimensions the number of possibile pair-copulae constructions grows up significantly (for example, for five variables, there are 240 possible constructions), Bedford and Cooke (2001, 2002) proposed a graphical representation called regular vine (R-vine) in order to organize them.

More generally, a n-dimensional R-vine is a set of $n-1$ trees such that the first tree comprises n nodes, identifying $n-1$ pairs of variables and also $n-1$ corresponding edges. Therefore each subsequent tree is derived such that all the edges of tree $T_{i}$ turn into nodes of the tree $i+1$; furthermore, two edges in $T_{i}$, which become nodes in $T_{i+1}$, are joined by an edge in $T_{i+1}$ only if these edges share a common node in $T_{i}$.

To each edge is associated a (conditional) rank correlation (r), as in the NPBNs, that can be arbitrarily chosen in the interval $[-1,1]$ using a copula; hence, a joint distribution based on the copula-vine specification can be defined and it is always consistent.

But, each vine branch may also be associated with partial correlations $(\rho )$. Therefore, it is possible to assign to each edge of the vine a partial correlation, dealing with a partial correlation vine specification.

The correlations could be computed by means of Pearson’s transformation, valid both for normal and normal copula distributions:

$$\begin{aligned} {\rho }= 2 \sin \left( \frac{\pi }{6}\cdot {r}\right) \end{aligned}$$

(5)

The above transformation holds both for marginal and partial correlation coefficients.

Bedford and Cooke (2002) showed that each such partial correlation vine specification uniquely determines the correlation matrix.

Moreover, it could not uniquely identify a joint distribution given a set of marginal distributions; the latter could not be consistent with the defined partial correlations unless joint normal distribution is used for which there is only one joint normal distribution satisfying all partial correlation specifications (Hanea et al. 2006). Only for both joint normal and joint normal copula distributions, it holds that a zero partial correlation implies conditional independence.

A joint distribution could be portrayed as a vine equivalent to a BN remarking that the translation of the rank correlation specification for a BN in that corresponding to a vine could be cumberstome, involving the numerical evaluations of multiple integrals, unless the joint normal copula is assumed.

Now, given a Non-Parametric continuous BN for which the nodes represent continuous univariate random variables with invertible distribution functions and the arcs are associated with (conditional) parent–child rank correlations (that has been proved to be algebraically independent), its joint distribution is specified by means of the copula-vine approach, sampling the BN structure by using the procedures for normal vines as well explained in following steps by Hanea et al. (2006).

Given the random variables $X_{1},\ldots ,X_{n}$, with continuous, invertible distribution functions $F_{1},\ldots ,F_{n}$:

• 1. $X_{1},\ldots ,X_{n}$ are transformed to standard normal variables $Y_{1},\ldots ,Y_{n}$ via $Y_{i}=\varPhi ^{-1}(F_{i}(X_{i}))$ $\forall \, i=1,\ldots ,n$;

• 2. the vine on $Y_{1},\ldots ,Y_{n}$ is constructed; given that $\varPhi ^{-1}(F_{i}(X_{i}))$ are strictly increasing functions, the (conditional) rank correlations associated to the edges of the vine are the same; by Pearson’s transformation, they are then converted to partial correlations;

• 3. the correlation vine specification is obtained and there is only one joint normal distribution for $Y_{1},\ldots ,Y_{n}$ that satisfies it.

• 4. given the (unique) correlation matrix, it is possible to sample the joint normal distribution of $Y_{1},\ldots ,Y_{n}$;

• 5. For each sample, $(F_{1}^{-1}(\varPhi (y_{1})),\ldots ,F_{n}^{-1}(\varPhi (y_{n})))$ is finally computed specifying, in this way, the joint distribution of the variables $X_{1},\ldots ,X_{n}$.

The partial correlations are also important, in this context, since they are involved in the computation of an overall measure of multivariate linear dependence equal to the determinant of the correlation matrix. In the following theorem Hanea et al. (2010) states that:

Theorem 1

Let D the determinant of a n-dimensional correlation matrix, with $D>0$. For any partial correlation BN specification:

$$\begin{aligned} D = \prod \left( 1- \rho _{ij;D_{ij}}^{2}\right) \end{aligned}$$

where $\rho _{ij;D_{ij}}^{2}$ is the partial correlation assigned to the arc connecting node i and j, with conditioning set$D_{ij}$, and the product is taken over all arcs in the BN.

D varies in [0, 1], attaining 1 if all variables are independent, 0 in case of multivariate linear dependence. All values in such interval take into account the different degree of dependence. As shown in the next paragraph, this overall measure of linear dependence plays a key role since it is involved in the model selection procedure.

2.4 Learning the NPBNs

When the DAG is not known, one needs to define both the structure and parameters using data and$\setminus$or experts’ elicitation.

When learning the NPBN directly from data, following the procedure proposed by Hanea et al. (2010), the univariate marginal distributions are the empirical ones, and the only assumption is that the joint distribution is modeled by a normal copula. Also the conditional rank correlations are estimated from data.

The learning algorithm, proposed by Hanea et al. (2010) and implemented in the UniNet software, consists of two steps:

• 1. the joint normal copula distribution has to be validated in order to accept it as a valid model for the multivariate data;

• 2. if the joint normal copula is not rejected, the chosen NPBN (entailing conditional independence relationships) has to be validated as an adequate model of the saturated graph.

To perform these two validation steps, the determinant of the rank correlation matrix is used, being a suitable measure of multivariate dependence (see Theorem 1).

More formally, the following three determinants are involved:

• DER, the determinant of the empirical rank correlation matrix;

• DNR, the determinant of the empirical normal rank correlation matrix computed on the transformed variables (that are standard normals) applying the inverse Pearson transformation to obtain rank correlations;

• DBBN, the determinant of the rank correlation matrix of a BN under the assumption of joint normal copula.

Obviously, the DNR and DER do not coincide since the former assumes the normal copula distribution; the DNR, being equal to the determinant of the saturated model, could be equal to the DBBN only when the BN is a saturated graph. In all other cases, the following inequality holds: $DBBN>DNR$.

The first validation step is accomplished by simulating the sampling distribution of DNR and checking whether DER is within the 90% central confidence band of DNR.

Only if the normal copula assumption could not be rejected on the basis of the above test, we can next search for a non saturated NPBN which represents the DNR parsimoniously. Therefore, to select a good model that does not differ significantly from that induced by the saturated graph, the idea is to remove from the graph all the edges with very small rank correlations. Since they less contribute to the value of the approximated determinant (DBBN) induced by the non saturated graph, the difference between its associated DBBN and the DNR could be negligible.

Furthermore, it is worth remembering that a zero conditional rank correlation implies conditional independence that is represented in the DAG structure with the absence of the arc.

In this work, we followed the same model selection procedure proposed by Hanea et al. (2010). Properly, the BN is built by adding arcs between variables only if their (unconditional) rank correlation is among the largest (the threshold value is fixed by the researcher). Therefore, this second validation step consists in constructing a skeletal BN: starting from a BN with no arcs, all the edges whose rank correlation (in the normal rank correlation matrix) is greater than the given threshold are added in the network.

Then, if DNR is within the 90\% central confidence band of the DBBN (the determinant of the skeletal BN), the selected structure could be considered a good approssimation of the saturated graph; otherwise, we proceed to add an arc between the pair of nodes for which their rank correlation is greater (in absolute value) than the rank correlation of any other not connected pair. The arcs are added, once a time, until the DNR is within the 90\% central confidence band of DBBN (that is recomputed whenever an arc is added).

The last step could also include the possibility to set very small correlations to zero (without too much perturbing the determinant of the correlation matrix) in order to get a more parsimonious model, with less arcs.

Obviously, in a selected BN, we could have nodes with more than one parent and DBBN changes according to the ordering of the parents. As argued in Hanea et al. (2010), there is no the “best” model: the ordering of parents nodes and the choice of the arcs’ directions may be based on expert knowledge and other non statistical considerations. For example, not all edges corresponding to very small rank correlations have to be excluded in the model if the researcher is interested to study them. The conclusion is that there will be different BNs that well approximate the saturated model.

3 Dependence Relationships Between Local BES Indicators

The learning procedure based on NPBNs theory will be, here, applied to infer the dependence relationships between the BES indicators at the local level, with reference to the dashboard of indicators defined in the 2019 edition.

This analysis, focused on the Italian provinces’ dinamics, can enhance the knowledge about the well-being determinants in the territories, intrinsically characterized by high eterogeneity and variability.

Many factors influencing people’s well-being are local issues, in particular in Italy, historically affected by strong territorial disparities. We also argue that many political and social choices in the territories have an impact on national policies.

The analysis based on “local” indicators, on the one hand, allows to identify the main distinctive features of well-being of large communities and areas but, on the other hand, it could be less accurate (depending on data quality and availability).

Different from National BES framework, the equity and sustainability are not well investigated and measured at the provincial level. The Subjective well-being domain is completely missing while the Innovation and Social relationships domains are composed of only two basic indicators do not covering all the main themes established in the National BES program.

In the 2019 edition, 56 basic indicators are provided by Istat grouped in 11 BES domains. Many basic indicators are available until the year 2016; therefore, we focused the analysis on the reference year 2016 for which holds the old partition of Italian Provinces in 110 units.

In order to deal with a reduced number of variables, we applied the learning algorithm procedure to a dashboard of 12 composite indicators.

The definition of a composite indicator depends on the used aggregation function that, in turn, is strictly connected to the concept of compensability among variables. As in Casadio Tarabusi and Guarini (2013), by compensability we mean the possibility of compensating any deficit in a dimension with a suitable surplus in another.

In this paper we adopted the aggregation method proposed by Istat in the national BES framework: the Mazziotta–Pareto Index (MPI, Mazziotta and Pareto (2016)), that is a partially non-compensatory composite indicator.

We acknowledge that the debate on composite indicators’ construction is an open-research problem. For a deepened analysis about the interpretation and the possible fallacy of the compensatory composite indicators we can refer to Alaimo and Maggino (2020) who argued that there is no “such thing as the best method”, meaning that all proposed aggregation methods show strengths and weaknesses.²

Using the Mazziotta–Pareto approach, each composite indicator was computed under the hypothesis of no substitutability of the components; properly, the basic indicators were first standardized and adjusted according to its polarity, i.e. the sign of the relationship between the indicator and the phenomenon to be measured (its composite indicator). Then, they were aggregated by the arithmetic mean adjusted by a coefficient that penalyzes all units that, mean being equal, have a greater balance among the indicators values. In this study, each MPI was chosen with negative penalty.³

Missing values were few and imputed using the last available value of the time series; otherwise the regional datum were imputed.

In this context, the main issue concerns the appropriate choice of the basic indicators defining the synthetic ones, according to the formative approach.

The basic indicators, for each domain, were chosen according to their relevance with the investigated phenomenon, their clear interpretation and, above all, according to data availability and quality. The selected indicators try to mimic those of national BES but with many limits since, for some of them, their sample estimates are not available at the local level.

In Table 1 are reported the individual indicators used to construct the corresponding 12 composite indicators. They are one more than the number of domains since, for Security, as for national BES, two composite indices were computed.

In Figs. 1, 2, 3 and 4, we reported the maps of values (in deciles) for each composite indicator. While for some indicators, like those beloging to the economic pillar, the well-known gap between North and South of Italy is more evident, for other domains, a strong eterogeneity also emerges between contiguous territories. This confirms the requirement of an in-depth analysis of well-being that must be investigated also at the provincial level to discover similarities and inequalities between urban areas and territories.

Fig. 1

Maps of Health, Education and Work

Fig. 2

Maps of Economic well-being, Social relationships and Politics

Fig. 3

Maps of Security (property crimes), Security (violent crimes) and Environment

Fig. 4

Maps of Landascape Quality of services and Innovation

We also point out that the selected indicators, for each domain, are in line with those proposed in the works of Chelli et al. (2016), Mazziotta (2018) and Davino et al. (2018).

We are aware that some domains, especially Innovation and Social relationships, are poorly measured: other basic indicators covering other important aspects of the domain under consideration need to be included. It is worth noting that this work does not claim to provide a consolidated dashboard of the composite indicators at the provincial level, but only focuses on modeling the dependence structure of BES indicators by means of NPBNs.

Table 1 Composite and basic indicators for the 11 BES provinces domains

3.1 The Estimated BN Based on Composite Indicators

The model selection procedure has been mainly data-driven even if arcs’ direction and parents’ ordering have been set on the basis of experts’ knowledge and some other logical constraints.

We remember that no distributional assumptions are required for the univariate marginal distributions that are taken directly from data. Also the conditional rank correlations⁴ are computed from data.

Following the Hanea et al. (2010) procedure described in Sect. 2.4, the first step consists in validating the multivariate normal copula assumption for the variables in Fig. 5.

Fig. 5

The Non-Parametric Bayesian network with no arcs

Fig. 6

The Non-Parametric Bayesian Network with no arcs whose nodes are substituted by monitors showing the empirical marginal distributions

Based on 1.000 simulations, the $90\%$ central confidence interval for DNR is [0.0007823, 0.005867]. The determinant of the empirical rank correlation matrix (DER) is 0.0017598 thus falling within the above interval; therefore, we can not reject, at the 10$\%$ level, the hypothesis that data were generated from the joint normal copula.

In Fig.  6, the same variables are reported but the nodes are replaced by monitors showing the associated empirical marginal distributions (also the mean ± the standard deviation is reported). By inspecting the histograms, we can notice that some distribution are far from Gaussian.

In the second step we build the so called skeletal BN: starting from the empty graph, we add to it all arcs whose (unconditional) rank correlation between the corresponding variables (in the normal rank correlation matrix) is greater than 0.29. The corresponding NPBN is shown in Fig.  7.

Fig. 7

The estimated NPBN

In order to verify if the selected NPBN adequately summarize the saturated graph, the determinants DBBN and DNR must be compared.

Based on 1.000 simulations, the 90% confidence interval for DBBN is $\left[ 0.0013101 ;0.010968\right]$. The DNR is 0.0037651 falling within the above interval. Then the NPBN, in Fig. 7, can be considered a valid model, well approximating the saturated one.

We can notice that it has some arcs with very small associated conditional rank correlations (as we can see looking at the number associated with each arc of the network). We search for a more convenient representation deleting all arcs whose conditional rank correlation is less than a threshold value fixed to 0.16.

The new NPBN, with less arcs than the previous one, is reported is Fig. 8.

Fig. 8

The estimated NPBN with arcs whose conditional rank correlation is grater or equal to 0.16

Its determinant slightly varies with respect to that associated with the previous NPBN, from 0.0069879 to 0.00825332, and its 90\% confidence interval is $\left[ 0.0016859; 0.011718\right]$. The DNR falls within the above interval, thus, we choose the last network as the final estimated model.

As expected, the NPBN is able to describe the complexity of the dependence structure of the well-being domains. By inspecting the estimated NPBN of Fig. 8, looking at the parent - child relationships, it is worth underlining the link among the educational level, the employment and the economic prosperity confirming the key role of the school system as a source of the economic growth and of the labour market development. From the graph we can also read off that the node Education, as expected, directly influences the rate of cultural employment (node Innovation). The latter, in turn, together with the Quality of services, affects the presence of city parks and historical green in the urban areas, highlighting the positive link between culture and landscape care. The node Education itself influences Landscape through an indirect path.

It is not surprising that the node Qual_serv has the highest number of parents nodes: in particular, the Labour Market conditions, the economic prosperity, the educational level and the political leadership, actively involved at the local level, directly influence the quality of public services for the citizen.

As regards the node Soc_rel, we infer that the job conditions, the economic prosperity and the educational system promote the birth of no profit associations and higher levels of school services.

Moreover, the quality of the Environment directly depends on the economic and work conditions while the citizens’ health is directly related to the educational level and to the landscape maintenance.

The security, represented by the two indices accounting for violent crimes and property crimes, are positively correlated. The property crimes tend to increase if the levels of landscape maintenance and quality of services are high, most likely because these crimes are more frequent in the North of Italy.

The violent crimes, instead, tend to increase if there is low attention to the environmental issues. As a matter of fact the rate of homicides is higher in the South of Italy where some municipal services such the share of waste landfilled and that of separate collection are insufficient.

Moreover, from the network, we can read off all conditional independence relationships between variables, since each node can influence the others also through indirect paths. Using the concept of the Markov blanket⁵ of a node, one can indentify the subset of all nodes in the graph carrying information about the node. Hence, the Markov blanket contains all information one needs to infer a target variable X, making all the variables not belonging to it redundant. Looking at the estimated network, we can read off, for example, that, given Work, Education, Politics, Qual_serv, Environment and Soc_rel, the variable Ec_well_being and all remaining variables in the network are conditional independent.

Also Politics, if Work, Ec_well_being, Education and Qual_serv are known, becomes conditional independent from all other variables in the network. Moreover, knowing the state of the variables Work, Education, Qual_serv and Landscape, no other information is needed to do inference on the variable Innovation.

Given Work, Ec_well_being, Security_PC and Security_VC, the variable Environment and all remaining variables in the network are conditional independent.

As far as the variables Soc_Rel and Health are concerned, we can observe that their Markov Blankets consist of only their parents; therefore, the information carried by all other variables in the model is redundant when that on own parents nodes is given.

In the last application, based on the expert knowledge, we include in the model the variable called Pop_density that measures the provincial population density. The final estimated network, after performing the same validation steps as before, are reported in Fig. 9.

By inspecting the network, we can notice that Pop_density is directly connected with the nodes Qual_serv, Landscape and Security_PC. In particular, to more densely populated cities correspond higher levels of services and landscape maintenance but lower levels of security providing evidence that social unrest and uncertainty affect the suburbs of the large Italian cities.

Fig. 9

The estimated NPBN taking into account population density

Given the estimated structure, the NPBN could also be used to address a number of queries, operating conditioning analitically thanks to the normal copula assumption (Kurowicka and Cooke 2006), as explained in the Sec.  2.2.

In particular, UniNet allows the visualization of both the original unconditional (showed in gray) and the new conditional distributions (showed in black). Therefore, in the next paragraph, some examples of possible scenarios will be simulated.

3.1.1 Conditioning

In the first simulated scenario, the interest is to observe the impact of the employment on all other indicators, fixing the mean value of the node Work to 110 (see Fig. 10).

As expected, a province with a very high level of employment and a reduced gender gap in Labour Market seems to show an high level of general prosperity since, except for Security_PC, all the mean values of all other indicators are greater or almost equal to the mean value of the unconditional marginal distributions (see Fig. 6). The same conclusion could be addressed by inspecting the monitors: the conditional distributions, shown in black, are shifted towards the right with respect to the unconditional ones, shown in gray.

Fig. 10

Fist scenario

In the second scenario, we focus on the important role of services for the citizens. In Fig. 11a, we have simulated a situation in which there is an high level of economic properity while, in Fig. 11b, a situation in which there is economic prosperity but a low quality of services.

Fig. 11

Second scenario

If we compare the conditional distributions of Fig. 11a, b, it is evident that, even in case of economic prosperity, a low level of public services shifts the conditional distributions of the indicators Landscape and Politics towards the left. Lower levels of the services are also correlated with lower levels of the indicators Work, Education and Social_relationships. It is worth noting also the strong relationship with the indicators Security_PC and Pop_density.

The urban areas characterized by a high level of economic prosperity and a low level of services do not show a high level of employment even if it is above the mean. Moreover, these areas are characterized by a low level of landscape maintenance, a low population density and high levels of security, especially with reference to the property crimes. We argue that the evident shift of the conditional distribution of the node Politics towards the left could deserve further investigations about the incidence of the political choices, at the local level, on the quality and efficiency of the social and public services.

4 Conclusions

In this paper we focus on the use of the Non-Parametric BNs framework to deal with complex multivariate distributions. Relaxing the hypothesis of multivariate normality in favour of the normal copula, this class of BNs becomes more flexible and can be applied in many real contexts in order to discover complex dependence relationships between variables, without any distributional assumption on the marginals.

Their use is particularly suitable in the context of BES analysis since well-being is intrinsically multidimensional and could be adequately measured only by means of a multivariate approach.

This study clearly showed that all dimensions of well-being are strictly interdependent. The impact of the educational system on the labour market conditions (gender gaps and employment rate) and on the economic growth is confirmed. The public services play a key role and could be identified as one of the main determinants of well-being perception. In this regards, a more active role of political leaders in the territories is mandatory in order to improve the levels of social and public services, the level of job placement and, more generally, the quality of life of their citizens. Also the lower levels of security in the densely populated cities could merit further attention since it is a symptom of the climate of growing social unrest that characterizes many large Italian cities. More generally, the application to BES of Provinces enriched the analysis disclosing many strong disparities also among contiguous territories, suggesting more in-deep studies on the local dinamics involving the social, economic and environmental aspects of daily life.

From a theoretical point of view, many other open research problems have to be addressed in the future such that of embedding the temporal component in the model allowing comparisons over the time. Another mathematical issue concerns the possibility to include in the model the spatial component whose proxy, usually, is a nominal variable for which the categories’ ordering is meaningless.