Modelling trend life cycles in scientific research using the Logistic and Gompertz equations

Abstract

Scientific topics vary in popularity over time. In this paper, we model the life cycles of 200 trending topics by fitting the Logistic and Gompertz models to their frequency over time in published abstracts. Unlike other work, the topics we use are algorithmically extracted from large datasets of abstracts covering computer science, particle physics, cancer research, and mental health. We find that the Gompertz model produces lower median error, leading us to conclude that it is the more appropriate model. Since the Gompertz model is asymmetric, with a steep rise followed a long tail, this implies that scientific topics follow a similar trajectory. We also explore the case of double-peaking curves and find that in some cases, topics will peak multiple times as interest resurges. Finally, when looking at the different scientific disciplines, we find that the lifespan of topics is longer in some disciplines (e.g. cancer research and mental health) than it is others, which may indicate differences in research process and culture between these disciplines.

Article Highlights

• 1. We use a method called MACD to extract 200 trending topics from 5.4 million abstracts spanning the period 1975-2017.

• 2. We compare the Logistic and Gompertz growth curves for the task of modelling trend publication counts over time

• 3. Some trends experience multiple peaks in publications.

• 4. We compare the data for four different scientific disciplines, and find that trends in cancer and mental health research are popular for longer, on average, than topics in computer science and particle physics.

Introduction

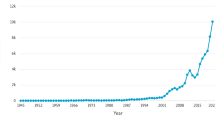
In scientific research, it often seems as if a small number of topics occupy just about every student, researcher, and funding body. A recent example in the field of computer science is deep learning, which is the idea that a neural network with multiple layers outperforms conventional machine learning methods. While deep learning is not a completely new idea (Fukushima, 1980; LeCun et al., 1989), deep neural networks rose to widespread prominence when they were applied to an image classification competition by Krizhevsky et al. (2017). The rise in interest since 2012 has been steep—a search for “deep learning” in the computer science bibliography dblp (DBLP 2021) yields 47 titles from 2011, but 10,368 from 2020. Using dblp, we can also find other topics which behaved in a similar way (Fig. 1). For example, ontologies rose very quickly in popularity before reaching a saturation point in 2006. The rise of cloud computing was even swifter, taking place between 2008–2015. Finally, neural networks peaked twice, once in the 1990s and then again in present times with the advent of machine learning.

Fig. 1

The proportional popularity of the terms “ontologies”, “cloud”, and “neural networks” in dblp. Proportional popularity is the percentage of documents in a given year that mention the term at least once

The three graphs in Fig. 1 share certain characteristics, such as exponential rises and peaks. This work aims to determine which mathematical model is the most appropriate for modelling this behaviour. Being able to do this would be both interesting and useful, for scientific research often foreshadows technological advancement. A mathematical model of the trend life cycle would make it possible to predict how long a trend is likely to be popular for, and how much publishing activity may result from it. This could aid researchers and funding bodies in making decisions about research.

While various models for scientific growth have been proposed, there is as of yet no consensus on which specific model should be used. In previous work researchers chose a number of known trends, searched for their frequency in one or more databases, then fitted their candidate models to the resulting curves (Bettencourt et al., 2006; Trappey & Wu, 2008; Adamuthe & Thampi, 2019). However, the weakness in these approaches lies in the small number of trends used, and in the fact that they are manually chosen by the researchers, which introduces the prospect of selection bias. This work differs in that we use a burst detection algorithm to automatically select 200 emerging trends from four large datasets of abstracts. We fit two candidate models to the publications-over-time trajectories of the detected trends, then compare the error of the models to determine which one best fits the data. We also consider the case of double-peaking trends such as neural networks, and investigate whether this behaviour can be modelled via a superposition of curves. To our knowledge this is the first study of its type to use trends that are automatically detected.

Background

Attempts to model scientific growth date from as early as the 1930s. For example, Wilson and Fred (1935) fitted a growth model to the frequency of publications on nitrogen fixation by plants (see Fig. 2) and used it to predict that almost 100 papers per year would be published on the topic by 1960.

Fig. 2

The number of publications per year on the topic of nitrogen-fixation by leguminous plants in the period 1860–1935. The solid line shows the best-fit s-curve model fitted to the data. This figure was taken from Wilson and Fred (1935)

One of the key publications in the modern study of trend modelling is Bettencourt et al. (2006). In this work the authors manually searched the post-World War 2 physics literature for mentions of Feynman diagrams, then plotted the number of authors publishing on the topic over time. They fitted several epidemiological models and compared the error. In their follow-up work, Bettencourt et al. (2008) they repeated this process with literature searches for cosmological inflation, cosmic strings, prions, H5N1 influenza, carbon nanotubes, and quantum computing. They found that a SEIR epidemic model provided the best fit to the data. SEIR splits the population of authors into four states (susceptible, exposed, infected, recovered) and models the transition between states. The fact that it can be used to model the number of authors publishing on a topic might imply that ideas grow and spread much like viruses do. However, in comparison to other models, SEIR is complex, requiring five parameters to be fitted. One of the parameters, which here corresponds to the total population of authors who might be susceptible to an idea, is particularly difficult to estimate.

Alternative approaches make use of simpler models. Campani and Vaglio (2014) and Ho et al. (2014) applied the Logistic model (a classical symmetrical S-curve growth model with just three parameters) to publication-over-time counts for Organic Light Emitting Diodes (OLEDs) and fuel cells respectively. Both groups gathered their data via a keyword search in the scientific bibliography Web of Science. They reported a reasonable level of fit, although Campani and Vaglio (2014) commented that the symmetric Logistic model did not quite match their asymmetric data. Trappey and Wu (2008) tackled the same problem with a slightly different dataset—the sales volumes for a number of different electronic products. They fitted the Logistic, Gompertz, and time-varying Logistic models to their data, and found that the time-varying Logistic model gave the lowest error, followed by the asymmetric Gompertz model.

Egghe and Rao (1992) use 20 datasets gathered from another work. All of their datasets span the period 1965–1987, and include e.g. MEDLINE, smoking and health, world aluminum abstracts. They fit exponential, Logistic, Gompertz, and power model curves to their datasets, finding that the power model and Gompertz model are the best performers. The other models do not fit very well. Young (1993) incorporates a larger sample of trends: 46 datasets gathered from correspondence with other authors. They fit nine different models. An issue with this work is that the datasets are not described—it is not clear whether they correspond to publication rates in science, industry, or something else entirely.

Perhaps the most similar work to ours is Adamuthe and Thampi (2019). They fit the Logistic and Gompertz models to six time series gathered via keyword searches for mainframes, minicomputers, cluster computing, grid computing, autonomic computing, and cloud computing on four datasets (two patent datasets, IEEE, and Science Direct). They find that the Gompertz model provides lower error in the majority of cases, although there was considerable variation between the results from the four datasets.

In most of the studies above, the typical procedure followed by researchers is to identify a list of key terms, search for them in patent and/or scientific bibliographies, then fit one or more models to the resulting time series and compare the error. The most common models used are the Logistic and Gompertz models. In this paper, we will gather a much larger dataset of time series by detecting trends automatically from scientific literature. Otherwise, we intend to follow the typical procedure shown in Fig. 3. The next subsections will deal with the methodological hurdles this presents, such as the choice of datasets, how to detect trends automatically, and the mathematical formulations of the growth curve models we will be using.

Fig. 3

A typical methodology workflow for a technology life cycle modelling paper. We follow the same workflow, except that that we use a trend detection algorithm in place of the known key terms

Dataset choice

For this work, we require one or more datasets of scientific texts. Ideally, these would be large datasets that span decades, each focussed on a relatively narrow subject area so that fine-grained trends can be revealed. They must also be freely available on the web, both for ease of access and to make our work reproducible by others.

Happily, several such datasets exist in the form of bibliographies of abstracts. While scientific abstracts contain less text than full papers, they have several advantages. Firstly, since abstracts are used to summarise the content of papers, they contain important information in a dense format. Secondly, unlike full papers, they are rarely hidden in PDFs that would need to be decoded. Finally, many abstract repositories have free bulk download APIs to facilitate this kind of natural language research.

Among the largest abstract repositories on the web are PubMed (biomedical abstracts), arXiv (abstracts and pre-prints from a range of subjects, most notably physics), and Semantic scholar (a range of subjects, including computer science abstracts (Ammar et al., 2018)). We chose to work with subsets of these three databases to form the four datasets described in the list below, and in Table 1.

• 1. Computer Science: Semantic scholar abstracts which contain the dblp tag in their metadata.

• 2. Particle Physics: arXiv abstracts in the categories hep-ex, hep-lat, hep-ph and hep-th.

• 3. Mental Health: PubMed abstracts tagged with the MeSH keyword “Mental Health” or one of its sub-terms.

• 4. Cancer: PubMed abstracts tagged with the MeSH keyword “Neoplasms” or one of its sub-terms.

Table 1 Descriptions of all four datasets. Note that the last two are subsets of the much larger PubMed abstract database

The documents in each dataset consist of title, abstract, and year fields. To preprocess this data, we combine title and abstract, then remove all punctuation (preserving acronyms), convert letters to lowercase, and then lemmatize each word using NLTK’s WordNetLemmatizer (Bird et al., 2009).

Detecting trends automatically

Rotolo et al. (2015) define an emerging technology as having radical novelty, relatively fast growth, coherence, prominent impact, uncertainty, and ambiguity. The easiest of these properties to measure is fast growth—in this case, a sudden change in the number of publications mentioning a term over a short span of years. The practice of detecting events like these is called burst detection, and in text mining it has been used, for example, to classify emails as spam (Kleinberg, 2002) and to detect trends on Twitter (Mathioudakis & Koudas, 2010) and in news streams (Takahashi et al., 2012).

Various forms of burst detection exist. For instance, Kleinberg (2002)’s popular method uses a two-state automaton which transitions from a non-bursty to bursty state as the flow of emails increases. However, applying burst detection methods meant for emails and news streams to scientific literature is not straightforward because of the ways the domains differ. Kleinberg’s algorithm relies on the assumption that the size of the dataset remains stable over time. By contrast, scientific literature has undergone vast growth in the last few decades.

A method previously applied to trend detection in scientific literature is based on Moving Average Convergence-Divergence (MACD). MACD was originally developed for the stock market, and, when applied to price histories for stocks, gives quick assessments of whether the price is trending up or down (Murphy, 1999). MACD makes use of two moving averages of a time series, one with a long span (which is the number of datapoints used to create the average) and one with a short span. When the trajectory of the time series changes, the shorter moving average responds more quickly, causing the two moving averages to cross. These intersections can be interpreted as buy/sell signals.

MACD was first applied to scientific literature by He and Parker (2010) who used it to detect bursts in the MeSH keywords of PubMed papers. We adapted their method in our later work, in which we demonstrated that it could be used to detect bursty terms in computer science (Tattershall et al., 2020). We will also be using it in this work to detect trends in our chosen datasets.

In order to apply MACD-based burst detection, we first create a vocabulary for each dataset. This vocabulary contains all unique words in the full set of abstracts, along with phrases between 2 and 5 words. The least common terms are then excluded from the vocabulary to reduce noise/conserve memory. For each remaining term in the vocabulary, we count the number of documents it appears in each year. This creates a time series of document frequency/time for each term. Since the total number of documents in each dataset has increased over the years (see Fig. 4), we divide the data for each year by the number of documents in that year.

Fig. 4

The number of documents per year in each of our four datasets. There is a substantial increase in yearly publishing in the period 1975–2017. The dip in publishing experienced in the very last year of the dataset occurs because publications are often backdated, so the data for these years is slightly incomplete

We then apply our algorithm to each time series to create a burstiness score for each term (Tattershall et al., 2020). These terms are then clustered based on their co-occurrence in documents (e.g. “internet of things” and “iot” are grouped as they often appear together). At this point, we manually examine the most bursty clusters and remove publishing artefacts such as “elsevier science bv right reserved”. We also split clusters where substantially different terms have been grouped together. Finally, we select the top 50 burstiest remaining clusters in each dataset. This forms the set of 200 terms upon which we will test our models.

The Logistic and Gompertz models

For this part, we compare two relatively simple models, the Logistic and Gompertz curves. The Logistic model was first introduced as a model of population growth by (Verhulst, 1845). It is symmetric about its peak, and describes a form of growth that is initially exponential, but slows as an upper limit is reached (Fig. 5a). The mathematical formulation that explains the model and that we will be using is:

$$\begin{aligned} y_{\mathrm{L}} = \frac{k}{1+e^{-r(t-b)}} \end{aligned}$$

(1)

The curve is controlled by three parameters: r, which determines the width of the curve, k, which determines the cumulative frequency at the upper limit, and b, which determines the location of the peak on the x-axis.

Fig. 5

The Logistic and Gompertz models, visualised. The graphs on the left show the cumulative frequency over time, while those on the right show the rate

The Gompertz model differs from the Logistic model in that it is asymmetric about its peak. It assumes that the rate of growth is inversely proportional to the current cumulative frequency, such that as cumulative frequency increases, growth slows. The peak—or point of inflection on the cumulative frequency graph—occurs at 37.79% of the eventual maximum cumulative frequency of the model (Fig. 5b). The formulation of the Gompertz model that we use is:

$$\begin{aligned} y_{\mathrm{G}} = ke^{-e^{r(t-b)}} \end{aligned}$$

(2)

We can calculate double-peaked variants of these two models using curve superposition. For example, a double-peaked Logistic model is represented by:

$$\begin{aligned} y_{\mathrm{L}} = \frac{k_1}{1+e^{-r_1(t-b_1)}} + \frac{k_2}{1+e^{-r_2(t-b_2)}} \end{aligned}$$

(3)

while a double-peaked Gompertz model is

$$\begin{aligned} y_{\mathrm{G}} = k_1e^{-e^{r_1(t-b_1)}} + k_2e^{-e^{r_2(t-b_2)}} \end{aligned}$$

(4)

These equations have twice as many parameters as their single-peaked equivalents.

Since the parameter r corresponds to the width of the curve, we can use it to find a proxy for trend duration. We follow Burg and Schachter (2017) by deriving the time period $\Delta t$ in which the central 80% of documents are published (full derivations can be found in the Appendix). For the Logistic model this is:

$$\begin{aligned} \Delta t_{\mathrm{L}} = \frac{\ln (81)}{r} \end{aligned}$$

(5)

The derivation is similar for the Gompertz model and yields the result:

$$\begin{aligned} \Delta t_{\mathrm{G}} = \frac{1}{\log (-\log (0.9))-\log (-\log (0.1))} \end{aligned}$$

(6)

Curve fitting

We used the Loglet Lab software (Burg & Schachter, 2017) to fit the Logistic and Gompertz models to our 200 trends. Loglet Lab uses a sophisticated fitting algorithm based on Monte-Carlo annealing which we have translated into Python for this project. It acts to minimise the root mean-squared error when compared to the original time series. In the double-peaked case, this is the error of the superposition of the two curves. Since initial constraints are required for the parameters r, k, and b, we set these following Loglet Lab’s example (see Table 2).

Table 2 Initial constraints for the parameters r, k, and b, as used in Loglet Lab (Burg & Schachter, 2017)

After fitting, we scale each time series so that it scales between 0 and 1, then calculate the mean-squared error between the time series and the Logistic and Gompertz models for each. Scaling ensures that the error measurements are comparable across different trends.

Results and discussion

As described in the previous section, our burst detection method identifies 50 trends for each of the four datasets. For illustration, the 10 burstiest terms for each discipline are shown in Table 3.

Table 3 The top 10 burstiest historical and current trends detected in the four datasets. A full list of clusters can be found in the GitHub repository for this paper in the file 200clusters.csvA full list of clusters can be found in the GitHub repository for this paper in the file 200clusters.csv

We then calculate the popularity of each term over time, and use the Loglet Lab algorithm to fit Logistic and Gompertz models to each time series. An example result for the term “XML” is shown in Fig. 6. In this case, we can see that both models fit the curve relatively well, although they slightly overestimate the year at which XML’s popularity peaks.

Fig. 6

An example of the Logistic and Gompertz models fitted to the data for “XML”

In order to compare the models more quantitatively, we calculate the error of the Logistic and Gompertz models for each time series, then compare the mean error across the dataset (Table 4. We find that the Gompertz model produces a lower error than the Logistic model, and an independent t-test tells us that this result is significant (p value 0.0001). This implies that publication activity on a trend tends to be asymmetric, with the bulk of work occurring after the year in which publications peak.

Table 4 A statistical comparison of the error of the Logistic and Gompertz models across the entire dataset

Double-peaking trends

By inspection, we know that some of our trends experience multiple peaks. In order to investigate this behaviour further, we fit the double-peaked Gompertz equation (Eq. 4) to each of our trends, then compare the error with that produced by the single-peaked equation.

We find that using the double-peaked equation reduces the error in 157 of 200 cases. This is not unexpected, because the greater number of parameters in the double-peaked equation allows it more easily overfit the data. However, the situation becomes more nuanced when we look at individual trends. For example, in the case of “big data” (Fig. 7a), the single-peaked equation is still superior in terms of both subjective fit and error reduction. “Cloud” (Fig. 7b) is a more ambiguous example. Changing from single to double-peaked reduces the error slightly, but without much impact on fit. Finally, in the last two examples, “internet” and “recurrent” (Fig. 7c, d), the double-peaked model is clearly superior. Therefore, it is our opinion that the best way to detect double-peaked curves is through setting a threshold of proportional error reduction at which a term is deemed to have multiple peaks.

Fig. 7

Comparison between the single- and double-peaked Gompertz models for four computer science examples. The error of the models is shown in the legend of each graph

Variation between different scientific disciplines

We are interested in learning whether trend duration differs between disciplines. In this subsection, we calculate trend duration using Eq. 6, then compare the results for the 50 trends from each dataset (Table 5). Since the data is strongly skewed towards lower values (see Fig. 8), we compare medians rather than means.

The median trend duration in particle physics and computer science appears to be about a decade shorter than in mental health and cancer research. Using Mood’s median test, we calculate the p value of this difference to be 0.0001. There are smaller differences in trend duration in particle physics and computer science, and between mental health and cancer research, but these are not significant (p values 0.55 and 0.84 respectively). This implies that trends last, on average, for much longer in some disciplines than in others.

Table 5 The median time-span into which 80% of the publications on a given trend fall, by dataset

Fig. 8

Boxplots of the trend durations (as calculated using Eq. 6) for the four different datasets

Finally, we investigate the relationship between peak year (the year in which the model predicts that the greatest number of documents will be published on a trend) and trend duration. Our hypothesis was that modern trends last are shorter lived, but to our surprise, this is not true. When we plot the two variables against each other in Fig. 9, we find that the trendline is positive in every discipline, indicating that trend durations have slightly increased over time. There is, however, greater variation in trend lifespan for more recently peaking trends.

Fig. 9

The relationship between the predicted peak year and the predicted duration for each trend. The solid black line in each plot represents the regression line, while the shaded area is the 95% confidence interval. The regression line has a positive slope for all four disciplines, although the correllation is not strong

Examples of trends and fitted models across all four disciplines

To illustrate the effectiveness of Gompertz curve for the task of modelling trend lifecycles, in this subsection we present the best-fitted Gompertz model for the 36 most bursty trends in each discipline. These can be seen in Figs. 10, 11, 12 and 13. In cases where the error reduction gained by moving to the double-peaked equation is greater than a threshold (set empirically to 0.005), we use that equation instead.

The fit is good in most cases, and the longer trend durations in the PubMed datasets are clearly visible. We see many examples of double-peaked trends, such as “Higgs” and “neutrino oscillation” in particle physics, “depression” in mental health research, and “HR” (hormone receptor) in cancer research. There are also rare cases in which there is almost no decline in publishing activity for decades after the peak, such as “Magnetic Resonance Imaging” (MRI) and “Polymerase Chain Reaction” (PCR) in cancer research. Perhaps this behaviour is due to the fact that, after discovery, both MRI and PCR went on to become tools that facilitated further research.

Regarding the limitations of the model, we see that it has some difficulty with publication spikes that last for only one or two years. These are common in the particle physics dataset (which is much smaller than the other three; see Table 1). Additionally, it has difficulty modelling the rare cases where trends experience sudden drops in popularity, such as “beta-catenin” in the cancer research dataset.

Fig. 10

The Gompertz model fitted to trends in the computer science dataset. The dashed line represents the model, while the solid line is the observed data for each trend

Fig. 11

The Gompertz model fitted to trends in the particle physics dataset gathered from arXiv. The dashed line represents the model, while the solid line is the observed data for each trend

Fig. 12

The Gompertz model fitted to trends in the mental health dataset. The dashed line represents the model, while the solid line is the observed data for each trend

Fig. 13

The Gompertz model fitted to trends in the cancer research dataset. The dashed line represents the model, while the solid line is the observed data for each trend

Conclusion

We have fitted the Logistic and Gompertz models to 200 trends gathered from four separate datasets of scientific abstracts. While both of these models have been used before, prior work has not been on this scale and has relied upon manually-selected trends. We found that the fit of the Gompertz model is superior, having lower error on average than the Logistic model. Our results further support the view that the Gompertz model is applicable across different scientific domains. This leads us to the conclusion that the growth of scientific interest in a new idea is asymmetric, with the bulk of publications occurring after the year of peak productivity. We also note double-peaked trends in the data, supporting the idea that topics can go in and out of fashion. Finally, we calculated the median trend duration for four different scientific disciplines and found that trends tend to be popular for shorter periods in computer science and particle physics than in cancer and mental health research.

Appendix: A derivation of trend duration

This section follows Burg (2017)’s derivation of the Logistic curve’s span, then extends it to find an equivalent span for the Gompertz curve. By span, or duration, we mean the time taken for a curve to go from 10% of k (the maximum cumulative frequency) to 90% of k. This time period covers the central 80% of activity.

The Logistic equation is:

$$\begin{aligned} y_{\mathrm{L}} = \frac{k}{1+e^{-r(t-b)}} \end{aligned}$$

We are searching for the points $(t_1, y_1)$ where $y_1$ is 0.1k and $(t_2, y_2)$ where $y_2$ is 0.9k.For $y_1$:

$$\begin{aligned} y_1 &= \frac{k}{10} = \frac{k}{1+e^{-r(t_1-b)}} \\ 10 &= 1+e^{-r(t_1-b)} \\ 9 &= e^{-r(t_1-b)} \end{aligned}$$

(7)

And for $y_2$:

$$\begin{aligned} y_2& = \frac{9k}{10} = \frac{k}{1+e^{-r(t_2-b)}} \\ \frac{10}{9} &= 1+e^{-r(t_2-b)} \\ \frac{1}{9} &= e^{-r(t_2-b)} \end{aligned}$$

(8)

Combining Eqs. (7) and (8) , we have:

$$\begin{aligned} 9*9& = \frac{e^{-r(t_1-b)}}{e^{-r(t_2-b)}} \\ 81& = e^{-r(t_1-b)+r(t_2-b)} \\ 81& = e^{r(t_2-t_1)} \end{aligned}$$

Therefore:

$$\begin{aligned} \varDelta t_L = t_2 - t_1 = \frac{\ln {(81)}}{r} \end{aligned}$$

(9)

The derivation for the Gompertz curve is more complex, and while a result is included in Burg and Schachter (2017), it does not match our calculation. We start with the Gompertz equation, which is:

$$\begin{aligned} y_{\mathrm{G}}& = ke^{-e^{r(t-b)}} \\ y_1& = \frac{k}{10} = ke^{-e^{r(t_1-b)}} \\ \frac{1}{10}& = e^{-e^{r(t_1-b)}} \\ \ln {\left(\frac{1}{10}\right)}& = -e^{r(t_1-b)} \\ \ln {\left(-\ln {\left(\frac{1}{10}\right)}\right)}& = r(t_1-b) \\ t_1& = \frac{\ln {\left(-\ln {\left(\frac{1}{10}\right)}\right)}}{r}+b \end{aligned}$$

(10)

Likewise:

$$\begin{aligned} t_2 = \frac{\ln {(-\ln {(\frac{9}{10})})}}{r}+b \end{aligned}$$

(11)

Therefore:

$$\begin{aligned} \varDelta t_G = t_2 - t_1 = \frac{\ln {(-\ln {(\frac{9}{10})})}-\ln {(-\ln {(\frac{1}{10})})}}{r}{.} \end{aligned}$$

(12)