Gender bias in journals of gender studies

Abstract

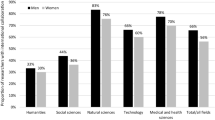
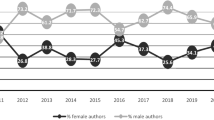
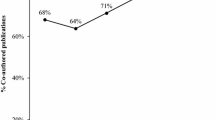
The causes of gender bias favoring men in scientific and scholarly systems are complex and related to overall gender relationships in most of the countries of the world. An as yet unanswered question is whether in research publication gender bias is equally distributed over scientific disciplines and fields or if that bias reflects a closer relation to the subject matter. We expected less gender bias with respect to subject matter, and so analysed 14 journals of gender studies using several methods and indicators. The results confirm our expectation: the very high position of women in co-operation is striking; female scientists are relatively overrepresented as first authors in articles. Collaboration behaviour in gender studies differs from that of authors in PNAS. The pattern of gender studies reflects associations between authors of different productivity, or “masters” and “apprentices” but the PNAS pattern reflects associations between authors of roughly the same productivity, or “peers”. It would be interesting to extend the analysis of these three-dimensional collaboration patterns further, to see whether a similar characterization holds, what it might imply about the patterns of authorship in different areas, what those patterns might imply about the role of collaboration, and whether there are differences between females and males in collaboration patterns.

Appendix

Theory and mathematical model for the intensity function of interpersonal attraction

The mathematical function for describing the three-dimensional distribution of co-author pairs’ frequencies (N _ij ) is a special case derived from Kretschmer’s mathematical model for the intensity function of interpersonal attraction (Who is attracting whom? “Intensity” means the extent of this attraction).

In the wake of a tangible change of paradigm in science a number of holistic theories have emerged which are based on the idea of holographic interacting entities in the world, with several of them also implying a field concept.

For example:

• magnetic fields in physics

• morphogenetic fields of living organisms in evolutionary biology

• psychological fields in psychology or sociology (Gestalts)

• etc.

The field concept says a force, which emanates from a field generates a balanced evenness among all the individual components taken in their totality. However, the field fails to determine completely the behaviour of individual components in terms of the predictability of these individual components.

This is called conciseness (or‘Prägnanz’) tendency in Gestalt psychology, i.e. there is a ′tendency towards a good Gestalt′ of the totality. The stable final state is, if possible, built up in a simple, well-ordered, harmonic and uniform manner in line with definite rules. Several authors take the view that these fields can be mathematically described.

Interpersonal attraction is a major area of study in social psychology.

Whereas in physics, attraction may refer to gravity or to the electromagnetic force, interpersonal attraction can be thought of force acting between two people tending to draw them together.

When measuring interpersonal attraction, one must refer to the qualities of the attracted as well as the qualities of the attractor. That means one must refer to their personal characteristics. For example, in terms of the degree of the node F _x and the degree of the node F _y (Newman 2002) or in terms of productivity: X = log i of co-author F _x and Y = log j of co-author F _y (Kretschmer and Kretschmer 2007, 2009).

The notion of “birds of a feather flock together” points out that similarity is a crucial determinant of interpersonal attraction.

But: Do birds of a feather flock together or do opposites attract?

This leads to a model of complementarities:Complementarities are a crucial determinant of the Intensity Function of Interpersonal Attraction.

Derivation of the Intensity Function of Interpersonal Attraction:

We assume the intensity structure of mutual attraction Z _XY can be described by a function of a special power functions’ combination (X is the value of a special personality characteristic (quality) of an attracted and Y is the value of the same personality characteristic (quality) of the attractor and in case of mutual attraction also vice versa).

The crucial determinant of interpersonal attraction (similarity or dissimilarity) suggests considering the distance A between the qualities of persons $(A = |X - Y|)$ as the independent variable of a power function:

$$ Z^{*} = c_{1} \cdot (A + 1)^{\alpha } $$

with c ₁ = constant; the 1 is added because log A is not possible in case A = 0. We see that as A increases, dissimilarity increases.

A power function with only one parameter (unequal to zero) is either only monotonically decreasing or only monotonically increasing; when referred to both proverbs we obtain: either “birds of a feather flock together” or “the opposites attract”, cf. Fig 3.

Fig. 3

Power functions with different values of parameter α (non-log presentation). In both patterns X – Y is the abscissa with X – Y = 0 (similarity is highest) in the middle and Z*is the ordinate. On the left pattern, the parameter α is negative: “Birds of a feather flock together”, i.e. decrease of interpersonal relations with increasing dissimilarity. On the right pattern, the parameter α is positive: “Opposites attract”, i.e. increase of interpersonal relations with increasing dissimilarity (this figure is a copy of a figure in Kretschmer and Kretschmer 2007)

In order to fulfil the inherent requirement that both proverbs with their extensions can be included in the representation, the second step of approximation follows.

Information in brief: There is a complementary variation of similarity and dissimilarity. As dissimilarity increases between persons, similarity decreases, and vice versa. Similarity is greatest at the minimum of A and least at the maximum and vice versa, dissimilarity is greatest at the maximum and least at the minimum.

A is a variable with the two opposite poles A _min and A _max. The sum of A _min and A _max is a constant. Thus,

$$ A_{\text{complement}} = A_{ \min } + A_{ \max } - A $$

That means, the variable A _complement increases by the same amount as the variable A decreases and vice versa.

Example: $A_{ \min } = 0,\; A_{ \max } = 3$:

A	A complement
0	3
1	2
2	1
3	0

• the model of complementarities leads to the conclusion to use additionally the “complement of the distance A” (A _complement) as the independent variable of a second power function:

$$ \begin{aligned} Z^{**}& = c_{2} \cdot (A_{\text{complement }} + 1)^{\beta } \\ Z_{\text{A}} & = {\text{constant}}_{\text{A}} \cdot (A + 1)^{\alpha } \cdot (A_{\text{complement}} + 1)^{\beta } . \\ \end{aligned} $$

The relationships of the two parameters α and β to each other determine the expressions of the complementarities (similarities, dissimilarities) in each of the eight shapes, cf. Fig. 4. In correspondence with changing relationships of the two parameters α and β to each other a systematic variation is possible from “Birds of a feather flock together” to “Opposites attract” and vice versa.

Fig. 4

Patterns with varying combinations of the two parameters α and β (non-log presentation). In all of the eight patterns X – Y is the abscissa with X – Y = 0 in the middle and Z _A is the ordinate

While in the upmost pattern “Birds of the feather flock together” is more likely to be in the foreground, the bottom pattern reveals that “Opposites attract” is more likely to be salient.

Starting pattern by pattern counter clockwise from the upmost pattern towards the bottom pattern, “Birds of the feather flock together” diminishes as “Opposites attract” emerges. Vice versa, starting pattern by pattern counter clockwise from the bottom pattern towards the upper pattern, “Opposites attract” diminishes as “Birds of the feather flock together” emerges.

For the purpose of completion,

• Let the addition $(B = X + Y)$ as the opposite of subtraction $(A = |X - Y|),$ be the independent variable of the third power function

  $$ {\text{Z}}^{***} = c3 \cdot (B + 1)^{\gamma } $$

• and the complement (B _complement) be the independent variable of the fourth power function

$$ Z^{****} = c4 \cdot (B_{\text{complement}} + 1)^{\delta } $$

In analogy to A and A_complement:

$$ B_{\text{complement}} = B_{\min } + B_{\max } - B $$

$$ Z_{\text{B}} = {\text{constant}}_{\text{B}} \cdot (B + 1)^{\gamma } \cdot (B_{\text{complement}} + 1)^{\delta } $$

Because the function Z _A can vary independently from the function Z _B we assume the intensity of mutual attraction Z _XY is proportional to the product of the two functions Z _A and Z _B :

$$ Z_{XY} \sim Z_{A} \cdot Z_{B} $$

Therefore, the Intensity Function of Interpersonal Attraction (Social Gestalt) can be formalized as follows (Prototypes of Social Gestalts, cf. Fig. 5 ):

$$ \begin{aligned} Z_{\text{XY}} & = {\text{constant}} \cdot (A + 1)^{\alpha } \cdot (A_{\text{complement}} + 1)^{{{\upbeta}}} \cdot (B + 1)^{\gamma } \cdot(B_{\text{complement}} + 1)^{\delta } \\ {\text{with }} A &= |X -Y|\,{\text{and}} \, B{ = }X + Y \\ A_{\text{complement}} &= A_{\min } + A_{\max } - A \\ B_{\text{complement}} &= B_{\min } + B_{\max } - B \\ A_{\min } &= \left( {\left| {X - Y} \right|} \right)_{\min } \\ A_{\max } & = \left( {\left| {X - Y} \right|} \right)_{\max } \\ B_{\min } & = \left( {\left| {X + Y} \right|} \right)_{\min } \\ B_{\max }& = \left( {\left| {X + Y} \right|} \right)_{\max } \end{aligned} $$

Fig. 5

Prototypes of social Gestalts (non-logarithmic presentation). Several empirical patterns matching the five Prototypes were already taken out and presented in Kretschmer (2002). The distribution of co-author pairs’ frequencies N _ij is one of the examples. The non-logarithmic presentation is similar to the left prototype. However, in this paper we are showing the corresponding log–log–log presentation only (log N _ij with log i and log j)

Measurement of the variables X, Y and Z _XY including $X_{\min } = Y_{\min }$ and $X_{\max } = Y_{\max }$ depends on the subject being studied.

Examples (types) of social interactions (Z _XY) are collaboration, friendships, marriages, etc., while examples (types) of characteristics or of qualities of these individual persons (X or Y) are age, labor productivity, education, professional status, degree of a node in a network, etc.

Whereas Z _A and Z _B are each alone produce two-dimensional patterns, the bivariate function Z _XY shows three-dimensional patterns (non-logarithm presentation).

We show one example of how to measure the variables X and Y in relation to the function of the distribution of co-author pairs’ frequencies$Z_{\text{XY}} = N_{ij}$. The physicist and historian of science de Solla Price (1963) conjectured that the logarithm of the number of publications has greater importance than the number of publications per se.

Thus, using the logarithm of the number of publications (log i or log j, respectively) as an indicator of the personal characteristic ‘productivity’, we define:

$$ X{ = }\log i \quad Y{ = }\log j $$

$$ A = |\log i - \log j| \quad B = \log i + \log j $$

Consequently:

$$ \begin{gathered} A_{\min } = |X - Y|_{\min } = 0{\text{ with }}\log i = \log j \hfill \\ A_{ \max } = |X - Y |_{ \max } = | ( {\text{log }}i )_{ \max } - {\text{log1}} | = |{\text{log1}}- (\log j )_{\text{max }} | = (\log i )_{ \max } = (\log j )_{ \max } \hfill \\ B_{\min } = (X + Y)_{\min } = \log 1 + \log 1 = 0 \hfill \\ B_{\max } = (X + Y)_{\max } = (\log i)_{\max } + (\log j)_{\max } = 2({ \log }i)_{\max } = 2({ \log }j)_{\max } \hfill \\ \end{gathered} $$

Let us assume a specific value for the maximum possible number of publications i (or j, respectively) of an author as a standard for such studies, which does not vary depending upon the given sample. We assume that the maximum possible number of publications of an author is equal to 1000, i.e.

$$ A_{\max } = \log 1000 = 3\quad B_{\max } = 2A_{\max } = 6 $$

Thus, it follows that:

$$ \begin{gathered} A_{\text{COMPLEMENT}} = 3 - |\log i--\log j|,{\text{with }}A_{\text{COMPLEMENT}} + 1 = 4 - |\log i - \log j| \hfill \\ B_{\text{COMPLEMENT}} = 6 - (\log i + \log j),{\text{with }}B_{\text{COMPLEMENT}} + 1 = 7 - \left( {\log i + \log j} \right) = 7 - \log i - \log j \hfill \\ \end{gathered} $$

Thus, the theoretical mathematical function for describing the social Gestalts of the distribution of co-author pairs’ frequencies results in the previously mentioned logarithmic version (log N _ij ):

$$ \log N_{ij} = c + \alpha \cdot \log \left( {\left| {X - Y} \right| + 1} \right) + \beta \cdot \log \left( {4 - \left| {X - Y} \right|} \right) + \gamma \cdot \log \left( {X + Y + 1} \right) + \delta \cdot \log (7 - X - Y) $$

with X = logi and Y = logj and with c = constant.