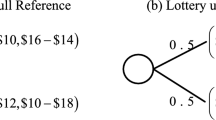Abstract
We experimentally investigate the effect of an independent and exogenous background risk to initial wealth on subjects’ risk attitudes and explore an appropriate incentive mechanism when identical or similar tasks are repeated in an experiment. Taking a simple chance improving decision model under risk where the winning probabilities are negatively related to the potential gain, we find that such a background risk tends to make risk-averse subjects behave more risk aversely. Furthermore, we find that risk-averse subjects tend to show decreasing absolute risk aversion (DARA), and that a random round payoff mechanism (RRPM) would control the possible wealth effect. This suggests that RRPM would be a better incentive mechanism for an experiment where repetition of a task is used.


Similar content being viewed by others
Notes
In this kind of chance improving decision situation, the comparative static prediction is usually ambiguous and it crucially depends on the probability distribution of outcomes. The general comparative statics are analysed by McGuire, Pratt, and Zeckhauser (1991) where the decision situation problem is similar to ours in principle but different in some specific aspects. For example, their decision problem can be regarded as choosing an optimal expenditure with the possibility of the loss of the initial wealth while our problem is choosing an optimal giving-up amount among potential gains without the loss of the initial wealth.
In the real world, there are a few situations similar to this. For example, consider a firm’s problem trying to merge with a company taking on its debt (instead of paying for the merge), a salesman who attempts to sell a car giving up a large part of his or her own potential profit, a job seeker who would be willing to lower his or her willingness-to-accept wage to take a job, and so on.
Repeating an identical or similar task has been one of the norms in economics experiments. Repetition is generally used for two purposes. First, it gives subjects an opportunity to learn about the experiment. Second, it gives experimenters an opportunity to get more data. Whatever the purpose is, experimenters are usually interested in subjects’ decision at the individual task. For more details, see Lee (2007).
We actually used the set of numbers {2, 4, 5, 6, 7, 8, 16, 21, 24, 27} for x and y, 35 for m, and 40 pence (4 pence multiplied by 10 since the actual earnings for Task 1 are multiplied by 10 as explained below) for c in the actual experiment. In this paper, we need to consider these numbers when we estimate the risk aversion coefficient using a utility functional.
For Task 2, there was one more treatment related to matching as shown in Table 1: Strangers vs. partners. But, for the purpose of this paper, we find that it is natural to pool the data. So, we pool APM&Strangers and APM&Partners to define the APM group. We define the RRPM group by the same way.
The real earnings for Task 1 in the actual experiment were decided by the following manner: subjects choose a number x at each round, a round is randomly drawn by each subject after the experiment is completed, a random number y at the round is randomly drawn by the subject, the earnings in the round are computed according to the equation (2) using the actual numbers used in the experiment, and then those are multiplied by 10.
It is well known that subjects’ choices in experiments are in general not constant when they repeatedly make a choice for the same risky decision problems (Isaac and James 2000).
For the estimation, we calculated the payoff p i using the actually used decision numbers in the experiment: x={2, 4, 5, 6, 7, 8, 16, 21, 24, 27}, m = 35 and c = 40 pence.
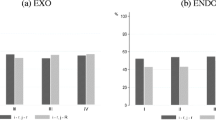
There was one risk-loving subject and two subjects’ risk attitude was indecisive.
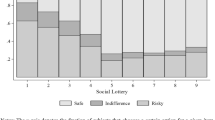
At this round, the abrupt decrease of the mean chosen number in the APM group is not a result of one or two subjects’ choice. Most subjects in the APM group decreased the number accidentally. So, it is more appropriate to exclude all data in the sixth round if we consider it as an outlier. In this case, the difference is still significant (p = 0.089). If we exclude the data up to the second round as we did in the previous subsection, the qualitative results do not change but the statistical significances are improved: p = 0.004 in the case including the sixth round, and p = 0.021 in the case excluding the sixth round.
For example, see Cox and Grether (1996). They report that there is no significant wealth effect in their experiment on preference reversal.
It should be noted that we are here investigating whether the increase of wealth from Task 2 affects subjects’ decisions for Task 1. Thus this is a different question from our first hypothesis which is related to the effect of riskiness in an initial wealth level between APM and RRPM.
It should be noted that there is no possibility that subjects lose money in future rounds and subjects know that in advance. In fact, most experiments are not allowed to make subjects lose money. Of course, money for initial wealth may be given by an experimenter before the experimental session in that case. However, this could also bring up an empirical question called the “house money effect”: a tendency that subjects may behave less risk aversely (e.g., higher marginal propensity to consumer or more risky investment) with such a given endowment than with their own endowment (Clark 2002; Thaler and Johnson 1990).
One would argue that subjects’ decisions in the RRPM group are affected by the potential earnings even if they are not influenced by the accumulated earnings: under RRPM, the potential earnings would be cognitively more relevant than the accumulated earnings. We ran a regression using the potential earnings for the RRPM group, and the results do not change qualitatively: RRPM controls the effect of the potential earnings too. We also ran a regression including both the accumulated earnings and the potential earnings for each group, and the results were qualitatively identical to those which we present here.
If the remaining opportunities (e.g. lotteries) are not identical while those are independent, the answer could be the opposite since such remaining lotteries could be regarded as a background risk. For analysis on the background risk, see Gollier (2001), Eeckhoudt, Gollier, and Schlesinger (1996), and Pratt and Zeckhauser (1987).
References
Binswanger, Hans P. (1980). “Attitudes Toward Risk: Experimental Measurement in Rural India,” American Journal of Agricultural Economics 62, 395–407.
Clark, Jeremy. (2002). “House Money Effects in Public Good Experiments,” Experimental Economics 5, 223–231.
Cox, James C. and David M. Grether. (1996). “The Preference Reversal Phenomenon: Response Mode, Markets and Incentives,” Economic Theory 7, 381–405.
Cubitt, Robin P., Chris Starmer, and Robert Sugden. (1998). “On the Validity of the Random Lottery Incentive System,” Experimental Economics 1, 115–131.
Eeckhoudt, Louis, Christian Gollier, and Harris Schlesinger. (1996). “Changes in Background Risk and Risk Taking Behavior,” Econometrica 64, 683–689.
Eeckhoudt, Louis, Christian Gollier, and Harris Schlesinger. (2005). Economic and Financial Decisions under Risk. Princeton, NJ: Princeton University Press.
Fischbacher, Urs. (1999). “Z-Tree: Zurich Toolbox for Readymade Economic Experiments: Experimenter’s Manual,” Working Paper 21, Institute for Empirical Research in Economics, University of Zurich.
Friedman, Daniel and Alessandra Cassar. (2004). Economics Lab: An Intensive Course in Experimental Economics. London: Routledge.
Gollier, Christian. (1996). “Repeated Optional Gambles and Risk Aversion,” Management Science 42(11), 1524–1530.
Gollier, Christian. (2001). The Economics of Risk and Time. Cambridge, MA: MIT Press.
Gollier, Christian and John W. Pratt. (1996). “Weak Risk Aversion and the Tempering Effect of Background Risk,” Econometrica 64, 1109–1123.
Grether, David M. and Charles R. Plott. (1979). “Economic Theory of Choice and the Preference Reversal Phenomenon,” American Economic Review 69, 623–638.
Guiso, Luigi and Monica Paiella. (1999). “Risk Aversion, Wealth and Background Risk,” unpublished manuscript.
Harless, David W. and Colin F. Camerer. (1994). “The Predictive Utility of Generalized Expected Utility Theories,” Econometrica 62, 1251–1289.
Harrison, Glenn W. (1989). “Theory and Misbehavior of First Price Auctions,” American Economic Review 79, 749–762.
Harrison, Glenn W., Eric Johnson, Melayne M. McInnes, and E. Elisabet Rutström. (2005). “Individual Choice and Risk Aversion in the Laboratory: A Reconsideration,” Working Paper 03–18, Department of Economics, University of Central Florida.
Hey, John D. and Jinkwon Lee. (2005a). “Do Subjects Separate (or Are They Sophisticated)?” Experimental Economics 8, 233–265.
Hey, John D. and Jinkwon Lee. (2005b). “Do Subjects Remember the Past?” Applied Economics 37, 9–18.
Hey, John D. and Chris Orme. (1994). “Investigating Generalizations of Expected Utility Theory Using Experimental Data,” Econometrica 62, 1291–1326.
Holt, Charles A. (1986). “Preference Reversals and the Independence Axiom,” American Economic Review 76, 508–515.
Holt, Charles A. and Douglas D. Davis. (1993). Experimental Economics. Princeton, NJ: Princeton University Press.
Holt, Charles A. and Susan K. Laury. (2002). “Risk Aversion and Incentive Effects,” American Economic Review 92(5), 1644–1655.
Isaac, R. Mark and Duncan James. (2000). “Just Who Are You Calling Risk Averse?” Journal of Risk and Uncertainty 20(2), 177–187.
Kimball, Miles S. (1993). “Standard Risk Aversion,” Econometrica 61, 589–611.
Laury, Susan K. (2005). “Pay One or Pay All: Random Selection of One Choice for Payment,” Working Paper 06-13, Andrew Young School of Policy Studies, Georgia State University.
Lee, Jinkwon. (2006). “Accumulated or Random: An Experimental Investigation on the Payoff Mechanisms under Repetition,” unpublished manuscript.
Lee, Jinkwon. (2007). “Repetition and Financial Incentives in Economics Experiments,” Journal of Economic Surveys 21(3), 628–681.
Lee, Jinkwon and Jose L. Lima. (2004). “The Restart Effect.” In D. Friedman and A. Cassar (eds.), Economics Lab: An Intensive Course in Experimental Economics. London: Routledge.
Loomes, Graham and Robert Sugden. (1998). “Testing Different Stochastic Specifications of Risk Choice,” Economica 65, 581–598.
Loomes, Graham, Peter G. Moffatt, and Robert Sugden. (2002). “A Microeconometric Test of Alternative Stochastic Theories of Risky Choice,” Journal of Risk and Uncertainty 24(2), 103–130.
McGuire, Martin, John W. Pratt, and Richard J. Zeckhauser. (1991). “Paying to Improve Your Chances: Gambling or Insurance?” Journal of Risk and Uncertainty 4, 329–338.
Pratt, John W. and Richard J. Zeckhauser. (1987). “Proper Risk Aversion,” Econometrica 55, 143–154.
Saha, Atanu. (1993). “Expo-Power Utility: A ‘Flexible’ Form for Absolute and Relative Risk Aversion,” American Journal of Agricultural Economics 75, 905–913.
Starmer, Chris and Robert Sugden. (1991). “Does the Random Lottery Incentive System Elicit True Preferences? An Experimental Investigation,” American Economics Review 81, 971–978.
Thaler, Richard H. and Eric J. Johnson. (1990). “Gambling with the House Money and Trying to Break Even: The Effects of Prior Outcomes on Risky Choice,” Management Science 36, 643–660.
Acknowledgements
This paper is a revised version of a chapter in the author’s Ph.D thesis and the main revision was done when the author was affiliated with the Centre for Experimental Economics, University of York. The author is very grateful to John Hey for his comments and supports. The author also thanks Miguel Costa-Gomes, Werner Güth, Dan Levine, Chris Starmer, the editor and an anonymous referee for their helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Appendix A: Proofs of propositions
(Proof of Proposition 1)
First we show that x N = M/2. Define \( D{\left( x \right)} = u{\left( {w_{0} + M - x} \right)} - u{\left( {w_{0} } \right)} - x \cdot u\prime {\left( {w_{0} + M - x} \right)} \). For a risk-neutral person, \( {{\left( {u{\left( {w_{0} + M - x} \right)} - u{\left( {w_{0} } \right)}} \right)}} \mathord{\left/ {\vphantom {{{\left( {u{\left( {w_{0} + M - x} \right)} - u{\left( {w_{0} } \right)}} \right)}} {{\left( {M - x} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {M - x} \right)}} = u\prime {\left( {w_{0} + M - x} \right)} \). Hence, \( D_{N} {\left( {x_{N} } \right)} = u{\left( {w_{0} + M - x_{N} } \right)} - u{\left( {w_{0} } \right)} - x_{N} \cdot {{\left( {u{\left( {w_{0} + M - x_{N} } \right)} - u{\left( {w_{0} } \right)}} \right)}} \mathord{\left/ {\vphantom {{{\left( {u{\left( {w_{0} + M - x_{N} } \right)} - u{\left( {w_{0} } \right)}} \right)}} {{\left( {M - x_{N} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {M - x_{N} } \right)}} = 0 \). Solving this gives x N = M/2. Now we show that x A > M/2. Since x N = M/2, we need to check D A (x N ). Note that for a risk-averse person, \( {{\left( {u{\left( {w_{0} + M - x} \right)} - u{\left( {w_{0} } \right)}} \right)}} \mathord{\left/ {\vphantom {{{\left( {u{\left( {w_{0} + M - x} \right)} - u{\left( {w_{0} } \right)}} \right)}} {{\left( {M - x} \right)} > u\prime {\left( {w_{0} + M - x} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {M - x} \right)} > u\prime {\left( {w_{0} + M - x} \right)}} \). Hence, \( D_{A} {\left( {x_{N} } \right)} - D_{N} {\left( {x_{N} } \right)} = D_{A} {\left( {M \mathord{\left/ {\vphantom {M 2}} \right. \kern-\nulldelimiterspace} 2} \right)} = u{\left( {w_{0} + M \mathord{\left/ {\vphantom {M 2}} \right. \kern-\nulldelimiterspace} 2} \right)} - u{\left( {w_{0} } \right)} - M \mathord{\left/ {\vphantom {M 2}} \right. \kern-\nulldelimiterspace} 2 \cdot u\prime {\left( {w_{0} + M \mathord{\left/ {\vphantom {M 2}} \right. \kern-\nulldelimiterspace} 2} \right)} > 0 \). But, dD A /dx < 0 by SOC. Hence, To satisfy D A (x A ) = 0, x A should be higher than x N = M/2. Thus, x A > M/2. (Q.E.D.)
(Proof of Proposition 2)
Define v = k(u(.)) where k is a concave transformation of u(.), i.e., k(.) > 0, k′(.) > 0, and k″(.) < 0. Hence, k(u)/u > k′(u) ⬄ k(u) > u·k′(u). Then, v is more risk averse than u at every initial wealth level. If we show that v gives up more than u does, we are done. Solving v’s optimization problem generates FOC as following: \( H{\left( x \right)} = k{\left( {u{\left( {w_{0} + M - x} \right)}} \right)} - x \cdot k\prime {\left( {u{\left( {w_{0} + M - x} \right)}} \right)} \cdot u\prime {\left( {w_{0} + M - x} \right)} - k{\left( {u{\left( {w_{0} } \right)}} \right)} = 0 \). Suppose x = x A which was the solution of D A (x A ) = 0 which implies \( x_{A} \cdot u\prime {\left( {w_{0} + M - x_{A} } \right)} = u{\left( {w_{0} + M - x_{A} } \right)} - u{\left( {w_{0} } \right)} \). Denote \( u{\left( {w_{0} + M - x_{A} } \right)} = u_{A} \), u(w 0 ) = u 0 and H(x A ) = H A where u A > u 0 > 0. Then, by a simple calculation, we can show \( H_{A} = k{\left( {u_{A} } \right)} - k{\left( {u_{0} } \right)} - {\left( {u_{A} - u_{0} } \right)}k\prime {\left( {u_{A} } \right)} \). Note that since k′(u) > 0, k″(u) < 0, and u A > u 0 > 0, \( {{\left( {k{\left( {u_{A} } \right)} - k{\left( {u_{0} } \right)}} \right)}} \mathord{\left/ {\vphantom {{{\left( {k{\left( {u_{A} } \right)} - k{\left( {u_{0} } \right)}} \right)}} {{\left( {u_{A} - u_{0} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {u_{A} - u_{0} } \right)}} > k\prime {\left( {u_{A} } \right)} \). That is, \( k{\left( {u_{A} } \right)} - k{\left( {u_{0} } \right)} - {\left( {u_{A} - u_{0} } \right)}k\prime {\left( {u_{A} } \right)} > 0 \). Thus, H A > 0 while D A = 0. Since it is easily seen that dH A /dx < 0, we find that x A ′ which satisfies H A = 0 should be higher than x A . Thus, x A ′ > x A . In other words, a more risk-averse person v chooses a higher x than u does. (Q.E.D.)
(Proof of Proposition 3)
By totally differentiating FOC, we get \({dx_{A} } \mathord{\left/ {\vphantom {{dx_{A} } {dw_{0} }}} \right. \kern-\nulldelimiterspace} {dw_{0} } = {{\left( {u\prime {\left( {w_{0} + M - x_{A} } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \cdot u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)}} \mathord{\left/ {\vphantom {{{\left( {u\prime {\left( {w_{0} + M - x_{A} } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \cdot u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)}} {{\left( {2u\prime {\left( {w_{0} + M - x_{A} } \right)} - x_{A} \,u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {2u\prime {\left( {w_{0} + M - x_{A} } \right)} - x_{A} \,u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)}}\). Since u′ > 0, u″ < 0, \(\operatorname{sgn} {\left( {{dx_{A} } \mathord{\left/ {\vphantom {{dx_{A} } {dw_{0} }}} \right. \kern-\nulldelimiterspace} {dw_{0} }} \right)} = \operatorname{sgn} {\left( {u\prime {\left( {w_{0} + M - x_{A} } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \cdot \,u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)}\). Thus \( u\prime {\left( {w_{0} + M - x_{A} } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \,u\prime \prime {\left( {w_{0} + M - x_{A} } \right)} < 0 \) would imply dx A /dw 0 < 0. But note that DARA preference implies that v = −u′ is a concave transformation of u where v′ > 0 and v″ < 0 (Eeckhoudt, Gollier and Schlesinger 2005). That is, DARA implies that v is more risk averse than u. If we solve the maximisation problem of v, then we get the FOC, \( {\text{I}}{\left( {x_{A} \prime } \right)} = - {\left\{ {u\prime {\left( {w_{0} + M - x_{A} \prime } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \prime \cdot \,u\prime \prime {\left( {w_{0} + M - x_{A} \prime } \right)}} \right\}} = 0 \) where x A ′ is a giving-up amount satisfying FOC, I(x A ′) = 0. From Proposition 2, we know x A ′ > x A since v is more risk averse than u. This implies that I(x A ) > 0 since x A ′, which is higher than x A , should satisfy I(x A ′) = 0 and by SOC, dI(x A )/dx A < 0 if and only if v is concave.
Note that \({\text{I}}{\left( {x_{A} } \right)} = - {\left( {u\prime {\left( {w_{0} + M - x_{A} } \right)} - u\prime {\left( {w_{0} } \right)} - x_{A} \cdot \,u\prime \prime {\left( {w_{0} + M - x_{A} } \right)}} \right)} = { - dx_{A} } \mathord{\left/ {\vphantom {{ - dx_{A} } {dw_{0} }}} \right. \kern-\nulldelimiterspace} {dw_{0} }\). Thus, I(x A ) > 0 implies dx A /dw 0 < 0. (Q.E.D.)
(Proof of Proposition 4)
We here mainly follow Gollier and Pratt (1996). Note from Proposition 2 that if a person is more risk averse at any wealth level, then he or she would choose a higher x. Hence, if we show that a risk-averse person who faces an independent and exogenous background risk to initial wealth would be more risk averse than one who does not face the background risk to initial wealth, then we are done. Denote \( v{\left( {w_{0} + M - x} \right)} = Eu{\left( {w_{\varepsilon } + M - x} \right)} \). If we denote \( z = w_{0} + M - x \), then \( v{\left( z \right)} = Eu{\left( {z + \varepsilon } \right)} \). Since we know that \( { - v\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - v\prime \prime {\left( z \right)}} {v\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {v\prime {\left( z \right)}} > { - u\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - u\prime \prime {\left( z \right)}} {u\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {u\prime {\left( z \right)}} \) implies x v > x u at any z, we only need to show \( { - v\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - v\prime \prime {\left( z \right)}} {v\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {v\prime {\left( z \right)}} > { - u\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - u\prime \prime {\left( z \right)}} {u\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {u\prime {\left( z \right)}} \). Rearranging \( { - v\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - v\prime \prime {\left( z \right)}} {v\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {v\prime {\left( z \right)}} = { - Eu\prime \prime {\left( {z + \varepsilon } \right)}} \mathord{\left/ {\vphantom {{ - Eu\prime \prime {\left( {z + \varepsilon } \right)}} {Eu\prime {\left( {z + \varepsilon } \right)}}}} \right. \kern-\nulldelimiterspace} {Eu\prime {\left( {z + \varepsilon } \right)}} > { - u\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - u\prime \prime {\left( z \right)}} {u\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {u\prime {\left( z \right)}} \), the condition implies \( Eg{\left( {z,\varepsilon } \right)} = Eu\prime \prime {\left( {z + \varepsilon } \right)} \cdot u\prime {\left( z \right)} - Eu\prime {\left( {z + \varepsilon } \right)} \cdot u\prime \prime {\left( z \right)} < 0 \). By noting g(z,E(ɛ)) = 0 since E(ɛ) = 0, we find the condition implies that g(z,ɛ) should be concave in ɛ at any z, that is, g 22 (z,ɛ) < 0. This implies −u″(z)/u′(z) < −u″″(z)/u‴(z) when evaluated at ɛ = 0. By our assumptions of u‴ > 0 and u″″ < 0, this could be satisfied. So this is the necessary condition. In fact, it is easily shown that u‴ > 0 and u″″ < 0 are sufficient for \( { - v\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - v\prime \prime {\left( z \right)}} {v\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {v\prime {\left( z \right)}} > { - u\prime \prime {\left( z \right)}} \mathord{\left/ {\vphantom {{ - u\prime \prime {\left( z \right)}} {u\prime {\left( z \right)}}}} \right. \kern-\nulldelimiterspace} {u\prime {\left( z \right)}} \) by using the implied relationship of \( - Eu\prime \prime {\left( {z + \varepsilon } \right)} = E{\left[ {A{\left( {z + \varepsilon } \right)} \cdot u\prime {\left( {z + \varepsilon } \right)}} \right]} > EA{\left( {z + \varepsilon } \right)} \cdot Eu\prime {\left( {z + \varepsilon } \right)} > A{\left( z \right)} \cdot Eu\prime {\left( {z + \varepsilon } \right)} \) where A(.) denotes the absolute risk aversion coefficient. (Q.E.D.)
1.2 Appendix B: Instructions
These instructions have been used for the RRPM&Stranger group. The instructions for the other treatments are almost identical to this except only a few sentences to explain Partner treatment and/or APM treatment.
1.2.1 Instructions
This is an experiment in the economics of decision-making. If you follow the instructions carefully and make good decisions you may earn a considerable amount of money. You will be paid in private and in cash at the end of the whole session. It is important that you remain silent and do not communicate with the other participants. If you have any questions, please raise your hand and an experimenter will answer your question in private.
1.2.2 Overview
This experiment consists of 10 Rounds. Each Round consists of two Tasks, Task 1 and Task 2 in that order. In each task, your decision problem is to choose your number, which we call x. In each task, another number, which we call y, will be determined. Your potential earnings for each task and for each round will depend on x and y. Your final cash earnings from this experiment will depend on your potential earnings in each round and in each task.
Choosing your number x
In each Task of each Round, you have to choose one number from the set of numbers 2, 4, 5, 6, 7, 8, 16, 21, 24, and 27.
How the other number y will be determined
In Task 1, the other number y will be chosen at random from the same set of numbers 2, 4, 5, 6, 7, 8, 16, 21, 24, and 27.
In Task 2, the other number y will be chosen from the same set of numbers by some other participant in the experiment, who we call your partner for that Round. Your partner will be changed in each Round. Hence, you will never meet the same partner more than once through the 10 Rounds. Your partner will face exactly the same decision task as you, and you and your partner will not know the identity of each other.
How your potential earnings are determined
In every Round and in both Tasks, your potential earnings will depend on x and y in the following way:
-
If x is greater than y then your potential earnings will be (35 − x) times 4 pence.
-
If x is equal to y then your potential earnings will be (35 − x) times 2 pence.
-
If x is less than y then your potential earnings will be zero.
Tables 1 and 2, which are provided on separate sheets, show you the calculated potential earnings for Task 1 and for Task 2 corresponding to your various choices, respectively. Please see the tables and read the examples on those sheets now.
What feedback is given to you after each Task in each Round
For Task 1, a history table for Task 1 on the screen will present you with only the number x you chose for Task 1.
For Task 2, a history table for Task 2 on the screen will present you with the following: the number x you chose in Task 2, the number y your partner chose in Task 2, and your potential earnings for Task 2.
1.2.3 How your cash earnings will be determined
Your cash earnings for Task 1 will be 10 times your potential earnings for Task 1 from a randomly chosen Round: that is, after you completed all the ten Rounds, one of the ten Rounds will be selected at random and the number x , which you choose for Task 1 in that Round, will be recalled. Then, y will be chosen at random. Your potential earnings for Task 1 in that Round are calculated by Table 1 with the x and y, and your cash earnings for Task 1 will be 10 times your potential earnings for Task 1 in that Round.
Your cash earnings for Task 2 will be 10 times your potential earnings for Task 2 from a randomly chosen Round: that is, after you completed all the ten Rounds, one of the ten Rounds will be selected at random, and your potential earnings for Task 2 in that Round will be recalled. Your cash earnings for Task 2 will be 10 times your potential earnings for Task 2 of that randomly selected Round.
Your cash earnings for the experiment as a whole will be the sum of your cash earnings for Task 1 and your cash earnings for Task 2.
1.2.4 An Example
Your cash earnings from Task 1
Suppose that Round 2 is randomly selected after you completed all the ten Rounds and that you chose 4 in Task 1 in that Round. That number will be recalled from your history table for Task 1. Then, the other number y is randomly chosen. For example, if the randomly chosen y is 2, then your potential earnings from Task 1 will be 124p as shown in Table 1 (with x = 4, y = 2). Hence, your cash earnings from Task 1 will be £12.40 (= 10 times 124p). Similarly, if the randomly chosen y is 4, then your potential earnings are 62p as shown in Table 1 (with x = 4 and y = 4) and so your cash earnings from Task 1 will be £6.20 (= 10 times 62p). If the randomly chosen y is 7, then your potential earnings will be 0p as shown in Table 1 (with x = 4 and y = 7) and so your cash earnings from Task 1 will be £0 (10 times 0p).
Your cash earnings from Task 2
Suppose that Round 5 is randomly selected for Task 2 after you completed all the ten Rounds. Your potential earnings in Task 2 in that Round will be recalled from your history table for Task 2. For example, if your potential earnings for Task 2 in that Round was 124p, then your cash earnings from Task 2 will be £12.40 (=10 times 124p). Similarly, if your potential earnings for Task 2 in that Round was 44p, then your cash earnings from Task 2 will be £4.40 (=10 times 44p), and if your potential earnings for Task 2 in that Round was 0p, then your cash earnings from Task 2 will be £0 (=10 times 0p).
Your final cash earnings for the experiment as a whole
For example, if your cash earnings from Task 1 and Task 2 are £5.00 and £3.50 respectively, then your final cash earnings for this experiment will be £8.50 (=£5.00+£3.50).
1.2.5 Some details
Throughout this experiment, the Round number and the Remaining time for the Task will appear on the upper-left part and the upper right part of the screen, respectively. The Task number will be on the center of the screen. Each Round begins with Task 1 and ends with Task 2.
In each Task, please put the number that you choose in the box on the screen, and then click the OK button.
After each Task of each Round, you will have feedback about your choice in that task of that Round, and your history tables for Task 1 and Task 2 will be in the bottom of the feedback screen.
After you finish the 10th Round, an experimenter will come over to you. You will pick one coin at random from an opaque bag (labeled with ‘Round for Task 1’) containing 10 coins numbered from 1 to 10: the number on it determines the Round in which your chosen number x for Task 1 will be recalled. Then, you will pick one coin at random from an opaque bag (labeled with ‘y for Task 1’) containing 10 coins numbered from the set 2, 4, 5, 6, 7, 8, 16, 21, 24 and 27 to decide y for Task 1. As explained above, your cash earnings from Task 1 will be 10 times the potential earnings determined by these x and y. After doing this, you will pick one coin at random again from an opaque bag (labeled with ‘Round for Task 2’) containing 10 coins numbered from 1 to 10 to decide the Round in which your potential earnings for Task 2 will be recalled, and as explained above, your cash earnings from Task 2 will be 10 times the potential earnings for Task 2 of that Round. Your final cash earnings from this experiment will be the sum of your cash earnings from Task 1 and Task 2 as already explained.
The experiment will be finished after you have answered a brief questionnaire and you have been paid your final cash earnings.
Many thanks for taking part.
Rights and permissions
About this article
Cite this article
Lee, J. The effect of the background risk in a simple chance improving decision model. J Risk Uncertainty 36, 19–41 (2008). https://doi.org/10.1007/s11166-007-9028-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-007-9028-3