Abstract
By numerically simulated Bray–Liebhafsky (BL) reaction under a continuously fed well stirred tank reactor (CSTR) conditions, we discussed the attractors and Poincaré 1D maps with respect to flow rate as the control parameter. The new technique of the return maps from transient trajectories over the slow manifold is developed and applied in order to explore its multilayered structure related to dynamical states (periodic and aperiodic -chaotic oscillating modes) of the system. Kinetic relations underlying the slow manifold structure are briefly discussed.





Similar content being viewed by others
Notes
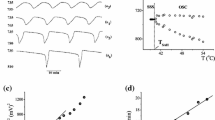
The position of the section plane is indicated in the Fig. 2 by right part of the black horizontal line 2.
References
Field RJ, Burger M (1985) Oscillations and travelling waves in chemical systems. Wiley, New York
Strizhak PE, Ali F, Menzinger M (1999) J Phys Chem A 103:10866–10873
Field RJ, Schneider FW (1989) J Chem Educ 66:195–204
Kawczynski AL, Strizhak PE (2000) J Phys Chem 112:6122–6130
Bray WC (1921) J Am Chem Soc 43:1262–1267
Furrow SD, Noyes RM (1982) J Am Chem Soc 104:38–42
Furrow SD, Noyes RM (1982) J Am Chem Soc 104:42–45
Bray WC, Liebhafsky HA (1931) J Am Chem Soc 53:38–44
Khavrus VO, Strizhak PE, Kawczynski AL (2003) Chaos 13:112–122
Kawczynski AL, Khavrus VO, Strizhak PE (2000) Chaos 10:299–310
Strogatz SH (1994) Non-linear dynamics and chaos with applications to physics, biology, chemistry and engineering, Perseus Books Publishing. L.L.C, Reading
Kolar-Anić Lj, Mišljenović Đ, Anić S, Nikolis G (1995) React Kinet Catal Lett 54:35–41
Kolar-Anić Lj, Čupić Ž, Schmitz G, Anić S (2010) Chem Eng Sci 65:3718–3728
Blagojević S, Čupić Ž, Ivanović-Šašić A, Kolar-Anić Lj (2015) Russ J Phys Chem A 13:2349–2358
Ivanovic-Šašić A, Marković V, Anić S, Kolar-Anić Lj, Čupić Ž (2011) Phys Chem Chem Phys 13:20162–20171
Čupić Ž, Ivanović-Šašić A, Anić S, Stanković B, Maksimović J, Kolar-Anić Lj, Schmitz G (2013) MATCH Commun Math Comput Chem 69:805–830
Maselko J, Swinney HL (1986) J Chem Phys 85:6430–6441
Popović N (2008) J Phys 138:012020. doi:10.1088/1742-6596/138/1/012020
Schmitz G, Kolar-Anić Lj, Anić S, Grozdić T, Vukojević V (2006) J Chem Phys A 110:10361–10368
Stanković B, Čupić Ž, Pejić N, Kolar-Anić Lj (2013) JAND J Appl Nonlinear Dyn 2:285–301
Ivanović AZ, Čupić ŽD, Janković MM, Kolar-Anić Lj, Anić SR (2008) Phys Chem Chem Phys 10:5848–5858
Scott S (1991) Chemical chaos. Clarendon press, Oxford
Desroches M, Krauskopf B, Osinga HM (2008) SIAM J Appl Dyn Syst 7:1131–1162
Acknowledgments
The support of this research by the Ministry of Education and Science of Republic of Serbia through projects No.172015 and 45001 is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix: Standard numerical methods
Appendix: Standard numerical methods
In the return map method, the attractor is first cut by the selected surface in the phase space. Furthermore, only those points are identified where trajectory passes through the selected surface from one chosen direction. Hence, each cycle is counted only once. Thus, quasi-continuous trajectory (line) is completely discretized—transformed to a set of points in the surface. However, the connection between the points is not obvious any more leaving us without the information about their sequence in time. Since we have this information from the original data series, we can use it to construct two-dimensional map, equivalent to the Poincare section, by plotting one chosen variable of the precursor point, against the same variable for the successor point. The Poincaré map, or return map is created this way [22]. Period doubling is indicated by duplicated number of corresponding cross points in the map in comparison to their number in previous dynamical state of the period doubling sequence. Thus, in the case of periodic motions, cross points have finite number and are distinctively localized in the map. In the case of chaotic dynamics, in contrast to periodicity, cross points continuously fill in a part of the map.
Rights and permissions
About this article
Cite this article
Čupić, Ž., Ivanović-Šašić, A., Blagojević, S. et al. Return map analysis of the highly nonlinear Bray–Liebhafsky reaction model. Reac Kinet Mech Cat 118, 27–38 (2016). https://doi.org/10.1007/s11144-016-0998-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11144-016-0998-5