The fluid limit of the multiclass processor sharing queue

Abstract

Consider a single server queueing system with several classes of customers, each having its own renewal input process and its own general service times distribution. Upon completing service, customers may leave, or re-enter the queue, possibly as customers of a different class. The server is operating under the egalitarian processor sharing discipline. Building on prior work by Gromoll et al. (Ann. Appl. Probab. 12:797–859, 2002) and Puha et al. (Math. Oper. Res. 31(2):316–350, 2006), we establish the convergence of a properly normalized state process to a fluid limit characterized by a system of algebraic and integral equations. We show the existence of a unique solution to this system of equations, both for a stable and an overloaded queue. We also describe the asymptotic behavior of the trajectories of the fluid limit.

Appendices

Appendix A: Multidimensional renewal equations

Consider F(t)=(F _ij (t)) _i,j a matrix of increasing and r.c.l.l. functions, such that F _ij (t)=0 when t<0. Let $\hat {F}(\theta)$ denote the Laplace–Stieltjes transform of F. With the definition of matrix-matrix and matrix-vector convolutions assumed in Sect. 1.4, define the renewal matrix as

$$U(t) = \sum_{k=0}^{\infty}F^{*k}(t) .$$

Let H be a vector of measurable and bounded functions. The matrix-renewal equation is the system of equations:

$$V_i(t) = H_i(t) + \sum _{j} \int_{0}^{t}V_j(t-s) \,\mathrm {d}F_{ij}(s) ,$$

for all i. In vector notation, this equation can be written as

$$V(t) = H(t) + ( F * V ) (t) .$$

The following result is quoted from [24] (see also [3, Lemma 2.1]). The notation ϱ(A) is used here for the spectral radius of matrix A.

Lemma A.1

([24], Lemma 3, p. 23)

The function U(t) is finite for all t if, and only if, ϱ(F(0))<1.

If ϱ(F(0))<1, then V=U∗H is the unique measurable and bounded solution to the matrix-renewal equation.

The matrix F will be called lattice if there exists a real value λ such that: as a distribution function, F _ij is concentrated on b _ij +n _ij λℤ (with n _ij ∈ℕ, b _ii =0) and if, assuming that a _ij is a point of increase for F _ij , all values (a _ij +a _jk −a _ki )/λ are integer. A nonnegative matrix F is said to be reducible if there exists a permutation matrix P such that

$$P^{\prime}FP= \left ( \begin{array}{l@{\quad}l}A & B\\0 & C\end{array} \right ),$$

where A and C are square matrices, and it is called irreducible if it is not reducible. The following proposition summarizes the asymptotic results we need. They are a direct consequence of the results of [3] or [24]. The irreducibility condition, which is implicit in [3], is explicitly added here.

Proposition A.1

Let g be a directly integrable function. Then:

• (i) If ϱ(F(∞))=1, F(∞) is irreducible and F(⋅) not lattice, then, for u and v left- and right-eigenvectors of F(∞) for the eigenvalue 1, such that u.v=1,

  $$\lim_{t\to\infty} (U_{ij} * g) (t) = \frac{v_i u_j}{u \varGamma v} \int _0^{\infty} g(s) \, \mathrm {d}s ,$$

  with

  $$\varGamma = \int_{0}^{\infty} s \, \mathrm {d}F(s) = -\frac{\mathrm {d}\hat {F}}{\mathrm {d}\theta}(0) .$$

  If one component of Γ is infinite, the limit above is 0.

• (ii) If $\varrho(F(\infty))\not= 1$, and if there exists a positive θ ₀ such that $\varrho(\hat {F}(\theta_{0}))=1$ and $\hat {F}(\theta_{0})$ is irreducible, then for $\tilde{u}$ and $\tilde{v}$ left- and right-eigenvectors of $\hat {F}(\theta_{0})$ for the eigenvalue 1, such that $\tilde{u}.\tilde{v}=1$,

  $$\lim_{t\to\infty} (U_{ij} * g) (t) e^{-\theta_0 t} =\frac{\tilde{v}_i \tilde{u}_j}{\tilde{u}\tilde{\varGamma}\tilde{v}} \int_0^{\infty} e^{-\theta_0 s}g(s) \, \mathrm {d}s ,$$

  where

  $$\tilde{\varGamma} = \int_{0}^{\infty} se^{-\theta_0 s}\, \mathrm {d}F(s) = - \frac{\mathrm {d}\hat {F}}{\mathrm {d}\theta}(\theta_0) .$$

  If one component of $\tilde{\varGamma}$ is infinite, the limit above is 0.

Appendix B: Convergence of shifted convolutions

This section is devoted to the following technical result:

Lemma B.1

Consider:

• A sequence of increasing functions A ⁿ:ℝ₊→ℝ, which are such that A ⁿ(0)=0 and which converges uniformly on compacts to a function A which is Lipschitz-continuous, and such that A(t)>0 if t>0.

• A sequence of functions $f^{n}: \mathbb {R}_{+}^{2} \to \mathbb {R}$ which converges uniformly on every compact of (0,∞)×(0,∞), to a continuous function f which satisfies:

• for every t>0 the function f _t (⋅):(0,t]→ℝ₊ defined by f _t (s)=f(t,s) is continuous and strictly decreasing, and f(t,t)=0.

Then for every probability measure ν on ℝ₊, the following statements hold, for every function g∈C _b (ℝ₊), extended with g(x)=0 for x<0:

• (i) for each t>0 the function s∈(0,t]↦〈g(⋅−f(t,s)),ν〉 is continuous, except for the at most countable set of values s where $\nu(\{f(t,s)\})\not= 0$;

• (ii) for every ε>0 and for every T>T ₀>0 there exists η ₀>0 and N ₀>0 such that

  

  (B.1)

  for all n≥N ₀ and t∈[T ₀,T];

• (iii) the sequence of functions $h_{n}(t)=\int_{0}^{t}\langle g( \cdot- f(t,s) ) , \nu \rangle \, \mathrm {d}A^{n}(s)$ is equicontinuous on finite intervals;

• (iv) for every T>0, the following convergence holds:

  

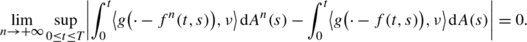  (B.2)

Proof of (i)

Denote with h _t (s) the function:

$$h_t(s) = \int_{f(t,s)}^{\infty} g\bigl( x- f(t,s) \bigr) \nu(\mathrm {d}x) .$$

Let s≤t be such that ν({f(t,s)})=0. Let s _n be a decreasing sequence converging to s. We have

(B.3)

When rewriting the first term in (B.3), we have used the fact that s<s _n and that f _t (⋅) is decreasing. This first term tends to 0 as n→+∞ because ν({f(t,s)})=0. By the continuity of both f and g, g(x−f(t,s _n ))−g(x−f(t,s))→0 as n→∞. The dominated convergence theorem implies that the second term in (B.3) tends to 0 as well. Hence, h _t is right-continuous. A similar argument proves that it is left-continuous, hence continuous at s. □

Proof of (ii)

Note that, for all t ₁<t ₂,

$$A^{n}(t_{2})-A^{n}(t_{1}) =A^{n}(t_{2})-A(t_{2}) - \bigl(A^{n}(t_{1})-A(t_{1})\bigr) +A(t_{2}) - A(t_{1}) .$$

Let L be the Lipschitz constant of the function A(⋅). Using the uniform convergence of A ⁿ(⋅) on the interval [0,T], there exists N ₀∈ℕ such that

$$A^{n}(t_{2})-A^{n}(t_{1}) \leq \frac{\varepsilon}{4}+ L (t_{2}-t_{1} ) $$

(B.4)

for all 0≤t ₁≤t ₂≤T and n≥N ₀. Let $\varDelta =\frac{\varepsilon}{4}+ L (T-T_{0} )$. Note that A ⁿ(T)−A ⁿ(T ₀)≤Δ. The difficulty in proving (B.1) lies in the fact that ν can have atoms. Let $\mathcal{A}\subset \mathbb {R}_{+}$ denotes the set of all the atoms of ν, which is countable. Let $\nu^{d}=\sum_{a\in \mathcal{A}}\nu(\{a\})\delta_{a}$ be the Borel measure formed with the atoms of ν, and ν ^c=ν−ν ^d be the measure that has no atoms. By Lemma A.1 of [18], there exists η ₁>0 such that for all η≤η ₁ we have

$$\sup_{y\in \mathbb {R}_{+}}\bigl\langle1_{(y-\eta, y+\eta)} , \nu^{c} \bigr \rangle < \frac{\varepsilon}{4\varDelta} . $$

(B.5)

Since $\sum_{a\in\mathcal{A}}\nu({a})\leq1$, there exists a finite set $\mathcal{A}_{\varepsilon}\subset\mathcal{A}$ such that

$$\sum_{a\in\mathcal{A}\backslash\mathcal{A}_{\varepsilon}}\nu\bigl(\{ a\}\bigr)\leq \dfrac{\varepsilon}{4\varDelta} . $$

(B.6)

Let T ₀<T, t∈[T ₀,T], n≥N ₀ and η≤η ₁. We have:

(B.7)

In the third line, we have used (B.5) and in the last line we have used the fact that A ⁿ(t)−A ⁿ(T ₀)≤Δ and (B.6). If $\mathcal{A}_{\varepsilon}=\varnothing$, let η ₀=η ₁. The right-hand side in (B.7) is ε/2. Otherwise, for any 0<η≤η ₁, T ₀≤s≤t and $a\in\mathcal{A}_{\varepsilon}$, we have

$$a\in \bigl[ \bigl( f(t,s) -\eta\bigr)^{+}, f(t,s)+\eta \bigr) \quad \implies\quad s\in \bigl[ f_{t}^{-1}(a + \eta), f_{t}^{-1}\bigl((a-\eta)^+\bigr) \bigr) .$$

This implies for 0<η≤η ₁, t∈[T ₀,T], $a\in \mathcal{A}$ and n≥N ₀, that

$$\int_{T_{0}}^{t}\langle1_{ [ ( f(t,s) - \eta)^{+}, f(t,s)+\eta )},\delta_{a}\rangle\, \mathrm {d}A^{n}(s) \leq A^{n}\bigl( f_t^{-1}\bigl((a-\eta)^+\bigr) \bigr) -A^{n}\bigl( f_t^{-1}(a+\eta)\bigr) . $$

(B.8)

Since n>N ₀ and $f_{t}^{-1}(a+\eta)\leq f_{t}^{-1}((a-\eta)^{+})\leq f_{t}^{-1}(0)=t\leq T$, by (B.4) we have

(B.9)

On the other hand, since $\nu(\{a\})( f_{t}^{-1}((a-\eta)^{+}) -f_{t}^{-1}( a+\eta))\leq t \nu(\{a\})$ and $\sum_{a\in\mathcal {A}_{\varepsilon}} t\nu(\{a\})\leq t$, the function of η:

$$\eta\mapsto\sum_{a\in\mathcal{A}_{\varepsilon}} \nu\bigl(\{a\}\bigr) \bigl(f_t^{-1}\bigl((a-\eta)^+\bigr) - f_t^{-1}(a+\eta) \bigr)$$

is continuous, and there exists 0<η ₀<η ₁ such that

$$\sum_{a\in\mathcal{A}_{\varepsilon}} \nu\bigl(\{a\}\bigr) \bigl(f_t^{-1}\bigl((a-\eta_0)^+\bigr) -f_t^{-1}( a+\eta_0) \bigr)\leq \frac{\varepsilon}{4L} . $$

(B.10)

Finally, using (B.8), (B.9), and (B.10) in (B.7), we have, for η ₀,

The inequality (B.1) is therefore proved. This concludes the proof of (ii). □

Proof of (iii)

For each n≥0, the function h _n (⋅) is continuous on each interval [0,T]. Indeed, s↦A ⁿ(s) is a continuous and increasing function, so that it is differentiable almost everywhere, and h _n can be written as

$$h_n(t)=\int_0^T\bigl\langle g\bigl(\cdot-f(t,s)\bigr),\nu\bigr\rangle1_{[0,t]}(s) \dot{A}^n(s)\,\mathrm {d}s$$

for all t≤T. On the other hand, the function

$$\begin{array}{rcl}\lambda: [0,T]\times[0,T]&\rightarrow&\mathbb{R}^+,\\(t,s)&\mapsto&\bigl\langle g\bigl(\cdot-f(t,s)\bigr),\nu\bigr\rangle1_{[0,t]} \dot{A}^n(s)\end{array} $$

has the following properties. First, for each T≥t≥0 the function s↦λ(t,s) is bounded by $\|g\|_{\infty}\dot{A}^{n}(s)$ which is integrable independently of t. Second, for each T≥s≥0 the function t↦λ(t,s) is continuous except for a denumerable set of t≤T.

Hence, by Lebesgue’s theorem, the function h _n is continuous on [0,T]. To prove the equicontinuity of (h _n (⋅),n≥0) on finite intervals, it suffices to show that, for every T>0 and ε>0, there exists η>0 and N ₀∈ℕ such that if 0≤t ₁, t ₂≤T and |t ₂−t ₁|<η then

$$\bigl \vert h_n(t_2)-h_n(t_1)\bigr \vert <\varepsilon $$

for all n≥N ₀. Note that for each 0≤t ₁, t ₂≤T,

(B.11)

Let ε>0. By the uniform convergence of A ⁿ(⋅) on [0,T], there exists N ₀∈ℕ such that

$$\bigl \vert A^{n}(t_2)-A^{n}(t_1)\bigr \vert \leq \frac{\varepsilon}{16( \Vert g \Vert _{\infty} \vee1)} + L\vert t_2-t_1\vert . $$

(B.12)

Let $T_{1}=\frac{\varepsilon}{16L( \Vert g \Vert _{\infty} \vee1)}$. Inequality (B.12) implies, for t ₂=T ₁ and t ₁=0

(B.13)

For all n≥N ₀. Thus for t ₁∈[0,T ₁] and n≥N ₀, using the fact that A ⁿ(0)=0,

(B.14)

The second inequality follows from the increasingness of A ⁿ(⋅), and the third one uses (B.13). Then by (B.11), (B.12), and (B.14), we have

$$\vert t_2-t_1\vert \leq\frac{11\varepsilon}{16L(\Vert g\Vert _{\infty}\vee1 )} \quad \implies\quad \bigl \vert h_n(t_2)-h_n(t_1)\bigr \vert \leq\varepsilon .$$

Since in (B.11) the variables t ₁,t ₂ play a symmetrical role, the same estimate as above is derived when t ₂∈[0,T ₁] and t ₁∈[0,T].

It remains to consider the case where t ₁, t ₂∈[T ₁,T]. Let therefore be two such real numbers with $\vert t_{2}-t_{1}\vert \leq\frac{3\varepsilon}{16L(\Vert g\Vert _{\infty}\vee 1)}$. We have

(B.15)

for all n≥N ₀. We have used (B.11) in the first inequality, and (B.12) and (B.14) in the last inequality.

In order to conclude on the equicontinuity of h _n , it suffices to show that there exists η ₀>0 such that if t ₁, t ₂∈[T ₁,T] are such that |t ₂−t ₁|<η ₀, then

$$\int_{T_1}^{t_1} \bigl\langle\bigl \vert g\bigl(\cdot- f(t_2,s) \bigr) -g\bigl( \cdot- f(t_1,s) \bigr)\bigr \vert , \nu \bigr\rangle \, \mathrm {d}A^{n}(s) \leq \frac{\varepsilon}{2} $$

(B.16)

for all n≥N ₀. An estimate for the integrand in (B.16) can be derived as follows. We first introduce the shorthand notation m ₁(s):=f(t ₁,s) and m ₂(s):=f(t ₂,s), where we shall omit the argument s when no ambiguity occurs. Let $\varDelta= \frac{\varepsilon}{16(\Vert g \Vert _{\infty}\vee 1)}+ L(T-T_{1})$. From (B.12), A ⁿ(T)−A ⁿ(T ₁)≤Δ for all n≥N ₀. Next, let M>0 be such that

$$\langle1_{[M,\infty)},\nu\rangle\leq\frac{\varepsilon}{8\varDelta (\Vert g\Vert _{\infty}\vee1)} . $$

(B.17)

Such an M exists, since ν is a proper probability measure. Therefore, for every fixed s, the integral:

$$\bigl\langle\bigl \vert g( \cdot- m_2 ) - g( \cdot- m_1) \bigr \vert , \nu \bigr\rangle = \int_{0}^{\infty}\bigl \vert g( x - m_2 ) - g( x - m_1 ) \bigr \vert \nu(\mathrm {d}x)$$

can be decomposed according to the intervals [0,m ₁∧m ₂), [m ₁∧m ₂,m ₁∨m ₂), [m ₁∨m ₂,M] and (M,+∞). Using the fact that g(⋅) is zero on negative half line, we obtain the bound:

(B.18)

Since g(⋅) is continuous, it is uniformly continuous on [0,M] and there exists δ>0 such that

$$\bigl|g(x)-g(y)\bigr| \leq \frac{\varepsilon}{4\varDelta} $$

(B.19)

for all x,y∈[0,M] verifying |x−y|≤δ. On the other hand the function f(⋅ ,⋅) is continuous on (0,∞)×(0,∞), it is uniformly continuous on [T ₁,T]×[T ₁,T] then for each δ′∈(0,δ] there exists η(δ′)>0 such that if (t ₁,s ₁), (t ₂,s ₂)∈[T ₁,T]×[T ₁,T] and |t ₂−t ₁|+|s ₂−s ₁|≤η(δ′) then |f(t ₁,s ₁)−f(t ₂,s ₂)|<δ′. In particular for all t ₁, t ₂∈[T ₁,T] such that |t ₂−t ₁|≤η(δ′),

$$\sup_{T_1\leq s\leq T}\bigl \vert m_1(s) - m_2(s) \bigr \vert = \sup_{T_1\leq s\leq T}\bigl \vert f(t_1,s)-f(t_2,s)\bigr \vert < \delta^{\prime} . $$

(B.20)

Thus, for all s∈[T ₁,T], x∈[f(t ₁,s)∧f(t ₂,s),M] and t ₁, t ₂∈[T ₁,T] such that |t ₂−t ₁|<η(δ′). So, by (B.20) we have |(x−f(t ₂,s))−(x−f(t ₁,s))|=|f(t ₂,s)−f(t ₁,s)|≤δ′ and by (B.19), we have

$$\bigl \vert g(x- m_2)-g(x-m_1)\bigr \vert \leq \frac{\varepsilon}{4\varDelta} . $$

(B.21)

Note that (B.20) implies (f(t ₁,s)−δ′)⁺≤f(t ₂,s)≤f(t ₁,s)+δ′. Consequently, we have

$$\bigl(f(t_1,s)-\delta^{\prime}\bigr)^+\leq f(t_1,s)\wedge f(t_2,s)\leq f(t_1,s)\vee f(t_2,s)\leq f(t_1,s)+\delta^{\prime} .$$

(B.22)

We combine the estimates (B.17), (B.21), and (B.22) in (B.18) to obtain the following bound:

(B.23)

Coming back to the left-hand side of (B.16), we conclude that for all δ′∈(0,δ], t ₁, t ₂∈[T ₁,T] such that |t ₂−t ₁|≤η(δ′) and n≥N ₀

(B.24)

where the second inequality uses the fact that A ⁿ(T)−A ⁿ(T ₁)≤Δ for all n≥N ₀ and t ₁≤T. Replacing ε by ε/2∥g∥_∞ in (ii), there exists δ ₀>0 and N ₀∈ℕ such that

$$\int_{T_{1}}^{t_1} \langle1_{ [ ( f(t_1,s) -\delta_{0})^{+}, f(t_1,s)+\delta_{0}) } , \nu \rangle \, \mathrm {d}A^{n}(s) \leq \frac{\varepsilon}{2\Vert g \Vert _{\infty}}$$

for all n≥N ₀. Therefore, if δ ₀≥δ, then the second term of right-hand side of (B.24) is less than ε/2 in this case it suffices to take η ₀=η(δ) and (B.16) holds. Otherwise, there exists η(δ ₀) such that (B.24) is verified, consequently (B.16) holds for η ₀=η(δ ₀). □

Proof of (iv)

Fix T>0. Using a double difference, we have

(B.25)

(B.26)

For the term (B.25), we use the following reasoning. Let 0<t≤T. Choose N>0 such that A ⁿ(t)>0 for all n≥N. This N exists because A ⁿ(t)→A(t). Define for all n≥N, F _n (s)=A _n (s)/A _n (t) if s<t and F _n (s)=1 if t≤s. It is clear that {F _n (⋅);n≥N} is a sequence of distribution functions that satisfies F _n (⋅)⟶F(⋅), where F(s)=A(s)/A(t) if s<t and F(s)=1 if s≥t. From (i), the function s↦〈g(⋅−f(s)),ν〉 is bounded and continuous, except for countably many values of s∈(0,t]. Then, by the continuous mapping theorem (cf. [13, Theorem 2.3, Chap. 2]):

$$\lim_{n\rightarrow\infty} \int_{0}^{t} \bigl\langle g\bigl( \cdot- f(t,s) \bigr) , \nu \bigr\rangle \, \mathrm {d}F^{n}(s) =\int_{0}^{t} \bigl\langle g\bigl( \cdot- f(t,s)\bigr) , \nu \bigr\rangle \, \mathrm {d}F(s) .$$

Then, replacing F _n and F by their expressions and using the fact that A ⁿ(t)→A(t) one deduces

$$\int_{0}^{t} \bigl\langle g\bigl( \cdot- f(t,s)\bigr) , \nu \bigr\rangle \, \mathrm {d}A^{n}(s) \to \int _{0}^{t} \bigl\langle g\bigl( \cdot- f(t,s) \bigr), \nu \bigr\rangle \, \mathrm {d}A(s) .$$

Then by (iii) the uniform convergence of the above limit holds on every finite interval, thus (B.25) tends to 0. For the term (B.26), we adopt the following strategy which is similar to that of the proof (ii). First, we isolate and bound the integral when s is close to 0. Indeed, we have not specified the behavior of the function f(t,s) when s→0, and the difference |f _n (t,s)−f(t,s)| is not necessarily uniformly bounded for (t,s)∈[0,T]×[0,T]. Next, we eliminate the unbounded part of the integral with respect to the measure ν, in order to reduce the integral to a compact. Finally, we bound the difference on this compact. The objective is therefore to prove that, for each given T>0, g∈C _b (ℝ₊) and ε>0, there exists N>0 such that for all n≥N,

$$\sup_{0\leq t\leq T}\int_{0}^{t} \bigl\langle \bigl \vert g\bigl( \cdot- f^{n}(t,s) \bigr) - g\bigl( \cdot- f(t,s)\bigr) \bigr \vert , \nu \bigr\rangle\, \mathrm {d}A^{n}(s) <\varepsilon. $$

(B.27)

Observe first that the steps (B.12)–(B.14) of the proof of (iii) do not depend on the nature of the shift inside g, and are still valid here. For each ε>0, let therefore $T_{1}= \frac{\varepsilon}{16L(\Vert g \Vert _{\infty} \vee1)}$: for all t∈[0,T ₁] and n≥N ₀ we have

The next step is to bound the part of the integral in (B.27) for the range t∈[T ₁,T]. In order to obtain (B.27), it suffices to find some N ₁>0 such that for n ≥N ₁:

$$\int_{T_{1}}^{t}\bigl\langle\bigl \vert g\bigl(\cdot- f^{n}(t,s) \bigr)-g\bigl(\cdot- f(t,s) \bigr) \bigr \vert ,\nu \bigr\rangle \, \mathrm {d}A^{n}(s)\leq\frac{3\varepsilon}{4} . $$

(B.28)

Set m ₁(s):=f ⁿ(t,s) and m ₂(s):=f(t,s). The arguments of the proof of (iii) between (B.17) and (B.18) still apply. Set therefore $\varDelta=\frac{\varepsilon}{16(\Vert g \Vert _{\infty} \vee 1)}+L(T-T_{1})$, and fix M>0 be such that (B.17) holds. We then (B.18) holds as well. Since f ⁿ(⋅ ,⋅)→f(⋅ ,⋅) uniformly on [T ₁,T]×[T ₁,T], for each δ′≤δ there exists N ₁(δ′)>0 such that

$$\sup_{T_1\leq s\leq T}\bigl\vert m_1(s) - m_2(s) \bigr\vert \leq \sup_{T_1\leq t,s\leq T}\bigl\vert f^n(t,s)-f(t,s)\bigr\vert \leq \delta^{\prime} . $$

(B.29)

This bound implies: |(x−m ₁(s))−(x−m ₂(s))|=|m ₁(s)−m ₂(s)|≤δ′≤δ|, for all T ₁≤t,s≤T, f ⁿ(t,s)∨f(t,s)≤x≤M and n≥N ₁(δ′). Then by (B.19), we have

$$\bigl\vert g\bigl(x-f^n(t,s)\bigr)-g\bigl(x-f(t,s)\bigr)\bigr\vert\leq \frac{\varepsilon}{4\varDelta} $$

(B.30)

for all T ₁≤t,s≤T, f ⁿ(t,s)∨f(t,s)≤x≤M and n≥N ₁(δ′). From (B.29), we have (f(t,s)−δ′)⁺≤f ⁿ(t,s)≤f(t,s)+δ′. So,

$$\bigl(f(t,s)-\delta^{\prime}\bigr)^+\leq f^n(t,s)\wedge f(t,s)\leq f^n(t,s)\vee f(t,s)\leq f(t,s)+\delta^{\prime} . $$

(B.31)

Coming back to (B.18), we have

(B.32)

for all T ₁≤t,s≤T and n≥N ₁(δ′). The first inequality is by (B.31), (B.30), and (B.17). Then the estimate of the integral in (B.28) is obtained by integrating (B.32) on [T ₁,t] with respect to dA ⁿ(s),

(B.33)

for all T ₁≤t≤T and n≥N ₁(δ′)∨N ₀. The estimate of the last term in (B.33) is obtained as that of the last term in (B.24) by using (ii). □

Appendix C: Relationship with the single-class case

We begin by stating in the following lemma the properties of the sequences {V _k (i);i≥1} and $\{V^{0}_{k}(i);i \geq1\}$ defined in Sect. 5.1. Where there is no ambiguity, we shall denote also with V _k (x) the common distribution function of the random variable V _k , and similarly for $V^{0}_{k}$.

Lemma C.1

We have the following properties:

• (i) The sequence {V _k (i);i≥1} is i.i.d. with common distribution function given by

  $$ V_k (x) = \bigl( e \bigl(I-P'\bigr) (\mathcal{B} * B) (x) \bigr) _k ,$$

  (C.1)

  with Laplace transform given by

  $$ \hat{V}_k (s) = \bigl( e \bigl( I -P'\bigr) \bigl( I - \hat {B}(s)P'\bigr)^{-1} \hat {B}(s) \bigr) _k ,$$

  (C.2)

  and with the first two moments:

  $$ \mathbb{E}(V_k) = ( e\beta Q)_k , \qquad \mathbb{E}\bigl(V^2_k\bigr) =\bigl( e\bigl( \beta^{(2)}+ 2 \beta P'Q \beta\bigr) Q\bigr)_{k} ,$$

  (C.3)

  where $\beta=\operatorname{diag}\{\langle\chi,\nu_{k}\rangle\}$ and $\beta^{(2)}=\operatorname{diag}\{\langle\chi^{2},\nu_{k}\rangle\}$.

• (ii) The sequence $\{V^{0}_{k} (i); i \geq1\}$ is i.i.d. with common distribution function given by

  $$ V^0_k (x) = \bigl( e\bigl(I-P'\bigr) \bigl(\mathcal{B} * B^0\bigr) (x) \bigr) _k .$$

  (C.4)

Proof

The proofs of (i) and (ii) are similar. Let us prove (i). The total service time of a customer of class k is the sum of one service time v _k and of the service it requires after the end of this service. The latter duration is distributed according to V _j with probability p _kj and is zero with probability p _k0. The service time after reentering the queue is independent from the first service. Accordingly, we have the identity for distribution functions:

$$ V_k(x) = \sum _{j} p_{kj} ( B_k * V_j) (x) + p_{k0} B_k(x) .$$

(C.5)

Expressed in vector-matrix form, with $V(x) = (V_{k}(x); k\in\mathcal{K})$ (a row vector), we have

$$V(x) = \bigl( V * \bigl(P'B\bigr) \bigr) (x) + e \bigl(I-P'\bigr) B(x) ,$$

and this is a multidimensional renewal equation in the sense of Lemma A.1. By application of the lemma, we obtain $V(x) = e (I-P') ( \mathcal{B} * B )(x)$, hence (C.1). □

Coming back to our multiclass queue, a customer taken “at random” in the external input flow will be of class k with probability α _k /α _e , where $\alpha_{e} := \sum_{k\in\mathcal{K}}\alpha_{k} = e.\alpha$ is the “equivalent” arrival rate of single-class customers. Accordingly, the service time distribution of such a typical customer should be a mixture of the distributions V _k with these probabilities. The following result summarizes the properties of this distribution.

Lemma C.2

Consider the random variable v ^s whose distribution B ^s is formed as a mixture of the V _k , proportionally to the arrival rates α _k :B ^s(x)= $\sum_{k\in\mathcal{K}} \alpha_{k} V_{k}(x) /\alpha_{e}$. The Laplace transform of this distribution is given by:

$$\hat {B}^{s}(\theta) = \frac{1}{\alpha_e} e \bigl(I-P'\bigr) \bigl(I-P'\hat {B}(\theta)\bigr)^{-1} \hat {B}(\theta) \alpha.$$

Its first two moments $\beta^{s} = \mathbb {E}{v^{s}}$ and $\beta^{s,2}= \mathbb {E}{(v^{s})^{2}}$ are given by:

Let the excess life distribution associated to B ^s(⋅) be denoted by $B^{s}_{e}(\cdot)$, with first moment $\beta_{e}^{s}$. Its Laplace transform satisfies the identities:

(C.6)

(C.7)

(C.8)

Proof

The formulas for the Laplace–Stieltjes transform and the moments are direct consequences of Lemma C.1. Expression (C.6) is the application of the classical formula $\hat {B}^{s}_{e}(\theta) = (1-\hat {B}^{s}(\theta))/(\theta\beta^{s})$. The second expression (C.7) is derived from the first one as

and simplifying. Finally, the expansion (C.8) follows from the fact that $\beta^{s}_{e} = \beta^{s,2}/2\beta^{s}$. □

Consider now the Processor Sharing queue with a single class of customers having the service time distribution B ^s with their first and second moment are denoted by β ^s and β ^s,2, and the arrival rate α _e . We have the following result, the two first statements of which is Proposition 2 of [21], and the last statement of which is a simple consequence, using flow conservation equations.

Proposition C.1

Assume that α _e β ^s>1. There exists a unique positive solution θ ₀ to the equation:

$$\theta _0= \alpha_e \bigl( 1 - \hat {B}^{s}(\theta _0)\bigr).$$

If L(t) is the number of customers in the single class system at time t, then a.s.:

$$\lim_{t\to\infty} \frac{L(t)}{t} = \theta _0.$$

If D(t) is the number of customers that have departed the system at time t, then a.s.:

$$\lim_{t\to\infty} \frac{D(t)}{t} = \alpha_e -\theta _0.$$

We have now gathered enough information to state the correspondence results with the single-class case. We refer to [23] for the terminology associated to the single-class queue.

Lemma C.3

Consider a processor sharing queue with arrival rate α _e and service time distribution B ^s, associated to the Borel measure ν ^s. Assume that the data (α _e ,ν ^s) is supercritical. Consider the initial measure ξ such that

$$\langle1_{(x,+\infty)} , \xi \rangle = e \bigl(I-P'\bigr) (\mathcal{B}*C) (x)\bar {Z}(0) ,$$

where $\mathcal{B}(t)=\sum_{n\geq0} ( BP')^{*n}(t)$ and C(t)=(I−B ⁰(t))+(I−B(t))QP′. Then the function T is given by:

$$T(u) = (H*U_e) (u),$$

where $U_{e}(u) = \sum_{n=0}^{\infty} \rho^{n}(B^{s}_{e})^{*n}(u), H(x)=\int_{0}^{x}\langle1_{(y,+\infty)} , \xi \rangle \,\mathrm{d}y$, and $B^{s}_{e}(\cdot)$ is the excess life distribution associated to B ^s(⋅). Its Laplace–Stieltjes transform is given by

$$ \hat{T}(\theta) = \frac{\hat {H}(\theta)}{1-\psi(\theta)} ,$$

(C.9)

where

(C.10)

(C.11)

Proof

From (4.12), it is easy to see that the Laplace–Stieltjes transform of T must satisfy: $\hat {T}(\theta) =\hat {H}(\theta) + \rho \hat {F}_{e}(\theta) \hat {T}(\theta)$, which readily gives (C.9). The expression for $\hat {H}(\theta)$ uses the identity $\mathcal{B}*C = Q - \mathcal{B}*B^{0}$ mentioned in the proof of Lemma 4.2, and the fact that if $H(t) =\int_{0}^{t} h(u)\, \mathrm {d}u$, then $\hat {H}(\theta) = \theta^{-1}\hat{h}(\theta)$. □

Appendix D: Laws of large numbers for visits and residual times

In the following lemmas we give the properties of the sequences {N _lk (i), i≥1} and {V _lk (i,n),i≥1,n≥1} introduced in Sect. 5.2, where $l,k\in \mathcal{K}$. For each j=1,…,N _lk (i) let $\tilde{V}_{lkk}(i,j)$ be the sum of service times experienced by the ith customer, between just after its jth visit of class k until that of the (j+1)st, included. It is a simple consequence of the memoryless nature of customer routing, and the independence of successive service times, that for each $l,k\in\mathcal{K}$ and each i, the sequence $\{ \tilde{V}_{lkk}(i,j) \}_{j=1}^{N_{lk}(i)}$ is i.i.d. and the common distribution does not depend on l. Accordingly, we drop the reference to l in the notation, which becomes $\tilde{V}_{kk}$. For different i, the sequences are independent. Finally, for each n=1,…,N _lk (i), V _lk (i,n) can be expressed on the event {N _lk (i)≥m} as

$$ V_{lk}(i,n) =V_{lk}(i,1) + \sum_{j=1}^{n-1}\tilde{V}_{kk}(i,j),$$

(D.1)

for all n=1,…,m.

Lemma D.1

For each $l,k\in\mathcal{K}$, the sequence {N _lk (i),i≥1} is i.i.d. with distribution given by ℙ(N _lk (i)=0)=1−f _lk , and for m≥1:

$$\mathbb{P}\bigl(N_{lk}(i)=m\bigr) = f_{lk}(f_{kk})^{m-1}(1-f_{kk}). $$

(D.2)

Here, f _lk =Q _kl /Q _kk if l≠k and f _kk =(P′Q) _kk /Q _kk .

Proof

Actually, N _lk (i) is the number of visits of state k starting from state l in a time-homogeneous Markov chain with state space $\mathcal{K}$ and transition matrix P. The sequence is i.i.d. because routing events of different customers are independent. Since the spectral radius of P is less than 1, we have (D.2) (cf. [13, Sect. 5.3, Chap. 5]). □

A shorthand notation will be useful in the following. An element k of $\mathcal{K}$ being fixed (its value will always be clear from the context), let $\bar{\mathcal{K}}=\mathcal{K}\backslash\{k\}$.

Lemma D.2

Provided that f _lk >0 and f _kk >0 respectively, the distributions V _lk and $\tilde{V}_{kk}$ of the random variables (V _lk (1,1)|{N _lk (1)≥1}) and $(\tilde{V}_{kk}(1,1) |$ {N _kk (1)≥1}) are given by

(D.3)

(D.4)

Moreover, we have

(D.5)

(D.6)

for all m≥2 and n=2,…,m.

Proof

Conditioning on the sequence of classes visited by the customer:

Since ℙ(N _lk ≥1)=f _lk, we have (D.3). A similar reasoning holds for (D.4). The proof of (D.6) is by (D.1). Since V _lk (1,n)−V _lk (1,n−1) represents the sum of service times for one cycle around a class k, so we conclude from (D.4). □

Lemma D.3

For each $l,k\in\mathcal{K}$, we have

$$ \sum_{m=1}^{\infty}V_{lk}\ast\tilde{V}^{\ast (m-1)}_{kk}\mathbb{P}\bigl(N_{lk}(1)\geq m\bigr)=\mathcal{B}_{kl}\ast \nu_l .$$

(D.7)

Moreover, we have the following expected value:

$$ \mathbb{E}\Biggl(\sum_{n=1}^{N_{lk}(1)}g\bigl(V_{lk}(1,n)\bigr)\Biggr) = \langle g,\mathcal{B}_{kl}\ast\nu_{l}\rangle .$$

(D.8)

Proof

Let us prove (D.7). For each $l,k\in\mathcal{K}$, denote by

$$\varPsi_{lk}:=\bigl(BP'\bigr)_{kl}+\sum_{n=0}^{\infty}\bigl(BP'\bigr)_{k\bar{\mathcal{K}}} \ast\bigl(\bigl(BP'\bigr)_{\bar{\mathcal{K}}\bar{\mathcal{K}}}\bigr)^{\ast n} \ast \bigl(BP'\bigr)_{\bar{\mathcal{K}}l}$$

and observe that Ψ _lk ∗B _l =V _lk f _lk and $\varPsi_{kk}=\tilde{V}_{kk}f_{kk}$. It suffices to prove that

$$\sum_{n=0}^{\infty}\varPsi^{\ast(n)}_{kk}=\mathcal{B}_{kk} \quad \text{and}\quad \sum_{n=0}^{\infty}\varPsi_{kk}^{\ast (n)}\ast\varPsi_{lk}=\mathcal{B}_{kl} . $$

(D.9)

For each $k\in\mathcal{K}$, let $\hat {B}_{k}$ be the Laplace Transform of the distribution B _k and $\hat{\mathcal{B}}$ be the Laplace transform of the matrix function $\mathcal{B}:=\sum_{n=0}^{\infty}(BP')^{\ast n}$, which is $\hat{\mathcal{B}}=(I-\hat {B}P')^{-1}$. The formula for inverting partitioned matrix (see, e.g., [20, p. 18]) yields for the partition $\{k\},\bar{\mathcal{K}}$:

(D.10)

(D.11)

Since the Laplace transform of Ψ _kk is $(\hat {B}P')_{k\bar {\mathcal{K}}}(I-(\hat {B}P')_{\bar{\mathcal{K}}\bar{\mathcal{K}}})^{-1}(\hat {B}P')_{\bar{\mathcal{K}}k}$ and $\hat{\mathcal{B}}_{kk}>0$, we have from (D.10)

$$\hat{\mathcal{B}}_{kk}=\dfrac{1}{1-\hat{\varPsi}_{kk}} .$$

Hence, $\sum_{n=0}^{\infty}(\hat{\varPsi}_{kk})^{n}=\hat{\mathcal{B}}_{kk}$ and by the uniqueness of the Laplace transform, the first identity in (D.9) is satisfied. For the second identity and by definition of Ψ _lk , we have

where $\hat{\varPsi}_{\bar{\mathcal{K}}k}=(\hat{\varPsi}_{lk},l\in\bar {\mathcal{K}})$ and $\hat{\varPsi}_{lk}$ is the Laplace transform of Ψ _lk . By (D.11), for $l\in\bar{\mathcal{K,}}$ we have $\hat{\varPsi}_{lk}=\hat{\mathcal{B}}_{kk}^{-1}\hat{\mathcal{B}}_{kl}$. Then the Laplace transform of $\sum_{n=0}^{\infty}(\varPsi_{kk})^{\ast (n)}\ast\varPsi_{lk}$ is $\hat{\mathcal{B}}_{kl}$.

For (D.8), we have from (D.1)

This proves the lemma. □

Lemma D.4

(Convergence of random sums)

Consider a sequence of nonnegative real numbers r→∞. For each r, let N ^r be an integer-valued random variable with distribution ρ ^r, and $\{ z^{r}_{i} \}_{i=1}^{\infty}$ be a sequence of random variables such that $z^{r}_{1}$ and the increments $z^{r}_{i+1} - z^{r}_{i}$ are conditionally independent and have the following conditional distributions:

Let ρ, ν ₀ and ν be probability distributions, and let:

$$\nu_s = \sum_{m=0}^\infty \rho\bigl(\{\geq m\}\bigr) \nu_0 * \nu^{*m} .$$

Finally, let g be a Borel-measurable, ν _s -a.e. continuous function. Assume that the following holds as r→∞: $\nu^{r}\stackrel{w}{\longrightarrow} \nu$, $\nu_{0}^{r}\stackrel{w}{\longrightarrow} \nu_{0}$, and $\rho^{r}\stackrel{w}{\longrightarrow} \rho$. Then the sequence of random variables

$$X^r = \sum_{n=1}^{N^r} g\bigl( z^r_n \bigr)$$

converges in distribution.

Proof

Let h:ℝ⁺→ℝ⁺ be a bounded and continuous function, it suffices to prove that the limit as r→∞ of

$$A_r := \mathbb{E}^r \bigl(h \bigl( X^r\bigr) \bigr)$$

exists and is finite. Conditioning on the value of N ^r, we have

(D.12)

Let p≥1 be such that ρ({p})>0 (which implies ρ({≥p})>0). As a consequence of the ν _s -a.e. continuity, g is a.e. continuous with respect to the measure ν ₀∗ν ^∗(p−1), and each term g(x ₁+⋯+x _p ) is a.e. continuous with respect to the product measure $\nu_{0}^{r}(\mathrm {d}x_{1}) \times\nu^{r}(\mathrm {d}x_{2})\times\cdots\times\nu^{r}(\mathrm {d}x_{p})$. Since h is bounded and continuous, the function

$$(x_1,x_2,\ldots,x_m) \mapsto h\bigl(g(x_1)+\cdots+g(x_1+x_2+\cdots+x_m) \bigr)$$

is bounded and also a.e. continuous with respect to the product measure. Therefore, the integral inside the second member of (D.12) converges as r→∞. Since h is bounded, the limit is bounded above by ∥h∥ρ({m}). This implies the normal convergence of the series in the right-hand term of (D.12). Limit of A ^r thus exists and finite. □

Lemma D.5

Assume that conditions (3.9)–(3.12) and (3.14) holds. For $l,k \in \mathcal{K}$ given, let g:ℝ₊→ℝ₊ be a Borel measurable and $(\mathcal{B}_{lk}\ast\nu_{l})$-a.e. continuous such that as r→∞,

$$\bigl\langle g,\bigl(\mathcal{B}^r_{kl}\ast \nu^r_{l} \bigr)\bigr\rangle \rightarrow \bigl\langle g , (\mathcal{B}_{kl}\ast\nu_{l} ) \bigr\rangle < \infty . $$

(D.13)

Then we have, as r→∞

$$\frac{1}{r}\sum_{i=1}^{r\bar{E}_{l}^{r}(t)} \sum _{n=1}^{N_{lk}^{r}(i)}g\bigl(V_{lk}^{r}(i,n)\bigr) \Rightarrow \bigl\langle g,(\mathcal{B}\ast\nu)_{kl}\bigr\rangle \alpha_{l}t .$$

Proof

The proof uses two steps.

Step 1: :

According to Lemma D.3, the sequence $\{X_{lk}^{r}(i)\}_{i = 1}^{\infty}$ defined as

$$X_{lk}^{r}(i) = \sum_{n=1}^{N_{lk}^{r}(i)}g\bigl(V_{lk}^{r}(i,n)\bigr)$$

is i.i.d. with common expectation

$$ \mathbb{E}^r\bigl(X_{lk}^{r}(1)\bigr) = \bigl\langle g,\mathcal{B}_{kl}^{r}\ast \nu_{l}^{r}\bigr\rangle .$$

(D.14)

By (D.5) and (D.6) of Lemma D.2, $\{ V_{lk}^{r}(1,n)\}_{n=1}^{\infty}$ and $N^{r}_{lk}(1)$ satisfy the first two conditions of Lemma D.4 with $\nu_{0}^{r}(\cdot)=V^{r}_{lk}(\mathrm{d}x)$, $\nu^{r}(\cdot)=\tilde{V}^{r}_{kk}(\mathrm{d}x)$ and the distribution of $N_{lk}^{r}(1)$ is given in Lemma D.1. Under assumptions (3.11), (3.12), the distributions $V^{r}_{lk}(\mathrm{d}x),~\tilde{V}^{r}_{kk}(\mathrm{d}x)$ and that of $N_{lk}^{r}$ converge as r→∞. This is due to the continuity of the linear operations involved in the definition of these distributions in Lemmas D.1 and D.2. On the other hand, it follows from (D.7) in Lemma D.3 that the measure ν _s defined in Lemma D.4 corresponds here to $\mathcal{B}_{lk}\ast \nu_{l}$. The conditions of Lemma D.4, are therefore fulfilled, and the distribution of the random sums $X_{lk}^{r}(1)$, say $\nu^{r}_{g,s}$ converges in distribution to some limit measure ν _g,s .

Step 2: :

Consider the counting process $\bar{E}_{l}^{r}(t)$ of customers arriving to class l. We apply Lemma A.2 of [18] to this process, with the function χ as the lemma’s function g, and the measure $\nu^{r}_{g,s}$ as the lemma’s measure ν. Assumption (A.2) of the lemma holds under assumption (3.10). Assumption (A.3) holds thanks to Lemma D.4. Assumption (A.4) is equivalent to (D.13) because $\langle\chi, \nu^{r}_{g,s} \rangle = \langle g , \mathcal{B}_{kl}^{r}\ast\nu_{l}^{r} \rangle$, according to (D.14). Assumption (A.5) is trivial, and Assumptions (A.6)–(A.7) are a consequence of (3.14). Therefore,

$$\frac{1}{r}\sum_{i=1}^{r\bar{E}_{l}^{r}(t)} \sum _{n=1}^{N_{lk}^{r}(i)}g\bigl(V_{lk}^{r}(i,n)\bigr) \Rightarrow \alpha_{l} t \langle\chi, \nu_{g,s}\rangle = \alpha_{l} t \langle g , \mathcal{B}_{kl}\ast\nu_{l} \rangle $$

which was to be proved.

 □