Resource analysis of quantum computing with noisy qubits for Shor’s factoring algorithms

Abstract

We decompose two implementations of Shor’s algorithm for prime factorization into universal gate units at the logical level and predict the number of physical qubits and execution time when surface codes are used. Logical qubit encoding using a rotated surface code and logical qubits with all-to-all connectivity are assumed. We express the number of physical qubits and execution time in terms of the bit length of the number to be factorized and error rate of the physical quantum gate. We confirm the relationship between the number of qubits and the execution time by analyzing two algorithms using various bit lengths and physical gate error rates .

1 Introduction

Since Peter Shor introduced a polynomial-time quantum algorithm for factoring integers and computing discrete logarithms in 1994, interest in quantum computing has increased significantly [1]. Several companies such as Google and IBM are leading efforts toward the practical use of quantum computers [2, 3].

However, technological advances are still needed to perform large scale operations such as Shor’s algorithm. Only noisy-intermediate-scale-quantum operations can be performed, and even quantum error correcting (QEC) codes cannot be used properly [4].

We need to know the required quantum computing resources to implement Shor’s algorithm. With this knowledge, quantum computer developers can set goals regarding which areas deserve further attention, and the crypto industry can estimate how soon a cryptosystem that is safe against quantum computing attacks can be developed.

Fig. 1

Overall structure of quantum computing resource analysis. K is the number of logical qubits required by the algorithm, and Q is the elementary gate step. KQ formalism is used to determine the logical gate error rate required by the algorithm

The quantum resources and expected performance required for practical large-scale quantum computing have been investigated [5,6,7,8]. However, because the results of these analyses vary widely depending on the underlying assumptions, it is necessary to analyze the resources required under different conditions.

We perform resource analysis as illustrated in Fig. 1; the structure is similar to the typical resource analysis structure, with some differences. The similarities to other studies are as follows. To achieve a low gate error rate, a QEC code is used. As a result, the algorithm is decomposed into universal gates. To determine what distance to use, we analyze the number of elementary gate steps Q in the algorithm, and because T gates are used, we confirm the number of additional qubits used for magic-state distillation. In addition, it is possible to determine how many T gate factories to prepare by obtaining the number of T gates used simultaneously. The differences are as follows. We assume all-to-all connectivity between logical qubits. To reduce the number of physical qubits, we use a rotated planar surface code. Because this code requires lattice surgery when the CNOT operation is performed, we use additional ancilla qubits for the CNOT gate. We also use the magic-state distillation protocol of Fowler and Gidney [9].

Our study is based on several assumptions. First, as shown in Fig. 1, we assume logical qubits with all-to-all connectivity. Second, we assume that the cycle time of the surface code $c_t$ is $1\mu s$.

Our contributions are as follows. First, we obtain the minimum number of physical qubits required for one T gate factory while satisfying the physical gate error rate and logical gate error rate conditions by controlling $d_1$ and $d_2$, the code distance for magic-state distillation in the method of Fowler and Gidney [9]. Second, we express the number of physical qubits and execution time required for two implementations of Shor’s algorithm as a closed-form equation for the bit length of the number to be factorized. In addition, the relationship between the number of qubits and time required is confirmed by analyzing the two algorithms using various numbers of logical qubits.

The remainder of this paper is organized as follows. Section 2 briefly explains Shor’s factorization algorithm and introduces the algorithms of Beauregard [10] and Pavlidis and Gizopoulos [11], which are decomposed in Sect. 4. In addition, previous works are reviewed and compared with our work. Section 3 explains how logical qubits and logical T gates are generated and identifies the cost of the QEC and magic-state distillation. In Sect. 4, the Beauregard and Pavlidis algorithms for factorization at a logical level are decomposed, and the elementary gate step Q and T depth are determined. In Sect. 5, the equation for the physical qubits and time required is derived using the bit length of the number to be factorized and the error rate of the physical quantum gate as parameters. In Sect. 6 the estimated resource use of the two algorithms for various bit lengths and physical quantum gate error rates are compared. The paper concludes with discussion in Sect. 7.

2 Related works

In this section, we briefly introduce Shor’s algorithm and review the two algorithms used in this work. We then introduce several previous works that analyzed the resources required by Shor’s algorithm and compare them with our work.

2.1 Shor’s algorithm

Since the introduction of Shor’s algorithm in 1994, several methods of implementing the algorithm have been developed. Although the algorithm was implemented in different ways in previous studies, they share a general structure of Shor’s algorithm for factorization, which is shown in Fig. 2. The modular exponentiation operator $U_a$ performs the following operation.

$$\begin{aligned} U_a|1\rangle =|a~mod~N\rangle . \end{aligned}$$

(1)

In Eq. (1), N is the number to be decomposed, and a is the randomly chosen number during the implementation of Shor’s algorithm. Several algorithms exist depending on how the modular exponentiation is implemented. Among several methods, we chose to analyze the $2n+3$ logical qubit algorithm of Beauregard [10] and the $9n+2$ logical qubit algorithm of Pavlidis and Gizopoulos [11]. We chose the Beauregard algorithm because it uses a small number of logical qubits. Because quantum algorithms cannot be implemented without a sufficient number of qubits, it can be expected that the Beauregard algorithm can be implemented on quantum computers more easily than other algorithms that use more logical qubits. The first reason for analyzing the Pavlidis algorithm is to analyze its advantage over the Beauregard algorithm in terms of depth when logical qubits are used. Second, because the Beauregard and Pavlidis algorithms are both phase-based algorithms, it is valid to compare them.

Fig. 2

General structure of Shor’s algorithm for factorization

2.2 Previous works

We review several quantum computing frameworks in terms of performance and quantum resources required for quantum computing. Table 1 briefly summarizes the previous works and our work.

Fowler et al. [5] used surface code quantum computing to approximate the number of physical qubits and the execution time of the Shor’s algorithm when N is a 2000-bit integer. They assumed all-to-all connectivity between logical qubits and used the algorithm of Vedral et al. [12], which uses a bit-based adder. They found that Shor’s algorithm for a 2000-bit integer requires 26.7 h and approximately $2.20\times 10^8$ physical qubits when the physical gate error rate is $10^{-3}$. However, they performed resource analysis by a parallel method using 800 magic-state factories; by contrast, the implementation in our work minimizes the number of magic-state factories. They also consider only modular exponentiation circuit and the Toffoli gate as a required resource and did not consider the decomposition of the rotation gate. For this reason, the resource analysis of Fowler et al. requires more physical qubits and has a smaller volume and longer execution time than ours.

By contrast, O’Gorman and Campbell [6] analyzed the resources required by Shor’s algorithm by presenting a detailed resource analysis of the magic-state factory within a surface code quantum computer. They used surface code that requires fewer physical qubits to create a single logical qubit [13], which is identical to that in our work. They found that the magic-state factory required for factoring can be as small as 6.3 million physical qubits, ignoring ancilla qubits, assuming a physical gate error rate of $10^{-4}$, a $p_{fail}$ value of 0.1, where $p_{fail}$ is the probability of failure of the algorithm, and all-to-all connectivity. However, as in the resource analysis of Fowler et al. [5], they considered only the modular exponentiation circuits, not the entire algorithm.

Hwang et al. [7] performed analysis using Steane code and Surface code considering nearest-neighbor connectivity. They used the magic-state distillation protocol described in [5]. They analyzed the number of physical qubits and the time required to execute the Shor’s factoring algorithm described in [11], but they did not specify the formula for determining these required resources. In contrast to the other two works, their decomposition of the algorithm was more detailed and thus produced more plausible results. They found that the factorization of a 512-bit integer by Shor’s algorithm requires $8.78\times 10^5$ h and $9.5\times 10^{10}$ physical qubits assuming a physical gate error rate of $10^{-3}$ and $p_{fail}$ value of 0.3.

Gidney and Ekerå [8] also estimated the approximate cost of their construction using plausible physical assumptions for large-scale superconducting qubit platforms. They reduced the cost of factoring integers on a quantum computer by combining various techniques and developed an efficient modular exponentiation circuit to reduce the resources required by the algorithm. Using this result, they found that Shor’s algorithm requires 0.31 days and $20\times 10^{6}$ physical qubits to factorize a 2048-bit integer, assuming physical gate error of $10^{-3}$ and nearest-neighbor connectivity. They compared the resources required by various algorithms, but not under the same conditions and assumptions. In addition, they did not express the required resources in a closed-form formula.

Table 1 Summary of considerations when analyzing resources of Shor’s algorithm in previous works and our work

Our analysis was performed using a rotated planar surface code, which uses fewer physical qubits than the method described in [14]. We consider all-to-all connectivity and used the magic-state distillation protocol described in [9]. Unlike other studies, our study describes the number of physical qubits and time required in a closed-form formula. Additionally, we compared the required resources for two algorithms under the same conditions.

3 Logical qubit encoding using quantum error correcting code

Physical qubits cannot perform operations on themselves because they have a very high error probability at the current level. Therefore, we used QEC codes to reduce the gate error rate and protect quantum information from various errors. QEC codes collect several qubits with a high error probability to create a single logical qubit with a low error rate. There are various types of error-correcting codes, such as concatenated codes and surface codes [14, 17]. Surface codes are generally used because they are easy to implement and exhibit high performance [14]. Among various types of surface codes, we chose a rotated planar surface code [13].

3.1 Rotated planar surface code

When a rotated planar surface code is used, the number of physical qubits required to make one logical qubit with code distance d is $2d^2-1$ [13]. In the rotated planar surface code, CNOT operations are performed using the lattice surface method, which requires one additional logical qubit for the computation. Therefore, because we assume all-to-all logical qubit connectivity, the number of additional logical qubits required is the number of CNOT gates used simultaneously [13].

The performance of logical qubits is determined by the code distance. The code distance d is set to satisfy the following condition [9].

$$\begin{aligned} \epsilon _L=0.1\times (100\epsilon _p)^{(d+1)/2}. \end{aligned}$$

(2)

In Eq. (2), $\epsilon _L$ is the logical gate error rate, and $\epsilon _p$ is the physical gate error rate. Therefore, to obtain the desired code distance d, we need to know the $\epsilon _L$ value required by the algorithm, which depends on the algorithm complexity. When $\epsilon _{L}$ is the required logical gate error rate, the code distance d can be obtained by modifying Eq. (2) as follows.

$$\begin{aligned} d=2\cdot \left\lceil \frac{\log (10\epsilon _{L})}{\log (100\epsilon _p)}\right\rceil -1. \end{aligned}$$

(3)

In Eq. (3), $\lceil x \rceil$ means the function that takes as input a real number x, and gives the least integer greater than or equal to x. Therefore, if we know the value of $\epsilon _{L}$, we can obtain the desired code distance d. In Sect. 4, we explain how $\epsilon _{L}$ can be obtained using KQ formalism [18]. KQ formalism is a method to find the probability that an algorithm to fail by multiplying the number of logical qubits K, the elementary gate step Q and the logical error rate $\epsilon _L$.

3.2 Magic-state distillation

To implement a quantum algorithm using logical qubits, QEC codes need to form a universal quantum gate set, that is, Clifford gates and T gates. The rotated surface code executes T gate operation by state injection and gate teleportation, and the error rate of the T gate is determined by the error probability of the $|A\rangle = |0\rangle +\exp (i\cdot \pi /4)|1\rangle$ state. Magic-state distillation reduces the error rate of the T gate by using several T gates with higher error rates.

Among several magic-state distillation methods, the method of Fowler and Gidney [9] is used in this study. When the code distance of the logical qubit used for magic-state distillation is $d_1$, the improved T gate error rate obtained by a magic-state distillation $p_{out,1}$ is as follows [9].

$$\begin{aligned} p_{out,1}=35\cdot (\epsilon _p+10\cdot (100\epsilon _p)^{(\lfloor \frac{d_1}{2}\rfloor +1)/2})^3+100\cdot (100\epsilon _p)^{\frac{d_1+1}{2}}. \end{aligned}$$

(4)

In Eq. (4), $d_1\ge 15$ and $\lfloor x \rfloor$ means the function that takes as input a real number x, and gives the greatest integer less than or equal to x. If the desired result is obtained by performing only one level of magic-state distillation, the time required for this magic-state distillation, $t_{T,1}$, is as follows [9].

$$\begin{aligned} t_{T,1}=6.5\cdot d_1\cdot c_t. \end{aligned}$$

(5)

In Eq. (5), $c_t$ is the cycle time of the surface code [9]. Some researchers have assumed that $c_t=1\mu s$ [7, 9]; we adopted the same assumption in this study. The number of physical qubits required to perform one level of magic-state distillation, $n_{T,1}$, is as follows [9].

$$\begin{aligned} n_{T,1}=32\cdot (2d_1^2-1). \end{aligned}$$

(6)

From Eq. (4), we can find the lower bound of $p_{out,1}$. Let the lower bound of $p_{out,1}$ be $p_{Low,1}$. Then $p_{Low,1}$ can be expressed as a function of $\epsilon _p$.

$$\begin{aligned} p_{Low,1}=35\cdot \epsilon _p^3. \end{aligned}$$

(7)

For example, if $\epsilon _p$ is $10^{-3}$, $p_{out,1}$ cannot be less than $3.5\times 10^{-8}$ for any value of $d_1$. Therefore, if $p_{Low,1}\le \epsilon _{L}$, the desired result can be obtained using only one level of magic-state distillation. Otherwise, we need to collect several improved T gates obtained by one level of magic-state distillation and perform two levels of magic-state distillation. When the code distance of the two-level magic-state distillation process is $d_2$, the new T gate error rate obtained by two levels of magic-state distillation, $p_{out,2}$, is as follows [9].

$$\begin{aligned} p_{out,2}=35\cdot (p_{out,1}+10\cdot (100\epsilon _p)^{\frac{d_1+1}{2}})^3+100\cdot (100\epsilon _p)^{\frac{d_2+1}{2}}. \end{aligned}$$

(8)

In Eq. (8), $d_2\ge 15$. Let the lower bound of $p_{out,2}$ be $p_{Low,2}$. Then $p_{Low,2}$ can also be expressed as function of $\epsilon _p$.

$$\begin{aligned} p_{Low,2}=35\cdot (35\epsilon _p^3)^3. \end{aligned}$$

(9)

If $p_{Low,2}\le \epsilon _{L,R}$, the desired result can be obtained by two levels of magic-state distillation. Otherwise, we need to collect several T gates obtained by two-level magic-state distillation and perform three levels of magic-state distillation. The number of physical qubits required to perform two levels of magic-state distillation, $n_{T,2}$, is as follows [9].

$$\begin{aligned} n_{T,2}=32\cdot (2d_2^2-1)+8\cdot 32\cdot (2d_1^2-1). \end{aligned}$$

(10)

The time required for this magic-state distillation, $t_{T,2}$, is as follows [9].

$$\begin{aligned} t_{T,2}=6.5\cdot \max (2d_1,d_2)\cdot c_t. \end{aligned}$$

(11)

According to Eq. (13), (19), and (27) in Sect. 4, when $p_{fail}=0.01$ and $n=2048$, the logical error rate required by the Beauregard algorithm for 2048-bit prime factorization is $\epsilon _{L}=4.28\times 10^{-21}$, and the Pavlidis algorithm requires an error rate of $\epsilon _{L}=1.40\times 10^{-19}$. Table 2 shows the minimum number of physical qubits required to make one T gate, $T_m$, according to the physical error rate $\epsilon _p$.

Table 2 Number of physical qubits required to make one T gate for various physical error rates

We set $d_1$ and $d_2$ such that $T_m$ is as small as possible while satisfying the required logical gate error rate. The number of qubits used was found to increase greatly between the first and second distillation steps; therefore, the parameter was set so that the first distillation step could end the process, if possible. Table 2 shows that overall, the Beauregard algorithm requires more physical qubits than the Pavlidis algorithm, because the Beauregard algorithm requires a lower logical gate error rate. In addition, a physical error rate of $10^{-5}$ to $10^{-6}$ requires the same number of physical qubits. The reason is that the first distillation step does not solve the problem by increasing $d_1$ because the physical gate error rate is too high to obtain the desired result, and the weakest second distillation of $d_2=15$ is sufficient to obtain the required logical gate error rate.

4 Decomposition of algorithms at the logical level

Because the surface code is used, the gates used in the algorithm should be decomposed into X, Z, CNOT, and T gates. The KQ formalism will be used to analyze the algorithm; thus, the elementary gate step Q has to be obtained. The T depth must also be known to identify the time required to implement the algorithm. To determine how many T gate factories to create, we obtain the number of T gates that are used simultaneously. We also require as many additional logical qubits as there are concurrent CNOT gates.

First, we use the KQ formalism to determine the logical gate error rate required by the algorithm. The KQ formalism is described as follows [18].

$$\begin{aligned} p_{fail}=KQ\epsilon _L. \end{aligned}$$

(12)

In Eq. (12), $p_{fail}$ is the probability of failure of the algorithm, K is the number of logical qubits required by the algorithm, and Q is the elementary gate step. We rearrange the equation as follows.

$$\begin{aligned} \epsilon _{L}=\frac{p_{fail}}{KQ}. \end{aligned}$$

(13)

Therefore, we can find $\epsilon _{L}$ by obtaining K and Q. Previous studies have made various assumptions regarding $p_{fail}$. For example, O’Gorman and Campbell [6] assumed $p_{fail}=0.1$, and Hwang et al. [7] assumed $p_{fail}=0.3$. If $p_{fail}$ becomes large, $\epsilon _L$ increases, which reduces the resources required to implement the algorithm once; however, it can lead to incorrect results, which causes the algorithm to be implemented again. As $p_{fail}$ becomes smaller, the accuracy of the algorithm increases, but $\epsilon _L$ increases, which increases resources required to implement the algorithm once. In our study, we derived formulas for the number of physical qubits and time required by designating $p_{fail}$ as a variable and confirmed the required resources for $p_{fail}$ values of 0.01,  0.1, and 0.3.

Because the values of K and Q depend on the algorithm, we analyze both algorithms to find K and Q. As described above, because QEC codes are used, the gates used in the algorithm, such as the Toffoli and rotation gates, must be created through X, Z, CNOT, H, S, and T gates. First, we decompose the Toffoli gate into universal gates. Several studies on the decomposition of the Toffoli gate have been reported. Among the various methods, we used the method described in [19]. In this method, the number of elementary gate steps is 12, and the T depth is five steps.

An arbitrary rotation gate can be represented by approximating it as S, H, and T gates using the Gridsynth algorithm [20]. According to [20], when the degree of approximation is set to $10^{-10}$ , a total of 253 S, H, and T gates are needed, and 102 T gates are needed regardless of the angle of rotation. Hwang et al. [7] also assumed a degree of approximation of $10^{-10}$. Although this value may change depending on the required logical error rate, our study assumes a degree of approximation of $10^{-10}$. Because the number of gates required for the approximation is proportional to the physical gate error rate on a log scale, adjusting the level of approximation to a higher level does not significantly affect the obtained value.

The controlled rotation gate is also decomposed using the method described in [19]. Applying the result of the Gridsynth algorithm and the result of the decomposition of the controlled rotation gate, the number of elementary steps is 508, and the T depth is 204 steps.

Fig. 3

Decomposition of doubly controlled rotation gate

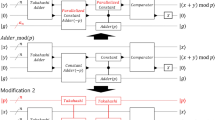
The doubly controlled rotation gate is decomposed as shown in Fig. 3. Therefore, when it is decomposed by a universal gate unit using the result described above, the number of elementary steps is 1295, and the T depth is 520.

Both the Beauregard and Pavlidis algorithms use the approximate quantum Fourier transform (AQFT) instead of the QFT. Suppose $R_d$ is a $\pi /2^d$ Z rotation gate. According to [21], when the n-bit QFT is implemented, it is sufficient to use the Z rotation gate with $d_{max}=\lceil \log _4{n}+1\rceil$, and Z rotation gates with $d\ge d_{max}$ need not be implemented. Using this result and combining it with the result in [20], the elementary step $Q_{AQFT}(n)$ and T depth $D_{AQFT}(n)$ of the n-bit AQFT are as follows.

$$\begin{aligned} \begin{aligned} Q_{AQFT}(n)&=n+1+508\cdot n\lceil \log _4 n\rceil ,\\ D_{AQFT}(n)&=204\cdot n\lceil \log _4 n\rceil . \end{aligned} \end{aligned}$$

(14)

Using these results, we decompose the Beauregard and Pavlidis algorithms.

4.1 Decomposition of Beauregard algorithm

Most of the operations in the Beauregard algorithm are modular operations, which requires a constant addition gate. In phase-based operation, the constant addition gate consists of n A gates. An A gate is a rotation operation that performs $A_k^j\rightarrow 2\pi i\cdot j/2^{n+1-k}$ Z rotation. A gates can be implemented simultaneously, but in that case, the number of T gates used simultaneously increases, and therefore the number of T gate factories must be increased. To reduce the number of T gate factories, we configured a constant addition gate serially by performing one A rotation per time step. The elementary step $Q_{A,Bea}$ and T depth $D_{A,Bea}$ of the constant addition gate are as follows.

$$\begin{aligned} Q_{A,Bea}=253n,~D_{A,Bea}=102n. \end{aligned}$$

(15)

As shown in [10], the modular adder is constructed using three doubly controlled adders, one constant adder, one controlled constant adder, four AQFTs, two CNOT gates, and two X gates. The controlled adder uses $n+1$ controlled rotation gates, and the doubly controlled adder uses $n+1$ doubly controlled rotation gates. Therefore, the elementary step $Q_{MA,Bea}$ and T depth $D_{MA,Bea}$ of the modular adder are as follows.

$$\begin{aligned} \begin{aligned} Q_{MA,Bea}&=2032n\lceil \log _4 n\rceil +4650n+4401,\\ D_{MA,Bea}&=816n\lceil \log _4 n\rceil +1818n+1716. \end{aligned} \end{aligned}$$

(16)

The controlled multiplier gate in [10] uses 2 n-bit AQFTs, and n modular adder gates. Therefore, the elementary step $Q_{Mul,Bea}$ and T depth $D_{Mul,Bea}$ of the controlled multiplier gate are as follows.

$$\begin{aligned} \begin{aligned} Q_{Mul,Bea}&=2Q_{AQFT}(n)+nQ_{MA,Bea},\\ D_{Mul,Bea}&=2D_{AQFT}(n)+nD_{MA,Bea}. \end{aligned} \end{aligned}$$

(17)

The $U_a$ gate in [10] uses two controlled multiplier gates and one controlled swap gate. Therefore, the elementary step $Q_{U_a,Bea}$ and T depth $D_{U_a,Bea}$ of $U_a$ are given as follows.

$$\begin{aligned} \begin{aligned} Q_{U_a,Bea}&=2Q_{Mul,Bea}+14n,\\ D_{U_a,Bea}&=2D_{Mul,Bea}+5n. \end{aligned} \end{aligned}$$

(18)

The Beauregard algorithm uses 2n controlled $U_a$ gates, 2n H gates, $2n-1$ rotation gates, and 2n measurements. The total elementary step $Q_{Bea}$ and T depth $D_{Bea}$ are as follows.

$$\begin{aligned} \begin{aligned} Q_{Bea}&=2n\cdot Q_{U_a,Bea}+2n+253\cdot (2n-1)+2n\\&= 8128n^3\lceil \log _4 n\rceil +18600n^3+4064n^2\lceil \log _4 n\rceil \\&\quad +17640n^2+518n-253,\\ D_{Bea}&=2n\cdot D_{U_a,Bea}+102\cdot (2n-1)\\&= 3264n^3\lceil \log _4 n\rceil +7272n^3+1632n^2\lceil \log _4 n\rceil \\&\quad +6874n^2+204n-102. \end{aligned} \end{aligned}$$

(19)

When the algorithm is implemented, only the rotation gates are executed simultaneously. Therefore, $N_{CNOT}=1$. In addition, because three T gates are used simultaneously in the doubly controlled rotation gate, it can be confirmed that the maximum number of T gates used simultaneously in the entire algorithm is $N_T=3$.

4.2 Decomposition of Pavlidis algorithm

The Pavlidis algorithm resembles the Beauregard algorithm in a large framework. The algorithms differ in the configuration of the modular exponentiation ($U_a$) circuit. The Pavlidis algorithm reduces the depth of the circuit by using more logical qubits than the Beauregard algorithm. Although the constant addition gate in the Pavlidis algorithm performs the same operation as that in the Beauregard algorithm, which adds a constant a to the input state, the difference is that the constant addition gate in the Pavlidis algorithm is constructed in parallel. Because the Pavlidis algorithm already requires n T gate factories to implement other parts, we can use these T gate factories when implementing the constant addition gate. Therefore, the number of elementary step $Q_{\varPhi ADD_a}$ and T depth $D_{\varPhi ADD_a}$ of the constant addition gate $\varPhi ADD_a$ are as follows.

$$\begin{aligned} Q_{\varPhi ADD_a}=253,~D_{\varPhi ADD_a}=102. \end{aligned}$$

(20)

The cost of the controlled version of $\varPhi ADD_a$, $C\varPhi ADD_a$, is the same as that of the controlled adder in [10]. As shown in [11], the $\varPhi ADD$ circuit that receives the number a to be added as input and adds it to the existing quantum state in the Pavlidis algorithm uses n controlled rotation gates per time step. Therefore, the numbers of CNOT gates and T gates executed simultaneously are given as $N_{CNOT}=n$, $N_T=n$. Thus, the gates of the algorithm are executed in parallel, which is a characteristic of the Pavlidis algorithm. The elementary step $Q_{\varPhi ADD}$ and T depth $D_{\varPhi ADD}$ of the $\varPhi ADD$ gate are as follows.

$$\begin{aligned} Q_{\varPhi ADD}=508n,~D_{\varPhi ADD}=204n. \end{aligned}$$

(21)

The operation $\varPhi MAC$ in [11] multiplies the fixed number a by the input state. Although $\varPhi MAC$ uses $2n^2$ controlled rotation gates, it can be parallelized, and the elementary step $Q_{\varPhi MAC}$ and T depth $D_{\varPhi MAC}$ of $\varPhi MAC$ are as follows.

$$\begin{aligned} Q_{\varPhi MAC}=1016n,~D_{\varPhi MAC}=408n. \end{aligned}$$

(22)

The $C\varPhi MAC$ operation in [11] multiplies the fixed number a by the input state according to the controlled qubit. It can also be parallelized, and the elementary step $Q_{C\varPhi MAC}$ and T depth $D_{C\varPhi MAC}$ of $C\varPhi MAC$ are as follows.

$$\begin{aligned} Q_{C\varPhi MAC}=3050n,~D_{C\varPhi MAC}=1224n. \end{aligned}$$

(23)

The $GM\varPhi DIV_N$ operation in [11] obtains the quotient and remainder of the number entering the input divided by the fixed number N. $GM\varPhi DIV_N$ uses 10 $\phi ADD$s, 7 $C\varPhi ADD_a$s, 2 2n-bit $\varPhi ADD_a$s, 5 $\varPhi MAC$, 16 n bit AQFTs, 10 2n-bit AQFTs, 8 CNOT gates, and 2 X gates. Therefore, the elementary step $Q_{GM\varPhi DIV_N}$ and T depth $D_{GM\varPhi DIV_N}$ of $GM\varPhi DIV_N$ are as follows.

$$\begin{aligned} \begin{aligned} Q_{GM\varPhi DIV_N}&= 9144n\lceil \log _4 2n\rceil +5588n\lceil \log _4 n\rceil +11684n+506,\\ D_{GM\varPhi DIV_N}&= 3672n\lceil \log _4 2n\rceil +2244n\lceil \log _4 n\rceil +4692n+204. \end{aligned} \end{aligned}$$

(24)

The $\varPhi MAC\_MOD$ operation, which calculates ay MOD N, where y is the input, uses two $C\varPhi MAC$s, two $GM\varPhi DIV$s, four 2n-bit AQFTs, and n CNOT gates. Therefore, the elementary step $Q_{\varPhi MAC\_MOD}$ and T depth $D_{\varPhi MAC\_MOD}$ of $\varPhi MAC\_MOD$ are as follows.

$$\begin{aligned} \begin{aligned} Q_{\varPhi MAC\_MOD}&= 2Q_{C\varPhi MAC}+2Q_{GM\varPhi DIV}+4Q_{AQFT}(2n)+n,\\ D_{\varPhi MAC\_MOD}&= 2D_{C\varPhi MAC}+2D_{GM\varPhi DIV}+4D_{AQFT}(2n). \end{aligned} \end{aligned}$$

(25)

The $U_{a,Pav}$ operation in [11] uses two $\varPhi MAC\_MOD$s and one controlled swap gate. The elementary step $Q_{U_{a,Pav}}$ and T depth $D_{U_{a,Pav}}$ of $U_{a,Pav}$ are as follows.

$$\begin{aligned} \begin{aligned} Q_{U_{a,Pav}}&= 2Q_{\varPhi MAC\_MOD}+17n,\\ D_{U_{a,Pav}}&= 2D_{\varPhi MAC\_MOD}+5n. \end{aligned} \end{aligned}$$

(26)

Like the Beauregard algorithm, the Pavlidis algorithm uses 2n controlled $U_a$ gates, 2n H gates, $2n-1$ rotation gates, and 2n measurements. The elementary step $Q_{Pav}$ and T depth $D_{Pav}$ of the Pavlidis algorithms are as follows.

$$\begin{aligned} \begin{aligned} Q_{Pav}&=2n\cdot Q_{U_a,Pav}+2n+253\cdot (2n-1)+2n\\&= 89408n^2\lceil \log _4 2n\rceil +44704n^2\lceil \log _4 n\rceil \\&\quad +1179000n^2+4652n-253,\\ D_{Pav}&=2n\cdot D_{U_a,Pav}+102\cdot (2n-1)\\&= 35904n^2\lceil \log _4 2n\rceil +17952n^2\lceil \log _4 n\rceil \\&\quad +47338n^2+1836n-102. \end{aligned} \end{aligned}$$

(27)

5 Equation for number of physical qubits and time required

The number of physical qubits required can be obtained by taking the product of the number of logical qubits plus the number of CNOT gates used simultaneously and the number of physical qubits required to create one logical qubit, and adding it to the product of the number of physical qubits required to create one T gate through magic-state distillation and the number of T gates used simultaneously. Therefore, by inserting Eq. (3) into the code distance d and inserting Eq. (13) into Eq. (3), the number of physical qubits $N_{phy}$ can be expressed as follows.

$$\begin{aligned} \begin{aligned} N_{phy}&=(2d^2-1)\cdot (K+N_{CNOT})+N_T\cdot T_m\\&=(2\cdot (2\lceil \frac{\log (10\epsilon _{L})}{\log (100\epsilon _p)}\rceil -1)^2-1) \cdot (K+N_{CNOT})+N_T\cdot T_m\\&=(2\cdot (2\lceil \frac{\log (\frac{10 p_{fail}}{KQ})}{\log (100\epsilon _p)}\rceil -1)^2-1) \cdot (K+N_{CNOT})+N_T\cdot T_m. \end{aligned} \end{aligned}$$

(28)

In Eq. (28), $N_{CNOT}$ is the number of CNOT gates used simultaneously, $N_T$ is the number of T gates used simultaneously, and $T_m$ is the number of physical qubits required to create one T gate by magic-state distillation. The Beauregard algorithm has $K=2n+3$, and the Pavlidis algorithm has $K=9n+2$.

The time required for the algorithm is based on the time required for the T gates, because the execution time of T gates is much longer than that of the other gates used in the algorithm [5]. Therefore, the time required to run the algorithm once, $T_{one}$, can be expressed as follows.

$$\begin{aligned} T_{one}=D\cdot t_T. \end{aligned}$$

(29)

Assuming that the second level of magic-state distillation is performed considering the current physical gate error rate, and assuming $c_t=10^{-6}~sec$, if we insert Eq. (11) into $t_T$, the time required to run the algorithm once can be expressed as follows.

$$\begin{aligned} T_{one}=D\cdot 6.5\cdot \max (2d_1,d_2)\times 10^{-6} (s). \end{aligned}$$

(30)

Because $p_{fail}$ is the probability of failure of the algorithm, $1-p_{fail}$ is the probability of success of the algorithm. Accordingly, the average number of trials for the success of the algorithm, $A_T$, is as follows.

$$\begin{aligned} A_T=\frac{1}{1-p_{fail}}. \end{aligned}$$

(31)

Therefore, as in the study of Hwang et al. [7], the time required to successfully execute the algorithm, $T_r$, can be expressed as the product of $T_{one}$ and $A_T$ [7].

$$\begin{aligned} \begin{aligned} T_r&=T_{one}\cdot A_T\\&=\frac{D\cdot 6.5\cdot \max (2d_1,d_2)\times 10^{-6}}{1-p_{fail}} (s). \end{aligned} \end{aligned}$$

(32)

6 Analysis of results

Table 3 shows the number of physical qubits, time, and volume required by the Beauregard and Pavlidis algorithms for 2048-bit factorization at $p_{fail}=0.01$ for various physical gate error rates. The volume in our study is a value multiplied by the number of physical qubits and the time, and is a value representing the overall complexity of the algorithm. The Beauregard algorithm uses fewer physical qubits than the Pavlidis algorithm. The main reason is the difference in the number of T gates used simultaneously, $N_T$. For example, when $n=2048$ and $\epsilon _p=10^{-3}$, the Beauregard algorithm requires approximately 12 million physical qubits for data and approximately 1 million physical qubits for magic-state factories, and the Pavlidis algorithm requires approximately 50 million physical qubits for data and approximately 600 million physical qubits for magic-state factories. The Pavlidis algorithm requires only approximately four times the number of physical qubits required by the Beauregard algorithm, whereas it required approximately 600 times the number of physical qubits for the magic-state factories.

The required number of physical qubits for the Pavlidis algorithm decreases sharply when the physical gate error rate decreases from $10^{-6}$ to $10^{-7}$ because at a rate of $10^{-7}$, one level of magic-state distillation is sufficient. The Beauregard algorithm allows one level of magic-state distillation for physical gate error rates of $10^{-8}$ or lower.

Table 3 Resource estimation for Beauregard and Pavlidis algorithms for various physical gate error rates for factoring $n=2048$ RSA integers

If we assume a physical gate error rate of $10^{-3}$, the Beauregard algorithm requires a logical gate error rate of $\epsilon _{L}=8.33\times 10^{-22}$ for 3072-bit factorization. However, the lower bound of the T gate performance that can be obtained through two levels of magic-state distillation is $1.50\times 10^{-21}$; thus, the use of three levels of magic-state distillation should be considered, although it greatly increases the required resources.

As shown in Eq. (32), the time required for the algorithm is determined by the distances $d_1$ and $d_2$ of the magic-state distillation and the T depth. Table 3 shows that the time required for these two algorithms does not vary significantly with the physical gate error rate. The reason is that the T depth, which consumes much of time required for the algorithm, is independent of the physical gate error rate. In addition, there is a flat region for the physical gate error rate, as the gate error rate required by the algorithm can be obtained only for $d_1=15$ and $d_2=15$, that is, at the lowest stage of two-level magic-state distillation, and the gate error rate cannot be obtained using one level of magic-state distillation. The time required for the Pavlidis algorithm decreases when the physical gate error rate decreases from $10^{-6}$ to $10^{-7}$ because at a physical gate error rate of $10^{-7}$, one level of magic-state distillation is sufficient. The Beauregard algorithm requires only one level of magic-state distillation for physical gate error rates of $10^{-8}$ or lower. Both algorithms use the minimum distance, $d_1=15$, in the interval where one level of magic-state distillation is sufficient; thus, even if the physical gate error rate is further reduced, it is impossible to further reduce the time required if logical qubits are used. Table 3 also shows the volume, which was obtained by multiplying the number of physical qubits and the time, to compare the total resources required by each algorithm. As the physical gate error rate decreases, the volume of both algorithms decreases slightly. The volume difference between the two algorithms is small. The volume of the Pavlidis algorithm is generally smaller, but for some physical error rate, the Beauregard algorithm has a smaller volume. Therefore, if we consider the number of physical qubits and time required to be equally important, the performance of the two algorithms does not differ greatly. By contrast, if we consider the number of qubits to be more important, the Beauregard algorithm is more efficient, and if we consider the execution time to be more important, we can choose the Pavlidis algorithm.

Fig. 4

Number of physical qubits and required time with different bit length

Figure 4 shows the number of physical qubits and time required for a physical gate error rate of $10^{-4}$ and $p_{fail}$ values of 0.01, 0.1, 0.3, and 0.9 for the prime factorization of numbers of various bit lengths. We assume that the cycle time of the surface code is $c_t=10^{-6}~sec$. The number of qubits required by the two algorithms differs by a factor of approximately 100, regardless of the length of the number to be factorized. The time required by the two algorithms is proportional to the length of the number to be factorized. The reason is that the order of the T depth of the two algorithms differs by n. Although the number of physical qubits increases and the time required tends to decrease as $p_{fail}$ decreases, the required resources do not vary significantly with $p_{fail}$. The reason is that variation of $\epsilon _L$ with $p_{fail}$ is not large enough to dramatically change the code distance d of the surface code and code distance $d_1$, $d_2$ of magic-state distillation. However, if $p_{fail}$ approaches 1, the time required becomes infinite because $A_T$ approaches infinity. In addition, because d, $d_1$, and $d_2$ all have discrete values, the same number of physical qubits is required even if $p_{fail}$ changes.

Figure 5 shows the volume, number of physical qubits, and time required for the Beauregard and Pavlidis algorithms when the physical gate error rate is $\epsilon _p=10^{-3}$ for Fig. 5(a) and $\epsilon _p=10^{-4}$ for Fig. 5(b) and the bit length is 2048 for various $p_{fail}$s. We also assume that the cycle time of the surface code is $c_t=10^{-6}~sec$. In both algorithms, the number of physical qubits increases gradually as $p_{fail}$ decreases. Compared to when $\epsilon _p=10^{-4}$, the increase in the number of physical qubits according to the decrease in $p_{fail}$ is larger when $\epsilon _p=10^{-3}$. For example, Fig. 5(a) shows that the number of physical qubits of Pavlidis algorithm increases rapidly when $p_{fail}=0.0001$, because three levels of magic-state distillation is required under corresponding condition. Figure 5(b) shows that the time required decreases as $p_{fail}$ decreases, and the decrease is very large when $p_{fail}$ is near 1, whereas the decrease is very small when $p_{fail}$ is small. On the other hand, Fig. 5(a) shows that the time required decreases and increases from a certain moment as the $p_{fail}$ gets smaller. The reason is that the changes of d, $d_1$, and $d_2$ according to the change of $p_{fail}$ at $\epsilon _p=10^{-3}$ is larger than at $\epsilon _p=10^{-4}$. For these reasons, as $p_{fail}$ decreases, the volume of both algorithms decreases and increases at some point. When $\epsilon _p=10^{-4}$, the volume of two algorithms are the smallest when $p_{fail}$ is near 0.01. On the other hand, the volume of two algorithms are the smallest when $p_{fail}$ is near 0.1 for $\epsilon _p=10^{-3}$. Therefore, in order to perform an effective algorithm, it is necessary to select an appropriate $p_{fail}$ value that is neither too large nor too small, and the optimal $p_{fail}$ value varies depending on conditions such as the physical error rate.

Fig. 5

Volume, Number of physical qubits, and time required for Beauregard and Pavlidis algorithms for various $p_{fail}$s when (a) $\epsilon _p=10^{-3}$ and (b) $\epsilon _p=10^{-4}$

Figure 6 shows the volume of the Beauregard and Pavlidis algorithms according to the length of the number to be prime factorized and physical gate error rate. Overall, as the physical gate error rate and bit length increase, the volume of the algorithm increases. Although the difference in volume between the two algorithms is not large, the Beauregard algorithm has a smaller volume than the Pavlidis algorithm for short bit lengths. By contrast, as the bit length increases, the volume of the Beauregard algorithm becomes larger than that of the Pavlidis algorithm. The reason is that the T depth and elementary step in the Beauregard algorithm have smaller coefficients and are of higher order than those of Pavlidis algorithm. Overall, there is a large change in volume when the level of magic-state distillation changes. In particular, the volume gap of the Beauregard and Pavlidis algorithm is very large when the physical error rate is $10^{-3}$ and the bit length is 3072 or longer, because Beauregard algorithm requires three levels of magic-state distillation in the corresponding region, whereas the Pavlidis algorithm only requires two levels of magic-state distillation.

Fig. 6

Volume of Beauregard and Pavlidis algorithms for various bit lengths and physical gate error rates

7 Discussion

We formulated closed-form equations for the number of physical qubits and execution time required by two quantum factoring algorithms, the Beauregard and Pavlidis algorithms, assuming all-to-all connectivity. We used the magic-state distillation method of Fowler and Gidney [9]. The AQFT was used instead of the QFT, and an arbitrary rotation gate was decomposed into a universal gate set using the Gridsynth algorithm. Based on the formulas obtained under various conditions, we compared the number of physical qubits, execution time, and volume used by the two algorithms under various number of the bit lengths, the probabilities of failure of the algorithm, and the physical gate error rates. The results show that the resource required of the two algorithms are greatly influenced by the level of the magic state distillation. Therefore, to implement an algorithm effectively, efforts are needed such as lowering the physical error rate to use the magic state distillation as low level as possible. Although the difference in volume between the two algorithms is not large, but the more complex the system becomes, the more advantageous Pavlidis algorithm becomes. Therefore, it is necessary to select the appropriate algorithm according to the given environment. It is advantageous in terms of volume to choose an appropriate value that is neither too small nor too large for algorithm failure probability. In addition, the probability of algorithm failure has a greater impact on the execution time than the number of physical qubits.

Several things could be done to improve our study. First, the magic-state distillation method we used has a large number of minimally required resources and exhibits over-performance. Consequently, the required resources did not decrease significantly even when the physical gate error rate decreased. Therefore, it is expected that the resources required by the algorithm when the physical gate error rate is low can be reduced by using magic-state distillation with lower performance and fewer resources. Second, we compared only algorithms based on phase rotation. The rotation operation uses a number of T gates during decomposition into a universal gate set, which increases the required resources. Therefore, interesting results can be obtained if we compare the required resource of the bit-based quantum factoring algorithm, which generally uses fewer phase rotation gates and uses more logical qubits [12], and our results. Third, a comparison with the resources required assuming nearest-neighbor connectivity is necessary. Nearest-neighbor connectivity requires additional bus qubits and swapping operations because two data qubits to be calculated must be moved. This results in excessive increases in execution time and the number of physical qubits.