Quantum regularized least squares solver with parameter estimate

Abstract

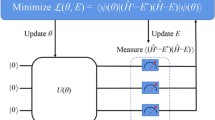
For ill-conditioned least squares problems, regularization techniques such as Tikhonov regularization are the key ingredients to obtain meaningful solutions, and the determination of the proper regularization parameter is the most difficult step. This paper focuses on the choice of regularization parameter on a quantum computer. We combine the classical L-curve or Hanke–Raus rule with the HHL algorithm and quantum amplitude estimation that compute the regularized solution and the corresponding residual and their norms. When a series of regularization parameters are tested, we then apply Grover’s search algorithm to find the best one that gives the meaningful solution. This yields a quadratic speedup in the number of regularization parameters.

Appendices

Appendix A: The procedure of HHL algorithm to generate state (12)

Suppose the SVD of ${\widetilde{A}}_\mu =\sum _j \tilde{\sigma }_j|\tilde{u}_j\rangle \langle \tilde{u}_j|$, and the smallest nonzero singular value is represented by $\tilde{\sigma }_{\min }$. We formally decompose $|\tilde{b}\rangle =\sum _j \tilde{\beta }_j |\tilde{u}_j\rangle$. Then by QPE, we obtain

$$\begin{aligned} \sum _j \tilde{\beta }_j |\tilde{u}_j\rangle |\tilde{\sigma }_j\rangle . \end{aligned}$$

Denote ${\widetilde{C}}$ as a lower bound of $\sigma _{\min }$, and define $f(z) = \arccos ({\widetilde{C}}/z)$, then apply $U_f$ to the above state to get

$$\begin{aligned} \sum _j \tilde{\beta }_j |\tilde{u}_j\rangle \left| \tilde{\sigma }_j\right\rangle \left| \arccos \left( {\widetilde{C}}/\tilde{\sigma }_j\right) \right\rangle . \end{aligned}$$

Now use control rotation to generate

$$\begin{aligned} \sum _j \tilde{\beta }_j |\tilde{u}_j\rangle \left| \tilde{\sigma }_j\right\rangle \left| \arccos \left( {\widetilde{C}}/ \tilde{\sigma }_j\right) \right\rangle \left[ \frac{{\widetilde{C}}}{\tilde{\sigma }_j}|0\rangle + \sqrt{1- \frac{{\widetilde{C}}^2}{\tilde{\sigma }^2_j}} |1\rangle \right] . \end{aligned}$$

At last, undo $U_f$ and QPE, then we have

$$\begin{aligned} \sum _j \tilde{\beta }_j |\tilde{u}_j\rangle \left[ {\widetilde{C}}\tilde{\sigma }_j^{-1}|0\rangle + \sqrt{1- {\widetilde{C}}^2\tilde{\sigma }_j^{-2}} |1\rangle \right] = {\widetilde{C}} \Vert x_\mu \Vert |x_\mu \rangle |0\rangle + P_1 |\phi _1\rangle |1\rangle . \end{aligned}$$

Appendix B: Multiply A on state (12)

Denote the SVD of $A=\sum _j \sigma _j |u_j\rangle \langle v_j|$, then the eigenvalue decomposition of ${\widetilde{A}} = \left( \begin{array}{c@{\quad }c} 0 &{} A \\ A^\dag &{} 0 \\ \end{array} \right)$ is $\sum _j \pm \sigma _j |w_j^\pm \rangle \langle w_j^{\pm }|$, where $|w_j^\pm \rangle = \frac{1}{\sqrt{2}}(|0\rangle |u_j\rangle \pm |1\rangle |v_j\rangle )$.

Formally, we can rewrite $|1,x_\mu \rangle = \sum _j x_{\mu ,j}|1,v_j\rangle = \sum _j \frac{x_{\mu ,j} }{\sqrt{2}}(|w_j^+\rangle -|w_j^-\rangle )$. Then

$$\begin{aligned} |1,X_\mu \rangle = {\widetilde{C}} \Vert x_\mu \Vert \sum _j \frac{x_{\mu ,j} }{\sqrt{2}}\left( |w_j^+\rangle -|w_j^-\rangle \right) |0\rangle + P_1 |0,\phi _1\rangle |1\rangle . \end{aligned}$$

By viewing $|0\rangle$ in the third register as control qubit, we perform QPE to $\hbox {e}^{\mathbf{i}t_0 {\widetilde{A}}}$ with initial state $|1,X_\mu \rangle$, then we obtain

$$\begin{aligned} {\widetilde{C}} \Vert x_\mu \Vert \sum _j \frac{x_{\mu ,j} }{\sqrt{2}}(|w_j^+\rangle |\sigma _j\rangle -|w_j^-\rangle |-\sigma _j\rangle ) |0\rangle + P_1 |0,\phi _1\rangle |1\rangle . \end{aligned}$$

Denote $f(z) = \arccos (z/{\widehat{C}})$, where ${\widehat{C}}$ is a upper bound of $\sigma _{\max }$. Apply $U_f$ to the above state to prepare

$$\begin{aligned} {\widetilde{C}} \Vert x_\mu \Vert \sum _j \frac{x_{\mu ,j} }{\sqrt{2}}\left( |w_j^+\rangle |\sigma _j\rangle \left| \arccos \left( \frac{\sigma _j}{{\widehat{C}}}\right) \right\rangle - |w_j^-\rangle |-\sigma _j\rangle \left| \arccos \left( -\frac{\sigma _j}{{\widehat{C}}}\right) \right\rangle \right) |0\rangle + P_1 |0,\phi _1\rangle |1\rangle . \end{aligned}$$

Now apply control rotation to generate

$$\begin{aligned}&\displaystyle {\widetilde{C}} \Vert x_\mu \Vert \sum _j \frac{x_{\mu ,j} }{\sqrt{2}}\left( |w_j^+\rangle |\sigma _j\rangle \left| \arccos \left( \frac{\sigma _j}{{\widehat{C}}}\right) \right\rangle \otimes \left[ \frac{\sigma _j}{{\widehat{C}}} |0\rangle + \sqrt{1- \frac{\sigma _j^2}{{\widehat{C}}^2}} |1\rangle \right] \right. \\&\quad \left. \displaystyle -\, |w_j^-\rangle |-\sigma _j\rangle \left| \arccos \left( -\frac{\sigma _j}{{\widehat{C}}}\right) \right\rangle \otimes \, \left[ -\frac{\sigma _j}{{\widehat{C}}} |0\rangle + \sqrt{1- \frac{\sigma _j^2}{{\widehat{C}}^2}} |1\rangle \right] \right) |0\rangle + P_1 |0,\phi _1\rangle |1\rangle . \end{aligned}$$

Finally, undo $U_f$ and QPE we obtain

$$\begin{aligned}&\displaystyle \frac{{\widetilde{C}}}{{\widehat{C}}} \Vert x_\mu \Vert \sum _j \frac{x_{\mu ,j}}{\sqrt{2}} \sigma _j (|w_j^+\rangle +|w_j^-\rangle ) |0,0\rangle + {\text {orthogonal terms}} \nonumber \\&\quad = \displaystyle \frac{{\widetilde{C}}}{{\widehat{C}}} \Vert x_\mu \Vert \sum _j x_{\mu ,j} \sigma _j |0,u_j\rangle |0,0\rangle + \, {\text {orthogonal terms}} \nonumber \\&\quad = \displaystyle \frac{{\widetilde{C}}}{{\widehat{C}}} \Vert x_\mu \Vert |0\rangle A |x_\mu \rangle |0,0\rangle + \, \mathrm{orthogonal~terms}. \end{aligned}$$

(22)

Therefore, there is a unitary that maps $|1,X_\mu \rangle$ to state (22). The first qubit $|0\rangle$ is ancillary.