Entanglement concentration service for the quantum Internet

Abstract

Here, we define the entanglement concentration service for the quantum Internet. The aim of the entanglement concentration service is to provide reliable, high-quality entanglement for a dedicated set of strongly connected quantum nodes in the quantum Internet. The objectives of the service are to simultaneously maximize the entanglement throughput of all entangled connections and to minimize the hop distance between the high-priority quantum nodes. We propose a method for the resolution of the entanglement concentration problem and provide a performance analysis.

1 Introduction

A fundamental aim of the quantum Internet [2,3,4,5,6,7,8,9,10,11,12,13] is to provide the standard network functions of the traditional Internet with an unconditional security for the users as quantum computers [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] become available. A basic concept of the quantum Internet is the entangled quantum network structure established via quantum entanglement [2, 4, 5, 10, 30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. The primary function of quantum Internet is to generate quantum entanglement [11, 42, 43, 70,71,72,73,74] between a distant sender and receiver quantum node through several intermediate repeater quantum nodes [3, 75,76,77,78,79,80,81,82,83,84,85,86,87,88,89]. The process of entanglement sharing consists of several steps of entanglement transmission and entanglement swapping (extension) between the quantum nodes [6, 7, 9, 90,91,92,93,94,95,96,97,98,99,100]. The entanglement throughput of an entangled connection quantifies the number of transmittable entangled states per sec at a particular fidelity over that quantum connection [11, 43, 44]. Entangled connections can be characterized by a cost function, which is practically the inverse of the entanglement throughput of a given connection [11, 42, 43]. Therefore, it is important to find the shortest entangled path (a set of entangled connections) in an entangled quantum network with respect to the particular cost function [8, 80, 81, 101,102,103,104,105,106]. A given quantum node of an entangled network could store several entangled systems in the local quantum memory, which can then be utilized for the entanglement distribution [11,12,13, 42,43,44, 77,78,83]. In our current modeling environment, the entangled states of a given quantum node are referred to as entangled ports; therefore, the aim is to find the shortest path between the entangled ports of the entangled network. The entanglement switching operation is therefore analogous to the problem of assignment of an entanglement switcher port. The entanglement switcher port models a quantum switcher node that switches between entangled connections and also applies entanglement swapping on selected entangled connections. The field of VLSI (very-large-scale integration) design [107,108,109,110], the automatic generation of integrated circuits (IC) and the tools of electronic design automation (EDA) [107,108,109,110] also address similar problems; however, the subject and final goal of our quantum networking setting are different. There are some fundamental ideas that can open a path between the field of EDA and the open problems of entangled quantum networks. As we have found, this path does not only exist, but also allowed us to merge the tools of EDA and the most recent results of quantum Shannon theory [11, 41] to derive valuable results for the quantum Internet.

Here, we define the entanglement concentration service for the quantum Internet. The entanglement concentration service aims to provide entangled connections between a strongly connected subset of high-priority quantum nodes such that an entangled connection exists between each pair of nodes. The primary requirements of the service are as follows: (1) the entanglement throughput between all connected nodes is maximized, and (2) the hop distance (number of spanned quantum nodes, which depends on the entanglement level of the connection) between the quantum nodes is minimized. The importance of the primary requirements is as follows. The maximization of the entanglement throughput of the links aims to provide a seamless and efficient quantum communication for high-priority users. The minimization of the hop distance aims to reduce the noise added from the physical environment (link loss, losses in the nodes) and to reduce the delay connected to the procedures of quantum transmission and entanglement distribution. We approach the problem of entanglement concentration through the entangled states that are available in the quantum nodes, which are referred to as entangled ports.

To handle the several different constraints, such as the entanglement throughput of the entangled connections or the hop distance, we organize the entangled ports of the quantum nodes into a base graph. The base graph contains the maps of the entangled ports in a square base lattice, which allows us to find the shortest path in the entangled network in a multiconstrained network setting. The base graph is also extended into a multilayer structure with a different set of entangled ports in each level. In the multilayer structure, each layer is classified by the supported maximally available entanglement throughput of the given entangled connection. The shortest path in the multilayer structure of base graphs identifies the shortest entangled path between a source and target node at multiple parallel constraints on the entanglement throughput of the entangled connections of the path. Since the entanglement concentration formulates a multiconstraint, multiobjective problem, we propose an algorithmic framework for an efficient tool problem solution and optimization. We also prove the complexity of the proposed framework.

The novel contributions of our manuscript are as follows:

• We conceive the entanglement concentration for the quantum Internet. The entanglement concentration service provides entangled connections for a subset of high-priority quantum nodes in the entangled quantum network.

• We define a multiobjective optimization that covers the maximization of entanglement throughput between all entangled connections of the strongly connected subset of quantum nodes, and the minimization of the hop distance between the quantum nodes to maximize the reliability.

• We prove the computational complexity of the service.

This paper is organized as follows. Section 2 summarizes the related works and preliminaries. Section 3 presents the problem statement and system model. Section 4 defines a method for optimal entanglement swapping. Section 5 provides a solution for the problem of entanglement concentration. Finally, Sect. 6 concludes with the results. Supplemental information is included in “Appendix”.

2 Related works and preliminaries

2.1 Related works

Quantum communication networks can be classified into two main classes [11, 42, 43]: unentangled and entangled quantum networks. In an unentangled quantum network, the connections between the quantum nodes are formulated via unentangled quantum states. In an entangled quantum network, the connections between the quantum nodes are formulated via entangled states. The entangled states are stored within the internal quantum memories of the quantum nodes, such that the entangled connections span several hops and are established over long distances. The characteristics and aims of the two types of quantum network models are fundamentally different. While the main purpose in an unentangled quantum network is to implement a standard (unentangled) QKD (quantum key distribution) protocol [11, 42, 43] between the nodes in a point-by-point manner to ensure the security of the quantum communication, the main task in an entangled quantum network is to distribute quantum entanglement over long distances. The services of unentangled and entangled quantum networks can be used as supplemental services for the tasks of traditional networks (to ensure stronger encryption and security services via QKD—such as IPSec with QKD [11] or TLS with QKD [11], to reduce the dependency on public key methods and on one-way functions, and to reduce the computational complexities of cryptographic methods, authentications, and privacy services). On the other hand, while unentangled quantum networks can provide only these supplemental services for traditional networks in short distances due to the point-by-point QKD-based quantum communication, the structure of entangled quantum networks allows us to construct a more complex network—called the quantum Internet. In a quantum Internet scenario, the core network is an entangled quantum network, and the main aim is to provide a general network structure for quantum computers (legal users) to establish reliable and secure long-distance quantum communications. A fundamental of the quantum Internet concept is therefore quantum entanglement and quantum repeaters. Quantum repeaters serve as intermediate transmitter quantum nodes between a sender quantum node (Alice) and a receiver quantum node (Bob) in the entanglement distribution process. By utilizing quantum entanglement, communication distances can be extended to long distances (unlimited, by theory) via the entanglement distribution process.

The entangled connections of entangled quantum networks span multiple nodes (i.e., these connections are multihop connections). An entangled connection is created via the entanglement distribution process, that is, via many physical links. A given physical link (i.e., optical fiber, wireless optical link) serves only temporarily in the distribution process because a physical link can create entanglement only over short distances. This is the reason the entanglement distribution process is realized in a step-by-step manner via many physical links and by many short-distance entangled states. The end of the entanglement distribution process is an end-to-end entangled state between the distant sender and receiver. The end-to-end entangled state spans over the intermediate nodes and physical links used in the distribution process between the sender and the receiver.

In an unentangled quantum network, the achievable communication distances are limited because of the requirement of (primarily) point-by-point QKD between the quantum nodes. In an entangled quantum network, the entanglement distribution procedure eliminates the requirement of point-by-point quantum communications and extends it to a multihop quantum communication.

Entangled quantum networks allow us to utilize all quantum protocols, such as QKD, and other quantum cryptographic primitives similar to untangled networks, but with the additional exploitation of the improved network structure, higher transmission reliability and transmission rates, and significantly longer achievable communication distances. As long-distance end-to-end entangled states are available, the entangled quantum network can be utilized as a quantum LAN (local area network), a quantum MAN (metropolitan area network), a quantum WAN (wide area network), or a global quantum Internet network.

The main uses of the quantum Internet include the field of distributed computations [70] (quantum secret sharing [11], blind quantum computation [11, 70], client–server quantum communications [11, 70], system-area networks [11, 70]), distributed cryptographic functions (Byzantine agreement [73], leader election [11, 70], QKD [11, 70]), and the field of sensor technology [11] (interferometry, clocks, reference frames).

Since an entangled network architecture represents a core of the quantum Internet, our network model is also based on the entangled quantum network model.

2.2 Preliminaries

A d-dimensional superposed quantum system ${\left| \psi \right\rangle }$ is a d-level system, $| \psi \rangle ={{\alpha }_{1}}| {{B}_{1}}\rangle +\cdots +{{\alpha }_{d}}| {{B}_{d}} \rangle$, where the $\alpha _{i}$-s are complex numbers, $\left| \alpha _{1} \right| ^{2} +\cdots +\left| \alpha _{d} \right| ^{2} =1$, while ${\left| B_{i} \right\rangle }$ is the ith basis state, $i=1,\ldots ,d$ [11, 41, 42]. For a qubit system, the dimension is $d=2$, and a superposed ${\left| \psi \right\rangle }$ can be written as ${\left| \psi \right\rangle } =\alpha _{1} {\left| 0 \right\rangle } +\alpha _{2} {\left| 1 \right\rangle }$, with $\left| \alpha _{1} \right| ^{2} +\left| \alpha _{2} \right| ^{2} =1$. A two-qubit system formulates quantum state

$$\begin{aligned} {\left| \psi \right\rangle } =\alpha _{1} {\left| 00 \right\rangle } +\alpha _{2} {\left| 01 \right\rangle } +\alpha _{3} {\left| 10 \right\rangle } +\alpha _{4} {\left| 11 \right\rangle }, \end{aligned}$$

(1)

where $\sum \left| \alpha _{i} \right| ^{2} =1$. A separable two-qubit system ${\left| \psi \right\rangle } _{s}$ can be decomposed into a tensor product form as ${\left| \psi \right\rangle } _{s} ={\left| \phi \right\rangle } \otimes {\left| \varphi \right\rangle }$, where ${\left| \phi \right\rangle }$ and ${\left| \varphi \right\rangle }$ are one-qubit systems, while $\otimes$ is the tensor product. An example for a ${\left| \psi \right\rangle } _{s}$ system is obtained at $\alpha _{1} =\alpha _{2} =\alpha _{3} =\alpha _{4} ={\textstyle \frac{1}{2}}$ in (1). On the other hand, if $\alpha _{1} =\alpha _{4} ={\textstyle \frac{1}{\sqrt{2} }}$ and $\alpha _{2} =\alpha _{3} =0$, the two-qubit system ${\left| \psi \right\rangle }$ in (1) cannot be decomposed, ${\left| \psi \right\rangle } \ne {\left| \phi \right\rangle } \otimes {\left| \varphi \right\rangle }$, and the qubits formulate an entangled system.

In an entangled system, operations performed on one half of the state affect the other, and the probabilities of the entangled qubits are not independent. The $d=2$-dimensional two-partite maximally entangled states are the Bell states [11, 41, 42] (or EPR states, named after Einstein, Podolsky and Rosen [11, 41, 42]). The Bell states are ${\left| \beta _{00} \right\rangle } ={\textstyle \frac{1}{\sqrt{2} }} \left( {\left| 00 \right\rangle } +{\left| 11 \right\rangle } \right) ,{\left| \beta _{01} \right\rangle } ={\textstyle \frac{1}{\sqrt{2} }} \left( {\left| 01 \right\rangle } +{\left| 10 \right\rangle } \right) ,{\left| \beta _{10} \right\rangle } ={\textstyle \frac{1}{\sqrt{2} }} \left( {\left| 00 \right\rangle } -{\left| 11 \right\rangle } \right)$ and ${\left| \beta _{11} \right\rangle } ={\textstyle \frac{1}{\sqrt{2} }} \left( {\left| 01 \right\rangle } -{\left| 10 \right\rangle } \right)$. In the entanglement distribution process, we assume the use of the $| \beta _{00} \rangle$ state.

A quantum system ${\left| \psi \right\rangle }$ can also be represented via a density matrix $\rho$. For an n-length, d-dimensional system, $\rho$ is a $d^{n} \times d^{n}$ size matrix, as $\rho ={\left| \psi \right\rangle } {\left\langle \psi \right| }$, such that $\mathrm{Tr}\left( \rho \right) =1$ for a general state, and for pure states $\mathrm{Tr}\left( \rho ^{2} \right) =1$. The density of ${\left| \beta _{00} \right\rangle }$ is $\rho ={\textstyle \frac{1}{2}} {\left| 00 \right\rangle } {\left\langle 00 \right| } +{\textstyle \frac{1}{2}} {\left| 00 \right\rangle } {\left\langle 11 \right| } +{\textstyle \frac{1}{2}} {\left| 11 \right\rangle } {\left\langle 00 \right| } +{\textstyle \frac{1}{2}} {\left| 11 \right\rangle } {\left\langle 11 \right| }$.

The fidelity [41, 42] for two pure quantum states ${\left| \psi \right\rangle }$ and ${\left| \varphi \right\rangle }$ is defined as $F\left( {\left| \varphi \right\rangle } ,{\left| \psi \right\rangle } \right) =\left| {\left\langle \varphi \mathrel {\left| \right. } \psi \right\rangle } \right| ^{2}$. The fidelity for a pure quantum system ${\left| \psi \right\rangle }$ and a mixed quantum system $\sigma =\sum _{i=0}^{n-1}p_{i} \rho _{i} =\sum _{i=0}^{n-1}p_{i} {\left| \psi _{i} \right\rangle } {\left\langle \psi _{i} \right| }$ is as $F\left( {\left| \psi \right\rangle } ,\sigma \right) =\left\langle \psi | \left. \sigma \right| \psi \right\rangle =\sum _{i=0}^{n-1}p_{i} \left| {\left\langle \psi \mathrel {\left| \right. } \psi _{i} \right\rangle } \right| ^{2}$. Fidelity can also be defined for mixed states $\sigma$ and $\rho$, as $F\left( \rho ,\sigma \right) =\sum _{i}p_{i} \left[ \text {Tr}\left( \sqrt{\sqrt{\sigma _{i} } \rho _{i} \sqrt{\sigma _{i} } } \right) \right] ^{2}$.

2.3 Operations in the quantum Internet

In a quantum Internet scenario, quantum repeaters aim to create high-fidelity entangled systems over long distances. For practical reasons, let us assume that we are operating on $d=2$-dimensional quantum systems. At a given target Bell state ${\left| \beta _{00} \right\rangle }$ subject to be created at the end of the entanglement distribution procedure, the entanglement fidelity at an actually created noisy quantum system $\sigma$ is therefore evaluated as $F\left( \sigma \right) =\langle {{\beta }_{00}} | \sigma |{{\beta }_{00}} \rangle$. In particular, F is a value between 0 and 1, with $F=1$ for a perfect Bell state and $F<1$ for an imperfect state.

The entangled system between two distant points A and B is distributed in a step-by-step manner through a set of intermediate quantum repeater nodes. In the first step, the neighboring quantum nodes create entanglement between each other. In the next step, particular quantum nodes apply a special operation called entanglement swapping [11, 42, 43] to double the number of spanned quantum nodes. The entanglement swapping operation splices two short-distance Bell states into a longer-distance Bell pair via operations applied in the quantum node and via classical side information (i.e., a similar mechanism to quantum teleportation [11, 42, 43]). This type of entanglement distribution mechanism is referred to as doubling architecture [11].

An important problem connected to the entanglement distribution is the handling of the noise on the entangled states. Considering the noisy physical links and other effects of the environment, the received quantum states are noisy. Particularly, the fidelity of the actually created entangled system $\sigma$ is far from the target fidelity F. To handle the situation, the noisy states should be purified—this process is called entanglement purification [11, 42, 43]. The entanglement purification process takes two imperfect systems $\sigma _{1}$ and $\sigma _{2}$ with $F_0<1$, and outputs a higher-fidelity system $\rho$ such that $F\left( \rho \right) >F_0$. The purification is a high-cost procedure since it requires a huge amount of resources (quantum systems, transmissions, and internal procedures in the nodes), causes delay in the transmission, and is probabilistic.

As follows, a network optimization is essential for a quantum Internet setting to reduce the purification steps. The problem is handled via our modeling scheme by determining optimal paths and via the application of entanglement switching nodes to switch between the entangled connections without the requirement of high-cost steps.

2.4 Network and service management in the quantum Internet

The quantum Internet requires the utilization of advanced network and service management. The main task in the physical layer of the quantum Internet is the reliable transmission of quantum states and the faithful internal storage of the received quantum systems in the quantum memories of the quantum nodes. The quantum transmission and quantum storage processes in the physical layer of the quantum Internet require a collaboration with network and service management services in a higher, logical layer. The logical layer utilizes classical side information available from the quantum network through traditional communication channels to provide feedback and adaption mechanism for the physical layer of the quantum network. The logical layer contains controlling and post-processing tasks, such as error correction, dynamic monitoring of the quantum links and quantum memories, controlling of the internal storage and error correction mechanisms of the quantum nodes, network optimization, and advanced service management processes.

The field of the quantum Internet dynamically improves and also challenges with several open questions. Since the structure and the processes of the quantum Internet are fundamentally different from the mechanisms of the traditional Internet, it requires the development of novel and advanced services. The main challenge regarding these services is to provide an optimal solution for the transmission of entangled systems, for the optimization of the network architecture, and for the development of the networking services connected to the entanglement distribution. The networking procedures of the quantum Internet should consider the fundamentals of quantum mechanics (such as superposition, quantum entanglement, and no-cloning theorem) that require a significantly different network and service management compared with the networking services of the traditional Internet.

This work defines a novel service for the quantum Internet. The service considers the physical attributes of quantum transmission and the procedures of entanglement distribution. The proposed service utilizes the fundamental architectural attributes of the quantum Internet, establishes advanced service management for the processes of entanglement distribution, and develops a network optimization by controlling the physical layer.

2.5 Experimental implementation

The entanglement concentration service can be implemented via the standard optical and physical devices of quantum networking. In practical applications, the preparation of long-distance entangled connections requires the utilization of high-fidelity quantum channels in the physical layer. On the aspects of entanglement transmission and repeater-assisted quantum communications in a practical quantum Internet, we suggest [3, 4]. On the bounds for multiend communication over experimental quantum networks, see [4]. For further reading on the feasibility of the quantum networks from experimental aspects, we suggest [6,7,8,9]. On the problem of entanglement routing in the quantum Internet, see [46,47,48, 96, 97, 101, 103]. For the different aspects of entanglement distribution problem in a quantum Internet setting, see [85,86,87,88, 111]. On the utilization of quantum channels in heterogeneous experimental networking environments, we suggest [11, 41].

The problem of entanglement localization in practical quantum networking scenarios is studied in [51]. In [52], a quantum network stack and protocols are defined for reliable entanglement-based experimental networks. On the problem of practical entanglement distillation, see [55]. The method of deterministic delivery of entanglement in an experimental quantum network is discussed in [56]. Satellite-to-ground quantum communications and quantum teleportation in experimental quantum networking scenarios are studied in [57, 58, 61]. The description of modular entanglement of atomic qubits using photons and phonons and its experimental quantum networking aspects can be found in [60]. For a review on quantum repeaters units based on atomic ensembles and linear optics, see [62]. On some aspects of network coding in experimental quantum networking, we suggest [64,65,66]

On current research topics and directions in the experimental quantum Internet, we suggest the descriptions of the Quantum Internet Research Group (QIRG) [112].

3 Problem statement and system model

3.1 Problem statement

The entanglement concentration problem is defined via Problems 1 and 2.

Problem 1

Determine a set of entangled connections for a set of high-priority unconnected quantum nodes such that the hop distance for all entangled connections is minimal and the entanglement throughput for all entangled connections is maximal.

Problem 2

(Strong connectivity property) Assure that all sets of high-priority quantum nodes selected for the entanglement concentration service are interconnected.

3.2 System model

3.2.1 Basic terms

The quantum Internet scenario is modeled through the concept of entangled overlay quantum network. The entangled overlay quantum network represents a logical layer over the physical-layer quantum repeater network. The overlay quantum network $N=\left( V,E \right)$ is defined via a set V of quantum nodes, and via a set E of entangled connections (edges). Set V consists the $U_{i}^{A}\in V$ source and $U_{i}^{B}\in V$ receiver nodes of ${{U}_{i}}$ legal users, $i=1,\ldots ,K$, where K is the number of transmit and receiver users, and quantum repeater nodes $R_i\in V$, $i=1, \ldots ,q$, with $E=\left\{ E_j\right\}$, $j=1, \ldots ,m$ edges between the nodes of V. Each $E_j$ identifies an l-level entanglement,¹$l=1, \ldots ,r$, between quantum nodes $x_j$ and $y_j$ of edge $E_j$, respectively.

In the quantum Internet, an $N=\left( V,E\right)$ entangled overlay quantum network integrates single-hop and multihop entangled nodes. The single-hop entangled nodes are directly connected through an $l=1$ level entanglement, while the multihop entangled nodes are connected through $l>1$ level entanglement.

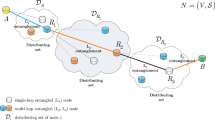
An entangled overlay quantum network N in a quantum Internet setting is depicted in Fig. 1. The network model consists of a set of legal users and intermediate quantum repeaters in V, with a set E of different level l of entangled connections. The model assumes a doubling architecture in the physical layer.

Fig. 1

An entangled overlay quantum network in a quantum Internet scenario. The quantum network consists of K source users (depicted by yellow nodes), $U_{i}^{A}$, $i=1,\ldots ,K$, K receiver users (depicted by blue nodes), $U_{i}^{B}$ $i=1,\ldots ,K$, and a set of intermediate quantum repeaters (depicted by gray nodes in the clouds) ${{R}_{i}}$, $i=1,\ldots ,q$, between the senders and receivers. The quantum nodes are connected via l-level entangled connections, where $l=1$ refers to a direct connection (black line), while $l>1$ are multilevel connections. For $l=2$ (blue thick line), the hop distance between the connected nodes is ${{d}_{l}}=2$, while for $l=3$ (orange thicker line), the hop distance between the connected nodes is ${{d}_{l}}=4$ (Color figure online)

Let us assume that there are m source nodes in the entangled quantum network and n receiver nodes. Let $E_{{l} } \left( A_{i} ,B_{j} \right)$, $i=0,\ldots ,m-1$, $j=0,\ldots ,n-1$, be an l -level entangled connection between source node $A_{i}$ and receiver node $B_{j}$, and let $B_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right)$ refer to the entanglement throughput of a given l -level entangled connection $E_{{l} } \left( A_{i} ,B_{j} \right)$ between nodes $\left( A_{i} ,B_{j} \right)$ as measured in the number of d-dimensional entangled states per sec at a particular fidelity F [41,42,43].

Without loss of generality, for an l -level entangled connection $E_{{l} } \left( A_{i} ,B_{j} \right)$, the hop distance $d\left( A_{i} ,B_{j} \right) _{{l} }$ refers to the number of spanned nodes. In a doubling architecture [11, 42,43,44], the number of spanned nodes is doubled on each entanglement level l, and $d\left( A_{i} ,B_{j} \right) _{{l} }$ is expressed as $d\left( A_{i} ,B_{j} \right) _{{l} } =2^{l-1}$.

To distinguish between the source and target nodes for a particular connection $E_{{l} } \left( A_{i} ,B_{j} \right)$, let $B_{F} \left( A_{i} \right)$, $B_{F} \left( A_{i} \right) \ge 0$ refer to the number of generated entangled states per sec of a particular fidelity in node $A_{i}$, and let $B_{F} \left( B_{j} \right)$ be the number of received entangled states per sec of a particular fidelity in node $B_{j}$, where $B_{F} \left( B_{j} \right) \le 0$. Therefore, in function of $B_{F} \left( A_{i} \right)$ and $B_{F} \left( B_{j} \right)$, an upper bound ${\tilde{B}}_{F}$ on $B_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right)$ can be defined for the entangled connection $E_{{l} } \left( A_{i} ,B_{j} \right)$ as

$$\begin{aligned} {\tilde{B}}_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) =\min \left( \max (B_{F}(A_{i})), \max (|B_{F}(B_{j})|)\right) , \end{aligned}$$

(2)

which corresponds to the maximum entanglement throughput that can be assigned to the entangled connection $E_{{l} } \left( A_{i} ,B_{j} \right)$.

Therefore, at m source and n receivers, the problem of entanglement concentration formulates a minimization via objective function $\Phi$ as

$$\begin{aligned} \Phi =\min \sum _{i=1}^{m}\sum _{j=1}^{n}d\left( A_{i} ,B_{j} \right) _{{l} } (\max (B_{F}(A_{i})), \max (|B_{F}(B_{j})|)). \end{aligned}$$

(3)

Assuming an entangled connection $E_{{l} } \left( A_{i} ,B_{j} \right)$ with an actual entanglement throughput $B_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) \le {\tilde{B}}_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right)$ between $A_{i}$ and $B_{j}$, the quantity $\Delta {B_{F}^{*}}\left( {{E}_{l}}\left( {{A}_{i}},{{B}_{j}} \right) \right)$ of maximal residual entanglement throughput for the direction from $A_{i}$ to $B_{j}$ is defined as

$$\begin{aligned} \Delta {B_{F}^{*}} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) ={\tilde{B}}_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) -B_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) . \end{aligned}$$

(4)

The result in (4) indicates that for a given entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$ with a current entanglement throughput $B_{F} \left( E_{l} \left( A_{i} ,B_{j} \right) \right)$, it is not possible to inject more entanglement throughput than $\Delta {B_{F}^{*}} \left( E_{l} \left( A_{i} ,B_{j} \right) \right)$. Let $\Delta d\left( A_{i} ,B_{j} \right) _{{l} }$ refer to the residual hop distance function, as

$$\begin{aligned} \Delta d\left( A_{i} ,B_{j} \right) _{{l} } =d\left( A_{i} ,B_{j} \right) _{{l} } , \end{aligned}$$

(5)

and let $B_{F} \left( E_{{l} } \left( B_{j} ,A_{i} \right) \right)$ refer to the entanglement throughput from $B_{j}$ to $A_{i}$, with maximal residual entanglement throughput $\Delta {B_{F}^{*}} \left( E_{{l} } \left( B_{j} ,A_{i} \right) \right)$ as

$$\begin{aligned} \Delta {B_{F}^{*}} \left( E_{{l} } \left( B_{j} ,A_{i} \right) \right) =-B_{F} \left( E_{{l} } \left( A_{i} ,B_{j} \right) \right) , \end{aligned}$$

(6)

and negative residual hop distance function as

$$\begin{aligned} \Delta d\left( B_{j} ,A_{i} \right) _{{l} } =-d\left( A_{i} ,B_{j} \right) _{{l} } . \end{aligned}$$

(7)

For a particular entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$, we define a forward residual edge, $e_{l} \left( A_{i} ,B_{j} \right)$, and a backward residual edge, $e_{l} \left( A_{j} ,B_{i} \right)$. The forward and backward residual edges are used for the increment and decrement of an actual entanglement throughput $B_{F} \left( E_{l} \left( A_{i} ,B_{j} \right) \right)$ over a particular entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$. An $e_{l} \left( A_{i} ,B_{j} \right)$ forward direction residual edge is associated with a particular $\Delta B_{F} \left( E_{l} \left( A_{i} ,B_{j} \right) \right) \le {B_{F}^{*}}\left( E_{l} \left( A_{i} ,B_{j} \right) \right)$, and it is maximized as given in (4).

An $e_{l} \left( A_{j} ,B_{i} \right)$ backward direction residual edge is associated with the quantity $\Delta B_{F} \left( E_{l} \left( A_{j} ,B_{i} \right) \right) \ge \Delta {B_{F}^{*}} \left( E_{l} \left( A_{j} ,B_{i} \right) \right)$ that describes the amount of entanglement throughput that can be removed from the entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$, and it is maximized as given in (6). As follows at most $\Delta B_{F} \left( E_{l} \left( A_{j} ,B_{i} \right) \right)$ entanglement throughput can be removed from the entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$.

Then, for a particular $A_{i}$ and $B_{j}$ with entangled connection $E_{l} \left( A_{i} ,B_{j} \right)$, the maximum allowed entanglement throughput that can be injected is $\eta \left( E_{l} \left( A_{i} ,B_{j} \right) \right)$, defined via (4) and (6) as

$$\begin{aligned} \eta \left( E_{l} \left( A_{i} ,B_{j} \right) \right) = \min ({\Delta B_{F} \left( E_{l} \left( A_{i}, B_{j} \right) \right) , \left| \Delta B_{F} \left( E_{l} \left( A_{j}, B_{i} \right) \right) \right| )}. \end{aligned}$$

(8)

Note that if negative cycles occur in the graph, some basic algorithmic solutions (e.g., Bellman–Ford algorithm [107]) can be straightforwardly applied to remove it.

Practically, an $E_{l} \left( x,y\right)$ entangled connection is implemented via an optical fiber ${{{\mathcal {N}}}}$ (or a wireless optical link, etc.) in the physical layer. The $E_{l} \left( x,y\right)$ link is associated with a particular link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ measured in dB, and with a transmittance coefficient $T\left( E_{l} \left( x,y\right) \right) \in \left[ 0,1\right]$ that characterizes the ratio of successfully transmitted photons. The link loss and transmittance values determine the achievable ${\tilde{B}}_{F}$ at a particular F over $E_{l} \left( x,y\right)$.

3.2.2 Evolutionary model

The motivation behind the utilization of an evolutionary model in the entanglement concentration problem is as follows. The modeled networking scenario assumes a quantum Internet environment with dynamically changing link and node attributes. The characteristic of the entangled links depends not just on the attributes of the physical link (entanglement throughput, link loss, link transmittance) used for the transmission of the entangled states, but also on the internal attributes of the quantum nodes (quantum memory status, error corrections, entanglement purification, etc.). These conditions overall result in a highly diverse networking environment. As a corollary, the path-finding algorithms and other related procedures should consider the diverse and dynamic conditions and should be able to adapt and modify their working mechanism according to a current situation. Another constraint is that the possible solutions should be explored simultaneously in the search space, with a parallel optimization in the overlay network. These conditions require the elimination of the need of deterministic procedures, and the solutions should be determined in an evolutionary manner. The utilization of the evolutionary model therefore eliminates the requirement of high-cost reiterations, redesigning, and rerouting steps and results overall in an optimal approach for the problems of entanglement concentration service in a quantum Internet scenario.

3.2.3 Base graph

The quantum nodes are approached through their available entangled states, which are referred to as entangled ports. We define the multiport multinode (MP/MN) [107,108,109,110] base graph and the multilayer MP/MN structure for the selection of entangled connections in the entanglement concentration service. The algorithm for the selection of the optimal entangled state $B_{j}^{c*}$ (referred to as optimal entangled port) in a target node $B_{j}$, where

$$\begin{aligned} B_{j} =\left\{ B_{j}^{c_{1} } ,\ldots ,B_{j}^{c_{k} } \right\} , \end{aligned}$$

(9)

where $B_{j}^{c_{i} }$ is the ith entangled port available in target node $B_{j}$ while c identifies an actual cycle in the base graph; requires the determination of an optimal multilayer path ${{{\mathcal {P}}}}^{*}$ and the definition of a particular cost function. The problem of constructing a multiport multimode base graph is therefore analogous to the problem of MP/MN signal nets [107,108,109,110].

Assuming a set of k entangled ports $P_{j} =\left\{ P_{j}^{c_{1} } ,\ldots ,P_{j}^{c_{k} } \right\}$ for a given quantum node j, each set corresponds to a different quantum node. For an overlay quantum network $N=\left( V,{{{\mathcal {S}}}}\right)$ with $\left| V\right|$ nodes, we defined a d-dimensional square lattice multiport multinode base graph $G^{d}$ ($d=2$) that contains the sets $P_{j}$, $j=1,\ldots ,\left| V\right|$.

Figure 2 depicts a $G^{2}$ two-dimensional square lattice base graph of entangled overlay quantum network N. The $d\left( P_{i}^{c_{k} } ,P_{j}^{c_{h} } \right) _{{l} }$ hop distance between l -level entangled ports $P_{i}^{c_{k} }$ and $P_{j}^{c_{h} }$ is identified by $\mathrm{l1}$ distance function in $G^{2}$ (intermediate entangled ports are depicted by empty dots).

Fig. 2

A $G^{2}$ two-dimensional square lattice base graph of an entangled overlay quantum network $N=\left( V,{{{\mathcal {S}}}}\right)$. Each quantum node (framed boxes) i, $i=1,\ldots ,\left| V\right|$, $\left| V\right| =5$ is assigned to a given set of entangled ports (depicted by black dots) $P_{i} =\{P_{i}^{c_{1} } ,\ldots ,P_{i}^{c_{k} } \}$, where k is the set of available entangled states in quantum node i. The unassigned entangled ports are depicted by empty dots

3.2.4 Strong connectivity

The aim of the topology construction method is to ensure strong connectivity between the entangled ports of the quantum nodes.

Procedure ${{{\mathcal {M}}}}_{S}$ of connection topology construction outputs a minimum spanning tree to ensure strong connectivity between the entangled ports of the subset $\Gamma$ of selected nodes. The steps of ${{{\mathcal {M}}}}_{S}$ are given in Procedure 1.

Note that in Step 5 of Procedure 1, the basic Kruskal algorithm [113] can be applied straightforwardly to compute the minimum spanning tree. The minimum spanning tree ensures strong connectivity and minimizes the number of required entangled connections. The resulting connection topologies can then be used as inputs for a shortest path-finding algorithm.

3.2.5 Multilayer structure

Each layer of the $G_\mathrm{ep}$ multilayer grid consists of a d-dimensional square lattice $G^{d}$ base graph that contains the maps of the quantum ports of the entangled overlay quantum network N. Assume that the network consists of n entangled ports. Depending on the maximal entanglement throughput available at the ports, the entangled ports of the graph are organized into a $G_\mathrm{ep}$ multilayer grid structure.

In $G_\mathrm{ep}$, a given Li, $i=0,\ldots ,q$ layer is a $d=2$-dimensional square lattice base graph $G^{d=2}$. The availability of the entangled ports in Li depends on the supported entanglement throughput of the ports. As the layer index i increases, the available entanglement throughput supported by the entangled ports of the layer also increases. Let ${\tilde{B}}_{F}^{\left( Li\right) }$ be the maximal supported entanglement throughput of layer Li. Then, the corresponding relation for the maximal entanglement throughput of the layers is

$$\begin{aligned} {\tilde{B}}_{F}^{\left( L0\right) }<{\tilde{B}}_{F}^{\left( L1\right) } \cdots <{\tilde{B}}_{F}^{\left( L\mathrm{q}\right) } . \end{aligned}$$

(10)

The steps for finding a shortest path in the multilayer base graph are summarized in Procedure 2.

Note in Step 2, an $A^{*}$ search² [107] can be applied to expand all possible routes in parallel.

Figure 3 depicts the multilayer structure. The entangled ports of the quantum network are organized into a four-layer structure with layers $L0-L3$. Each layer is a square lattice base graph with the map of the entangled ports of the entangled overlay quantum network. The entangled ports are extended to all layers and depicted by dots. A blue dot refers to the availability of a given entangled port in a given layer and a gray dot means that a current port is unavailable in the current layer. The white dots refer to intermediate ports that are not the ports of the target node. The source node is represented by $A_{i}$, and the target node is represented by $B_{j}$.

In Fig. 3a, target node $B_{j}$ has four entangled ports: $B_{j} =\left\{ B_{j}^{c_{1} } ,B_{j}^{c_{2} } ,B_{j}^{c_{3} } ,B_{j}^{c_{4} } \right\}$. All ports are depicted in all layers and colored according to their actual availability. The source node targets the four L2-layer entangled ports (dashed line and green area), since these support the actual entanglement throughput requirements of the source node (target level is L2). In the current target level, only two entangled ports are available in $B_{j}$.

Figure 3b shows the determination of the shortest path in the multilayer structure between $A_{i}$ and an available port $B_{j}^{c*}$ of $B_{j}$. The vertical line between the layers has a virtual cost $\kappa$.

Fig. 3

Selection of entangled port in the multilayer structure. a The sender node $A_{i}$ would like to share an entangled connection with target node $B_{j}$. The target node has 4 entangled ports, $B_{j} =\{B_{j}^{c_{1} } ,\ldots ,B_{j}^{c_{4} }\}$ on the target level L2 (thick line). An available port on an ith quality layer Li is depicted by blue dots, the unavailable ports are depicted by gray dots. b Determination of shortest path in the multilayer structure between entangled port $B_{j}^{c*}$ of target node $B_{j}$ and source node $A_{i}$. The intermediate nodes of the shortest paths are depicted by empty dots. The shortest path between $A_{i}$ and $B_{j}^{c*}$ is depicted by the red line (and light blue between the layers of an intermediate node) (Color figure online)

4 Network optimization

The constrained assignment for entanglement swapping covers the problem of optimal assignment of an entanglement switcher port (an entangled port for entanglement switching and swapping), which is constrained by the supported maximal entanglement throughput of the ports. The aim of the optimal constrained assignment of the entangled port is to minimize the path cost between a source quantum node A and target quantum nodes $B_{j}$, $j=1,\ldots ,t$. The assignment procedure is established in the multilayer grid structure of base graphs.

4.1 Optimization method

Minimization yields a minimal cost path for which the overall cost is minimal. If two or more paths have the same cost, the path is selected for which the overlapped length cost $\zeta _{A\rightarrow S}$ between a source node A and an entanglement switcher port S is maximal. The switcher port is selected from a set of entangled ports of a quantum node, which is referred to as the quantum switcher node.

The method for assigning a quantum switcher port in a $G_\mathrm{ep}$ multilayer grid structure is summarized in Procedure 3.

Note that in Step 2, an $A^{*}$ search [107] can straightforwardly be applied.

Let $\kappa$ be a cost function defined between the layers in the multilayer structure. Figure 4 depicts the procedure for assigning an entanglement switcher port S in the multilayer structure. The assignment problem is depicted in Fig. 4a, b. When the cost $\kappa$ associated with the vertical lines (depicted by blue) between the layers is $\kappa <1$, the optimal assignment of the switcher port is as depicted in Fig. 4c. If $\kappa \ge 1$, the optimal solution is as depicted in Fig. 4d, since the overlapped length is $\zeta _{A\rightarrow S} =9$. In Fig. 4e, the overlapped length is $\zeta _{A\rightarrow S} =7$ for a same path length $c_{A\rightarrow B} =c_{A\rightarrow B_{1} } +c_{A\rightarrow B_{2} } =15$ between source node A and target ports $B_{1}$ and $B_{2}$.

Fig. 4

Assignments of an entanglement switcher port in the multilayer structure. a The source node A would like to establish an entangled connection with target ports $B_{1}$ or $B_{2}$; however, an optimal assignment of switcher port S would require an entangled port from the set of inaccessible entangled ports of the switcher node (grey area). b Possible suboptimal assignments (black dots) of the switcher S in current layer L1 and lower-quality layer L0. c The entanglement switcher port S is assigned into layer L0 with path length $c_{A\rightarrow B} =c_{A\rightarrow B_{1} } +c_{A\rightarrow B_{2} } =12+3\kappa$ and overlapping path length $\zeta _{A\rightarrow S} =6+\kappa$ (depicted by thick orange line). Intermediate ports are depicted by empty dots. d The switcher port S is assigned into L1, with path length $c_{A\rightarrow B} =c_{A\rightarrow B_{1} } +c_{A\rightarrow B_{2} } =15$ and overlapping path length $\zeta _{A\rightarrow S} =9$. e The switcher port S is assigned into L1, with path length $c_{A\rightarrow B} =c_{A\rightarrow B_{1} } +c_{A\rightarrow B_{2} } =15$, and overlapping path length $\zeta _{A\rightarrow S} =7$ (Color figure online)

4.2 Entanglement throughput symmetry axis

The aim of the extraction of the entanglement throughput symmetry axis is to inject symmetry attributes to the connection of entangled ports and to the selection of entanglement switcher ports.

The entanglement throughput symmetry axis is extracted as follows. Let $\left( I,J\right)$ be an entangled port pair, where I is a source entangled port and J is a target entangled port with same maximal entangled throughputs ${{{\tilde{B}}}_{F}}\left( I \right) =\max \left( {{B}_{F}}\left( I \right) \right)$ and ${{{\tilde{B}}}_{F}}\left( J \right) =\max \left( \left| {{B}_{F}}\left( J \right) \right| \right)$. These entangled ports formulate a symmetry pair (SP) [107] as

$$\begin{aligned} {\mathrm{SP}}({\tilde{B}}_{F} (I),{\tilde{B}}_{F} (J)). \end{aligned}$$

(11)

For SP pair $\mathrm{SP}({\tilde{B}}_{F} (I),{\tilde{B}}_{F} (J))$, the $\Delta {\tilde{B}}_{F} (\mathrm{SP}({\tilde{B}}_{F} (I),{\tilde{B}}_{F} (J)))$ difference of entanglement throughput of the ports is negligible, thus

$$\begin{aligned} \Delta {\tilde{B}}_{F} (\mathrm{SP}({\tilde{B}}_{F} (I),{\tilde{B}}_{F} (J)))=\left| {\tilde{B}}_{F} \left( I\right) -{\tilde{B}}_{F} \left( J\right) \right| \rightarrow 0. \end{aligned}$$

(12)

Ordering the SP pairs of entangled ports in descending order with respect to their maximally supported entanglement throughput level defines a symmetry axis. We refer to this axis as the entanglement throughput symmetry axis. This vertical axis separates the entangled ports of the sender and receiver. Since an entanglement switcher port S is placed on this axis, the switcher port is referred to as self-symmetric (SS) [107] and denoted by $\mathrm{SS}\left( S\right)$.

Ordering the SP pairs at distance $l_{S,j}$ with respect to their entanglement throughput between the switcher port and an entangled port j of a given SP pair allows us to rewrite the minimization problem of (3) as

$$\begin{aligned} \Phi \left( S,\mathrm{SP}m\right) =\min \sum _{j=1}^{m}l_{S,\mathrm{SP}j} \left( {\tilde{B}}_{F} \left( \mathrm{SP}j\right) \right) , \end{aligned}$$

(13)

where m is the total number of SP pairs and ${\tilde{B}}_{F} \left( \mathrm{SP}j\right)$ quantifies the maximal entanglement throughput of the jth SP pair $\mathrm{SP}j$, where $l_{S,\mathrm{SP}j}$ is the distance function in the grid structure evaluated as

$$\begin{aligned} l_{S,\mathrm{SP}j} =\left| x_{S} -x_{\mathrm{SP}j} \right| +\left| y_{S} -y_{\mathrm{SP}j} \right| +\left| z_{S} -z_{\mathrm{SP}j} \right| \kappa , \end{aligned}$$

(14)

where $\kappa$ is the cost associated to the vertical lines and $\left\{ x_{\mathrm{SP}j} ,y_{\mathrm{SP}j} ,z_{\mathrm{SP}j} \right\}$ identifies a given port from the jth SP pair in the multilayer grid $G_\mathrm{ep}$.

Figure 5 illustrates the entanglement symmetry axis. The SP pairs are ordered with respect to their entanglement throughput $B_{F}$. To manage the connection rules between the switcher port S and the entangled ports, we define heuristics ${{{\mathcal {H}}}}1,{{{\mathcal {H}}}}2$ and ${{{\mathcal {H}}}}3$.

The first rule, ${{{\mathcal {H}}}}1$, assumes no switcher port and allows entangled connections only between SP ports from two different side of the symmetry axis; thus, a connection is not allowed between two sender or two receiver ports.

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}1:\\&\lnot \text {SS}\left\{ S \right\} \wedge \\&\lnot \left( \text {C}\left\{ I,P \right\} \wedge \text {C}\left\{ J,Q \right\} \right) \wedge \lnot \left( \text {C}\left\{ I,E \right\} \wedge \text {C}\left\{ J,F \right\} \right) \wedge \\&\left( \text {C}\left\{ E,P \right\} \wedge \text {C}\left\{ Q,F \right\} \right) \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( I \right) ,{{{{\tilde{B}}}}_{F}}\left( J \right) \right) \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( P \right) ,{{{{\tilde{B}}}}_{F}}\left( Q \right) \right) \wedge \text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( E \right) ,{{{{\tilde{B}}}}_{F}}\left( F \right) \right) . \end{aligned} \end{aligned}$$

(15)

The second rule, ${{{\mathcal {H}}}}2$, assumes no switcher port and allows no connection between entangled ports with different entanglement throughput capabilities.

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}2:\\&\lnot \text {SS}\left\{ S \right\} \wedge \\&\lnot \left( \text {C}\left\{ J,P \right\} \wedge \text {C}\left\{ I,Q \right\} \wedge \text {C}\left\{ J,E \right\} \wedge \text {C}\left\{ I,F \right\} \right) \wedge \\&\left( \text {C}\left\{ I,J \right\} \wedge \text {C}\left\{ P,Q \right\} \right) \wedge \text {C}\left\{ E,F \right\} \wedge \text {C}\left\{ E,Q \right\} \wedge \text {C}\left\{ P,F \right\} \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( I \right) ,{{{{\tilde{B}}}}_{F}}\left( J \right) \right) \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( P \right) ,{{{{\tilde{B}}}}_{F}}\left( Q \right) \right) \wedge \text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( E \right) ,{{{{\tilde{B}}}}_{F}}\left( F \right) \right) . \end{aligned} \end{aligned}$$

(16)

The third rule, ${{{\mathcal {H}}}}3$, assumes a switcher port. It defines the valid connections between a switcher port S and the entangled ports of the SP pairs separated by the entanglement throughput axis. Valid connections are allowed only between the SP symmetry pairs, which assures that the source and target ports support the same level of entanglement throughput to optimize performance.

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}3:\\&\text {SS}\left\{ S \right\} \wedge \\&\left( \text {C}\left\{ I,S \right\} \wedge \text {C}\left\{ J,S \right\} \right) \wedge \\&\left( \text {C}\left\{ P,S \right\} \wedge \text {C}\left\{ Q,S \right\} \right) \wedge \left( \text {C}\left\{ E,S \right\} \wedge \text {C}\left\{ F,S \right\} \right) \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( I \right) ,{{{{\tilde{B}}}}_{F}}\left( J \right) \right) \wedge \\&\text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( P \right) ,{{{{\tilde{B}}}}_{F}}\left( Q \right) \right) \wedge \text {SP}\left( {{{{\tilde{B}}}}_{F}}\left( E \right) ,{{{{\tilde{B}}}}_{F}}\left( F \right) \right) . \end{aligned} \end{aligned}$$

(17)

Fig. 5

Entanglement throughput symmetry axis with respect to an entanglement switcher port S. The SP pairs are ordered according to their associated entanglement throughput $B_{F}$. The possible symmetry pairs (SP) are (SP1): $\mathrm{SP}({\tilde{B}}_{F} (I),{\tilde{B}}_{F} (J))$, (SP2): $\mathrm{SP}({\tilde{B}}_{F} (P),{\tilde{B}}_{F} (Q))$ and (SP3): $\mathrm{SP}({\tilde{B}}_{F} (E),{\tilde{B}}_{F} (F))$. Switcher port S is a self-symmetric port, as denoted by $\mathrm{SS}\left( S\right)$. The lines between the ports identify a given entangled connection $\mathrm{C}$. The heuristics ${{{\mathcal {H}}}}1,{{{\mathcal {H}}}}2$, and ${{{\mathcal {H}}}}3$ are depicted by dashed, dotted, and solid lines, respectively. (For ${{{\mathcal {H}}}}1$, the allowed connections are depicted by black and the not-allowed connections are depicted by purple. For ${{{\mathcal {H}}}}2$, the allowed connections are depicted by black and the not-allowed connections are depicted by red) (Color figure online)

5 Entanglement concentration service

The problem of entanglement concentration can be viewed as a multiobjective optimization problem [107,108,109,110, 114,115,116] with the previously discussed constraints (Sects. 3, 4). Therefore, it is convenient to use a multiconstraint, multiobjective algorithmic framework to solve the optimization problem. We therefore propose a straightforward exploitation of a modified and re-constrained evolutionary approach [108].

Let x be a vector of $\mathrm{H}$ optimization variables, let $g_{j} \left( x\right)$ refer to the jth constraint of the multiobjective optimization problem and let $f_{m} \left( x\right)$ be the mth objective function. The problem is therefore to find an x that minimizes $f_{m} \left( x\right)$, $m=1,\ldots ,M$, subject to $g_{j} \left( x\right) =0$, $j=1,\ldots ,J$.

Assume that the number of subnets is $\mathrm{H}$, $l_{i}$ is the number of entangled connections in subnet i, K is the fixed number of segments in entangled connection j, $c_{ijk}$ is the length of a segment k of entangled connection j of net i, $r_{ijk}$ is the number of layers of a segment k of entangled connection j of net i, and $\left| S_{i} \right|$ is the number of switcher ports in subnet i [107,108,109,110]. Therefore, the D dimension of the search space is

$$\begin{aligned} \begin{aligned}&D\\ =&\sum _{i=1}^{\mathrm{H} }\left( \sum _{j=1}^{l_{i} }\sum _{k=1}^{K}\left( \left( c_{ijk} +r_{ijk} \right) +\left| A\right| +\left| B\right| \right) +\sum _{j=1}^{\left| S_{i} \right| }\left( x_{j} +y_{j} \right) \right) {}, \end{aligned} \end{aligned}$$

(18)

where $\left| A\right|$ is the number of source ports and $\left| B\right|$ is the number of target ports with respect to entangled connection j of net i.

A multiobjective evolutionary algorithm ${{{\mathcal {A}}}}_{G}$ can be straightforwardly applied to solve the problem. Algorithm ${{{\mathcal {A}}}}_{G}$ is summarized in Algorithm 1.

5.1 Discussion

For a detailed description of the subprocedures of Step 0 of ${{{\mathcal {A}}}}_{G}$, see [108].

5.2 Computational complexity

The computational complexity of the ${{{\mathcal {A}}}}_{G}$ algorithm is

$$\begin{aligned} {{{\mathcal {O}}}}\left( MW^{2} \right) , \end{aligned}$$

(19)

where M is the number of objectives and W is the size of population. Since the complexity of subprocedure ${{{\mathcal {A}}}}^{\prime }_\mathrm{nds}$ is ${{{\mathcal {O}}}}\left( M\left( 2W\right) ^{2} \right)$ [108], the complexity of ${{{\mathcal {A}}}}^{\prime }_\mathrm{assign.}$ is ${{{\mathcal {O}}}}\left( M\left( 2W\right) \log \left( 2W\right) \right)$ [108] and the complexity of subprocedure ${{{\mathcal {A}}}}^{\prime }_\mathrm{sorting}$ is ${{{\mathcal {O}}}}\left( 2W\log \left( 2W\right) \right)$ [108].

5.3 Numerical evidence

We study the entanglement concentration problem in a practical scenario, at a set ${{{\mathcal {S}}}}_{f}$ of objective functions ${{{\mathcal {S}}}}_{f} =\left\{ f_{1} ,f_{2} ,f_{3} ,f_{4} \right\}$, where $f_{1} ={\tilde{B}}_{F}$, $f_{2} =d_{l}$, $f_{3} ={\tilde{F}}$ and $f_{4} =\Phi$. Objective function $f_{1}$ identifies the maximal entanglement throughput at a target fidelity $F\ge 0.98$, $f_{2}$ is the hop distance function at an l-level entangled connection $E_{l}$, $f_{3}$ is associated with the ${\tilde{F}}$ maximal achievable fidelity of entanglement, while $f_{4}$ is the objective function defined in (3).

The numerical evidences consider a realistic quantum network setting with optical fiber link ${{{\mathcal {N}}}}$ between nodes x and y, with a particular link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$, and transmittance $T\left( E_{l} \left( x,y\right) \right)$. The link loss is measured in dB, while the transmittance is the ratio of photons (a value between 0 and 1) successfully transmitted through the physical link.

5.3.1 Entangled connections

First, we study the achievable ${\tilde{B}}_{F}$ (Bell pairs per second at a fidelity condition $F\ge 0.98$) values in function of the hop distance $d_{l}$. The analysis considers $\left| A\right| =\left| B\right| =5$ for the number of source and target entangled ports in x and y.

In Fig. 6a the effects of $d_{l}$ on ${\tilde{B}}_{F}$ are depicted. The system model assumes that the initial link loss at $l=1$ is ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2\,\mathrm{dB}$, and ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.1 dB per a unit increase of l. The network setting in Fig. 6b considers the situation if ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.2 dB per a unit increase of l. The results reveal the characteristic of the decrement of maximal entanglement throughput at improved link loss values.

The analysis in Fig. 6c reveals the connection between the achievable ${\tilde{B}}_{F}$ values and the $T\left( E_{l} \left( x,y\right) \right)$ transmittance, at $T\left( E_{l} \left( x,y\right) \right) \in \left[ 0.2,0.6\right]$, $l=1$. An increment of $T\left( E_{l} \left( x,y\right) \right)$ from $T\left( E_{l} \left( x,y\right) \right) =0.4273$ to $T\left( E_{l} \left( x,y\right) \right) =0.46$ doubles the ${\tilde{B}}_{F}$ values, because at these $T\left( E_{l} \left( x,y\right) \right)$ values the resulting link loss decreases from ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) \approx 3.7\,\mathrm{dB}$ to ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) \approx 3.3\,\mathrm{dB}$.

The ${\tilde{F}}$ maximal achievable entanglement fidelity in function of the $d_{l}$ hop distance is depicted in Fig. 6d. The initial link loss at $l=1$ is ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2\,\mathrm{dB}$, and ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.1 dB per a unit increase of l. The analysis considers $\left| A\right| =\left| B\right| =5$ for the number of source and target ports in x and y. The ${\tilde{F}}$ values varies random due to the probabilistic nature of the entanglement purification procedure. Due to link loss characteristic, the ${\tilde{F}}$ values remain in the target range $\left[ 0.98,1\right]$ for $l\le 3$. As $l>3$, ${\tilde{F}}$ varies more significantly and picks up values from outside of the target range, due to the increased link loss. (The lower bound of the target fidelity range is depicted by the dashed line.)

Fig. 6

The achievable ${\tilde{B}}_{F}$ values (entangled pairs per second at $F\ge 0.98$) in function of the hop distance $d_{l}$, at initial link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2\,\mathrm{dB}$. a The loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.1 dB per a unit increase of l, ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2+\left( l-1\right) 0.1\,\mathrm{dB}$. b The loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.2 dB per a unit increase of l, ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2+\left( l-1\right) 0.2\,\mathrm{dB}$. c The achievable ${\tilde{B}}_{F}$ values ($F\ge 0.98$) and the $T\left( E_{l} \left( x,y\right) \right)$ transmittance, at $T\left( E_{l} \left( x,y\right) \right) \in \left[ 0.2,0.6\right]$, $l=1$. d The ${\tilde{F}}$ maximal achievable entanglement fidelity in function of the $d_{l}$ hop distance. The link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ increases 0.1 dB per a unit increase of l, ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) =3.2+\left( l-1\right) 0.1\,\mathrm{dB}$. The ${\tilde{F}}$ values remain in the target range of $\left[ 0.98,1\right]$ for $l\le 3$

5.3.2 Objective function

The results in Fig. 7 reveal the impacts of link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ (dB) on the objective function value $\Phi$ (see (3)) for a particular node pair $\left\{ x,y\right\}$ with an entangled connection $E_{l} \left( x,y\right)$, $l=1$. Assuming a practical optical fiber for the transmission of the entangled systems, the range of the ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$ loss of the $E_{l} \left( x,y\right)$ entangled connection is considered in the range of ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) \in \left[ 3.2\,\mathrm{dB},4.4\,\mathrm{dB}\right]$. The evaluation assumes target fidelity $F\ge 0.98$. As the link loss increases above 3.5 dB, the $\Phi$ objective function decreases significantly, because the ${\tilde{B}}_{F}$ values start to converge to 0.

Fig. 7

Evaluation of the objective function $\Phi$ in function of link loss ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right)$, ${{{\mathcal {L}}}}\left( E_{l} \left( x,y\right) \right) \in \left[ 3.2\,\mathrm{dB},4.4\,\mathrm{dB}\right]$ for a particular node pair x, y, and entangled connection $E_{l} \left( x,y\right)$, at $l=1$

6 Conclusions

Entanglement concentration service is a complex problem in the quantum Internet aimed at providing reliable, high-quality entanglement for a dedicated set of strongly connected quantum nodes. Distribution of entanglement in the strongly connected subset is related to the problem of the optimal switching and swapping of entangled connections. In the problem solving, we integrated the fundamentals of VLSI design and analysis and evolutionary computations with the recent results of the quantum Internet.

Appendix

1.1 Abbreviations

EDA:

Electronic design automation

IC:

Integrated circuit

MP/MN:

Multiport multinode

QKD:

Quantum key distribution

SP:

Symmetry pair

SS:

Self-symmetric

VLSI:

Very-large-scale integration

1.2 Notations

The notations of the manuscript are summarized in Table 1.

Table 1 Summary of notations