Preservation of entanglement and quantum correlations next to periodic plasmonic nanostructures

Abstract

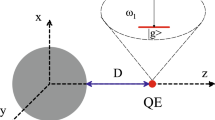
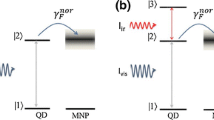
We study quantum correlations dynamics of two identical V-type quantum systems initially prepared in an extended Werner-like state, where each one independently interacts with a plasmonic nanostructure. Each V-type system can be decomposed as a two-level system with an additional third external level acting as an “umbrella level.” As the plasmonic nanostructure, we use a two-dimensional array of metal-coated dielectric nanoparticles. For the calculations, we combine quantum dynamics calculations using the density matrix equations and classical electromagnetic calculations. In order to describe the entanglement, we use the measure of entanglement of formation, while we use quantum discord to describe the total quantum correlations of our composite system. We find that the presence of the plasmonic nanostructure leads to high suppression of spontaneous emission rates along with a high degree of quantum interference. These phenomena affect the evolution of both entanglement and quantum discord, while they significantly prolong their dynamics.

Appendices

Appendix A

Here, we give the expressions for the elements of the composite density matrix $\rho ^{(2)}_{AB}(t)$. Since the elements of the single-qubit density matrix are given in Eq. (2) and the composite two-qubit density matrix is given by the tensor product $\rho ^{(2)}_{AB}(t)=\rho ^{(1)}_A(t) \otimes \rho ^{(1)}_B(t)$, following Ref. [49], we take

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KK}}(t)= & {} \rho ^{(2)}_{\mathcal{KK}}(0)|q(t)|^4, \end{aligned}$$

(22)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{LL}}(t)= & {} \rho ^{(2)}_{\mathcal{KK}}(0)|q(t)|^2(1-|q(t)|^2)+\rho ^{(2)}_{\mathcal{LL}}(0)|q(t)|^2, \end{aligned}$$

(23)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{MM}}(t)= & {} \rho ^{(2)}_{\mathcal{KK}}(0)|q(t)|^2(1-|q(t)|^2)+\rho ^{(2)}_{\mathcal{MM}}(0)|q(t)|^2, \end{aligned}$$

(24)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{NN}}(t)= & {} 1-[\rho ^{(2)}_{\mathcal{KK}}(t)+\rho ^{(2)}_{\mathcal{LL}}(t)+\rho ^{(2)}_{\mathcal{MM}}(t)], \end{aligned}$$

(25)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KL}}(t)= & {} \rho ^{(2)}_{\mathcal{KL}}(0)q(t)|q(t)|^2, \end{aligned}$$

(26)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KM}}(t)= & {} \rho ^{(2)}_{\mathcal{KM}}(0)q(t)|q(t)|^2, \end{aligned}$$

(27)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KN}}(t)= & {} \rho ^{(2)}_{\mathcal{KN}}(0)q^2(t), \end{aligned}$$

(28)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{LM}}(t)= & {} \rho ^{(2)}_{\mathcal{LM}}(0)|q(t)|^2, \end{aligned}$$

(29)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{LN}}(t)= & {} \rho ^{(2)}_{\mathcal{KM}}(0)q(t)(1-|q(t)|^2)+\rho ^{(2)}_{\mathcal{LN}}(0)q(t), \end{aligned}$$

(30)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{MN}}(t)= & {} \rho ^{(2)}_{\mathcal{KL}}(0)q(t)(1-|q(t)|^2)+\rho ^{(2)}_{\mathcal{MN}}(0)q(t), \end{aligned}$$

(31)

where $\rho ^{(2)}_{ij}(t)={\rho ^{(2){^*}}_{ij}}(t)$, with $i,j={{\mathcal {K}}},{{\mathcal {L}}},{{\mathcal {M}}},{{\mathcal {N}}}$.

Appendix B

Here, we give the details for the derivation of concurrence and QD for a composite system consists by two two-level systems. Since the states given by Eqs. (9) are X-states, the concurrence is given by

$$\begin{aligned} C=\max \left\{ 0, C_1, C_2 \right\} , \end{aligned}$$

(32)

with $C_1=2(|\rho ^{(2)}_{\mathcal{KN}}|-\sqrt{\rho ^{(2)}_{\mathcal{LL}}\rho ^{(2)}_{\mathcal{MM}}})$ and $C_2=2(|\rho ^{(2)}_{\mathcal{LM}}|-\sqrt{\rho ^{(2)}_{\mathcal{KK}}\rho ^{(2)}_{\mathcal{NN}}})$.

For the initial state $\rho ^{(2)}_{\varPhi }(0)$ [see Eq. (9a)], the element $\rho ^{(2)}_{\mathcal{KN}}$ is initially zero and remains zero for every t [49]. Therefore, from Eq. (32), one obtains that $C_1$ is always negative, leading to the concurrence $C_\varPhi (t)$ for the initial state $\rho ^{(2)}_{\varPhi }(0)$ being equal to $C_2$. Furthermore, for $0\le a \le 1$ and $0\le r \le 1$, one can easily prove [6]

$$\begin{aligned} C_{\varPhi }(t)= & {} 2\max \left\{ 0,|q(t)|^2 \left[ ra\sqrt{1-a^2}\right. \right. \nonumber \\&\quad \left. \left. -\frac{1}{2}\sqrt{(1-r)\left( 1-|q(t)|^2+\frac{1-r}{4}|q(t)|^4 \right) } \right] \right\} . \end{aligned}$$

(33)

Now, when the initial state is $\rho ^{(2)}_{\varPsi }(0)$ [see Eq. (9b)], the matrix element $\rho ^{(2)}_{\mathcal{LM}}(t)$ in $\rho ^{(2)}_{\varPsi }(t)$ is zero at all times; thus, we essentially obtain that the concurrence $C_\varPsi (t)$ for this initial state equals $C_1$. From Ref. [6] again, we write

$$\begin{aligned} C_{\varPsi }(t)= & {} 2\max \left\{ 0,|q(t)|^2 \left[ ra\sqrt{1-a^2}+\frac{1}{4}\left( |q(t)|^2(1+3r-4ra^2)\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +4ra^2-2(1+r) \right) \right] \right\} . \end{aligned}$$

(34)

Substituting Eqs. (33)–(34) into Eq. (3), we can also compute EoF for $\rho _{\varPhi }^{(2)}(0)$ and $\rho _{\varPsi }^{(2)}(0)$, correspondingly. Because the final analytical expression for EoF is rather complex, we will not present it here.

Writing Eq. (9) in a matrix form, we take

$$\begin{aligned} \rho ^{(2)}_{\varPhi }(0)= & {} \left[ \begin{array}{cccc} \frac{1-r}{4} &{} 0 &{} 0 &{} 0 \\ 0 &{} r(1-a^2)+\frac{1-r}{4} &{} ra \sqrt{1-a^2} &{} 0 \\ 0 &{} ra\sqrt{1-a^2} &{} ra^2+\frac{1-r}{4} &{} 0 \\ 0 &{} 0 &{} 0 &{} \frac{1-r}{4} \end{array} \right] , \end{aligned}$$

(35)

$$\begin{aligned} \rho ^{(2)}_{\varPsi }(0)= & {} \left[ \begin{array}{cccc} r(1-a^2)+\frac{1-r}{4} &{} 0 &{} 0 &{} ra\sqrt{1-a^2} \\ 0 &{} \frac{1-r}{4} &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{1-r}{4} &{} 0 \\ ra\sqrt{1-a^2} &{} 0 &{} 0 &{} ra^2+\frac{1-r}{4} \end{array} \right] \, . \end{aligned}$$

(36)

The composite density matrix elements for $t > 0$ and for the initial states $\rho ^{(2)}_{\varPhi }(0)$ and $\rho ^{(2)}_{\varPsi }(0)$ are given [6, 48, 49, 52] as follows: In case of $\rho ^{(2)}_{\varPhi }(t)$, the matrix elements read

$$\begin{aligned}&\rho ^{(2)}_{\mathcal{KK}}(t)=\frac{1-r}{4}|q(t)|^4, \end{aligned}$$

(37a)

$$\begin{aligned}&\rho ^{(2)}_{\mathcal{LL}}(t)=\left[ r(1-a^2)+\frac{1-r}{2} \right] |q(t)|^2-\frac{1-r}{4}|q(t)|^4, \end{aligned}$$

(37b)

$$\begin{aligned}&\rho ^{(2)}_{\mathcal{MM}}(t)=\left[ ra^2+\frac{1-r}{2} \right] |q(t)|^2-\frac{1-r}{4}|q(t)|^4, \end{aligned}$$

(37c)

$$\begin{aligned}&\rho ^{(2)}_{\mathcal{NN}}(t)=1-|q(t)|^2+\frac{1-r}{4}|q(t)|^4, \end{aligned}$$

(37d)

$$\begin{aligned}&\rho ^{(2)}_{\mathcal{LM}}(t)=ra\sqrt{1-a^2}|q(t)|^2, \end{aligned}$$

(37e)

and in case of $\rho ^{(2)}_{\varPsi }(t)$, the matrix elements read

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KK}}(t)&=\left[ r(1-a^2)+\frac{1-r}{4} \right] |q(t)|^4, \end{aligned}$$

(38a)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{LL}}(t)&=\left[ r(1-a^2)+\frac{1-r}{2} \right] |q(t)|^2-\left[ r(1-a^2)+\frac{1-r}{4}\right] |q(t)|^4, \end{aligned}$$

(38b)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{MM}}(t)&=\left[ r(1-a^2)+\frac{1-r}{2} \right] |q(t)|^2-\left[ r(1-a^2)+\frac{1-r}{4}\right] |q(t)|^4, \end{aligned}$$

(38c)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{NN}}(t)&=1-2\left[ r(1-a^2)+\frac{1-r}{2} \right] |q(t)|^2+\left[ r(1-a^2)+\frac{1-r}{4} \right] |q(t)|^4, \end{aligned}$$

(38d)

$$\begin{aligned} \rho ^{(2)}_{\mathcal{KN}}(t)&=ra\sqrt{1-a^2} q^2(t), \end{aligned}$$

(38e)

with $\rho ^{(2)}_{ij}={\rho ^{(2)}_{ji}}^*$ and all the other elements equal to zero in both cases. So, using these equations for the elements of density matrix, we can derive Eqs. (33)–(34).

Now, we turn our attention to QD. As before, our initial states, Eqs. (9), are X-states, which can be written in the most general form in the basis ${{\mathcal {B}}}=\{ |{{\mathcal {K}}}\rangle \equiv |11\rangle , |{{\mathcal {L}}}\rangle \equiv |10\rangle , |{{\mathcal {M}}}\rangle \equiv |01\rangle , |{{\mathcal {N}}}\rangle \equiv |00\rangle \}$; we thus obtain

$$\begin{aligned} \rho ^{(2)}_{AB}(0)= \left[ \begin{array}{cccc} \rho ^{(2)}_{\mathcal{KK}} &{} 0 &{} 0 &{} \rho ^{(2)}_{\mathcal{KN}} \\ 0 &{} \rho ^{(2)}_{\mathcal{LL}} &{} \rho ^{(2)}_{\mathcal{LM}} &{} 0 \\ 0 &{} \rho ^{(2)}_{\mathcal{ML}} &{} \rho ^{(2)}_{\mathcal{MM}} &{} 0 \\ \rho ^{(2)}_{\mathcal{NK}} &{} 0 &{} 0 &{} \rho ^{(2)}_{\mathcal{NN}} \end{array} \right] \, . \end{aligned}$$

(39)

We note that $\sum _{i=1}^4 \rho ^{(2)}_{ii}=1$ holds in the above equation. Here, we assume that all the elements of the matrix are real. By diagonalizing the density matrix $\rho ^{(2)}_{AB}(0)$, we obtain its eigenvalues, given by

$$\begin{aligned} \lambda _0= & {} \frac{\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{NN}}+\sqrt{(\rho ^{(2)}_{\mathcal{KK}}-\rho ^{(2)}_{\mathcal{NN}})^2+4|\rho ^{(2)}_{\mathcal{KN}}|^2}}{2}, \end{aligned}$$

(40)

$$\begin{aligned} \lambda _1= & {} \frac{\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{NN}}-\sqrt{(\rho ^{(2)}_{\mathcal{KK}}-\rho ^{(2)}_{\mathcal{NN}})^2+4|\rho ^{(2)}_{\mathcal{KN}}|^2}}{2}, \end{aligned}$$

(41)

$$\begin{aligned} \lambda _2= & {} \frac{\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{MM}}+\sqrt{(\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{MM}})^2+4|\rho ^{(2)}_{\mathcal{LM}}|^2}}{2}, \end{aligned}$$

(42)

$$\begin{aligned} \lambda _3= & {} \frac{\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{MM}}-\sqrt{(\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{MM}})^2+4|\rho ^{(2)}_{\mathcal{LM}}|^2}}{2}. \end{aligned}$$

(43)

By substituting Eqs. (40)–(43) into Eq. (4), we obtain for the mutual information

$$\begin{aligned} I(\rho ^{(2)}_{AB})=S(\rho ^{(1)}_A)+S(\rho ^{(1)}_B)+\sum _{j=0}^3 \lambda _j \log _2\lambda _j. \end{aligned}$$

(44)

In general, a von Neumann measurement on the subsystem B can be written [51] as

$$\begin{aligned} \varPi ^B_i=V\varPi _iV^\dagger , \quad i=0,1 \quad , \end{aligned}$$

(45)

with $\varPi _i=|i\rangle \langle i|$ and $V\in SU(2)$. After such a measurement, the composite density matrix is given by Eq. (5) with the corresponding probabilities [see Eq. (5)]. A matrix $V \in SU(2)$ can be written in the form

$$\begin{aligned} V=t {{\mathbb {I}}}+ i\mathbf {y}\cdot \varvec{\sigma } \end{aligned}$$

(46)

where $\varvec{\sigma }=\left\{ \sigma _1, \sigma _2, \sigma _3 \right\}$ with the Pauli matrices $\sigma _i$, ($i=1,2,3$) and $t, y_1, y_2, y_3$ being real numbers, for which $t^2+y_1^2+y_2^2+y_3^2=1$ holds. Equation (46) thus implies that three of the four parameters are independent taking values in the interval $[-1,1]$. The most general way to write a X-structured state is given [51] by

$$\begin{aligned} \rho ^{(2)}_{AB}=\frac{1}{4}\left( {{\mathbb {I}}}_{4 \times 4}+\varvec{\alpha }\cdot \varvec{\sigma }\otimes {{\mathbb {I}}}_{2 \times 2}+{{\mathbb {I}}}_{2 \times 2} \otimes \varvec{\beta }\cdot \varvec{\sigma }+\sum _{j=1}^3 c_j \sigma _j \otimes \sigma _j\right) , \end{aligned}$$

(47)

where after some algebra, we can rewrite it as [50]

$$\begin{aligned} \rho ^{(2)}_{AB}(0)=\frac{1}{4} \left[ \begin{array}{cccc} 1+d_1 &{} 0 &{} 0 &{} c_1-c_2 \\ 0 &{} 1+d_2 &{} c_1+c_2 &{} 0 \\ 0 &{} c_1+c_2 &{} 1+d_3 &{} 0 \\ c_1-c_2 &{} 0 &{} 0 &{} 1+d_4 \end{array} \right] , \end{aligned}$$

(48)

where all the coefficients are real numbers, $d_1=c_3+a_3+b_3$, $d_2=-c_3+a_3-b_3$, $d_3=-c_3-a_3+b_3$ and $d_4=c_3-a_3-b_3$. Now, using the elements of the composite density matrix of Eq. (39), we have: $a_3=\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{MM}}-\rho ^{(2)}_{\mathcal{NN}}$, $b_3=\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{MM}}-\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{NN}}$, $c_3=\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{NN}}-\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{MM}}$, $c_1=2(\rho ^{(2)}_{\mathcal{LM}}+\rho ^{(2)}_{\mathcal{KN}})$ and $c_2=2(\rho ^{(2)}_{\mathcal{LM}}-\rho ^{(2)}_{\mathcal{KN}})$.

In order to evaluate the matrix $\rho ^{(2)}_{AB_i}$ of Eq. (5), with $i=0,1$, we write the projective measurement in the form of Eq. (45), starting from Eq. (5) and following the procedure given in Ref. [51], we obtain that

$$\begin{aligned} p_0\rho ^{(2)}_{AB_0}= & {} \frac{1}{4}\left[ {{\mathbb {I}}}_{4 \times 4}+b_3z_3+z_1c_1\sigma _1+z_2c_2\sigma _2+(a_3+c_3z_3)\sigma _3 \right] , \end{aligned}$$

(49)

$$\begin{aligned} p_1\rho ^{(2)}_{AB_1}= & {} \frac{1}{4}\left[ {{\mathbb {I}}}_{4 \times 4}-b_3z_3-z_1c_1\sigma _1-z_2c_2\sigma _2+(a_3-c_3z_3)\sigma _3 \right] , \end{aligned}$$

(50)

where we have used the unit vector $\mathbf {z}=(z_1,z_2,z_3)$ as defined in Ref. [51], $z_1=2(-ty_2+y_1y_3)$, $z_2=2(ty_1+y_2y_3)$ and $z_3=t^2+y_3^2-y_1^2-y_2^2$. Now, taking the trace of Eqs. (49) and (50), we find the probabilities

$$\begin{aligned} p_0= & {} \frac{1+b_3z_3}{2} , \end{aligned}$$

(51)

$$\begin{aligned} p_1= & {} \frac{1-b_3z_3}{2}. \end{aligned}$$

(52)

By diagonalizing Eqs. (49) and (50), we obtain their eigenvalues. Rewriting the probabilities of Eqs. (51) and (52) using the density matrix elements, we have $p_0=(\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{MM}})k+(\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{NN}})l$ and $p_1=(\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{MM}})l+(\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{NN}})k$, and finally, one obtains the eigenvalues of $\rho ^{(2)}_{AB_0}$ and $\rho ^{(2)}_{AB_1}$ as

$$\begin{aligned} \upsilon _{\pm }(\rho ^{(2)}_{AB_0})= & {} \frac{1 \pm \theta }{2}, \end{aligned}$$

(53)

$$\begin{aligned} w_{\pm }(\rho ^{(2)}_{AB_1})= & {} \frac{1 \pm \theta ^\prime }{2}, \end{aligned}$$

(54)

respectively, where the parameters $\theta$ and $\theta ^\prime$ are provided by

$$\begin{aligned} \theta= & {} \sqrt{\frac{\left[ (\rho ^{(2)}_{\mathcal{KK}}-\rho ^{(2)}_{\mathcal{MM}})k+ (\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{NN}})l \right] ^2+\varTheta }{ \left[ (\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{MM}})k+ (\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{NN}})l \right] ^2}}, \end{aligned}$$

(55)

$$\begin{aligned} \theta ^\prime= & {} \sqrt{\frac{\left[ (\rho ^{(2)}_{\mathcal{KK}}-\rho ^{(2)}_{\mathcal{MM}})l+ (\rho ^{(2)}_{\mathcal{LL}}-\rho ^{(2)}_{\mathcal{NN}})k \right] ^2+\varTheta }{ \left[ (\rho ^{(2)}_{\mathcal{KK}}+\rho ^{(2)}_{\mathcal{MM}})l+ (\rho ^{(2)}_{\mathcal{LL}}+\rho ^{(2)}_{\mathcal{NN}})k \right] ^2}}, \end{aligned}$$

(56)

and $\varTheta =4\left[ ((\rho ^{(2)}_{\mathcal{LM}})^2+(\rho ^{(2)}_{\mathcal{KN}})^2)(n+m)+2\rho ^{(2)}_{\mathcal{LM}}\rho ^{(2)}_{\mathcal{KN}}(n-m) \right]$. The k, l, m, n parameters used above are given by

$$\begin{aligned} k= & {} t^2+y_3^2, \quad l=y_1^2+y_2^2, \nonumber \\ m= & {} (ty_1+y_2y_3)^2, \quad n=(ty_2-y_1y_3)^2. \end{aligned}$$

(57)

Using $t^2+y_1^2+y_2^2+y_3^2=1$ and $t, y_1, y_2, y_3 \in [-1,1]$, we derive the following useful relations: $k+l=1$, $k-l=z_3$, $4m=z_2^2$ and $4n=z_1^2$. Thus, we have: $k, l \in [0,1]$ and $m, n \in [0,1/4]$. So, the three out of four parameters are independent. (We choose k, l and m to be independent following Ref. [50].)

Now, using the eigenvalues of the matrices $\rho ^{(2)}_{AB_0}$ and $\rho ^{(2)}_{AB_1}$ [see Eqs. (53) and (54), respectively], we can finally compute the corresponding von Neumann entropies. Thus, we obtain

$$\begin{aligned} S\left( \rho ^{(2)}_{AB_0}\right)= & {} -\sum _{i=\pm } \upsilon _i \log _2 \upsilon _i, \end{aligned}$$

(58)

$$\begin{aligned} S\left( \rho ^{(2)}_{AB_1}\right)= & {} -\sum _{i=\pm } w_i \log _2 w_i. \end{aligned}$$

(59)

The quantum conditional entropy in Eq. (7) can be thus written as

$$\begin{aligned} S\left( \rho ^{(2)}_{AB} | \{ \varPi ^B_i \}\right) =p_0S\left( \rho ^{(2)}_{AB_0}\right) +p_1S\left( \rho ^{(2)}_{AB_1}\right) , \end{aligned}$$

(60)

and as a result, the classical correlation of our system is given by

$$\begin{aligned} CC\left( \rho ^{(2)}_{AB}\right) =\max _{\{ \varPi ^B_i \}} J\left( \rho ^{(2)}_{AB} | \{ \varPi ^B_i \}\right) =S\left( \rho ^{(1)}_A\right) - \min _{\{ \varPi ^B_i \}} S\left( \rho ^{(2)}_{AB} | \{ \varPi ^B_i \}\right) . \end{aligned}$$

(61)

Therefore, in order to compute the classical correlation of our system, we need to minimize $S(\rho ^{(2)}_{AB} | \{ \varPi ^B_i \})$ given by Eq. (60); subsequently, we can obtain the QD.

In order to minimize Eq. (60), we follow the procedure of Ref. [50]. Initially, we observe that Eq. (60) is symmetric under the interchange of the parameters $k \leftrightarrow l$. Thus, Eq. (60) is an even function of $(k-l)$ and as a result, it has endpoints for $k=l=1/2$ and $k=0$, $l=1$ (or $k=1$, $l=0$ since it is symmetric under $k \leftrightarrow l$). From Eqs. (57), we find that $t=y_3=0$ (or $y_1=y_2=0$) is required at the endpoint $k=0$, $l=1$ (or $k=1$, $l=0$). This fact implies that also $m=n=0$ holds at these points. In case of $k=l=1/2$, we find that the parameters $\theta$ and $\theta ^\prime$ become equal ($\theta =\theta ^\prime$) and as a result, this leads to $S(\rho ^{(2)}_{AB_0})=S(\rho ^{(2)}_{AB_1})$, and the minimization of $S(\rho ^{(2)}_{AB} | \{ \varPi ^B_i \})$ simply requires the minimization of $S(\rho ^{(2)}_{AB_0})$ (or $S(\rho ^{(2)}_{AB_1})$). Moreover, $\varTheta$ depends linearly on the parameters m and n and as a result, it takes its extreme values at the endpoints of these parameters, i.e., for $m=0, 1/4$ and $n=0, 1/4$. So, in this way, the maximum classical correlations of our composite system as well as all its quantum correlations can be computed at last.