Dynamics of entanglement and uncertainty relation in coupled harmonic oscillator system: exact results

Abstract

The dynamics of entanglement and uncertainty relation is explored by solving the time-dependent Schrödinger equation for coupled harmonic oscillator system analytically when the angular frequencies and coupling constant are arbitrarily time dependent. We derive the spectral and Schmidt decompositions for vacuum solution. Using the decompositions, we derive the analytical expressions for von Neumann and Rényi entropies. Making use of Wigner distribution function defined in phase space, we derive the time dependence of position–momentum uncertainty relations. To show the dynamics of entanglement and uncertainty relation graphically, we introduce two toy models and one realistic quenched model. While the dynamics can be conjectured by simple consideration in the toy models, the dynamics in the realistic quenched model is somewhat different from that in the toy models. In particular, the dynamics of entanglement exhibits similar pattern to dynamics of uncertainty parameter in the realistic quenched model.

Appendix A

In this appendix we examine how to extend the main results of this paper to the excite states. If, for example, two oscillators are in ground and first-excited states initially, the reduced density matrix becomes

$$\begin{aligned} \rho _{(0, 1)}^A \left( x_1, x'_1: t\right)= & {} 2 \omega '_2 \rho _{(0, 0)}^A (x_1, x'_1: t) \nonumber \\&\left[ \frac{\cos ^2 \alpha }{2 D} + F_1 x_1^2 + F_1^* {x'_1}^2 + F_2 x_1 x'_1 \right] \end{aligned}$$

(A.1)

where $\rho _{(0, 0)}^A (x_1, x'_1: t)$ is given in Eq. (4.2) and

$$\begin{aligned} F_1= & {} \frac{\sin ^2 \alpha \cos ^2 \alpha }{4 D^2} \bigg [ \left( \omega '_1 - \omega '_2 \right) \left\{ \omega '_1 (1 + \sin ^2 \alpha ) + \omega '_2 \cos ^2 \alpha \right\} \nonumber \\&\quad - \cos ^2 \alpha \left( \frac{\dot{b_1}}{b_1} - \frac{\dot{b_2}}{b_2} \right) ^2 - 2 i \omega '_1 \left( \frac{\dot{b_1}}{b_1} - \frac{\dot{b_2}}{b_2} \right) \bigg ] \nonumber \\ F_2= & {} \frac{1}{D} \left( 2 a_3 \cos ^2 \alpha + \omega '_1 \sin ^2 \alpha \right) . \end{aligned}$$

(A.2)

The explicit expression of $a_3$ is given in Eq. (4.3). Then one can show

$$\begin{aligned} \text{ Tr } \left[ \rho _{(0,1)}^A \right]\equiv & {} \int \text {d}x \rho _{(0,1)}^A (x, x: t) = 1 \nonumber \\ \text{ Tr } \left[ \left( \rho _{(0,1)}^A \right) ^2\right]\equiv & {} \int \text {d}x \text {d}x' \rho _{(0,1)}^A (x, x': t) \rho _{(0,1)}^A (x', x: t) \nonumber \\= & {} \text{ Tr } \left[ \left( \rho _{(0,0)}^A \right) ^2\right] r(t) \end{aligned}$$

(A.3)

where r(t) is ratio of mixedness between $\rho _{(0,0)}^A$ and $\rho _{(0,1)}^A$ and its explicit expression is

$$\begin{aligned} r(t)= & {} 4 {\omega '_2}^2 \Bigg [ \frac{\cos ^4 \alpha }{4 D^2} + \frac{\cos ^2 \alpha }{4 D a_1 (a_1 + 2 a_3)} \left\{ \left( F_1 + F_1^*\right) a_1 + \left( F_1 + F_1^* + F_2\right) a_3 \right\} \nonumber \\&\quad + \frac{1}{16 a_1^2 (a_1 + 2 a_3)^2} \bigg [ a_1^2 \left\{ \left( F_1 + F_1^*\right) ^2 + 4 |F_1|^2 + F_2^2 \right\} + a_3^2 \nonumber \\&\quad \left\{ 3 \left( F_1 + F_1^*\right) ^2 + 3 F_2 \left( 2 F_1 + 2 F_1^* + F_2\right) \right\} \nonumber \\&\quad + 2 a_1 a_3 \left\{ \left( F_1 + F_1^*\right) ^2 + 4 |F_1|^2 + F_2 \left( 3 F_1 + 3 F_1^* + F_2\right) \right\} \bigg ] \Bigg ]. \end{aligned}$$

(A.4)

We expect that the entanglement between ground and first-excited harmonic oscillators is very small compared to that between two ground state harmonic oscillators. However, it is difficult to show this explicitly because the analytic derivation of eigenvalues and eigenfunctions for $\rho _{(0,1)}^A (x, x': t)$ does not seem to be simple matter, at least for us. We hope to discuss the dynamics of entanglement for general excited (m, n) state in the future. The time dependence of the uncertainty $\Delta x_1 \Delta p_1$ for $\rho _{(0,1)}^A$ can be computed analytically. The Wigner function $W_{(0,1)} (x_1, p_1, t)$ for this state becomes

$$\begin{aligned} W_{(0,1)} (x_1, p_1, t)= & {} W_{(0,0)} (x_1, p_1, t) \nonumber \\&\left[ h_0 (t) + h_1 (t) x_1^2 + h_2 (t) p_1^2 + 2 h_3 (t) x_1 p_1 \right] \end{aligned}$$

(A.5)

where $W_{(0,0)} (x_1, p_1, t)$ is the Wigner function for $\psi _{0,0} (x_1, x_2, t)$ given in Eq. (5.5) and

$$\begin{aligned} h_0 (t)= & {} \frac{\omega '_1 \omega '_2}{\bar{\eta }} \cos 2 \alpha \nonumber \\ h_1 (t)= & {} \frac{2 \omega '_2 \sin ^2 \alpha }{\bar{\eta }^2} \nonumber \\&\left\{ \left[ \omega '_1 \tilde{D} + \cos ^2 \alpha \frac{\dot{b}_1}{b_1} \left( \frac{\dot{b}_1}{b_1} - \frac{\dot{b}_2}{b_2} \right) \right] ^2 + \left[ \omega '_1 \frac{\dot{b}_2}{b_2} \sin ^2 \alpha + \omega '_2 \frac{\dot{b}_1}{b_1} \cos ^2 \alpha \right] ^2 \right\} \nonumber \\ h_2 (t)= & {} \frac{2 \omega '_2 \sin ^2 \alpha }{\bar{\eta }^2} \left[ D^2 + \cos ^4 \alpha \left( \frac{\dot{b}_1}{b_1} - \frac{\dot{b}_2}{b_2} \right) ^2 \right] \nonumber \\ h_3 (t)= & {} \frac{2 \omega '_2 \sin ^2 \alpha }{\bar{\eta }^2} \Bigg \{ \cos ^2 \alpha \left( \frac{\dot{b}_1}{b_1} - \frac{\dot{b}_2}{b_2} \right) \left[ \omega '_1 \tilde{D} + \cos ^2 \alpha \frac{\dot{b}_1}{b_1} \left( \frac{\dot{b}_1}{b_1} - \frac{\dot{b}_2}{b_2} \right) \right] \nonumber \\&+ D \left[ \omega '_1 \frac{\dot{b}_2}{b_2} \sin ^2 \alpha + \omega '_2 \frac{\dot{b}_1}{b_1} \cos ^2 \alpha \right] \Bigg \}. \end{aligned}$$

(A.6)

Then, it is straightforward to show that the uncertainty relation for $\rho _{(0,1)}^A$ becomes $(\Delta x_1 \Delta p_1)^2 = \Gamma (t) / 4$, where

$$\begin{aligned} \Gamma (t)= & {} \left( \frac{\bar{\eta }}{\omega '_1 \omega '_2} \right) ^2 \left[ \left( h_0 \alpha _2 + \frac{h_2}{2} \right) + \frac{3 \bar{\eta }}{2 \omega '_1 \omega '_2} \left( h_1 \alpha _2^2 + h_2 \alpha _3^2 + 2 h_3 \alpha _2 \alpha _3 \right) \right] \nonumber \\&\quad \times \left[ \left( h_0 \alpha _1 + \frac{h_1}{2} \right) + \frac{3 \bar{\eta }}{2 \omega '_1 \omega '_2} \left( h_2 \alpha _1^2 + h_1 \alpha _3^2 + 2 h_3 \alpha _1 \alpha _3 \right) \right] \end{aligned}$$

(A.7)

where $\alpha _j$ are defined in Eq. (5.6).

Fig. 4

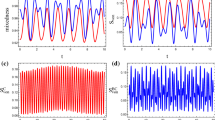
(Color online) The time dependence of ratio for mixedness r(t) (a) and uncertainties $\Gamma (t) / \Omega (t)$ (b) between $\rho _{(0,0)}^A$ and $\rho _{(0,1)}^A$ in the realistic quenched model. We choose $\omega _{1, i} = 1$, $\omega _{1, f} = 1.3$, $\omega _{2, i} = 1.5$, and $\omega _{2, f} = 1.8$ for $J = 1.1$ (red solid line), $J = 0.9$ (blue dashed line), and $J = 0.6$ (black dotted line). Since $r(t) < 1$ in the full range of time. a Indicates that $\rho _{(0,1)}^A$ is more mixed state than $\rho _{(0,0)}^A$. It is of interest to note that $\rho _{(0,1)}^A$ becomes more and more mixed compared to $\rho _{(0,0)}^A$ with increasing the coupling constant J. b Shows that the uncertainty $\Delta x_1 \Delta p_1$ increases in $\rho _{(0,1)}^A$ compared to that of $\rho _{(0,0)}^A$. The increasing rate becomes larger with increasing the coupling constant J

The time dependence of the ratios r(t) and $\Gamma (t) / \Omega (t)$ for the realistic quenched model is plotted in Fig. 4, where $\omega _{1, i} = 1$, $\omega _{1, f} = 1.3$, $\omega _{2, i} = 1.5$, and $\omega _{2, f} = 1.8$ are chosen. The red solid, blue dashed, and black dotted lines correspond to $J=1.1$, $J=0.9$, and $J=0.6$, respectively. The fact $r(t) < 1$ in the full range of time indicates that $\rho _{(0,1)}^A$ is more mixed than $\rho _{(0,0)}^A$. It is of interest to note that $\rho _{(0,1)}^A$ becomes more mixed compared to $\rho _{(0,0)}^A$ with increasing the coupling constant J. Figure 4b indicates that the uncertainty $\Delta x_1 \Delta p_1$ increases in $\rho _{(0,1)}^A$ compared to that of $\rho _{(0,0)}^A$. The increasing rate becomes larger with increasing the coupling constant J.