Abstract
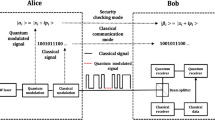
In the quantum illumination protocol for secure communication, Alice prepares entangled signal and idler beams via spontaneous parametric downconversion. She sends the signal beam to Bob, while retaining the idler. Bob imposes message modulation on the beam he receives from Alice, amplifies it, and sends it back to her. Alice then decodes Bob’s information by making a joint quantum measurement on the light she has retained and the light she has received from him. The basic performance analysis for this protocol—which demonstrates its immunity to passive eavesdropping, in which Eve can only listen to Alice and Bob’s transmissions—is reviewed, along with the results of its first proof-of-principle experiment. Further analysis is then presented, showing that secure data rates in excess of 1 Gbps may be possible over 20-km-long fiber links with technology that is available or under development. Finally, an initial scheme for thwarting active eavesdropping, in which Eve injects her own light into Bob’s terminal, is proposed and analyzed.










Similar content being viewed by others
Notes
The low-gain OPA is a downconverter to which non-vacuum signal and idler inputs are applied. That it converts phase-sensitive cross-correlation between those inputs into intensity modulation of the idler output follows from standard coupled-mode analysis [13]. The low-gain condition maximizes the resulting signal-to-noise ratio on the idler output by suppressing the ASE noise present on the returned light.
The ASE threshold for entanglement breaking is \(N_B^\mathrm{thresh} = \kappa G_B\). Because phase-insensitive amplifiers must obey \(N_B \ge G_B-1\), any \(\kappa \le (G_B-1)/G_B\) will make the channel entanglement breaking. For \(G_B \gg 1\), this condition will always be satisfied in long-distance communication.
The impact of non-idealities, such as idler-storage loss, will be addressed explicitly in Sect. 3, when we review our proof-of-principle experiment from [9].
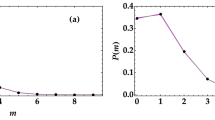
Fig. 2 Bit-error-probability bounds versus mode-pair number (time-bandwidth product for a single bit) \(M\). All curves assume \(N_S = 0.004,\,\kappa = 0.1\), and \(G_B = N_B = 10^4\). Solid curves Chernoff bounds for Alice and Eve’s optimum quantum receivers. Dashed curve lower bound for Eve’s optimum quantum receiver. Dot-dashed curve Bhattacharyya bound for Alice’s OPA receiver with \(G_A = 1 + N_S/\sqrt{\kappa N_B}\)
We will use bit-error rate and bit-error probability interchangeably. The former term is commonly used in describing experiments, whereas the latter is preferred for the theory.
The dc level is removed prior to amplification. The equivalent dc level for the inset in Fig. 6 is \(\sim \)33 V.
The classicality threshold employed here accounts for the non-idealities in the experimental system, see [17].
All other non-idealities will be neglected, e.g., Alice’s dispersion compensation will be taken to be perfect.
For the parameter values given below, we have found that this approximation has 0.23 % error at \(M = 200\)—the \(M\) value associated with \(R = 10\,\)Gbps—by comparison with the exact results for that \(M\) value. That exact analysis shows that increasing \(R\) to \(2\,\)Tbps (reducing \(M\) to 1) does not appreciably increase \(\Delta I^\mathrm{LB}_{AB}\) beyond the value shown in Fig. 7 for \(R = 10\) Gbps.
At \(R=10\) Gbps, Alice’s OPA receiver detects an average of 15.3 photons/bit when Bob send a 0, and 11.2 photons/bit when Bob sends a 1.
Of course, if Alice and Bob use optical time-domain reflectometers (OTDRs) to monitor the integrity of their fiber links, they should be able to detect the presence of a discrete loss element at an unexpected location. We shall ignore that possibility for now.
Because the idler is now detected immediately, rather than stored in a fiber, \(\kappa = 0.9\) can be used, representing a coupling efficiency from the SPDC source to the homodyne detector.
The upper bound on the bit-error rate for an individual homodyne detector—from which a lower bound on Alice and Bob’s Shannon information is obtained—is derived in Appendix 1. The derivation of the upper bound on Eve’s Holevo information is the same as previously described.
One could also carp that the coupling efficiencies in Table 1 need to be augmented to account for the coupling efficiencies of the DWDMs that are employed.
The \(\{\theta _k^{(b)}\}\) are thus a version of Yuen’s alpha-eta scheme [23].
This authentication requirement is no different from what is needed in QKD protocols.
Note that Fig. 10 applies even if Eve could use spread spectrum over the full 2 THz optical bandwidth of Bob’s terminal. Also, note that Alice and Bob could increase the number of bases they employ, leading to an increase in the power that Eve must inject to glean information from her active attack, and thus reducing the amount of time Bob needs to detect her intrusion with his power monitor.
The two components of \(\mathbf{x}_m\) are the outputs from the returned-light and idler homodyne detectors for the \(m\)th mode: \(\mathbf{x}_m = \left[ \begin{array}{cc}x_{m_R}&\quad x_{m_I}\end{array}\right] ^T\).
The symmetry of the \(\{\theta _k^{(b)}\}\) make the Chernoff and Bhattacharyya bounds coincide.
In other words, the real and imaginary parts of \(\mathbf{x}\) are the in-phase (\(I\)) and quadrature (\(Q\)) components of standard coherent communications.
References
Bennett, C.H., Brassard, G.: Quantum cryptography, public key distribution, and coin tossing. Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 1984. pp. 175–179. IEEE, New York (1984)
Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991)
Grosshans, F., Grangier, P.: Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002)
Peev, M., Pacher, C., Alléaume, R., et al.: The SECOQC quantum key distribution network in Vienna. New J. Phys. 11, 075001 (2009)
Sasaki, M., Fujiwara, M., Ishizuka, H., et al.: Field test of quantum key distribution in the Tokyo QKD network. Opt. Express 19, 10387–10409 (2011)
Shannon, C.E.: Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715 (1949)
Gallager, R.G.: Information Theory and Reliable Communication, chap. 3. Wiley, New York (1968)
Shapiro, J.H.: Defeating passive eavesdropping with quantum illumination. Phys. Rev. A 80, 022320 (2009)
Zhang, Z., Tengner, M., Zhong, T., Wong, F.N.C., Shapiro, J.H.: Entanglement’s benefit survives an entanglement-breaking channel. Phys. Rev. Lett. 111, 010501 (2013)
Lloyd, S.: Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463–1465 (2008)
Tan, S.-H., Erkmen, B.I., Giovannetti, V., et al.: Quantum illumination with Gaussian states. Phys. Rev. Lett. 101, 253601 (2008)
Guha, S., Erkmen, B.I.: Gaussian-state quantum-illumination receivers for target detection. Phys. Rev. A 80, 052310 (2009)
Louisell, W.: Radiation and Noise in Quantum Electronics, chap. 7. McGraw-Hill, New York (1964)
Audenaert, K.M.R., Calsamiglia, J., Muñoz-Tapia, R., et al.: Discriminating states: the quantum Chernoff bound. Phys. Rev. Lett. 98, 160501 (2007)
Calsamiglia, J., Muñoz-Tapia, R., Masanes, Ll., Acin, A., Bagan, E.: Quantum Chernoff bound as a measure of distinguishability between density matrices: application to qubit and Gaussian states. Phys. Rev. A 77, 032311 (2008)
Pirandola, S., Lloyd, S.: Computable bounds for the discrimination of Gaussian states. Phys. Rev. A 78, 012331 (2008)
Zhang, Z., Tengner, M., Zhong, T., Wong, F.N.C., Shapiro, J.H.: Supplemental material for Phys Rev. Lett. 111, 010501 (2013). http://link.aps.org/supplemental/10.1103/PhysRevLett.111.010501
Nair, R.: Discriminating quantum-optical beam-splitter channels with number-diagonal signal states: applications to quantum reading and target detection. Phys. Rev. A 84, 032312 (2011)
Marsili, F., Verma, V.B., Stern, J.A., et al.: Detecting single infrared photons with 93% system efficiency. Nat. Photonics 7, 210–214 (2013)
Rosenberg, D., Kerman, A.J., Molnar, R.J., Dauler, E.A.: High-speed and high-efficiency superconducting nanowire single photon detector array. Opt. Express 21, 1440–1447 (2013)
Bower, P., Dedic, I.: High speed converters and DSP for 100G and beyond. Opt. Fiber Technol. 17, 464–471 (2011)
Xu, W., Shapiro, J.H.: Defeating active eavesdropping with quantum illumination. in Quantum Communication Measurement and Computing (QCMC). Ralph, T., Lam, P. K., eds. AIP Conf. Proc. No. 1363. AIP, New York (2011).
Barbosa, G.A., Corndorf, E., Kumar, P., Yuen, H.P.: Secure communication using mesoscopic states. Phys. Rev. Lett. 90, 227901 (2003)
Stinson, D.R.: Cryptography: Theory and Practice. Chapman and Hall, Boca Raton (2006)
Lloyd, S.: Quantum enigma machines. arXiv:1307.0380 [quant-ph]
Guha, S., Hayden, P., Krovi, H., et al.: Quantum enigma machines and the locking capacity of a quantum channel. arXiv:1307.5368 [quant-ph]
Shapiro, J.H.: Near-field turbulence effects on quantum key distribution. Phys. Rev. A 67, 022309 (2003)
Shapiro, J.H.: Scintillation has minimal impact on far-field Bennett-Brassard 1984 protocol quantum key distribution. Phys. Rev. A 84, 032340 (2011)
Chandrasekaran, N., Shapiro, J.H.: Photon information efficient communication through atmospheric turbulence—Part I: channel model and propagation statistics. J. Lightw. Technol. (submitted)
Chandrasekaran, N., Shapiro, J.H., Wang, L.: Photon information efficient communication through atmospheric turbulence—Part II: bounds on ergodic classical and private capacities. J. Lightw. Technol. (submitted)
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by an ONR Basic Research Challenge grant and the DARPA Quiness Program.
Appendices
Appendix 1
Here we shall derive the bit-error rate for a single channel of the homodyne receiver that Alice uses in the QI-DWDM setup from Sect. 4. We will assume \(R_c \ll W_c\). Then, given the value, \(k\), of Bob’s message bit, the outputs from Alice’s idler and returned-light homodyne detectors during the \(T_c = 1/R_c\) duration bit interval can be regarded as a set of \(M_c = W_c/R_c\) statistically independent, identically distributed, zero-mean, 2-D Gaussian random-vector modes \(\{\mathbf{x}_m : 1\le m \le M_c\}\) Footnote 20 with common covariance matrix
when \(k=0\), and
when \(k=1\). In these expressions:
and
When Bob’s message bits are equally likely to be 0 or 1, the minimum error-probability decision rule reduces to the following threshold test:
The upper bound on Alice’s bit-error probability that we used in Sect. 4 is the Bhattacharyya bound,
Appendix 2
Here we show how the bit-error-probability bounds for Eve’s heterodyne receiver, plotted in Fig. 10a, were obtained. The upper bound is a Chernoff bound,Footnote 21
and the lower bound is
where \(p(\mathbf{x}\mid k)\) for \(k = 0,\,1\) is the conditional probability density function for the normalized, complex-valued output \(\mathbf{x}\) from bit-interval-matched filtering of Eve’s heterodyne photocurrent.Footnote 22 For our basis-encoded system, Eve’s conditional probability densities are
Rights and permissions
About this article
Cite this article
Shapiro, J.H., Zhang, Z. & Wong, F.N.C. Secure communication via quantum illumination. Quantum Inf Process 13, 2171–2193 (2014). https://doi.org/10.1007/s11128-013-0662-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-013-0662-1