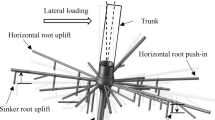
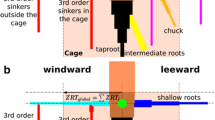
Abstract
Aim
(1) To understand the tree root-soil interaction under lateral and moment loading using a physical modelling technique; (2) To detect the possible factors (e.g. root architecture, water condition, and stress level) influencing a tree’s push-over behaviour; (3) To identify suitable scaling laws to use in physical modelling.
Methods
Two 1:20 scaled root models with different architectures (namely, deep and narrow, and shallow and wide) were reconstructed and 3D printed based on the field-surveyed root architecture data. Push-over tests were performed both in elevated-gravity (centrifuge 20-g) and normal-gravity (1-g) conditions.
Results
The shallow and wide model showed higher anchorage strength than the deep and narrow model. Regardless of the root architecture, the root anchorage strength measured from dry soil was higher than that from saturated soil. However, once the effective stress was the same, regardless of water conditions, the root anchorage strength would be the same.
Conclusions
The presence of water decreasing the soil effective stress and key lateral roots extending along the wind direction play a significant role on a tree’s push-over resistance. Centrifuge tests showed comparable results to the field pull-over measurements while 1-g model tests overestimated the root-soil interaction, which could be corrected for soil strength by using modified scaling laws.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Understanding tree root anchorage behaviour under lateral and moment loads has long been of interest in forestry, where heavy winds, which are predicted to be stronger due to the increase of power of major Atlantic tropical hurricanes (Dekker et al. 2018), are the main causes of destruction in European forests (Gandhi et al. 2008; McCarthy et al. 2010) and responsible for more than 50% of damage in European forests (Schelhaas et al. 2003). Besides, it is important for understanding how much of a commercial crop may be damaged by windstorms and how stand management and forest management plans can mitigate wind risks (Gardiner and Quine 2000; Mickovski et al. 2005; Dupont and Brunet 2008; Moore et al. 2008). It is also of interest in Civil Engineering, where windthrown trees in sloping ground may be a trigger for landslides (Larsen and Torres Sanchez 1992; Jakob and Lambert 2009). Additionally, it is desirable to protect old and culturally valuable trees; for example, Typhoon Mangkhut (Hong Kong) in September 2018 damaged or uprooted some trees estimated to be more than 100 years old. Furthermore, fallen trees can become a potential threat to life (e.g. Storm Ali, United Kingdom, September 2018) and infrastructure (e.g. Storm Doris, United Kingdom, February 2017).
In recent decades, an increasing body of research has focused on tree anchorage under lateral and moment loading. Earlier studies empirically correlated the stability of a tree to the branching structure of the crown, biomass distribution and geometric properties of the trunk and wind exposure (Guitard and Castera 1995; Ruel 2000; Sellier and Fourcaud 2009) due to the invisibility of the roots buried in the soil and the complexity of their anchorage mechanisms. Some correlations were developed by wind tunnel modelling of physical models across a range of scales (Gromke and Ruck 2008; Cao et al. 2012). Root-soil interaction has been studied by measuring root architecture in trees having experienced varying levels of storm damage (Danjon et al. 2005; Danquechin Dorval et al. 2016) or damage from typical winching (pulling) tests, where lateral forces are applied to the stem with a winch to pull the tree over. The latter experimental method has been widely used in the field to determine moment-rotation curves (Wessolly and Erb 1998) and anchorage resistance of tree root systems (e.g. Coutts 1983, 1986; Crook and Ennos 1998; Nicoll et al. 2008). However, in field winching tests it is impossible to find another identical root system for systematic studies of the impact of soil type, ground water conditions or rate of loading.
To overcome these difficulties and develop a better understanding of tree root anchorage mechanisms in soil, efforts have been made through analytical and numerical modelling, as well as scaled physical modelling in the lab. Three principal analytical modelling methods, namely Blackwell, Rennolls and Coutts model (Blackwell et al. 1990), Fibre Bundle Model (Pollen and Simon 2005) and Root Bundle Model (Schwarz et al. 2010), which all rely on highly simplified root system architecture and root biomechanical properties, have been developed to predict root anchorage strength. The Finite Element Method has then been employed to simulate mechanical soil-root system interaction under horizontal loading (Dupuy et al. 2005; Yang et al. 2014, 2017, 2018). More recently, the Macroelement approach, treating the root system as an embedded shallow foundation, has also been proposed to model root soil interaction of tree pull-over (Dattola et al. 2019). Only limited physical model tests on root anchorage mechanism of trees can be found in the literature for validation of such models (e.g. Rahardjo et al. 2015; Zhang et al. 2018). However, these model tests were conducted at reduced-scale under single gravity (1-g) conditions, where soil confining effective stress levels did not fully represent the field and hence the soil-root mechanical interaction that would have been expected in the field might not be correctly captured without the application of appropriate scaling laws (Wood 2004; Liang et al. 2015, 2017b). In addition, little is known about how soil conditions affect the mechanical interaction.
This paper aims to address these issues associated with physical model tests. 1:20 scaled 3D printed tree root models, based on detailed field-surveyed 3D root architecture data reported in the literature (Danjon and Reubens 2008; Danjon et al. 2008), were created for conducting controlled push-over tests at both 20-g in a geotechnical beam centrifuge, where full-scale root-soil interaction could be simulated, and under 1-g conditions. The main objective of testing the tree root behaviour at both 20-g and 1-g was to investigate and identify appropriate scaling laws whereby the root-soil mechanical interaction may be approximated and tested under 1-g conditions by satisfying similitudes with prototype conditions (as achieved in the centrifuge). However, the root models were also used to study the effects of root morphology and stress levels on the failure mechanism and moment-rotation relationships of the root systems.
Material and methods
Soil characteristics
The soil used in this study was a mixture of 70% HST95 sand and 30% A50 silt (silica flour), which attempted to recreate a compacted field sandy loam (known as Bullionfield soil, see Liang et al. 2017a) in terms of shear strength and particle size distribution (PSD), but which could be pluviated around 3D printed root models. The particle size distribution of the soil, determined by the laser diffraction method (BS1377: 1990 Part 1), is shown in Fig. 1a, compared with those of the HST95 sand, A50 silt and Bullionfield soil. The PSD of the model soil is closer to that of the Bullionfield soil compared with HST95 sand that was used in previous research utilising 3D printed root analogues (Zhang et al. 2018). The coefficients of uniformity and curvature of the model soil were 15.1 and 2.4, respectively. Other basic index properties are summarised in Table 1. A series of drained direct shear apparatus (DSA) tests were conducted to determine the shear strength properties of the soil at a pluviated relative density of 45–50% under fully saturated condition. The critical state friction angle of the model soil under conventional stress levels (10 kPa to 200 kPa) was 37.8°, which is close to that of saturated compacted Bullionfield soil tested under similar conditions (36.4°; Liang et al. 2017a). It should be noted that the soil-root mechanical interaction considered in this study is not a plane-strain problem because of the complexity of the root distribution involved. Although some lateral roots with low tortuosity might be analogous to a horizontal pipeline (which is a plane-strain structure), most sinker roots cannot. However, the uplift mechanism for a pipeline (lateral root) is controlled by the formation of shear bands in plane strain, and the pull-out resistance of sinker roots will be controlled by interface shear. Therefore, the friction angle derived from the direct-shear apparatus is considered to provide the most appropriate reference measurement for the shear properties of the soil.
A 16 mm-diameter cone penetration test (CPT) was conducted at 1-g to further measure the variation of soil strength with depth. A soil bed of 300 mm thick was pluviated at a fixed height of 450 mm from the soil free surface. Trial pluviation suggested that this method can produce a soil bed with a relative density ranging between 45% and 50%. The cone was driven at a constant rate of 5.5 mm/min and using Eq. (1) (Knappett and Craig 2019), a vertical profile of peak friction angle (\( {\phi}_{max}^{\prime } \)) was obtained:
where \( {\sigma}_{vo}^{\prime } \) is the vertical effective stress in kPa, at the depth of measurement of tip resistance qc. Effective stress is an average of the inter-particle stresses across a section of the soil skeleton and is therefore equal to the total stress (e.g. from soil self-weight) minus the pore water pressure. Figure 1b shows the distribution of \( {\phi}_{max}^{\prime } \) with depth. Some noise is found at very shallow depth due to the disturbance of the cone. Below 20 mm (covering most of the rooted soil depth), \( {\phi}_{max}^{\prime } \) appears to increase from 53° to 59° approximately linearly with depth, broadly consistent with results from DSA tests conducted at extremely low confining pressures (around 1 kPa) using a light 3D printed cap (in plastic instead of the conventional brass cap). The higher soil strength obtained under 1-g conditions is expected because soil subjected to low confining pressure would have increased ability to exhibit shearing-induced dilation, causing an increase in friction angle compared to the critical state value (Bolton 1986).
General description of root system
Two types of 3D root models with realistic architecture were considered in this investigation. The first model (ND) had a relatively narrow and deep architecture, whereas the other was wider and shallower (WS). The ND model was created from root architecture data obtained from a 27-year-old Pinus pinaster tree grown in a deep sandy spodosol, which is similar to the soil used in this study, in the “Landes de Gascogne” forest in south-west France (Fig. 2a, after Danjon and Reubens 2008). The WD model was from a 19-year-old P. pinaster tree also grown in a shallower sandy spodosol in Cestas, France (Fig. 2b, after Danjon et al. 2013). The prevailing wind direction experienced by the two selected trees in the field is indicated in Fig. 2. The 3D-digitized root architecture data was expressed in the form of a Multi-scale Tree Graph file (Godin et al. 1999) and was input into AMAPmod software for display (Fig. 2a,b).
To scale root models purely geometrically, with material properties (e.g. Young’s modulus) unchanged, scaling laws (typical ones shown in Table 2), which relate the parameters at model scale to the full-scale prototype, are needed. In order to benefit most from using centrifuge modelling to model a prototype root-soil system at a reduced scale (1:N), without generating unwanted boundary effects from the model container, it is desirable to select a high value of N. Indeed, the value of N cannot be too small since the root model must fit within the build envelope of the 3D printer and also the centrifuge model container. The value of N must also be small enough to avoid any grain-size effect and suit the resolution of the 3D printer (where the minimum root diameter that can be printed was 1.2 mm). An optimum value of N = 20 was eventually selected as a suitable compromise across these competing factors. The mean particle size (D50) of the model soil was 0.12 mm, while the weighted average diameter of the 3D printed root model (dr, ave) was 2 mm. Hence the ratio of dr, ave/D50 was 17. This was higher than 15, which was the minimum threshold above which grain-size effects of a soil-structure interaction problem in the centrifuge can be effectively ignored (Stone and Wood 1992). Root models were printed in Acrylonitrile Butadiene Styrene (ABS) plastic, which has been used by other studies to create root analogues for studying problems of slope stabilisation by vegetation and development of in-situ test methods for rooted soil (e.g. Liang et al. 2015, 2017b; Meijer et al. 2015; Liang and Knappett 2017). Liang et al. (2015) conducted a series of uniaxial tensile tests of 3D printed ABS plastic cylinders of different uniform diameters from 0.8 to 12 mm. It was demonstrated that irrespective of the cylinder diameter, the ABS plastic behaved largely elastically until an ultimate tensile strength was reached. Brittle failure was observed, similarly to what is conventionally observed for tree roots. The ABS plastic rods were also found to display diameter dependency on both the tensile strength and Young’s modulus, following a negative power law relationship as has often been observed for tree roots (Fig. S1, after Liang et al. 2017a, 2017b). The fabrication process, which involved progressive layering of the ABS plastic, was exploited to print the root analogues with the layering running along the longitudinal axes of the principal lateral roots near the ground surface, to approximate the fibrous structure of real roots (Liang et al. 2014). From this point onward, all dimensions quoted are at model scale, unless stated otherwise.
After applying the dimension scaling factor N to the coordinates in the MTG files, these were input into Solidworks 2012, the output from which was then sent to a Fortus 250mc 3D printer.
Root architecture
Following Liang et al. (2017b), in both 3D printed root models, all individual roots (except the tap root) were assumed to be of constant diameter for the idealization of ongoing numerical analysis. Based on the field root architecture data, the root diameters were divided into four representative classes (Table 3) for practical reasons. Each class was represented by a single average diameter (1.6, 2, 2.4 and 3 mm at model scale). The smallest diameter chosen was well within the printer’s resolution. The first three diameters were selected following a constant interval of 0.4 mm, while the last one, 3.0 mm, was determined based on the average diameter of the remaining roots. According to the root diameter classification suggested by Watson et al. (1995), all roots considered in the models were structural roots (either large or coarse). It should be noted that any root segments smaller than 1.2 mm (at model scale) were discarded to make the average diameter of individual roots not smaller than the smallest representative diameter (1.6 mm). For the tap root, the only simplification was to remove segments with diameters smaller than 1.2 mm. The diameter of the tap root varies along its length, according to the field survey data.
Root architectures were reconstructed in the sequence of orders (Danjon et al. 2008) following the flow chart in Fig. S2. Due to the limit of the printing resolution, only roots down to the fifth branching order were considered in this study. There was no significant effect on total root volume when using the average diameter to represent the whole root system, however, root volume was decreased after removing the segments smaller than 1.2 mm. To compensate for this effect, a global root volume scale-up factor Kv was applied. Coordinates of each vertex were enlarged Kv times, with volume enlarged \( {K}_v^3 \) times, to match the real root volume in the printed model. The scale-up factors for ND and WS models are given in Table 4. Although model ND (27 years old) is older than WS (19 years old), it has less total root volume, because the soil where WS grew had greater water availability and soil organic matter (Augusto et al. 2010).
The main stem of a tree (the trunk) transfers lateral loading mechanically to the root system via the stump. Here a 14 mm diameter dowel was used to model the tree trunk. The diameter of the dowel was determined based on the average diameter at breast height (DBH) of the ND and WS trees, which were 288 mm and 291 mm respectively at prototype scale. The main reason to model the trunk was (i) to provide a lever arm for applying horizontal load and converting this into an overturning moment on the root system; and (ii) to take into account any possibilities of flexural breakage of the trunk in case the model roots had sufficient anchorage to the ground (though this did not subsequently occur in any of the centrifuge tests presented). The trunk was connected with the root system through a coupler into which the printed root system and dowel trunk were glued using epoxy resin. The dimensions of the coupler were determined following Zhang et al. (2018). In total, 7 root models were 3D printed, taking approximately one day for each model.
General description of physical modelling
The stress level in a 1-g test is N times lower than that in the field for a 1:N scaled root system. Geotechnical centrifuge modelling (Fig. 3a) is an approach which can simulate the global performance of a full-scale soil and root prototype to a high level of fidelity, by achieving similitude of stresses at homologous points within the model and prototype (Liang et al. 2017a). In this case, the global performance of a full-scale root system prototype can be simulated within a small-scale model (Fig. 3b). A series of 1-g physical model tests was also undertaken to investigate whether the prototype responses, after scaling by appropriate 1-g scaling factors (summarised in Table 2) were comparable with those obtained from the centrifuge tests. All key variables (e.g. model root properties, root architecture, soil properties, groundwater conditions and loading conditions) were closely controlled in all tests.
Centrifuge test set-up and procedures
Three centrifuge tests were performed using the Actidyn C67–2 geotechnical beam centrifuge (Fig. 3a) at the University of Dundee, UK. 1:20 scale models of the ND and WS models were tested to investigate the role of root architecture on anchorage behaviour. Both models were installed in fully saturated model soil to consider windthrow under a winter storm condition. The third test utilised the ND root model but was buried in fully dry soil and tested at 12-g so as to create an identical effective soil stress regime experienced by roots at homologous points to those in fully saturated soil at 20-g, following Eq. (2):
where Nd, γd and Ns, γs are g-levels and unit weights of the soil for the dry and saturated case, respectively, γ′ is effective unit weight of the saturated soil and γw is unit weight of the water.
A strongbox container with internal dimensions of 800 mm × 500 mm × 550 mm was used. At the bottom of the box, a 10 mm pea-gravel layer was placed to facilitate bottom drainage. This was overlain by a 100 mm thick HST95 sand layer (Fig. 4a). Two 1:20 root models were installed within the same container, since the plan area of the container was big enough to test two root models without affecting each other (Fig. 4b). Each root model was suspended at the desired position and the model soil was pluviated around them through a 1.18 mm sieve at a fixed height of 450 mm from the soil surface to create a uniform 300 mm thick soil bed with relative density of 45–50% (corresponding to the dry bulk density 1.67 ± 0.02 g/cm3). Pluviation was complete when the soil surface reached the bottom of the coupler. For saturated tests, a water head 500 mm higher than the soil surface was applied at the bottom of the model soil for bottom-up saturation.
After spinning the centrifuge to the designed g-level, a lateral force was applied under displacement control to the trunk 60 mm above the top of the coupler (Fig. 4a) to induce an overturning moment on the root system. This position maximised the rotation angle achievable for a given travel of the actuator. The loading rate applied in the saturated tests at 20-g was 0.6 mm/min at model scale to achieve fully drained behaviour of the root-soil interaction. The loading rate in the dry test at 12-g was 0.4 mm/min at model scale such that the prototype velocity was identical with the saturated tests. Root models could be pushed to approximately a 30° maximum rotation in the centrifuge (50° in 1-g tests) due to limitations of the apparatus. The horizontal force was applied to the root systems in the direction of the prevailing wind experienced in the field (Fig. 2). The rotation (θ) and moment (M) curves were determined from the measurements of horizontal displacement and force, respectively, via:
where d and h are the horizontal displacement and the distance between the loading point and the top of root (Fig. 4a), respectively, F is the horizontal force measured, m is the mass of the trunk, N is the g-level and g is the gravitational acceleration.
1-g test set-up and procedures
Four 1-g tests were conducted to investigate the root anchorage behaviour provided by the ND and WS root models installed in dry and saturated soil. All these 1-g tests were conducted using a model container with similar dimensions to the centrifuge strong box. The preparation procedures of both the soil and the root models were identical to those described previously for the centrifuge tests. In all 1-g tests, the lateral load was applied under displacement control at a constant rate of 0.03 mm/min. For the given loading rate acting on the model tree trunk, the rate of shearing v of soil occurring at the farthest end of the lateral root was estimated as 0.075 mm/min. For the weighted-average root diameter dr, ave of 2 mm and the coefficient of consolidation cv of the model soil of 2.6 mm2/s, Peclet number, defined as \( \frac{v{d}_{r, ave}}{c_v} \) (Finnie and Randolph 1994), can be determined to be 9.6 × 10−4, which is a thousand times smaller than the threshold value of 1, below which shearing may be considered as drained.
Results
Architecture and root distribution of 3D printed tree root models
The root systems reconstructed from the field survey data are compared with those 3D printed in Fig. 2 c,d with vertical distribution of root volume at prototype scale demonstrated in Fig. 5. WS generally had more root material than ND however it was around 0.5 m shorter than ND. The rapid increase of root volume in the top 400 mm was due to the untapered part of tap root as well as the appearance of shallow lateral roots. The overview of the spatial structure of root reinforcement in this zone (top 400 mm) will be discussed in the following section. Below this depth, central sinkers and tap roots mainly dominate and largely contribute to the anchorage strength.
From centrifuge tests
For all three tests, windward horizontal roots were pulled out of the soil. The broken roots recovered from the soil post-test for these two systems are shown in Fig. 6, where they are nearly identical for the ND model under different water conditions. All breakage points observed in the three centrifuge tests are marked in Fig. 7a, b. It was found that one windward lateral (A, G in Fig. 7), as well as central sinkers (including the tap root) was vulnerable to be broken for both root models.
Validity of dry-saturated equivalency
Figure 8a shows the moment-rotation curves, expressed at model scale, obtained from the centrifuge tests. The curves for the ND roots at the same effective stress level but different water conditions are in excellent agreement for the first 10° of trunk rotation, and the initial rotational stiffness was practically the same. Also, in both cases, three prominent drops of moments were captured, most probably indicating breakages of main structural roots from amongst those shown in Figs. 6 and 7. Beyond 10° rotation, however, a maximum difference in peak moment resistance of 14% was observed. Based on careful inspection of exhumed root models post-test (Fig. 7 c, d), the positions of root breakage were found to be similar between the two cases. Two minor differences were identified: (i) one more breakage (F in Fig. 7) occurred close to the tip of the tap root in the saturated test; and (ii) one of the broken sinker roots (B marked in Fig. 7) attached to the tap root was still stuck on the root system in the dry test whereas this became detached in the saturated case. These explain the small reduction in moment capacity in the saturated case.
Effects of root architecture
To better quantify the root morphology, the rooted area was divided into 8 zones relative to the wind direction and numbers of roots in each zone are presented in Fig. 9. Based on the final root breakage, only roots originating from the top 20 mm at model scale (400 mm at prototype scale) were recorded for comparison and roots passing through several zones rather than extending radially were not counted. This figure shows that although the WS model has more roots in total than the ND model, they have very similar numbers of lateral roots in zone I, IV, V and VIII. Therefore, there was no significant difference in leeward and windward horizontal roots which were believed to provide most resistance to lateral loading. As shown in Fig. 8a, the initial rotational stiffness provided by the WS case was similar to that by the ND case, until a rotation of about 5°. By 30° rotation, the peak moment capacity of the WS case was only 35% higher than that of the ND root, even though it had 65% higher total root volume and a wider spread of the second-order horizontal roots. Besides the similar horizontal root distribution along the predominant wind direction, the ND root system was 35% longer in the vertical direction than the WS case, meaning that the tap and sinker roots in the ND case could have gained greater resistance from greater soil effective confining pressure for resisting uprooting. The longer root length for the ND system translates to 35% higher soil confining pressure, hence causing an estimated 150% increase in soil confining moment due to lateral earth pressure during rotation.
From 1-g tests
The failure patterns of all 1-g tests were similar to each other, with examples of models ND and WS tested in saturated soil shown in Fig. S3. More roots were pulled out of the soil on the windward side compared to the centrifuge tests due to greater rotation applied in 1-g tests, resulting in small differences in root breakage.
Figure 8b shows the moment-rotation curves of the ND and WS root systems buried in dry and saturated soil under 1-g conditions. Regardless of the model root type, the moment capacity measured from dry soil was higher than that from saturated soil due to the effects of water buoyancy (with the effective unit weight of the soil being reduced from 16.4 kN/m3 (dry soil) to 10.2 kN/m3 (saturated soil)), translating to a reduction of 38% in soil effective confining pressure. As indicated in Fig. 6, in general, the breakage of root systems was similar for these two different water conditions. Additionally, similarly to centrifuge tests, WS exhibited greater stiffness and higher moment capacity than ND.
The comparison of the moment-rotation curves between the ND and WS roots in Fig. 8b suggests that the WS root has approximately 10% higher moment capacity than the ND root for similar groundwater conditions. Compared with the centrifuge tests (Fig. 8a), though the stiffness of the roots was not scaled, moment capacity was much smaller as soil stress levels were 1/20th of the 20-g condition for the same groundwater conditions, resulting in effective confining stresses on structural lateral roots (buried by 6.5 mm at model scale) lowered from 1.3 kPa to 0.06 kPa (saturated case), which largely reduced the gap of the moment capacities, which was much more obvious in the centrifuge tests due to different morphologies, between two types of root systems.
Discussion
Comparisons between centrifuge and field testing
Following the scaling laws summarised in Table 2, the moment-rotation curves obtained from the ND and WS root tests in saturated soil were scaled to prototype scale for comparison with the field data obtained from in-situ winching tests on Larch (Larix europea × L. japonica) in wet sandy clay (Crook and Ennos 1996) and on Sitka spruce (Picea sitchensis) in peaty gley soil (Coutts 1983, 1986) in Fig. 10a. These two specific case studies, among many in the literature, were selected for comparison because the field soil was known to be saturated and the tree roots were observed pulling-out from soil, which was consistent with the centrifuge test conditions. In addition, the field tree dimensions were similar to those considered in the present study (Table 5). As shown in Fig. 10a, the centrifuge test data showed comparable initial rotational stiffness to the field measurements below 10° rotation. Beyond this there were greater discrepancies, however the overturning moments measured in the centrifuge (9 to 12 kNm) fell within the range of field measurements (7 to 20 kNm). By normalizing the curves by their peak moment Mp and corresponding rotation at peak moment (θp, Fig. 10b), it was found that the shapes of the centrifuge test curves were consistent with the field tests up to peak moment.
Based on the field data collected, Crook and Ennos (1996) used stepwise multiple regression to empirically correlate the total cross-sectional area of windward lateral roots Awr with peak moment, giving:
In this study, Awr = 0.0049 and 0.0083 (m2) for the models ND and WS, respectively (at prototype scale). Eq 5 thus predicts the peak moments to be 8.88 and 10.6 kNm, respectively, which are close to the measured values. These comparisons suggest that the data obtained from the centrifuge tests simulated root anchorage strengths of the correct order of magnitude with field observations. Despite the close agreement of the normalised curves between the centrifuge tests and field tests, the caveats are: (i) the loading applied in the centrifuge test was horizontal rather than inclined through a rope as in most field winching tests and hence the vertical-horizontal-moment loading conditions between the two types of tests were different even though rotational uprooting predominates in both; (ii) root architectures considered in the physical tests were simplified (e.g. fine roots as normally found in the field root system were ignored as they could not be printed); (iii) the structure/fabric, and hence the mechanical properties, of the model soil being tested in the centrifuge would be different from the field soil which has been subjected to cycles of wetting and drying and hence a complex stress history; (iv) the drainage condition of field winching tests is generally unknown and the winch pulling applied might not always achieve a fully drained condition like in the centrifuge tests, as cv is not routinely measured.
Failure mechanism
For WS at 1-g in the two different water conditions, the leeward root with branches broke (Fig. 6), which is consistent with observation in the field winching tests by Crook and Ennos (1996), who also found that the anchorage resistance started to reduce after the leeward roots were damaged. In the 1-g tests in this study, rapid decreases were observed when rotation exceeded 30°. There were no clear drops in the centrifuge tests indicating that the rotation angle limit of the apparatus (≤ 30°) was not sufficient to activate the failure of the leeward roots. However, by applying realistic overburden pressure, centrifuge tests gave a better representation of root-soil behaviour before 30°, as windward roots in the centrifuge tests were more vulnerable to be broken, consistent with field observations (Coutts 1983, 1986). It should be noted that the difference here between centrifuge and 1-g tests did not contribute significantly to differences in the final moment-rotation curve because in the early stages, the stress was redistributed when breakage occurred and it was the whole root system that dominated the root-soil interaction, which could be seen in Fig. 8a, where sharp decreases in moment were then followed by gradual increases.
Development of 1-g scaling laws
To compare the behaviour obtained from the 1-g and centrifuge high-g tests, the moment-curvature curves were scaled up to the same prototype initially following the scaling laws given in Table 2. The comparison, after scaling, is shown in Fig. 11. The 1-g model tests exhibited higher moment capacity than the centrifuge results, regardless of which root morphology or groundwater conditions were considered. This is, however, somewhat expected as at the low confining soil effective stresses in the 1-g tests, the soil exhibited much greater dilatancy, which was significantly suppressed in the high-g tests. For example, considering a soil depth of 45 mm (i.e., half of the length of ND root), the confining pressure of saturated soil at 1-g and high-g was 0.46 and 9.2 kPa, respectively, and the corresponding peak friction angle could be as high as 55° in the 1-g case but only 38° in the 20-g case based on the results of DSA tests shown in Fig. 1b. Therefore, the soil tested at 1-g provided much greater soil strength to the roots upon relative root-soil deformation. In order to take into account the effects of soil dilatancy in the scaling of the 1-g tests, the transverse effective soil stresses acting normal to a root segment at depth z may be approximated as:
where σ′n and σ′v are the transverse normal and vertical effective soil stresses, respectively, Kp is the passive earth pressure coefficient, and z is the depth from the ground surface. Most of the existing literature in soil bioengineering (e.g. Mickovski et al. 2010; Liang et al. 2019) has demonstrated that the lateral earth pressure coefficient, K, of the soil in the vicinity of the roots being axially uprooted was higher than K0 (coefficient at rest) but lower than Kp, which is consistent with the theory of cavity expansion. However, due to the complexity of the root models being investigated in this study, it was difficult (if not impossible) to precisely determine the values of K mobilised at different positions within the root system. Therefore, for simplicity, Kp was used in the scaling as a limit state condition of the soil. Based on the friction angles given in Fig. 1b, the ratio of Kp at 1-g compared to 20-g (effective over-strength factors) for the cases of ND and WS root models are 2.6 and 2.2, respectively. If considering Kp as the non-dimensional number for scaling the dilation effects, this ratio can then be applied to reduce the values of prototype moment obtained from 1-g tests, to remove the over-strength effect. After applying this correction, Fig. 11 demonstrates a much closer match between 1-g and high-g tests, particularly in terms of the moment capacity.
Although the prototype moment is now better matched between the 1-g and high-g tests, especially at intermediate and large rotations, discrepancies of initial rotational stiffness are still observed at low rotations in Fig. 11. The central tap root and sub-vertical sinker roots in both root models, may be considered as individual piles subjected to a lateral load at their head (transferred from the root system at the connection point). Assuming the soil responds elastically at low rotation, the relative root-soil stiffness may be described by the following non-dimensional number proposed by Broms (1964):
where Er, Ir, l and G are the Young’s Modulus of the root, second moment of area of the root, length of root and shear modulus of the soil, respectively. To maintain similitude, this non-dimensional number evaluated at model scale must be identical to that at the prototype scale. Hence, the ratio αΛ, of Λ between model and prototype scale, as calculated below, has to be 1.0:
where nG, nl nI and nE are the scaling factors for G, l, Er and Er, respectively. The values of nG and nl can be found from Table 2. nE is taken to be 1.0 for both the 1-g and high-g cases, because the same root material was used at both scales. To evaluate nI, since the model roots are circular, the second moment of area can be calculated by:
where dr is the diameter of the root. Thus, nI is 1/204 for both 1-g and high-g case. Therefore, as a result of the scaling, the corresponding value of αΛ is 1 and 1/200.5 for the high-g and 1-g tests. This means that the relative soil-root stiffness in the high-g case has been correctly scaled, yet was underestimated in the 1-g case (i.e. the roots were too stiff compared to the soil, which explains why the prototype M-θ behaviour was stiffer in the 1-g tests in Fig. 11). In order to maintain complete similitude in 1-g tests (i.e., keeping αΛ to be 1), it is not desirable to modify dr as this would also influence the moment capacity given the root pull-through failure mechanisms observed in the tests (which depends on dr). Instead, it would be desirable to identify a printable material that has the same tensile strength as the ABS plastic used herein but with a Young’s Modulus reduced by 200.5 times (i.e. Er, 1 − g = 0.22 Er, ABS).
Implications for engineering application
The testing method employing the combined use of 3D printing and centrifuge modelling shows promise for: (i) further mechanistically-based study of tree-root-soil interaction in research (e.g. the effects of loading rate, partially-saturated ground conditions); (ii) non-destructively assessing the push-over hazard to historically important trees near infrastructure; and (iii) back-analysing uprooted trees to estimate applied loads or soil conditions. To use the method currently requires: (1) field mapping of root architecture for detailed 3D reconstruction and 3D printing and (2) the growth soil being considered to be cohesionless. Furthermore, it has been demonstrated that it may be possible to conduct relatively cheap and simple 1-g tests (without requiring a centrifuge) that are representative of high-g tests, as long as the effect of soil dilatancy at lower effective stresses is considered in the scaling (via the passive lateral earth pressure coefficient). Although the moment capacity obtained from the 1-g tests quantitatively matched the prototype (high-g) value, it should be acknowledged that there were some differences in individual root failure modes, because of the different soil stress states that controlled the different modes of root failure against breakage and slippage.
Conclusions
This paper has presented an investigation into the push-over behaviour of tree root systems under lateral loading using both 1-g physical modelling tests and high-g centrifuge tests. The protocols used to convert field-measured root architecture data into printable 1:20 scale physical model root systems were presented. Two main factors influencing stiffness and capacity of tree root systems under lateral loading were considered, namely: (i) groundwater condition and (ii) root morphology.
It was found that the fully saturated case where the roots respond in a drained manner can be appropriately simulated by dry soil centrifuge tests at reduced g-level (compensating for the higher effective soil unit weight), or 1-g tests with appropriate allowance made for effective unit weight within the scaling laws applied to obtain prototype response. In terms of root architecture, it was noted that the presence of key lateral roots along the predominant wind direction contributed more to the moment capacity than the total root volume.
Centrifuge results showed similar moment-rotation behaviour and moment capacities to data from winching tests on trees of similar size from the literature. Using conventional scaling laws, 1-g model tests overestimated moment capacity because of the high soil dilation operating at very low confining effective stresses. This could be corrected for using a simple modification for soil strength which was developed in the paper. Some distortion was also observed in terms of the behaviour at low rotation angles due to root-soil relative stiffness and suggestions were made for changes to the properties of the model root material that could remove these unwanted effects in 1-g tests.
The discarding of fine roots within the scaled models did not appear to result in significant effects on the overall push-over behaviour; however, further research with simulation of fine roots (e.g. fibres or prints using future higher resolution 3D printers) is required to generalise this finding. The model test data in this paper will be a valuable data set for validating future numerical and analytical modelling developments under more controlled conditions that are possible in field testing.
Abbreviations
- ABS:
-
Acrylonitrile Butadiene Styrene
- CPT:
-
cone penetration test
- DBH:
-
diameter at breast height
- DSA:
-
direct shear apparatus
- ND:
-
narrow and deep (root model)
- PSD:
-
particle size distribution
- WS:
-
wide and shallow (root model)
References
Augusto L, Bakker MR, Morel C, Meredieu C, Trichet P, Badeau V, Arrouays D, Plassard C, Achat DL, Gallet-Budynek A, Merzeau D, Canteloup D, Najar M, Ranger J (2010) Is ‘grey literature’ a reliable source of data to characterize soils at the scale of a region? A case study in a maritime pine forest in southwestern France. Eur J Soil Sci 61:807–822. https://doi.org/10.1111/j.1365-2389.2010.01286.x
Blackwell PG, Rennolls K, Coutts MP (1990) A root anchorage model for shallowly rooted Sitka spruce. Forestry 63:73–91. https://doi.org/10.1093/forestry/63.1.73
Bolton MD (1986) The strength and dilatancy of sands. Géotechnique 36:65–78. https://doi.org/10.1680/geot.1986.36.1.65
British Standards Institution (1990) Methods of test for soils for civil engineering purposes - part 1: General requirements and sample preparation
Broms BB (1964) Lateral resistance of piles in cohesive soils. J Soil Mech Found Div 90:27–64
Cao J, Tamura Y, Yoshida A (2012) Wind tunnel study on aerodynamic characteristics of shrubby specimens of three tree species. Urban For Urban Green 11:465–476. https://doi.org/10.1016/j.ufug.2012.05.003
Coutts MP (1983) Root architecture and tree stability. Plant Soil 188:171–188
Coutts MP (1986) Components of tree stability in Sitka spruce on peaty gley soil. Forestry 59:173–197. https://doi.org/10.1093/forestry/59.2.173
Crook MJ, Ennos AR (1996) The anchorage mechanics of deep rooted larch, Larix europea × L. japonica. J Exp Bot 47:1509–1517. https://doi.org/10.1093/jxb/47.10.1509
Crook MJ, Ennos AR (1998) The increase in anchorage with tree size of the tropical tap rooted tree Mallotus wrayi, King (Euphorbiaceae). Ann Bot 82:291–296. https://doi.org/10.1006/anbo.1998.0678
Danjon F, Reubens B (2008) Assessing and analyzing 3D architecture of woody root systems, a review of methods and applications in tree and soil stability, resource acquisition and allocation. Plant Soil 303:1–34. https://doi.org/10.1007/s11104-007-9470-7
Danjon F, Fourcaud T, Bert D (2005) Root architecture and wind-firmness of mature Pinus pinaster. New Phytol 168:387–400. https://doi.org/10.1111/j.1469-8137.2005.01497.x
Danjon F, Barker DH, Drexhage M, Stokes A (2008) Using three-dimensional plant root architecture in models of shallow-slope stability. Ann Bot 101:1281–1293. https://doi.org/10.1093/aob/mcm199
Danjon F, Caplan JS, Fortin M, Meredieu C (2013) Descendant root volume varies as a function of root type: estimation of root biomass lost during uprooting in Pinus pinaster. Front Plant Sci 4:1–16. https://doi.org/10.3389/fpls.2013.00402
Danquechin Dorval A, Meredieu C, Danjon F (2016) Anchorage failure of young trees in sandy soils is prevented by a rigid central part of the root system with various designs. Ann Bot 118:747–762. https://doi.org/10.1093/aob/mcw098
Dattola G, Ciantia MO, Galli A et al (2019) A macroelement approach for the stability assessment of trees. InNational conference of the researchers of geotechnical engineering. Springer, Cham, pp 417–426. https://doi.org/10.1007/978-3-030-21359-6_44
Dekker MM, Haarsma RJ, de Vries H et al (2018) Characteristics and development of European cyclones with tropical origin in reanalysis data. Clim Dyn 50:445–455. https://doi.org/10.1007/s00382-017-3619-8
Dupont S, Brunet Y (2008) Impact of forest edge shape on tree stability: a large-eddy simulation study. Forestry 81:299–315. https://doi.org/10.1093/forestry/cpn006
Dupuy L, Fourcaud T, Stokes A (2005) A numerical investigation into the influence of soil type and root architecture on tree anchorage. Plant Soil 278:119–134. https://doi.org/10.1007/s11104-005-7577-2
Finnie IMS, Randolph MF (1994) Punch-through and liquefaction induced failure of shallow foundations on calcareous sediments. In Seventh Int Conf Behav Offshore Struct 1:217–230
Gandhi KJK, Gilmore DW, Katovich SA, Mattson WJ, Zasada JC, Seybold SJ (2008) Catastrophic windstorm and fuel-reduction treatments alter ground beetle (Coleoptera: Carabidae) assemblages in a north American sub-boreal forest. For Ecol Manag 256:1104–1123. https://doi.org/10.1016/j.foreco.2008.06.011
Gardiner BA, Quine CP (2000) Management of forests to reduce the risk of abiotic damage - a review with particular reference to the effects of strong winds. For Ecol Manag 135:261–277. https://doi.org/10.1016/S0378-1127(00)00285-1
Godin C, Costes E, Sinoquet H (1999) A method for describing plant architecture which integrates topology and geometry. Ann Bot 84:343–357. https://doi.org/10.1006/anbo.1999.0923
Gromke C, Ruck B (2008) Aerodynamic modelling of trees for small-scale wind tunnel studies. Forestry 81:243–258. https://doi.org/10.1093/forestry/cpn027
Guitard DGE, Castera P (1995) Experimental analysis and mechanical modelling of windinduced tree sways. In: Coutts MP, Grace J (eds) Wind and trees: 182–194. https://doi.org/10.1017/cbo9780511600425.010
Jakob M, Lambert S (2009) Climate change effects on landslides along the southwest coast of British Columbia. Geomorphology 107:275–284. https://doi.org/10.1016/j.geomorph.2008.12.009
Knappett JA, Craig RF (2019) Craig’s soil mechanics. CRC press, Boca Raton
Larsen MC, Torres Sanchez AJ (1992) Landslides triggered by hurricane Hugo in eastern Puerto Rico, September 1989. Caribb J Sci 28:113–125
Liang T, Knappett JA (2017) Centrifuge modelling of the influence of slope height on the seismic performance of rooted slopes. Géotechnique 67:855–869. https://doi.org/10.1680/jgeot.16.P.072
Liang T, Knappett JA, Bengough AG (2014) Scale modelling of plant root systems using 3-D printing. ICPMG2014–physical Model Geotech 1:361–366
Liang T, Knappett JA, Duckett N (2015) Modelling the seismic performance of rooted slopes from individual root–soil interaction to global slope behaviour. Géotechnique 65:995–1009. https://doi.org/10.1680/jgeot.14.P.207
Liang T, Bengough AG, Knappett JA, MuirWood D, Loades KW, Hallett PD, Boldrin D, Leung AK, Meijer GJ (2017a) Scaling of the reinforcement of soil slopes by living plants in a geotechnical centrifuge. Ecol Eng 109:207–227. https://doi.org/10.1016/j.ecoleng.2017.06.067
Liang T, Knappett JA, Bengough AG, Ke YX (2017b) Small-scale modelling of plant root systems using 3D printing, with applications to investigate the role of vegetation on earthquake-induced landslides. Landslides 14:1747–1765. https://doi.org/10.1007/s10346-017-0802-2
Liang T, Knappett JA, Leung A, Carnaghan A, Bengough AG, Zhao R (2019) A critical evaluation of predictive models for rooted soil strength with application to predicting the seismic deformation of rooted slopes. Landslides. 17:93–109. https://doi.org/10.1007/s10346-019-01259-8
McCarthy JK, Hood IA, Brockerhoff EG et al (2010) Predicting sapstain and degrade in fallen trees following storm damage in a Pinus radiata forest. For Ecol Manag 260:1456–1466. https://doi.org/10.1016/j.foreco.2010.07.044
Meijer GJ, Knappett JA, Nicoll BC et al (2015) New in situ techniques for measuring the properties of root-reinforced soil – laboratory evaluation. Géotechnique 66:27–40. https://doi.org/10.1680/jgeot.15.p.060
Mickovski SB, Stokes A, Van Beek LPH (2005) A decision support tool for windthrow hazard assessment and prevention. For Ecol Manag 216:64–76. https://doi.org/10.1016/j.foreco.2005.05.043
Mickovski SB, Bransby MF, Bengough AG, Davies MCR, Hallett PD (2010) Resistance of simple plant root systems to uplift loads. Can Geotech J 47:78–95. https://doi.org/10.1139/T09-076
Moore JR, Tombleson JD, Turner JA, van der Colff M (2008) Wind effects on juvenile trees: a review with special reference to toppling of radiata pine growing in New Zealand. Forestry 81:377–387. https://doi.org/10.1093/forestry/cpn023
Nakahara T, Iai S, Tobita T (2005) Generalised scaling relations for dynamic centrifuge tests. Géotechnique 55:355–362. https://doi.org/10.1680/geot.2005.55.5.355
Nicoll BC, Gardiner BA, Peace AJ (2008) Improvements in anchorage provided by the acclimation of forest trees to wind stress. Forestry 81:389–398. https://doi.org/10.1093/forestry/cpn021
Pollen N, Simon A (2005) Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour Res 41:1–11. https://doi.org/10.1029/2004WR003801
Rahardjo H, Leong EC, Ow LF et al (2015) Stability of containerized urban street trees. Landsc Ecol Eng 12:13–24. https://doi.org/10.1007/s11355-015-0272-4
Ruel J (2000) Factors influencing windthrow in balsam fir forests: from landscape studies to individual tree studies. For Ecol Manag 135:169–178
Schelhaas MJ, Nabuurs GJ, Schuck A (2003) Natural disturbances in the European forests in the 19th and 20th centuries. Glob Chang Biol 9:1620–1633. https://doi.org/10.1046/j.1365-2486.2003.00684.x
Schwarz M, Cohen D, Or D (2010) Root-soil mechanical interactions during pullout and failure of root bundles. J Geophys Res Earth Surf 115:1–19. https://doi.org/10.1029/2009JF001603
Sellier D, Fourcaud T (2009) Crown structure and wood properties:influence on tree sway and response to high winds. Am J Bot 96:885–896. https://doi.org/10.3732/ajb.0800226
Stone KJL, Wood DM (1992) Effects of dilatancy and particle size observed in model tests on sand. Soils Found 32:43–57
Watson A, Marden M, Rowan D (1995) Tree species performance and slope stability. Vegetation and slopes: 161-171. Thomas Telford :Press, London
Wessolly L, Erb M (1998) Handbuch der Baumstatik und Baumkontrolle (in German). Patzer-Verlag, Berlin
Wood DM (2004) Geotechnical modelling. Spon Press, Abingdon
Yang M, Défossez P, Danjon F, Fourcaud T (2014) Tree stability under wind: simulating uprooting with root breakage using a finite element method. Ann Bot 114:695–709. https://doi.org/10.1093/aob/mcu122
Yang M, Défossez P, Danjon F, Dupont S, Fourcaud T (2017) Which root architectural elements contribute the best to anchorage of Pinus species? Insights from in silico experiments. Plant Soil 411:275–291. https://doi.org/10.1007/s11104-016-2992-0
Yang M, Défossez P, Danjon F, Fourcaud T (2018) Analyzing key factors of roots and soil contributing to tree anchorage of Pinus species. Trees - Struct Funct 32:703–712. https://doi.org/10.1007/s00468-018-1665-4
Zhang X, Knappett JA, Leung AK, et al (2018) Physical modelling of soil-structure interaction of tree root systems under lateral loads. In: Physical modelling in geotechnics 1:481–486. CRC Press
Acknowledgments
The first author would like to acknowledge the financial support of the China Scholarship Council (CSC) and the Norman Fraser Design Trust. The third author would like to acknowledge the grant GRF/16212818 funded by the Hong Kong Research Grant Council (RGC) as well as the grant no. 51922112 provided by the National Natural Science Foundation of China (NSFC) for the time spent on this work. Gary Callon is also gratefully acknowledged for 3D root printing, as are Mark Truswell and Grant Kydd for their assistance in centrifuge tests at the University of Dundee.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing financial interest.
Additional information
Responsible Editor: Alexia Stokes.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOCX 1773 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, X., Knappett, J.A., Leung, A.K. et al. Small-scale modelling of root-soil interaction of trees under lateral loads. Plant Soil 456, 289–305 (2020). https://doi.org/10.1007/s11104-020-04636-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11104-020-04636-8