Abstract
We present experimental evidence that supports the thesis (advanced recently by Stefánsson and Bradley in Philos Sci 82(4):602–625, 2015, Br J Philos Sci 70(1):77–102, 2019; Bradley in Decisions theory with a human face, Cambridge University Press, Cambridge, 2017; Goldschmidt and Nissan-Rozen in Synthese 198:7553–7575, 2021) that people might positively or negatively desire risky prospects conditional on only some of the prospects’ outcomes obtaining. We argue that this evidence has important normative implications for the central debate in normative decision theory between two general approaches on how to rationalize several common patterns of preference, which are ruled out as irrational by orthodox decision theory, namely the re-individuation approach and the non-expected utility approach.


Similar content being viewed by others
Notes
It is important to remember, however, that finding no statistically significant evidence for a correlation between two variables is not statistically significant evidence for lack of correlation. We discuss this point in the discussion sub-section of Sect. 3.
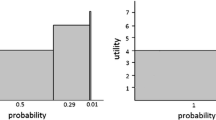
The variance of a lottery is the average deviation between the possible outcomes of the lottery and the expected value (in terms of G) of the lottery. It is a standard measure for what Weirich (2020) calls “a lottery’s exposure to risk” and economists sometimes call the “riskiness” of a lottery. See Weirich (2020) chapter 1 for a discussion of the limitation of this measure. Nothing in this paper depends, however, on the specific measure chosen for the initial characterization of the phenomenon.
This is not meant to be an exhaustive list, though. Some suggestions in the literature seem not to fall neatly into any one of these two families. A notable example is Loomes and Sugden’s (1982) regret theory.
This is the case because it violates Savage’s) 1954) “sure-thing principle”: the choice between a and b is identical to the choice between c and d as long as one ignores state w3 in which a and b, as well as c and d, give the same outcome.
We thank Naly Thaler for this example.
Nissan-Rozen (2021) explores several possible strategies proponents of the non-expected utility approach can adopt in order to overcome this problem. However, the fact that the problem does not even arise for the re-individuation strategy seems like a clear advantage.
Another recent normative re-individuation account is that of Weirich (2020). However, Weirich’s account does not allow for different risk-attitudes conditional on different possible outcomes, which is the feature of Stefansson’s and Bradley’s account that we will make use of.
Because it is a weighted sum of the conditional desires for the lottery given each one of its possible outcomes and every such conditional desire represents—as explained above—what getting the outcome via this specific lottery adds to the prospect of getting the outcome, and not the desirability of the outcome itself.
This immediately follows from the conditional desirability formula: d(L|A) = d(AL) − d(A) + d(T) and so. d(AL) = d(L|A) + d(A) − d(T). Using the last equation, we can rewrite the conditional desirability formula applied to d(A|L) as d(A|L) = d(L|A) + d(A) − d(T) − d(L) + d(T) = d(L|A) + d(A) − d(L).
We did not ask participants directly about their d(L|A)s because that would have defeated the purpose of the study. Asking this question (i.e., asking participants how much they desire a certain probability of winning an item, under the assumption that they will win it) already assumes that conditional risk-attitudes exist (i.e., that people sometime positively or negatively desire not only certain outcomes, but also getting these outcomes with certain probabilities). However, their existence is the hypothesis our experiments aim to examine. If we would asked participants directly about their d(L|A)s we could not have ruled out the possibility that the participants misinterpreted out question in some way. On the other hand, asking people how much they desire winning an item, while letting them know the probability that they will win it, assumes nothing of the sort.
Some readers might prefer to skip the next few pages and move straight to the discussion sub-section.
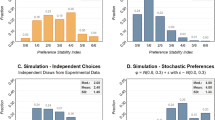
An anonymous referee has raised the worry that the results might be explained by a small percentage of the participants opting for the alternative (wrong) interpretation of the question as explained in the main text. In order to rule this explanation out we checked for outliers. In the first experiment there were 2 outliers (more than 3.5 standard deviations from the average difference between the desire under the high probability condition and the desire under the low probability condition): one had an average desire 8 times higher under the high probability condition and the other had an average desire 13 times higher. In the second experiment there was one outlier with an average desire 5 times higher under the high probability condition. We ran the analysis again for the two experiments without the outliers and still got significant results. For the first experiment the significant main effect of Probability was: \([F(\mathrm{1,68.47}) = 12.24,p<0.001]\). For the second experiment the significant main effect of Probability was: \([F(\mathrm{1,90.6})=23.26,p<0.001]\).
References
Allais, M. (1953). Le Comportement de l’Homme Rationnel Devant le Risque: Critique des Postulats et Axiomesde l’Ecole Americaine. Econometrica, 21, 503–546.
Blessenohl, S. (2020). Risk attitudes and social choice. Ethics, 130(4), 485–513.
Bolker, D. (1966). Functions resembling quotients of measures. Transactions of the American Mathematical Society, 124(2), 292–312.
Bradley, R. (1999). Conditional desirability. Theory and Decision, 47(1), 23–55.
Bradley, R. (2017). Decisions theory with a human face. Cambridge University Press.
Briggs, R. (2015). Cost of abandoning the sure-thing principle. Canadian Journal of Philosophy, 45(5–6), 827–840.
Broome, J. (1991). Weighing goods. Basil Blackwell.
Buchak, L. (2013). Risk and rationality. Oxford University Press.
Ellsberg, D. (1961). Risk, ambiguity, and the savage axioms. Quarterly Journal of Economics, 75, 643–669.
Gawronski, B., & Hahn, A. (2019). Implicit measures: Procedures, use, and interpretation. In H. Blanton, J. M. LaCroix, & G. D. Webster (Eds.), Measurement in social psychology (pp. 29–55). Taylor & Francis.
Goldschmidt, Z., & Nissan-Rozen, I. (2021). The intrinsic value of risky prospects. Synthese, 198, 7553–7575.
Jeffrey, R. (1965). The logic of decision. University of Chicago Press.
Lejuez, C. W., Read, J. P., Kahler, C. W., Richards, J. B., Ramsey, S. E., Stuart, G. L., Strong, D. R., & Brown, R. A. (2002). Evaluation of a behavioral measure of risk taking: The Balloon Analogue Risk Task (BART). Journal of Experimental Psychology: Applied, 8(2), 75.
Loomes, G., & Sugden, R. (1982). Regret theory: an alternative theory of rational choice under uncertainty. The Economic Journal, 92(368), 805–824.
Murray, D., & Buchak, L. (2019). Risk and motivation: when the will is required to determined what to do. Philosophers’ Imprint, 19(16), 1–16.
Nebel, J. (2020). Rank-weighted utilitarianism and the veil of ignorance. Ethics, 131(1), 87–106.
Nissan-Rozen, I. (2019). The value of chance and the satisfaction of claims. The Journal of Philosophy., 116(9), 469–493.
Nissan-Rozen, I. (2021). Weighing and aggregating reasons under uncertainty: a trilemma. Philosophical Studies, 178, 2853–2871.
Pettigrew, R. (2015). Risk, rationality and expected utility theory. Canadian Journal of Philosophy, 45(5–6), 798–826.
Quiggin, J. (1982). A theory of anticipated utility. Journal of Economic Behavior and Organization, 5, 323–343.
Rabin, M. (2000). Risk aversion and expected utility theory: A calibration theorem. Econometrica, 68, 1281–1292.
Savage, J. L. (1954). The foundations of statistics. Dover.
Stefánsson, H. O., & Bradley, R. (2015). How valuable are chances? Philosophy of Science, 82(4), 602–625.
Stefánsson, H. O., & Bradley, R. (2019). What is risk aversion? The British Journal for the Philosophy of Science, 70(1), 77–102.
Thoma, J. (2019). Risk aversion and the long run. Ethics, 129(2), 230–253.
Thoma, J., & Weisberg, J. (2019). No escape from Allias: Reply to Buchak. Philosophical Studies. https://doi.org/10.1007/s11098-019-01322-z
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.
Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science, 211(4481), 453–458.
Tversky, A., & Wakker, P. (1995). Risk attitudes and decision weights. Econometrica, 63(6), 1255–1280.
Von Neumann, J., & Morgenstern, O. (1947). Theory of games and economic behavior (2nd ed.). Princeton University Press.
Wakker, P. (2010). Prospect theory: For risk and uncertainty. Cambridge University Press.
Weirich, P. (2020). Rational responses to risk. Oxford University Press.
Acknowledgements
Earlier versions of this paper were presented in the “Lab” forum of the Edelstein Center for Philosophy of Science in the Hebrew University and in the Cork-Trinity departmental seminar (both via Zoom). We thank the participants of these events for their helpful comments. We also thank Richard Bradley, Ryan Doody, Graham Oddie, Orri Stefansson and two anonymous referees for helpful discussions and suggestions. This work was supported by Ittay Nissan-Rozen’s Israel Science Foundation Grant (Grant No. 327/18) and by a fellowship from the Edelstein Center for the Philosophy of Science to Haim Cohen.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Cohen, H., Maril, A., Bleicher, S. et al. Attitudes toward risk are complicated: experimental evidence for the re-individuation approach to risk-attitudes. Philos Stud 179, 2553–2577 (2022). https://doi.org/10.1007/s11098-022-01778-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-022-01778-6