1 Introduction

A wide range of nonlinear evolution equations (NLEEs) have been widely utilized in recent decades to represent a number of physical situations that occur in many scientific domains, including applied biological science, engineering, hydrology, plasma physics, chemistry, and applied mathematics (Gao 2015; Jiang et al. 2010; Gao 2015a, b; Zhen et al. 2015; Sun et al. 2015; Xie et al. 2015; Ablowitz and Clarkson 1991; Wazwaz 2005, 2010a, b, 2012, 2013, 2014; Duan et al. 2013; Sebogodi et al. 2023; Podile et al. 2022; Ma 2021, 2022, 2023; Ye et al. 2021) It is crucial to get these NLEEs’ precise solutions in order to gain deeper understanding of the physical principles that underlie subsequent applications. Numerous potent and successful techniques (Chen and Lü 2023; Cao et al. 2023; Gao et al. 2023; Chen et al. 2024, 2023a, b; Liu et al. 2023; Yin and Lü 2023; Yin et al. 2022; Liu et al. 2022; Yin et al. 2021; Lü et al. 2021; Lü and Chen 2021; Zhao et al. 2022) that enable the generation of precise traveling wave solutions to NLEEs have been put forward in the literature. The Lie symmetry approach, sine-cosine method, inverse scattering transform method, and tanh method are a few of these well-known techniques (Wang and Wazwaz 2022a, b; Wang 2021a, b, c; Wang et al. 2020; Hu et al. 2020). A Gwaxa et al. (2023) special class of third-order polynomial evolutionary equations that admitted the same one-parameter point transformations which left the evolutionary equations invariant resulted in highly nonlinear third-order ordinary differential equations, finally a power series established interesting solutions. Solutions (Gwaxa et al. 2023) of general bond-pricing model that satisfy a given terminal condition were systematically illustrated via point symmetries.

Many different physical processes, including fluid mechanics, plasma waves, solid state physics, and plasma physics, are represented by the theory of nonlinear evolution equations. The interactions of the nonlinear and dispersive components of nonlinear partial differential equations result in solitons, also known as solitary waves (Sebogodi et al. 2023). A complete analysis of nonlinear partial differential equations must thus include calculating these sorts of solutions. There is no one approach that can be used to solve nonlinear partial differential equations, despite several efforts, and conservation laws are crucial for solution extraction. The initial step in issue solving is often determining the conservation laws of a system of nonlinear partial differential equations. A system of nonlinear partial differential equations is considered to be integrable if it has a significant number of conservation laws (Sebogodi et al. 2023).

The Boussinesq equation

$$\begin{aligned} \mu _{\tau \tau } + \mu _{\chi \chi } - b (\mu ^{2})_{\chi \chi } - c \mu _{\chi \chi \chi \chi } =0, \end{aligned}$$
(1.1)

where b and c are constants, was introduced by Boussinesq in 1871 to describe the propagation of long waves in shallow water under gravity propagating in both directions (Boussinesq 1877; Clarkson and Kruskal 1989). It also arises in several physical applications such as nonlinear lattice waves, iron sound waves in plasma and in vibrations in a nonlinear string and in the percolation of water in porous subsurface of a horizontal layer of material. The Boussinesq equation has been widely studied for its ability to describe solitons in various physical systems (Wazwaz 2007, 2006, 2010). These solitons are localized, stable waves that can propagate without changing their shape or amplitude. They are often observed in nonlinear systems such as water waves, optical fibers, and plasma waves. The presence of solitons in the Boussinesq equation has attracted significant attention due to its connection to incompressible Navier–Stokes equations and its relevance in mathematical fluid dynamics. Moreover, the Boussinesq equation not only allows for the study of solitons but also provides insights into wave motion in weakly nonlinear and dispersive media.Researchers have explored different aspects of solitons in the Boussinesq equation, such as their existence, properties, and behaviour under various conditions. These studies have contributed to our understanding of nonlinear wave phenomena and have practical implications in fields such as oceanography, optics, and plasma physics. The study of solitons in the Boussinesq equation is of great significance due to its wide range of applications and its contribution to our understanding. Furthermore, the discovery of solitons in the Boussinesq equation has paved the way for advancements in mathematical modelling and numerical simulations of buoyancy-driven flows, wave propagation, and nonlinear dynamics. Moreover, the soliton solutions of the Boussinesq equation have been used to explain various physical phenomena, such as wave-breaking events and rogue waves. Overall, the Boussinesq equation and its soliton solutions play a crucial role in advancing our understanding of nonlinear wave phenomena and their applications in diverse scientific disciplines (Wazwaz 2001; Liu et al. 2020; Li et al. 2022).

In this paper we study a (2 + 1)-dimensional Boussinesq equation (Wazwaz 2022)

$$\begin{aligned} \mu _{\tau \tau } + \mu _{\chi \chi } -\beta (\mu ^{2})_{\chi \chi } - \gamma \mu _{\chi \chi \chi \chi }+\frac{\alpha ^2}{4}\mu _{\varsigma \varsigma }+\alpha \mu _{\varsigma \tau } =0, \end{aligned}$$
(1.2)

where \(\alpha \),\(\beta \) and \(\gamma \) are non-zero constants. The Boussinesq (1.2) explains the propagation of gravity waves over the water surface, more specifically, the head-on collision of oblique wave profiles. The Boussinesq (1.2) equation involves two dissipative terms \(\mu _{\chi \chi }\) and \(\mu _{\varsigma \varsigma }\) and also fourth-order derivative term \(\mu _{\chi \chi \chi \chi }\), which represents dispersion effects. Although in Wazwaz (2022) the author has given a recommendable effort to solve (1.2), there is no unified method. The method employed in Wazwaz (2022) cannot be used to construct conservation laws or point symmetries and hence this prompted the utilization of the symmetry approach for the underlying Eq. (1.2).

This paper is planned into three sections. In Sect. 2 we compute courtesy of Lie point symmetry analysis leads to similarity reductions and exact solutions. We compute several waves of physical interest with innovative general wave frequencies and phase shifts via the multiple exp-function approach, which is a generalization of Hirota’s perturbation strategy in Sect. 3. Section 4 deals with conservation laws of with the aid of a variational approach. Finally, in Sect. 5 concluding remarks are given.

2 Lie symmetries analysis and exact solutions of (1.2)

Symmetry analysis (Sebogodi et al. 2023; Podile et al. 2022; Wang and Wazwaz 2022a, b; Wang 2021a, b, c; Wang et al. 2020; Hu et al. 2020; Gwaxa et al. 2023; Yildirim and Yasar 2018) is a powerful tool in the study of differential equations. By analyzing the intrinsic symmetries of equations, researchers can gain valuable insights into the underlying structures and properties of the system being studied. This analysis can help identify invariant solutions, which are solutions that remain unchanged under certain transformations. These invariant solutions often have physical significance and can provide a deeper understanding of the system’s behavior. Additionally, symmetry analysis allows for the reduction of the dimensionality of differential equations. This reduction can simplify the equations and make them more tractable for further analysis or numerical simulations. Not only does symmetry analysis provide insights into the structure and properties of differential equations, but it also helps identify invariant solutions with physical significance. Using the symmetry method, researchers can transform the solutions of simple linear differential equations to find solutions of more complex nonlinear differential equations. Furthermore, symmetry analysis is not limited to differential equations alone, but can also be applied to difference equations. Through symmetry analysis, researchers can find traveling wave solutions of differential equations. In summary, symmetry analysis is a powerful tool in the study of differential equations.

We now compute the point symmetries (Sebogodi et al. 2023; Podile et al. 2022; Wang and Wazwaz 2022a, b; Wang 2021a, b, c; Wang et al. 2020; Hu et al. 2020; Gwaxa et al. 2023; Yildirim and Yasar 2018) of a (2 + 1)-dimensional Boussinesq equation (1.2). The vector field of the form

$$\begin{aligned} \mho= & {} \Lambda ^1 (\tau ,\chi ,\varsigma ,\mu ) \displaystyle \frac{\partial }{\partial \tau } + \Lambda ^2 (\tau ,\chi ,\varsigma ,\mu )\displaystyle \frac{\partial }{\partial \chi } + \Lambda ^3 (\tau ,\chi ,\varsigma ,\mu ) \displaystyle \frac{\partial }{\partial \varsigma }+\Delta (\tau ,\chi ,\varsigma ,\mu ) \displaystyle \frac{\partial }{\partial \mu }. \end{aligned}$$

would generate all the desired Lie point symmetries of (1.2). It should be noted that this would be initiated by applying the fourth prolongation pr\(^{(4)} \mho \) to (1.2). This algorithmic procedure yields an overdetermined system of linear partial differential equations (PDEs). The general solution of the overdetermined system of linear PDEs is given by

$$\begin{aligned}{} & {} \Lambda ^1 (\tau ,\chi ,\varsigma ,\mu )= \digamma _{2}(\tau ,\varsigma ),\\{} & {} \Lambda ^2 (\tau ,\chi ,\varsigma ,\mu )=\digamma _{4}(t,\varsigma )-\chi \digamma _{3}(\tau ,\varsigma ),\\{} & {} \Lambda ^3 (\tau ,\chi ,\varsigma ,\mu )=\digamma _{1}(\tau ,\varsigma ),\\{} & {} \Delta (\tau ,\chi ,\varsigma ,\mu )=\digamma _{3}(\tau ,\varsigma )(2\mu \beta -1), \end{aligned}$$

where \(\digamma _{1},\digamma _{2},\digamma _{3}\) and \(\digamma _{4}\) are arbitrary functions of \(\tau \) and \(\varsigma \). For simplicity we confined the arbitrary functions to quadratic functions. As a results we obtain the 12-dimensional Lie algebra spanned by the following linearly independent operators:

$$\begin{aligned}{} & {} \mho _{1}=\left( 2\,\mu \beta -1 \right) \frac{\partial }{\partial \mu }- \tau \alpha \,\beta \frac{\partial }{\partial \varsigma } -2\, \tau \beta \frac{\partial }{\partial \tau } - \chi \beta \frac{\partial }{\partial \chi }, \\{} & {} \mho _2 = \left( {\alpha }^{2}{\tau }^{2}-4\,\alpha \,\tau \varsigma +4\,{\varsigma }^{2} \right) \frac{\partial }{\partial \varsigma }, \,\,\,\, \mho _3 = \left( 2\varsigma -\,\alpha \,\tau \right) \frac{\partial }{\partial \varsigma },\\{} & {} \mho _4 = \frac{\partial }{\partial \varsigma }, \,\,\,\, \mho _{5} = \left( {\alpha }^{2}{\tau }^{2}-4\,\alpha \,\tau \varsigma +4\,{\varsigma }^{2} \right) \frac{\partial }{\partial \tau },\,\,\,\ \mho _{6} = \left( 2\varsigma -\,\alpha \,\tau \right) \frac{\partial }{\partial \tau },\\{} & {} \mho _7 = \frac{\partial }{\partial \tau },\,\,\,\, \mho _{8} = \left( {\alpha }^{2}{\tau }^{2}-4\,\alpha \,\tau \varsigma +4\,{\varsigma }^{2} \right) \frac{\partial }{\partial \chi },\,\,\,\, \mho _{9} = \left( 2\varsigma -\,\alpha \,\tau \right) \frac{\partial }{\partial \chi },\,\,\,\ \mho _{10} = \frac{\partial }{\partial \chi },\\{} & {} \mho _{11} = \left( 2\,\mu {\alpha }^{2}\beta \,{\tau }^{2}-8\,\mu \alpha \,\beta \,\tau \varsigma +8\,\mu \beta \,{\varsigma }^{2}-{\alpha }^{2}{\tau }^{2}+4\,\alpha \,\tau \varsigma -4\,{\varsigma }^{2} \right) \frac{\partial }{\partial \mu }- \left( 2\,{\alpha }^{2}\beta \,{\tau }^{3}-8\, \alpha \,\beta \,{\tau }^{2}\varsigma +8\,\beta \,\tau {\varsigma }^{2} \right) \frac{\partial }{\partial \tau }\\{} & {} - \left( {\alpha }^{2}\beta \,{\tau }^{2}\chi -4\,\alpha \, \beta \,\tau \chi \varsigma +4\,\beta \,\chi {\varsigma }^{2} \right) \frac{\partial }{\partial \chi }- \left( {\alpha }^{3}\beta \,{\tau }^{3}-4\,{\alpha }^{2}\beta \,{\tau }^{2} \varsigma +4\,\alpha \,\beta \,\tau {\varsigma }^{2} \right) \frac{\partial }{\partial \varsigma },\\{} & {} \mho _{12} = -\left( 2\,\mu \alpha \,\beta \,\tau -4\,\mu \beta \,\varsigma -\alpha \,\tau +2\,\varsigma \right) \frac{\partial }{\partial \mu }+ \left( 2\,\alpha \,\beta \,{\tau }^{2}-4 \,\beta \,\tau \varsigma \right) \frac{\partial }{\partial \tau }+ \left( \alpha \,\beta \,\tau \chi -2\,\beta \,\chi \varsigma \right) \frac{\partial }{\partial \chi }\\{} & {} +\left( {\alpha }^{2}\beta \,{\tau }^{2}-2\,\alpha \,\beta \,\tau \varsigma \right) \frac{\partial }{\partial \varsigma }. \end{aligned}$$

2.1 Symmetry reductions and group invariant solutions (1.2)

To obtain symmetry reduction, one has to solve the associated Lagrange equations

$$\begin{aligned} \frac{d\tau }{\Lambda ^1 (\tau ,\chi ,\varsigma ,\mu ) }= \frac{d\chi }{ \Lambda ^2 (\tau ,\chi ,\varsigma ,\mu )}=\frac{d\varsigma }{\Lambda ^3 (\tau ,\chi ,\varsigma ,\mu )}=\frac{d\mu }{\Delta (\tau ,\chi ,\varsigma ,\mu )}. \end{aligned}$$

We consider the following cases:

Case 1. \(\mho _1\).

The symmetry \(\mho _{1}\) gives rise to the invariants

$$\begin{aligned} \vartheta =\frac{\alpha \tau -2\varsigma }{\alpha },\,\,\varrho =\frac{\chi }{\sqrt{\tau \alpha }},\,\,\,\varOmega =\frac{\mu \alpha \beta \tau -\varsigma }{\beta }. \end{aligned}$$

Considering \(\vartheta \) and \(\varrho \) as the new independent variable and \(\varOmega \) as the new dependent variable, system (1.2) transforms to

$$\begin{aligned} \varrho ^2\alpha ^2\beta \varOmega _{\varrho \varrho }+7\varrho \alpha ^2\varOmega _{\varrho }+4\vartheta \alpha \beta \varOmega _{\varrho \varrho }-4\vartheta \alpha ^2+8\alpha ^2\beta \varOmega -8\beta ^2\varOmega \varOmega _{\varrho \varrho }-8\beta ^2\varOmega ^2_{\varrho }-4\gamma \beta \varOmega _{\varrho \varrho \varrho \varrho }=0, \end{aligned}$$
(2.1)

which is a nonlinear PDE in two independent variables. We now use the Lie point symmetries of (2.1) to reduce it to an ordinary differential equation (ODE). We obtain one Lie point symmetry of (2.1) as follows:

$$\begin{aligned} \varOmega = 2\beta \frac{\partial }{\partial \vartheta } + \alpha \frac{\partial }{\partial \varOmega }, \end{aligned}$$

using the above symmetry, we obtain the following two invariants:

$$\begin{aligned} \zeta =\varrho ,\,\,\,\,\,\phi =\frac{ 2 \beta \varOmega -\alpha \vartheta }{2\beta }, \end{aligned}$$

which give rise to a group-invariant solution \(\phi =\phi (\zeta )\). Using these invariants, equation (2.1) is transformed into the fourth-order nonlinear ODE

$$\begin{aligned} \zeta ^2 \alpha ^2 \phi ''+7\zeta \alpha ^2 \phi '-8\beta \phi '^2-8\beta \phi \phi ''+8\alpha \phi -4\gamma \phi ''''=0, \end{aligned}$$
(2.2)

where \('\)denotes the differentiation with respect to the variable \(\zeta \).

Case 2. \(\mho _2+\mho _5\)

The symmetry \(\mho _{2}+\mho _5\) gives rise to the invariants

$$\begin{aligned} \vartheta =\chi ,\,\,\varrho =\tau -\varsigma ,\,\,\,\varOmega =\mu . \end{aligned}$$

Treating \(\varOmega \) as the new dependent variable and \(\vartheta ,\varrho \) as new independent variables, Eq. (1.2) transforms to

$$\begin{aligned} \varOmega _{\varrho \varrho }+\varOmega _{\vartheta \vartheta }-2\beta \varOmega _{\vartheta \vartheta }-2\beta \varOmega ^2_{\vartheta \vartheta }-\gamma \varOmega _{\vartheta \vartheta \vartheta \vartheta }+\frac{1}{4}\alpha ^2\varOmega _{\varrho \varrho }-\alpha \varOmega _{\varrho \varrho }=0 \end{aligned}$$
(2.3)

which is a nonlinear partial differential equation in two independent variables, whose solution is

$$\begin{aligned} \varOmega (\vartheta ,\varrho )=-\frac{6\gamma C^{2}_{2}}{\beta }\tanh ^2 \left( \vartheta C_{2}+\varrho C_{3}+C_{1}\right) +\frac{1}{8\beta C^{2}_{2}}\bigg (32\gamma C^{4}_{2}+\left( \alpha ^{2}-4\alpha +4\right) C^{2}_{3}+4C^{2}_{2}\bigg ). \end{aligned}$$
(2.4)

Where \(C_1,C_{2}\) and \(C_{3}\) are arbitrary parameters. Reverting back to our original variables, the topological soliton solution of (1.2) takes the form

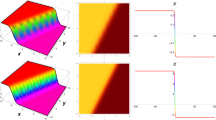
$$\begin{aligned} \mu (\tau ,\chi ,\varsigma )=-\frac{6\gamma C^{2}_{2}}{\beta }\tanh ^2 \left( C_{2}\chi +C_{3}(\tau -\varsigma )+C_{1}\right) +\frac{1}{8\beta C^{2}_{2}}\bigg (32\gamma C^{4}_{2}+\left( \alpha ^{2}-4\alpha +4\right) C^{2}_{3}+4C^{2}_{2}\bigg ). \end{aligned}$$
(2.5)

A profile of the solution (2.5) is given in Fig. 1. below.

Fig. 1
figure 1

Evolution of solitary wave solution (2.5), with the help of suitable choices of parameters \(\beta =\frac{1}{16}\), \(\alpha =2\), \(C_{2}=C_{3}=1\)

Full size image

Case 3. \(\mho _{2}+\mho _5+\mho _8\)

Symmetry \(\mho _{2}+\mho _5+\mho _8\) gives rise to the invariants

$$\begin{aligned} \vartheta =\varsigma -\chi ,\,\,\varrho =\tau -\chi ,\,\,\,\varOmega =\mu . \end{aligned}$$
(2.6)

Considering \(\vartheta \) and \(\varrho \) as the new independent variable and \(\varOmega \) as the new dependent variable, Eq. (1.2) transforms to

$$\begin{aligned}{} & {} 2 \varOmega _{\varrho \varrho }+\varOmega _{\vartheta \vartheta }+2\varOmega _{\varrho \vartheta }-2\beta \varOmega \varOmega _{\vartheta \vartheta }-4\beta \varOmega \varOmega _{\varrho \vartheta }-2\beta \varOmega \varOmega _{\varrho \varrho }-2\beta \varOmega ^{2}_{\vartheta }-4\beta \varOmega _{\vartheta }\varOmega _{\varrho }-2\beta \varOmega _{\varrho }-\gamma \theta _{\vartheta \vartheta \vartheta \vartheta }\nonumber \\{} & {} -4\gamma \varOmega _{\varrho \vartheta \vartheta \vartheta }-6\gamma \varOmega _{\varrho \varrho \vartheta \vartheta }-4\gamma \varOmega _{\vartheta \varrho \varrho \varrho }-\gamma \varOmega _{\varrho \varrho \varrho \varrho }+\frac{1}{4}\alpha \varOmega _{\vartheta \vartheta }+\alpha \varOmega _{\varrho \vartheta }=0, \end{aligned}$$
(2.7)

which gives the solution of the form

$$\begin{aligned} \varOmega (\vartheta ,\varrho )= & {} -\frac{6\gamma }{\beta }\left( C^2_{2}+2C_{2}C_{3}+C^2_{3}\right) ^2\tanh ^2(C_{2}\vartheta +C_{3}\varrho +C_{1})\nonumber \\{} & {} +\frac{1}{8\beta \left( C^2_{2}+2C_{2}C_{3}+C^2_{3}\right) }\bigg (32\gamma C^4_{2}+128\gamma C^3_{2}C_{3}+192\gamma C^2_{2}C^2_{3}+128\gamma C_{2}C^2_{3}\nonumber \\ {}{} & {} +32 \gamma C^4_{3}+\alpha ^2 C^2_{2}+4\alpha C_{2}C_{3}+4C^2_{2}+8C_{2}C_{3}+8C^2_{3}\bigg ). \end{aligned}$$
(2.8)

Using the invariants (2.6) together with Eq. (2.7), we obtain a topological soliton solution of (1.2) as

$$\begin{aligned} \mu (\tau ,\chi ,\varsigma )= & {} -\frac{1}{8\beta \left( C^2_{2}+2C_{2}C_{3}+C^2_{3}\right) }\bigg (48C^4_{2}\gamma \tanh ^2(C_{2}(\varsigma -\chi )+C_{3}(\tau -\chi )+C_{1})\nonumber \\ {}{} & {} -192C_{2}C^2_{3}\gamma \tanh ^2(C_{2}(\varsigma -\chi )+C_{3}(\tau -\chi )+C_{1})-32C^4_{2}\gamma -128C^3_{2}C_{3}\gamma \nonumber \\ {}{} & {} +288C^2_{2}C^2_{3}\gamma \tanh ^2(C_{2}(\varsigma -\chi )+C_{3}(\tau -\chi )+C_{1})-192\gamma C^2_{2}C^3_{3}-\alpha ^2 C^2_{2}\nonumber \\ {}{} & {} +48C^4_{3}\gamma \tanh ^2(C_{2}(\varsigma -\chi )+C_{3}(\tau -\chi )+C_{1})-192C^2_{2}C^2_{3}\gamma -128C_{2}C^2_{3}\gamma \nonumber \\{} & {} -32C^4_{3}\gamma -4C_{3}C_{2}\alpha -4C^2_{2}-8C_{2}C_{3}-8C^2_{3}\bigg ). \end{aligned}$$
(2.9)

Case 4. Also considering the combinations \(\mho _{4},\mho _7\) and \(\mho _{10}\), we obtain the following three invariants

$$\begin{aligned} \vartheta =\tau -\varsigma ,\,\,\varrho =\chi -\varsigma ,\,\,\,\varOmega =\mu . \end{aligned}$$
(2.10)

By treating \(\varOmega \) as the new dependent variable and \(\vartheta \) and \(\varrho \) as the new independent variables, (1.2) transforms to

$$\begin{aligned}{} & {} \varOmega _{\vartheta \vartheta }+\varOmega _{\varrho \varrho }-2\beta \varOmega \varOmega _{\varrho \varrho }-2\beta \varOmega ^2_{\varrho \varrho }-\gamma \varOmega _{\varrho \varrho \varrho \varrho }+\frac{1}{4}\alpha ^2\varOmega _{\vartheta \vartheta }+\frac{1}{2}\alpha ^2\varOmega _{\varrho \vartheta }+\frac{1}{4}\alpha ^2\varOmega _{\varrho \varrho }-\alpha \varOmega _{\vartheta \vartheta }\nonumber \\ {}{} & {} -\alpha \varOmega _{\varrho \vartheta }=0, \end{aligned}$$
(2.11)

which is a nonlinear PDE in two independent variables and its solution is given by

$$\begin{aligned} \varOmega (\vartheta ,\varrho )= & {} \frac{6\gamma C^2_{1}C^2_{4} \text {cn}^2 (C_{3}\vartheta +C_{4}\varrho +C_{2}|C_{1})}{\beta }-\frac{1}{8\beta C^2_{4}}\bigg (32\gamma C^{2}_{1}C^4_{4}-16\gamma C^4_{4}-C^2_{3}\alpha ^2\nonumber \\ {}{} & {} -2C_{4}C_{3}\alpha ^2-C^2_{4}\alpha ^2 +4C^2_{3}\alpha +4C_{4}C_{3}\alpha -4C^2_{3}-4C^2_{4}\bigg ). \end{aligned}$$
(2.12)

Now we revert back to our original variables, the cnoidal wave solution of (1.2) takes the form

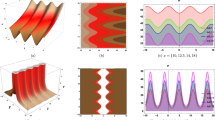
$$\begin{aligned} \mu (\tau ,\chi ,\varsigma )= & {} \frac{1}{8\beta C^2_{4}}\bigg (48\gamma C^2_{1}C^4_{4}\text {cn}^2(C_{3}(\tau -\varsigma )+C_{4}(\chi -\varsigma )+C_{2}|C_{1})-32\gamma C^{2}_{1}C^4_{4}\nonumber \\ {}{} & {} +16\gamma C^4_{4}+C^2_{3}\alpha ^2+2C_{4}C_{3}\alpha ^2+C^2_{4}\alpha ^2 -4C^2_{3}\alpha -4C_{4}C_{3}\alpha +4C^2_{3}+4C^2_{4}\bigg ). \end{aligned}$$
(2.13)

A profile of the solution (2.13) is given in Fig. 2.

Fig. 2
figure 2

Evolution of periodic wave solution (2.13), with the help of suitable choices of parameters \(\beta =\frac{1}{8}\), \(\alpha =2\), \(\gamma =\frac{9}{64}\), \(C_{1}=\frac{1}{3}\),\(C_{2}=\frac{1}{2}\),\(C_{3}=\frac{1}{4}\),\(C_{4}=\frac{2}{4}\)g

Full size image

It should be pointed out that in the aforementioned technique, one could obtain more group invariants solutions of the generalized (2 + 1)-dimensional Boussinesq equation by using the other symmetries. In many applications, group invariant solutions describe the limiting behaviour of physical problems that are extremely far away from their initial or boundary conditions.

3 Multiple exp-function method

For exact multiple wave solutions of nonlinear partial differential equations, a multiple exp-function approach was suggested in Ma et al. (2010) The approach offers a straightforward and systematic solution process that generalizes Hirota’s perturbation technique. The assumption is made that polynomials of exponential functions can be used to define the multisoliton solutions. A generalization of Hirota’s perturbation system is what the multiple expfunction algorithm essentially is. Generic phase shifts and wave frequencies are also included in the following solutions. The crucial steps of the multiple exp-function method can be summarized as follows (Adem 2016; Ma et al. 2010; Sebogodi et al. 2023; Podile et al. 2022; Yildirim and Yasar 2017):

Step 1 Let us consider the following (1 + 1)-dimensional NLEE:

$$\begin{aligned} P(\chi , \tau , \mu _\chi , \mu _\tau ,\cdots \,) = 0. \end{aligned}$$
(3.1)

Step 2 Suppose the solution of above NLEE can be expressed as

$$\begin{aligned}{} & {} \mu (\tau ,\chi )=\frac{p(\eta _1, \eta _2,\cdots ,\eta _n)}{q(\eta _1, \eta _2,\cdots ,\eta _n)}, \quad p=\sum ^{n}_{r,s=1}\sum ^{M}_{i,j=0} p_{rs,ij} \eta ^{i}_{r}\eta ^{j}_{s},\nonumber \\{} & {} q=\sum ^{n}_{r,s=1}\sum ^{N}_{i,j=0}q_{rs,ij} \eta ^{i}_{r}\eta ^{j}_{s}, \end{aligned}$$
(3.2)

in which \(p_{rs,ij}\) and \(q_{rs,ij}\) are unknowns to be determined and

$$\begin{aligned} \eta _{i} = c_ie^{\xi _i},\quad \xi _i = k_i \chi - \omega _i \tau ,\quad 1 \leqslant i \leqslant n, \end{aligned}$$
(3.3)

Step 3 Substituting (3.2) and its derivatives into (3.1) yields the following transformed equation

$$\begin{aligned} Q(\chi ,\tau ,\eta _1, \eta _2,\cdots ,\eta _n)=0. \end{aligned}$$
(3.4)

Step 4 By setting the numerator of the function \(Q(\chi ,\tau ,\eta _1, \eta _2,\cdots ,\eta _n)\) to zero, we will reach an algebraic system which its solution yields the multiple wave solution of (3.1) as

$$\begin{aligned} \mu (\tau ,\chi )=\frac{p(c_1 e^{k_1 \chi - \omega _1 \tau },\cdots ,c_n e^{k_n \chi - \omega _n \tau })}{q(c_1 e^{k_1 \chi - \omega _1 \tau },\cdots ,c_n e^{k_n \chi - \omega _n \tau })}. \end{aligned}$$
(3.5)

3.1 Application of the multiple exp-function algorithm to the generalized (2 + 1)-dimensional Boussinesq equation (1.2)

In this subsection, we will employ the multiple exp-function method to obtain one- and two-wave solutions of (1.2). We use the potential \(\mu =\nu _\chi \) so that Eq. (1.2) takes this form

$$\begin{aligned} \nu _{\chi \tau \tau }+\nu _{\chi \chi \chi }-2 \beta \nu _{x} \nu _{\chi \chi \chi }-2 \beta \nu _{\chi \chi }^{2}-\gamma \nu _{\chi \chi \chi \chi \chi }+\frac{1}{4} \alpha ^{2} \nu _{\chi \varsigma \varsigma }+\alpha \nu _{\chi \varsigma \tau }=0. \end{aligned}$$
(3.6)

It should be noted that the solutions that will be appear in the next two subsections are soliton type solutions.

3.1.1 One-wave solution of (1.2)

We start with one-wave function

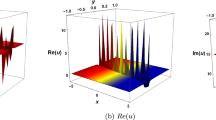
$$\begin{aligned} \mu (\tau ,\chi ,\varsigma )=\nu _\chi =\frac{A_1 k_1}{2 \cosh \left( k_1 \chi +l_1 \varsigma -\tau \omega _1\right) +2}, \end{aligned}$$
(3.7)

where \(A_{1}\) is a constant (Fig. 3). By applying the multiple exp-function algorithm, we obtain with the aid of Maple:

$$\begin{aligned} A_{1}=\frac{6\gamma k_{1}}{\beta },\,\,\, \omega _{1}=\frac{1}{2}\theta , \end{aligned}$$
(3.8)

where \(\theta \) is any solution \(-4\,\gamma \,{k_{{1}}}^{4}+{\alpha }^{2}{l_{{1}}}^{2}-2\,{ \theta }\, \alpha \,l_{{1}}+{{ \theta }}^{2}+4\,{k_{{1}}}^{2}=0\).

Fig. 3
figure 3

Evolution of the one-wave solution (3.7)

Full size image

3.1.2 Two-wave solution of (1.2)

We consider two-wave solutions based on the statement in Step 2, we assume that Eq. (1.2) has the rational function of two-wave solutions as shown in the following form:

$$\begin{aligned} \mu (\tau ,\chi ,\varsigma )=\nu _\chi =\frac{P}{Q} \end{aligned}$$
(3.9)

with P and Q being defined by

$$\begin{aligned} P= & {} 2 \left( \sinh \left( k_1 \chi +k_2 \chi +l_1 \varsigma +l_2 \varsigma +\tau \omega _1+\tau \omega _2\right) +\cosh \left( k_1 \chi +k_2 \chi +l_1 \varsigma +l_2 \varsigma +\tau \omega _1+\tau \omega _2\right) \right) \nonumber \\{} & {} \bigg (k_1^2 \big (A_{1,2} \left( \sinh \left( k_2 \chi +l_2 \varsigma -\tau \omega _2\right) +\cosh \left( k_2 \chi +l_2 \varsigma -\tau \omega _2\right) +1\right) -\sinh \left( k_2 \chi +l_2 \varsigma -\tau \omega _2\right) \nonumber \\{} & {} +\cosh \left( k_2 \chi +l_2 \varsigma -\tau \omega _2\right) +1\big )+k_2^2 \big (A_{1,2} \left( \sinh \left( k_1 \chi +l_1 \varsigma -\tau \omega _1\right) +\cosh \left( k_1 \chi +l_1 \varsigma -\tau \omega _1\right) +1\right) \nonumber \\{} & {} -\sinh \left( k_1 \chi +l_1 \varsigma -\tau \omega _1\right) +\cosh \left( k_1 \chi +l_1 \varsigma -\tau \omega _1\right) +1\big )+2 k_2 k_1 \left( A_{1,2}-1\right) \bigg )\nonumber \\ Q= & {} \bigg (A_{1,2} \left( \sinh \left( k_1 \chi +k_2 \chi +\left( l_1+l_2\right) y\right) +\cosh \left( k_1 \chi +k_2 \chi +\left( l_1+l_2\right) \varsigma \right) \right) +\sinh \left( k_2 \chi +l_2 \varsigma +\tau \omega _1\right) \nonumber \\{} & {} +\sinh \left( k_1 \chi +l_1 \varsigma +\tau \omega _2\right) +\cosh \left( k_2 \chi +l_2 \varsigma +\tau \omega _1\right) +\cosh \left( k_1 \chi +l_1 \varsigma +\tau \omega _2\right) \nonumber \\{} & {} +\sinh \left( \tau \left( \omega _1+\omega _2\right) \right) +\cosh \left( \tau \left( \omega _1+\omega _2\right) \right) \bigg ){}^2 \end{aligned}$$
(3.10)

where

$$\begin{aligned} \lambda _{i}=k_{{i}}\chi +l_{i}\varsigma -\omega _{{i}}\tau ,\quad i=1,2. \end{aligned}$$
(3.11)

Applying the multiple exp-function algorithm, with the aid of Maple leads to the following case:

$$\begin{aligned}{} & {} \beta ={\frac{3({\alpha }^{2}{l_{{2}}}^{2}-4\,\alpha \,l_{{2}}\omega _ {{2}}+4\,{k_{{2}}}^{2}+4\,{\omega _{{2}}}^{2})}{4{k_{{2}}}^{4}}},\\{} & {} \gamma ={\frac{({\alpha }^{2}{l_{{2}}}^{2}-4\,\alpha \,l_{{2}}\omega _{{2}}+4\,{k_{{2}}}^{2}+4\,{\omega _{{2}}}^{2})}{4{k_{{2}}}^{4}}},\\{} & {} \omega _{1}=\frac{\sigma }{2k^2_{2}},\\{} & {} A_{{12}}=\frac{\mu +\alpha \,k_{{2}}l_{{2}} \sigma +\tau -2\,k_ {{2}}\omega _{{2}} \sigma }{\xi +\alpha \,k_{{2}}l_{{2}} \sigma +\phi -2\,k_ {{2}}\omega _{{2}} \sigma },\\{} & {} L_{1}=2\,{\alpha }^{2}{k_{{1}}}^{3}{l_{{2}}}^{2}-3\,{\alpha }^{2}{k_{{1}}}^{2} k_{{2}}{l_{{2}}}^{2}+2\,{\alpha }^{2}k_{{1}}{k_{{2}}}^{2}{l_{{2}}}^{2}- {\alpha }^{2}{k_{{2}}}^{3}l_{{1}}l_{{2}}-8\,\alpha \,{k_{{1}}}^{3}l_{{2} }\omega _{{2}}\\{} & {} +12\,\alpha \,{k_{{1}}}^{2}k_{{2}}l_{{2}}\omega _{{2}}-8\, \alpha \,k_{{1}}{k_{{2}}}^{2}l_{{2}}\omega _{{2}}+2\,\alpha \,{k_{{2}}}^{ 3}l_{{1}}\omega _{{2}},\\{} & {} L_{2}=8\,{k_{{1}}}^{3}{k_{{2}}}^{2}+8\,{k_{{1}}}^{3}{\omega _{{2}}}^{2}-12\,{ k_{{1}}}^{2}{k_{{2}}}^{3}-12\,{k_{{1}}}^{2}k_{{2}}{\omega _{{2}}}^{2}+4 \,k_{{1}}{k_{{2}}}^{4}+8\,k_{{1}}{k_{{2}}}^{2}{\omega _{{2}}}^{2},\nonumber \\{} & {} \xi =2\,{\alpha }^{2}{k_{{1}}}^{3}{l_{{2}}}^{2}+3\,{\alpha }^{2}{k_{{1}}}^{2} k_{{2}}{l_{{2}}}^{2}+2\,{\alpha }^{2}k_{{1}}{k_{{2}}}^{2}{l_{{2}}}^{2}- {\alpha }^{2}{k_{{2}}}^{3}l_{{1}}l_{{2}}-8\,\alpha \,{k_{{1}}}^{3}l_{{2} }\omega _{{2}}\\{} & {} -12\,\alpha \,{k_{{1}}}^{2}k_{{2}}l_{{2}}\omega _{{2}}-8\, \alpha \,k_{{1}}{k_{{2}}}^{2}l_{{2}}\omega _{{2}}+2\,\alpha \,{k_{{2}}}^{ 3}l_{{1}}\omega _{{2}},\\{} & {} \phi =8\,{k_{{1}}}^{3}{k_{{2}}}^{2}+8\,{k_{{1}}}^{3}{\omega _{{2}}}^{2}+12\,{ k_{{1}}}^{2}{k_{{2}}}^{3}+12\,{k_{{1}}}^{2}k_{{2}}{\omega _{{2}}}^{2}+4 \,k_{{1}}{k_{{2}}}^{4}+8\,k_{{1}}{k_{{2}}}^{2}{\omega _{{2}}}^{2}, \end{aligned}$$

where \(\sigma \) is any solution of \(-{\alpha }^{2}{k_{{1}}}^{4}{l_{{2}}}^{2}+{\alpha }^{2}{k_{{2}}}^{4}{l_{{ 1}}}^{2}+4\,\alpha \,{k_{{1}}}^{4}l_{{2}}\omega _{{2}}-4\,{k_{{1}}}^{4}{ k_{{2}}}^{2}-4\,{k_{{1}}}^{4}{\omega _{{2}}}^{2}+4\,{k_{{1}}}^{2}{k_{{2 }}}^{4}-2\,{ \sigma }\,\alpha \,{k_{{2}}}^{2}l_{{1}}+{{ \sigma }}^{2}=0. \)

4 Conservation laws (1.2)

Conservation laws (Sebogodi et al. 2023; Podile et al. 2022; Gwaxa et al. 2023) are fundamentally important because they give physical, conserved values for every solution \(\mu (\tau ,\chi ,\varsigma )\) and preserved standards that are helpful for solving problems and verifying the accuracy of numerical solution techniques. Indeed conservation laws of partial differential equations are essential in understanding the behavior and properties of physical systems. By studying the conservation laws, we can determine how quantities such as mass, energy, momentum, and charge are conserved or transformed within a system. These laws provide valuable insights into the dynamics and evolution of various phenomena in fields such as mathematics, physics, chemistry, and biology. Conservation laws of partial differential equations are fundamental principles that govern the behavior and evolution of physical systems. They provide a framework for understanding how certain quantities, such as mass, energy, momentum, and charge, are conserved or transformed within a system. Furthermore, the generation of conservation laws has practical applications in fields such as fluid dynamics, solid mechanics, electromagnetism, and thermodynamics. By studying conservation laws, researchers can gain valuable insights into the properties and behavior of solutions to nonlinear partial differential equations. Additionally, the existence of a large number of conservation laws in a system of partial differential equations is a strong indication of its integrability. In summary, conservation laws play a crucial role in the study of differential equations as they describe physical conserved quantities and provide insights into the behavior and properties of solutions to partial differential equations. The knowledge of conservation laws for systems of partial differential equations allows one to gain useful information on the properties of the solutions. For example, conservations laws can help in determining the stability and uniqueness of solutions, as well as providing a foundation for developing numerical methods to approximate thesesolutions. The study of conservation laws of partial differential equations is an essential step in understanding the behavior and properties of physical systems. It allows us to determine how quantities such as mass, energy, momentum, and charge are conserved or transformed within a system, providing valuable insights into the dynamics and evolution of various phenomena in fields such as mathematics, physics, chemistry, and biology.

A local conservation law of (1.2) is a continuity equation

$$\begin{aligned} D_{\tau }T^{\tau }+D_{\chi }T^{\chi }+D_{\varsigma }T^{\varsigma }=0 \end{aligned}$$
(4.1)

holding for all solutions of (1.2), where \(T^{\tau }\) is the conserved density and \((T^{\chi },T^{\varsigma })\) is the spatial flux.

In this section we construct conservation laws (Sebogodi et al. 2023; Podile et al. 2022; Gwaxa et al. 2023) of the (2 + 1)-dimensional Boussinesq equation (1.2). Consider a differential equation \(E=0\), and \({\Lambda }\) being the characteristic function. \({\Lambda E}\) is divergent if and only if \(E_\mu (QE) = 0\), where \(E_\mu \) is the Euler–Lagrange operator. Without loss of generality, we can now state the following theorems.

Theorem 1

The (2 + 1)-dimensional Boussinesq equation (1.2) admits a characteristic function of the form:

$$\begin{aligned} {\Lambda }= & {} H_{1}(2\varsigma -\alpha \tau )\tau \chi +H_{2}(2\varsigma -\alpha \tau )\chi +H_{4}(2\varsigma -\alpha \tau )\tau +H_{3}(2\varsigma -\alpha \tau ), \end{aligned}$$
(4.2)

where \(H_{1}(2\varsigma -\alpha \tau ),....,H_{4}(2\varsigma -\alpha \tau )\) are arbitrary functions of \(2\varsigma -\alpha \tau \).

The proof of the above theorem is a straightforward but lengthy computation can be carried out from \(\varepsilon _\mu ( \Lambda E)=0\). The expansion of this equation leads to an over-determined system of linear differential equations in the unknown characteristic function \(\Lambda \). Solving these equations, one obtains the characteristic function (4.2).

Theorem 2

The (2 + 1)-dimensional Boussinesq equation (1.2) strictly admits an infinite set of conservation laws corresponding to the above characteristic function (4.2), namely:

$$\begin{aligned} T_{1}^\tau= & {} \bigg (\left( \frac{\alpha \mu _{\varsigma }}{2}+\mu _{\tau }\right) \tau -\mu \bigg )H_{1}(2\varsigma -\alpha \tau )\chi ,\\ T_{1}^{\chi }= & {} \big (\beta \mu ^2-(2\beta \chi \mu _{\chi }+1)\mu +(\mu _{\chi }-\gamma \mu _{\chi \chi \chi })\chi +\gamma \mu _{\chi \chi }\big )H_{1}(2\varsigma -\alpha \tau )\tau ,\\ T_{1}^\varsigma= & {} -\frac{1}{2}H_{1}(2\varsigma -\alpha \tau )\alpha \chi \big (\mu -\frac{1}{2}\alpha \tau \mu _{\varsigma }-\tau \mu _{\tau }\big ); \\ T_{2}^\tau= & {} \frac{1}{2}H_{2}(2\varsigma -\alpha \tau )\chi \big (\alpha \mu _{\varsigma }+2\mu _{\tau }\big ),\\ T_{2}^{\chi }= & {} H_{2}(2\varsigma -\alpha \tau )\big (\beta \mu ^2-(2\beta \chi \mu _{\chi }+1)\mu +(\mu _{\chi }-\gamma \mu _{\chi \chi \chi })\chi +\gamma \mu _{\chi \chi }\big ),\\ T_{2}^\varsigma= & {} \frac{1}{2} H_{2}(2\varsigma -\alpha \tau )\alpha \chi \big (2\mu _{\tau }+\alpha \mu _{\varsigma }\big );\\ \\ T_{3}^\tau= & {} \frac{1}{2}H_{3}(2\varsigma -\alpha \tau )\big (2\mu _{\tau }+\alpha \mu _{\varsigma }\big ),\\ T_{3}^{\chi }= & {} H_{3}(2\varsigma -\alpha \tau )\big (\mu _{\chi }-2\beta \mu \mu _{\chi }-\gamma \mu _{\chi \chi \chi }\big ),\\ T_{3}^\varsigma= & {} \frac{1}{4}\alpha H_{3}(2\varsigma -\alpha \tau )\big (2\mu _{\tau }+\alpha \mu _{\varsigma }\big );\\ \\ T_{4}^\tau= & {} H_{4}(2\varsigma -\alpha \tau )\bigg (\big (\frac{1}{2}\alpha \mu _{\varsigma }+\mu _{\tau }\big )\tau -\mu \bigg ),\\ T_{4}^{\chi }= & {} H_{4}(2\varsigma -\alpha \tau )\big (\mu _{\chi }-2\beta \mu \mu _{\chi }-\gamma \mu _{\chi \chi \chi }\big ),\\ T_{4}^\varsigma= & {} \frac{1}{2} \alpha H_{4}(2\varsigma -\alpha \tau )\big (\frac{1}{2}\alpha \tau \mu _{\varsigma }+\tau \mu _{\tau }-\mu \big ). \end{aligned}$$

The proof of Theorem 2 is straightforward but long. It consists of applying the divergence equation \(\partial _\tau T^\tau +\partial _\chi T^\chi +\partial _\varsigma T^\varsigma =0\), which vanishes for all solutions of the (2 + 1)-dimensional Boussinesq equation (1.2).

We consider the physical implications and justifications that follow from conserved vectors, or conservation laws. There are conservation laws in fundamental branches of physics, as well as in its applications and related fields. Physical laws like the conservation of energy, momentum, and mass are essentially expressed mathematically. Conservation laws (Sebogodi et al. 2023; Podile et al. 2022) preserve commanding physical information about the complicated processes of non-linear systems. For the (2 + 1)-dimensional Boussinesq equation, a family of arbitrarily infintely many conservation laws can be obtained due to the existence of arbitrary functions in the multiplier.

5 Concluding remarks

We constrained the arbitrary functions in the infinitesimal generators to take the form of quadratic functions, which resulted in symmetry reductions and group invariant solutions for the (2 + 1)-dimensional Boussinesq equation. In certain cases, the group invariant solutions were of the of a topological soliton type. In order to find one-wave and two-wave solutions, we have used the multiple exp-function approach resulting in further soliton type solutions. In addition, we used the multiplier approach to construct the conservation laws for the (2 + 1)-dimensional Boussinesq equation. The exact solutions can be used as yardsticks against the numerical simulations in theoretical physics and fluid mechanics. The conserved vectors obtained here can be used to construct new solutions and this will be reported elsewhere.