Electromagnetically induced grating in double quantum dot system

Abstract

Electromagnetically induced grating (EIG) in the ladder-plus-Y double quantum dot system is modeled and the diffraction grating properties are explored in this structure. A high transmission function is obtained under the high pump field. This function is reduced under increasing the probe field due to the Kerr effect. The phase of this function depends on pumping. It is shown that the application of another two fields from the wetting layer (WL)-quantum dot (QD) type is more efficient in obtaining very high diffraction intensity. So, EIG with high diffraction intensity is obtained under a four-field application. Note that, WL-QD field effect is not studied earlier. Neglecting the WL effect reduces the transmission by five times. The diffraction intensity of this system is six times higher than that obtained from a single QD structure.

Appendices

Appendix 1: Ladder-plus-Y type DQD structure

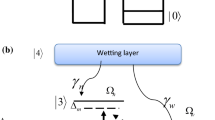
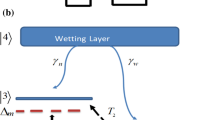
The ladder-plus-Y DQD system used in this work, see Fig. 1, has two subsystems: the first one is |0〉, |2〉 and |4〉 subbands, which forms a ladder-type subsystem with the $\left| 0 \right\rangle \to \left| 2 \right\rangle$ transition ($\hbar w_{02}$ energy) that was driven by a weak probe field $E_{k}$ (frequency $w_{k}$) with Rabi frequency ($\varOmega_{k} = E_{k} \mu_{02} /\hbar$). Also, we have the $\left| 2 \right\rangle \to \left| 4 \right\rangle$ transition ($\hbar w_{24}$ energy) due to the coupling field $E_{w}$, with Rabi frequency ($\varOmega_{w} = E_{w} \mu_{24} /\hbar$) which gives QD-WL coupling. The second subsystem contains |0〉, |1〉, |2〉, |3〉 and |4〉 subbands, which form a Y-type subsystem with the three tunneling component $T_{0}$, $T_{1}$ and $T_{2}$ between $\left| 0 \right\rangle \to \left| 1 \right\rangle$, $\left| 1 \right\rangle \to \left| 2 \right\rangle$, and $\left| 2 \right\rangle \to \left| 3 \right\rangle$ transitions. Also, we have the $\left| 1 \right\rangle \to \left| 3 \right\rangle$ transition ($\hbar w_{13}$ energy) due to the probe field $E_{m}$ with Rabi frequency ($\Omega _{m}$). There is another transition coupling between QD-WL which is the $\left| 3 \right\rangle \to \left| 4 \right\rangle$ transitions ($\hbar w_{34}$ energy) due to the strong coupling field $E_{n}$ with Rabi frequency ($\Omega _{n} = E_{n} \mu_{34} /\hbar$).

Appendix 2: The Hamiltonian of the ladder-plus-Y DQD system

The dynamical equation of the density matrix for the atomic systems can be written as (Kazarinov et al. 1982),

$$i\hbar \rho^{ \cdot } = \left[ {H_{0} ,\rho } \right] + \left[ {H_{\text{int}} ,\rho } \right] + \left[ {H_{\text{relax}} ,\rho } \right]$$

(9)

$\rho$ is the density matrix operator and $(\rho^{ \cdot } = d\rho /dt)$. For the ladder-plus-Y configuration in Fig. 1, the unperturbed Hamiltonian $H_{0}$ is diagonal in $\left| i \right\rangle \,,\,\,(i = 0,\,\,1,\,2,\,\,3,\,\,4)$ states and results in $w_{i}$ frequency which is the central transition frequency, i.e.

$$H_{0} = \hbar w_{0} \left| 0 \right\rangle \left\langle 0 \right| + \hbar w_{1} \left| 1 \right\rangle \left\langle 1 \right| + \hbar w_{2} \left| 2 \right\rangle \left\langle 2 \right| + \hbar w_{3} \left| 3 \right\rangle \left\langle 3 \right| + \hbar w_{4} \left| 4 \right\rangle \left\langle 4 \right|$$

(10)

In Eq. (9), $H_{relax}$ is the relaxation Hamiltonian which takes into account the relaxations that result from scattering processes. They are represented by $\gamma_{r} ,(r = k,m,w,n,0,2)$ where $\gamma_{k} ,\gamma_{m}$ are the relaxation rates from $\left| 2 \right\rangle$ to $\left| 0 \right\rangle$ and $\left| 3 \right\rangle$ to $\left| 1 \right\rangle$, $\gamma_{w} ,\gamma_{n}$ are from WL to states $\left| 2 \right\rangle$ and $\left\langle 3 \right|$, while $\gamma_{0} ,\gamma_{2}$ are from $\left| 1 \right\rangle$ to $\left| 0 \right\rangle$ and $\left| 3 \right\rangle$ to $\left| 2 \right\rangle$, respectively. Its dynamical equation is written as follows (Kazarinov et al. 1982),

$$i\hbar \rho_{ij}^{ \cdot } = \left[ {H_{relax} ,\rho } \right]_{ij} = \gamma_{r} (\rho_{ij} - \rho_{ij}^{(0)} )$$

(11)

with $\rho_{ij}^{(0)} ( = \rho_{ij}^{(0)} \delta_{ij} )$ is refer to the initial distribution. Note that i and j refer to the states $\,(0,\,\,1,\,2,\,\,3,\,\,4)$.

Appendix 3: Formulation of WL-QD transition

In addition to the interdot transitions, WL-QD transitions between QD subbands and a quasi-continuum WL state at higher energy are considered. These transitions are principal in the QD simulation. In the WL, the in-plane wavefunction can be represented by plane waves multiplied by the state due to the confinement comes from the barrier of finite height in the perpendicular direction. For WL-QD transitions, orthogonality between WL-QD states is required. This situation may represent the orthogonalized plane wave (OPW) (Mandel and Wolf 1995). In the QD structure, the wave function is,

$$\mathop \varphi \nolimits_{QD} (\vec{r}) = \mathop \varphi \nolimits_{QD} (\vec{\rho })\zeta (\vec{z})u(\vec{r})$$

(12)

where u (r) is the periodic Bloch function. The in-plane component in the QD is described by the Bessel function of the first kind J_m (pρ) (Kim and Chuang 2006),

$$\mathop \varphi \nolimits_{QD} (\vec{\rho }) = \mathop C\nolimits_{nm} \mathop J\nolimits_{m} (p\vec{\rho })$$

(13)

where C_nm is the normalization constant, p is a constant that determined from the boundary conditions at the interface between the quantum disk and the surrounding material. In the WL, the in-plane wavefunction is described by the OPWs which are constructed from WL wave functions (plane waves) in the absence of QDs. OPW is defined as (Al-Ameri et al. 2019),

$$\left| {\mathop \psi \nolimits_{WL} } \right\rangle = \frac{1}{{\mathop N\nolimits_{WL} }}\quad \left[ {\left| {\mathop \varphi \nolimits_{WL} } \right\rangle - \sum\limits_{\ell } {\left| {\mathop \varphi \nolimits_{QD}^{\ell } } \right\rangle \left\langle {\mathop \varphi \nolimits_{QD}^{\ell } } \right.\left| {\mathop \varphi \nolimits_{WL} } \right\rangle } } \right]$$

(14)

where the index $\ell$ refers to the QD state. $\mathop \varphi \nolimits_{WL} (\vec{\rho })$ is the in-plane (x–y plane) quantum well WL wave function defined by (Asada et al. 1984),

$$\mathop \varphi \nolimits_{WL} (\vec{\rho }) = A_{{WL_{\rho } }} \exp (i\vec{k}_{\rho } .\vec{\rho })$$

(15)

$\vec{k}_{\rho }$ is the in-plan WL wave vector and $A_{{WL_{\rho } }}$ is the in-plane WL normalization constant. The normalization coefficient in Eq. (14) is defined as (Al-Ameri et al. 2019)

$$\mathop N\nolimits_{WL} = \sqrt {1 - \mathop {\left| {\sum\limits_{\ell } {\left\langle {{\mathop \varphi \nolimits_{QD}^{\ell } }} \mathrel{\left | {\vphantom {{\mathop \varphi \nolimits_{QD}^{\ell } } {\mathop \varphi \nolimits_{WL} }}} \right. \kern-0pt} {{\mathop \varphi \nolimits_{WL} }} \right\rangle } } \right|}\nolimits^{2} } .$$

(16)

Appendix 4: Single QD system

Taking the right QD, only, as a single QD system. In this case, only $\left| 0 \right\rangle ,\,\,\left| 2 \right\rangle ,\,\,\left| 4 \right\rangle$ states are considered in the simulation, see Fig. 14. Then, the system in Eq. (4) is reduced from $5 \times 5$ into $3 \times 3$ matrix. The dynamical equations for the DQD system, in Eq. (5), are reduced into six equations, for the single QD system. They are:

$$\rho_{00}^{ \cdot } = (\gamma_{k} \rho_{22} - \,\gamma_{0R} \rho_{00} \,) + \,i\left[\Omega _{k} \sin \left( {\frac{\pi x}{\lambda }} \right)(\rho_{20} - \rho_{02} )\right]$$

(17.1)

$$\rho_{22}^{ \cdot } = [ - \gamma_{k} \rho_{22} + \gamma_{W} \rho_{44} ] + i\left\{ \left[\Omega _{w} (\,\rho_{42} \, - \rho_{24} )\right] + \left[\Omega _{k} \sin \left( {\frac{\pi x}{\lambda }} \right)(\rho_{02} - \rho_{20} )\right]\right\}$$

(17.2)

$$\rho_{44}^{ \cdot } = [ - (\gamma_{w} \rho_{44} + \gamma_{w} R_{inc} \rho_{44} )] + [i\Omega _{w} (\rho_{24} - \rho_{42} )]$$

(17.3)

$$\rho_{20}^{ \cdot } = \left\{ { - (\gamma_{k} + i\Delta_{k} )\rho_{20} } \right\}\, + i\left\{ {[\Omega _{k} \sin \left( {\frac{\pi x}{\lambda }} \right)(\rho_{00} - \rho_{22} )] -\Omega _{w} \rho_{40} } \right\}$$

(17.4)

$$\rho_{40}^{ \cdot } = \left\{ { - (\gamma_{w} + \gamma_{k} ) - i(\Delta_{w} + \Delta_{k} )\rho_{40} } \right\} + i\left\{ {(\Omega _{w} \rho_{20} ) - [\Omega _{k} \sin \left( {\frac{\pi x}{\lambda }} \right)\rho_{42} ]} \right\}$$

(17.5)

$$\rho_{42}^{ \cdot } = \left\{ { - (\gamma_{w} + i\Delta_{w} )\rho_{42} } \right\} + i\left\{ {[\Omega _{w} (\rho_{22} - \rho_{44} )] -\Omega _{k} \sin \left( {\frac{\pi x}{\lambda }} \right)\rho_{40} } \right\}$$

(17.6)

with the condition

$$\rho_{00} + \rho_{22} + \rho_{44} = 1$$

(17.7)

Fig. 14

Schematic representation of the single QD system with WL