1 Introduction

For optoelectronic devices, the light–matter interaction is essential. In nonequilibrium Green’s function (NEGF) formalism (Lake et al. 1997), it can be included either through appropriate selfenergy (Henrickson 2002; Aeberhard and Morf 2008; Steiger 2009; Shedbalkar and Witzigmann 2018) or time-dependent (ac) potential incorporated into device Hamiltonian (Wacker et al. 2013). For light-emitting devices, utilizing intersubband transitions, only the “ac” approach was used (Wacker et al. 2013; Winge et al. 2014; Lindskog et al. 2014). This approach requires solving the full set of NEGF equations for several higher harmonics of fundamental frequency what generates huge numerical load. On the contrary, the selfenergy approach generates only little additional load as the light–matter selfenergy (like other selfenergies) is included into NEGF equations for the steady state. In this paper, the selfenergy approach is used to perform simulations of quantum cascade laser (QCL).

2 Model and method

In QCLs, light is emitted due to intersubband transitions occurring in the conduction band. Therefore, one-band effective mass Hamiltonian, parametrized for the in-plane momentum k, provides the sufficient description (Kubis et al. 2009):

$$\begin{aligned} H= \frac{-\hbar ^2}{2}\frac{d}{dz}\frac{1}{m(E,z)} \frac{d}{dz}+V(z)+\frac{\hbar ^2k^2}{m(E,z)}, \end{aligned}$$
(1)

where z is the coordinate along the transport direction and other symbols have the usual meaning. In Eq. (1), mixing with valence bands is taken into account by the use of energy (E) dependent effective mass m. The potential V(z) includes both the variation of the conduction band edge and the Hartree term of the electron–electron interaction. For such a formulation, the Green’s functions \(G(z,z',E,k)\) are the functions of 4 arguments, namely: two spatial coordinates \(z, z'\), energy E, and lateral momentum k.

In QCLs, the radiative intersubband transitions are stimulated by the z-polarized light propagating along the y-axis. The electromagnetic (e-m) field can be described in the terms of the vector potential \(\mathbf{A }=[0\;0\;A_{z}]\) which can be related to the photon flux \(\Phi\) through the time-averaged Poynting vector S: for monochromatic field, \(S= \Phi E_{\gamma }=2nc \epsilon _{0} E^{2}_{\gamma } \hbar ^{-2}|A_{z}|^{2}\), where n is the material refractive index, c is the speed of light, and \(E_{\gamma }=h\nu\) is the photon energy. For such a case, the electron–photon selfenergies are given by Eqs. (32) and (33) of Henrickson’s (2002) paper. Alternatively, they can be also inferred from more general Steiger’s (2009) Eq. (4.51) which holds as well for intraband transitions for the case of light polarized along the direction of transport (\(\lambda = \hat{z}\)): under dipole approximation and for orthogonal basis (\(M_{ij} = 1\)) one gets

$$\begin{aligned} P^{\gamma }_{\alpha \mu }=P^{\gamma }_{(i,1)(j,1)} =M_{ij}(0)\frac{p^{z}_{11}}{m_{0}} =\frac{\text{i}}{\hbar }\left\langle i|[H,z]|j\right\rangle, \end{aligned}$$

where index 1 stands for the conduction band and [ ] denotes the commutator. When laser works, the terms responsible for spontaneous emission are irrelevant and can be omitted. Then, the electron–photon selfenergies can be obtained assuming suitable expression for the photon population \(N_{\mathbf{q }\lambda }\). This would require evaluation of photon Green’s functions in the laser cavity which is quite demanding (see, e.g., Pereira and Henneberger 1996; Miloszewski and Wartak 2012) and left for future studies. In a simplified approach presented here, the confinement of optical field by laser cavity is accounted for through the average waveguide losses and the confinement factor which modify the threshold condition whereas photon density in laser’s cavity is related to the vector potential as \(|C_{{\mathbf{q }}}|^{2}N_{{{\mathbf{q }}} \lambda } =e^{2}\hbar /(2V\omega _{{\mathbf{q }}}\epsilon _{0}) N_{{\mathbf{q }}\lambda }=e^{2}|A_{z}|^{2}\). Such an assumption makes the value of low-density internal quantum efficiency, \(QE=[J( \Phi )-J(0)]/e \Phi\), equal the product of absorbing length (QCL period) and the small-signal gain. The latter can be calculated independently using the theory developed by Wacker et al. (2013). As shown in the right Fig. 2, both approaches give identical current-flux dependence in the low density limit \(\Phi \longrightarrow 0\) what proves their consistency.

Adopting all above simplifications and the relation between photon flux and the vector potential, the electron–photon selfenergies can be expressed as

$$\begin{aligned} \Sigma ^{\lessgtr }(z,z',E,k)&= {} e^{2}\hbar ^{-2}|A_{z}|^{2}[H,z] (G^{\lessgtr }(z,z',E+E_{\gamma },k)\nonumber \\&\quad +G^{\lessgtr }(z,z',E-E_{\gamma },k)) [H,z']. \end{aligned}$$
(2)

The retarded selfenergy can be calculated from Henrickson’s Eq. (33)

$$\begin{aligned} \Sigma ^{\text{R}}=\frac{\text{i}}{2} \Gamma =\frac{1}{2}( \Sigma ^{{>}}- \Sigma ^{{<}}), \end{aligned}$$
(3)

which neglects the principal value integral in more general Lake et al.’s (1997) Eq. (17). As discussed by Esposito et al. (2009), such simplification ignores renormalization of energy and can be a source of errors, especially in the low current region. For higher currents, the errors drop below \(5 \%\). This estimate was obtained for scatterings with polar optical phonons. For the photons, the estimate can be obtained comparing the currents induced by these scattering mechanisms: the phonon-induced current equals approximately the total current J as almost no current flows when this scattering is absent. The I–V curves, presented in the left Fig. 3, reveal that photon induced current, \(J( \Phi ) - J(0)\), is always a fraction of J(0) so similar relation is expected for the errors mentioned above. These errors can be lowered adopting another formulation for \(\Sigma ^{\text{R}}\) used, e.g., by Aeberhard and Morf (2008) which contains a fraction of the Hermitian part of retarded selfenergy. Though this method was effective in the case of polar optical phonon (Esposito et al. 2009), it might be less effective in the case of photon field with nonequilibrium population of photon modes: it introduces factors to \(\Sigma ^{\text{R}}\) which are of the order of spontaneous emission term and (like that) can be ignored as being small compared to \(N_{\mathbf{q }\lambda }\). Eventually, one more possibility is to calculate \(\Sigma ^{\text{R}}\), like in Eq. (2), replacing \(G^{{>}}\) with \(G^{\text{R}}\). With this formulation, the principal value integral is performed analytically but Pauli blocking is not accounted for Lake et al. (1997). Therefore, this approximation is valid only for low electron densities. Due to these limitations, tests were performed in which \(\Sigma ^{\text{R}}\) was calculated either as in Eq. (3) (accounts for Pauli blocking, ignores energy renormalization) or as in Eq. (2) with > replaced with R (accounts for energy renormalization, ignores Pauli blocking). In the latter case, the occupation function was evaluated to verify that Pauli principle was not violated (see “Appendix”). For those two approaches, the current-flux dependence differs by no more than several percent what is consistent with the estimates made by Esposito et al. (2009) for the scattering with polar optical phonons. Therefore, in the following, the results are presented which were obtained using the approximation of Eq. (3) for the retarded selfenergy.

The electron–photon selfenergies were included into the steady-state NEGF formalism like other selfenergies. The formulations for LO-phonon, interface roughness, ionized impurity, and alloy disorder selfenergies were taken from Lake et al.’s (1997) paper, whereas, for the acoustic phonons, the energy-averaged approximation of Kubis et al. (2009) was used. The full set of model parameters used in the simulations can be found elsewhere (Hałdaś et al. 2017). The calculations were made in the position basis: the base vectors were defined by the points discretizing the Hamiltonian of Eq. (1). As QCL core is periodic, the structure subjected to the calculations was limited to a bit more than one QCL period connected to the leads that reliably imitate device periodicity (Kubis et al. 2009; Hałdaś et al. 2011). The Dyson and Keldysh equations were iterated until the selfconsistent solution was achieved. Then, the gain/absorption was calculated from the linear response to small ac field perturbation (Lee and Wacker 2002).

3 Tests and validation

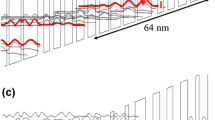
The model described in Sect. 2 was tested on GaAs/AlGaAs QCL, emitting at mid-IR wavelength \(\lambda \cong 9.5\, \upmu \text{m}\), described by Page et al. (2001). The NEGF-based analysis of the electronic transport in this device, however without the light–matter interaction, has already been presented (Hałdaś et al. 2017). The results that include this interaction are presented below. The self-consistent band structure of one device period, laser levels, and the corresponding wavefunctions are shown in Fig. 1. As one can see, the upper level is occupied by the electrons, whereas there are no carriers in the lower laser level. Then, the conditions for light amplification are fulfilled. This is confirmed by the direct calculations of the optical gain (see Fig. 2). Plots in Fig. 2 illustrate that when the selfenergy for the monochromatic e-m field with photon energy of 126 meV, corresponding to the emitted wavelength, is included in the calculations, the optical gain decreases with the increasing photon flux. Simultaneously, the total current increases. The calculated gain-flux and current-flux dependencies can be compared with the relations predicted by the 2-state rate equations model (Winge et al. 2014; Lindskog et al. 2014)

$$\begin{aligned} g( \Phi )= \frac{g(0)}{1+eg_{0}d \Phi }, \;\;\;J( \Phi ) =J(0)+edg( \Phi ) \Phi , \end{aligned}$$
(4)

where g is the gain at energy \(E_{\gamma }\), J is the current density, \(g_{0}\) is the gain coefficient, and d is the period length. In the case of the gain, the agreement with the semiclassical result is excellent. Note that the value of parameter \(g_{0}\) was taken from independent calculations in the “off state”, i.e., without the electron–photon selfenergy (see Fig. 3), so that no fitting parameters were used when drawing the lines. For the current density, the agreement is poorer, but still very good, especially for small photon fluxes. The discrepancy observed for larger fluxes may indicate that the nonradiative component J(0) of the current slowly decreases with the increasing flux. Such explanation is quite probable because the radiative current discharges upper state population, and there are fewer carriers to flow through the nonradiative channels. Data presented in Fig. 2 prove that the calculations of the optical gain (ac field perturbation) are consistent with the calculations of electronic transport that include scattering electron–photon selfenergies. Then, the alternative way to calculate small-signal gain is to make use of right Eq. (4) for the infinitesimal photon flux.

Fig. 1
figure 1

Conduction band profile, laser (3, 2) and depopulating (1) levels wavefunctions (modulus squared) and electron density in units \(\text{eV}^{-1}\,\text{nm}^{-3}\) (contour color plot) calculated with the NEGF method. (Color figure online)

Full size image
Fig. 2
figure 2

(Left) Gain spectra for the increasing photon flux (up-to-down) set at \(h\nu =E_{\gamma }=126\, \text{meV}\). (right) Gain at \(h\nu =E_{\gamma }\) and current density as a function of photon flux set at \(h\nu =E_{\gamma }=126\, \text{meV}\) calculated with the NEGF method (symbols). The cyan and blue lines in the right graph were drawn according to Eq. (4). (Color figure online)

Full size image
Fig. 3
figure 3

(Left) Current–voltage and light–current characteristics calculated with or without light–matter selfenergies included into NEGF formalism; (right) gain peak for these two cases. The slope of the line approximating the data in the off state is \(g_{0}=12.9\, \text{cm}/\text{kA}\). Lines show experimental data (Page et al. 2001)

Full size image

4 Results and discussion

The calculations have been done for Page et al.’s (2001) QCL for the number of bias voltages with light–matter interaction turned off or on. For the latter case, the monochromatic field with energy \(E_{\gamma }=0.126\, \text{eV}\) was used, and the flux \(\Phi\) was increased until the gain was clamped to its threshold value, \(g_{\text{th}}\cong 60 \; \text{cm}^{-1}\), described by the total losses and the confinement factor (Page et al. 2001). Then, the power of light leaving the cavity through one of the mirrors was related to \(\Phi\) as (Winge et al. 2014; Lindskog et al. 2014)

$$\begin{aligned} P=(1-R)N_{p}dw \Phi E_{\gamma }, \end{aligned}$$
(5)

where \(R=0.27\) is the facet reflectivity, \(N_{p}\) is the number of periods in a cascade, and \(w=30\, \upmu \text{m}\) is the waveguide width. Results of these calculations are shown in Fig. 3 and compared to the experimental data of Page et al. (2001). The agreement for current densities lower than \(\sim 15 \; \text{kA cm}^{-2}\) is not bad if we take into account that the only adjustable parameter of the model is the roughness of the interfaces which was assumed as \(\frac{1}{3}\) of the monolayer spacing (Hałdaś et al. 2017). The discrepancies observed for higher current densities can arise from several reasons. The first and best documented is the leakage of the carriers to continuum. As already mentioned, the calculations were made for \(\sim\) one QCL period, and the rest of the QCL structure was mimicked by the contact selfenergies. It was then assumed that the calculated current equals the current measured at device terminations. However, this is true only when electrons fully relax their energy while traveling through one stage of the cascade. The left Fig. 4, made for low bias voltage, illustrates such situation. In the right Fig. 4, it is demonstrated that when the bias voltage increases, some of the carriers escape to continuum. This happens in each period, therefore the “escaping” part of the current should be multiplied by the number of periods what makes the total QCL current larger than the current of one period. Similar effect may take place due to the tunneling or thermally activated tunneling to X-valley states. This scattering mechanism is not included in the calculations, but is highly probable, because in this QCL material system the X-band edge in the barrier layers lies \(\sim 30 \; \text{meV}\) below \(\Gamma\)-band edge. Hence the upper \(\Gamma\)-band states can align with the lowest X-valley states, allowing for the tunneling (Gao et al. 2007). Another reason that could lead to larger currents could be overestimated losses in the cavity. To verify this hypothesis, the calculations were made for the lower value of the threshold gain, \(g_{\text{th}}=30 \; \text{cm}^{-1}\). Results of these calculations, presented in the right Fig. 5, reveal that the current in the on state indeed increases, but simultaneously the calculated threshold current and the output power depart from the experimental curves. Therefore this hypothesis must be rejected.

Fig. 4
figure 4

Spatially resolved energetic spectrum of current density calculated for devices biased with the voltage: (left) 0.246 mV and (right) 0.336 mV per period

Full size image
Fig. 5
figure 5

L–I–V characteristics calculated for: (left) different doping densities of the core region, (right) different values of threshold gain

Full size image

Eventually, the last possibility that was tested was an underestimation of the core doping density. In the simulations, the value of \(4\times 10^{17}\;\text{cm}^{-3}\) declared in the experiment was used. However, this is hardly measurable quantity, and the real value could be different. Thus other values were tried, and it was found that the higher values of doping can indeed lead to the increase of the current and the output power, while keeping the slope efficiency of the light–current characteristic unchanged (see left Fig. 5). Therefore this reason of the observed discrepancies is also realistic.

5 Summary and conclusions

In this paper, the light–matter interaction selfenergy was implemented in the NEGF simulations of QCL. This approach is attractive as it significantly saves simulation time, numerical load, and complexity of the method. The method was tested and good agreement with the semiclassical analysis was obtained. It was also shown that in the limit of small photon flux, the gain calculated from the right Eq. (4) is consistent with those extracted from the linear response of the Green’s functions. As an example, the light–current (L–I) characteristics of QCL emitting in mid-IR (\(9.5\ \upmu \text{m}\)) was calculated and good agreement with the experimental data was found. The observed discrepancies can arise from the leakage currents and the underestimated doping.