Theoretical investigation of metal–metal waveguides for terahertz quantum-cascade lasers

Abstract

We report our theoretical investigations of metal–metal waveguides for terahertz quantum-cascade lasers. The device is considered as a planar, multilayer structure. The optical properties of constituent materials are calculated according to Drude–Lorenz model. The Helmholtz equation is solved numerically using transfer matrix method. We concentrate on selecting the proper metallic material for claddings to minimize the waveguide losses. In addition, we analyze the consequences of inserting Ti separation layers between claddings and semiconductor core for blocking the destructive diffusion of metals into the active layer and improving the adhesion.

1 Introduction

The terahertz region of the electromagnetic spectrum proves its usability in number of applications including security screening, (bio)chemical detection, remote sensing, nondestructive materials evaluation, communications, astronomy, biology and medicine (Williams 2007; Belkin 2009). Therefore the development of compact, cheap, high-power and convenient continuous-wave radiation sources in this range is strongly desired. The terahertz-emitting quantum-cascade lasers (THz QCLs) seem to be an excellent response for these needs.

The first THz QCL was demonstrated in 2002 as a cryogenic device. Obviously, for most practical applications, such feature is not acceptable. A lot of efforts are made to fabricate devices able to lase in higher, at least TEC-controlled, temperatures. Here, it is useful to recall the formula for threshold gain, valid for any semiconductor laser:

$$\begin{aligned} g_{th}={{\alpha _{wg}+\alpha _m}\over \varGamma }. \end{aligned}$$

(1)

List of symbols can be found in Table 1. All the parameters on the right side of Eq. (1) are determined by the passive waveguide structure, while the material gain depends on the carrier transport and radiative properties of the quantum-well gain medium. Minimizing the threshold gain generally results in reduced threshold current densities and increased operating temperatures (Kohen 2005). Therefore two ways leading to improvements of THz QCL can be distinguished: (i) designing new lasing schemes with higher gain and (ii) lowering the waveguide loss. For example, present temperature performance record of 200 K has been achieved mainly due to approach (i), namely by optimizing the lasing transition oscillator strength of the resonant phonon based three-well design (Fathololoumi 2012).

Table 1 List of symbols used in the paper

In this theoretical work, we explore the path (ii). Our investigations deal with metal–metal waveguides commonly used for THz QCL’s. Our goal is to select the proper metallic material for claddings and thus to minimize the waveguide losses $\alpha _{wg}$. In addition, we analyze the consequences of inserting separation layers between claddings and semiconductor core for blocking the destructive diffusion of metals into the active layer and improving the adhesion.

2 The model

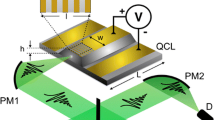
THz QCLs can be considered as planar waveguides. Schematic view of such a structure is shown in Fig. 1. It is well known that QCLs support TM modes only (Sirtori 2002). The further analysis will be based on these two facts.

Fig. 1

Geometry of the planar waveguide. Coordinates $x, y, z$ indicate the directions: across the epitaxial layers, lateral and of wave propagation, respectively. To the right one can see the field components

2.1 Modes of the laser waveguide

The total electromagnetic field of TM mode can be determined by $H_y$, which satisfies the Helmholtz equation (Marcuse 1974):

$$\begin{aligned} {d^2 H_y(x) \over d x^2} + \left[ \tilde{n}(x)^2k_0^2 -\tilde{n}_{eff}^2k_0^2 \right] H_y(x)=0, \end{aligned}$$

(2)

According to the transfer matrix method and boundary conditions imposed on the layer interfaces we get the following dispersion equation (Chilwell and Hodgkinson 1984):

$$\begin{aligned} \chi (\beta )=\gamma _{M+1} m_{11}+\gamma _{M+1}\gamma _0m_{12}+m_{21}+\gamma _0m_{22}=0, \end{aligned}$$

(3)

where $m_{pq}$ are elements of the transfer matrix defined as

$$\begin{aligned} {{\mathbb M}=\prod _{m} {\mathbb M}_m =\prod _{m}\begin{pmatrix} \cos {\phi _m}&{}(-i/\gamma _m)\sin {\phi _m}\\ -i\gamma _m\sin {\phi _m}&{}\cos {\phi _m} \end{pmatrix}}. \end{aligned}$$

(4)

In Eqs. (3) and (4) $\gamma _m={\kappa _m \over {\tilde{n}_m^2k_0}}\sqrt{\mu _0/\epsilon _0}$, $\kappa _m=\sqrt{(k_0^2 \tilde{n}_m^2 -\beta ^2)}$ and $\phi _m=\kappa _md_m$. Numerical solution of Eq. (3) provides the propagation constant $\beta =\tilde{n}_{eff}k_0$. The waveguide loss can be calculated as:

$$\begin{aligned} \alpha _{wg}=2k_0Im(\tilde{n}_{eff}). \end{aligned}$$

(5)

2.2 Material parameters

The optical properties of metals as well as highly doped semiconductors are determined by the behaviour of free carriers, which exhibit well known collective charge oscillations, i.e. plasmons. Introducing the volume plasma frequency

$$\begin{aligned} \omega _p=\sqrt{N_de^2 \over \epsilon _0\epsilon _bm_{eff}}, \end{aligned}$$

(6)

and using the classical Drude–Lorenz model, it is possible to calculate the refractive index as (Lu 2009):

$$\begin{aligned} \tilde{n}=\sqrt{\epsilon _b \left[ 1-{\omega _p^2 \over \omega \eta }\left( 1+{i \over \omega \tau }\right) \right] }, \end{aligned}$$

(7)

where $\eta =1+1/(\omega \tau )^2$ and $\tau =m_{eff} \cdot \mu _e/e$ is the relaxation time.

For calculating $\tilde{n}_{GaAs}$ with different doping levels, we created our own software. We assumed $m_{eff}=0.063~m_e$ (http://www.ioffe.ru/SVA/NSM/), $\mu _e=0.85~\text {m}^2/(\text {Vs})$ for low doping (http://www.ioffe.ru/SVA/NSM/), $\mu _e=0.2~\text {m}^2/(\text {Vs})$ for highly doped contact layers (Zivanov and Zivanov 1995) and $\epsilon _b=\tilde{n}_{GaAs}^2$, where $\tilde{n}_{GaAs}=2.99$ is the value measured for $\lambda _0=100\,\upmu \text {m}$ by transient terahertz time-domain spectroscopy (Schall and Jepsen 2000). For calculating $\tilde{n}$ for metals we used shareware Matlab code LD.m described in Ung and Sheng (2007).

3 The results

We started the investigations from testing our numerical tools for simplified case. We considered a TM wave of wavelength $\lambda _0=100~\upmu \text {m}$ propagating through the planar structure consisted of $w=10.2~\upmu \text {m}$ thick, undoped GaAs between infinitely thick Au plates. For such a simple case the analytical expression for the effective index is known (Collin 2007):

$$\begin{aligned} \tilde{n}_{eff}=\sqrt{\epsilon _{GaAs}} \left( 1+{\lambda _0 \over \pi w \sqrt{-\epsilon _{Au}}}\sqrt{1-{\epsilon _{GaAs} \over \epsilon _{Au}}}\right) ^{1/2}. \end{aligned}$$

(8)

Substituting $\epsilon _{GaAs}=2.99^2$ and $\epsilon _{Au}=(188.3+i 237.4)^2$ into Eq. (8) yielded $n_{eff}=3.0021 + 0.0096 i$, which turned out to be identical with our numerical solution of Eq. (3). The plot of $H_y$ revealed features characteristic for narrow waveguides (width much smaller than the wavelength), i.e. almost flat profile between the metal plates and rapid, exponential decay inside the metal plates (see Fig. 1(c) in Collin 2007).

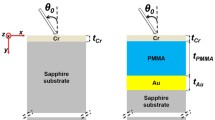
After gaining confidence to our numerical tools, we started to deal with the analysis of particular device, namely THz QCL designed to emit $\lambda _0=100\,\upmu \text {m}$. Its active layer consists of hundreds of alternating GaAs and $Al_{0.15}Ga_{0.85}As$ layers and is surrounded by highly doped GaAs:Si contact layers. Metal claddings on both sides form the metal–metal waveguide structure. The data concerning the planar structure (schematically shown in Fig. 1) have been collected in Table 2. Some additional simplifications are briefly described below.

Table 2 Description of THz QCL structure ($\lambda _0=100\,\upmu \text {m}$)

Standard thickness of THz QCL cladding is about 1,000 nm. On the other hand, the penetration depth of electromagnetic radiation into metals is usually much less than 100 nm (Collin 2007). These two facts allow us to consider claddings to be infinitely thick.

The active layer is substituted by one equivalent layer marked number 2. Its thickness $d_2$ is the sum of constituent GaAs and $Al_{0.15}Ga_{0.85}As$ layers. To calculate $\tilde{n}_2$ we averaged the Al content and doping thus obtaining homogeneous material $Al_{0.037}Ga_{0.963}As$ with $N_d=6.8\cdot 10^{15}~\text {cm}^{-3}$. Then we used our software based on Drude–Lorenz model dedicated for pure $GaAs$ and calculated $\tilde{n}_2=2.8117 + i 0.0289$, where $Re(\tilde{n}_2)$ has been reduced of 0.6 % according to tendency reported by http://www.ioffe.ru/SVA/NSM/.

We considered THz QCL structures with several metals used as claddings. The calculated waveguide losses are presented in Table 3. The results are lined up monotonically from smallest to highest values of $\alpha _{wg}$. Considering the order, we can say, we achieved the qualitative convergence with Belkin (2009), where Au and Cu claddings were considered and lower losses in the latter case were found out. Looking at the particular values, we note the divergence with many authors, who report significantly smaller waveguide losses, namely 10–20 cm$^{-1}$ (Williams 2007; Belkin 2009; Kohen 2005). We explain this divergence by taking by us into account losses in the active layer. Assuming $Im(\tilde{n}_2)=0$ (instead of $Im(\tilde{n}_2)=0.0289$ in Table 2), we obtained $7.5\le \alpha _{wg}\le 41~\text {cm}^{-1}$, while the order of results shown in Table 3 remained unchanged.

Table 3 Results for the THz QCL ($\lambda _0=100\,\upmu \text {m}$) with different metal claddings

Figure 2 shows normalized $/H_y/^2$ profiles for selected cases. Comparison of the plot and Table 3 indicates that there is a correlation between mode confinement and waveguide losses. The less the field leaks into the claddings, the lower $\alpha _{wg}$ is found.

Fig. 2

Normalized field profiles for different claddings. The structure is symmetrical around $x=5.1\,\upmu \text {m}$

The result presented in Table 3 might bring one to conclusion that using, say, Cu, Ag or Au as cladding materials is clearly advantageous for THz QCL, while Ti is a material which should be definitely avoided. Unfortunately, the metals providing low $\alpha _{wg}$ have drawbacks:

• they tend to diffuse into semiconductor layers (which is detrimental for device operation),

• their adhesion to semiconductor layers is relatively weak.

Ti exhibits the opposite features and this is why it is sometimes used for separation layers between the core and cladding. We decided to investigate the influence of such layers on waveguiding.

The modified THz QCL structure is described in Table 4. Our calculations show that $\alpha _{wg}$ is a quadratic-like function in the range of $d_{Ti} \le 200\,\text {nm}$ (Fig. 3). We claim that fabricating a device with Ti layers of thickness, say, $d_{Ti}<30~\text {nm}$ will not increase waveguide losses significantly on the one hand and—on the other—will eliminate the technological drawbacks mentioned above.

Table 4 Description of the THz QCL structure ($\lambda _0=100\,\upmu \text {m}$) with Ti separation layers

Fig. 3

The influence of Ti separation layer thickness on waveguide losses

4 Conclusions

In conclusion, we investigated theoretically metal–metal waveguides designed for THz QCL. We considered the device designed to emit radiation of wavelength $\lambda _0=100\,\upmu \text {m}$. We used Drude–Lorenz model to find out the optical properties of constituent materials. Solving Helmholtz equation by transfer matrix method allowed us to calculate waveguide losses for structures with claddings made of different metals. The obtained results show that copper (Cu), silver (Au) and gold (Au) are the most conducive cladding materials for laser operation. To block the destructive diffusion of metals into the active layer and improving the adhesion, titanium (Ti) separation layers of thicknesses not exceeding 30 nm can be used.