Design of compact tunable wavelength division multiplexing photonic phased array switches using nano-electromechanical systems on a silicon-on-insulator integration platform

Abstract

We present the design of novel $2\times 2$ and $4\times 4$ photonic phased array switch elements with the capability to actively tune wavelength division multiplexing pass-bands. The switch elements use nano-electromechanical systems phase shifters located on the two longitudinal sides of the structures; offering advantages of compact footprint and low-power consumption. The design is verified using the complex finite difference mode three-dimensional full-vectorial solver of the simulation tool FIMMPROP and utilizing custom numerical analysis.

1 Introduction

The number of reports in the literature of the design of advanced silicon on insulator (SOI) photonic integrated circuits (PICs) has been increasing reflecting the growing appreciation by designers of the tight light confinement of the high refractive index between the silicon guiding ridge and the surrounding cladding that offers compact size and low loss as well as their compatibility with complementary metal-oxide-semiconductor (CMOS) technology. The introduction of the nano-electromechanical system (NEMS)-operated phase shifters of cascaded under-etched slot waveguides has paved the way to produce ultra-small size low-power consumption voltage controlled active SOI devices (Acoleyen et al. 2012). Designs using splitter/combiner multimode interference (MMI) couplers interconnected by a network of path imbalances were considered for the realization of wavelength division multiplexed (WDM) wavelength routing (de)multiplexers (Paiam and MacDonald 1997). The introduction of the generalized Mach–Zehnder (MZI) interference structures promised the capability to implement multiple-input/multiple-output (MIMO) light routing devices (Cahill 2004).

Integrated Photonic Phased Array Switches (IPPAS) and the concept of tunable WDM light routing has been introduced recently (Hussein et al. 2013). Tunable WDM–IPPAS elements are generalized MZI structures having both phase shifters and path length imbalances in the interconnection network between the splitter/combiner MMI couplers each of size $\hbox {N}\times \hbox {N}$. They provide the capability of actively routing the light between the MIMO ports in tunable WDM bands. Both novel $2\times 2$ and $4\times 4$ WDM–IPPAS elements are presented in this work. The phase shifting elements used in IPPAS are NEMS-operated; each has a compact size and all are located on the longitudinal sides of the switch structure in-line with the ports of the splitter/combiner MMI couplers.

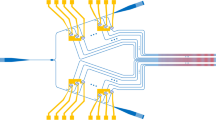
The schematic diagram of the $2\times 2$ and $4\times 4$ tunable WDM–IPPAS elements shown in Fig. 1 depicts the novel features of this family of photonic integrated circuits (PICs). The pitch size between the port centers of all of the MMI couplers is the same enabling the nano-dimensions NEMS-operated phase shifters to be aligned with the ports of the interconnected MMI couplers and eliminating the need to use waveguide loops to compensate for path length imbalance. One of the two silicon beams of each phase shifter is electrically isolated and is biased from one (exterior) side, whereas the other is excited through the rest of the system silicon structure taken as the electrical ground. This avoids the need to use waveguide crossovers and facilitates the electrical probing to the chip compared with analogous conventional switches. Edge couplers, as shown in Fig. 1, or grating couplers can be used to couple the light in/out of each PIC. The $2\times 2$ MMI coupler crossovers at the output ports facilitate coupling the ground to the structures. These can be eliminated in case of the use of grating couplers. The overall structures are symmetrical and losses are well-balanced for all paths.

Fig. 1

Schematic diagrams of the $2\times 2$ (on the top) and $4\times 4$ (on the bottom) tunable WDM–IPPAS elements

2 NEMS-operated phase shifter

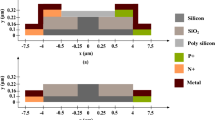
The NEMS-operated phase shifter is built by cascading under-etched slot waveguides. The structure of the under-etched slot waveguide is explained in Fig. 2. It consists of two suspended silicon beams each of width $W_{gs}$ (230 nm) and height $h$ (300 nm) equal to the thickness of the silicon top layer of the SOI wafer. The slot-width between the suspended silicon beams at quiescence, i.e. when no potential difference is applied between the silicon beams, is $W_{s0}$ (100 nm). An applied voltage difference modulates the slot width between the suspended silicon beams to $W_{s}$ as a function of the propagation distance along the under-etched slot. Alternatively, the excursion width $W_{ex}$ is described as: $W_{ex} = (W_{s0}-W_{s})/2$. The length of the under-etched slot is $L_{s}$.

Fig. 2

Under-etched slot waveguide

The width of each one of the freestanding silicon beams and the slot width are selected to support the fundamental mode in the under-etched slot waveguide. The simulation of the effective index $n_{e}$ of the under-etched slot waveguide for the fundamental mode is depicted as a function of the modulated slot width in Fig. 3. Here, we allow a minimum slot width $W_{s,min}$ of 20 nm as a guard before the applied voltage reaches the pull-in instability which causes the two silicon beams to come in direct touch with each other at the midpoint along the under-etched slot length. The two silicon beams of the under-etched slot waveguide behave as a capacitor. The resulting electrostatic force causes the reduction of the slot width with increasing applied potential difference. This results in large modulation in the effective index of the guided mode. The positive z-axis is taken as the direction of propagation. The phase difference ${\varDelta } \phi$ introduced due to modulating the slot width of the NEMS-operated slot waveguide is given by:

$$\begin{aligned} {\Delta } \phi =\frac{2\pi }{\lambda }\left[ {\int \limits _{0}^{L_s } {n_e dz} -n_{e0} L_s } \right] \end{aligned}$$

(1)

In Eq. (1), $n_{e}$ is a function of the $W_{s}$ which by itself is a function of $z$. The term $(2\pi /\lambda ){n}_{e0}L_{s}$ in Eq. (1) corresponds to the phase without applying voltage to the under-etched slot waveguide. Therefore, $n_{e0}$ represents the effective index when the slot width equals to $W_{s0}$. We removed the dependency on $W_{s}$ and $z$ from Eq. (1) for simplicity. The wavelength $\lambda$ is taken here as the free-space wavelength.

Fig. 3

Simulation of the effective index for the fundamental mode versus the slot width of the under-etched slot waveguide

When applying voltage to the silicon beams, the excursion of the beams caused by the lateral force due to the electrostatic attraction can be described by the Euler–Bernoulli beam equation, which provides a means for calculating small deflections in beams due to an applied distributed load. The axial stress is neglected in the formulation. Further relating the distributed force to the stored electrostatic energy of the capacitor formed by the silicon beams reveals the following nonlinear forth-order differential equation that describes the beam excursion (Acoleyen et al. 2012):

$$\begin{aligned} \frac{d^{4}W_{ex}}{dz^{4}}=\frac{\varepsilon _o hV^{2}}{2EI\left( {W_{s0} -2W_{ex}} \right) ^{2}} \end{aligned}$$

(2)

$V$ is the voltage applied across the slot between the two suspended silicon beams. $E$ is Young’s modulus and is equal to 169 GPa in the core silicon in the direction of interest. $I = hW_{gs}^{3}/12$ is the beam moment in the direction of interest. The solution of Eq. (2) is achieved numerically subjected to fixed and hinged boundary conditions. Fixed boundary conditions allow no displacement and no rotation at the clamping points: $W_{ex} = 0$ and $dW_{ex}/dz = 0$ at both $z = 0$ and $z = L_{s}$. Hinged boundary conditions allow no displacement, but do allow rotation around the clamping points: $W_{ex} = 0$ and $d^{2}W_{ex}/dz^{2} = 0$ at both $z=0$ and $z =L_{s}$.

The phase difference due to a modulation of the slot width can be predicted using the data on the effective index versus slot width obtained by simulation (Fig. 3) and the numerical solution of Eq. (2) subject to fixed or hinged boundary conditions. The speed of the NEMS-operated slot waveguides depends on the mechanical relaxation time of the suspended silicon beams. The expected speed is in the MHz range. The fundamental resonance frequency of the nanomechanical structure is given in (Acoleyen et al. 2012) by:

$$\begin{aligned} f_o =\frac{K^{2}}{2\pi L_s^2 }\sqrt{\frac{EI}{\rho hW_{gs} }} \end{aligned}$$

(3)

$\rho = 2.329\text { g cm}^{-3}$ is the silicon mass density. The factor $K$ equals to 4.73 for fixed boundary conditions and equals to $\pi$ for hinged boundary conditions. Increasing the speed of the system requires decreasing $L_{s}$. However, a smaller value of $L_{s}$ means that the phase shift which can be achieved by each under-etched slot waveguide is smaller. This in turn requires cascading more under-etched slot nanowire sections to achieve the desired total phase shift, which results in more excess loss. The design, therefore, is a compromise between speed of the system and its excess loss. We set the length of the under-etched slot waveguide to $\hbox {L}_\mathrm{s} = 5.4\,\upmu \hbox {m}$. Midway between fixed and hinged boundary conditions, the achieved phase shift is about $16.58^{\circ }$ at operational voltage 15 V and the fundamental resonance frequency is 50 MHz. The pull-in voltage is about 17.7 V based on hinged boundary conditions.

The total phase shift element, illustrated in Fig. 4, is composed of 15 cascaded under-etched slot waveguides coupled though a high efficiency straight transition slot couplers that provide electrical isolation to the two silicon beams of the phase shift line. The length of each straight transition slot coupler is 100 $\upmu \hbox {m}$. The total length of the designed phase shifter is only 349 $\upmu \hbox {m}$ and is intended to provide $0^{\circ }$–$180^{\circ }$ of phase shift. Simulations of the phase shifter and the straight transition slot couplers show that an excess loss of about 1.1 dB is introduced by this phase shifter design and that each straight transition slot coupler is 96.7 % efficient.

3 MMI couplers

The excellent properties including the compact size, low loss, low reflection, low crosstalk and wide bandwidth response have entitled MMI couplers to be used in a number of PICs. The presented two WDM–IPPAS elements make use of a crossover $2\times 2$ and equal-split-ratio $2\times 2$ ($-$3 dB) and $4\times 4$ ($-6$ dB) MMI couplers. The width of each input/output (I/O) access port is setup to $W_{a} = 1.49\,\upmu \hbox {m}$ centered in the case of equal-split-ratio MMI couplers at the maximum possible width of the access port of $W_{am} = 2\,\upmu \hbox {m}$. The $-$3 dB $2\times 2$ and $-$6 dB $4\times 4$ MMI couplers have widths of 4 and 8 $\upmu \hbox {m}$, respectively. The width of the crossover $2\times 2$ MMI coupler is set to 3.49 $\upmu \hbox {m}$ such that the centers of its adjacent access ports are separated by the same distance of 2 $\upmu \hbox {m}$ as those of the other equal-split-ratio MMI couplers. The imbalance $I_{k/l,j}$ between outputs $k$ and $l$ due to input $j$ is given by:

$$\begin{aligned} I_{k/l,j} =10\log \left( {\frac{T_{kj} }{T_{lj} }} \right) \end{aligned}$$

(4)

$T_{ij}$ is the transmission for output $i$ and input $j$. The excess loss $L_{j}$ due to input $j$ for an $\hbox {N}\times \hbox {N}$ MMI coupler is given by:

$$\begin{aligned} L_j =-10\log \left( \, {\sum _{i=1}^N {T_{ij} } } \right) \end{aligned}$$

(5)

Fig. 4

Schematic diagram of the NEMS-operated phase shifter of 15 cascaded under-etched slot waveguides

Simulations of the coupler-length-dependant excess loss show that the length $L_{c}$ of the crossover $2 \times 2$ and $-$3 dB $2\times 2$ MMI couplers are about 60.66 and 94.55 $\upmu \hbox {m}$, respectively, at minimum excess loss. The designed $-$3 dB $2 \times 2$ MMI coupler has an imbalance of 0.053 dB and excess loss of 0.11 dB based on simulation. The designed crossover $2 \times 2$ MMI coupler has excess loss of 0.122 dB and crosstalk of $-$31.9 dB based on simulation. The simulation of the imbalances $I_{1/4,1}$, $I_{2/3,1}, I_{1/4,3}$ and $I_{2/3,3}$ and excess losses $L_{1}$ and $L_{3}$ for the $-$6 dB $4 \times 4$ MMI coupler is depicted in Fig. 5.

Fig. 5

Simulation of the coupler-length-dependant imbalances and excess losses for the $-$6 dB $4\times 4$ MMI coupler

The design of the $-$6 dB $4 \times 4$ MMI coupler can be optimized between minimum imbalances and minimum excess losses for the different inputs. An appropriate objective function for the minimization of the non-uniformity in the output powers and the minimization of loss taking into account all the inputs has been introduced and used in design. The optimum MMI coupler length for the minimization of non-uniformity in the output powers and loss is $L_{c}= 122.094\;\upmu \hbox {m}$ and $L_{c} = 122.281\;\upmu \hbox {m}$, respectively. The two coupler length values are close to each other. The designed coupler length is set at $L_{c} = 122.2\, \upmu \hbox {m}$. The designed $-$6 dB $4 \times 4$ MMI coupler has a maximum imbalance of 0.074 dB and maximum excess loss of 0.377 dB based on simulation.

4 Wavelength-dependant responses and tunable WDM design optimization

The interferogram of a WDM–IPPAS element represents the prediction of the transmission or magnitude responses of the system versus the wavelength for the different combinations of inputs and outputs by utilizing the wavelength-dependant simulation data for the different components of the structure. The wavelength-dependant phase shift ${\Delta } \varphi$ introduced by a path length imbalance ${\Delta } {L}$ is given by:

$$\begin{aligned} {\Delta } \varphi =2\pi n_e (\lambda )\frac{{\Delta } L}{\lambda } \end{aligned}$$

(6)

$\hbox {n}_\mathrm{e}(\lambda )$ in Eq. (6) is the wavelength-dependant effective index of the nanowire path imbalance. The simulation of $\hbox {n}_\mathrm{e}(\lambda )$ for the path imbalance is depicted in Fig. 6. Simulations of the wavelength-dependant magnitudes and phases of the fundamental mode for the scattering parameters of the different MMI couplers are performed and used together with Eq. (6) and the simulation data of Fig. 6 in a custom code for the prediction of the interferogram response and to facilitate the design of the path length imbalances for proper WDM applications. For the $2\times 2$ tunable WDM–IPPAS element, the path imbalance is setup to: $L_{1}- L_{2} = 100\, \upmu \hbox {m}$. For the $4\times 4$ tunable WDM–IPPAS element, the path imbalances are setup to: $L_{1} - L_{4} = 150$, $L_{2} - L_{4} = 100.12$ and $L_{3} - L_{4} = 50\,\upmu \hbox {m}$.

Fig. 6

Simulation of the wavelength-dependant effective index of the nanowire imbalance

The interferogram response for both outputs $O_{1}$ and $O_{2}$ and input $I_{1}$ of the designed $2 \times 2$ WDM–IPPAS element when the two phase shifters are at reset is shown in the left side of Fig. 7. A progressive phase shift ${\Delta } \phi ={\Delta } \phi _{1}-{\Delta } \phi _{2}$ causes the passbands of the interferogram to be steered along the wavelength as in steerable phased array antennas. The right side of Fig. 7 depicts the tuning capability in the location of $O_{1}$ passband. The top of Figure 8 depicts the interferogram response for the designed $4 \times 4$ WDM–IPPAS element for the four outputs and input $I_{1}$. The steering capability of the same structure is demonstrated by the lower part of the same figure when applying a progressive phase shift of: ${\Delta } \phi ={\Delta } \phi _{1} - {\Delta } \phi _{2} = {\Delta } \phi _{2} - {\Delta } \phi _{3} = {\Delta } \phi _{3} - {\Delta } \phi _{4} =60^{\circ }$.

Fig. 7

(on the left) Interferogram response of the $2 \times 2$ WDM–IPPAS element for input $I_{1}$. (on the right) Steering of output $O_{1}$

Fig. 8

(on the top) Interferogram response of the $4 \times 4$ WDM–IPPAS element for input $I_{1}$. (on the bottom) Steering for ${\Delta } \upphi = 60^{\circ }$

5 Summary

The design and characteristic of novel $2\times 2$ and $4\times 4$ integrated photonic phased array switches with active capability to steer the passbands is presented. The designed switches can rout the light through the control of external voltages applied to the electrodes of the NEMS-operated phase shifters utilized in the designed PICs.