50 Years of Capital Mobility in the Eurozone: Breaking the Feldstein-Horioka Puzzle

Abstract

This paper assesses capital mobility for the Eurozone countries by studying the long-run relationship between domestic investment and savings for the period 1970-2019. Our main goal is to analyze the impact of economic events on capital mobility during this period. We apply the cointegration methodology in a setting that allows us to identify endogenous breaks in the long-run saving-investment relationship. Precisely, the breaks coincide with relevant economic events. We find a downward trend in the saving-investment retention since the 70s for the so-called “core countries”, whereas this trend is not so evident in the peripheral, where the financial and sovereign crises have had a more substantial impact. In addition, our analysis captures other economic events: the Exchange Rate Mechanism (ERM) crisis, the German reunification, the European financial assistance program, and the post-crisis period. Our results also indicate that the original euro design had some flaws that remain unsolved.

1 Introduction

The free movement of capital in the European Union (EU) is one of the fundamental economic freedoms established in the founding treaties. However, the level of restrictions in this field has long been considered secondary in European construction. Until the mid-1980s, the regime for the liberalization of intra-Community capital movements had its origin in the 1960s and was limited to those capital operations most closely linked to compliance with the other fundamental freedoms of the Treaty of Rome. Obviously, the integration of the EU capital markets is a long-term structural endeavor, and much effort has been devoted over the years. During the 60s, apart from two directives adopted in 1960 and 1962, other initiatives to facilitate the harmonization or convergence of national regulations were paralyzed; moreover, due to the instability of the financial markets in the 70s and the crisis of the European Monetary System (EMS) at the beginning of the 90s, some Member States (i. ex. France, Italy, Ireland, Denmark, and Greece) called in for safeguard clauses to stop and reverse the process of financial integration.

Nevertheless, European capital markets should be as integrated and developed as possible, as in the context of a monetary union, the failure to achieve it may have serious consequences. First, if private risk-sharing is grossly insufficient, it can limit the resilience of Eurozone Member States, measured as the capacity to absorb and recover from adverse shocks. Second, capital mobility may also strengthen the effectiveness of the single monetary policy as fragmentation and frictions may prevent the pass-through of the policy interest rate to market interest rates. Therefore, the assessment of capital mobility in the EU deserves further attention.

According to Meyermans et al. (2018), the three main structural barriers that hamper the development of a well-functioning financial architecture in the Eurozone (EZ) are: (i) the fragmented regulatory and institutional frameworks; (ii) the corporate sector’s over-reliance on bank financing¹ and, finally, (iii) the strong “home bias” of credit and capital markets. Home bias, measured as the holding of domestic assets versus their optimal intra-EU allocation, relates to the quantity approach to financial integration (Feldstein and Horioka 1980). This should be closely monitored, as a high home bias may amplify output shocks during the financial crisis (Furceri and Zdzienicka 2013).

After the findings of Feldstein and Horioka (1980), many papers have attempted to identify factors impeding capital mobility; Niehans (1986) argues that the removal of barriers to capital transfers does not ensure its mobility across countries. In the same vein, Obstfeld and Rogoff (2000) developed a model with transaction costs for international trade in goods, finding that the sole existence of frictions in the goods markets might prevent capital mobility across countries. More recently, Ford and Horioka (2017) maintain that financial markets integration is not a sufficient condition to achieve capital mobility, i.e., they state that Feldstein and Horioka (1980) results can be due to the absence of globally integrated goods markets. Hence, both financial and goods markets integration are needed for capital mobility to existing.

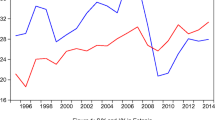
The EU is a natural test for capital mobility because there are no barriers neither to capital nor to goods mobility. In case capital mobility remains persistently low, we should conclude that there are other reasons for this result, probably the so-called “home bias”. Unlike most of earlier literature, which focuses on the price approach, we adopt the quantity one based on Feldstein and Horioka (1980); we consider this approach is especially suited to assess the evolution of capital mobility within a monetary union where external imbalances have been persistently growing up to the Great Recession. External disequilibria are caused by macroeconomic imbalances between national savings and investment (S and I, respectively, hereafter) in a context of financial liberalization. Persistent imbalances between national S and I would be at odds with the existence of a Feldstein-Horioka (FH hereafter) puzzle. In Fig. 1, we plot the current account (CA) balance of the core² and peripheral EU countries as the average value of the difference between domestic I and domestic S. The two groups of countries show a mirroring evolution. Indeed, the visual inspection shows a diverging trend between core and peripheral countries, especially since the convergence of interest rates in the EU from 1995 to 1997 on the euro’s launching eve. While eliminating currency risk and the broader and deeper financial markets would facilitate the financing of external deficits allowing domestic savings to drift apart from domestic investment, the situation for the peripheral countries changed dramatically with the 2007 financial crisis and the subsequent adjustment afterward. The latter gave rise to a credit crunch in the area, with a subsequent financial fragmentation process. Thus, the financial crisis triggered a double reduction in capital mobility and the gap between core and periphery external positions. However, beyond the former general patterns, and according to Lane and Milesi-Ferretti (2007), the exposures across Europe are very heterogeneous (differences in trade patterns, financial exposures, and net external positions); this can be seen in Fig. 2. Therefore, to tackle this heterogeneity across countries, a more disaggregated analysis using individual time series seems a convenient empirical approach.

In this paper, we evaluate capital mobility using the FH regression and complement its interpretation by examining the time-series properties of the individual series involved and the stability of the long-run relationship linking domestic saving and investment.³ Bearing in mind all the arguments stated above, in this paper, we seek to measure capital mobility over the period 1970-2019, accounting for the different stages of the EU financial integration: the initial process of financial integration since the 70s (more intense after the Maastricht Treaty signature in 1992), the creation of the euro and the subsequent large capital imbalances along 2000-2007, the global financial crisis and the post-crisis period. The econometric methodology is based on the tests proposed by Kejriwal and Perron (2010) that allow us to identify if there is a long-term relationship between domestic savings and investment as well as its stability by the endogenous identification of potential breaks. Moreover, we test for cointegration using tests allowing for multiple structural breaks in the coefficients as proposed by Arai and Kurozumi (2007) and Kejriwal (2008). Finally, for the cases where we find cointegration between the two variables, we estimate the model including the breaks to assess if the relationship between domestic investment and saving (the slope parameter $\beta$) has changed over time. In order to check for the robustness or our results we implement two additional estimations. First, we test for cointegration in a panel for different groupings using the MG/PMG estimators and, second, we apply rolling window regressions to assess the evolution of the saving retention parameters over time.

Our contributions are the following: first, we reassess the FH puzzle for the Eurozone countries for the most extended sample available. Surprisingly, there is little empirical literature on the Feldstein-Horioka puzzle covering financial integration from the very beginning of the monetary integration process, the only exceptions to the best of our knowledge being Katsimi and Zoega (2016), Drakos et al. (2018), ECB (2018, 2020) and Camarero et al. (2020), although they use different empirical approaches and cover a shorter time span compared to the present study; second, for this purpose, we take into account the non-stationarity properties of the variables in the same vein of recent literature both in large panels and time series; third, we relate our econometric methodology, that accounts for structural changes (breaks) in the long-run relationship, with the changes in the degree of financial integration and capital mobility as measured by the savings-retention coefficient in the FH equation; fourth, we deal with the expected degree of heterogeneity within the EU considering the existence of several country groups. The groupings are determined endogenously relying on the breaks found and signal a clear difference between core countries and the rest of the sample; fifth, we present robustness checks using in a complementary way both MG/PMG estimators⁴ and rolling window regressions. Finally, our results have relevant economic policy implications.

This paper is organized as follows: in Section 2, we succinctly present how capital mobility is measured using the FH approach and review the empirical literature on the subject focusing on the time series perspective. Section 3 summarizes the econometric methodology and describes the database, while Section 4 discusses the empirical results and robustness tests. Finally, Section 5 concludes.

2 Theoretical and Empirical Background

2.1 Capital Mobility: FH Condition for Financial Integration

The measurement of the degree of capital mobility is not an easy task. Although the literature provides several alternative definitions, financial market integration is closely related to the law of one price. The law of one price states that if assets have identical risks and returns, they should b priced identically regardless of where they are transacted. However, to get this result, different conditions should be met, and the literature has traditionally considered three approaches⁵. While the first one is known as the price approach and focuses on the co-movement between domestic and foreign rates linked by the exchange rate, the second approach - also known as the quantity approach - studies the co-movement of the variables that directly materialize capital mobility, that is, investment and savings. More recently, alternative measures investigating the impact of common shocks on prices (news-based measures) have been added as a valuable complement to the traditional price-based measures. Feldstein and Horioka (1980) estimated using OLS the relationship between the ratios of saving and investment over GDP for the period 1960-1974, as well as for three subperiods (1960-1964, 1965-1969 and 1970-1974). In particular, they estimate the following equation:

$$\begin{aligned} (\frac{I_{i}}{Y_{i}})=\alpha +\beta (\frac{S_{i}}{Y_{i}}) \end{aligned}$$

(1)

where $({I_i}/{Y_i})$ is the ratio of gross domestic investment to GDP and $({S_i}/{Y_i})$ is the ratio of gross domestic saving to GDP. The $\beta$ coefficient is called the saving-retention coefficient that measures how changes in the national investment ratio are explained by exogenous changes in the domestic saving ratio.

The authors argue that in a world with perfect capital mobility, $\beta$ should be zero for small countries, whereas it would represent their share of the world capital stock for large countries. The reason for $\beta$ to be zero is that in a world with fully integrated capital markets, any exogenous variation in domestic savings should not affect domestic investment, arguing that capital would move to the countries with the highest return. In contrast, in a closed economy, the saving-retention coefficient should be 1 because the domestic savings accommodate all variations in domestic investment.

Feldstein and Horioka (1980) found a $\beta$ coefficient of 0.88. They argued that this coefficient implied that international capital mobility and the degree of integration of the international capital markets were low. This unexpected result has been tested in many papers but has remained robust in the cross-section analysis. However, as it confronts what international macroeconomics predicts in a process of globalization, it has been coined as the “Feldstein-Horioka puzzle”.

2.2 Survey On the Main Empirical Literature

Obstfeld and Rogoff (2000) refer to it as “the mother of all puzzles” and, consequently, has given rise to extensive literature trying to solve it. This literature can be classified into three categories⁶. While the first focuses on theoretical developments, the second line of research explores possible problems present in the studies (sample selection problems, endogeneity problems, or data problems). Finally, a third strand of the literature has emphasized the need to improve the econometric techniques since the seminal cross-section studies might overestimate or underestimate the value of the saving-retention coefficient. We will limit ourselves to surveying the time series or panel data literature, but always with a time perspective.

Among the time-series studies, Feldstein and Horioka (1980) also ran annual time-series for the original FH sample finding an average saving-retention coefficient of 0.64. Obstfeld (1986) obtained a saving-retention coefficient from 0.13 to 0.91. Tesar (1991) and Frankel (1991) also used time series and the latter showed that the saving-investment correlation had fallen from the 1980s in the US. Also, in this literature, Miller (1988) studies the existence of cointegration between saving and investment over the period 1946-1987, finding that there only was cointegration under a fixed exchange rate regime. However, Gulley (1992) did not find any cointegrating relationship between the variables in any exchange rate regime. This result was confirmed by Sarno and Taylor (1998). Leachman (1991) and Sinha (2002) did not find cointegration using a sample of 23 OECD economies, probably due to the low power of the Engle-Granger two-step procedure. To overcome this problem, other authors such as Jansen and Schulze (1993) used an error correction model to verify the existence of a long-run relationship and found more evidence in favor of cointegration.

The analysis implemented in Kejriwal (2008) deserves special attention, as it revisits the FH puzzle for 21 OECD countries with data ending in 2000. He finds evidence from 1 to 3 regime changes and considers that part of the evidence in favor of the puzzle may be due to non-accounting for the non-stationarity of the variables and the existence of structural breaks. Ketenci (2012) applies the same econometric methodology than Kejriwal (2008) and estimates the $\beta$ coefficients determined by the breaks. However, her findings do not support FH’s result for the EU countries.

Concerning panel data techniques, the literature is non-conclusive. While some papers, like Krol (1996), Coakley and Kulasi (1997), Corbin (2001), Kim (2001), Coakley et al. (2004) and Narayan (2005), find similar results as using time-series, other authors criticize the panel methodology, as the results would not be valid if no regime change is allowed for. However, there is not much literature on the FH puzzle allowing for structural breaks. A prominent example is Ho (2000), who includes structural changes in the cointegrated relationship as well, arguing that the saving-investment relationship may be subject to regime changes.⁷

Focusing on the European case, Katsimi and Zoega (2016) use the difference-in-difference method in a panel of 19 EU countries for 1960-2014, with promising results; Drakos et al. (2018) assess the relationship between domestic saving and investment for 14 EU countries for the period 1970-2015, finding that there is weak evidence in favor of the FH and that the long-run solvency condition is achieved. But and Morley (2017), applying panel techniques for a sample of OECD countries (therefore including some Eurozone countries), found that the correlation between domestic saving/investment dropped to record levels right before the 2008 financial crisis, and the puzzle returns afterward. Their results also suggest that the puzzle for net capital-importing and capital-exporting countries differs. In this line, Ketenci (2018) using GMM techniques analyzes the impact of the 2008 financial crisis on the level of capital mobility, finding an insignificant impact. Finally, Camarero et al. (2020) developed a time-varying parameters state-space model applied to panel data covering 12 EU countries, where they show the evolution along time of the FH coefficient as a by-product of a more general OECD sample.⁸

Finally, the ECB performs periodical studies on the degree of financial integration in the Eurozone. ECB (2018) and ECB (2020) analyzes how financial integration has evolved in the Eurozone⁹ concluding that it increased after the creation of the euro with a reversion of the trend after the 2007 financial crisis that stopped after the introduction of the Outright Monetary Transactions (OMT) program and the banking union announcement. To assess the degree of financial integration, the ECB uses two approaches. First, in ECB (2018), following the two seminal papers of Lewis (1995) and Asdrubali et al. (1996), the ECB examines the evolution of cross-country risk-sharing in the Eurozone and finds that risk-sharing is still low and unstable, with an increase in the correlation between consumption and output dynamics after the financial and sovereign crisis. Second, in ECB (2018) appears an analysis of the degree of financial integration in the Eurozone and the fulfillment of the FH puzzle. The approach followed was to augment the usual FH equation with country-specific variables to account for global shocks affecting those economies. However, the report highlights that the estimation is highly volatile, making the interpretation of the results difficult, which calls for further research.

3 Econometric Analysis: Unit Roots, Cointegration and Stability

This section examines the link between domestic investment and saving using cointegration techniques that allow for multiple structural breaks. Although we closely follow the empirical strategy developed by Kejriwal (2008), we first apply Perron and Yabu (2009) stability test, and only then, depending on whether the individual series are found to be stable, we use the proper specification of the unit root tests. Sequentially, the econometric procedure is as follows. First, we apply Perron and Yabu (2009) pre-test to assess the stability of each individual saving and investment series. Next, to determine the order of integration of the variables, if the series were found stable (that is, when we cannot reject the null hypothesis of stability in the Perron-Yabu test), we use the unit root test proposed by Ng and Perron (2001). For the non-stable series, we apply the unit root tests with breaks by Carrion-i Silvestre et al. (2009). In a third step, we test for the stability of the domestic saving-investment relationship (and select the number of breaks) using the test proposed by Kejriwal and Perron (2010). After that, we verify that the variables are cointegrated with tests allowing for multiple structural breaks in the coefficients as proposed by Arai and Kurozumi (2007) and Kejriwal (2008). Finally, for the cases where we find cointegration between the two variables, we estimate the model including the breaks to assess if the relationship between domestic investment and saving (the slope parameter $\beta$) has changed over time.

The robustness of our findings is checked using two alternative methodologies: MG/PMG estimators in panel data for the analysis of the cointegration relationships and rolling windows regressions to assess the time-varying nature of the savings retention coefficient. The rationale for both robustness checks goes as follows. First, given that we have a large panel of countries for a very long-time span, it can be an interesting exercise to run a mean group estimator and a pooled mean group estimator to uncover how the savings retention coefficient changes both in the long run and short run. Indeed, the recent literature on dynamic heterogeneous panel estimation in which both N and T are large suggests using the MG estimator proposed by Pesaran and Smith (1995) where the intercepts, slope coefficients, and error variances are all allowed to differ across groups. Moreover, the PMG estimator (Pesaran et al. 1999) combines both pooling and averaging, allowing the intercept, short-run coefficients, and error variances to differ across groups (as would the MG estimator) but constraining the long-run coefficients to be equal for all the groups (as would the FE estimator). In a second stage, as it may seem unlikely that international capital mobility is governed only by abrupt events, we use a rolling window regression to analyze the discontinuities along time in the savings retention coefficient. Indeed, due to different reasons (menu cost, technological progress, or policy time lags), we think that letting the FH regression parameter vary overtime to capture this effect can be an interesting robustness check.¹⁰

As our interest is focused on the evolution of the savings-investment relationship in the EU and the role of the economic-integration related events¹¹ on this relationship, we have tried to obtain as much information as possible from the data. Annual data is only available for some of the countries: Austria (Aus), Belgium (Bel), Finland (Fin), Germany (Ger), Ireland (Ire), Italy (Ita), Luxembourg (Lux), Portugal (Por) and Spain (Spa) for the period 1970-2019. In the case of Cyprus (Cyp), it starts in 1975, Greece (Gre) and France (Fra) in 1960, and the Netherlands (Net) in 1969. The source is the World Bank (WB) database. Quarterly data was available for all the EU countries, for most of them starting in 1995 and has been obtained from the International Financial Statistics (IFS) of the IMF. Estonia, Latvia, Lithuania, Malta, Slovak Republic, and Slovenia have been only included in the quarterly analysis¹². The reason for the combination of annual and quarterly data is that annual data is generally available for a longer sample period, usually from 1970, whereas quarterly data is only available from 1995. We are applying the analysis to the data in the two frequencies. First, to include as many EU countries as possible, but more importantly, because the techniques used to endogenously detect the instabilities leave out observations from the beginning and the end of the sample due to the trimming. Therefore, to capture potential structural breaks at the end of the sample (after the 2007 financial crisis), quarterly data is necessary¹³.

The variable used to measure investment is gross fixed capital formation, whereas, for saving, we use “basic saving”, as recommended by Baxter and Crucini (1993). This variable is defined as GDP minus total consumption (both public and private); the two variables are expressed as a percentage of GDP. Quarterly data has been seasonally adjusted.

3.1 Stability. Perron and Yabu (2009) Test

As a pre-test, we start by applying the Perron and Yabu (2009) test for structural changes in the deterministic components of a univariate time series when it is a priori unknown whether the series is stationary – I(0) case – or contains an autoregressive unit root – I(1) case. The Perron-Yabu test statistic, called $EXP-Wfs$, is based on a quasi-Feasible Generalized Least Squares (FGLS) approach using an autoregression for the noise component, with a truncation to 1 when the sum of the autoregressive coefficients is in some neighborhood of 1, along with a bias correction. For given break dates, Perron and Yabu (2009) propose an F-test for the null hypothesis of no structural change in the deterministic components using the Exp function.

Table 1 shows the Perron and Yabu (2009) stability test. Models I, II, and III have been included since there is no common pattern in the series to discard the others (level change, trend change or both). For annual data, the results of the $Exp-WRQF$ test show stronger evidence in favor of structural breaks in the time series, rejecting the null hypothesis of absence of structural breaks for 15 out of 26 cases. In line with the annual data analysis, from the quarterly results we reject the null hypothesis for 25 out of 38 time series.

In the case of quarterly data, the two variables follow different behavior: investment is found to be unstable for most of the countries (except for 4 out of 19); for savings, in contrast, there is stronger evidence in favor of stability. This may be due to the dependence of investment on the economic cycle, hence its higher volatility. The savings rate may be affected by long-term factors that change more slowly, such as demography or the cultural propensity to save.

3.2 Order of Integration

Once stability has been assessed, we apply the unit root tests proposed by Ng and Perron (2001) to the stable series, whereas for the unstable ones (the cases in which we could reject the null of stability), we have applied the GLS-based unit root tests with multiple structural breaks –both under the null and the alternative hypotheses– proposed in Carrion-i Silvestre et al. (2009)¹⁴. Previous unit root tests with a structural change in an unknown break date, such as Zivot and Andrews (1992) or Perron (1997), assumed that if a break occurs it does so only under the alternative hypothesis of stationarity. Carrion-i Silvestre et al. (2009) propose a class of modified tests, called $M^{GLS}$, as M tests¹⁵, that use GLS detrending of the data as proposed in Elliott et al. (1996), and the Modified Akaike Information Criterion (MAIC) to select the order of the autoregression. We use Model III and II (structural breaks with trend and constant change and structural break with trend change, respectively) allowing for up to three breaks.

Table 2 shows the Ng and Perron (2001) unit root test for the stable variables. For both, annual and quarterly time series, with the exception of Germany (annual data) the null of a unit root cannot be rejected at the $1\%$ level of significance (although Luxembourg (investment) and Portugal is rejected at the $5\%$ of significance).

Concerning the variables that are considered unstable, Tables 3, 4, 5 and 6 show the unit root tests results proposed by Carrion-i Silvestre et al. (2009) for annual and quarterly data. For annual data, Carrion-i Silvestre et al. (2009) test allowing up to 3 breaks shows that all the time series contain a unit root. For quarterly data, evidence in favor of a unit root in the time series is generally found, except for some cases¹⁶.

3.3 Cointegration and Structural Breaks Tests

As the results of Subsection 3.1 point to instabilities in many variables across countries, in this subsection we test for cointegration accounting for potential structural breaks. We follow mostly the proposals of Kejriwal (2008) and Kejriwal and Perron (2010), as they allow for both I(1) and I(0) regressors and multiple breaks. However, we also apply Arai and Kurozumi (2007) test of the null of cointegration against the alternative of non-cointegration.

Kejriwal and Perron (2010) consider a sequential test of the null hypothesis of k breaks versus the alternative of $k+1$ breaks. As a complementary procedure to select the number of breaks we use the Bayesian Information Criterion (BIC) proposed by Yao (1988) and the LWZ criterion proposed by Liu et al. (1997). Kejriwal (2008) and Kejriwal and Perron (2010) show that the structural change tests can suffer from important lack of power against spurious regression (i.e., no cointegration). This means that these tests could reject the null of stability when the regression is really a spurious one. In this sense, tests for breaks in the long run relationship are used in conjunction with tests for the presence or absence of cointegration allowing for structural changes in the coefficients. This is the way we proceed in this subsection.

First, we test for structural changes in the relationship between saving and investment. In Table 7, we report the stability tests and the number of breaks selected using the sequential procedure (S) and the two information criteria, the BIC (B) and LWZ (L). Given the span of data, we allow for up to three breaks¹⁷ in both the annual and quarterly analysis. Based on the recommendation of Bai and Perron (2003), we rely on the BIC and the Sequential criterion¹⁸. Using annual data (section A of Table 7), we find between one and three breaks, with the exception of Belgium, Greece, the Netherlands, Portugal and Spain that, according to the sequential and LWZ method have no break. Concerning the quarterly data, in section B, the majority of the countries have two or three breaks. Cyprus, Ireland, Latvia, Luxembourg, Malta and the Netherlands have just one, whereas Finland, France and Italy have none.

The previous stability tests may also reject the null of coefficient stability when both variables are not cointegrated. Thus, we need to test for cointegration, used as confirmatory test¹⁹.

We consider two different tests²⁰. First, the traditional Phillips-Perron and ADF tests for the null hypothesis of no cointegration without breaks²¹. The second cointegration test takes into account possible breaks in the cointegrated relationship. Arai and Kurozumi (2007) allows up to three structural breaks, the number being selected by the sequential procedure, the BIC and LWZ criteria.

For the relationships that were found to be stable, we report in Table 8 the traditional Phillips-Perron and ADF tests. For annual data, in section A of the table, the null of non-cointegration is rejected for Greece and the Netherlands. However, for quarterly data, the null hypothesis of non-cointegration is rejected for Finland, Ireland, Luxembourg and the Netherlands.

Then, we use the residual-based test of the null of cointegration with an unknown single break against the alternative of no cointegration proposed in Arai and Kurozumi (2007). They propose a LM test based on partial sums of residuals where the break point is obtained by minimizing the sum of squared residuals and consider three models: i) Model I, level shift; ii) Model II, level shift with trend; iii) and Model III, regime shift.

For our analysis and given what economic theory suggests, we only consider model III, that can be written as follows:

$$\begin{aligned} y_t=c_i+z^{\prime }_t\beta _i+u_t \ \ \ if \ \ (T_{i-1}<t\leqslant T_i) \end{aligned}$$

(2)

To correct for potential endogeneity of the regressors, equation (2) is augmented with leads and lags of the first differences of the I(1) regressors, such as:

$$\begin{aligned} y_t=c_i+z^{\prime }_t\beta _i+\sum ^{l_T}_{J=-l_{T}}\Delta Z^{\prime }_{t-j}\prod _j+u^{*}_t \ \ \ if \ \ T_{i-1}<t\leqslant T_i \end{aligned}$$

(3)

The LM test statistic (for one break), $\tilde{V}_{1}(\hat{\lambda })$, is given by:

$$\begin{aligned} \tilde{V}_{1}(\hat{\lambda })=(T^{-2}\sum \limits _{t=1}^{T}S_{t}(\hat{\lambda })^{2})/\hat{\Omega }_{11} \end{aligned}$$

(4)

where $\hat{\Omega }_{11}$ is a consistent estimate of the long run variance of $u_{t}^{*}$ in (7), the date of break $\hat{\lambda }=(\hat{T}_{1}/T,...,\hat{T}_{k}/T)$ and $(\hat{T}_{1},...\hat{T}_{k})$ are obtained using the dynamic algorithm proposed in Bai and Perron (2003).

The Arai and Kurozumi (2007) test is more restrictive, as only a single structural break is considered under the null hypothesis. Hence, the test may tend to reject the null of cointegration when the true data generating process exhibits cointegration with multiple breaks. To avoid this problem, Kejriwal (2008) extended its test by including multiple breaks under the null hypothesis of cointegration. The Kejriwal (2008) test of the null of cointegration with multiple (k) structural changes is denoted $\tilde{V}_{k}(\hat{\lambda })$.

Concerning the results, Tables 9 and 10 show the Arai and Kurozumi (2007) cointegration test up to three breaks. Using annual data, we cannot reject the null of cointegration for any country, whereas for the quarterly data the null is rejected for the case of one break for Cyprus, as well as of two breaks for Belgium, The Netherlands and the Slovak Republic (sequential criteria). Finally, when three breaks are considered, the null is rejected for Austria (Sequential, BIC and LWZ criteria), France, Greece, Italy and Portugal (sequential criteria).

4 A Linear Cointegrated Regression Model with Multiple Structural Changes

Accounting for parameter shifts is crucial in cointegration analysis since it typically involves long data spans that are more likely to be affected by structural breaks. In particular, Kejriwal (2008) and Kejriwal and Perron (2010) provide a comprehensive treatment of the problem of testing for multiple structural changes in cointegrated systems. More specifically, they consider a linear model with m structural changes (i.e., $m+1$ regimes) such as:

$$\begin{aligned} y_t=c_t+z_{ft}^\prime \delta _f+z_{bt}^\prime \delta _{bj}+x_{ft}^\prime \beta _f+x_{bt}^\prime \beta _{bj}+u_t\ \ \ \ \ (t=T_{J-1}+1,...,T_J) \end{aligned}$$

(5)

for $j=1,...,m+1$, where $T_{0}=0$, $T_{m+1}=T$ and T is the sample size. In this model, $y_{t}$ is a scalar dependent I(1) variable, $x_{ft}(p_{f}\times 1)$ and $x_{bt}(p_{b}\times 1)$ are vectors of I(0) variables while $z_{ft}(q_{f}\times 1)$ and $z_{bt}(q_{b}\times 1)$ are vectors of I(1) variables²². The break points $(T_{1},...,T_{m})$ are treated as unknown.

The general model (5) is a partial structural change model in which the coefficients of only a subset of the regressors are subject to change. In our case, we assume that $p_{f}=p_{b}=q_{f}=0$, and the estimated model is a pure structural change model where all coefficients of the I(1) regressors and deterministic components are allowed to change across regimes:

$$\begin{aligned} y_{t}=c_{j}+z_{bt}^{\prime }\delta _{bj}+u_{t} \ \ \ \ (t=T_{j-1}+1,...,T_{j}) \end{aligned}$$

(6)

Generally, the assumption of strict exogeneity is too restrictive and the test statistics for testing multiple breaks are not robust to the problem of endogenous regressors. To deal with the possibility of endogenous I(1) regressors, Kejriwal (2008) and Kejriwal and Perron (2010) propose to use the so-called dynamic OLS regression (DOLS)²³ where leads and lags of the first-differences of the I(1) variables are added as regressors, as suggested Saikkonen (1991) and Stock and Watson (1993):

$$\begin{aligned} y_{t}=c_{i}+z_{bt}^{\prime }\delta _{bj}+\sum \limits _{j=-l_{T}}^{l_{T}}\Delta z_{bt-j}^{\prime }\Pi _{bj}+u_{t}^{*} \ \ \ \ if \ \ T_{i-1}<t\le T_{i} \end{aligned}$$

(7)

for $i=1,...,k+1$, where k is the number of breaks, $T_{0}=0$ and $T_{k+1}=T$.

In order to test the relationship between domestic investment and domestic saving, the empirical studies commonly used a linear regression model such as:

$$\begin{aligned} I_{t}=\alpha +\beta S_{t}+\varepsilon _{t} \end{aligned}$$

(8)

As it has been earlier explained in this Section, and because there are only two variables in the estimated long-run relationship, when there is no structural break we will simply estimate the model by OLS (Table 11). When there are instabilities in the relationship, we estimate by DOLS and the results are presented in Tables 12, 13 and 14. Thus, if we find no evidence of cointegration for a given country (for any number of breaks), we will conclude that there is no long-run relationship between domestic saving and domestic investment. Therefore, this would be interpreted as “perfect capital mobility” (as this is the case using quarterly data for Austria or Belgium).

4.1 Individual Regression Results Including the Structural Breaks

We should emphasize that we have analyzed two different periods: 1970²⁴-2019 using annual data and 1995-2019 with quarterly data. In addition, we have estimated country-by-country equations, allowing for structural breaks and trying to use as much information as possible about each of the countries in the sample. Therefore, early stages of monetary integration may be captured with the annual sample, whereas the effects of deeper monetary integration are more likely to be detected in the quarterly data sample. It is worth to emphasize that there is not a priori classification in country groups for the analysis. On the contrary, the groupings are the output from our empirical results. Clearly, CEEC are not included in the annual data. Therefore, the patterns are confined to core and peripheral countries, and between bailed out and non-bailed out among the seconds. However, for the quarterly data (1995-2019), CEE countries are also included and they show particular features in the financial integration process reflected in common break points that differ from older member countries, either core or peripheral.

In Table 11, we present the results for the OLS regression. However, the OLS results are only interpretable in the case that 0 breaks have been identified with the Sequential, BIC and LWZ procedure, and the null hypothesis of non-cointegration is rejected for the ADF-PP Cointegration test (Table 8). Therefore, we can interpret the cases of Greece and the Netherlands for the annual data, whereas, for the quarterly data, we can interpret the OLS regression for Finland, Ireland, Luxembourg and Netherlands. The OLS results show a high degree of capital mobility except for Greece (annual data) and Ireland (quarterly data), which show a relatively larger coefficient. Next, we report the regression results with breaks, in which we would be able to analyze how capital mobility has changed over time.

We start by interpreting the annual data covering the different integration steps. The first salient feature of the results summarized in Table 12 is that most of the breaks are found in the 80s and 90s. However, in some cases, as in Ireland, Italy, Luxembourg and The Netherlands, the last break is found in 2010. To ease the interpretation of the results, we split the sample into three country groups: the first group includes the “core countries”: Austria, Belgium, France, Germany, Luxembourg and the Netherlands. There is clear evidence of a decrease in the value of the saving-retention coefficient over time that generally becomes statistically indistinguishable from zero (or negative, which will be taken as evidence of perfect capital mobility). Austria, Belgium, France and Germany achieved perfect capital mobility in the 1990s (with the start of the Single Market), even before the euro; in the case of Germany, later in the 1990s, due to the German reunification. For France, annual data shows that capital mobility was minimal from 1960 until 1992, with perfect capital mobility afterward. Some facts should be brought to attention: the period from mid-eighties until the EMS crisis (1992-1993) is one of financial turmoil; our analysis is able to capture this effect, as the evidence of capital mobility is very limited. Finally, in Austria and Belgium the third break occurred in 2007 and 2008, respectively. The parameter obtained for the last sample period increases for Austria (reaching a value between 0.55 and 0.62) with a decrease in capital mobility after the crisis, and around 1 for Belgium.²⁵

The second group of countries includes the periphery²⁶ (Cyprus, Greece, Ireland, Portugal and Spain). They share similar patterns: a continuous improvement in capital mobility in parallel with the integration process (the signature of the Maastricht Treaty and the road to EMU), altered by the financial turmoil in the beginning of the 90s (EMS crisis) and the 2007 financial crisis²⁷. The rest of the countries (i.e., Finland and Italy) show different patterns; for instance, Italy would have high capital mobility before the crisis and a large parameter (probably upwards biased) after the 2007 financial crisis. In Finland, evidence favoring capital mobility is found for the period 1979 to 1992; however, the coefficient increases after 1992, probably after being hit by the crash of the Soviet Union.

Having assessed capital mobility with annual data, we move to the quarterly analysis (Tables 13 and 14), starting in 1995 but extending our analysis for the period of the euro setup until the 2007 financial crisis and the subsequent events. We first find that the annual data regression provides similar results as the quarterly analysis for the shared period but, as the number of observations is considerably larger, the algorithm allows for more structural breaks to be found and richer results. As an illustration, we can take the case of Finland. Using annual data, we find a structural break in 1980 and the second one in 1992: the effects of a shock had relatively long-lasting effects, as the USSR crash was captured in 1992; however, for the quarterly analysis, the first structural break was found in 1994. In both cases, the conclusion is the same: the USSR crash caused the saving-retention coefficient to increase. However, the second break in Finland using quarterly data was found in 2005 and confirmed the maintenance of free capital mobility after joining the euro.

As in the case of annual data, we bundle the countries into different groups. Concerning the core countries (Austria, Belgium, Finland, France, Germany, Luxembourg and The Netherlands), we also obtain in this case that their degree of capital mobility is high (in the cases Austria, Belgium and France, this fact stems from the non-cointegrated relationship) and was achieved before the inception of the euro, or immediately afterward (as in Finland, Germany²⁸ or Luxembourg); moreover, the core countries do not seem to have suffered any impact from the crisis in terms of capital mobility. The case of the Netherlands is an outlier in this group since it is still displaying a relatively high coefficient. However, it should be pointed out that the Netherlands has a saving rate higher than the domestic investment rate, and the “saving glut” is invested abroad; therefore, the coefficient should not be interpreted as limited capital mobility.

The second set of countries are Central and Eastern countries (CEEC) that joined the EU and the euro later. Those countries received many capital inflows leading to increasing external disequilibria until the financial crisis in 2007. However, in terms of capital mobility, they show different behavior; Estonia (as Spain before) has received an increasing amount of capital inflows (until 2007) with a critical part invested in the non-tradable sector (housing). This fact is captured by a large coefficient explained by improved investment opportunities: domestic savings keep being invested at home. In 2009, when the housing bubble burst, it caused a large external disequilibrium and a dramatic fall in the level of capital mobility. Latvia’s (3 breaks)²⁹ shows a relatively low coefficient before the crisis; however, capital mobility started decreasing during the crisis as well as in the aftermath. In the case of Lithuania (3 breaks)³⁰ the situation is quite similar to Latvia’s, showing a “crisis effect” on capital mobility. However, in this case, the housing bubble explains the reason behind the reduction in capital mobility. The Slovak Republic displays, in turn, a high level of capital mobility since the first quarter of 2000, and the crisis seems not to have affected capital mobility (mainly because credit lending did not result in a large external disequilibrium). Concerning Slovenia, it had high capital mobility at the beginning of the sample but was altered by the crisis (a decrease in capital mobility). However, after 2010 the previous capital mobility levels have been restored (with a slight decrease in capital mobility after 2016 according to the (S) regression).

The third set of countries are Cyprus, Greece, Ireland, Portugal, and Spain. They were bailed out from 2010 to 2015, and our analysis captures their financial stability programs. In the case of Cyprus (BIC regression)³¹ shows no capital mobility until Q2 2012 (when it requested assistance from the Eurozone and the IMF). Afterward, it shows an increase in capital mobility; the other break (Q2 2016) closely coincides with the Cyprus exit of the bailout program; in this case, high capital mobility remains. The case of Greece is similar to Cyprus as it showed a low level of capital mobility before Q3 2010 when the first bailout occurred (May 2010). After the bailout, the retention coefficient would be compatible with capital mobility. However, as Greece’s exit of the financial assistance program took place in the third quarter of 2018, we cannot capture it. Ireland (sequential procedure)³² shows limited capital mobility (more restricted during the crisis period); however, the trend reverts during the period of the financial assistance program (displaying perfect capital mobility) and, again, returns to high capital mobility after the end of the program. We have obtained a large coefficient in both Portugal and Spain before the ESM programs (S)³³, decreasing afterward (perfect capital mobility for the case of Portugal and a slight improvement for Spain).

The remaining two countries are Malta and Italy, for which we conclude that there has been perfect capital mobility during the whole period.

4.2 Robustness Checks

In this Section, we perform two additional robustness checks³⁴. First, we test if the paper’s main conclusions can still be valid after using a panel framework instead of individual time series. The analysis of an economic integrated area as the EA can be improved using panel data, as it enriches the information included in the analysis. For that purpose, we use the Mean Group (MG) (Pesaran and Smith 1995) and the Pooled Mean Group (PMG) estimators (Pesaran et al. 1999)³⁵ to different groupings and time spans. Second, we perform a rolling-window regression over the individual series to assess the expected time-varying nature of the savings retention coefficients.

It is important to clarify that the country groups in the individual time series analysis and the one performed with panel data are not exactly the same. In the first case, we have followed an empirical approach to bundle the countries in different groups without any prior. This means that the classification is made based on the results obtained, when they share similar breaks, giving rise to 3 or 4 groupings, depending on the annual or quarterly nature of the data.³⁶ However, for the panel data analysis we only consider two groups: core vs. periphery with annual data (1070-2019) or core vs. rest of the countries (1996-2019); in the latter case CEEC are added to the peripheral countries. Due to the small n-dimension of the panel, we have limited the analysis to these two groupings instead of the more disaggregated assessment performed with the individual time series.

Regarding the panel approach, Table 15 shows the PMG/MG estimation of the annual and quarterly data. Some features become apparent for the annual data covering 1970-2019: first, the whole sample regression shows a low saving retention parameter in both the long and short term; therefore, an overall high degree of capital mobility is observed. Second, if we split our sample into core and periphery countries³⁷ our results point out that capital mobility is higher for the core countries. Concerning quarterly data covering from Q1 1996 to Q4 2019, our results capture an increase in the long-run parameter (decrease in capital mobility). The subgroups regression highlights two relevant conclusions: First, core countries have perfect capital mobility in both the long and short term. Second, the periphery and the CEEC show a moderate level of capital mobility in the long run; this can be seen as the relevant impact of those countries’ financial and sovereign crises. Overall conclusions of the panel approach give evidence in favor of a high degree of capital mobility for the core countries, whereas, for the periphery and CEEC, the results for the period Q1 1996-Q4 2019 point that the financial and sovereign crises have had a more substantial impact on capital mobility. Conclusions are in line with this paper’s overall conclusions and highlight the importance of taking into account structural breaks to properly isolate the impact of the financial crisis on the periphery and the CEEC.

As the last step, we have performed a simple rolling-window regression³⁸ over the individual time series. Conclusions are similar to the linear cointegrated regression with breaks presented in this paper. However, a few differences have been noted: first, for the case of Cyprus (quarterly data) from Q2 2016 (BIC approach), Cyprus does not show a perfect degree of capital mobility but a moderate degree instead. Second, Ireland shows a perfect degree of capital mobility from Q4 2015, whereas a moderate degree of capital mobility is observed with the rolling-window regression. In any case, we find that the overall conclusions of this paper are robust.

5 Conclusions

In this paper, we have studied the evolution of capital mobility for the 19 countries of the Eurozone during the period 1970-2019 using both annual and quarterly data. While most of the earlier literature focuses on the price approach, we adopt the quantity one. The latter can be especially suited to assess the evolution of capital mobility within a monetary union where external imbalances have been persistently growing up to the Great Recession. From an econometric approach standpoint, we base our analysis on the state-of-the-art cointegration econometrics of individual time series, allowing for discontinuities. One of the main benefits of the econometric methodology is that we are not imposing exogenously the breaks (that could bias the analysis), as they have been obtained endogenously as a result of the econometric analysis instead.

The main contributions of our analysis are, first, to identify different stages in the EU financial integration process up to the creation of the EMU; second, we analyze the evolution of the degree of capital mobility from the first years of the euro until the 2007 financial crisis distinguishing between core, peripheral and Central Eastern European countries; third, we can obtain a measure of the consequences of the financial crisis and the subsequent sovereign crisis on capital mobility; fourth, we have an appraisal of how the financial assistance programs affected the countries that were bailed out, and, finally, we can assess whether capital mobility increased after the European sovereign crisis.

Regarding our first question, our results confirm that the value saving-retention coefficient has, in general, been decreasing over time. This implies that the degree of capital mobility has been increasing during the 1990s after the Maastricht Treaty was signed, only to be affected by three critical events: the EMS crisis, the German reunification, and the USSR downfall.

Concerning the second question, our results confirm that European economic integration encouraged capital flows from the core countries to the periphery (Ireland, Greece, Portugal, and Spain). Our results also show a larger beta coefficient in these countries, meaning that a high domestic saving rate is invested domestically. Moreover, as a large proportion of foreign savings was invested in non-tradable sectors, such investment flows caused a boom and later created credit shortage after the 2007 financial crisis, ending with the sovereign crisis. As for the CEEC, in general, they have relatively low saving-retention coefficients after or even before their euro membership. Here, it is important to highlight two opposite cases: first, in Estonia (as in Spain), large capital inflows were invested in the non-tradable market (housing), causing a sizeable external disequilibrium. When the real state bubble burst, capital mobility decreased dramatically. Second, in the Slovak Republic, capital mobility was achieved after its EU membership, and despite the other CEEC, the financial crisis seems to have had no impact on capital mobility (such conclusion is in line with the quick recovery of the Slovak’s economy).

As for the impact of the financial (2007) and sovereign crises (2010-2015) on capital mobility, we find heterogeneous effects depending on the type of country. The impact can be summarized as follows: while core countries show no impact of the crisis on capital mobility, with some exceptions, in the periphery, capital mobility has decreased. Moreover, some countries’ capital mobility has not returned to its previous levels after the two crises.

Concerning the effects of the financial assistance programs on capital mobility, we find breaks in the series coinciding with the different financial assistance dates. More specifically, the period of financial assistance through the EFSM and ESM programs goes parallel with an improvement in capital mobility. However, after the program, some countries such as Cyprus and Ireland have returned to their previous levels of high capital mobility, whereas others (Portugal and Spain are prominent examples) have never recovered them.

Finally, in the period $2015-2019$, after the global financial and European sovereign crisis, capital mobility shows a signal of recovery for the majority of the Eurozone countries. That is the case for the core countries, Italy, Malta, Ireland, Latvia, Slovak Republic and Slovenia. However, it should be pointed out that the FH puzzle remains for Estonia, Lithuania, Portugal, and Spain. The likely explanation is that these countries were heavily affected by the boom and bust period (real state bubble)³⁹, which has harmed capital mobility, above all, after the bubble busted.

In terms of the FH puzzle, we have found that the value of the cointegrating relationship parameter between domestic saving and investment has been mostly dropping since the 1970s, along with the integration process until the euro’s creation. The first countries achieving a high degree of capital mobility have been from EU core. Driven by the financial crisis and market mistrust in the global financial and European sovereign crises, the puzzle returned for many peripheral countries, being more present in the countries with the highest external disequilibria.

Appendices

Figures

Fig. 1

Current Account

Fig. 2

Domestic saving and investment series

Tables

Table 1 Perron and Yabu (2009) tests for structural changes in the deterministic component

Table 2 Ng and Perron (2001) unit root test (stable series)

Table 3 Carrion-i Silvestre et al. (2009) unit root test with breaks (Unstable series)

Table 4 Carrion-i Silvestre et al. (2009) unit root test with breaks (Unstable series)

Table 5 Carrion-i Silvestre et al. (2009) unit root test with breaks (Unstable series). Quarterly data

Table 6 Carrion-i Silvestre et al. (2009) unit root test with breaks (Unstable series). Quarterly data. Continued

Table 7 Tests for the number of structural breaks (A-B)

Table 8 ADF and PP cointegration test without breaks (A-B)

Table 9 Arai and Kurozumi cointegration test: (1-2 breaks)

Table 10 Arai and Kurozumi cointegration test: (3 breaks)

Table 11 The individual OLS regression

Table 12 Estimated regression with breaks (annual data): 1970-2019

Table 13 estimated regression with breaks (quarterly data): Q1 1995 - Q4 2019

Table 14 estimated regression with breaks (quarterly data continued) Q1 1995 - Q4 2019

Table 15 Panel PMG/MG estimation