Skip to main content
SpringerLink
Log in

The mixed solutions of the (2+1)-dimensional Hirota–Satsuma–Ito equation and the analysis of nonlinear transformed waves

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

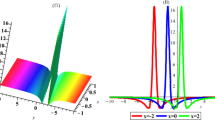
In this paper, we obtain the N-soliton solution for the \((2+1)\)-dimensional Hirota–Satsuma–Ito equation by the Hirota bilinear method. On this basis, the breathers and lumps can be obtained using the complex conjugate parameter as well as the long wave limit method, and the mixed solutions containing them are investigated. Then, different nonlinear transformed waves are obtained from breathers and lumps under specific conditions, which include quasi-anti-dark soliton, M-shaped soliton, oscillation M-shaped soliton, multi-peak soliton, quasi-periodic soliton and W-shaped soliton. Finally, on the basis of the two-breather solutions, we discuss in detail the mixed solutions consisting of one breather and one nonlinear transformed wave, and the mixed solutions formed by two nonlinear transformed waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  1. You, H.S.: Why teach science with an interdisciplinary approach: history, trends, and conceptual frameworks. J. Educ. Learn. 6(4), 66–77 (2017)

    Google Scholar 

  2. Dutta, H., Cortés, J.C., Agarwal, R.P.: Nonlinear hybrid systems and control in social and natural sciences. Chaos Solitons Fractals 165, 112900 (2022)

    MathSciNet  Google Scholar 

  3. Shen, S., Yang, Z.J., Pang, Z.G., Ge, Y.R.: The complex-valued astigmatic cosine-Gaussian soliton solution of the nonlocal nonlinear Schrödinger equation and its transmission characteristics. Appl. Math. Lett. 125, 107755 (2022)

    MATH  Google Scholar 

  4. Shen, S., Yang, Z.J., Li, X.L., Zhang, S.M.: Periodic propagation of complex-valued hyperbolic-cosine-Gaussian solitons and breathers with complicated light field structure in strongly nonlocal nonlinear media. Commun. Nonlinear Sci. Numer. Simul. 103, 106005 (2021)

    MathSciNet  MATH  Google Scholar 

  5. Wazwaz, A.M.: New \(\left(3+1 \right)\)-dimensional Painlev integrable fifth-order equation with third-order temporal dispersion. Nonlinear Dyn. 106(1), 891–897 (2021)

    Google Scholar 

  6. Wazwaz, A.M.: Painlevé integrability and lump solutions for two extended \(\left(3+1\right)\)- and \(\left(2+1\right)\)-dimensional Kadomtsev-Petviashvili equations. Nonlinear Dyn. 111(4), 3623–3632 (2023)

    Google Scholar 

  7. Zhang, R.F., Li, M.C., Gan, J.Y., Li, Q., Lan, Z.Z.: Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solitons Fractals 154, 111692 (2022)

    MathSciNet  MATH  Google Scholar 

  8. Zhang, R.F., Li, M.C., Albishari, M., Zheng, F.C., Lan, Z.Z.: Generalized lump solutions, classical lump solutions and rogue waves of the \(\left(2+1 \right)\)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada-like equation. Appl. Math. Comput. 403, 126201 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Zhang, R.F., Li, M.C., Cherraf, A., Vadyala, S.R.: The interference wave and the bright and dark soliton for two integro-differential equation by using BNNM. Nonlinear Dyn. 111(9), 8637–8646 (2023)

    Google Scholar 

  10. Biswas, A.: Soliton perturbation theory for Alfvén waves in plasmas. Phys. Plasmas 12(2), 022306 (2005)

    MathSciNet  Google Scholar 

  11. Pakzad, H.R.: Solitary waves of the Kadomstev-Petviashvili equation in warm dusty plasma with variable dust charge, two temperature ion and nonthermal electron. Chaos Solitons Fractals 42(2), 874–879 (2009)

    MATH  Google Scholar 

  12. Alexeev, B.V.: Application of generalized quantum hydrodynamics in the theory of quantum soliton’s evolution. J. Nanoelectron. Optoelectron. 3(3), 316–328 (2008)

    Google Scholar 

  13. Bonnemain, T., Doyon, B., El, G.: Generalized hydrodynamics of the KdV soliton gas. J. Phys. A: Math. Theor. 55(37), 374004 (2022)

    MathSciNet  MATH  Google Scholar 

  14. Crosignani, B., Porto, P.D.: Soliton propagation in multimode optical fibers. Opt. Lett. 6(7), 329–330 (1981)

    Google Scholar 

  15. Wang, Q., Wai, P.K.A., Chen, C.J., Menyuk, C.R.: Soliton shadows in birefringent optical fibers. Opt. Lett. 17(18), 1265–1267 (1992)

    Google Scholar 

  16. Beron-Vera, F.J.: Nonlinear dynamics of inertial particles in the ocean: from drifters and floats to marine debris and Sargassum. Nonlinear Dyn. 103(1), 1–26 (2021)

    MATH  Google Scholar 

  17. Guo, J., Hu, X., Ma, J., Zhao, L.M., Shen, D.Y., Tang, D.Y.: Anti-dark solitons in a single mode fiber laser. Phys. Lett. A 395, 127226 (2021)

    Google Scholar 

  18. Liang, A.H., Toda, H., Hasegawa, A.: High-speed soliton transmission in dense periodic fibers. Opt. Lett. 24(12), 799–801 (1999)

    Google Scholar 

  19. Dupac, M., Beale, D.G., Overfelt, R.A.: Three-dimensional lumped mass/lumped spring modeling and nonlinear behavior of a levitated droplet. Nonlinear Dyn. 42, 25–42 (2005)

    MATH  Google Scholar 

  20. Nakajima, H., Oh, P., Shin, S.: Quantum SUSY algebra of \(Q\)-lumps in the massive Grassmannian sigma model. J. Phys. A: Math. Theor. 42(12), 125401 (2009)

    MathSciNet  MATH  Google Scholar 

  21. Jian, Y.F., Bai, F.W., Falcoz, Q., Xu, C., Wang, Y., Wang, Z.F.: Thermal analysis and design of solid energy storage systems using a modified lumped capacitance method. Appl. Therm. Eng. 75, 213–223 (2015)

    Google Scholar 

  22. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, University of Colorado, Cambridge (1991)

    MATH  Google Scholar 

  23. Klibanov, M.V., Kolesov, A.E., Nguyen, D.L.: Convexification method for an inverse scattering problem and its performance for experimental backscatter data for buried targets. SIAM J. Imaging Sci. 12(1), 576–603 (2019)

    MathSciNet  Google Scholar 

  24. Ling, L.M., Zhao, L.C., Guo, B.L.: Darboux transformation and classification of solution for mixed coupled nonlinear Schrödinger equations. Commun. Nonlinear Sci. Numer. Simul. 32, 285–304 (2016)

    MathSciNet  MATH  Google Scholar 

  25. Chen, J.C., Ma, Z.Y., Hu, Y.H.: Nonlocal symmetry, Darboux transformation and soliton-cnoidal wave interaction solution for the shallow water wave equation. J. Math. Anal. Appl. 460(2), 987–1003 (2018)

    MathSciNet  MATH  Google Scholar 

  26. Ding, C.C., Gao, Y.T., Deng, G.F., Wang, D.: Lax pair, conservation laws, Darboux transformation, breathers and rogue waves for the coupled nonautonomous nonlinear Schrödinger system in an inhomogeneous plasma. Chaos Solitons Fractals 133, 109580 (2020)

    MathSciNet  MATH  Google Scholar 

  27. Huang, Q.M., Gao, Y.T., Jia, S.L., Wang, Y.L.: Bilinear Bäcklund transformation, soliton and periodic wave solutions for a \(\left(3+1 \right)\)-dimensional variable-coefficient generalized shallow water wave equation. Nonlinear Dyn. 87, 2529–2540 (2017)

    MATH  Google Scholar 

  28. Zhao, X.H., Tian, B., Xie, X.Y., Wu, X.Y., Sun, Y., Guo, Y.J.: Solitons, Bäcklund transformation and Lax pair for a \(\left(2+1 \right)\)-dimensional Davey–Stewartson system on surface waves of finite depth. Waves Random Complex Media 28(2), 356–366 (2018)

    MathSciNet  MATH  Google Scholar 

  29. Guo, B.L., Liu, N., Wang, Y.F.: A Riemann–Hilbert approach for a new type coupled nonlinear Schrödinger equations. J. Math. Anal. Appl. 459(1), 145–158 (2018)

    MathSciNet  MATH  Google Scholar 

  30. Li, Y., Tian, S.F., Yang, J.J.: Riemann–Hilbert problem and interactions of solitons in the component nonlinear Schrödinger equations. Stud. Appl. Math. 148(2), 577–605 (2022)

    MathSciNet  Google Scholar 

  31. Wang, D.S., Zhang, D.J., Yang, J.: Integrable properties of the general coupled nonlinear Schrödinger equations. J. Math. Phys. 51(2), 023510 (2010)

    MathSciNet  MATH  Google Scholar 

  32. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  33. Ma, W.X., Zhou, Y., Dougherty, R.: Lump-type solutions to nonlinear differential equations derived from generalized bilinear equations. Int. J. Mod. Phys. B 30(2829), 1640018 (2016)

    MathSciNet  MATH  Google Scholar 

  34. Hietarinta, J.: Hirota’s bilinear method and its generalization. Int. J. Mod. Phys. A 12(1), 43–51 (1997)

    MathSciNet  MATH  Google Scholar 

  35. Li, L., Duan, C.N., Yu, F.J.: An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation. Phys. Lett. A 383(14), 1578–1582 (2019)

    MathSciNet  MATH  Google Scholar 

  36. Yu, J.P., Sun, Y.L.: Study of lump solutions to dimensionally reduced generalized KP equations. Nonlinear Dyn. 87, 2755–2763 (2017)

    MathSciNet  Google Scholar 

  37. Gürses, M., Pekcan, A.: Nonlocal modified KdV equations and their soliton solutions by Hirota method. Commun. Nonlinear Sci. Numer. Simul. 67, 427–448 (2019)

    MathSciNet  MATH  Google Scholar 

  38. Zhang, R.F., Li, M.C.: Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 108(1), 521–531 (2022)

    Google Scholar 

  39. Zhang, R.F., Bilige, S.: Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 95, 3041–3048 (2019)

    MATH  Google Scholar 

  40. Scott, A.C., Chu, F.Y.F., McLaughlin, D.W.: The soliton: a new concept in applied science. Proc. IEEE 61(10), 1443–1483 (1973)

    MathSciNet  Google Scholar 

  41. Dang, Y.L., Li, H.J., Lin, J.: Soliton solutions in nonlocal nonlinear coupler. Nonlinear Dyn. 88, 489–501 (2017)

    Google Scholar 

  42. Singh, S., Sakkaravarthi, K., Tamizhmani, T., Murugesan, K.: Painlevé analysis and higher-order rogue waves of a generalized \(\left(3+1 \right)\)-dimensional shallow water wave equation. Phys. Scr. 97(5), 055204 (2022)

    Google Scholar 

  43. Wang, C.: Lump solution and integrability for the associated Hirota bilinear equation. Nonlinear Dyn. 87, 2635–2642 (2017)

    MathSciNet  Google Scholar 

  44. An, H.L., Feng, D.L., Zhu, H.X.: General M-lump, high-order breather and localized interaction solutions to the \(\left(2+1 \right)\)-dimensional Sawada-Kotera equation. Nonlinear Dyn. 98(2), 1275–1286 (2019)

    Google Scholar 

  45. Ma, W.X., Yong, X.L., Zhang, H.Q.: Diversity of interaction solutions to the \(\left(2+1 \right)\)-dimensional Ito equation. Comput. Math. Appl. 75(1), 289–295 (2018)

    MathSciNet  MATH  Google Scholar 

  46. Bi, K., Hao, H.Q., Zhang, J.W., Guo, R.: Soliton, breather-like and dark-soliton-breather-like solutions for the coupled long-wave-short-wave system. Nonlinear Dyn. 108(1), 543–554 (2022)

    Google Scholar 

  47. Liu, C., Yang, Z.Y., Zhao, L.C.: Vector breathers and the inelastic interaction in a three-mode nonlinear optical fiber. Phys. Rev. A 89(5), 055803 (2014)

    Google Scholar 

  48. Yuan, F., Cheng, Y., He, J.S.: Degeneration of breathers in the Kadomttsev–Petviashvili I equation. Commun. Nonlinear Sci. Numer. Simul. 83, 105027 (2020)

    MathSciNet  MATH  Google Scholar 

  49. Ma, W.X., Zhou, Y.: Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 264(4), 2633–2659 (2018)

    MathSciNet  MATH  Google Scholar 

  50. Sun, W.R., Wang, L., Xie, X.Y.: Vector breather-to-soliton transitions and nonlinear wave interactions induced by higher-order effects in an erbium-doped fiber. Physica A 499, 58–66 (2018)

    MathSciNet  MATH  Google Scholar 

  51. Bi, K., Guo, R.: The mixed solutions and nonlinear wave transitions for the \(\left(2+1 \right)\)-dimensional Sawada–Kotera equation. Phys. Scr. 97(10), 105205 (2022)

    Google Scholar 

  52. Liu, C., Yang, Z.Y., Zhao, L.C., Yang, W.L.: State transition induced by higher-order effects and background frequency. Phys. Rev. E 91(2), 022904 (2015)

    Google Scholar 

  53. Wang, C.J., Fang, H., Tang, X.X.: State transition of lump-type waves for the \(\left(2+1 \right)\)-dimensional generalized KdV equation. Nonlinear Dyn. 95, 2943–2961 (2019)

    MATH  Google Scholar 

  54. Zhang, X., Wang, L., Liu, C., Li, M., Zhao, Y.C.: High-dimensional nonlinear wave transitions and their mechanisms. Chaos 30(11), 113107 (2020)

    MathSciNet  MATH  Google Scholar 

  55. Chowdury, A., Kedziora, D.J., Ankiewicz, A., Akhmediev, N.: Breather-to-soliton conversions described by the quintic equation of the nonlinear Schrödinger hierarchy. Phys. Rev. E 91(3), 032928 (2015)

    MathSciNet  MATH  Google Scholar 

  56. Chowdury, A., Ankiewicz, A., Akhmediev, N.: Moving breathers and breather-to-soliton conversions for the Hirota equation. Proc. Math. Phys. Eng. Sci. 471(2180), 20150130 (2015)

    MathSciNet  MATH  Google Scholar 

  57. Wang, Z.J.: The interaction among kink, breather and lump in the \(\left(2+1 \right)\)-dimensional completely generalized Hirota–Satsuma–Ito equation. Phys. Scr. 96(3), 035202 (2020)

    Google Scholar 

  58. Hong, X., Manafian, J., Ilhan, O.A., Alkireet, A.I.A., Nasution, M.K.: Multiple soliton solutions of the generalized Hirota–Satsuma–Ito equation arising in shallow water wave. J. Geom. Phys. 170, 104338 (2021)

    MathSciNet  MATH  Google Scholar 

  59. Liu, W., Wazwaz, A.M., Zheng, X.X.: High-order breathers, lumps, and semi-rational solutions to the \(\left(2+1 \right)\)-dimensional Hirota–Satsuma–Ito equation. Phys. Scr. 94(7), 075203 (2019)

    Google Scholar 

  60. Zhou, Y., Manukure, S., Ma, W.X.: Lump and lump-soliton solutions to the Hirota–Satsuma–Ito equation. Commun. Nonlinear Sci. Numer. Simul. 68, 56–62 (2019)

    MathSciNet  MATH  Google Scholar 

  61. Zhou, Y., Manukure, S.: Complexiton solutions to the Hirota–Satsuma–Ito equation. Math. Methods Appl. Sci. 42(7), 2344–2351 (2019)

    MathSciNet  MATH  Google Scholar 

  62. Lü, X., Ma, W.X., Chen, S.T., Khalique, C.M.: A note on rational solutions to a Hirota–Satsuma-like equation. Appl. Math. Lett. 58, 13–18 (2016)

    MathSciNet  MATH  Google Scholar 

  63. Long, F., Alsallami, S.A., Rezaei, S., Nonlaopon, K., Khalil, E.M.: New interaction solutions to the \(\left(2+1 \right)\)-dimensional Hirota–Satsuma–Ito equation. Results Phys. 37, 105475 (2022)

    Google Scholar 

  64. Li, L.X., Dai, Z.D., Cheng, B.T.: Degeneration of \(N\)-soliton solutions for a \(\left(3+1 \right)\)-dimensional nonlinear model in shallow water waves. Nonlinear Dyn. 111(2), 1667–1683 (2023)

    Google Scholar 

  65. Zhao, X., Tian, B., Du, X.X., Hu, C.C., Liu, S.H.: Bilinear Bäcklund transformation, kink and breather-wave solutions for a generalized \(\left(2+1 \right)\)-dimensional Hirota–Satsuma–Ito equation in fluid mechanics. Eur. Phys. J. Plus 136(2), 1–9 (2021)

    Google Scholar 

  66. Aliyu, A.I., Li, Y.J.: Bell polynomials and lump-type solutions to the Hirota–Satsuma–Ito equation under general and positive quadratic polynomial functions. Eur. Phys. J. Plus 135, 1–10 (2020)

    Google Scholar 

  67. Zhang, Y., Zhao, H., Li, J.: The long wave limiting of the discrete nonlinear evolution equations. Chaos Solitons Fractals 42(5), 2965–2972 (2009)

    MathSciNet  MATH  Google Scholar 

  68. Zhang, Z., Yang, X.Y., Li, B., Wazwaz, A.M., Guo, Q.: Generation mechanism of high-order rogue waves via the improved long-wave limit method: NLS case. Phys. Lett. A 450, 128395 (2022)

    MathSciNet  MATH  Google Scholar 

  69. Kataoka, T.: Resonance theory of water waves in the long-wave limit. J. Fluid Mech. 722, 461–495 (2013)

    MathSciNet  MATH  Google Scholar 

  70. Ablowitz, M.J., Satsuma, J.: Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 19(10), 2180–2186 (1978)

    MathSciNet  MATH  Google Scholar 

  71. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20(7), 1496–1503 (1979)

Download references

Acknowledgements

We express our sincere thanks to each member of our discussion group for their suggestions. This work has been supported by the National Natural Science Foundation of China under Grant No. 11905155, and the Fund Program for the Scientific Activities of Selected Returned Overseas Scholars in Shanxi Province under Grant No. 20220008.

Funding

This work has been supported by the National Natural Science Foundation of China under Grant No. 11905155, the Fund Program for the Scientific Activities of Selected Returned Overseas Scholars in Shanxi Province under Grant No. 20220008.

Author information

Authors and Affiliations

  1. School of Mathematics, Taiyuan University of Technology, Taiyuan, 030024, China

    Yong-Ning An & Rui Guo

Authors
  1. Yong-Ning An
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rui Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rui Guo.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

An, YN., Guo, R. The mixed solutions of the (2+1)-dimensional Hirota–Satsuma–Ito equation and the analysis of nonlinear transformed waves. Nonlinear Dyn 111, 18291–18311 (2023). https://doi.org/10.1007/s11071-023-08791-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08791-2

Keywords

Search

Navigation