Skip to main content

Advertisement

SpringerLink
Log in

Nonlinear feedback synthesis and control of periodic, quasiperiodic, chaotic and hyper-chaotic oscillations in mechanical systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

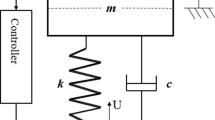
Self-excited periodic, quasiperiodic and chaotic oscillations have many significant applications in engineering devices and processes. In the present paper, a centralized nonlinear controller is proposed to artificially generate and control self-excited periodic, quasiperiodic, chaotic and hyper-chaotic oscillations of required characteristics in a fully actuated n-DOF spring-mass-damper mechanical system. The analytical relations among the amplitude, frequency and controller parameters for minimum control energy have been obtained using the method of two-time scale. It is shown that the proposed control can generate modal and nonmodal self-excited periodic and quasiperiodic oscillations of desired amplitude and frequency for minimum control energy. The analytical results have been verified numerically with MATLAB SIMULINK. Bifurcation analysis and extensive numerical simulations reveal a region of multistability in the plane of control parameters, where system responses may be periodic, quasiperiodic, chaotic and hyper-chaotic depending on initial conditions. However, it has been shown that the probability of obtaining chaotic and hyper-chaotic oscillations is very high for a wide range of controller parameters. The procedures of controlling the amplitude, frequency and characteristics of chaotic oscillations are also discussed. The results of the present paper are expected to find applications in various macro- and micro-mechanical systems and applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

Data availability

No Data are used in the current study.

References

  1. Babitsky, V.I.: Autoresonant mechatronic systems. Mechatronics 5(5), 483–495 (1995)

    Google Scholar 

  2. Kurita, Y.: Vibration transportation by cooperation of decentralized self-excited vibratory machines. Trans. Jpn. Soc. Mech. Eng., Ser. C 69(681), 1191–1196 (2003)

    Google Scholar 

  3. Ono, K., Furuichi, T., Takahashi, R.: Self-excited walking of a biped mechanism with feet. Int. J. Robot. Res. 23(1), 55–68 (2004)

    Google Scholar 

  4. Peigne, G., et al.: Self-excited vibratory drilling: a dimensionless parameter approach for guiding experiments. Proc. Inst. Mech. Eng., Part B: J. Eng. Manuf. 219(1), 73–84 (2005)

    Google Scholar 

  5. Lee, Y., Lim, G., Moon, W.: A piezoelectric micro-cantilever bio-sensor using the mass-micro-balancing technique with self-excitation. Microsyst. Technol. 13(5), 563–567 (2007)

    Google Scholar 

  6. Li, C., and Xiaojing H. "A bio-mimetic pipe crawling microrobot driven based on self-excited vibration. In" 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO). IEEE, (2007)

  7. Kobayashi, T., et al. "An electrostatic field sensor driven by self-excited vibration of sensor/actuator integrated piezoelectric micro cantilever. In: 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS). IEEE, (2012)

  8. Lin, Y., et al.: Highly sensitive AFM using self-excited weakly coupled cantilevers. Appl. Phys. Lett. 115(13), 133105 (2019)

    Google Scholar 

  9. Yabuno, H.: Review of applications of self-excited oscillations to highly sensitive vibrational sensors. ZAMM-J. Appl. Math. Mech. /Zeitschr. für Angew. Math. und Mech. 101(7), e201900009 (2021)

    MathSciNet  Google Scholar 

  10. Yang, R., et al.: Nanoscale cutting using self-excited microcantilever. Sci. Rep. 12(1), 1–12 (2022)

    Google Scholar 

  11. Van der Pol, B., Van der Mark, J.: London Edinburgh Dublin Philos. Mag. J. Sci. 6, 763 (1928)

    Google Scholar 

  12. Rayleigh, L.: XXXIII On maintained vibrations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 15, 229–235 (1883)

    MathSciNet  Google Scholar 

  13. Aguilar, L. T., et al. "Generation of periodic motions for underactuated mechanical system via second-order sliding-modes. In: 2006 American Control Conference. IEEE, (2006)

  14. Aguilar, L.T., et al.: Generating self-excited oscillations for underactuated mechanical systems via two-relay controller. Int. J. Control. 829, 1678–1691 (2009)

    MathSciNet  MATH  Google Scholar 

  15. Hernández, J., et al. "Generating self-excited oscillations with a second order sliding mode controller. In: Congreso Nacional de Control Automatico 2015. Asociación de México de Control Automático (AMCA), (2015)

  16. Kurita, Y., et al.: Driving at resonance point of multi-degree-of-freedom system by decentralized control development of control method and verification of basic performance. J. Syst. Des. Dyn. 51, 180–191 (2011)

    Google Scholar 

  17. Malas, A., Chatterjee, S.: Modal self-excitation by nonlinear acceleration feedback in a class of mechanical systems. J. Sound Vib. 376, 1–17 (2016)

    Google Scholar 

  18. Malas, A., Chatterjee, S.: Modal self-excitation in a class of mechanical systems by nonlinear displacement feedback. J. Vib. Control 24(4), 784–796 (2018)

    MathSciNet  Google Scholar 

  19. Zhou, K., Urasaki, S., Yabuno, H.: Cantilever self-excited with a higher mode by a piezoelectric actuator. Nonlinear Dyn. 106(1), 295–307 (2021)

    Google Scholar 

  20. Higuchi, E., et al.: Experimental amplitude and frequency control of a self-excited microcantilever by linear and nonlinear feedback. J. Micromech. Microeng. 323, 034001 (2022)

    Google Scholar 

  21. Lorenz, E.N.: Deterministic nonperiodic flow. J. Atmos. Sci. 20(2), 130–141 (1963)

    MathSciNet  MATH  Google Scholar 

  22. Barboza, R.U.Y.: Dynamics of a hyperchaotic Lorenz system. Int. J. Bifurc. Chaos 17(12), 4285–4294 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Wang, X., Wang, M.: A hyperchaos generated from Lorenz system. Phys. A 387(14), 3751–3758 (2008)

    MathSciNet  Google Scholar 

  24. Cuomo, K.M., Oppenheim, A.V.: Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 71(1), 65 (1993)

    Google Scholar 

  25. Fortuna, L., Frasca, M., Rizzo, A.: Chaotic pulse position modulation to improve the efficiency of sonar sensors. IEEE Trans. Instrum. Meas. 52(6), 1809–1814 (2003)

    Google Scholar 

  26. Klomkarn, A.J.K., and Sooraksa, P. "Further investigation on trajectory of chaotic guiding signals for robotic systems. In: IEEE International Symposium on Communications and Information Technology, 2004. ISCIT 2004. Vol. 2. IEEE, (2004)

  27. Yu, X., Zhu, S., Liu, S.: A new method for line spectra reduction similar to generalized synchronization of chaos. J. Sound Vib. 306(3–5), 835–848 (2007)

    MathSciNet  Google Scholar 

  28. Wang, Z., Chau, K.T.: Chaos in electric drive systems: analysis, control and application. John Wiley, Hong Kong (2011)

    Google Scholar 

  29. Aihara, K.: Chaos and its applications. Procedia Iutam 5, 199–203 (2012)

    Google Scholar 

  30. Miranda-Colorado, R., Aguilar, L.T., Moreno-Valenzuela, J.: A model-based velocity controller for chaotization of flexible joint robot manipulators: Synthesis, analysis, and experimental evaluations. Int. J. Adv. Robot. Syst. 155, 1729881418802528 (2018)

    Google Scholar 

  31. Sahin, S., et al.: Spatiotemporal chaotification of delta robot mixer for homogeneous graphene nanocomposite dispersing. Robot. Autonomous Syst. 134, 103633 (2020)

    Google Scholar 

  32. Madiot, G., et al. "Random number generation with a chaotic electromechanical resonator." arXiv preprint arXiv:2204.13403 (2022)

  33. Choi, I.: Interactive exploration of a chaotic oscillator for generating musical signals in real-time concert performance. J. Franklin Inst. 331(6), 785–818 (1994)

    MATH  Google Scholar 

  34. Buscarino, A., et al.: Chaos does help motion control. Int. J. Bifurc. Chaos 1710, 3577–3581 (2007)

    MATH  Google Scholar 

  35. Geiyer, D., Kauffman, J.L.: Chaotification as a means of broadband energy harvesting with piezoelectric materials. J. Vib. Acoust. (2015). https://doi.org/10.1115/1.4030024

    Article  Google Scholar 

  36. Zhang, J., et al.: Chaotification of vibration isolation floating raft system via nonlinear time-delay feedback control. Chaos, Solitons Fractals 45910, 1255–1265 (2012)

    MathSciNet  Google Scholar 

  37. Johnson, M.A., Moon, F.C.: Experimental characterization of quasiperiodicity and chaos in a mechanical system with delay. Int. J. of Bifurc. Chaos 9(01), 49–65 (1999)

    MATH  Google Scholar 

  38. Uçar, A.: On the chaotic behaviour of a prototype delayed dynamical system. Chaos, Solitons Fractals 16(2), 187–194 (2003)

    MATH  Google Scholar 

  39. Sun, K., Sprott, J.C.: Periodically forced chaotic system with signum nonlinearity. Int. J. Bifurc. Chaos 2005, 1499–1507 (2010)

    MathSciNet  MATH  Google Scholar 

  40. Banerjee, T., Biswas, D.: Theory and experiment of a first-order chaotic delay dynamical system. Int. J. Bifurc. Chaos 23(06), 1330020 (2013)

    MathSciNet  MATH  Google Scholar 

  41. Ablay, G.: Chaos in PID controlled nonlinear systems. J. Electr. Eng. Technol. 10(4), 1843–1850 (2015)

    MathSciNet  Google Scholar 

  42. Li, C., Lizhong, Xu., Zhang, J.: Bifurcation and chaotic vibration for an electromechanical integrated harmonic piezodrive system. J. Mech. Sci. Technol. 30(7), 2961–2970 (2016)

    Google Scholar 

  43. Buscarino, A., et al.: A new chaotic electro-mechanical oscillator. Int. J. Bifurc. Chaos 2610, 1650161 (2016)

    MathSciNet  MATH  Google Scholar 

  44. Moreno-Valenzuela, J., Torres-Torres, C.: Adaptive chaotification of robot manipulators via neural networks with experimental evaluations. Neurocomputing 182, 56–65 (2016)

    Google Scholar 

  45. Natiq, H., et al.: Self-excited and hidden attractors in a novel chaotic system with complicated multistability. Eur. Phys. J. Plus 13312, 1–12 (2018)

    Google Scholar 

  46. Abdul Rahim, M.F., et al.: Dynamics of a new hyperchaotic system and multistability. Eur. Phys. J. Plus 134(10), 1–9 (2019)

    Google Scholar 

  47. Natiq, H., et al.: Enhancing the sensitivity of a chaos sensor for internet of things. Internet Things 7, 100083 (2019)

    Google Scholar 

  48. Natiq, H., Banerjee, S., Said, M.R.M.: Cosine chaotification technique to enhance chaos and complexity of discrete systems. Eur. Phys. J. Spec. Topics 2281, 185–194 (2019)

    Google Scholar 

  49. Li, T., Wang, Yu., Zhou, X.: Bifurcation analysis of a first time-delay chaotic system. Adv. Differ. Equ. 2019(1), 1–18 (2019)

    MathSciNet  Google Scholar 

  50. Yan, M., Hui, Xu.: A chaotic system with a nonlinear term and multiple coexistence attractors. Eur. Phy. J. Plus 135(6), 1–9 (2020)

    Google Scholar 

  51. Burra, L., Zanolin, F.: Chaos in a periodically perturbed second-order equation with signum nonlinearity. Int. J. Bifurc. Chaos 30(02), 2050031 (2020)

    MathSciNet  MATH  Google Scholar 

  52. Zhang, X., et al.: A memristive chaotic oscillator with controllable amplitude and frequency. Chaos, Solitons Fractals 139, 110000 (2020)

    MathSciNet  MATH  Google Scholar 

  53. Defoort, M., et al.: A dynamical approach to generate chaos in a micromechanical resonator. Microsyst. Nanoeng. 71, 1–11 (2021)

    Google Scholar 

  54. Patel, B., Kundu, P.K., Chatterjee, S.: Nonlinear feedback anti-control of limit cycle and chaos in a mechanical oscillator: Theory and experiment. Nonlinear Dyn. 1044, 3223–3246 (2021)

    Google Scholar 

  55. Strogatz, S.H.: Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. CRC Press, London (2018)

    MATH  Google Scholar 

  56. Stender, M., Hoffmann, N.: bSTAB: an open-source software for computing the basin stability of multi-stable dynamical systems. Nonlinear Dyn. 107(2), 1451–1468 (2022)

    Google Scholar 

  57. Lyapunov, A.M.: The general problem of the stability of motion. Int. J. Control 55(3), 531–534 (1992)

    MathSciNet  Google Scholar 

  58. Calvo, M., Juan I. M., and Luis R. "User’s manual for DISODE45, a MATLAB integration code (v1. 0)." (2015)

  59. Chatterjee, S., Mallik, A.K.: Three kinds of intermittency in a nonlinear mechanical system. Phys. Rev. E 53(5), 4362 (1996)

    Google Scholar 

  60. Gelbrecht, M., Kurths, J., Hellmann, F.: Monte Carlo basin bifurcation analysis. New J. Phys. 22(3), 033032 (2020)

    MathSciNet  Google Scholar 

  61. Singh, J.P., Roy, B.K.: The nature of Lyapunov exponents is (+,+,-,-). Is it a hyperchaotic system? Chaos, Solitons Fractals 92, 73–85 (2016)

    MathSciNet  MATH  Google Scholar 

  62. Singh, J.P., Roy, B.K.: The simplest 4-D chaotic system with line of equilibria, chaotic 2-torus and 3-torus behaviour. Nonlinear Dyn. 893, 1845–1862 (2017)

    MathSciNet  Google Scholar 

Download references

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Engineering Science and Technology, Shibpur, P.O. Botanic Garden, Howrah, West Bengal, 711103, India

    Prasanjit Kumar Kundu & Shyamal Chatterjee

Authors
  1. Prasanjit Kumar Kundu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shyamal Chatterjee
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Analysis was performed by PKK. The first draft of the manuscript was written by PKK and SC. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Shyamal Chatterjee.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kundu, P.K., Chatterjee, S. Nonlinear feedback synthesis and control of periodic, quasiperiodic, chaotic and hyper-chaotic oscillations in mechanical systems. Nonlinear Dyn 111, 11559–11591 (2023). https://doi.org/10.1007/s11071-023-08402-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08402-0

Keywords

Search

Navigation