Performance analysis of a nonlinear inerter-based vibration isolator with inerter embedded in a linkage mechanism

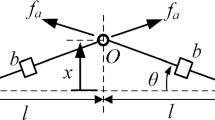
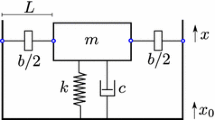
Abstract

This study presents an inerter-based nonlinear vibration isolator with geometrical nonlinearity created by configuring an inerter in a diamond-shaped linkage mechanism. The isolation performance of the proposed nonlinear isolator subjected to force or base-motion excitations is investigated. Both analytical and alternating frequency-time harmonic balance methods as well as numerical integration method are used to obtain the dynamic response. Beneficial performance of the nonlinear isolator is demonstrated by various performance indices including the force and displacement transmissibility as well as power flow variables. It is found that the use of the nonlinear inerter in the isolator can shift and bend the peaks of the transmissibility and time-averaged power flow to the low-frequency range, creating a larger frequency band of effective vibration isolation. It is also shown that the inertance-to-mass ratio and the initial distance of the nonlinear inerter can be effectively tailored to achieve reduced transmissibility and power transmission at interested frequencies. Anti-resonant peaks appear at specific frequency, creating near-zero energy transmission and significantly reducing vibration transmission to a base structure on which the proposed isolator is mounted.

Appendix

Using Eqs. (28), (29) and (43), governing Eq. (14) of the single-DOF oscillator with base-motion excitation (C2 configuration) becomes

$$ \begin{gathered} \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{2} \cos \left( {\Omega \tau - \theta } \right) \hfill \\ \quad - 2\zeta_{1} \Omega R_{2} \sin \left( {\Omega \tau - \theta } \right) = Q_{0} \Omega^{2} \cos \Omega \tau . \hfill \\ \end{gathered} $$

(61)

The coefficients of the corresponding harmonic terms in Eq. (61) can be balanced, leading to

$$ \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{2} = Q_{0} \Omega^{2} \cos \theta , $$

(62)

$$ - 2\zeta_{1} \Omega R_{2} = - Q_{0} \Omega^{2} \sin \theta . $$

(63)

By using the identity of $\cos^{2} \phi + \sin^{2} \phi = 1$, Eqs. (62) and (63) can be transformed into

$$ \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}^{2} R_{2}^{2} + \left( {2\zeta_{1} \Omega R_{2} } \right)^{2} = Q_{0}^{2} \Omega^{4} , $$

(64)

$$ \frac{{R_{2} }}{{Q_{0} }} = \frac{{\Omega^{2} }}{{\sqrt {\left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}^{2} + \left( {2\zeta_{1} \Omega } \right)^{2} } }}. $$

(65)

Note that Eq. (65) is obtained by rewriting Eq. (64), which can be solved by using a bisection method to obtain the amplitude $R_{2}$ of the relative displacement. The phase angle $\theta$ can then be determined by using Eqs. (62) and (63). When the excitation frequency $\Omega$ approaching infinity, Eq. (65) becomes

$$ \mathop {\lim }\limits_{\Omega \to \infty } \left( {\frac{{R_{2} }}{{Q_{0} }}} \right) = \frac{1}{{1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)}} , $$

(66)

in which, by denoting the corresponding value of $R_{2}$ as $R_{2,\infty }$, we have

$$ \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2,\infty }^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)R_{2,\infty } = Q_{0} , $$

(67)

which is a nonlinear algebraic equation which can be solved by a standard bisection method. It shows that the relative displacement amplitude $R_{2,\infty }$ is only related to the design parameters of $\lambda , D_{0}$ and $Q_{0}$ of the isolator.

It is noted that the nondimensional displacement response $X_{2} \left( \tau \right)$ of the mass in C2 is expressed by

$$ X_{2} \left( \tau \right) = Z_{2} \left( \tau \right) + Q_{0} \cos \Omega \tau \approx R_{2} \cos \left( {\Omega \tau - \theta } \right) + Q_{0} \cos \Omega \tau . $$

(68)

Therefore, the displacement amplitude $M_{2}$ of the mass in C2 can be obtained as

$$ \begin{gathered} M_{2} = \sqrt {\left( {R_{2} \cos \theta + Q_{0} } \right)^{2} + R_{2}^{2} \sin^{2} \theta } \hfill \\ \quad = \sqrt {R_{2}^{2} + Q_{0}^{2} + 2R_{2}^{2} \left\{ {\frac{1}{{\Omega^{2} }} - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)} \right\}} , \hfill \\ \end{gathered} $$

(69)

where Eq. (62) is used for the simplification.