Simulation and experimental studies of a vibro-impact capsule system driven by an external magnetic field

Abstract

This paper studies the electromagnetic field used for driving a vibro-impact capsule prototype for small bowel endoscopy. Mathematical models of the electromagnetic field and the capsule system are introduced, and analytical solution of the magnetic force applied on the capsule is derived and verified by experiment. The impact force between the inner mass of the capsule and the capsule body is also compared via numerical simulation and experimental testing. By comparing the capsule’s progressions under different control parameters (e.g. the excitation frequency and duty cycle), the merits of using the vibro-impact propulsion are revealed. Based on the experimental results, the optimised speed of the prototype can achieve up to 3.85 mm/s. It is therefore that the potential feasibility of using the external electromagnetic field for propelling the vibro-impact capsule system is validated.

1 Introduction

Bowel cancer is the second most common cause of cancer death in the UK [1]. Early detection of bowel cancer can increase the patient’s survival rate significantly [2]. Detection of bowel cancer is currently performed by regular surveillance [3] of the intestinal area through an endoscopic procedure. Capsule endoscopy, the primary modality for examining the surface lining of the small bowel, is prevalently chosen to assist or to substitute traditional endoscopy, selecting potential patients from regular surveillance and helping to decide whether a further treatment is required [4]. However, a long transit time of the capsule often results in a poor visualisation in the distal small bowel, and together with its peristalsis-dependent locomotion, capsule endoscopy has been reported to exclude some important syndromes during diagnosis [3]. Therefore, in small bowel endoscopic practice, there is an urgent need for new modalities that are controllable, accurate and reliable, which allow the practitioners to examine the areas of interest carefully. To satisfy this requirement, our present work aims to develop a controllable capsule robot by using the vibro-impact propelling method [5, 6] for small bowel endoscopy.

Fig. 1

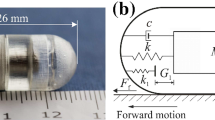
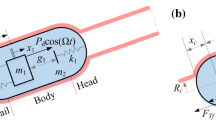
(Colour online) a Physical model, b conceptual design and c prototype of the vibro-impact capsule system, where $M_m$ and $M_c$ are the weights of the T-shaped magnet and the capsule, respectively. The forward and backward constraints are modelled as two linear springs with the stiffness $k_1$ and $k_2$; k and c are the stiffness and the damping coefficient of the helical spring connecting the magnet and the capsule, respectively. $G_1$ and $G_2$ represent the impact gaps between the constraints and the magnet, and $X_1$ and $X_2$ are the displacements of the magnet and the capsule, respectively

Developing a reliable propulsive mechanism in a standard-sized capsule, which is 26 mm in length and 11 mm in diameter, is a challenging task. Various propulsion methods have been proposed by researchers in the past few decades. For example, an integrated untethered swimming capsule with a camera and battery was designed by Falco et al. [7]. A jellyfish-mimicked capsule robot excited by a battery-powered rotor was designed by Valdastri et al. [8]. Woo et al. [9] developed an electric irritated capsule that can stimulate the peristalsis motion of the small intestine. Carta et al. [10] employed an on-board vibratory motor with a wireless powering unit for active capsule endoscopy. There are also other designs, such as the one with legs extended from the capsule’s body [11] and the one made anchors outside the capsule’s shell [12] to stabilise the capsule in the intestine. However, these additional accessories outside the capsule can potentially cause erosion and ulcers to the intestinal tract, so these designs may not be feasible for clinical use.

To manipulate the capsule in the intestinal tract remotely, a large number of research groups equipped the capsule with a small permanent magnet internally and utilised an external permanent magnet or electric coils, or a combination of both to control the inner magnet. Keller et al. [13] developed an integrated 12-coil electromagnetic guided capsule system that is feasible to control the capsule’s orientation to diagnose a water-filled stomach by using a joystick. In [14, 15], an external permanent magnet was manoeuvred by a robotic arm for guiding a small piece of permanent magnet inside a capsule, while in [16, 17], a hand-held manipulator adopted in the design provides a cheaper and less complex solution than the robotic arm. Other than employing the permanent magnet, Maxwell and Helmholtz coils are two common options for manipulating the capsule robot. Maxwell coils provide a strong gradient field that can induce a translational force on the magnet inside the capsule, while Helmholtz coils can generate a rotating torque on the magnet, thus leading to a helical “swimming”. In [18], a combination of Maxwell and Helmholtz coils was used to control the capsule’s speed and orientation in a collapsed small intestine in a water-filled rig. However, the control is only in one dimension (i.e. forward progression), and the controllable area of the capsule is very limited, so the feasibility of the design for practical use is in doubt. Furthermore, the helical movement of the capsule may also cause large and continuous torsion on the intestine, which could potentially cause patient’s discomfort and secondary damage during the examination.

In the present work, external electromagnetic coils were used and a new vibro-impact mechanism was employed to propel the capsule robot. Systems with such a mechanism have been adopted in many engineering applications, such as drilling [19], energy harvesting [20] and ground moling [21]. The idea of utilising the vibro-impact mechanism inside a capsule robot was firstly proposed by Liu et al. [22]. In the following studies, the system has been simulated under different friction models [23] and backward motion of the capsule has been observed under certain parameter configurations [24]. Also, feedback control was considered to avoid friction-induced chaotic motion. Based on the theoretical studies, a proof-of-concept experimental rig and a mesoscale prototype of the vibro-impact capsule system were developed in [5] and [25], respectively. In [26], the contact modelling of a standard-sized capsule moving in the small intestine was studied. Apart from the vibro-impact capsule system, Chernousko [27] proposed a three-dimensional motion control method that can be applied to the system with an internal movable mass based on a combination of three two-dimensional motions. Nguyen et al. [28] studied a vibro-impact Duffing system with bidirectional motion and verified the maximum progression rate within a range of parameters experimentally. In their later work [29], the influence of the varying friction on the vibrational model was discussed. Observation of the experimental results indicates that the friction does not only influence the progression speed, but also the direction of progression of the vibro-impact system. Recently, Zimmermann et al. [30] have adopted the smart magnetorheological fluid into their vibration system to adjust its friction in order to govern the system behaviour, which was validated both numerically and experimentally with an average speed of 2.87 cm/s. In [31], a vibro-impact model with two-sided constraint was studied from numerical simulation to experimental verification. Liu et al. [32] investigated a vibro-impact experimental rig with two-sided constraint and used the path-following techniques to optimise the progression of the system. Xu et al. [33] reviewed various vibration-driven locomotion systems driven by electric actuators. Later on, they designed a cascaded vibration robot with two modules, each with an inner vibrational mass, and the average velocity and the backward motion were recorded and compared with numerical results [34]. Furthermore, a vibrational prototype with an on-board linear actuator inside the capsule which was tethered for powering and designed in centimetre scale, was studied in [35, 36]. As the capsule that moves in a periodic pattern has difficulties in travelling in the fluid environment, the so-called scallop theorem [37], Bagagiolo et al. [38] utilised a switching control method to overcome this and validated it from a mathematical point of view.

The capsule prototype and its physical model to be studied in this work are presented in Fig. 1, where $M_m$ and $M_c$ are the weights of the permanent magnet and the capsule, respectively. The forward and backward constraints are modelled as two linear springs with the stiffness $k_1$ and $k_2$; k and c are the stiffness and the damping coefficient of the helical spring connecting the magnet and the capsule, respectively. $G_1$ and $G_2$ represent the impact gaps between the constraints and the magnet, and $X_1$ and $X_2$ are the displacements of the magnet and the capsule, respectively. In the present work, an analytical model for the external excitation of the capsule prototype will be studied to determine the magnetic force acting on the inner magnet. Experimental results will also be presented to demonstrate the validity of the proposed analytical model.

The rest of this paper is organised as follows. Sec. 2 presents an overview of capsule’s prototype design and the experimental set-up. In Sec. 3, the external magnetic field and the capsule system are modelled analytically and verified by simulations. Sec. 4 provides some experimental results on two case studies to reveal the moving patterns of the capsule. Finally, conclusions are drawn in Sec. 5.

2 Design and method

2.1 Prototype overview

The conceptual design of the capsule prototype is shown in Fig. 1b and the capsule prototype used in the experimental study is presented in Fig. 1c. The capsule’s shell that consists of two constraints and a linear bearing was printed using a stereolithography 3D printer. The pattern of the constraints was designed to reduce the weight of the capsule while providing sufficient impact forces on the capsule. A bearing was used to hold a T-shaped inner mass that was formed by two cascaded cylindrical neodymium magnets. A helical spring attached between the inner mass and the capsule can help the mass return to its original position after each excitation. The stiffnesses of the primary constraint, the secondary constraint and the helical spring were obtained by the static tests using an Instron machine. To determine the damping coefficient of the helical spring, a laser sensor was used to record its displacement under free vibration tests. A summary of all identified physical parameters of the capsule prototype is listed in Table 1.

Table 1 Identified physical parameters of the prototype

Fig. 2

a Schematic diagram and b photography of experimental set-up of the capsule system. The T-shaped magnet inside the capsule was excited through an on–off electromagnetic field leading to the movement of the prototype. The on–off excitation was generated using a signal generator producing a pulse-width modulation signal via a power amplifier, and the amplifier can control the voltage applied to the coils by adjusting the DC power supply. The prototype was put on a piece of cut-open synthetic small intestine supported by a halved black plastic tube, which was placed along the axis centre of the coils. A video camera was used to record the motion of the capsule, and recorded videos were analysed by using an open-source software to generate the time histories of capsules displacement and velocity

2.2 Experimental set-up and signal processing

The schematic diagram of the experimental set-up is shown in Fig. 2a, and its photograph is presented in Fig. 2b. A signal generator GW INSTEK AFG-2105 was used to generate the pulse-width modulation (PWM) signal in [0, 0.5] V. By using a power amplifier OPA544, which was powered by a DC power supply TENMA 72-10495, the PWM signal was then amplified up to 20 V for driving the electromagnetic coils. The capsule prototype was placed on a cut-open synthetic small intestine, and a video camera was on top of the prototype to record its movement. The coils winded by an automatic winding machine CNC-200A were designed after the simulation optimisation aiming to generate the required magnetic force on the prototype. Here, it should be noted that the two coils are identical, and only one coil was used in the present work. With a required voltage, the coil can provide the magnet with a varying electromagnetic field, so the magnet can vibrate inside the capsule to generate forward and backward impact motion. Three parameters, including the frequency, amplitude and duty cycle of the PWM signal, were used to modulate magnet’s vibration in experiment.

As shown in Fig. 2b, the coils were fixed, and a halved plastic tube was placed across the centre of the coils. On top of the tube, a piece of cut-open synthetic small intestine was used to simulate a straight path of real small intestine environment. Above the experimental set-up, a video camera was fixed to record the motion of the capsule. Recorded videos were analysed by an open-source software Tracker [39], and the planar displacements of the capsule and the magnet can be extracted.

Fig. 3

Schematic drawings for a a filament circular coil with the radius of R, b a cylindrical coil with the outer diameter of $2R+2a$, the thickness of 2a and the width length of 2b, c a filament square coil with the length of 2L and d a square cylindrical coil with the outer length of $2L+2a$, the thickness of 2a and the width length of 2b

3 Magnetic force calibration

3.1 Magnetic field modelling

For the case of magnetostatics, to calibrate the magnetic force acting on the magnet from the coils, the Biot–Savart’s law [40] was used, which can be expressed as

$$\begin{aligned} \vec {B}=\frac{\mu _0}{4\pi }\int _{}^{}\frac{I\cdot \mathrm {d}\vec {l}\times \vec {r}}{r^3}, \end{aligned}$$

(1)

where I is the current, d$\vec {l}$ is a vector, whose magnitude is the length of differential element of the wire, and direction is the direction of the current, $\vec {B}$ is the net magnetic field, $\mu _0$ is the magnetic constant and $\vec {r}$ is the displacement vector in the direction pointing from the wire element towards the point at where the field is being computed.

Consider a coordinate $\{o,x,y,z\}$ at the centre of a current loop as shown in Fig. 3a, and the magnitude of the magnetic field generated by a small element of the loop $\mathrm {d}l$ at $(x_c,0,0)$ can be written as

$$\begin{aligned} \mathrm {d}B=\frac{\mu _0}{4\pi }\frac{I\mathrm {d}l}{r^2}, \end{aligned}$$

(2)

where $r^2=x^2_c+R^2$, R is the radius of the current loop. If considering the magnet as a mass point moving along the x axis, only the magnetic field along the x axis should be taken into account, so

$$\begin{aligned} \mathrm {d}B_x=\mathrm {d}B\sin {\theta }, \end{aligned}$$

(3)

where $\sin {\theta }=\tfrac{R}{\sqrt{x_c^2+R^2}}$, and the magnitude of the magnetic field at $(x_c,0,0)$ can be obtained as

$$\begin{aligned} B=\int _{}^{}\mathrm {d}B_x=\frac{\mu _0 R^2 I}{2(x_c^2+R^2)^{\tfrac{3}{2}}}. \end{aligned}$$

(4)

When the number of turns of the coils is large, the width and thickness of the coil as shown in Fig. 3b need to be taken into account. In this case, the magnitude of the magnetic field generated by a small sectional area of the coil $\mathrm {d}x_i\mathrm {d}z_i$ at $(x_c,0,0)$ can be expressed as

$$\begin{aligned} B= & {} \int _{}^{}\mathrm {d}B_x=\int _{R+a}^{R-a}\int _{b}^{-b}\frac{n\mu _0 z_i^2 I}{2((x_c-x_i)^2+y^2)^{\tfrac{3}{2}}}\mathrm {d}x_i\mathrm {d}z_i \nonumber \\= & {} \tfrac{n\mu _0I}{2}\Bigl [(x_c+b)(\ln {(R+a+\sqrt{(x_c+b)^2+(R+a)^2})} \nonumber \\&-\ln {(R-a+\sqrt{(x_c+b)^2+(R-a)^2})}) \nonumber \\&-(x_c-b)(\ln {(R+a+\sqrt{(x_c-b)^2+(R+a)^2})} \nonumber \\&-\ln {(R-a+\sqrt{(x_c-b)^2+(R-a)^2})})\Bigr ], \end{aligned}$$

(5)

where n represents the number of turns per square metre cross-sectional area of the coil. It should be noted that we use (x, y, z) in general expressions where the orientation or the global coordinate needs to be used, use $(x_i, y_i, z_i)$ to indicate the wire’s position for integration purpose, and use $(x_c, y_c, z_c)$ to represent the magnet’s position.

When considering the magnetic field generated by the current loop on the xy plane, it is difficult to obtain its analytical solution. Thus, a current square is used here to approximate the magnetic field on the xy plane. As shown in Fig. 3c, the magnitude of the magnetic field generated by a small element of the square $\mathrm {d}l$ at $(x_c,y_c,0)$ is $\{\mathrm {d}B_x,\mathrm {d}B_y,\mathrm {d}B_z\}$. Because of the symmetry of the current square, one can obtain that $B_x\ne 0$, $B_y\ne 0$ and $B_z=0$.

According to Eq. (1), a small element of the top wire $\mathrm {d}l$ can generate the magnetic field at $(x_c,y_c,0)$ along the x axis as

$$\begin{aligned} \mathrm {d}B_{x}^t=\frac{\mu _0IL}{4\pi (L^2+x_c^2+(l-y_c)^2)^{\tfrac{3}{2}}}\mathrm {d}l, \end{aligned}$$

(6)

where L is the half width of the current square. Likewise, the bottom wire can generate the magnetic field at $(x_c,y_c,0)$ along the x axis as

$$\begin{aligned} \mathrm {d}B_{x}^b=\frac{\mu _0IL}{4\pi (L^2+x_c^2+(l-y_c)^2)^{\tfrac{3}{2}}}\mathrm {d}l. \end{aligned}$$

(7)

For the left and right wires of the current square, their magnetic fields along the x axis are

$$\begin{aligned} \mathrm {d}B_{x}^l=\frac{\mu _0I(L+y_c)}{2\pi ((L+y_c)^2+x_c^2+l^2)^{\tfrac{3}{2}}}\mathrm {d}l \end{aligned}$$

(8)

and

$$\begin{aligned} \mathrm {d}B_{x}^r=\frac{\mu _0I(L-y_c)}{2\pi ((L-y_c)^2+x_c^2+l^2)^{\tfrac{3}{2}}}\mathrm {d}l, \end{aligned}$$

(9)

respectively. The superscripts “t, b, l, r” denote the top, bottom, left and right wires, respectively. Thus, the net magnetic field generated by the small element $\mathrm {d}l$ at $(x_c,y_c,0)$ along the x axis can be written as

$$\begin{aligned} \mathrm {d}B_{x}=\mathrm {d}B_{x}^t+\mathrm {d}B_{x}^b+\mathrm {d}B_{x}^l+\mathrm {d}B_{x}^r. \end{aligned}$$

(10)

Since the top and bottom wires do not contribute to the magnetic field at $(x_c,y_c,0)$ along the y axis, only the left and right wires of the current square should be taken into account as

$$\begin{aligned} \mathrm {d}B_{y}^l=\frac{\mu _0Ix_c}{2\pi ((L+y_c)^2+x_c^2+l^2)^{\tfrac{3}{2}}}\mathrm {d}l \end{aligned}$$

(11)

and

$$\begin{aligned} \mathrm {d}B_{y}^r=\frac{\mu _0Ix_c}{2\pi ((L-y_c)^2+x_c^2+l^2)^{\tfrac{3}{2}}}\mathrm {d}l. \end{aligned}$$

(12)

So, the net magnetic field at $(x_c,y_c,0)$ along the y axis can be expressed as

$$\begin{aligned} \mathrm {d}B_{y}=\mathrm {d}B_{y}^l-\mathrm {d}B_{y}^r. \end{aligned}$$

(13)

Integrating Eqs. (10) and  (13), we have

$$\begin{aligned} B_{x1}= & {} \int _{L}^{-L}(\mathrm {d}B_{x}^t+\mathrm {d}B_{x}^b+\mathrm {d}B_{x}^l+\mathrm {d}B_{x}^r)\nonumber \\= & {} \frac{\mu _0IL}{2\pi }(\frac{L+y_c}{(L^2+x_c^2)\sqrt{L^2+x_c^2+(L+y_c)^2}}\nonumber \\&+\frac{L-y_c}{(L^2+x_c^2)\sqrt{L^2+x_c^2+(L-y_c)^2}}\nonumber \\&+\frac{L+y_c}{((L+y_c)^2+x_c^2)\sqrt{(L+y_c)^2+x_c^2+L^2}}\nonumber \\&+\frac{L-y_c}{((L-y_c)^2+x_c^2)\sqrt{(L-y_c)^2+x_c^2+L^2}}) \end{aligned}$$

(14)

and

$$\begin{aligned} B_{y1}= & {} \int _{L}^{-L}(\mathrm {d}B_{y}^l-\mathrm {d}B_{y}^r)\nonumber \\= & {} \frac{\mu _0IL}{2\pi }(\frac{x_c}{((L+y_c)^2+x_c^2)\sqrt{(L+y_c)^2+x_c^2+L^2}}\nonumber \\&-\frac{x_c}{((L-y_c)^2+x_c^2)\sqrt{(L-y_c)^2+x_c^2+L^2}}). \end{aligned}$$

(15)

Here, it studies an ideal condition when the coil is formed by one filament. Thus, we use $B_{x1}$ and $B_{y1}$ in Eqs. (14) and (15) to indicate the magnetic field generated by the coil formed by one single filament. In this way, we can separate this result from the final result $B_{x}$ and $B_{y}$ which takes the coil’s geometric volume into account. To be more precise, a square cylindrical coil shown in Fig. 3d is considered further. After taking the thickness 2a and the width length 2b into account, the small sectional area $\mathrm {d}x_i\mathrm {d}z_i$ contains $n\mathrm {d}x_i\mathrm {d}z_i$ turns of coil, so $B_x$ and $B_y$ can be expressed as

$$\begin{aligned} B_x=\int _{L+a}^{L-a}\int _{b}^{-b}nB_{x1}\mathrm {d}x_i\mathrm {d}z_i \end{aligned}$$

(16)

and

$$\begin{aligned} B_y=\int _{L+a}^{L-a}\int _{b}^{-b}nB_{y1}\mathrm {d}x_i\mathrm {d}z_i. \end{aligned}$$

(17)

From Eqs. (10) and  (13), we can obtain

$$\begin{aligned} B_{x1}= & {} \tfrac{\mu _0I}{2\pi }\left( \tfrac{(L+y_c)z_i}{(z_i^2+(x_c-x_i)^2)\sqrt{z_i^2+(x_c-x_i)^2+(L+y_c)^2}}\right. \nonumber \\&+\tfrac{(L-y_c)z_i}{(z_i^2+(x_c-x_i)^2)\sqrt{z_i^2+(x_c-x_i)^2+(L-y_c)^2}}\nonumber \\&+\tfrac{L(z_i+y_c)}{((z_i+y_c)^2+(x_c-x_i)^2)\sqrt{(z_i+y_c)^2+(x_c-x_i)^2+L^2}}\nonumber \\&\left. +\tfrac{L(z_i-y_c)}{((z_i-y_c)^2+(x_c-x_i)^2)\sqrt{(z_i-y_c)^2+(x_c-x_i)^2+L^2}}\right) \nonumber \\ \end{aligned}$$

(18)

and

$$\begin{aligned} B_{y1}= & {} \tfrac{\mu _0I}{2\pi }\left( \tfrac{L(x_c-x_i)}{((z_i+y_c)^2+(x_c-x_i)^2) \sqrt{(z_i+y_c)^2+(x_c-x_i)^2+L^2}}\right. \nonumber \\&\left. -\tfrac{L(x_c-x_i)}{((z_i-y_c)^2+(x_c-x_i)^2)\sqrt{(z_i-y_c)^2+(x_c-x_i)^2+L^2}}\right) .\nonumber \\ \end{aligned}$$

(19)

Rewriting Eqs. (16) and  (17), it gives

$$\begin{aligned} B_x= & {} \frac{\mu _0nI}{2\pi }\int _{L+a}^{L-a}(\sum _{j=1}^{4} (\tan ^{-1}\tfrac{L_j(x_c+b)}{z_{ij}\sqrt{z_{ij}^2+(x_c+b)^2+L_j^2}} \nonumber \\&-\tan ^{-1}\tfrac{L_j(x_c-b)}{z_{ij}\sqrt{z_{ij}^2+(x_c-b)^2+L_j^2}}))\mathrm {d}z_i \end{aligned}$$

(20)

and

$$\begin{aligned} B_y= & {} \frac{\mu _0nI}{2\pi }\int _{L+a}^{L-a}(\sum _{j=3}^{4}(-1)^{j+1}(\tanh ^{-1} \tfrac{\sqrt{z_{ij}^2+(x_c-b)^2+L^2}}{L}\nonumber \\&-\tanh ^{-1}\tfrac{\sqrt{z_{ij}^2+(x_c+b)^2+L^2}}{L}))\mathrm {d}z_i, \end{aligned}$$

(21)

where $L_1=L-y_c$, $L_2=L+y_c$, $L_3=L_4=L$, $z_{i1}=z_{i2}=z_i$, $z_{i3}=z_i+y_c$ and $z_{i4}=z_i-y_c$.

It is worth noting that when solving Eqs. (20) and  (21), due to the term $\tanh ^{-1}(\kappa )$ containing a singularity point at $\kappa =1$, integrations of these terms cannot be expressed analytically, so the numerical integration was adopted here to get the final results for $B_y$.

3.2 Analytical and numerical results

Next, the electromagnetic simulation software ANSYS Maxwell was used to validate the magnetic field modelling for both the cylindrical and the square coils. The simulation environment was set up with an air boundary surrounding the coil and the magnet. At each self-converge step during the simulation, the size of tetrahedrons was refined by 40%. When the last step resulted in an error within 0.05% compared with its previous step, the result was considered as converged.

Table 2 Parameters of the cylindrical coil used in experiment

First, we will make a comparison between the cylinder and the square coils. It should be noted that the parameters of the coils, R, a and b, and the location of the magnetic field on the xy plane, ($x_c, y_c$), are influenced interactively by the ratio of R and L. Here we chose the coil parameters from Table 2 and used $x_c=30$ mm as a standard to find the ratio of R and L that can provide the best match for the cylindrical and the square coils. Based on our simulation, it was found that when $L/R=0.83$, where $R=29$ mm and $L=24$ mm, we can get the best matching results for both coils as shown in Fig. 4a. Figure 4b compares the magnetic fields generated by both coils along the x axis obtained from the analytical solutions, Eqs. (5) and  (20), and ANSYS Maxwell. It can be seen that all the analytical and numerical results for both coils fix well from $x_c>20$ mm.

Fig. 4

a Cylindrical coil’s radius R and half length of the square coil L as the functions of their magnetic fields generated along the x axis, $B_x$, at $x_c=30$ mm, calculated from Eqs. (5) and  (20). The square coil has the best match with the cylindrical coil at $L/R=0.83$. b Distance $x_c$ along the x axis as a function of the magnetic field generated along the x axis, $B_x$, calculated for $R=29$ mm, $L=24$ mm and $L/R=0.83$. Analytical solutions for the cylindrical and the square coils were calculated by using Eqs. (5) and  (20), respective. Simulation results for both coils were obtained from ANSYS Maxwell

Figure 5 presents the magnitude of magnetic fields generated by the cylindrical and the square coils on the xy plane obtained from ANSYS Maxwell. It can be found that the magnitude of the fields in the area that $x_c\in [10, 20]$ mm and $y_c\in [-20, 20]$ mm are slightly different in the neighbourhood of the coils, but are consistent around the centres of the coils. For the area that $x_c>20$ mm, the distributions of fields of both coils are very similar. Thus, it is fair to use the analytical solution of the square coil, Eqs. (20) and  (21), to approximate the analytical solution of the cylindrical coil on the xy plane.

Fig. 5

Magnetic fluxes (i.e. the magnitude of magnetic fields) generated by a the cylindrical ($R=29$ mm) and b the square ($L=24$ mm) coils on the xy plane obtained from ANSYS Maxwell, where colour bars indicate the magnetic fluxes, and internal panels illustrate the shapes of the coils and their fluxes in the xyz coordinate

3.3 Magnetic force on the inner mass

With the coil’s parameters given in Table 2, the analytical equations of the magnetic field generated by the coils, Eqs. (5),  (20) and  (21), can be solved to derive the magnetic force acting on the inner mass of the capsule system. When the current flows through a coil, a non-uniform magnetic field can be generated, and a magnetic force, $\vec {P}_d$, will act on the inner mass along its magnetised direction once the capsule is within the neighbourhood of the coil. When the voltage of the coil is controlled by a PWM signal, the periodic excitation of the inner mass can be expressed as

$$\begin{aligned} F_e(t)=\bigg \{\begin{array}{cl} P_d, &{} t\in [\frac{N}{f}, \frac{N+D}{f}], \\ 0, &{} t\in [\frac{N+D}{f}, \frac{N+1}{f}], \end{array} \end{aligned}$$

(22)

where $P_d=|\vec {P}_d|$ is the magnitude of the magnetic force, N is the period number, f is the frequency, and $D\in (0,1)$ is the duty cycle ratio of the PWM signal. By changing these key parameters of the driving signal, the capsule will behave differently: it can move with the modulated speed and bidirectional orientations.

The magnetic excitation force, exerted on the magnet can be written as [41]

$$\begin{aligned} \vec {P}_d= & {} \nabla (\vec {m} \cdot \vec {B})\nonumber \\= & {} (\vec {m} \cdot \nabla ) \vec {B} + (\vec {B} \cdot \nabla ) \vec {m} \nonumber \\&+ \vec {m} \times (\nabla \times \vec {B}) + \vec {B} \times (\nabla \times \vec {m}), \end{aligned}$$

(23)

where $\nabla$ is the vector gradient operator $[\frac{\partial }{\partial x} \ \frac{\partial }{\partial y} \ \frac{\partial }{\partial z}]^T$, $\vec {m}$ is the magnetic dipole moment of the magnet which can also be expressed as $\vec {m} = v\vec {M}$, i.e. multiplication of the volume of the magnet v and density of the magnetic dipole moment $\vec {M}$. According to Maxwell’s equation, we have the following conditions.

• For the case of magnetostatics, we assume that the electric displacement field and the magnetic field are time-independent and no current displacement is through the occupied region, so $\nabla \times \vec {H} = 0$, where $\vec {H}$ is the magnetic field intensity.

• We also assume no spatial variation for the magnetisation inside the permanent magnet, so $\vec {m}$ has no coordinate dependence, leading to $(\vec {B} \cdot \nabla ) \vec {m} = 0$ and $\nabla \times \vec {m} = 0$ [42].

• Since $\vec {H}=\frac{1}{\mu _0}\vec {B}-\vec {M}$, where $\mu _0$ is the permeability of vacuum, the relations $\nabla \times \vec {H} = 0$ and $\nabla \times \vec {m} = 0$ can lead to $\nabla \times \vec {B} = 0$.

According to the above conditions, Eq. 23 can be transformed to

$$\begin{aligned} \vec {P}_d = (\vec {m}\cdot \nabla )\vec {B}=v \ (\vec {M}\cdot \nabla )\vec {B}. \end{aligned}$$

(24)

As we have discussed the magnetic fields along the x, y and z directions in Sect. 3.1, here we are going to calculate the forces exerted along the x, y and z directions. To this end, Eq. 24 can be expanded as

$$\begin{aligned} \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix} = v \begin{bmatrix} M_x \frac{\partial B_x}{\partial x} + M_y \frac{\partial B_x}{\partial y} + M_z \frac{\partial B_x}{\partial z}\\ M_x \frac{\partial B_y}{\partial x} + M_y \frac{\partial B_y}{\partial y} + M_z \frac{\partial B_y}{\partial z}\\ M_x \frac{\partial B_z}{\partial x} + M_y \frac{\partial B_z}{\partial y} + M_z \frac{\partial B_z}{\partial z} \end{bmatrix} \end{aligned}$$

(25)

or

$$\begin{aligned} \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix} = v \begin{bmatrix} M_x \frac{\partial B_x}{\partial x} + M_y \frac{\partial B_y}{\partial x} + M_z \frac{\partial B_z}{\partial x}\\ M_x \frac{\partial B_x}{\partial y} + M_y \frac{\partial B_y}{\partial y} + M_z \frac{\partial B_z}{\partial y}\\ M_x \frac{\partial B_x}{\partial z} + M_y \frac{\partial B_y}{\partial z} + M_z \frac{\partial B_z}{\partial z} \end{bmatrix} \end{aligned}$$

(26)

where (25) and (26) are equivalent due to $\nabla \times \vec {B} = 0$.

Let the magnetic field at the point (x, y, z) be oriented along the x axis and let the magnetisation vector $\vec {M}$ be aligned to the magnetic field, i.e. $M_x=M$, $M_y=M_z = 0$. For this case, we have

$$\begin{aligned} \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix} = vM\begin{bmatrix} \frac{\partial B_x}{\partial x}\\ \frac{\partial B_y}{\partial x} \\ \frac{\partial B_z}{\partial x} \end{bmatrix} = vM\begin{bmatrix} \frac{\partial B_x}{\partial x}\\ \frac{\partial B_x}{\partial y} \\ \frac{\partial B_x}{\partial z} \end{bmatrix}. \end{aligned}$$

(27)

If $\tfrac{\partial B_y}{{\partial x}} = \tfrac{\partial B_z}{{\partial x}} = 0$ (or $\tfrac{\partial B_x}{{\partial y}} = \tfrac{\partial B_x}{{\partial z}} = 0$) which means the magnetic force is directed along the x axis, then

$$\begin{aligned} \vec {P}_d = \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix} = vM\begin{bmatrix} \frac{\partial B_x}{\partial x}\\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

(28)

If $\tfrac{\partial B_z}{{\partial x}} = 0$ (or $\tfrac{\partial B_x}{{\partial z}} = 0$), then the z component of the magnetic force is equal to zero, which means the magnetic force is exerted on the xy plane

$$\begin{aligned} \vec {P}_d = \begin{bmatrix} F_x \\ F_y \\ F_z \end{bmatrix} = vM\begin{bmatrix} \frac{\partial B_x}{\partial x}\\ \frac{\partial B_y}{\partial x} \\ 0 \end{bmatrix} = vM\begin{bmatrix} \frac{\partial B_x}{\partial x}\\ \frac{\partial B_x}{\partial y} \\ 0 \end{bmatrix}. \end{aligned}$$

(29)

Full explicit expressions of the magnetic forces along the x and y axes, $F_x$ and $F_y$, can be found in Appendix.

Fig. 6

a Experimental set-up for calibrating the coil’s magnetic force acting on the magnet. b Comparison of analytical solutions (blue square line) calculated by Eq. (28), numerical results (green dot line) obtained from ANSYS Maxwell and experimental results (red triangle line)

In the present experiment, we used the NdFeB magnet with $\text {M} = 8.91\times 10^5$ A/m and $v=2.41\times 10^{-7}$ $\hbox {m}^3$. To validate Eq. (28), an experimental rig as shown in Fig. 6a was built to calibrate the magnetic force of the coil acting on the magnet. The coil was fixed above the magnet with a changeable distance $x_c$ along the x axis, and the magnitude of the magnetic force $\vec {P}_d$ can be obtained from the scale after zeroing out the gravity of the magnet. The experiment was repeated for five times with a distance interval of 5 mm and taken the average value for each distance. A comparison of the analytical solutions calculated by Eq. (28), the numerical results obtained from ANSYS Maxwell and the experimental results is shown in Fig. 6b, which shows a good agreement in the magnetic force $P_d$ as a function of the distance $x_c$.

Fig. 7

Comparison between the semi-analytical solutions by solving Eq. (29) and the numerical results obtained from ANSYS Maxwell for a the force acting on the magnet along the x axis, $F_x$, and b the force acting on the magnet along the y axis, $F_y$. Semi-analytical solutions and numerical results are denoted by solid lines and dots, respectively

Fig. 8

Comparison between a the semi-analytical solutions and b the numerical results of the magnetic forces on the xy plane generated by the square coil, where the length and the direction of the arrows indicate the magnitudes and the orientations of the magnetic forces, respectively. The semi-analytical map was obtained by solving Eqs. (20),  (21) and  (29), and the numerical map was acquired from ANSYS Maxwell

To examine the magnetic force on the xy plane, Eq. (29) was used. However, it contains the non-integrable term $\tanh ^{-1}(x)$, which cannot be expressed explicitly in an analytical form, so numerical methods must be applied here by solving Eq. (29). To test Eq. (29), a comparison between its semi-analytical solutions and the numerical results obtained from ANSYS Maxwell is presented in Fig. 7. Furthermore, a force map on the xy plane obtained by solving Eq. (29) is plotted in Fig. 8a to show how the magnetic forces are distributed in the neighbourhood of the coil. To validate the accuracy of the semi-analytical solutions, numerical results obtained from ANSYS Maxwell is presented in Fig. 8b.

4 Capsule system modelling

Before starting this section, it should be clear that when considering the magnetic force calculation in the previous section, the inner magnet of the capsule was considered as a mass point; while considering the dynamic impact in this section, the capsule and its inner magnet are considered as two 3D rigid bodies. As shown in Fig. 1, the magnet (inner mass) is constrained by a primary and a secondary constraints, and a helical spring is mounted between the magnet and the capsule, which can store the energy during the compression and release when the magnetic excitation $P_d$ is turned off. Here we define $X_r=X_1-X_2$ and $V_r=V_1-V_2$ as the relative displacement and relative velocity of the magnet and the capsule. Under the magnetic excitation, the magnet moves in three phases: no impact ($-G_2\le X_r\le G_1$), impact with the primary constraint ($X_r\ge G_1$), and impact with the secondary constraint ($X_r\le -G_2$). The interaction force between the magnet and the capsule can be written as

$$\begin{aligned} F_i=\left\{ \begin{array}{ll} kX_r+cV_r+F_2, &{} ~X_r\le -G_2 \\ kX_r+cV_r, &{} ~-G_2\le X_r\le G_1,\\ kX_r+cV_r+F_1, &{} ~X_r\ge G_1, \\ \end{array}\right. \end{aligned}$$

(30)

where $F_1=k_1(X_r-G_1)$ is the impact force of the primary constraint, and $F_2=k_2(X_r+G_2)$ is the impact force of the secondary constraint. The capsule moves in a stick-slip manner in the presence of Coulomb friction between the capsule and its contact surface which can be expressed as

$$\begin{aligned} F_f=\left\{ \begin{array}{ll} -\mathrm {sign}(F_i)P_f, &{} V_2 = 0, \mid F_i\mid \ge P_f, \\ -F_i, &{} V_2 = 0, \mid F_i\mid < P_f, \\ \mathrm {-sign}(V_2)P_f, &{} V_2 \ne 0 \\ \end{array}\right. \end{aligned}$$

(31)

where $P_f=\mu _s(M_m+M_c)g$ and g is the acceleration due to gravity. Finally, the equations of motion of the capsule system can be written as

$$\begin{aligned} \bigg \{\begin{array}{l} M_m\ddot{X}_1 = F_e - F_i,\\ M_c\ddot{X}_2 = F_f + F_i, \end{array} \end{aligned}$$

(32)

It is worth noting that Eq. (32) is applicable to the rectilinear motion of the capsule system along the x axis. For the planar motion on the xy plane, since the inner mass is excited by a PWM signal, the capsule moves in a stick-slip manner. For every period of excitation, which is a very small interval, the locomotion of the capsule on the xy plane can be approximated as a series of rectilinear motions. The orientation of the inner mass (so that the capsule) will be changed slightly during the procedure of each rectilinear motion according to the direction of magnetic gradient. Since the capsule contacts with the plane along a generatrix of its cylindrical shell, its friction model during rotation may be more complex. However, based on our experimental investigation in [26] and negligible capsule rotations in steps, Eqs. (31) and  (32) are still sufficient for assessing the planar motion of the capsule system.

4.1 Impact force evaluation

The capsule starts to move without any impact between the magnet and the constraints when $F_i>|F_f|$ and $-G_2\le X_r\le G_1$. When $F_i<|F_f|$ and $-G_2\le X_r\le G_1$, the magnet will impact with the constraints generating the impact force, $F_1$ or $F_2$. Usually moving on a smooth surface, the impact will not happen; while encountering any barriers, such as the circular folds of the small intestine, impact will take place, and an impact force will be generated to help the capsule to overcome the barriers.

Fig. 9

a Front and b side views of the experimental set-up for evaluating the impact force between the magnet and the constraint. An internal structure of the capsule was fixed on a platform with a bearing holding the magnet. The magnet was excited by the coil and may contact with the force sensor mounted on the constraint. Once the coil was switched off, the magnet will revert to its original position by the helical spring mounted between the magnet and the bearing

To evaluate the impact force, an experimental rig shown in Fig. 9 was built to measure the impact force, where a thin piezoelectric force sensor was attached in front of the constraint, and the magnet may contact with the sensor through a bearing under the excitation of the coil. As can be seen from Eq. (25), the magnetic force generated on the magnet is only related to the gradient of the magnetic field if magnet’s size and material are fixed. Eq. (3) reveals that the magnetic field’s gradient can be calculated from both the current applied to the coil and the distance from the coil, so the magnetic force $P_d$ can be determined from these two parameters.

Results from the experiment (denoted as dot line) and the numerical simulation (marked as red crosses) obtained from Eq. (32) by fixing the capsule on the supporting surface (i.e. $F_f$ was set as infinity) are presented in Fig. 10. It can be seen from the figure that there are some slightly differences between the maximum impact forces obtained from the numerical simulation and the experiment, which are about 53.8 mN and 63.1 mN, respectively. This may be due to the approximation when calculating the magnetic force as the magnet was considered as a mass point at one coordinate on the x axis only, i.e. $(x_c, 0, 0)$. Hence, the actual magnetic force acting on the magnet in experiment must be greater than the theoretical result, so leading to a greater impact force.

Fig. 10

Comparison of experimental (black dot line) and numerical (red crosses) results of the impact forces between the magnet and the constraint under the magnetic excitation of $P_d=97.86$ mN, $f=1$ Hz and $D=10\%$

5 Experimental results and discussion

The experiment was carried out by using the set-up shown in Fig. 2, where the displacements of the capsule and the magnet were recorded by a high-resolution camera with a frame rate of 240 fps. To extract the locomotion information from the video sources, an open-source software Tracker was employed to track a targeted point on the object and trace the object’s displacement in real time, and then, the displacement data were used to calculate the average velocity of the capsule. For the rectilinear movement, the capsule was placed in a halved plastic tube with its inner surface covered by a synthetic small intestine; for the planar movement on the xy plane, the capsule was placed on a block of soft rubber-made tissue covered by the synthetic small intestine; for both cases, a coil with the parameters listed in Table 2 was fixed at one side of the platform to provide the magnetic driving force.

It is important to notice that the duty cycle and the frequency of the magnetic driving force may influence the movement of the capsule, so the first experimental result shown in Fig. 11 presents different trajectories of the capsule under the duty cycle of $10\%$, $30\%$, $60\%$ and $90\%$ and the frequency of 5, 10, 20, 40 Hz. Among these 16 cases, we can see that the fastest progression of the capsule is $D=60\%$ and $f=10$ Hz, reaching an average speed of 7.7 mm/s; a lower or higher frequency does not necessarily determine the speed, but a combination of the frequency and the duty cycle will do; and it tends to be that higher frequency always has a negative effect on the moving speed. For example, in the case of $D=10\%$ and $f=40$ Hz, the capsule vibrated around its original position, because the vibration was too fast, and the magnet had no chance to make a forward impact before the start of the next period. In addition, according to our observation, when $D=90\%$, as the duty cycle is too large, the magnetic force becomes a “pulling” force rather than a vibro-impact excitation, which is less effective for driving the capsule.

Fig. 11

Experimental trajectories of the capsule (red lines) and the magnet (black lines) with $D\in [10\%, 90\%]$ and $f\in [5, 40]$ Hz. The fastest progression of the capsule is $D=60\%$ and $f=10$ Hz, reaching an average speed of 7.7 mm/s; lower or higher frequency does not necessarily determine the speed, but a combination of the frequency and the duty cycle will do; and it tends to be that higher frequency always has a negative effect on the moving speed. When $D=90\%$, the magnetic force becomes a “pulling” force rather than a vibro-impact excitation, which is less effective for driving the capsule

A further comparison of the trajectories under the same frequency but different duty cycles is presented in Fig. 12, where $f=5$ Hz and $D=10\%$, $50\%$ and $80\%$. As can be seen from the figure, only the impacts with the secondary constraint were recorded. Since the intestinal friction is small, the capsule does not need the impact with the primary constraint to order to progress. In Fig. 12a, as the duty cycle was small ($D=10\%$), the magnet moved towards the secondary constraint forced by the helical spring after the excitation phase, causing a few small oscillations with the capsule (indicated by the green boxes). When the duty cycle was increased to $D=50\%$ as shown in Fig. 12b, such an oscillation moved to the excitation phase. As the duty cycle is further increased as in Fig. 12c, the duration of the oscillation was increased, and the contact duration for the magnet and the secondary constraint was shortened. However, this qualitative change did not improve the progression speed of the capsule, while causing more energy consumption due to the longer duration of the magnetic excitation.

Fig. 12

Experimental displacements (left panels) of the capsule (red lines) and the magnet (black lines) and phase trajectories (right panels) under $f=5$ Hz, a $D=10\%$, b $D=50\%$ and c $D=80\%$. Green boxes indicate the corresponding responses in time series and the trajectories on the phase portrait. Blue vertical lines denote the impact boundary of the secondary constraint

Fig. 13

a Average velocity of the capsule as a function of the excitation frequency with a fixed duty cycle of $D=30\%$. b Average velocity of the capsule as a function of duty cycle of the excitation with a fixed frequency of $f=20$ Hz. Each average velocity was calculated from 5 repeated tests and standard derivations were marked on the plot

Fig. 14

Experiment on the xy plane under $f=5$ Hz and $D=30\%$, where the coil was positioned at the left of the capsule, and the capsule was put on a flat and soft surface of the synthetic small intestine supported by a block of soft silicon rubber mimicking the real body environment. a Traces of the capsule (indicated by the blue arrows) starting from 10 different initial positions. Displacements of the capsule (red lines) and the magnet (black lines) along the b x and c y directions. Velocities of the capsule (red lines) and the magnet (black lines) along the d x and e y directions

Two series of experiments with either a fixed frequency or a fixed duty cycle were carried out to find out the optimised control parameters for generating the fastest progression of the capsule. The experimental results are shown in Fig. 13, where for each case, the experiment was repeated for 5 times to get an averaged velocity. As shown in Fig. 13a, when the duty cycle was fixed at $D=30\%$, the fastest progression of the capsule occurred at $f=15$ Hz with an averaged speed of 3.85 mm/s; when the frequency was fixed at $f=20$ Hz as presented in Fig. 13b, the fastest progression occurred at $D=50\%$ with an averaged speed of 2.99 mm/s. Increasing the frequency, as mentioned before, will have a negative effect on the capsule’s progression, thus the best frequency range is within $f\in [10, 20]$ Hz. On the other hand, increasing the duty cycle will have a negative effect on the capsule’s progression too, which strongly indicates that the vibro-impact driving method works much better than the “pulling” method (e.g. using an external permanent magnet to drag the magnet inside the capsule for progression). According to our experimental result, the best duty cycle range falls within $D\in [20\%, 70\%]$.

The following discussion will move from the rectilinear motion study to a more complex steering, where the capsule is able to move along the direction of the magnetic field on the xy plane. In the experiment, the capsule was put on a flat and soft surface of the synthetic small intestine, which was supported by a block of soft silicon rubber mimicking the real body environment. An external coil was fixed at one side of the surface, and the capsule was placed at 10 different initial positions and their traces are plotted in Fig. 14a. The trend in the plot indicated by the blue arrows fits well with the force vectors shown in Fig. 8. Figures 14b–e show the displacement and velocity of the magnet and the capsule along the x and y directions, respectively. It can be seen from the figure that, within a very short distance of progression, the dynamics of the capsule became stable rapidly.

6 Conclusions

This paper presents a force calibration study for a vibro-impact capsule prototype that can be swallowed by patients for small bowel endoscopy. The capsule system, containing a capsule body with an inner permanent magnet, a helical spring and two constraints, can be controlled by an external electromagnetic coil driven by a pulse-width modulation signal with tunable frequency, amplitude and duty cycle.

A mathematical model of the electromagnetic force generated by the coil was built based on the experimental prototype. The model depicts the force interactions between the coil and the inner magnet, and its accuracy was verified by comparing the analytical (for rectilinear motion), the semi-analytical (for planar motion), numerical (obtained by ANASYS Maxwell) and experimental results, which showed a good agreement. To better understand the impact interaction between the inner magnet and the capsule body, the dynamic model of the capsule system was reviewed, and the impact force was validated by experiments.

Experimental studies for rectilinear motion were carried out by placing the capsule in a halved plastic tube with its inner surface covered by a synthetic small intestine. The electromagnetic coil was fixed at one side of the capsule with its axis aligned to the capsule body. The trajectories of the capsule and the inner magnet were recorded, and different frequencies and duty cycles of the external excitation were tested to observe the best progression for the capsule. During the experiments, it was observed that using the vibro-impact driving method was more efficient compared to the method of constant pulling. Since different combinations of duty cycles and frequencies may result in different dynamic behaviours of the capsule, comparisons were made by changing one of the parameters at one time and record the average velocity of the capsule. Finally, planar steering ability of the coil was validated by placing the capsule on a flat surface covered by the small intestine. Trajectories and orientations of the capsule were depicted and compared with the semi-analytical results, which showed a good consistency.

Future work includes expanding the two-dimensional analytical model to two-dimensional for controlling the capsule’s motion in a more realistic environment and developing a feedback control system for automation of the endoscopic procedure.

Appendix

From Eqs. (5) and  (28), the magnitude of the magnetic force exerted on the magnet along the x axis by the cylindrical coil can be explicitly written as

$$\begin{aligned} P_d= & {} vM\frac{\partial B_x}{\partial x} \nonumber \\= & {} \frac{n\mu _0I}{2}\left[ \ln {(R+a+\sqrt{(x_c+b)^2+(R+a)^2})} \right. \nonumber \\&-\ln {(R-a+\sqrt{(x_c+b)^2+(R-a)^2})} + (x_c+b)^2 \nonumber \\&\left( \tfrac{1}{(R+a+\sqrt{(x_c+b)^2+(R+a)^2})\sqrt{(x_c+b)^2+(R+a)^2}}\right. \nonumber \\&-\left. \tfrac{1}{(R-a+\sqrt{(x_c+b)^2+(R-a)^2})\sqrt{(x_c+b)^2+(R-a)^2}}\right) \nonumber \\&-\ln {(R+a+\sqrt{(x_c-b)^2+(R+a)^2})} \nonumber \\&+\ln {(R-a+\sqrt{(x_c-b)^2+(R-a)^2})} - (x_c-b)^2\nonumber \\&\left( \tfrac{1}{(R+a+\sqrt{(x_c-b)^2+(R+a)^2})\sqrt{(x_c-b)^2+(R+a)^2}} \right. \nonumber \\&\left. \left. -\tfrac{1}{(R-a+\sqrt{(x_c-b)^2+(R-a)^2})\sqrt{(x_c-b)^2+(R-a)^2}}\right) \right] . \end{aligned}$$

(33)

Based on Eqs. (20) and  (29), the magnitude of the magnetic force along the x direction of the xy plane by the square coil can be explicitly written as

$$\begin{aligned} F_x= & {} vM\frac{\partial B_x}{\partial x} = vM\tfrac{n\mu _0I}{2\pi }\Bigl [\sum _{j=1}^{8} \Bigl (\alpha _j (L+(-1)^j a) \nonumber \\&\tan ^{-1}\tfrac{(x_c+\beta _j b)(L-\beta _j y_c)(L+(-1)^j a)^{-1}}{\sqrt{(L+(-1)^j a)^2+(x_c+\beta _j b)^2+(L-\beta _j y_c)^2}}\Bigr )\nonumber \\&-\sum _{j=1}^{8} \Bigl (\alpha _j (x_c+\beta _j b) \nonumber \\&\tanh ^{-1}\tfrac{\sqrt{(L+(-1)^j a)^2+(x_c+\beta _j b)^2+(L-\beta _j y_c)^2}}{L-\beta _j y_c}\Bigr )\nonumber \\&-\sum _{j=1}^{8} \Bigl (\alpha _j (L-\beta _j y_c) \nonumber \\&\tanh ^{-1}\tfrac{\sqrt{(L+(-1)^j a)^2+(x_c+\beta _j b)^2+(L-\beta _j y_c)^2}}{x_c+\beta _j b}\Bigr )\nonumber \\&+\sum _{j=1}^{8} \Bigl (\alpha _j (L+(-1)^j a+\gamma _j y_c) \nonumber \\&\tan ^{-1}\tfrac{(x_c+\beta _j b)(L+(-1)^j a+\gamma _j y_c)^{-1}L}{\sqrt{(L+(-1)^j a+\gamma _j y_c)^2+(x_c+\beta _j b)^2+L^2}}\Bigr )\nonumber \\&-\sum _{j=1}^{8} \Bigl (\alpha _j (x_c+\beta _j b) \nonumber \\&\tanh ^{-1}\tfrac{\sqrt{(L+(-1)^j a+\gamma _j y_c)^2+(x_c+\beta _j b)^2+L^2}}{L}\Bigr )\nonumber \\&-\sum _{j=1}^{8} \Bigl (\alpha _j L \tanh ^{-1}\nonumber \\&\tfrac{\sqrt{(L+(-1)^j a+\gamma _j y_c)^2+(x_c+\beta _j b)^2+L^2}}{x_c+\beta _j b}\Bigr )\Bigr ],\nonumber \\ \end{aligned}$$

(34)

where $\alpha _{1,2,3...8} = \{1, -1, -1, 1, 1, -1, -1, 1\}$ and $\beta _{1,2,3...8} = \{1, 1, -1, -1, 1, 1, -1, -1\}$ and $\gamma _{1,2,3...8} = \{1, 1, 1, 1, -1, -1, -1, -1\}$.

Based on Eqs. (21) and  (29), the magnitude of the magnetic force along the y direction of the xy plane by the square coil can be semi-explicitly written as

$$\begin{aligned} F_y= & {} vM\frac{\partial B_y}{\partial x} \nonumber \\= & {} vM\frac{\partial }{\partial x}\left[ \tfrac{\mu _0nI}{2\pi }\int _{L+a}^{L-a}\left[ \sum _{j=3}^{4}(-1)^{j+1}\right. \right. \nonumber \\&\left( \tanh ^{-1}\tfrac{\sqrt{z_{ij}^2+(x_c-b)^2+L^2}}{L}\right. \nonumber \\&\left. \left. \left. -\tanh ^{-1}\tfrac{\sqrt{z_{ij}^2+(x_c+b)^2+L^2}}{L}\right) \right] \mathrm {d}z_i\right] . \end{aligned}$$

(35)

Finally, the resultant magnitude of the magnetic force on the xy plane can be calculated as $|\vec {P}_d| =\sqrt{F_x^2+F_y^2}$ in the direction of $\theta _{xy} = \arctan (\tfrac{F_y}{F_x})$.