Zero-dispersion point in curved micro-mechanical beams

Abstract

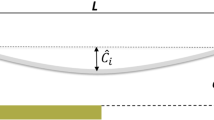
In doubly clamped curved mechanical beams, there are inherent hardening and softening nonlinearities. Thus, their frequency of oscillation is a non-monotonic function of the energy. However, for a sufficiently high energy level there is a zero-dispersion point, where the frequency of oscillation is locally independent of energy even though the beam oscillates deep in its nonlinear regime. This zero-dispersion point is a highly desirable feature in micro-mechanical beams that are used in sensing and time-keeping applications because it effectively eliminates the amplitude-to-frequency noise conversion, and thereby, stabilizes the oscillation frequency. In this paper, we present a detailed analysis of the conservative strongly nonlinear dynamics of curved micro-mechanical beams. Our analysis includes a numerically validated closed-form analytical solution for the strongly nonlinear oscillation of beam, derivation of the condition for the zero-dispersion point in curved beams, and a design scheme for the optimal initial depth of the curved beam that maximizes the frequency of oscillation and the energy level at the zero-dispersion point. We apply our methodology to a physical MEMS device reported in the literature and find the optimal values for this device. Our analysis provides the first step in the development of design tools for exploiting the inherent nonlinearities of curved micro-mechanical beams for frequency stabilization.

Appendices

Appendix A: Exact solution of the conservative strongly nonlinear dynamics

By rearranging the expression for conservation of energy ${\dot{q}}^2/2+U(q)=E_{\mathrm{tot}}$, we find that

$$\begin{aligned} dt=\pm \frac{dq}{\sqrt{2(E_{\mathrm{tot}}-U(q))}}, \end{aligned}$$

(24)

where the ± reflects the change of sign in the velocity $\dot{q}$ when crossing the turning points $q^{(1)},q^{(2)}$. In half cycle, the resonator starts its motion from the lower turning point $q^{(2)}$ with a positive velocity and arrives to the higher turning point $q^{(1)}$ . Therefore, we can write

$$\begin{aligned} \int _{0}^{\frac{T}{2}}{dt}=\int _{q^{(2)}}^{q^{(1)}}{\frac{dq}{\sqrt{2[E_{\mathrm{tot}}-U(q)]}}}. \end{aligned}$$

(25)

Furthermore, we can rewrite the quadratic polynomial under the square root sign in the following way

$$\begin{aligned}&2[E_{\mathrm{tot}}-U(q)]\nonumber \\&\quad =\frac{\gamma }{4}\left( -q^{4}-\frac{4\beta }{3\gamma }q^{3}-\frac{2\omega _{0}^{2}}{\gamma }q^{2}+\frac{4}{\gamma }E_{\mathrm{tot}}\right) \nonumber \\&\quad = \frac{\gamma }{4}(q^{(1)}-q)(q-q^{(2)})(q-q^{(3)})(q-q^{(4)}). \end{aligned}$$

(26)

Thus, from Eq. (25) we find that

$$\begin{aligned} \frac{T}{2}&=\sqrt{\frac{2}{\gamma }} \int _{q^{(2)}}^{q^{(1)}}{}\nonumber \\&\quad \frac{dq}{\sqrt{(q^{(1)}-q)(q-q^{(2)})(q-q^{(3)})(q-q^{(4)})}}. \end{aligned}$$

(27)

We normalize the modal coordinate q by the highest real root $q^{(1)}$, and hence, Eq. (25) yields

$$\begin{aligned} \frac{T}{2}&=\sqrt{\frac{2}{ q^{(1)}\gamma }}\int _{q'^{(2)}}^{1}{}\nonumber \\&\quad \frac{dq'}{\sqrt{(1-q')(q'-q'^{(2)})(q'-q'^{(3)})(q'-q'^{(4)})}} \end{aligned}$$

(28)

where $q'=q/q^{(1)}$, $q'^{(1)}=q^{(1)}/q^{(1)}=1$, $q'^{(2)}=q^{(2)}/q^{(1)}$, $q'^{(3)}=q^{(3)}/q^{(1)}$ and $q'^{(4)}=q^{(4)}/q^{(1)}$. The solution of the elliptic integral in Eq. (28) is given by (cf. Ref. [68], Eq. (259.00))

$$\begin{aligned} T=4g'\sqrt{\frac{2}{\gamma }}K(k'), \end{aligned}$$

(29)

where

$$\begin{aligned} k'^{2}= & {} \frac{1}{4}\frac{(q'^{(1)}-q'^{(2)})^2-(z'^{(1)}-z'^{(2)})^2}{z'^{(1)}z'^{(2)}},\nonumber \\ z'^{(1)^2}= & {} (q'^{(1)}-{\mathfrak {R}}\{q'^{(3)}\})^2+({\mathfrak {I}}\{q'^{(3)}\})^2,\nonumber \\ z'^{(2)^2}= & {} (q'^{(2)}-{\mathfrak {R}}\{q'^{(3)}\})^2+({\mathfrak {I}}\{q'^{(3)}\})^2,\nonumber \\ g'= & {} \frac{1}{\sqrt{(z'^{(1)}z'^{(2)})}}, \end{aligned}$$

(30)

$K(k')$ is an elliptic integral of the first kind, and ${\mathfrak {R}}\{\bullet \}$ and ${\mathfrak {I}}\{\bullet \}$ are the real and imaginary parts of $\{\bullet \}$, respectively. Thus, by switching back to the non-normalized variables $q, q^{(1)}, q^{(2)}, q^{(3)}$ and $q^{(4)}$, we find that the fundamental frequency is given by

$$\begin{aligned} \omega =\frac{2\pi }{T}=\frac{\pi }{2K(k)}\sqrt{\frac{\gamma }{2}z^{(1)}z^{(2)}}, \end{aligned}$$

(31)

and by inverting the relation ${\text {cn}}\tau =[(q^{(1)}-q)z^{(2)}-(q-q^{(2)})z^{(1)}]/[(q^{(1)}-q)z^{(2)}+(q-q^{(2)})z^{(1)}]$, we find that

$$\begin{aligned} q=\frac{q^{(1)}z^{(2)}+q^{(2)}z^{(1)}-(q^{(1)}z^{(2)}-q^{(2)}z^{(1)}){\text {cn}}(\tau |k)}{(z^{(1)}-z^{(2)}){\text {cn}}(\tau |k)+(z^{(1)}+z^{(2)})}, \end{aligned}$$

(32)

where $\tau =t\sqrt{\frac{\gamma }{2}z^{(1)}z^{(2)}}$.

Appendix B: Quintic order nonlinear equation of motion

We consider the nonlinearities that stem from the midline stretching and induced by the large deflections of the beam compared to its thickness.

Fig. 8

Kinematic and free-body diagrams. Left panel: kinematic diagram of a segment from the midline of the beam before and after deformation. Right panel: free-body diagram of an element of the beam after deformation

Following [57], we assume planar motion, linear stress–strain law (i.e. Hooke’s law), an initially curved beam [$w_0(x)$], and constant beam properties (E, I, A and $\rho$). From the kinematics of the beam, we find that location of point $p({{\tilde{x}}},{{\tilde{y}}})$ of the deformed segment (Fig. 8, left panel) is given by

$$\begin{aligned} {\tilde{x}}=x+u, \qquad {\tilde{y}}=w_0+w. \end{aligned}$$

(33)

Thus, by differentiation of Eq. (33), we find that the horizontal and transverse stretches of the segment are given by

$$\begin{aligned}&d{\tilde{x}}=dx+\frac{\partial u}{\partial x}dx=(1+u')dx,\nonumber \\&d{\tilde{y}}=\frac{\partial w_{0}}{\partial x}dx+\frac{\partial w}{\partial x} dx=(w_{0}'+w')dx. \end{aligned}$$

(34)

Consequently, the length of the deformed segment is $d{{\tilde{s}}}=\sqrt{d{\tilde{x}}^2 + d{\tilde{y}}^2}=dx\sqrt{(1+u')^2+(w_{0}'+w')^2}$, which can be subtracted from the initial length of the segment, $ds=\sqrt{dx^2 + dy^2}=dx\sqrt{1+w_0'^2}$, and then divided by ds to yield the axial strain

$$\begin{aligned} \varepsilon&=\frac{ds^{*}-ds}{ds}\nonumber \\&\quad =\frac{dx\sqrt{(1+u')^2+(w_{0}'+w')^2}-dx\sqrt{1+w_0'^2}}{dx\sqrt{1+w_0'^2}}\nonumber \\&\approx \sqrt{(1+u')^2+w'^2+2w'w_{0}'}-1, \end{aligned}$$

(35)

where we have assumed that $w_0'^2\ll 1$. To complete the description of the deformed segment, we also define (see, Fig. 8, left panel)

$$\begin{aligned} \sin {\theta }=\frac{d{\tilde{y}}}{ds^{*}}=\frac{w'+w'_{0}}{\sqrt{(1+u')^2+(w'+w'_{0})^2}}, \end{aligned}$$

(36)

$$\begin{aligned} \cos {\theta }=\frac{d{\tilde{x}}}{ds^{*}}=\frac{1+u'}{\sqrt{(1+u')^2+(w'+w'_{0})^2}}. \end{aligned}$$

(37)

Using Taylor expansion, we find that

$$\begin{aligned} \varepsilon&\approx u'+w'_{0}w'+\frac{w'^{2}}{2}-\frac{w'_{0}w'^{3}}{2}-\frac{w'^{4}}{8}+...\,, \end{aligned}$$

(38)

$$\begin{aligned} \sin {\theta }&\approx w'_{0}+w'-w'_{0}u'-w'u'-\frac{3w'_{0}w'^{2}}{2}\nonumber \\&\quad -\frac{w'^3}{2}+\frac{15w'_{0}w'^{4}}{8}+\frac{3w'^{5}}{8}+...\,, \end{aligned}$$

(39)

$$\begin{aligned} \cos {\theta }&\approx 1-w'_{0}w'-\frac{w'^{2}}{2}+\frac{3w'_{0}w'^{3}}{2}+\frac{w'^4}{8}+...\,. \end{aligned}$$

(40)

Furthermore, the deformed angle at the other end of the deformed segment is approximately $\theta +\theta 'd{\tilde{x}}$ (Fig. 8, right panel), and therefore,

$$\begin{aligned} \sin {(\theta +\theta 'd{\tilde{x}})}\approx \sin {\theta }+(\sin {\theta })'d{\tilde{x}}+...\,, \end{aligned}$$

(41)

$$\begin{aligned} \cos {(\theta +\theta 'd{\tilde{x}})}\approx \cos {\theta }+(\cos {\theta })'d{\tilde{x}}+...\,. \end{aligned}$$

(42)

Now, we consider the free-body diagram (Fig. 8, right panel) and apply Newton’s second law in the horizontal and transverse directions

$$\begin{aligned}&(N+N'd{\tilde{x}})\cos {(\theta +\theta 'd{\tilde{x}})}-N\cos {\theta }=\rho Ad{\tilde{x}}\ddot{u}, \end{aligned}$$

(43)

$$\begin{aligned}&V-(V+V'd{\tilde{x}})-N\sin {\theta }+(N+N'd{\tilde{x}})\nonumber \\&\times \sin {(\theta +\theta 'd{\tilde{x}})}=\rho Ad{\tilde{x}}\ddot{w}. \end{aligned}$$

(44)

Substitutions of Eq. (42) into Eqs. (43), and (41) into Eq. (44), yield

$$\begin{aligned}&(N\cos {\theta })'=\rho A\ddot{u}, \end{aligned}$$

(45)

$$\begin{aligned}&-V+(N\sin {\theta })'=\rho A\ddot{w}. \end{aligned}$$

(46)

Using the relation between the shear force and the bending moment, $V=-\frac{\partial M}{\partial x}$, the relation between the bending moment and the beam curvature, $M=EI\frac{\partial ^2 w}{\partial x ^2}$ [15, 69], and Hooke’s law

$$\begin{aligned} N&=EA\varepsilon =EA\nonumber \\&\quad \left( u'+w'_{0}w'+\frac{w'^{2}}{2}-\frac{w'_{0}w'^{3}}{2}-\frac{w'^{4}}{8}+...\right) , \end{aligned}$$

(47)

we find that Eqs. (45), (46) reduce to

$$\begin{aligned}&\rho A\ddot{u}-EAu''=EA\nonumber \\&\quad \left( \frac{w'^{2}}{2}+w'_{0}w'-\frac{3w'_{0}w'^{3}}{2}-\frac{3w'^{4}}{8} \right) ', \end{aligned}$$

(48)

$$\begin{aligned}&\rho A\ddot{w}+EIw^{IV}=EA\left( u'(w'_{0}+w')+\frac{3w'_{0}w'^{2}}{2}\right. \nonumber \\&\quad \left. +\frac{w'^{3}}{2}-\frac{15w'_{0}w'^{4}}{8}-\frac{3w'^{5}}{8} \right) '. \end{aligned}$$

(49)

Eqs. (48), (49) are a pair of coupled nonlinear partial differential equations that govern the dynamics of the beam. However, in our case of a slender beam with small radius of gyration $r=\sqrt{I/A}\ll 1$, the analysis can be simplified significantly. In particular, the inertia term in Eq. (48) can be neglected, since the axial natural frequency is much higher than the transverse natural frequency [57], and therefore

$$\begin{aligned} u''=-\left( \frac{w'^{2}}{2}+w'_{0}w'-\frac{3w'_{0}w'^{3}}{2}-\frac{3w'^{4}}{8} \right) '. \end{aligned}$$

(50)

Integrating Eq. (50) twice with respect to x yields

$$\begin{aligned} u&=-\int _{0}^{x}{\left( \frac{w'^{2}}{2}+w'_{0}w'-\frac{3w'_{0}w'^{3}}{2}-\frac{3w'^{4}}{8}\right) dx}\nonumber \\&\quad +c_{1}(t)x+c_{2}, \end{aligned}$$

(51)

where $c_{1}(t)$ and $c_{2}(t)$ can be found from the clamped–clamped boundary conditions, i.e. $u(0,t)=u(\ell ,t)=0$, and are given by

$$\begin{aligned}&c_{1}=\frac{1}{\ell }\int _{0}^{\ell }{\left( \frac{w'^{2}}{2}+w'_{0}w'-\frac{3w'_{0}w'^{3}}{2}-\frac{3w'^{4}}{8}\right) dx},\nonumber \\&c_{2}=0. \end{aligned}$$

(52)

Substituting Eq. (52) into Eq. (51) and the outcome into Eq. (49), we obtain the following single integro-differential equation for the transverse motion of the beam

$$\begin{aligned} \rho&A\ddot{w}+EIw^{IV}=\frac{EA}{2\ell }(w''_{0}+w'')\int _{0}^{\ell }\nonumber \\&\quad {\left( w'^{2}+2w'_{0}w'-3w'_{0}w'^{3}-\frac{3w'^{4}}{4}\right) dx}. \end{aligned}$$

(53)