Abstract
In view of the facts in the infection and propagation of COVID-19, a stochastic reaction–diffusion epidemic model is presented to analyse and control this infectious diseases. Stationary distribution and Turing instability of this model are discussed for deriving the sufficient criteria for the persistence and extinction of disease. Furthermore, the amplitude equations are derived by using Taylor series expansion and weakly nonlinear analysis, and selection of Turing patterns for this model can be determined. In addition, the optimal quarantine control problem for reducing control cost is studied, and the differences between the two models are compared. By applying the optimal control theory, the existence and uniqueness of the optimal control and the optimal solution are obtained. Finally, these results are verified and illustrated by numerical simulation.
Similar content being viewed by others
1 Introduction
By the end of 2019, a new virus infection named COVID-19 (SARS-CoV-2) was recorded in China [1,2,3]. The symptoms of infected individuals are respiratory problem, fever, dry cough, etc. and it seriously affects the lungs. The incubation period of this infectious disease is 3–14 days or longer [4], the asymptomatic period is on an average 3 days [5].
The evolution that followed the outbreak indicated that the world mechanisms for preventing the transmission and quarantine of COVID-19 were considerably limited, and almost all areas are suffering from its serious impact. The epidemic models are often used to forecast and control the spread of diseases as much as possible, so as to the relevant government departments to prepare in advance and make necessary decisions. As early as the eighteenth century, the work on constructing mathematical models [6] of epidemiology has begun. From Bernoulli [7] at that time to Kermack and McKendrick [8] more than 100 years later, many changes have taken place in the models, and now most of the models used in epidemic research are based on the latter. These models which constitute a set of nonlinear ordinary differential equations are called compartment models. As we all know, classical differential equations are often used to analyse and study infectious diseases, such as SI [9], SIS [10], SIR [11], SIRC [12], SEIR [13] models and so on. Since the discovery of the COVID-19, many models have been constructed to describe and study its dynamics [14,15,16]. With the increase of real data and available information, the models for COVID-19 pandemic are also developing, what followed was increasingly complex epidemiological models [17,18,19,20]. Sun et al. [21] proposed an SEIQR model in light of the influences of lockdown and medical resources on the propagation of COVID-19. Zhang et al. [22] considered the threshold of a stochastic SIQS epidemic model with varying total population and its corresponding deterministic epidemic model. Zhang et al. [23] constructed a SIQRS model on networks and investigate the related optimal control problems. Tang et al. [24] studied the effects of isolation and quarantine on the tendency of this novel coronavirus-caused pneumonia in China.
The present novel coronavirus (SARS-CoV-2) infection has spread all over the world in a large scale, but there is no specific effective vaccine, anti-viral medicine for such infection. The UK, which has made rapid progress in COVID-19 vaccine trials, has only approved the use of the vaccine in emergency situations [25]. There are still many questions about the effect when it is promoted to millions of people. Thus, at present, the most effective method is still early detection and isolation treatment. This approach has been practiced forcefully in China. In the face of a sudden epidemic, China built Fangcang shelter hospitals [26] which are large-scale, extemporaneous hospitals for the first time to cope with it in February 2020. They transformed the existing public places, for example exhibition centres and gymnasium, into the Fangcang shelter hospitals to quarantine patients with COVID-19 and prevent further infection. This measure reduce the incidence and maintain it at a very low level by strict social distancing, localized and targeted measures. China has generally controlled the propagation of COVID-19 by implementing these measures. Thus, quarantine treatment is still the most effective treatment until specific effective vaccines and drugs are developed. Although continuous control can effectively control the epidemic of infectious diseases, it usually costs a lot of manpower and material resources. In order to achieve the control goal and reduce the control cost, the optimal control is a effective method to better control the epidemic situation [27, 28]. The research on COVID-19 is developing vigorously. Some meaningful results are obtained to recognize this infectious disease, for example, clinical studies have shown that the immune system’s memory of the new coronavirus lingers for at least 6 months in most people [29]. According to the facts and inspired by [30], a stochastic reaction–diffusion epidemic model is presented. Diffusion is introduced into it to better understand and analyse COVID-19, this model will be elaborated in the next section.
The structure of this paper is as follows. In Sect. 2, the epidemic models studied in this paper are introduced in detail. In Sect. 3, the sufficient criteria for the persistence and extinction of disease are derived. In Sect. 4, we deal with this stochastic model by the given method and obtain the conditions of how the Turing instability arises. In Sect. 5, the amplitude equations for Turing pattern are derived by using Taylor series expansion and weakly nonlinear analysis. And the stability of these equations are analysed, by which the selection of Turing patterns for this model can be determined. In Sect. 6, the optimal quarantine control problems of the stochastic model and its corresponding deterministic model are studied. The existence and uniqueness of the optimal control and the optimal solution are got by using the optimal control theory. In Sect. 7, an approximation based on the solution of the deterministic model is used to solve the stochastic optimal control problem numerically. These results are verified and illustrated by numerical simulations. Finally, some discussions and conclusions are made in Sect. 8.
2 The model
In 2020, Anwarud Din et al. [30] had proposed a stochastic coronavirus (COVID-19) epidemic model, which consists of three stochastic differential equations. This model is based on stochastic theories and study the transmissions dynamic of the novel virus. The stochastic model is obviously better than the deterministic model in describing most phenomena in nature. That’s because stochastic model has some inherent randomness, while the deterministic model is completely determined by initial condition and parameter value.
Different from the temporal development of epidemics that most researchers have focused on in the past. Many significant epidemiological behaviours are keenly impacted by space in the process of their transmission and development due to the relevant characteristics of the transmission environment or other interactions. And its spread can also lead to strong spatial pattern changes, resulting in some new phenomena. The subjects which are related to the spatial variation in disease risk or incidence have attracted more attention [31]. When the distribution of people is in different spatial locations, the diffusion terms should be taken into consideration to accord with the actual situation of infectious diseases. Hence, on the basis of [30], we propose novel susceptible-infected-quarantined epidemic models with spatial diffusion term that are more in line with the actual characteristics. This model can better research the spatial and temporal transmission laws of population epidemics, and improve the awareness of the epidemiological characteristics of population.
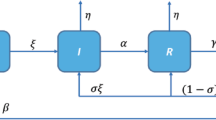
According to the characteristics of COVID-19, the following assumptions are given.
- (i):
-
\(N(t)=S(t)+I(t)+Q(t)\) is the total population which is changing with time t.
- (ii):
-
The state variables and parameters in the model are nonnegative throughout this paper.
- (iii):
-
The initially infected individuals move to the quarantined class.
- (iv):
-
Once the infection is confirmed, then the quarantined will be sent back to the infected area.
Based on the above assumptions (i)–(iv), we proposed the following model
where S is the susceptible individuals. I denotes the infected individuals. Q represents the quarantine individuals. \(\nabla ^{2}=\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\) is the Laplacian operator in two-dimensional space and \(d_{i}\ (i=1, 2, 3)\) are diffusion coefficients. \(B_{i}\ (i=1, 2, 3)\) is the Brownian motion, \( R_{i}=R_{i}(S,I,Q),\ (i=1,2,3) \) are locally Lipschitz-continuous functions. According to the different problems studied, the specific forms of \( R_{i} \) are also different. In the problems investigated in this paper, they have two forms:
- \( H_{1} \)::
-
One recorded as form \( H_{1} \) is \( R_{1}=S,\ R_{2}=I,\ R_{3}=Q \), i.e., the environmental influence on the individuals described by stochastic perturbations [32].
- \( H_{2} \)::
-
Second one recorded as form \( H_{2} \) is \(R_{1}=S-S_{0},\) \( R_{2}=I-I_{0},\) \( R_{3}=Q-Q_{0}\) where \((S_{0},I_{0},Q_{0})\) is the equilibrium point of (2.1) after removing diffusion terms and stochastic terms, i.e., the situation of stochastic perturbations around the equilibrium state [33].
The parameters in (2.1) are summarized as follows:
-
A : the per capita constant fecundity rate;
-
\(\beta :\) transmission coefficient between S and I;
-
\(\mu _{0}:\) the per capita natural mortality rate;
-
\(r_{1}:\) the rate for individuals leaving I for Q;
-
\(\mu _{1}:\) disease-caused death rate of infectious individuals;
-
\(\sigma \): the rate for individuals leaving Q for I;
-
\(\mu :\) disease-caused death rate of quarantined individuals;
-
\(\eta _{i}:\) noise magnitude \((i=1, 2, 3)\).
If \( d_{1}=d_{2}=d_{3}=0 \), then (2.1) is reduced to the following model,
The difference between (2.2) and the model from [30] is that the incidence rate varies in form, one is bilinear incidence rate \( \beta SI \), and the other is standard incidence rate \( \dfrac{\beta SI}{N} \). If \( \eta _{1}=\eta _{2}=\eta _{3}=0 \), then (2.2) is simplified to the underlying deterministic model. With regard to this deterministic system, we give the following results according to [34].
The total population N(t) satisfies \( \dfrac{\mathrm{d}N(t)}{\mathrm{d}t}=A-\mu _{0} N{(t)}-\mu _{1} I{(t)}-\mu Q{(t)} \). When there is no disease, the population size N(t) approaches the carrying capacity \( \dfrac{A}{\mu _{0}} \). The solutions of the underlying deterministic model are always within \( \Gamma _{1}\in R_{+}^{3} \) which defined by
The basic reproduction number (or the threshold) \(R_{0}\) of the underlying deterministic model corresponding to (2.2) is determined by using the next generation matrix method [35]:
If \(R_{0}\le 1\), there exist a unique equilibrium point, i.e., the disease-free equilibrium \((S^{**}, I^{**}, Q^{**})=(\frac{A}{\mu _{0}}\), 0, 0). If \(R_{0}>1\), there are two equilibrium points, a disease-free equilibrium point and a positive endemic equilibrium point \((S^{*}, I^{*}, Q^{*})=\left( \dfrac{A-I^{*}R^{*}}{\mu _{0}},I^{*},\dfrac{r_{1}I^{*}}{\mu +\mu _{0}+\sigma } \right) ,\) where \(I^{*}=\dfrac{A}{R^{*}}-\dfrac{\mu _{0}}{\beta }\).
Next, some related theories in stochastic differential equations [36] are given.
Let \( (\Omega ,\ \lbrace \mathcal {F}_{t} \rbrace ,\ P^{*}) \) be the complete probability space with filtration \( \lbrace \mathcal {F}_{t} \rbrace _{t\ge 0} \) which satisfy \( X(t)=(S(t), I(t), Q(t)),\ |X(t)|=[S^{2}(t)+I^{2}(t)+Q^{2}(t)]^{\frac{1}{2}} \), and \( R_{+}^{d}=\lbrace x\in R^{d}:\chi > 0,\ j=1, \ldots , d \rbrace \). For some \( n \in N \), some \( x_{0} \in R^{n} \), and n-dimensional Brownian motion B(t), we have the general n-dimensional SDE as follows,
Define the differential operator \( \mathcal {L} \) related to the function in (2.4), and operate \( \mathcal {L} \) on a function \( U(t,x) \in C^{2,1}(R^{n}\times \left[ t_{0}, \infty \right] ; R_{+}) \) to obtain
Then, the following two theorems show the existence of the unique positive global solution of stochastic model (2.2) with form \( H_{1} \) and \( H_{2} \).
Theorem 2.1
There exist a unique solution \( (S((t), I(t), Q(t)) \) of model (2.2) with form \( H_{1} \) for all \( t\ge 0 \) with any initial condition \( (S((0), I(0), Q(0))\in R_{+}^{3} \). Moreover, this solution will always remain in \( R_{+}^{3} \) with probability one, i.e., \( (S((t), I(t), Q(t))\in R_{+}^{3} \) for \( \forall t\ge 0 \) almost surely (a.s.).
Proof
Owing to the local Lipschitz continuity of the coefficients in the equations with respect to any initial value \( (S((0), I(0), Q(0))\in R_{+}^{3} \), a unique local solution (S(t), I(t), Q(t)) on \( t\in [0, \tau _{e}) \) must exist. Next we need to prove the explosion time \( \tau _{e}= \infty \) (a.s.) to indicate this solution is global. Assume that all of the initial conditions belong to \( [\frac{1}{k_{0}}, k_{0}]\times [\frac{1}{k_{0}}, k_{0}] \times [\frac{1}{k_{0}}, k_{0}] \) where \( k_{0}\ge 0 \) is sufficiently large. For each integer \( k\ge k_{0} \), define the finishing time
We set \( \mathrm{inf} \phi = \infty \) (\( \phi \) is the empty set). As shown above, \( \tau _{k} \) is increasing as \( k\rightarrow \infty \). Setting \( \tau _{\infty }= \mathop {\lim }\nolimits _{k\rightarrow \infty } \tau _{k} \) with \( \tau _{\infty }\le \tau _{e} \) (a.s.). If we have \( \tau _{\infty }= \infty \), then \( \tau _{e}= \infty \) and \( (S(t), I(t), Q(t))\in R_{+}^{3} \) (a.s.) for \( \forall t\ge 0 \). In the opposite case, there have two constants \( \varsigma \in (0, 1) \) and \( T> 0 \) make
Thus, there exist an integer \( k_{1}\ge k_{0} \) makes
Next, defining a \( C^{2}\)-function \( {V}: R_{+}^{3}\rightarrow R_{+} \) by
From \( y-1-\log y\ge 0,\ \forall y>0 \), we can obtain this function is nonnegative. Assume that \( \forall {K}\ge k_{0} \) and \( \forall T> 0 \), and according to the It\(\hat{o}\) formula, we derive the following formula
where \( \mathcal {L}V:R_{+}^{3}\rightarrow R_{+} \) is as follows,
Now integrating both sides of (2.8) from 0 to \( \tau _{k}\wedge T \) where \( \tau _{k}\wedge T= \min \left\{ \tau _{k}, T \right\} \),
Therefore,
Set \( \Omega _{k}=\left\{ \tau _{k}\le T \right\} \) for \( k\ge k_{1} \) and \( P(\Omega _{k})\ge \varsigma \). For \( \forall \omega \in \Omega _{k} \), there is at least one \( S(\tau _{k}, \omega ),\ I(\tau _{k}, \omega ), Q(\tau _{k}, \omega ) \) which equals k or \( \frac{1}{k} \). Thus, \( V(S(\tau _{k}, {\omega }), I(\tau _{k}, {\omega }), Q(\tau _{k}, {\omega })) \) is no less than \( (k-1-\log k) \) or \( (\frac{1}{k}-1+\log k) \), then
According to (2.6) and (2.10), we derive
where \( 1_{\Omega (\omega )} \) represent the indicator function of \( \Omega \). Letting \( k\rightarrow \infty \) leads to the contradiction \( \infty = V(S(0), I(0), Q(0)){+KT}< \infty \), then we have \( \tau _{\infty }= \infty \) a.s. \(\square \)
Remark 2.1
The above Theorem 2.1 shows that the solution process of system (2.2) with form \( H_{1} \) is positive and global.
Theorem 2.2
There exist a unique solution \( (S((t), I(t), Q(t)) \) of model (2.2) with form \( H_{2} \) for all \( t\ge 0 \) with any initial condition \( (S((0), I(0), Q(0))\in R_{+}^{3} \). Moreover, this solution will always remain in \( R_{+}^{3} \) with probability one, i.e., \( (S((t), I(t), Q(t))\in R_{+}^{3} \) for \( \forall t\ge 0 \) almost surely (a.s.).
Proof
The essence of the proof of this theorem is the same as that of Theorem 2.1. The specific proof process is omitted here, and only the differences corresponding to (2.8) of Theorem 2.1 in the proof of this theorem are pointed out as follows,
Then, (2.9) corresponds to the following formula
The remaining proof process is the same as the previous theorem. Therefore, this theorem shows that the solution process of system (2.2) with form \( H_{2} \) is positive and global. \(\square \)
Remark 2.2
In the following sections, we mainly study two kinds of problems, one is the impact of the stochastic fluctuation of the environment on the existence and extinction of diseases, and the related optimal quarantine control problems, i.e., the form of stochastic perturbations in (2.2) is form \( H_{1} \). The other is the influence of stochastic perturbations around the equilibrium state on the pattern formations, i.e., the form of stochastic perturbations in (2.1) is form \( H_{2} \).
3 Extinction and stationary distribution criteria
In this section, we investigate the conditions for the extinction and stationary distribution criteria of this disease. For the sake of convenience, let
In order to prove the extinction and stationary distribution criteria, the following lemmas need to be used.
Lemma 3.1
[36](Strong Law of Large Number) Let \( M=\lbrace M \rbrace _{t\ge 0} \) be a continuous real valued local martingale and vanishing at \( t=0 \), then
and also
Lemma 3.2
Assume that (S(t), I(t), Q(t)) be a solution of (2.2) with form \( H_{1} \) along with initial values \( (S(0), I(0), Q(0))\in R_{+}^{3} \), then \( \mathop {\lim \mathrm{sup}}\limits _{t\rightarrow \infty } (S(t)+I(t)+Q(t))< \infty \) a.s. Further,
Proof
From (2.2) with form \( H_{1} \), we can obtain
Solving this above equation,
where \( M=\eta _{1} \int _{0}^{t} S(s)e^{-\mu _{0} (t-s)} dB_{1}(s)+\eta _{2} \int _{0}^{t} I(s)e^{-\mu _{0} (t-s)} dB_{2}(s)+\eta _{3} \int _{0}^{t} Q(s)e^{-\mu _{0} (t-s)} dB_{3}(s) \).
Obviously, M(t) is a continuous local martingale with \( M(0)=0 \). We define
where \( A(t)=\dfrac{A}{\mu _{0}} (1-e^{-\mu _{0} t}), Q(t)=(S(0)+I(0)+Q(0))(1-e^{-\mu _{0} t}), X(0)=S(0)+I(0)+Q(0) \).
Thus, we have \( S(t)+I(t)+Q(t)\le X(t)\ a.s. \) for all \( t\ge 0 \). It is clear that A(t) and Q(t) are continuous adapted increasing processes on \( t\ge 0 \) with \( A(0)=Q(0) \). By Theorem 1.3.9 in [36], we obtain \( \mathop {\lim }\limits _{t\longrightarrow \infty } X(t)\le \infty \). Therefore,
Then, the following results can be got
Setting
Since the quadratic variations, we have
By using Lemma 3.1, we obtain
Similarly, we can also obtain
\(\square \)
Lemma 3.3
[36, 37] Suppose that X(t) is a regular Markov process in \( R_{+}^{n} \) whose dynamics is given by
The diffusion matrix is defined as follows
The Markov process X(t) has a unique ergodic stationary distribution \( \pi (\cdot ) \) if there exists a bounded domain \( D\subset R^{d} \) with regular boundary \( \Gamma \) and
- (i):
-
There is a positive number M such that \( \sum _{i, j=1}^{3} a_{ij}(x)\kappa _{i}\kappa _{j}\ge M \mid \kappa \mid ^{2} \), \( x\in D,\ \kappa \in R^{d} \).
- (ii):
-
There exists a nonnegative \( C^{2} \)-function \( V^{*} \) such that \(\mathcal {L}V^{*} \) is negative for any \( R^{d}\setminus D \),then
$$\begin{aligned} P\left\{ \mathop {\lim }\limits _{T\rightarrow \infty } \frac{1}{T} \int _{0}^{T} F(X_{x}(t))\mathrm{d}t= \int _{R^{d}} F(x)\pi (\mathrm{d}x)\right\} = 1, \end{aligned}$$for all \( x\in R^{d} \), where \( F(\cdot ) \) is an integrable function with respect to measure \( \pi \).
In order to illustrate the extinction of disease, the following result can be obtained,
Theorem 3.1
Assume that the model (2.2) with form \( H_{1} \) has a solution (S((t), I(t), Q(t)) with initial value \( (S((0), I(0), Q(0))\in R_{+}^{3} \). If \( R_{0}^{S}=\frac{(A\beta +\sigma \mu _{0})}{\mu _{0}(\mu _{0}+\mu _{1}+r_{1}+\frac{\eta _{2}^{2}}{2})}<1 \), then
I(t) approaches zero exponentially a.s., i.e., the infection of COVID-19 will die out from the community with probability 1. And
Proof
We integrate (2.2) with form \( H_{1} \) directly, and apply the It\(\hat{o}\) formula to the second formula of (2.2),
By integrating relation (3.1) from 0 to t, then we can get
According to the theorem of large number in [36], we obtain
Taking the limit superior on both sides of (3.2) and when \( R_{0}^{S}< 1 \)
then, based on Lemma 3.2, we can obtain
and
Now, according to (2.2)
Adding both sides of each equations in (3.3) respectively, we get
the following formula is obtained by calculation
According to the third equation in (3.3), we obtain
Based on Lemma 3.2, we can get
\(\square \)
In order to illustrate the stationary distribution of disease, we can obtain the following result,
Theorem 3.2
The solution (S(t), I(t), Q(t)) of (2.2) with form \( H_{1} \) is ergodic and there is a unique stationary distribution \( \pi (\cdot ) \) when \( R_{1}^{S}=\frac{A\beta }{(\mu _{0}+\frac{\eta _{1}^{2}}{2})(\mu _{0}+\mu _{1}+r_{1}+\frac{\eta _{2}^{2}}{2})}> 1 \).
Proof
This theorem is mainly proved by Lemma 3.3. Firstly, the diffusion matrix of (2.2) with form \( H_{1} \) as follows
Furthermore, if we choose \( M=\min _{(S, I, Q)\in \overline{D}\subset R_{+}^{3}} \lbrace \eta _{1}^{2} S^{2}, \eta _{2}^{2} I^{2}, \eta _{3}^{2} Q^{2} \rbrace \), then we obtain
where \( (S, I, Q)\in \overline{D},\ \kappa =(\kappa _{1}, \kappa _{2}, \kappa _{3})\in R_{+}^{3} \). Then, (i) in Lemma 3.3 holds.
Secondly, the key is to construct a nonnegative \( C^{2} \)-function \( V^{*}: R_{+}^{3}\rightarrow R_{+} \). Firstly, we construct
where \( c_{1}, c_{2}, c_{3} \) are the positive constant and will be determined later, \( V_{2}=S+I+Q-c_{1}\mathrm{ln} S-c_{2}\mathrm{ln} I \). It is obvious that
where \( U_{k}=(\frac{1}{k}, k)\times (\frac{1}{k}, k)\times (\frac{1}{k}, k) \).
It can be obtained by calculation that
then, \( V_{1} \) have only one stagnation point \( (S_{0}^{*}, I_{0}^{*}, Q_{0}^{*})=(\dfrac{1+c_{1}c_{3}}{1+c_{3}}, \dfrac{c_{2}c_{3}}{1+c_{3}}, \dfrac{c_{3}}{1+c_{3}}) \). According to the Hesse matrix of \( V_{1} \) at this stagnation point is positive definite, we can obtain \( V_{1}(S, I, Q) \) has a minimum value \( V_{1}(S_{0}^{*}, I_{0}^{*}, Q_{0}^{*}) \). From (3.6), we can say that \( V_{1} \) has one unique minimum value inside \( R_{+}^{3} \).
Next, we construct a nonnegative \( C^{2} \)-function \( V^{*}: R_{+}^{3}\rightarrow R_{+} \) as follows
We consider \( V_{2} \) by using (2.2) and (2.5), the following formula can be obtained
Let
that means
which implies \( R_{1}^{S}=\dfrac{A\beta }{(\mu _{0}+\frac{\eta _{1}^{2}}{2})(\mu _{0}+\mu _{1}+r_{1}+\frac{\eta _{2}^{2}}{2})} \).
Then, we have
where \( c_{4}=3A[(R_{1}^{S})^{\frac{1}{3}}-1]> 0 \).
We divide \( R_{+}^{3}\setminus D \) into six regions as follows,
where \( D=\lbrace \delta _{1}<S< \dfrac{1}{\delta _{4}},\ \delta _{2}<I< \dfrac{1}{\delta _{5}},\ \delta _{3}<Q< \dfrac{1}{\delta _{6}} \rbrace ,\ \delta _{i}>0\ (i=1,\ldots , 6) \) are sufficiently small constants. In the set \( R_{+}^{3}\setminus D \), we can choose sufficiently small \( \delta _{i}>0\ (i=1,\ldots , 6) \) such that these conditions hold: \(\delta _{2}=\delta _{1}^{2},\delta _{3}=\delta _{1}^{3},-\dfrac{A}{\delta _{1}}+\overline{K}_{1}< 0,-\dfrac{r_{1}}{\delta _{1}}+\overline{K}_{1}< 0,-\dfrac{\mu _{0}}{\delta _{i}}+\overline{K}_{1}< 0,\ (i=4,5,6). \) where \( \overline{K}_{1} \) is positive constant which can be determined at later stages [37].
Next, we will prove \( \mathcal {L}V^{*}(S, I, Q)< 0 \) on \( R_{+}^{3}\setminus D \),
- (i):
-
If \( (S, I, Q)\in D_{1} \), then through (3.10), we can obtain
$$\begin{aligned}\begin{aligned} \mathcal {L}V^{*}&\le c_{1}c_{3}\beta {I}+c_{2}c_{3}\sigma +\dfrac{\beta A}{\mu _{0}}+2\mu _{0}\\&\quad +\dfrac{\eta _{1}^{2}+\eta _{3}^{2}}{2}+\mu +\sigma +A-\dfrac{A}{\delta _{1}},\\&{\le -\dfrac{A}{\delta _{1}}+\overline{K}_{1}< 0,} \end{aligned} \end{aligned}$$where
$$\begin{aligned} \overline{K}_{1}= & {} \mathop {\mathrm{sup}}\limits _{(S,I,Q)\in R_{+}^{3}} \left\{ c_{1}c_{3}\beta I+c_{2}c_{3}\sigma +\dfrac{\beta A}{\mu _{0}}+2\mu _{0}\right. \\&\left. +\dfrac{\eta _{1}^{2}+\eta _{3}^{2}}{2}+\mu +\sigma +A \right\} . \end{aligned}$$ - (ii):
-
If \( (S, I, Q)\in D_{2} \), then through (3.10), we can get
$$\begin{aligned} \mathcal {L}V^{*}\le & {} c_{1}c_{3}\beta \delta _{2}+c_{2}c_{3}\sigma +\dfrac{\beta A}{\mu _{0}}+2\mu _{0}\\&+\dfrac{\eta _{1}^{2}+\eta _{3}^{2}}{2}+\mu +\sigma +A-c_{3}c_{4}, \end{aligned}$$we select a big enough \( c_{3}> 0 \) and as small as possible \( \delta _{2}> 0 \) such that \( \mathcal {L}V^{*}<0 \) for \( (S, I, Q)\in D_{2} \).
- (iii):
-
If \( (S, I, Q)\in D_{3} \), then through (3.10), we can derive
$$\begin{aligned}\begin{aligned} \mathcal {L}V^{*}&\le c_{1}c_{3}\beta {I}+c_{2}c_{3}\sigma +\dfrac{\beta A}{\mu _{0}}+2\mu _{0}\\&\quad +\dfrac{\eta _{1}^{2}+\eta _{3}^{2}}{2}+\mu +\sigma +A-\dfrac{r_{1} \delta _{2}}{\delta _{3}},\\&{\le -\dfrac{r_{1}}{\delta _{1}}+\overline{K}_{1}< 0.} \end{aligned} \end{aligned}$$ - (iv):
-
If \( (S, I, Q)\in D_{i},\ (i=4,\ 5, \ 6) \), then through (3.10), we can gain
$$\begin{aligned}\begin{aligned} \mathcal {L}V^{*}&\le c_{1}c_{3}\beta {I}+c_{2}c_{3}\sigma +\dfrac{\beta A}{\mu _{0}}+2\mu _{0}\\&\quad +\dfrac{\eta _{1}^{2}+\eta _{3}^{2}}{2}+\mu +\sigma +A-\dfrac{\mu _{0}}{\delta _{i}},\\&{\le -\dfrac{\mu _{0}}{\delta _{i}}+\overline{K}_{1}< 0.} \end{aligned} \end{aligned}$$
Thus, under some above suitable conditions, \( \mathcal {L}V^{*}< 0 \) for all \( (S,I,Q)\in R_{+}^{3}\setminus D \). Then, (ii) in Lemma 3.3 holds.
In conclusion, through Lemma 3.3, we can get (2.2) with form \( H_{1} \) is ergodic and it has one and only one stationary distribution. These are further verified in the later numerical simulations (Figs. 2, 3). \(\square \)
4 Turing instability
In (2.1), let \(R_{1}=S-S_{0},\) \( R_{2}=I-I_{0},\) \( R_{3}=Q-Q_{0}\) where \((S_{0},I_{0},Q_{0})\) is the equilibrium point of the underlying deterministic model corresponding to (2.2), i.e., the form \( H_{2} \) of stochastic perturbations mentioned above. Then, this means the situation of a white noise stochastic perturbations around the equilibrium state of the underlying deterministic model corresponding to (2.2) is considered. From the relationship between the white noise \( \xi (t) \) and the Brownian motion B(t) , \( dB(t)=\xi (t)\mathrm{d}t \), we let
where \( \sigma _{0}\) is the variance of the Gaussian distribution satisfied. Then when \(R_{0}>1\), (2.1) has two equilibrium points, i.e., \((S^{**}, I^{**}, Q^{**})\) and \((S^{*}, I^{*}, Q^{*})\). In this section, Turing instability [38] of the positive equilibrium of (2.1) with form \( H_{2} \) is studied, i.e., the white noise perturbations around the endemic equilibrium state. In the following, the positive equilibrium point \((S^{*}, I^{*}, Q^{*})\) is denoted as \((S_{0},I_{0},Q_{0})\). And the zero-flux boundary conditions as follows,
where n is space, \((x,y)\in \partial \Omega \) and \(\Omega \) is spatial domain.
Next, linearising (2.1) with form \( H_{2} \) around \((S_{0},I_{0},Q_{0})\) which depends on time and space [39], here we expand the stochastic terms by Taylor expansion and then keep the linear terms, we can obtain
where \(\eta _{i1}=\dfrac{\eta _{i}}{\sqrt{2\pi }\sigma _{0}}, (i=1, 2, 3)\). And we can get the system governing the dynamics of P is defined by
where the coefficient matrix is given by
where
We assume P take the following form,
where \( \mathbf{k} \cdot \mathbf{k} =k^{2} \) and k is the wave number, \( \mathbf{r} =(x, y) \) is the spatial vector in two dimensions, i is the imaginary unit, \( i^{2}=-1 \), then we obtain the following characteristic matrix
Therefore, we have the following characteristic equation,
where
According to Routh–Hurwitz criterion, all the eigenvalues have negative real parts if and only if
Turing instability occurs if the equilibrium point \((S_{0},I_{0},Q_{0})\) is stable without diffusion, but driven unstable by diffusion, i.e., with respect to certain value of \( k(>0) \). It is clear that \((S_{0},I_{0},Q_{0})\) is locally asymptotically stable without diffusion if and only if
Therefore, if at least one of the three conditions in (4.8) does not hold, then Turing instability occurs. So according to (4.7), we let
where \( g_{3}> 0 \) and \( g_{0}> 0 \).
If we want to find some real number \(k^{2}(> 0)\) such that the value of \( p_{0} \) is negative, then \(\min \ p_{0}(k^{2})< 0 \) must be true, and here
where \(k_{c}^{2}\) is real and positive if
Therefore,
When \(p_{0}(k_{c}^{2})<0\) if
The conditions (4.12) and (4.14) are sufficient for the occurrence of Turing instability with noise. And conditions (4.9), (4.12) and (4.14) represent together the analytical Turing space in parametric space of model (4.1). Thus, from the perspective of diffusion, we must do our best to control the diffusion of the infectious to avoid another outbreak of COVID-19.
5 Amplitude equations for Turing patterns
The specific expression of amplitude equations for Turing patterns plays an important role in pattern selection theory. From the point of view of epidemiology, Turing patterns may lead to the homogeneous steady state in the spatial domain by changing the control parameter or diffusion parameter. In this section, we choose \( r_{1} \) as the control parameter, and use multiple scale analysis to derive the amplitude equations. We utilise the Taylor series expansion to expand the stochastic terms of (2.1) with form \( H_{2} \) at \( (S_{0}, I_{0}, Q_{0}) \), then we truncate the expansion at third order and higher order have no effect on the amplitude equations in the process. In order to obtain the amplitude equations, we write (2.1) with form \( H_{2} \) around the equilibrium point \( (S_{0}, I_{0}, Q_{0}) \) as follows
where \(\eta _{i2}=\dfrac{\eta _{i1}}{2\sigma _{0}^{2}}, (i=1, 2, 3)\).
In the following, we use multiple scale analysis to derive the amplitude equations with wave vector \( \mathbf{k} _{j} (j=1,2,3) \), \( \mathbf{k} _{j} (i=1,2,3) \) are different types of modes corresponding to the Turing patterns associated with an angle of \( \frac{2\pi }{3} \) within each pair, which satisfy \( \mid \mathbf{k} _{j} \mid =k_{c} \) and \( \mathbf{k} _{1}+\mathbf{k} _{2}+\mathbf{k} _{3}=0 \). Near the critical point, the solution of (5.1) can be expanded as
where \( \overline{P} \) is the eigenvector of the linearised operator, \( K_{j} \) are the amplitudes associated with the modes \( \mathbf{k} _{j} (j=1,2,3) \), and c.c. denotes complex conjugate. Now we rewrite (5.1) as the following form
where
Next, we investigate over the expansion around the Turing threshold constant \( r_{1c} \) and we obtain as follows,
where
such that,
where \( T_{1}=\epsilon t, T_{2}=\epsilon ^{2} t \).
Under the time scales \( T_{1}=\epsilon t, T_{2}=\epsilon ^{2} t \), we have
where K is amplitude.
The operator L at the point \( r_{1}=r_{1c} \) can be expanded as
where
and
Substituting the above formulas into (5.2) and expanding it with respect to different orders of \( \epsilon \), then the following three equations can be obtained,
where
By solving the first formula of (5.11), we have
where \( \xi _{1}=\frac{\beta S_{0}}{\eta _{11}-\beta I_{0}-\mu _{0}-d_{1}k_{c}^{2}} \), \( W_{j}\ (j=1, 2, 3)\) are termed as the amplitude of the mode \( e^{i\mathbf{k _{j} \cdot \mathbf{r} }} \) and its form is determined by the perturbational term of the higher order.
Then using the solvability condition of Fredholm to determine whether the second formula of (5.11) has a nontrivial solution or not. Next, considering of operator \( L_{c}^{+} \) which is the adjoint operator of \( L_{c} \), and the zero eigenvectors of operator \( L_{c}^{+} \) are
where \( \xi _{2}=\dfrac{\eta _{11}-\beta I_{0}-\mu _{0}-d_{1}k_{c}^{2}}{\beta I_{0}} \).
Substituting (5.12) into the second formula of (5.11), we can get
where
According to the Fredholm solubility condition, the vector function of the right hand of (5.14) must be orthogonal with the zero eigenvectors of operator \( L_{c}^{+} \) to ensure the existence of the nontrivial solution of this equation, then comparing the value of the coefficient of \( e^{i\mathbf{k _{j} \cdot \mathbf{r} }} \), we have
Now, we let
By replacing the (5.16) into the second formula of (5.11) and the results is as follows for \( j\ne k;\ j, k=1, 2, 3;\ (j, k)=(1, 2),\ (2, 3),\ (3, 1) \),
where
Substituting the (5.12), (5.16), (5.17) into the third formula of (5.11), and then we have
where
Then, utilizing the Fredholm solubility condition again, we can obtain
Therefore, \( K_{j}\ (j=1, 2, 3) \) can be expanded as below,
In summary, we can get the amplitude equations from (5.7) as follows,
where
Next, the stability conclusion of (5.22) is given for the subsequent numerical simulation and analysis. Each amplitude in (5.22) can be decomposed to mode \( \rho _{j}=|K_{j}| \) and a corresponding phase angle \( \varphi _{j} \). Then substituting \( K_{j}=\rho _{j} e^{i \varphi _{j}},\ (j=1, 2, 3) \) in (5.22), separating the real and imaginary parts and \( \varphi =\varphi _{1}+\varphi _{2}+\varphi _{3} \), we can get the following equation
and
For (5.24), this system lies the stationary state when \( \varphi =0 \) or \( \varphi =\pi \). For \( \rho _{j}\ge 0 \), we can know that the solution of \( \varphi =0 \) is stable when \( h_{1}> 0 \) and the solution of \( \varphi =\pi \) is stable when \( h_{1}< 0 \). If we only consider the stable solution, then the following equations are obtained,
By analysing (5.26), the following theorem is obtained,
Theorem 5.1
The system (5.26) has four kinds of solutions and the stability as follows,
- (i):
-
The stationary solution is stable for \( \tilde{r}_{1}< r_{11}=0 \) and unstable for \( \tilde{r}_{1}> r_{11} \).
- (ii):
-
Stripe patterns solution is stable for \( \tilde{r}_{1}< r_{12}=\frac{h_{1}^{2}h_{2}}{(h_{2}-h_{3})^{2}} \) and unstable for \( \tilde{r}_{1}> r_{12} \).
- (iii):
-
Hexagon patterns solution exist when \( \tilde{r}_{1}> \frac{-h_{1}^{2}}{4(2h_{3}+h_{2})} \), the solution is stable for \( \tilde{r}_{1}< r_{13}=\frac{h_{1}^{2}(2h_{2}+h_{3})}{(h_{2}-h_{3})^{2}} \) and unstable for \( \tilde{r}_{1}> r_{13} \).
- (iv):
-
The mixed state solution exist when \( h_{3}> h_{2}, \tilde{r}_{1}> h_{2}\rho _{1}^{2} \), which is always unstable.
Proof
Now, substituting \( \rho _{j}=\overline{\rho }_{j}+\bigtriangleup \rho _{j},\ (j=1, 2, 3)\) into (5.26) (ignoring higher order terms), and changing \( \overline{\rho }_{j} \) in the obtained equations to \( \rho _{j} \), then, we can obtain the following matrix,
Therefore,
- (i):
-
The stationary state \( \rho _{1}=\rho _{2}=\rho _{3}=0 \), according to (5.27), we can know that the stationary solution is stable for \( \tilde{r}_{1}< r_{11}=0 \), and vice versa.
- (ii):
-
Stripe patterns \( \rho _{1}=\rho =\sqrt{\frac{\tilde{r}_{1}}{h_{2}}}\ne 0, \rho _{2}=0, \rho _{3}=0 \), then (5.27) becomes
$$\begin{aligned} \begin{pmatrix} \tilde{r}_{1}-3h_{2}\rho ^{2} &{} 0 &{} 0\\ 0 &{} \tilde{r}_{1}-h_{3}\rho ^{2} &{} |h_{1}|\rho \\ 0 &{} |h_{1}|\rho &{} \tilde{r}_{1}-h_{3}\rho ^{2}\\ \end{pmatrix}. \end{aligned}$$(5.28)From (5.28) for stripe patterns, and through calculation, we get three eigenvalues as follows,
$$\begin{aligned} \lambda _{1}=-2\tilde{r}_{1},\ \lambda _{2, 3}=\tilde{r}_{1}\left( 1-\frac{h_{3}}{h_{2}}\right) \mp |h_{1}|\sqrt{\tilde{r}_{1}}{h_{2}}. \end{aligned}$$Then, stripe patterns solution is stable for \( \tilde{r}_{1}< r_{12}=\frac{h_{1}^{2}h_{2}}{(h_{2}-h_{3})^{2}} \), and vice versa.
- (iii):
-
Hexagon patterns \( \rho =\rho _{1}=\rho _{2}=\rho _{3}=\frac{|h_{1}|\pm \sqrt{[h_{1}^{2}+4(h_{2}+2h_{3})\tilde{r}_{1}]}}{2(h_{2}+2h_{3})} \), then (5.27) becomes
$$\begin{aligned} \begin{pmatrix} a_{1} &{} a_{2} &{} a_{2}\\ a_{2} &{} a_{1} &{} a_{2}\\ a_{2} &{} a_{2} &{} a_{1}\\ \end{pmatrix}, \end{aligned}$$(5.29)where
$$\begin{aligned}{\left\{ \begin{array}{ll} a_{1}=\tilde{r}_{1}-(3h_{2}+2h_{3})\rho ^{2},\\ a_{2}=|h_{1}|\rho -2h_{3} \rho ^{2}. \end{array}\right. } \end{aligned}$$From (5.29) for hexagon patterns, and through calculation, we get three eigenvalues as follows,
$$\begin{aligned} \lambda _{1}=a_{1}+2a_{2},\ \lambda _{2, 3}=a_{1}-a_{2}. \end{aligned}$$Then, we have \( \lambda _{1}> 0 \) for \( \rho ^{-}=\frac{|h_{1}|-\sqrt{[h_{1}^{2}+4(h_{2}+2h_{3})\tilde{r}_{1}]}}{2(h_{2}+2h_{3})} \), so the pattern is unstable; and \( \lambda _{j}< 0\ (j=1, 2, 3) \) for \( \rho ^{+}=\frac{|h_{1}|+\sqrt{[h_{1}^{2}+4(h_{2}+2h_{3})\tilde{r}_{1}]}}{2(h_{2}+2h_{3})} \) when \( \tilde{r}_{1}< r_{13}=\frac{h_{1}^{2}(2h_{2}+h_{3})}{(h_{2}-h_{3})^{2}} \), the pattern is stable.
- (iv):
-
The mixed state \( \rho _{1}=\frac{|h_{1}|}{h_{3}-h_{2}}, \rho _{2}=\rho _{3}=\sqrt{\frac{\tilde{r}_{1}-h_{2}\rho _{1}^{2}}{h_{2}+h_{3}}} \), then (5.27) becomes
$$\begin{aligned} \begin{pmatrix} a_{3} &{} a_{4} &{} a_{4}\\ a_{4} &{} a_{5} &{} a_{6}\\ a_{4} &{} a_{6} &{} a_{5}\\ \end{pmatrix} \end{aligned}$$(5.30)where
$$\begin{aligned}{\left\{ \begin{array}{ll} a_{3}=\tilde{r}_{1}-3h_{2}\rho _{1}^{2}-h_{3}(\rho _{2}^{2}+\rho _{3}^{2}),\\ a_{5}=\tilde{r}_{1}-3h_{2}\rho _{2}^{2}-h_{3}(\rho _{2}^{2}+\rho _{1}^{2}),\\ a_{4}=|h_{1}|\rho _{2}-2h_{3}\rho _{2}\rho _{1},\\ a_{6}=|h_{1}|\rho _{1}-2h_{3}\rho _{2}^{2}. \end{array}\right. } \end{aligned}$$
From (5.30), we can get
if all the eigenvalues are negative, we need
when \( \tilde{r}_{1}< \frac{(2h_{2}+h_{3})h_{1}^{2}}{(h_{3}-h_{2})^{2}} \), \( \lambda _{1}< 0 \) established, and \( \lambda _{2}\lambda _{3}=[\tilde{r}_{1}-\frac{(h_{2}h_{1}^{2}}{(h_{3}-h_{2})^{2}}][\tilde{r}_{1}-\frac{(2h_{2}+h_{3})h_{1}^{2}}{(h_{3}-h_{2})^{2}}]> 0 \). However, \( \rho _{2}=\rho _{3}=\sqrt{\frac{\tilde{r}_{1}-h_{2}\rho _{1}^{2}}{h_{2}+h_{3}}}> 0, \) and \( h_{2}+h_{3}> 0 \), i.e., \( \tilde{r}_{1}> \frac{(2h_{2}+h_{3})h_{1}^{2}}{(h_{3}-h_{2})^{2}} \). Thus, the conditions contradict each other, this means that is always unstable. \(\square \)
6 Optimal quarantine control
The spread of infectious diseases can be effectively suppressed under the continuous and high-intensity quarantine control. However, combined with practical factors, these are often difficult to implement \( 100\% \), which correspond to the cost of isolation, treatment and transportation, allocation of medical resources, even people’s psychological spirit, etc. Applying the time-varying optimal control theory [28] to control the epidemic situation can achieve the desired control objectives and reduce the related control costs to a certain extent.
In this section, optimal control problem of (2.2) with form \( H_{1} \) is studied. If \( \eta _{1}=\eta _{2}=\eta _{3}=0 \), then the model (2.2) with form \( H_{1} \) is reduced to the underlying deterministic model. Now, Let is study the deterministic optimal control problem firstly.
Define the time-varying quarantine control variables \( r_{1}(\cdot ) \in U_{ad}=\lbrace \zeta (t)\) is measurable, \(0\le \zeta (t)\le \overline{r}_{1}, t \in [0, T] \rbrace \), where \( 0\le \overline{r}_{1}\le 1 \) and \( T>0 \) is terminal time corresponding to the actual needs. Then, we have the following deterministic model,
Let
Problem 1
In view of our control objectives are to decrease the prevalence of epidemic and to balance control strengths, so the objective function is defined by
subject to (6.1) and \(S(0)=S_{0}\ge 0,\ I(0)=I_{0} \ge 0,\ Q(0)=Q_{0} \ge 0\), under these conditions, minimize the objective function (6.3).
Next, Problem 1 will be solved by applying the Pontryagin’s minimum principle [40]. We construct the Hamiltonian function H for this problem as
where \( \lambda _{1}(t)\), \( \lambda _{2}(t)\) and \( \lambda _{3}(t) \) are Lagrange multipliers introduced.
The Pontryagin’s minimum principle transforms Problem 1 into minimizing the Hamiltonian with regard to the controls at each time t, then the following result can be obtained.
Theorem 6.1
The Problem 1 has an optimal solution and this solution satisfies the following equations,
with transversality conditions \( \lambda _{i}(T)=0,\ (i=1,\ 2,\ 3)\). Moreover, the optimal quarantine rate is
Proof
Obviously, according to the convexity of Hamiltonian with respect to \( r_{1}(t) \), it is easily to know the existence of solution. The partial derivatives of the function H with respect to \( S,\ I,\ Q \) respectively, i.e., \( \dot{\lambda }_{1}(t),\ \dot{\lambda }_{2}(t),\ \dot{\lambda }_{3}(t) \) as follows,
the above formulas verify (6.5). We now calculate the optimal quarantine rate \( r_{1}^{*}(t) \). Now for a fixed value of t, on the basis of the Pontryagin’s minimum principle, \( r_{1}^{*}(t) \) must satisfy the following formula in the interval \( [0, \overline{r}_{1}] \),
then the optimal control \(r_{1}^{*}(t)\) has been worked out. If for \(\forall \overline{\overline{r}}_{1} \in [0, \overline{r}_{1}]\), there is \( 2\overline{\overline{r}}_{1}-I(\lambda _{2}-\lambda _{3})\ge 0\ (2\overline{\overline{r}}_{1}-I(\lambda _{2}-\lambda _{3})\le 0) \), then we must select \( r_{1}(t)=0 (r_{1}(t)=\overline{r}_{1}) \), hence, there is
\(\square \)
Remark 6.1
In view of the above deterministic optimality system has Lipschitz structure and the boundedness of the above variables, i.e., the state and adjoint variables, we can determine the uniqueness of the solution. Then, the uniqueness of the optimal control also can be guaranteed by the theories in Fister et al. [41].
Next, let is study the stochastic optimal control problem of (2.2), our objective is to seek an optimal quarantine rate \( r_{1}^{*} \) to minimizes the following objective function and \( x_{0} \) is an initial state,
what we obtain here is the expectation of the initial state of the system i.e. at time \(t=0\). For the deterministic problem studied above, a fixed constant \( \overline{r}_{1}\le 1 \) with \( r_{1}(t)\le \overline{r}_{1}\ (a.s.) \) is assumed. Then, we define the admissible control law as follows,
We define the following performance criterion for this problem of stochastic control,
where the expectation depends on the state of the system. Define the following value function,
We determine \( J : \mathcal {A}\rightarrow R_{+} \) given by (6.11). Next, the stochastic optimal control problem is proposed and solved.
Problem 2
Given (2.4), \( \mathcal {A} \) in (6.9) and J in (6.10), seek the value function
and the optimal control
Theorem 6.2
The Problem 2 about the optimal quarantine control has a solution as the following form
Proof
In order to determine (6.14) through the dynamic programming method, we need to calculate \( \mathcal {I}U(t) \) by utilizing (2.5),
According to the Hamilton–Jacobi–Bellman theory [42], we need to work out the following formula,
For this purpose, we obtain
According to the proof of the argument in the previous corresponding deterministic problem, and the bounds of \( r_{1} \), then \( r_{1}^{*}(t) \) emerges. \(\square \)
7 Case study and numerical simulation
In this section, we will show the relevant numerical simulations of the stochastic and deterministic model of coronavirus. The numerical simulations in this section are divided into four parts. Firstly, the values of relevant parameters in our proposed model are estimated by an indirect method based on the real data of COVID-19 in China and the USA. Secondly, the numerical simulations are used to show the difference between stochastic system (2.2) and its corresponding deterministic system, and to verify the extinction and stationary distribution criteria. Thirdly, numerical simulations of the proposed spatially COVID-19 epidemic model with diffusion are made to test the stability conclusion. Lastly, the numerical simulations are used to solve numerically the optimality system, and to test the feasibility and effect of the proposed optimal control strategy.
In order to obtain the proposed model parameters based on the real data of COVID-19 of China and the USA. We consider some of the parameters from some reports and literatures, and the rest of the parameters are fitted the model to some epidemiological data by the use of least-square fitting, which provides the minimized estimates of the needed parameters [43]. Here, we use the least square method to the proposed model to obtain the best-fit parameters for China and the USA. The procedure looks for the set of initial guesses and pre-estimated parameters for the model whose solutions best fit or pass through all the data points [44], by reducing the sum of the square difference between the observed data and the model solution.
Chinese authorities reported the new virus on January 4, 2020. From this period up to January 22, the statistics on the number of people contracting this disease are not comprehensive enough, and the relevant information is less. Since then, infection has received more attention. We consider the real data of COVID-19 in China from 22 January to 21 February 2020 obtained from worldometer [45]. According to [45, 46], considering the following estimates and values, \( N_{1}(0)=1400000000 \), \( S_{1}(0)=N_{1}(0)-571,\) \( I_{1}(0)=571,\) \( Q_{1}(0)=46 \). In Fig. 1a, we fitted the proposed COVID-19 model to the epidemic data of China using the least-squares fitting and the relevant best-fit curve is shown. At the same time, unlike China’s stricter quarantine measures, some countries have weak or almost no quarantine control, which greatly increases the risk of infection. Take the USA as an example. According to the statistical data of WHO [47], the outbreak in the USA occurred on March 4, 2020. According to [46, 48], considering the following estimates and values, \( N_{2}(0)=331000000 \), \( S_{2}(0)=N_{2}(0)-158,\) \( I_{2}(0)=158,\) \( Q_{2}(0)=16 \). In Fig. 1b, we fitted the proposed COVID-19 model to the epidemic data of the USA using the least-squares fitting and the relevant best-fit curve is shown. These fittings about China and the USA, i.e., Fig. 1a, b shows that our model relatively fit well to the reported data points and the accuracy of the development tendency of the infected class. From these, the obtained relevant parameter estimates about China and the USA are given in Tables 1 and 2. From the fitting results, development trend and estimated parameters in Tables 1 and 2, we can observe and summarize the differences between China and the USA in response and treatment measures. The start time of simulation and fitting in Fig. 1a, b is both the time of outbreak or data recording in each country. It can be seen that under the strong control and isolation measures in China, the number of infected people gradually stabilized after a period of time. However, both the number of infected persons and the development trend reflected in Fig. 1b almost show a trend that is difficult to control. This is inseparable from the way of regulation adopted by the government of the USA. In addition to the isolation of patients in the hospital, other people’s travel, work and life are basically unrestricted, and they do not wear masks and other protective measures in their daily activities. This greatly increases the probability of contact with susceptible persons in the incubation period, and makes the incidence rate high.
In the rest of this section, we will simulate and analyse the proposed model to compare the differences of the relevant contents and verify the results of the previous theoretical analysis. The simulations about the difference between the two systems, the extinction and stationary distribution of disease are obtained by the method in [51], the parameters with biological feasibility are set to two groups, which correspond to the extinction and persistence of disease respectively. The first group is \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1 \), \( \eta _{1}=0.5,\) \( \eta _{2}=0.4,\) \( \eta _{3}=0.2 \); the second group is \( A=0.5,\) \( \beta =0.7,\) \( r_{1}=0.3,\) \( \sigma =0.1,\) \( \mu =0.2 \), \( \eta _{1}=0.3,\) \( \eta _{2}=0.4,\) \( \eta _{3}=0.6 \). The initial values of different populations \( S(0)=0.9,\) \( I(0)=0.7,\) \( Q(0)=0.5 \), units of time 0-30. As we all know, the existence of noise disturbance can change the behaviour of evolution in the deterministic system. In view of this reason, we compare them in Fig. 2a, b. We can observe from Fig. 2a, b that the random fluctuations can eradicate the infectious disease, i.e., the infection vanishes, but even in the case of extinction, there will always be susceptible population. In the deterministic system with isolated treatment measures, although it can also reduce the number of infected people, it will not be eliminated, and it takes longer. In Fig. 3a, b, it can be observed that susceptible, infected and quarantine individuals always exist. According to the given parameter values, we can obtain \( R_{0}^{S}\approx 0.897< 1 \), \( R_{1}^{S}\approx 1.832> 1 \), these satisfy the conditions of the extinction and persistence. Thus, Figs. 2a and 3a verify the extinction and stationary distribution criteria. Figure 4a shows that in a reasonable range, no matter what changes I(0), I(t) approaches zero exponentially. Now, we select the first set of parameters to elaborate that the influence of white noise magnitude \( \eta _{2} \) on this epidemic. For this purpose, we select \( \eta _{2}=0.25,\) 0.45, 0.75, and other parameters remain unchanged. In Fig. 4b, we can observe that the infected population has decreased faster with the increase of the stochastic disturbance intensity and they all end up close to 0. Comparing the curves in Fig. 5a, b, we know that quarantine measure can decrease the number of the infected population whether in the stochastic system or in the corresponding deterministic system. But in the stochastic system, the effect is better because of the existence of stochastic term. Next, we show how the quarantine rate \( r_{1} \) and the noise intensity \( \eta _{2} \) influence the threshold \( R_{0} \) and \( R_{0}^{S} \). Figure 6 describes that \( R_{0} \) decreases with the isolation rate \( r_{1} \) increases and there exists a critical value \( r_{1}^{0}\approx 0.583 \). When \( r_{1}> r_{1}^{0}\), \( R_{0}<1 \). In addition, Fig. 7 shows that \( R_{0}^{S} \) decreases with the quarantine rate \( r_{1} \) or the noise magnitude \( \eta _{2} \) increase and there is a critical noise magnitude \( \eta _{2}^{*} \). If \( \eta _{2}> \eta _{2}^{*} \), then \( R_{0}^{S}< 1\). The above numerical simulations show that sufficiently big stochastic disturbance of the transmission rate can make this epidemic disease die out to some extent. Next, we will show the limit case of the system (2.2) with form \( H_{1} \) when S(t), I(t), Q(t) are perturbed by small noise. For this reason, we can assume that the noise magnitude of the small noise they are subjected to is the same, i.e., all of them are \( \varepsilon ,\ (\varepsilon \rightarrow 0) \). In this way, we can consider the following groups of parameters, namely \( \eta _{1}=\eta _{2}=\eta _{3}=0.5,\ 0.3,\ 0.1,\ 0.05,\ 0.001,\ 0.0001 \), to show the intermediate cases of transition from stochastic to deterministic, so as to analyse and show the limit system. Not only the representative parameters close to 0 are selected, but also some larger ones are selected, which can better reflect the asymptotic behaviour of the limit system. Other parameters used in this part of the simulations are in the first group described earlier, i.e., \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1 \). In fact, the noise magnitude can reach three decimal places, which is corresponding to the previous \( \varepsilon \rightarrow 0 \) in real life, i.e., it is only subject to very small noise disturbance or the limiting situation. Our smallest parameter is taken to four decimal places, so the numerical simulations will be closer to the deterministic system and this system can be used to study the limit properties more formally through \( \varepsilon \rightarrow 0 \). As shown in Fig. 8, it is not difficult to find that as the value of \( \eta _{i}\ (i=1,2,3) \) tend to 0, the trajectories of numerical simulations of S(t), I(t), Q(t) are closer to the deterministic system shown in Fig. 2b. And when 0.0001 is taken, the trend is basically the same as that of Fig. 2b, and the change of S(t), I(t), Q(t) with the change of \( \eta _{i}\ (i=1,2,3) \) is also in line with the previous analysis and practical significance.
Extinction: the simulation of the path \(S(t),\ I(t),\ Q(t)\) for model (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1 \), \( \eta _{1}=0.5,\) \( \eta _{2}=0.4,\) \( \eta _{3}=0.2 \) and its corresponding deterministic model, i.e., model (2.2) with \( \eta _{i}=0, (i=1,2,3) \)
Stationary distribution: the simulation of the path \(S(t),\ I(t),\ Q(t)\) for model (2.2) with \( A=0.5,\) \( \beta =0.7,\) \( r_{1}=0.3,\) \( \sigma =0.1,\) \( \mu =0.2 \), \( \eta _{1}=0.3,\) \( \eta _{2}=0.4,\) \( \eta _{3}=0.6 \) and its corresponding deterministic model, i.e., model (2.2) with \( \eta _{i}=0, (i=1,2,3) \)
The simulation of the path I(t) for model (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1 \), \( \eta _{1}=0.5,\) \( \eta _{3}=0.2 \), a \(I(0)=0.8,\) 0.4, 0.2 and b \(\eta _{2}=0.75,\) 0.45, 0.25
The simulation of the path I(t) for model (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( \sigma =0.2,\) \( \mu =0.1 \), \( \eta _{1}=0.5,\) \( \eta _{2}=0.4,\) \( \eta _{3}=0.2 \) and its corresponding deterministic model, i.e., model (2.2) with \( \eta _{i}=0, (i=1,2,3) \), a \( r_{1}=0.6,\) 0.2, 0 and b \( r_{1}=0.6,\) 0.2, 0.1
The numerical simulations of the spatially COVID-19 epidemic model with diffusion are made to test the stability conclusion. Next, we will simulate the continuous problem of spatially model with diffusion in a discrete region of \( M\times N \) lattice points by using the Euler method. Define the time step \( \Delta t \) and the lattice constant \( \Delta h \) between the lattice sites. Let \( r_{1} \) is a varied parameter, \( d_{1}=4.8 \), \( d_{2}=1.6 \), \( d_{3}=0.8 \), \( M=N=200 \) and other parameters are the same as above. We run the simulation until the characteristics and distribution of the simulated objects in the image do not seem to change, or reach a stable state, then stop and get the final image. In this section, the pattern formation of I is analysed by simulating the distribution of infected people. Figure 9a–d shows that the spatial distribution patterns of the infected class evolve with the small stochastic disturbance of the stationary solution in the spatially homogeneous state when the parameters are in the region of analytic Turing space. With the change of \( r_{1} \), the spatial pattern is different, the pattern transits from the hexagonal pattern (Fig. 9b) to the stripe pattern only (Fig. 9d), and in the process of change experienced the coexistence of the two states (Fig. 9c). When \( r_{1} \) is changed to an appropriate range, stripe patterns prevail in the whole dominant.
For the simulations of optimal control of (2.2) and its corresponding deterministic model, the parameters are set as \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( \sigma =0.2,\) \( \mu =0.1,\) \( c=0.3,\) \( \overline{r}_{1}=1 \), and \( S(0)=0.7,\) \( I(0)=0.02,\) \( Q(0)=0 \), terminal time \( T=150 \). An iterative scheme of Runge–Kutta method which is fourth order is utilized to deal with the deterministic optimal problem. Beginning by assuming an initial control based on the actual situation, and substituting it into the deterministic model (6.1) to solve \( S,\ I,\ Q \) forward in time by Runge–Kutta method. Then the above variables and the initial control are used to dispose of (6.5) with the transversality conditions backward in time through the same method. Thus, a new control \( r_{1} \) is obtained. After that, repeating the above process, and this algorithm is terminated when all the values of related variables in the above optimal system converge sufficiently [52, 53]. Numerical simulations to the system including the stochastic model corresponding to (6.1) compelled with the proxy adjoint system with transverslity conditions and characterization of the control variable \(r_{1}^{*}(t)\) in equation (6.14) are carried out using forward backward algorithm. Stochastic differential equations were first simulated using forth order Runge–Kutta method by introducing noise through Euler–Maruyama method [54] and then adjoint system (6.5) are simulated backward in time with final conditions. Particularly, we use as a proxy for \( (\lambda _{2}-\lambda _{3}) \) in the calculation of \(r_{1}^{*}(t)\) in this case. We note that makes U(t) becomes a stochastic variable because of the existence of I(t). For the sake of indicating the accuracy, effect and validity of the proposed optimal control strategy, optimal control \( r_{1}^{*} \) and other constant controls are contrasted on the basis of values of I(t) and objective function. Figures 10a and 11a tell us that the optimal control can make the value of I(t) to keep relatively low level contrasted to other seven constant controls (\( r_{1}=0,\) 0.1, 0.2, 0.3, 0.4, 0.5, 0.6). With the increase of quarantine control intensity, the overall level of the number of infected people, i.e., whether it is the peak or the end, will decrease in both deterministic system and stochastic system. Although low-intensity quarantine control will make the number of infected people reach a final stable trend and no longer increase, the number of infection is very high at this time, which will make COVID-19 long-term existence. On the contrary, high-intensity quarantine control will delay the time to reach the final stable trend, and the final level of infection is relatively low, even to achieve the purpose of elimination. Figures 10b and 11b represent the control profile of optimal control for the corresponding model. Further it is observed that control profile of optimal control for model (2.2) exhibits same state of affairs as that of deterministic control profile. The optimal control should be kept as high as possible from the beginning of the control policy and till the level of infection reaches a significantly stable low level. Then the quarantine measures maybe slightly relaxed. It is not a surprise that the corresponding optimal control is to keep the maximum value during almost the entire time period and then different kind of restrictions can be reduced to lower. It is worth noting that this approximation is desirable due to the expression of \( r_{1}^{*}(t) \). Though the constant control \( r_{1}=0.5 \) seems to make the value of I(t) lower than the optimal control \( r_{1}^{*} \), what’s more remarkable is that, the optimal control minimizes the value of objective function J from Fig. 12. Thus, it can be seen that the optimal control achieves the balance of control objective and control cost.
The relationship between \( r_{1} \) and \( R_{0} \) for the deterministic model corresponding to (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1, \) \( \eta _{i}=0, (i=1,2,3) \)
The relationship of \( R_{0}^{S} \), \( r_{1} \) and \( \eta _{2} \) for the stochastic model (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( \sigma =0.2,\) \( \mu =0.1 \), \( \eta _{1}=0.5,\) \( \eta _{3}=0.2 \)
8 Conclusion and further suggestions
The novel COVID-19 which broke out all over the world is one of the most severe disease today. In this paper, according to the facts in the infection and propagation of COVID-19, we have formulated a stochastic reaction–diffusion epidemic model to analyse and control this infectious diseases. Through the analysis, the sufficient criteria for the persistence and extinction of the disease are derived. This stochastic model is handled skilfully, by which the conditions of how the Turing instability arise have been obtained through stability analysis of local equilibrium. By using Taylor series expansion and weakly nonlinear analysis, amplitude equations for Turing patterns are derived. The results obtained from the stability analysis of amplitude equations determine the selection of patterns for this model. It is well-known that noise could make a bistable system which switches and regulates relevant mechanism [54]. And from this stochastic model and the results obtained, it can be seen that the white noise has a certain influence on pattern formation and the system with noise effect has more abundant spatial dynamics. These and general processing method for stochastic system are the contents that are worthy of further study.
From the current situation around the world, the outbreak of COVID-19 not only seriously endangers personal health, but also greatly affects the social and economic development. In terms of the scope, it also has a strong impact on the medical resources and systems of various countries. As soon as possible to develop specific and effective aversion and treatment is still the first to bear the brunt. In today’s situation, quarantine is the most popular and effective method to control and eliminate epidemic. Furthermore, the optimal quarantine control problem is studied. The optimal control strategies and solutions of deterministic and stochastic problems are derived by the Pontrygin’s Minimum Principle. Thanks to the difficulty of obtaining numerical results for stochastic optimal system, we utilise the solution of the deterministic problem to approximate them. The results of numerical simulation show that the premise of effectively restraining the prevalence of infectious diseases at present is constant and intensive quarantine control, which is corresponding to the cost, materials and manpower required. The blockade order issued by the government to a certain extent disrupt people’s work and life, leading to significant and widespread socio-economic costs [55]. On the contrary, it is the pressure of production and life caused by these restrictions that makes some enterprises and individuals gradually conflict with and lift the bans. That’s what we don’t want to happen. Thus, We can not blindly pursue the minimum number of infected people corresponding to the duration and intensity of quarantine. In order to promote the continuity of current and future development, we should seek the balance between control target and control cost. In view of the complexity and labor intensity of the formal method for numerical simulation of stochastic optimal control problems, the method adopted in this paper is a feasible approximation method. All the above analytical results are supported by numerical simulations.
The simulation of the path (a) S(t), (b) I(t), (c) Q(t) for model (2.2) with \( A=0.3,\) \( \beta =0.5,\) \( \mu _{0}=0.2,\) \( \mu _{1}=0.2,\) \( r_{1}=0.3,\) \( \sigma =0.2,\) \( \mu =0.1, \) \( \eta _{1}=\eta _{2}=\eta _{3}=0.5,\ 0.3,\ 0.1,\ 0.05,\ 0.001,\ 0.0001 \)
The simulation of the path I(t) for the deterministic system corresponding to model (2.2) with respect to seven kinds of constant control and optimal control, control profile of optimal control \( r_{1}(t) \)
The simulation of the path I(t) for model (2.2) with respect to seven kinds of constant controls and optimal control, control profile of optimal control \( r_{1}(t) \)
In the absence of full coverage of the vaccine, controlling the flow of infectious individuals is still the top priority. According to the World Health Organization recommendations [56, 57], 14 days of quarantine is one of the most effective means to guarantee safety, whether due to entering and leaving the country or having just come into contact with the carrier. Let’s take China and the USA shown in the first part of section 7 for example. As analysed in the previous paper, due to the different attitudes and measures of the two countries in dealing with the epidemic situation, the relevant simulations and analysis results are also different. The most obvious is the fitting results of the real COVID-19 data of the two countries in Sect. 7. The start time of fitting is the same time node with the same property, and the time span of data selection is the same, but one result is that the number of infected people gradually stabilizes after a period of time, and the other is that it is difficult to control. From the analysis results of this paper, we can see that this is inseparable from the quarantine control strategy of the two countries. It can be seen from the numerical simulations that the number of infected people in China has gradually stabilized about 60 days after the outbreak, which has to be admitted to have a great relationship with the strong control and quarantine measures implemented in China. This is in sharp contrast to the spread of the epidemic in the USA in the same period. With the overall improvement of China’s epidemic situation, not only the domestic population flow has increased, but also the entry-exit population increases relatively, which makes some unfavorable situations worthy of the attention of the relevant departments appear, that is, they are related to the rebound of the epidemic situation. How to deal with the coming situation is the top priority for the relevant departments in China and even other countries with better control of the epidemic situation facing similar situations. Through the investigation and the results of our study, we put forward the following suggestions:
- (i):
-
Strengthen the isolation and virus detection of entry-exit population to prevent overseas import.
- (ii):
-
Enhance the awareness of protection, do not take it lightly, maintain a certain social distance, and prevent a large-scale rebound in the territory. Especially, during the university holidays and the beginning of school, it should be carried out in batches and travel off peak.
- (iii):
-
For areas that have rebounded or have a rebound trend, i.e., relatively high risk areas, strict treatment and control measures should be taken immediately, and the source should be found out as soon as possible.
- (iv):
-
For some areas with low risk, normal work and life can be kept to some extent, but the corresponding monitoring and control mechanism should be further improved according to the local actual situation, in and out of public places to take temperature and wear masks, and so on.
One of the original purposes of this analysis and simulation in our paper is to emphasize the strategic position and importance of quarantine in the outbreak of COVID-19 by comparing the different results caused by different attitudes and implementation measures of quarantine between China and the USA in the same period. As for the USA, where the epidemic situation is still severe, the above suggestions on China may not be applicable to it in general because the epidemic situation is quite different from that of China. According to the research results and investigation, we also put forward the following trend suggestions, which are not only applicable to the USA, but also in line with some western countries with controversial implementation of quarantine measures like the USA.
- (i):
-
The government should issue more popular propaganda to make the public understand the importance of quarantine and less direct contact for the current situation. Understand what the people think, and issue effective quarantine measures on the premise of relaxing and appeasing policies. The process should not be too tough to avoid the loss outweighing the gain. And according to the celebrity effect combined with some more influential people to demonstrate the implementation.
- (ii):
-
It is true that it is difficult to implement isolation measures, but previous studies have found that in some countries, more people support quarantine than voluntary vaccination, which is due to the risk of early vaccination. And one infected individual at each site had less than one secondary infection. Even partial vaccination, the infection can be stabilized or even reduced by quarantine measures.
- (iii):
-
Even weak quarantine can promote the development of the situation, but it takes a long time, and the effect of strong quarantine in a short time is often unsatisfactory. One should not expect that even a short period of quarantine is sufficient to reduce the infection below its survival level. The above study found that implementation of longer quarantine measures, such as 70–80 days or even longer, is needed to achieve decisive results.
- (iv):
-
Keep as much quarantine as possible for most of the time in the controlled quarantine plan. Only when the infection reaches low level can quarantine restrictions be gradually reduced. During any quarantine period, even at the end of a predetermined time interval, control should not be zero. Some protective measures, such as wearing masks, avoiding crowds and maintaining good personal hygiene habits, should be continued and encouraged in society, even after strict isolation.
Through the findings of this paper, especially the section of optimal quarantine control, these show that it is far from enough to deal with the corresponding epidemic prevention and control problems by a single measure or a simple superposition of several measures. For example, the results obtained in Sect. 6 show that only one quarantine control measure is far from enough. Although it will also have some effects, it will take a long time, and some unstable and uncontrollable factors will be more. In order to control the epidemic as quickly as possible, a variety of measures should be cross coordinated response. We should be prepared to fight against coronavirus infection for a long time, rather than the current epidemic wave, so as to reduce the endemic burden and potentially eradicate the disease eventually. One can use model to short-term data which will enables us to comprehend deeply the existing data as well as to make predictions when data is unavailable. Due to the prevalence and concomitant of infectious diseases, if the current situation changes, the results of the model can be generally applied to the characterization of the mutated infectious diseases after improvement, or can be applied to any next disease. In the future, after verifying the safety, effectiveness and universality of the vaccine in daily life, combined with more actual data, we can further expand the model by adding a vaccinated class to the stochastic system proposed in this paper. And it is also the next step to further consider the effects of infectious disease treatment, vaccination, media publicity and other control in the model on the related optimal control problems.
Data availability statements
The data that support the findings of this study were derived from the following resources available in the public domain: https://www.worldometers.info/ and https://www.who.int/.
References
Li, Q., Guan, X., Wu, P., et al.: Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 382, 1199–1207 (2020)
World Health Organization: Pneumonia of unknown cause-China (2020). https://www.who.int/csr/don/05-january-2020-pneumonia-of-unkown-cause-china/en/. Accessed 5 Jan 2020
Hui, D., Azhar, E., Madani, T., et al.: The continuing 2019-nCoV epidemic threat of novel coronaviruses to global health-the latest 2019 Novel coronavirus outbreak in Wuhan, China. Int. J. Infect. Dis. 91, 264–266 (2020)
WHO: Report of the WHO China joint mission on coronavirus disease 2019 (COVID-19). World Health Organization (2020)
Wu, J., Leung, K., Leung, G.: Nowcasting and fore casting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 395, 689–697 (2020)
Bauer, F., Castillo-Chavez, C., Feng, Z.: Mathematical Models in Epidemiology. Springer, Berlin (2019)
Bernoulli, D.: Essai d’une nouvelle analyse de la mortalite causee par la petite verole. Mem. Math. Phys. Acad. R. Sci. (1766)
Kermack, W., McKendrick, A., Walker, G.: A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. 115, 700–721 (1972)
Duan, M., Chang, L., Jin, Z.: Turing patterns of an SI epidemic model with cross-diffusion on complex networks. Phys. A 533, 122023 (2019)
Xie, Y., Wang, Z., Lu, J., Li, Y.: Stability analysis and control strategies for a new SIS epidemic model in heterogeneous networks. Appl. Math. Comput. 383, 125381 (2020)
Sene, N.: SIR epidemic model with Mittag–Leffler fractional derivative. Chaos Solitons Fract. 137, 109833 (2020)
Rihan, F., Alsakaji, H., Rajivganthi, C.: Stochastic SIRC epidemic model with time-delay for COVID-19. Adv. Differ. Equ. (2020)
Rezapour, S., Mohammadi, H., Samei, M.: SEIR epidemic model for COVID-19 transmission by Caputo derivative of fractional order. Adv. Differ. Equ. (2020)
Fanelli, D., Piazza, F.: Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fract. 134, 109761 (2020)
Zhong, L., Mu, L., Li, J., et al.: Early prediction of the: novel coronavirus outbreak in the Mainland China based on simple mathematical model. IEEE Access 8, 51761–51769 (2020)
Wang, Y., Wei, Z., Cao, J.: Epidemic dynamics of influenza-like diseases spreading in complex networks. Nonlinear Dyn. 101, 1801–1820 (2020)
Kudryashov, N., Chmykhov, M., Vigdorowitsch, M.: Analytical features of the SIR model and their applications to COVID-19. Appl. Math. Model. 90, 466–473 (2021)
He, S., Peng, Y., Sun, K.: SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 101, 1667–1680 (2020)
Li, H., Jin, Y., Zhang, X., et al.: Transmission dynamics and control methodology of COVID-19: a modeling study. Appl. Math. Model. 89, 1983–1998 (2021)
Taghvaei, A., Georgiou, T., Norton, L., et al.: Fractional SIR epidemiological models. Sci. Rep. 10, 20882 (2020)
Sun, G., Wang, S., Li, M., et al.: Transmission dynamics of COVID-19 in Wuhan, China: effects of lockdown and medical resources. Nonlinear Dyn. 101, 1981–1992 (2020)
Zhang, X., Zhang, X.: The threshold of a deterministic and a stochastic SIQS epidemic model with varying total population size. Appl. Math. Model. 91, 749–767 (2021)
Zhang, L., Liu, M., Xie, B.: Optimal control of an SIQRS epidemic model with three measures on networks. Nonlinear Dyn. 103, 2097–2107 (2021)
Tang, B., Xia, F., Tang, S., et al.: The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China. Int. J. Infect. Dis. 95, 288–293 (2020)
Nature: The UK has approved a COVID vaccine-here’s what scientists now want to know (2020). https://www.nature.com/articles/d41586-020-03441-8. Accessed 3 Dec 2020
Chen, S., Zhang, Z., Yang, J., et al.: Fangcang shelter hospitals: a novel concept for responding to public health emergencies. Lancet 395, 1305–1314 (2020)
Li, K., Zhu, G.: Dynamic stability of an SIQS epidemic network and its optimal control. Commun. Nonlinear Sci. Numer. Simul. 66, 84–95 (2019)
Witbooi, P., Muller, G., Van Schalkwyk, G.: Vaccination control in a stochastic SVIR epidemic model. Comput. Math. Methods Med. (2015)
Nature: Immune responses to coronavirus persist beyond 6 months (2020). https://www.nature.com/articles/d41586-020-00502-w. Accessed 20 Nov 2020
Anwarud, D., Amir, K., Dumitru, B.: Stationary distribution and extinction of stochastic coronavirus (COVID-19) epidemic model. Chaos Solitons Fract. 139, 110036 (2020)
Sun, G.: Pattern formation of an epidemic model with diffusion. Nonlinear Dyn. 69, 1097–1104 (2012)
Rajasekar, S.P., Pitchaimani, M.: Qualitative analysis of stochastically perturbed SIRS epidemic model with two viruses. Chaos Solitons Fract. 118, 207–221 (2019)
Beretta, E., Kolmanovskii, V., Shaikhet, L.: Stability of epidemic model with time delays influenced by stochastic perturbations. Math. Comput. Simul. 45, 269–277 (1998)
Hethcote, H., Ma, Z.: Effects of quarantine in six endemic models for infectious disease. Math. Biosci. 180, 141–160 (2002)
Chukwu, A., Akinyemi, J.: On the reproduction number and the optimal control of infectious diseases in a heterogenous population. Adv. Differ. Equ. (2020)
Mao, X.: Stochastic Differential Equations and Applications. Ellis Horwood, Chichester (1997)
Liu, Q., Jiang, D., Shi, N., et al.: Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence. Phys. A 469, 510–517 (2017)
Kuwamura, M.: Turing instabilities in prey–predator systems with dormancy of predators. J. Math. Biol. 71, 125–149 (2015)
Zheng, Q., Wang, Z.: Turing bifurcation and pattern formation of stochastic reaction–diffusion system. Adv. Math. Phys. (2017)
Fleming, W., Rishel, R.: Deterministic and Stochastic Optimal Control. Springer, New York (1975)
Fister, K., Lenhart, S., Mcnally, J.: Optimizing chemotherapy in an HIV model. Electron. J. Diff. Equ. (1998)
Oksendal, B.: Stochastic Differential Equations: An Introduction with Applications, Universitext, vol. 5. Springer, Berlin (1998)
Chowell, G., Hyman, J.M., Bettencourt, L.M., Castillo-Chavez, C.: Mathematical and Statistical Estimation Approaches in Epidemiology. Springer, Berlin (2009)
Martcheva, M.: An Introduction to Mathematical Epidemiology. Springer, Berlin (2015)
COVID-19 Coronavirus Pandemic. 2020. https://www.worldometers.info/coronavirus/country/china/
worldometer. Countries in the world by population 2020. https://www.worldometers.info/world- population/population-by-country/
Coronavirus disease (COVID-2019) situation reports. Available from: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports
COVID-19 Coronavirus Pandemic. 2020. https://www.worldometers.info/coronavirus/country/us/
China Population 1950–2020. https://www.macrotrends.net/cities/20712/wuhan/population/
World health statistics. 2013. Available from: http://www.who.int/
Higham, D.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43, 525–546 (2001)
Gani, S., Halawar, S.: Optimal control analysis of deterministic and stochastic epidemic model with media awareness programs. Int. J. Optim. Control. Theor. Appl. IJOCTA 9, 24–35 (2019)
Okosun, K., Makide, O., Takaidza, I.: The impact of optimal control on the treatment of HIV/AIDS and screening of unaware infective. Appl. Math. Model. 37, 3802–3820 (2013)
Xu, Y., Zhu, Y., Shen, J., Su, J.: Switch dynamics for stochastic model of genetic toggle switch. Phys. A Stat. Mech. Appl. 416, 461–466 (2014)
Martin, A., Markhvida, M., Hallegatte, S., Walsh, B.: Socio-economic impacts of COVID-19 on household consumption and poverty. Econ. Disaster Clim. 4, 453–479 (2020)
Centers for Disease Control and Prevention. When to Quarantine (2020). https://www.cdc.gov/coronavirus/2019-ncov/if-you-are-sick/quarantine.html. Updated 10 Dec 2020
Wells, C., Townsend, J., Pandey, A., et al.: Optimal COVID-19 quarantine and testing strategies. Nat. Commun. 12, 356 (2021)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos:12172340 and 11772306), Zhejiang Provincial Natural Science Foundation of China (No. LY20A020001), and the Fundamental Research Funds for the Central Universities, China University of Geosciences (CUGGC05).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, Y., Wei, Z. Dynamics and optimal control of a stochastic coronavirus (COVID-19) epidemic model with diffusion. Nonlinear Dyn 109, 91–120 (2022). https://doi.org/10.1007/s11071-021-06998-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06998-9