Variable gain gradient descent-based reinforcement learning for robust optimal tracking control of uncertain nonlinear system with input constraints

Abstract

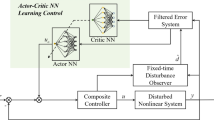
In recent times, a variety of reinforcement learning (RL) algorithms have been proposed for optimal tracking problem of continuous time nonlinear systems with input constraints. Most of these algorithms are based on the notion of uniform ultimate boundedness (UUB) stability, in which normally higher learning rates are avoided in order to restrict oscillations in state error to smaller values. However, this comes at the cost of higher convergence time of critic neural network weights. This paper addresses that problem by proposing a novel tuning law containing a variable gain gradient descent for critic neural network that can adjust the learning rate based on Hamilton–Jacobi–Bellman (HJB) approximation error. By allowing high learning rate the proposed variable gain gradient descent tuning law could improve the convergence time of critic neural network weights. Simultaneously, it also results in tighter residual set, on which trajectories of augmented system converge to, leading to smaller oscillations in state error. A tighter bound for UUB stability of the proposed update mechanism is proved. Numerical studies are then furnished to validate the variable gain gradient descent-based update law presented in this paper on a continuous time nonlinear system.

Appendices

Appendices

Lemma 1

Following equality holds true:

$$\begin{aligned}&2u_m\int _0^{-u_m\tanh {A(z)}}\tanh ^{-1}(\nu /u_m)^TRd\nu \nonumber \\&\quad =2u_m^2A^T(z)R\tanh {A(z)}+ u_m^2 \nonumber \\&\qquad \sum _{i=1}^{m}R_i\ln [1-\tanh ^2{A_i(z)}] \end{aligned}$$

(70)

Proof

$$\begin{aligned} \int \tanh ^{-1}\Big (\frac{x}{a}\Big )&=\frac{1}{2}a\ln {(a^2-x^2)} \nonumber \\&\quad +x\tanh ^{-1}\Big (\frac{x}{a}\Big )+I \end{aligned}$$

(71)

Therefore,

$$\begin{aligned} \int _0^u \tanh ^{-1} \Big (\frac{\nu }{u_m}\Big )d\nu&=\frac{1}{2}u_m\ln {(u_m^2-\nu ^2)} \nonumber \\&\quad +\nu \tanh ^{-1}\Big (\frac{\nu }{u_m}\Big )\Big |_0^u \nonumber \\&\qquad 2u_m\int _0^u \tanh ^{-1} \Big (\frac{\nu }{u_m}\Big )d\nu \nonumber \\&\quad =u_m^2\ln {(u_m^2-\nu ^2)} \nonumber \\&\quad +2u_m\nu \tanh ^{-1}\Big (\frac{\nu }{u_m}\Big )\Big |_0^u \nonumber \\&=u_m^2\ln {(1-\frac{u^2}{u_m^2})} \nonumber \\&\quad +2u_m^2\tanh {A(z)} \nonumber \\&=u_m^2\ln {(1-\tanh ^2{A(z)})} \nonumber \\&\quad +2u_m^2\tanh {A(z)} \end{aligned}$$

(72)

where $u=-u_m\tanh {A(z)}$ is scalar. Now if u is a vector, then,

$$\begin{aligned}&2u_m\int _0^u \tanh ^{-1} \Big (\frac{\nu }{u_m}\Big )Rd\nu \nonumber \\&=2u_m^2A^T(z)R\tanh {A(z)} \nonumber \\&+ u_m^2\sum _{i=1}^{m}R_i\ln [1-\tanh ^2{A_i(z)}] \end{aligned}$$

(73)

$\square$

Lemma 2

Following inequality holds true:

$$\begin{aligned} C(u_i)=2u_m\int _{0}^{u_i}\psi ^{-1}(\frac{\nu }{u_m})R_id\nu \ge 0 \end{aligned}$$

(74)

if $\psi ^{-1}$ is monotonic odd and increasing and $R_i>0$. Where $u_i \in {\mathbb {R}},i=1,2,...,m$

Proof

If $\psi ^{-1}$ is monotonic odd and increasing, then,

$$\begin{aligned} \begin{aligned} \Big (\frac{\nu }{u_m}\Big )\psi ^{-1}\Big (\frac{\nu }{u_m}\Big ) \ge 0 \end{aligned} \end{aligned}$$

(75)

or

$$\begin{aligned} \nu \psi ^{-1}\Big (\frac{\nu }{u_m}\Big ) \ge 0 \end{aligned}$$

(76)

where $\nu \in {\mathbb {R}}$ and $u_m>0$. Let $\theta =1/u_m$. In order to prove that $2u_m\times \int _{0}^{u_i}\psi ^{-1}(\nu /u_m)R_id\nu \ge 0$, it is enough to prove that, $\int _{0}^{u_i}\psi ^{-1}(\nu \theta )d\nu \ge 0$. In order to prove this inequality, a variable, ${\mathcal {K}}\in [0,\theta ]$ is assumed. Therefore,

$$\begin{aligned} \begin{aligned} \int _{0}^{u_i}\psi ^{-1}(\nu \theta )d\nu =\frac{1}{\theta }\int _{0}^{u_i\theta }\psi ^{-1}(l)dl \end{aligned} \end{aligned}$$

(77)

where $l=\nu \theta$. Similarly,

$$\begin{aligned} \begin{aligned} \frac{1}{\theta }\int _{0}^{u_i\theta }\psi ^{-1}(l)dl=\frac{1}{\theta }\int _{0}^{\theta }\psi ^{-1}(u_i{\mathcal {K}})u_id{\mathcal {K}} \end{aligned} \end{aligned}$$

(78)

by utilizing $l=u_i{\mathcal {K}}$

Since, $\psi ^{-1}(u_i{\mathcal {K}})u_i \ge 0$, which implies,

$$\begin{aligned} \frac{1}{\theta }\int _{0}^{\theta }\psi ^{-1}(u_i{\mathcal {K}})u_id{\mathcal {K}}\ge 0 \end{aligned}$$

(79)

$\square$

Lemma 3

Following equation holds true:

$$\begin{aligned} \begin{aligned} u&=-u_m\tanh {\Big (\frac{1}{2u_m}R^{-1}{\hat{G}}^T \nabla {\vartheta }^TW+\varepsilon _{u^*}\Big )}\\&=-u_m\tanh {(\tau _1(z))}\\&\quad +\varepsilon _{u} \end{aligned} \end{aligned}$$

(80)

where $\varepsilon _{u^*}=(1/2u_m)R^{-1}{\hat{G}}^T\nabla {\varepsilon }(z)= [\varepsilon _{{u^*}_{1}},\varepsilon _{{u^*}_{2}},...,\varepsilon _{{u^*}_{m}}]^T \in {\mathbb {R}}^m$. $\tau _{1}(z)=(1/2u_m)R^{-1}{\hat{G}}^T \nabla {\vartheta }^TW=[\tau _{11},...,\tau _{1m}]^T \in {\mathbb {R}}^m$ and $\varepsilon _{u}=-(1/2)\times ((I_m-diag(\tanh ^2{(q)}))R^{-1}{\hat{G}}^T\nabla {\varepsilon })$ with $q \in {\mathbb {R}}^m$ and $q_i \in {\mathbb {R}}$ considered between $\tau _{1i}+\varepsilon _{u^*_i}$ and $\varepsilon _{u^*_i}$ i.e., $i^{th}$ element of $\varepsilon _{u^*}$.

Proof

$$\begin{aligned} u=-u_m\tanh {(\tau _1+\varepsilon _{u^*})} \end{aligned}$$

(81)

Using mean value theorem,

$$\begin{aligned}&\tanh {(\tau _1+\varepsilon _{u^*})}-\tanh {(\tau _1)}=\tanh ^{'}{(q)}\varepsilon _{u^*} \nonumber \\&=(I_m-diag(\tanh ^2{(q)}))\varepsilon _{u^*} \end{aligned}$$

(82)

where $q \in {\mathbb {R}}^m$ and $q_i \in {\mathbb {R}}$ lying between $\tau _{1i}$ and $\tau _{1i}+\varepsilon _{u^*_i}$.

Now, using the expression for $\varepsilon _{u^*}$ in (82), $\tanh {(\tau _1+\varepsilon _{u^*})}$ can be rewritten as:

$$\begin{aligned} \tanh {(\tau _1+\varepsilon _{u^*})}&=\tanh {(\tau _1)}+(I_m-diag(\tanh ^2{(q)})) \nonumber \\&\quad \times \left( \frac{1}{2u_m}R^{-1}{\hat{G}}^T\nabla {\varepsilon }(z)\right) \end{aligned}$$

(83)

Multiplying $-u_m$ on both sides,

$$\begin{aligned} -u_m\tanh {(\tau _1+\varepsilon _{u^*})}&=-u_m\tanh {(\tau _1)} \nonumber \\&\quad -\frac{1}{2}(I_m-diag(\tanh ^2{(q)})) \nonumber \\&\quad \times \left( R^{-1}{\hat{G}}^T(z)\nabla {\varepsilon }(z)\right) \end{aligned}$$

(84)

Hence proved. $\square$

Lemma 4

Following vector inequality holds true:

$$\begin{aligned} \Vert \tanh {(\tau _1(z))}-\tanh {(\tau _2(z))}\Vert \le T_m \le 2\sqrt{m} \end{aligned}$$

(85)

where $T_m=\sqrt{\sum _{i=1}^mmin(|\tau _{1i}-\tau _{2i}|^2,4)}$, $\tau _1(z)$ and $\tau _2(z)$ both belong in ${\mathbb {R}}^m$; therefore, $\tanh {(\tau _i(z))} \in {\mathbb {R}}^m,~i=1,2$.

Proof

Since, $\tanh {(.)}$ is 1-Lipschitz, one can write,

$$\begin{aligned} \begin{aligned} |\tanh {(\tau _{1i})}-\tanh {(\tau _{2i})}| \le |\tau _{1i}-\tau _{2i}| \end{aligned} \end{aligned}$$

(86)

Therefore, using the above inequality and the fact that $-1\le \tanh {(.)} \le 1$

$$\begin{aligned} \begin{aligned} \Vert \tanh {(\tau _1(z))}-\tanh {(\tau _2(z))}\Vert ^2&= \sum _{i=1}^m|\tanh {\tau _{1i}}-\tanh {\tau _{2i}}|^2\\&\le \sum _{i=1}^mmin(|\tau _{1i}-\tau _{2i}|,2)^2\\&\le \sum _{i=1}^mmin(|\tau _{1i}-\tau _{2i}|^2,4) \end{aligned} \end{aligned}$$

(87)

One can also see, using the absolute upper bound of $\tanh {(.)}$.

$$\begin{aligned} \sum _{i=1}^mmin(|\tau _{1i}-\tau _{2i}|^2,4)\le 2\sqrt{m} \end{aligned}$$

(88)

which implies,

$$\begin{aligned} \begin{aligned} \Vert \tanh {(\tau _1(z))}-\tanh {(\tau _2(z))}\Vert \le T_m \le 2\sqrt{m} \end{aligned} \end{aligned}$$

(89)

$\square$