Abstract
Kinematics and its control application are presented for a Stewart platform whose base plate is installed on a floor in a moving ship or a vehicle. With a manipulator or a sensitive equipment mounted on the top plate, a Stewart platform is utilized to mitigate the undesirable motion of its base plate by controlling actuated translational joints on six legs. To reveal closed loops, a directed graph is utilized to express the joint connections. Then, kinematics begins by attaching an orthonormal coordinate system to each body at its center of mass and to each joint to define moving coordinate frames. Using the moving frames, each body in the configuration space is represented by an inertial position vector of its center of mass in the three-dimensional vector space ℝ3, and a rotation matrix of the body-attached coordinate axes. The set of differentiable rotation matrices forms a Lie group: the special orthogonal group, SO(3). The connections of body-attached moving frames are mathematically expressed by using frame connection matrices, which belong to another Lie group: the special Euclidean group, SE(3). The employment of SO(3) and SE(3) facilitates effective matrix computations of velocities of body-attached coordinate frames. Loop closure constrains are expressed in matrix form and solved analytically for inverse kinematics. Finally, experimental results of an inverse kinematics control are presented for a scale model of a base-moving Stewart platform. Dynamics and a control application of inverse dynamics are presented in the part II-paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When manipulators, which require precise positioning, operate in moving vehicles or ships, it becomes economical to utilize a Stewart platform [1], whose sole role is to stabilize the orientation and the translation of its top table onto which the manipulators are attached. In this way, the design and control of each tool for its precise positioning become simpler without coping with undesirable large rigid-body rotation and translation of the tool mount. In addition, such a platform is also useful for safe transportation of a sensitive equipment or a patient using a vehicle to mitigate the transmission of undesirable rotation and translation induced by the moving vehicle.
Fixed-base Stewart platforms have been popularly utilized in flight simulators, vehicle driving simulators, trajectory tracking apparatus, and immersed virtual-reality theaters in amusement parks. Kinematics and dynamics of fixed-base Stewart platforms have been investigated by many researchers to control the platforms to enable those applications, for example [2,3,4,5,6,7,8,9,10,11,12,13].
For base-moving Stewart platforms, only a few applications have been reported. As passive applications, Stewart platforms were utilized as vibration isolators utilizing bio-inspired X-shaped legs [14] and adjustable electromagnetic legs, which exhibit negative stiffness [15]. As actively controlled applications, previous researchers employed proportional-derivative (PD) controllers using inverse kinematics derived from geometrical relations [16, 17]. Due to the complexity of the problem, velocity computations and derivation of equations of motion for a base-moving Stewart platform have not been reported. For effective and fast position control of the top plate of a base-moving Stewart platform, it is desirable to derive equations of motion to explore nonlinear control schemes.
In response to the need described above, analytical equations of motion are derived in matrix form for a control application of inverse dynamics. In this part I-paper only kinematics is presented while the derivation of equations of motion and their control application are presented in the part II-paper.
Regarding the representation of configuration spaces of multi-body systems, Joseph-Louis Lagrange (1736–1813) defined configuration spaces using vectors consisting of generalized coordinates or displacements. Fortunately, in the early twentieth century, due to the advent of matrix Lie groups pioneered by Sophus Lie (1842–1899), in addition to vectors in \( {\mathbb{R}}^{n}\), the set of differentiable rotation matrices: the special orthogonal group SO(3) has been utilized to define the configuration space of multi-body systems [18]. Specifically, in the configuration space of a multi-body system each rigid body is mathematically expressed by the position vector of the origin of a body-attached coordinate system in \({\mathbb{R}}^{3}\), expressed with respect to an inertial coordinate system, and the rotation matrix in SO(3) of the body-attached coordinate axes from the inertial coordinate axes [19,20,21].
In this paper, first, the multi-body connection of a base-moving Stewart platform is expressed by using a directed graph to reveal closed loops [22]. Second, by attaching principal coordinate systems to constituent bodies at their centers of mass, moving coordinate frames are defined. Coordinate frames are also attached to joints. Third, to define the configuration space of the Stewart platform, the connections of body- and joint-attached coordinate frames are expressed mathematically employing the special Euclidian group, SE(3), which combines both SO(3) and \({\mathbb{R}}^{3}\). Fourth, loop closure constraints are obtained along a representative closed loop in the configuration space (as well as in velocities). They are solved analytically for inverse kinematics. Fifth, velocities of moving frames are computed incorporating the Lie algebra: so(3) of SO(3). The advantage of expressing the frame connections by using SE(3)-matrices is that the readers can compute frame velocities unambiguously since the coordinate vector bases are explicitly shown. Finally, experimental results of an inverse kinematics control are presented for a scale model of a base-moving Stewart platform. Furthermore, in Appendix A, workspace analysis is performed for the preliminary design of a Stewart platform. In the part II-paper, the velocities of body-attached coordinate frames computed here are utilized to derive analytical equations of motion for inverse dynamics control.
2 Description of a Stewart platform
Figure 1 illustrates a Stewart platform in its reference configuration. To identify bodies of the multi-rigid body system, body numbers are assigned to constituent bodies and shown in a pair of parentheses. Body-(0): base plate is attached to the floor of a moving ship or a vehicle. As a result, the base plate translates and rotates due to the motion of the vehicle. Body-(13) represents top plate or platform on which some sensitive equipment or a manipulator is mounted. Body-(0) and body-(13) are connected by six identical legs, referred to as leg-(k), k = 1,\(\cdots ,\) 6. Leg-(k) consists of lower leg, body-(2k-1), and upper leg, body-(2k), jointed by an actuated translational joint, ATJ-(k), between them. The objective of a controller is to maintain a desired attitude of the top plate to mitigate the motion of the base plate by changing their ATJ lengths at each time.
In leg-(k) shown in Fig. 1, the lower leg, body-(2k-1), is jointed to body-(0) by a universal joint (UJ), named UJ-(k), whereas the upper leg, body-(2k), is jointed to body-(13) by a spherical joint (SJ), called SJ-(k). The base yoke of UJ-(k) is fixed to body-(0), which journals one axis of the UJ cross. The cross of UJ-(k) is referred to as UJ-(k) cross. Its center is located at point \(B_{k}\). The attachment of the lower leg, body-(2k-1), to the other axis of UJ-(k) cross is facilitated by the yoke hub at the lower end of body-(2k-1) to pivot freely around this axis. The upper end of the upper leg, body-(2k), has a spherical ball, referred to as SJ-(k) ball with its center at point \(T_{k}\). The spherical ball fits into the SJ-(k) socket fixed to body-(13).
A directed graph of the Stewart platform is presented in Fig. 2a. In the graph vertices represent rigid bodies and lines show joint connections. The graph is “modified” by enlarging the vertices for the base plate, body-(0), and the top plate, body-(13), to show the leg attachment points \(B_{k}\) for universal joints, UJ-(k), and \(T_{k}\) for spherical joints, SJ-(k), for leg-(k), \(k = 1, \cdots , 6.\) In the graph body-(14), not shown in Fig. 1, represents a manipulator, which is rigidly attached to the top plate.
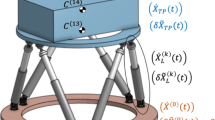
The graph in Fig. 2a reveals that there are closed loops formed by 15 pairs of different legs. Instead of dealing with individual pairs, the loop closure constraints can be treated efficiently by considering a generic closed loop shown in Fig. 2b. The loop is formed by a free link between body-(0) and body-(13), shown by a broken line, and leg-(k). In the figure, C(α) represent the center of mass of body-(α). Along path (i) one starts from the center of mass of body-(0), C(0), moves along the free link to that of body-(13), C(13), and heads toward the center Tk of the semi-spherical cavity of SJ-(k) socket, which is rigidly attached to body-(13). Along path (ii) one starts from C(0) to the center Bk of UJ-(k) cross, moves along the axis of leg-(k) passing the centers of mass of body-(2k-1), C(2k−1), and body-(2k), C(2k), and reaches the center Tk, of SJ-(k) ball. Finally, one fits SJ-(k) ball of the upper leg into SJ-(k) socket on body-(13). This fitting of SJ-(k) ball into SJ-(k) socket is mathematically described by loop closure constraints.
Using the vector method, kinematic equations of Stewart platforms were previously presented in vector form [4,5,6,7,8,9,10,11,12,13]. From the resulting vector equations to obtain component equations, readers need to define appropriate coordinate systems and perform necessary computations. This extra burden on readers is eliminated in the following by explicitly defining body-attached coordinate frames for kinematics.
To commence kinematics using moving frames, the configuration space is defined along the generic closed loop in Fig. 2b by attaching orthonormal coordinate systems at the centers of mass of constituent bodies as well as at the joints. The completion of both paths yields configurational loop closure constraints at SJ-(k). Then velocities of the attached coordinate frames will be computed to obtain: (1) the loop-closure constrains on velocities and (2) the translational and angular velocities of each body at its center of mass, which will be utilized in the part II-paper to compute the equations of motion for the Stewart platform.
3 Configuration space defined by coordinate frames
The configuration space is defined along each path of the generic closed loop in Fig. 2b by attaching moving coordinate frames at joints and the centers of mass of rigid bodies and expressing their interconnections.
3.1 Moving coordinate frames along path (i)
Figure 3 depicts the free link between body-(0) and body-(13), shown in Fig. 2b. To begin, an inertial coordinate frame is defined to express position vectors of the origins of moving coordinate frames.
3.1.1 Inertial frame
A fixed Cartesian coordinate system {x1 x2 x3} is defined with its origin, expressed by zero vector 0. The unit vectors of the coordinate axes define a vector basis \( \left( {{\mathbf{e}}_{1}^{I} \quad {\mathbf{e}}_{2}^{I} \quad {\mathbf{e}}_{3}^{I} } \right) \), which is compactly written as \({\mathbf{e}}^{I}\) utilizing Frankel’s notation [23]. The vector basis \({\mathbf{e}}^{I}\) and its origin 0 define the inertial coordinate frame written as: (\({\mathbf{e}}^{I}\), 0), [20, 21].
Using the inertial vector basis \({\mathbf{e}}^{I}\), the position vector of the center of mass, for example C(0) of body-(0) is expressed as:
where
In Frankel’s notation all vector bases are stored in 1 × 3 row matrices and components in 3 × 1 column matrices. In this paper, {x1 x2 x3} is exclusively used for the inertial coordinate system, while {s1 s2 s3} is used for body-attached, orthonormal coordinate systems. Furthermore, only right-handed coordinate systems are considered.
3.1.2 Body-(0) frame: (\({{\varvec{e}}}^{(0)}({\varvec{t}})\) \({{\varvec{r}}}_{{\varvec{C}}}^{(0)}({\varvec{t}})\))
To define the body-(0) coordinate frame, a principal coordinate system {\(s_{1}^{\left( 0 \right)}\) \(s_{2}^{\left( 0 \right)}\) \(s_{3}^{\left( 0 \right)}\)} is attached to body-(0) at its center of mass, C(0), with the \(s_{3}^{\left( 0 \right)}\)-axis normal to the plane of the base plate, spanned by the \(s_{1}^{\left( 0 \right)}\), \(s_{2}^{\left( 0 \right)}\)-axes. The coordinate unit vectors define the vector basis \({\mathbf{e}}^{\left( 0 \right)} \left( t \right) \equiv\) (\({\mathbf{e}}_{1}^{\left( 0 \right)} \left( t \right)\) \({\mathbf{e}}_{2}^{\left( 0 \right)} \left( t \right)\) \({\mathbf{e}}_{3}^{\left( 0 \right)} \left( t \right)\)). Using the vector basis \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) and the position vector of its origin \({\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)\), the body-(0) frame is defined as \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{\left( 0 \right)} \left( t \right)} & {{\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)} \\ \end{array} } \right)\). The configuration of body-(0) is defined by expressing its frame connection to (\({\mathbf{e}}^{I}\), 0). To this end, the attitude of \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) relative to \({\mathbf{e}}^{I}\) is expressed using a 3 × 3 rotation matrix \( R^{\left( 0 \right)} \left( t \right)\) with determinant one:
In expanded form, the rotation matrix is written as:
Equation (2a) is read as “\({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) is obtained by applying the rotation \(R^{\left( 0 \right)} \left( t \right)\) to \({\mathbf{e}}^{I}\)”.
The inverse relation of Eq. (2a) is
where a superposed ‘T’ attached to a matrix symbol implies the transposition of the matrix.
Using Eq. (2a) and the components \(x_{C}^{\left( 0 \right)} \left( t \right)\) of \({\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)\) in Eq. (1c), the connection of \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{\left( 0 \right)} \left( t \right)} & {{\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)} \\ \end{array} } \right)\) to \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{I} } & 0 \\ \end{array} } \right)\) is compactly expressed by using a 4 × 4 frame-connection matrix \(E^{\left( 0 \right)} \left( t \right)\) as:
where
and \(0_{1 \times 3} \equiv \left( {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right)\).
Equation (3a) shows that \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{\left( 0 \right)} \left( t \right)} & {{\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)} \\ \end{array} } \right)\) is obtained by applying the rotation \(R^{\left( 0 \right)} \left( t \right)\) and the parallel translation \(x_{C}^{\left( 0 \right)} \left( t \right)\) to \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{I} } & 0 \\ \end{array} } \right)\).
In this paper, an inertial coordinate frame is selected to be the body-(0) frame at t = 0:
Therefore, at t = 0 \(E^{\left( 0 \right)} \left( 0 \right)\) in Eq. (3b) is defined by the initial values \(x_{C}^{\left( 0 \right)} \left( 0 \right) = 0_{3x1}\) and \(R^{\left( 0 \right)} \left( 0 \right) = I_{3}\), which is the 3 × 3 identity matrix.
The set of differentiable rotation matrices forms the special orthogonal group: SO(3) [18, 23], and that of differentiable frame connection matrices forms the special Euclidean group [19,20,21]. (Here the adjective “special” means that all member matrices have determinant one.) Both SO(3) and SE(3) are matrix Lie groups with the basic group properties, expressed for SE(3): (i) their products belong to SE(3), (ii) their inverse matrices belong to SE(3), and (iii) associativity holds in matrix multiplications, see for example [18, 23]. The members of SO(3) also satisfy the same group properties. As Lie matrix groups, SO(3) and SE(3) come with their Lie algebras: so(3) and se(3), respectively, which describe the flow of matrix members with time near their identity matrix. In dynamics, the Lie algebras express angular velocities and translational velocities of each body [20, 21].
In robotics, frame connection matrices of SE(3) are called homogeneous transformations, see for example [24], where the time rate of transformations, comparable to the Lie algebra, are not mentioned. Also in robotics using the screw theory [25] and the product of exponentials formula [26], homogeneous coordinates of SE(3) were utilized to derive equations of motion by Murray et al. [27]. In this paper, the authors do not adopt the exponential matrix representation of rotation matrices, employed by the screw theory.
Returning to path (i) in Figs. 2b and 3 along the free link, a frame is defined for the top plate, body-(13).
3.1.3 Body-(13) Frame: (\({{\varvec{e}}}^{(13)}({\varvec{t}})\) \({{\varvec{r}}}_{{\varvec{C}}}^{(13)}({\varvec{t}})\))
A principal coordinate system {\({s}_{1}^{\left(13\right)}\) \({s}_{2}^{\left(13\right)}\,\,{s}_{3}^{\left(13\right)}\)} is attached to body-(13) at its center of mass, C(13), with the \({s}_{3}^{\left(13\right)}\)-axis normal to the plane of the plate. The coordinate vector basis \({\mathbf{e}}^{\left(13\right)}\left(t\right)\) is defined by the unit coordinate vectors as:\({\mathbf{e}}^{(13)}(t)\equiv \left(\begin{array}{ccc}{\mathbf{e}}_{1}^{(13)}(t)& {\mathbf{e}}_{2}^{(13)}(t)& {\mathbf{e}}_{3}^{(13)}(t)\end{array}\right)\). The position vector of C(13) is expressed by \({\mathbf{r}}_{C}^{(13)}(t)\). Now, body-(13) frame is defined as:\(\left(\begin{array}{cc}{\mathbf{e}}^{(13)}(t)& {\mathbf{r}}_{C}^{(13)}(t)\end{array}\right)\). As illustrated in Fig. 3, \({\mathbf{r}}_{C}^{(13)}(t)\) is expressed by adding the relative position vector of C(13) measured from C(0), written as \({\mathbf{s}}_{C}^{\left(13/0\right)}\left(t\right)={\mathbf{e}}^{\left(0\right)}\left(t\right){s}_{C}^{\left(13/0\right)}(t)\) to \({\mathbf{r}}_{C}^{\left(0\right)}\left(t\right)\). The rotation of \({\mathbf{e}}^{(13)}(t)\) relative to \({\mathbf{e}}^{(0)}(t)\) is expressed by \({R}^{\left(13/0\right)}(t)\). As a result, the connection of \(\left(\begin{array}{cc}{\mathbf{e}}^{\left(13\right)}\left(t\right)& {\mathbf{r}}_{C}^{\left(13\right)}\left(t\right)\end{array}\right)\) to \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{\left( 0 \right)} \left( 0 \right)} & {{\mathbf{r}}_{C}^{\left( 0 \right)} \left( 0 \right)} \\ \end{array} } \right)\) is expressed by the frame connection matrix \(E^{{\left( {13/0} \right)}} \left( t \right)\) as:
where
In this paper the matrices or vectors with superscript “(j/i)” imply those of frame-( j) relative to frame-(i). For example, in Eq. (4a), \(E^{{\left( {13/0} \right)}} \left( t \right)\) expressed the connection of body-(13) frame relative to body-(0) frame.
In the reference configuration at t = 0, shown in Fig. 1, \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{{\left( {13} \right)}} \left( 0 \right)} & {{\mathbf{r}}_{C}^{{\left( {13} \right)}} \left( 0 \right)} \\ \end{array} } \right)\) is obtained by parallel translating body-(0) frame \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{\left( 0 \right)} \left( 0 \right)} & {{\mathbf{r}}_{C}^{\left( 0 \right)} \left( 0 \right)} \\ \end{array} } \right)\) vertically from C(0) to C(13) by distance \(\hat{h}^{\left( 0 \right)}\) without any rotation. Therefore, the initial values of the elements of \(E^{{\left( {13/0} \right)}} \left( 0 \right)\) are: \(R^{{\left( {13/0} \right)}} \left( 0 \right) = I_{3}\) and \(s_{C}^{{\left( {13/0} \right)}} \left( 0 \right) = \hat{h}^{\left( 0 \right)} e_{3}\), where \(e_{3}\) represents a 3 × 1 unit column matrix: \(e_{3} \equiv \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)^{T}\).
Next along path (i) from C(13) one advances to SJ-(k) socket with its center at Tk.
3.1.4 SJ-(k) Socket Frame at \({{T}}_{{{k}}}\) on Body-(13): (\({{\mathbf e}}_{{{{T}}_{{{k}}} }}^{{\left( {{{SJ}} 13} \right)}} (t)\) \({{\mathbf r}}_{{{{T}}_{{{k}}} }} \left( {{t}}\right)\))
In Fig. 4a T1, T2, …, T6 on the circle of radius \(\hat{r}_{m}^{{\left( {13} \right)}}\) express the centers of semi-spherical cavity of sockets of six spherical joints (SJs). They form a hexagon, obtained by truncating an equilateral triangle by the radius \(\hat{r}_{m}^{{\left( {13} \right)}}\), which is slightly smaller than the radius of the circumscribing circle of the triangle. The relative coordinates \(\hat{s}_{{T_{k} }}^{{\left( {13} \right)}}\) of point Tk with respect to \( {\mathbf{e}}^{{\left( {13} \right)}} \left( t \right)\) remain constant:
where \(\hat{s}_{{3 T_{k} }}^{{\left( {13} \right)}} = - \hat{h}_{SJ}^{{\left( {13} \right)}}\) as shown in Fig. 4b:
and denoting the truncation angle by \(\Delta \hat{\theta }^{{\left( {13} \right)}}\), which is less than \(\pi\)/3, \(\hat{\theta }_{k}^{{\left( {13} \right)}}\) in Fig. 4a is expressed as:
In this paper, time-independent quantities are shown with superposed hat: ‘^’.
Along path (i) SJ-(k) socket frame at Tk on body-(13):\( \left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{T_{k} }}^{{\left( {{\text{SJ }}13} \right)}} \left( t \right)} & {{\mathbf{r}}_{{T_{k} }} \left( t \right)} \\ \end{array} } \right)\) is defined by parallel translating \({\mathbf{e}}^{{\left( {13} \right)}} \left( t \right)\) to Tk by \(\hat{s}_{{T_{k} }}^{{\left( {13} \right)}}\) and rotating the translated vector basis until \({\mathbf{e}}_{{1 T_{k} }}^{{\left( {{\text{SJ }}13} \right)}}\) points in the radial direction. Thus, the frame connection of \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{T_{k} }}^{{\left( {{\text{SJ }}13} \right)}} \left( t \right)} & {{\mathbf{r}}_{{T_{k} }} \left( t \right)} \\ \end{array} } \right)\) to body-(13) frame is written as:
where
and \(R_{{3 T_{k} }} \left( {\hat{\theta }_{k}^{{\left( {13} \right)}} } \right)\) represents the elementary rotation about \({\mathbf{e}}_{3}^{{\left( {13} \right)}} \left( t \right)\) by \(\hat{\theta }_{k}^{{\left( {13} \right)}}\) to point \({\mathbf{e}}_{{1 T_{k} }}^{{\left( {{\text{SJ }}13} \right)}}\) in the radial direction:
3.1.5 Summary of path (i) frame connections
Along path (i) SJ-(k) socket frame at Tk on body-(13) is also expressed with respect to body-(0) frame by combining Eqs. (6a) and (4a):
where the components of the frame connection matrix are defined as:
The computation of their components yields
This completes the definition of frame connections along path (i). However, at this point, for the computation of kinetic energy in the part II-paper, the configuration of a manipulator, mounted on the top plate, is defined.
3.1.6 Body-(14) Frame: (e (14)(t) r C (14)(t))
As shown in Figs. 2a and 3, a manipulator, body-(14), is mounted on the top plate. In this paper, the manipulator is approximated as a rigid body with its center of mass located on the \(s_{3}^{{\left( {13} \right)}}\)-axis at the elevation \(\hat{h}^{{\left( {14/13} \right)}}\). Body-(14) frame \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{{\left( {14} \right)}} \left( t \right)} & {{\mathbf{r}}_{C}^{{\left( {14} \right)}} \left( t \right)} \\ \end{array} } \right)\) is therefore established by parallel translating \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}^{{\left( {13} \right)}} \left( t \right)} & {{\mathbf{r}}_{C}^{{\left( {13} \right)}} \left( t \right)} \\ \end{array} } \right)\) along the \(s_{3}^{{\left( {13} \right)}}\)-axis by \(\hat{h}^{{\left( {14/13} \right)}}\) without any rotation:
where using \(e_{3} \equiv\) ( 0 0 1)T,
3.2 Moving coordinate frames along path (ii)
Moving coordinate frames necessary to define the frame connections of path (ii) are briefly discussed. On leg-(k), first, two frames are employed at the center Bk of UJ-(k) cross: UJ-(k) cross frame and UJ-(k) leg frame to describe the rotation of the lower leg, body-(2k-1). One axis of the cross is journaled by the base yoke fixed to body-(0) and the other axis is journaled by the yoke of body-(2k-1). Second, to describe the length change induced by the actuated translational joint, ATJ-(k), principal coordinate systems are attached to both body-(2k-1) and the upper leg, body-(2k), at their centers of mass of body-(2k-1) frame and body-(2k) frame. Third, advancing along the axis of the upper leg to the center \(T_{k}\) of the spherical ball, SJ-(k) ball frame at \( T_{k}\) on body-(2k) is defined. Finally, SJ-(k) ball frame at \(T_{k}\) on body-(2k) is connected to SJ-(k) socket frame at \( T_{k}\) on body-(13) to mathematically fit the spherical ball into the SJ socket on body-(13). This summarizes the frames to be defined along path (ii).
3.2.1 UJ-(k) Cross frame at Bk on body-(0): (e B k (UJcross)(t) r B k(t))
Figure 5a illustrates a plan view of the base plate, body-(0). In the figure the centers of cross of universal joints (UJs) are shown by points B1, B2, …, B6 on the circle of radius \(\hat{r}_{m}^{\left( 0 \right)}\), which are numbered in the counterclockwise direction. They form a hexagon, obtained by truncating an equilateral triangle by the radius \(\hat{r}_{m}^{\left( 0 \right)}\) which is slightly smaller than the circumscribing circle of the triangle. Figure 5b shows for leg-(k) an elevation of the base yoke of UJ-(k) with the center of cross at Bk. The base yoke on body-(0) journals one axis of the cross pointing in the radial direction. (The other axis of the cross is journaled by the yoke of the lower leg: body-(2k-1).)
The relative position vector \({\mathbf{s}}_{{B_{k} }}^{\left( 0 \right)} \left( t \right)\) of point Bk is expressed with respect to \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\):
where the coordinates \(\hat{s}_{{B_{k} }}^{\left( 0 \right)}\) are obtained from Fig. 5a and b with the elevation \(\hat{h}_{{{\text{UJ}}}}^{\left( 0 \right)}\) as:
and denoting the truncated angle by \(\Delta \hat{\theta }^{\left( 0 \right)}\), which is less than \(\pi\)/3, \(\hat{\theta }_{k}^{\left( 0 \right)}\)’s are defined as:
UJ-(k) cross rotates freely around the cross axis pivoted by the base yoke on body-(0). To describe the rotation of the cross, UJ-(k) cross frame \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{B_{k} }}^{{\left( {\text{UJ cross}} \right)}} \left( t \right)} & {{\mathbf{r}}_{{B_{k} }}^{{}} \left( t \right)} \\ \end{array} } \right)\) at Bk on body-(0): is defined. The unit coordinate vector \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) represents the axis of rotation of the cross, \({\mathbf{e}}_{{2 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) is the other axis of cross journaled by the yoke of the lower leg, body (2k-1), and \({\mathbf{e}}_{{3 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) is the normal of the plane of the cross. To define UJ-(k) cross frame, an intermediate frame \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{B_{k} }}^{\left( 0 \right)} \left( t \right)} & {{\mathbf{r}}_{{B_{k} }}^{{}} \left( t \right)} \\ \end{array} } \right)\) is defined first by parallel translating \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) to Bk by \(\hat{s}_{{B_{k} }}^{\left( 0 \right)}\), as shown in Fig. 5a, and rotating the translated \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) about \({\mathbf{e}}_{3}^{\left( 0 \right)} \left( t \right)\) by the angle \(\hat{\theta }_{k}^{\left( 0 \right)}\):
where the elementary rotation \(R_{{3 B_{k} }} \left( {\hat{\theta }_{k}^{\left( 0 \right)} } \right)\) about \({\mathbf{e}}_{3}^{\left( 0 \right)} \left( t \right)\) by the angle \(\hat{\theta }_{k}^{\left( 0 \right)}\) is
In Eq. (10a) the unit vector \({\mathbf{e}}_{{1 B_{k} }}^{ \left( 0 \right)}\) now points in the radial direction as illustrated in Fig. 5a.
UJ-(k) cross frame at \(B_{k}\) on body-(0) is now obtained by rotating \({\mathbf{e}}_{{B_{k} }}^{\left( 0 \right)} \left( t \right)\) about \({\mathbf{e}}_{{1 B_{k} }}^{ \left( 0 \right)}\) by angle \(\phi_{1}^{\left( k \right)} \left( t \right)\), as illustrated in Fig. 6b:
where \(R_{{1B_{k} UJ}}\) represents the elementary rotation about \({\mathbf{e}}_{{1 B_{k} }}^{ \left( 0 \right)}\) by \(\phi_{1}^{\left( k \right)} \left( t \right)\):
Finally, the connection of UJ-(k) cross frame at \(B_{k}\) on body-(0) to body-(0) frame is obtained by substituting Eq. (10a) into Eq. (10c):
The first column of Eq. (10e): \({\mathbf{e}}_{{B_{k} }}^{{\left( {\text{UJ cross}} \right)}} \left( t \right) = {\mathbf{e}}^{\left( 0 \right)} \left( t \right) R_{{3 B_{k} }} \left( {\hat{\theta }_{k}^{\left( 0 \right)} } \right)R_{{1 B_{k} UJ}} \left( {\phi_{1}^{\left( k \right)} \left( t \right)} \right)\) compactly expresses two sequence of rotations applied to the translated \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\) to Bk: the first rotation \(R_{{3 B_{k} }} \left( {\hat{\theta }_{k}^{\left( 0 \right)} } \right)\) to orient \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}} = {\mathbf{e}}_{{1 B_{k} }}^{ \left( 0 \right)}\) in the radial direction, and the second rotation \(R_{{1 B_{k} UJ}} \left( {\phi_{1}^{\left( k \right)} \left( t \right)} \right)\) about \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) by angle \(\phi_{1}^{\left( k \right)} \left( t \right)\) to describe the cross rotation.
Next, to describe the rotation of the lower leg, body-(2k-1), at \(B_{k}\) the second frame is defined.
3.2.2 UJ-(k) Leg frame at \({\varvec{B}}_{{\varvec{k}}}\) on body-(2k-1): (\({\varvec{e}}_{{{\varvec{B}}_{{\varvec{k}}} }}^{{\left( {\user2{UJ }2{\varvec{k}} - 1} \right)}} \left( {\varvec{t}} \right)\) \({\varvec{r}}_{{{\varvec{B}}_{{\varvec{k}}} }}^{{}} \left( {\varvec{t}} \right)\))
To describe the rotation of the lower leg at Bk, UJ-(k) leg frame at Bk on body-(2k-1): \(\left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)} & {{\mathbf{r}}_{{B_{k} }}^{{}} \left( t \right)} \\ \end{array} } \right)\) is defined in Fig. 6b and c. The coordinate vector basis \({\mathbf{e}}_{{B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\) is defined so that \({\mathbf{e}}_{{2 B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right) = {\mathbf{e}}_{{2 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}} \left( t \right)\) expresses the cross axis journaled by the yoke of body-(2k-1) and \({\mathbf{e}}_{{3 B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\) shows the leg axis. The associated coordinate system with the origin at Bk is defined as \(\left\{ {\begin{array}{*{20}c} {s_{{1B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } & {s_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } & {s_{{3 B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } \\ \end{array} } \right\}\). UJ-(k) leg frame on body-(2k-1) occupies the same origin \({\mathbf{r}}_{{B_{k} }}^{{}} \left( t \right)\) as that of UJ-(k) cross frame. However, \({\mathbf{e}}_{{B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\) is relatively rotated by angle \(\phi_{2}^{\left( k \right)} \left( t \right)\) with respect to \({\mathbf{e}}_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\), which shows the axis of the cross-link journaled by the yoke of body-(2k-1), as illustrated in Fig. 6c.
The lower leg, body-(2k-1), takes vertical position where the cross plane remains parallel to the plane of the base plate, i.e., no rotation about \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\), \(\phi_{1}^{\left( k \right)} = 0\), and no rotation about \({\mathbf{e}}_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\), \(\phi_{2}^{\left( k \right)} = 0\). The posture of the leg becomes that shown in Fig. 6b when only the cross rotates about \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) by \(\phi_{1}^{\left( k \right)} \ne 0\) without any rotation about \({\mathbf{e}}_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\), \(\phi_{2}^{\left( k \right)} = 0\). When both rotations take place about \({\mathbf{e}}_{{1 B_{k} }}^{{ \left( {\text{UJ cross}} \right)}}\) by \(\phi_{1}^{\left( k \right)} \ne 0\) and about \({\mathbf{e}}_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} \left( t \right)\) by \(\phi_{2}^{\left( k \right)} \ne 0\), the posture of the lower leg becomes that shown in Fig. 6c. Observing that in the reference configuration, shown in Fig. 1, the legs are not vertical to the plane of the base plate, both \(\phi_{1}^{\left( k \right)} \left( 0 \right)\) and \(\phi_{2}^{\left( k \right)} \left( 0 \right)\) take nonzero initial values (which are computed in Appendix A).
The connection of UJ-(k) leg frame at Bk on body-(2k-1) to UJ-(k) cross frame on body-(0) is expressed as:
where \(R_{{2B_{k} {\text{UJ}}}} \left( {\phi_{2}^{\left( k \right)} \left( t \right)} \right)\) represents the elementary rotation about \({\mathbf{e}}_{{2B_{k} }}^{{\left( {{\text{UJ }}2{\text{k}} - 1} \right)}} \left( t \right)\) by \(\phi_{2}^{\left( k \right)} \left( t \right)\):
To advance further along leg-(k) of path (ii), Fig. 7 illustrates the coordinate frames at joints and centers of mass which must be defined.
3.2.3 Body-(2k-1) frame: (\({\varvec{e}}^{{\left( {2{\varvec{k}} - 1} \right)}} \left( {\varvec{t}} \right)\) \({\varvec{r}}_{{\varvec{C}}}^{{\left( {2{\varvec{k}} - 1} \right)}} \left( {\varvec{t}} \right)\))
For the lower-leg, body-(2k-1) frame is defined at C(2k−1) by parallel translating the \(\left\{ {\begin{array}{*{20}c} {s_{{1B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } & {s_{{2B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } & {s_{{3 B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}} } \\ \end{array} } \right\}\) coordinate system of UJ-(k) leg frame at Bk on body-(2k-1) to C(2k−1). Since body-(2k-1) holds a motor for actuating the translational joint, the center of mass C(2k−1) may be slightly deviated from the axis of leg-(k). Including this deviation, the relative position vector of C(2k−1), \({\mathbf{s}}_{{C/B_{k} }}^{{\left( {2k - 1} \right)}} \left( t \right)\), measured by UJ-(k) leg frame at Bk is expressed as:
where \(\Delta \hat{s}_{{1C/B_{k} }}^{{\left( {2k - 1} \right)}}\) and \(\Delta \hat{s}_{{2C/B_{k} }}^{{\left( {2k - 1} \right)}}\) express the deviation of C(2k−1) from the axis of leg-(k), and \( \hat{l}_{{{\text{UJ}}}}^{{\left( {2k - 1} \right)}}\) denotes the \(s_{{3B_{k} }}^{{\left( {{\text{UJ }}2k - 1} \right)}}\)-coordinate of C(2k−1) measured from Bk, as illustrated in Fig. 7.
The connection of body-(2k-1) frame at C(2k−1) to the UJ-(k) leg frame at Bk on body-(2k-1) is expressed by the frame connection matrix \(E^{{(2k - 1/{\text{UJ }}2k - 1)}} \left( t \right)\):
To prepare for the computation of kinetic energy, body-(2k-1) frame is expressed with respect to body-(0) frame by substituting Eqs. (10a) and (11a) into Eq. (13):
where
and performing the multiplications using Eqs. (10b) and (11b), one finds
and where \(\hat{s}_{{B_{k} }}^{\left( 0 \right)}\) was defined in Eq. (9b).
3.2.4 Body-(2k) frame: (\({\varvec{e}}^{{\left( {2{\varvec{k}}} \right)}} \left( {\varvec{t}} \right)\) \({\varvec{r}}_{{\varvec{C}}}^{{\left( {2{\varvec{k}}} \right)}} \left( {\varvec{t}} \right)\))
The top end of the lower leg, body-(2k-1), has a mechanism to actively slide and passively rotate the cylindrical upper leg, body-(2k), to facilitate a translational joint. The \(s_{3}^{{\left( {2k - 1} \right)}}\)-distance between the center of mass of body-(2k-1), C(2k−1), and that of body-(2k), C(2k), is expressed by d(k)(t), as illustrated in Fig. 7. The passive rotation with \({\mathbf{e}}_{3}^{{\left( {2k - 1} \right)}} \left( t \right)\) by the angle \(\phi_{3}^{{\left( {2k/2k - 1} \right)}} \left( t \right)\) is expressed by the elementary rotation matrix: \(R_{{3 {\text{ATJ}}}} \left( {\phi_{3}^{{\left( {2k/2k - 1} \right)}} \left( t \right)} \right)\). Body-(2k) frame is now defined with respect to body-(2k-1) frame as:
where
and their component matrices defined as:
In Eq. (15d), the terms: \(- \Delta \hat{s}_{{1C/B_{k} }}^{{\left( {2k - 1} \right)}}\) and \(- \Delta \hat{s}_{{2C/B_{k} }}^{{\left( {2k - 1} \right)}}\) place C(2k) back on the axis of leg-(k).
3.2.5 SJ-(k) Ball frame at Tk on body-(2k): (\({\varvec{e}}_{{{\varvec{T}}_{{\varvec{k}}} }}^{{\left( {\user2{SJ }2{\varvec{k}}} \right)}} \left( {\varvec{t}} \right)\) \({\varvec{r}}_{{{\varvec{T}}_{{\varvec{k}}} }} \left( {\varvec{t}} \right)\))
The top end of body-(2k) is the spherical ball of SJ-(k), shown in Figs. 1 and 7. SJ-(k) ball frame is defined at the center Tk of the spherical ball. The axial distance of the center Tk from C(2k) is \(\hat{l}_{{T_{k} }}^{{\left( {2k} \right)}}\), as shown in Fig. 7. Therefore, SJ-(k) ball frame at Tk on body-(2k) is obtained by parallel translating body-(2k) frame to Tk by \(e_{3} \hat{l}_{{{\text{SJ}}}}^{{\left( {2k} \right)}}\) without any rotation:
3.2.6 SJ-(k) Socket frame at Tk on body-(13) along path (ii)
To conclude path (ii) the spherical ball must be fit into SJ-(k) socket at Tk on body-(13). This fitting is accomplished at Tk by rotating SJ-(k) ball frame to SJ-(k) socket frame at Tk on body-(13). The rotation is expressed by \(R_{{T_{k} {\text{SJ}}}}^{{\left( {{\text{SJ }}13/2k} \right)}} \left( t \right)\).
Combining Eqs. (6a) and (6b), SJ-(k) socket frame at Tk on body-(13) is expressed relatively with respect to body-(2k) frame as:
where the frame connection matrix \(E_{{T_{k} }}^{{({\text{SJ }}13/2k)}} \left( t \right)\) is computed as:
Finally, SJ-(k) socket frame is expressed with respect to body-(0) frame using the frame connection matrix \(\left( {E_{{T_{k} }}^{{({\text{SJ}} 13/0)}} \left( t \right)} \right)_{{path \left( {ii} \right)}}\) as:
where the components of the frame connection matrix are defined as Eq. (7b) for path (i):
and the components are obtained from Eqs. (14a), (15a) and (18a) as:
The above multiplications with Eqs. (14c) and (14d) yield:
where \(l^{\left( k \right)} \left( t \right)\) denotes the total length of leg-(k):
This completes the definition of frame connections along path (ii).
3.3 Loop closure constraints
The loop closure constraints are now expressed with respect to body-(0) frame by equating Eqs. (8a) and (8b) to Eqs. (9a) and (9b):
in components
Their components with respect to \({\varvec{e}}^{\left( 0 \right)} \left( t \right)\) are expressed using Eqs. (7d), (7e), (19d) and (19e) as:
The above constraints, expressed in configuration space, are classified as holonomic constraints [23]. As a result, the configuration is updated at each time by integrating the constraints on velocities starting from an initial configuration. The corresponding constraints on velocities will be computed in the next section.
In Appendix A, to facilitate design tools for determining dimensions of the platform both inverse and forward kinematics problems are solved analytically utilizing the loop closure equations. In the inverse kinematics problem, for a specified top-plate configuration: \({R}^{\left(13/0\right)}\) and \({s}_{C}^{\left(13/0\right)}\) one finds each leg configuration, \({\phi }_{1}^{\left(k\right)}\), \({\phi }_{2}^{\left(k\right)}\), \({l}^{\left(k\right)}\) and \({R}_{{T}_{k}\mathrm{SJ}}^{(\mathrm{SJ }13/\mathrm{SJ }2k)}\). The analytical equations for the inverse kinematics problem are utilized to find: (i) necessary stroke of the actuated translational joints (ATJs) and (ii) workspace, which shows the accessible top-plate configuration relative to the base plate.
4 Velocities of the moving frames
In this section velocities of the moving coordinate frames are computed. The input velocities of the base plate of the platform are measured at each time. Therefore, it is useful to express the loop closure constraints in velocities. In addition, for the computation of kinetic energy in the part II-paper, translational and angular velocities will be computed at each center of mass of constituent bodies. The kinematically admissible velocities are used to update the configuration at each time by integration since the loop closure constrains are holonomic as shown in Eqs. (20b) and (20c).
4.1 Velocities of the moving frames along path (i)
4.1.1 Body-(0) frame velocity: ( \(\dot{\user2{e}}^{\left( 0 \right)} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{\varvec{C}}}^{\left( 0 \right)} \left( {\varvec{t}} \right)\) )
The velocity of the origin of body-(0) frame, \({\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right)\), is obtained by taking the time derivative of Eq. (1a) expressing time differentiation with superposed dots:
in which \({\mathbf{e}}^{I}\) is independent of time.
The attitude of body-(0) frame changes with time. Its velocity is obtained by taking the time derivative of Eq. (2a) and expressing the result by its own basis, \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\), using Eq. (2d):
where \({\mathop{\omega^{\left( 0 \right)} \left( t \right)}\limits^{\longleftrightarrow}}\) is referred to as the skew symmetric angular velocity matrix [7b, 7c]:
which is a member the Lie algebra so(3) of SO(3).
The skew-symmetry of \({\mathop{\omega^{\left( 0 \right)} \left( t \right)}\limits^{\longleftrightarrow}}\) is easily proven by taking the time derivative of \(\left( {R^{\left( 0 \right)} \left( t \right)} \right)^{T} R^{\left( 0 \right)} \left( t \right)\) = I3. In Eq. (22a), expressing \({\dot{\mathbf{e}}}^{\left( 0 \right)} \left( t \right)\) with respect to its own basis, \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\), is consistent with the definition of Lie algebra so(3): the velocity \(\dot{R}^{\left( 0 \right)} \left( t \right)\) at \(R^{\left( 0 \right)} \left( t \right)\) is left translated by \(\left( {R^{\left( 0 \right)} \left( t \right)} \right)^{ - 1} = \left( {R^{\left( 0 \right)} \left( t \right)} \right)^{T}\) to the identity I3 where the Lie algebra is defined, see for example [23].
From the elements of \({\mathop{\omega^{\left( 0 \right)} \left( t \right)}\limits^{\longleftrightarrow}}\) the angular velocity vector \({{\varvec{\upomega}}}^{\left( 0 \right)} \left( t \right)\) is defined as:
For the computation of kinetic energy in the part II-paper, it is convenient to express the velocity of body-(0) frame as:
since the rotational kinetic energy is expressed by \(\omega^{\left( 0 \right)} \left( t \right)\) and mass moment of inertia with respect to \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\), while the translational kinetic energy is expressed by \(\dot{x}_{C}^{\left( 0 \right)} \left( t \right)\) with \({\mathbf{e}}^{I}\) [20, 21].
The translational velocity \(\dot{x}_{C}^{\left( 0 \right)} \left( t \right)\) is used to update \(x_{C}^{\left( 0 \right)} \left( t \right)\) using available integration schemes for vectors. However, the updating of rotation matrix \(R^{\left( 0 \right)} \left( t \right)\), using given \({\mathop{\omega^{\left( 0 \right)} \left( t \right)}\limits^{\longleftrightarrow}}\) in Eq. (22b) at each time increment, requires an appropriate integration algorithm, such as Rodrigues’ rotation formula [22], which assures that the updated rotation matrix remains in SO(3) [20, 28].
4.1.2 Body-(13) frame velocity: ( \({\dot{\mathbf{e}}}^{{\left( {13} \right)}} \left( {\mathbf{t}} \right)\) \({\dot{\mathbf{r}}}_{{\mathbf{C}}}^{{\left( {13} \right)}} \left( {\mathbf{t}} \right)\) )
The time derivative of Eq. (4a) expanded using Eq. (4b) yields the skew-symmetric angular-velocity matrix and the translational velocity at the center of mass of body-(13):
To familiarize readers with the computations, the steps for taking time derivative of the first column of Eq. (7a): \({\mathbf{e}}^{{\left( {13} \right)}} \left( t \right) = {\mathbf{e}}^{\left( 0 \right)} \left( t \right)R^{{\left( {13/0} \right)}} \left( t \right)\) are shown:
In the last right-hand side of Eq. (26a) in a pair of braces, the following formula is used to obtain the first term:
for \(R\left( t \right) = R^{(13/0)} \left( t \right)\) and \(\omega \left( t \right) = \omega^{\left( 0 \right)} \left( t \right)\), whose proof, presented in [20], is reproduced in Appendix B.
In the pair of braces the second term defines the relative skew-symmetric angular-velocity matrix:
In vector form the first column of Eqs. (25) and (26a) are written as:
The time derivative of the second column of Eq. (4a): \({\mathbf{r}}_{C}^{{\left( {13} \right)}} \left( t \right) = {\mathbf{r}}_{C}^{\left( 0 \right)} \left( t \right) + {\mathbf{e}}^{\left( 0 \right)} \left( t \right)R^{{\left( {13/0} \right)}} \left( t \right)\) is computed as:
where on the right-hand side in a pair of braces, the first term is obtained by using the formula:
which corresponds to the vector cross product: \({\varvec{\omega}}^{\left( 0 \right)} \left( t \right) \times {\mathbf{s}}_{C}^{(13/0)} \left( t \right) = - {\mathbf{s}}_{C}^{(13/0)} \left( t \right) \times {\varvec{\omega}}^{\left( 0 \right)} \left( t \right)\) (observing that both vectors are defined with respect to the body-(0) vector basis, \({\mathbf{e}}^{\left( 0 \right)} \left( t \right)\)).
Equation (28a) yields the translational velocity of C(13) with respect to \({\mathbf{e}}^{I}\):
In Eqs. (27) and (29), the velocities of the top-plate frame are expressed in terms of the excitation velocities, \(\omega^{\left( 0 \right)} \left( t \right)\) and \(\dot{x}_{C}^{\left( 0 \right)} \left( t \right)\), of the base plate and the relative velocities, \(\omega^{{\left( {13/0} \right)}} \left( t \right)\) and \(\dot{s}_{C}^{{\left( {13/0} \right)}} \left( t \right)\) of the top plate.
Next frame is the terminal frame of path (i).
4.1.3 SJ-(k) Socket frame velocities at Tk on body-(13): (\(\dot{\user2{e}}_{{{\varvec{T}}_{{\varvec{k}}} }}^{{\left( {\user2{SJ }13} \right)}} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{{\varvec{T}}_{{\varvec{k}}} }} \left( {\varvec{t}} \right)\))path(i)
To compute the velocity of SJ-(k) socket frame at Tk on body-(13):
the time derivative of Eq. (6a) is computed to utilize the body-(13) frame velocities just computed in Eqs. (9b) and (10a). The time derivative of the first column of Eq. (6a) is:
using the formula in Eq. (69).
In vector form, the first column of Eqs. (75) and (76) gives
Substituting Eq. (27) into Eq. (31b), one obtains
The time derivative of the second column of Eq. (6a) is computed as:
Using \(R^{{\left( {13} \right)}} \left( t \right) = R^{\left( 0 \right)} \left( t \right)R^{(13/0)}\), Eq. (33a) yields in components:
The substitution of Eqs. (27) and (29) into Eq. (33b) gives the velocity at \(T_{k}\) of SJ-(k) along path (i)
The velocity of SJ-(k) socket frame at \(T_{k}\) on body-(13) is now expressed by Eqs. (30), (33b) and (34).
4.1.4 Body-(14) frame velocity: (\(\dot{\user2{e}}^{{\left( {14} \right)}} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{\varvec{C}}}^{{\left( {14} \right)}} \left( {\varvec{t}} \right)\))
The velocities of body-(14) frame is computed by taking the time derivative of Eq. (8a):
The angular velocities and the translational velocities are easily obtained as:
Equations (35b) and (35c) are typical recursive equations along the graph tree and further expressed using Eqs. (27) and (29) as:
4.2 Velocities of the moving frames along path (ii)
Along path (ii) shown in Fig. 2b the velocities of body-(2k-1) frame of the lower leg and body-(2k) frame of the upper leg at their origins as well as those of SJ-(k) socket frame at \(T_{k}\) on body-(13) are computed.
4.2.1 Body-(2k-1) frame velocity: (\(\dot{\user2{e}}^{{\left( {2{\varvec{k}} - 1} \right)}} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{\varvec{C}}}^{{\left( {2{\varvec{k}} - 1} \right)}} \left( {\varvec{t}} \right)\))
The frame velocities of the lower leg, body-(2k-1):
are computed by taking the time derivatives of each column of Eq. (14a) using Eqs. (14b) and (14c).
The first column of Eq. (14a) is
and the second column:
where \(R^{(2k - 1/0)} \left( t \right)\) was defined in Eq. (14c).
The time derivative of Eq. (38a) yields using Eqs. (26a) and (26b):
where the relative skew-symmetric angular velocity matrix is defined as:
Its actual computation using Eq. (14c) gives
incorporating
in which \(e_{1} \equiv \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right)^{T}\) and \(e_{2} \equiv \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right)^{T}\).
In vector form, Eqs. (39a) and (39c) become, respectively,
The substitution of Eq. (40b) into Eq. (40a) gives in vector form:
Using Eq. (39b), the time derivative of Eq. (38b) yields
The velocity of C(2k−1) with \({\mathbf{e}}^{I}\) is obtained using Eqs. (2a), (22a) and (28b) as:
where
Equations (40c) and (41b) with Eq. (40b) express the velocity components of body-(2k-1) frame in Eq. (37).
4.2.2 Body-(2k) frame velocity: (\(\dot{\user2{e}}^{{\left( {2{\varvec{k}}} \right)}} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{\varvec{C}}}^{{\left( {2{\varvec{k}}} \right)}} \left( {\varvec{t}} \right)\))
The velocities of body-(2k) frame at C(2k) are computed from Eq. (15a) as:
The time derivative of the first column of Eq. (15a) yields in vector form:
while that of the second column yields, observing that in Eq. (15d) only \(d^{\left( k \right)} \left( t \right)\) is time dependent:
4.2.3 SJ-(k) Socket frame velocities at Tk on body-(13): (\(\dot{\user2{e}}_{{{\varvec{T}}_{{\varvec{k}}} }}^{{\left( {\user2{SJ }13} \right)}} \left( {\varvec{t}} \right)\) \(\dot{\user2{r}}_{{{\varvec{T}}_{{\varvec{k}}} }} \left( {\varvec{t}} \right)\))path(ii)
To compute the velocity of SJ-(k) socket frame at Tk on body-(13):
the time derivatives of the columns of Eq. (18a) are computed.
The time derivative of the first column gives in vector form:
where
The time derivative of the second column gives
To write closure equations, it is necessary to express the velocities of path (ii) in terms of \(\omega^{\left( 0 \right)} \left( t \right)\), \(\dot{\phi }_{1}^{\left( k \right)} \left( t \right)\), \(\dot{\phi }_{2}^{\left( k \right)} \left( t \right)\), and \(\omega_{{T_{k} {\text{SJ}}}}^{{\left( {{\text{SJ }}13/{\text{SJ }}2k} \right)}} \left( t \right)\). Thus Eq. (43b) is rewritten using Eqs. (42b) and (40c) as:
Similarly, Eq. (43d) is rewritten using Eqs. (42b), (42c), (41c), and (40c) as:
4.3 Loop closure constrains on velocities
The loop closure constraints on velocities in Fig. 2b are:
Equation (45a) is explicitly written using Eqs. (32) and (43b) as:
Similarly, Eq. (45b) is written explicitly using Eqs. (34) and (43d). After a slight simplification, it becomes
where
To simplify the subsequent presentation, the approximation \(\phi_{3}^{(2k/2k - 1)} \left( 0 \right) = 0\) is incorporated. \(\phi_{3}^{(2k/2k - 1)} \left( t \right)\), defined in Eqs. (15b) and (15c), expresses the axial rotation of the upper leg, body-(2k), relative to the lower leg, body-(2k-1) with initial value of: \(\phi_{3}^{(2k/2k - 1)} \left( t \right) = 0\). In the part II-paper, it will be shown that \(\phi_{3}^{(2k/2k - 1)} \left( t \right)\) remains zero since its axial moment of inertia is negligible and there is no external torque but some viscous damping. (For an example of the modeling of rotation of a rigid body subjected to perturbation and restoring torques, see [29].) With this hindsight \(\dot{\phi }_{3}^{(2k/2k - 1)} \left( t \right)\) is neglected in Eq. (46a). The resulting equation gives the angular velocity at the spherical joint, SJ-(k), as:
4.4 Equations for inverse instantaneous kinematics
For kinematics-based control, Eq. (46a) deserves careful interpretations. At each time step for measured input disturbance: \(\omega^{\left( 0 \right)} \left( t \right)\) and \(\dot{x}^{\left( 0 \right)} \left( t \right)\) of the base plate, to counter-measure the motion of the base plate, the desired values of the top-plate velocities: \(\omega^{{\left( {13/0} \right)}} \left( t \right)\) and \(\dot{s}_{C}^{{\left( {13/0} \right)}} \left( t \right)\) are computed. This task is accomplished by controlling the actuated translational joint velocities:\( \dot{d}^{\left( k \right)} \left( t \right)\) for inverse kinematics control (IKC) for \(k = 1, 2, \cdots , 6\). The actuation of the leg also induces the universal joint motion: \(\dot{\phi }_{1}^{\left( k \right)} \left( t \right)\), and \(\dot{\phi }_{2}^{\left( k \right)} \left( t \right)\).
For the instantaneous inverse kinematics control [24], Eq. (46b) is solved analytically for those velocities, stored in a 3 × 1 column matrix, \(\dot{q}_{L}^{\left( k \right)} \left( t \right)\):
where the left-hand side of Eq. (46b) is expressed by \(w^{vel} \left( t \right)\) as:
and
In Eq. (38a), one notes that \(l^{\left( k \right)} \left( t \right) \ne 0\) and \(\phi_{2}^{\left( k \right)} \left( t \right) \ne \pm \pi /2\) due to the leg constraints, discussed in Appendix A.
5 Experimental results
Experiments were performed on a scale model Stewart platform mounted on a motion generator to assess an inverse kinematics controller (IKC). The details of the apparatus are explained in Fig. 4 of the part II-paper, in which the performance of IKC is compared with that of an inverse-dynamics controller (IDC). Figure 8 illustrates a flowchart of IKC utilizing the inverse kinematics to feedforward the desired actuator displacements and proportional-integral-derivative (PID) for feedback control.
In Fig. 8, the desired relative top-plate translational vector \(s_{C*d*}^{{\left( {13/0} \right)}} \left( t \right)\) and rotation matrix \(R_{*d*}^{{\left( {13/0} \right)}} \left( t \right)\), and the corresponding velocities \(\left( {\dot{q}_{TP*d*} \left( t \right)} \right) \equiv \left( {\begin{array}{*{20}c} {\dot{s}_{C*d*}^{{\left( {13/0} \right)}} \left( t \right)} \quad \, {\omega_{*d*}^{{\left( {13/0} \right)}} \left( t \right)} \\ \end{array} } \right)^{T}\) with respect to the base-plate frame are computed from the desired top-plate translational vector \(x_{C*d*}^{{\left( {13} \right)}} \left( t \right)\) and rotation matrix \(R_{*d*}^{{\left( {13} \right)}} \left( t \right)\), and the corresponding velocities \(\left( {\dot{X}_{*d*}^{{\left( {13} \right)}} \left( t \right)} \right) \equiv \left( {\begin{array}{*{20}c} {\dot{x}_{C*d*}^{{\left( {13} \right)}} \left( t \right)} \quad \, {\omega_{*d*}^{{\left( {13} \right)}} \left( t \right)} \\ \end{array} } \right)^{T}\) for measured input base-plate velocities \(\left( {\dot{X}^{\left( 0 \right)} \left( t \right)} \right) \equiv \left( {\begin{array}{*{20}c} {\dot{x}_{C}^{\left( 0 \right)} \left( t \right)} \quad \, {\omega^{\left( 0 \right)} \left( t \right)} \\ \end{array} } \right)^{T}\) and the corresponding translational vector \(x_{C}^{\left( 0 \right)} \left( t \right)\) and rotation matrix \(R^{\left( 0 \right)} \left( t \right)\). From the inverse kinematics computation, desired velocities \(\dot{d}_{*d*}^{\left( k \right)} \left( t \right)\) and displacements \(d_{*d*}^{\left( k \right)} \left( t \right)\) of actuated translational joint are derived. Then, by employing a PID controller for each actuator, a control input: \(u_{ATJ}^{\left( k \right)} \left( t \right)\) is obtained from the errors, defined as the difference between the measured and the desired linear actuator velocities and extensions as:
where
and where \(K_{p}^{\left( k \right)}\), \(K_{i}^{\left( k \right)}\), and \(K_{d}^{\left( k \right)}\) are proportional, integral and derivative gains.
As a test case, a motion generator was used to move the bottom plate at a relatively low frequency to simulate the movement of a ship due to sea waves. Since the peak of the sea wave spectrum is around 0.1 Hz [30], three linear actuators changed their lengths at 0.02sin(2\(\pi f_{1} t\)) m, 0.02sin(\(2\pi f_{2} t\)) m, and 0.02sin(\(2{\pi} f_{3} t\)) m, respectively. These frequencies were \(f_{1}\) = 0.15 Hz, \(f_{2}\) = 0.1 Hz, and \(f_{3}\) = 0.05 Hz.
The control objective is to keep the top plate horizontal and stationary, against the motion of the base plate. The desired top-plate states are therefore set as: \(\dot{X}_{*d*}^{{\left( {13} \right)}} \left( t \right) = 0_{6 \times 1}\), \(x_{C*d*}^{{\left( {13} \right)}} \left( t \right) = e_{3} \hat{h}^{\left( 0 \right)}\), and \(R_{*d*}^{{\left( {13} \right)}} \left( t \right) = I_{3}\). For the PID controller, the gains are chosen by trial-and-error method. A time step of 0.01 s was selected as the minimum time-increment for the experimental system. The sequence of computations and signal transmission/reception was coded using MATLAB with Arduino microcontrollers.
The measured top-plate translational displacements \(x_{C}^{{\left( {13} \right)}} \left( t \right)\) and its rotation matrix are shown in Fig. 9a–f, where the rotation matrix is expressed by using Tait–Bryan angles \(\psi_{i}^{TB} \left( t \right), i = 1, 2, 3\) as: \(R^{{\left( {13} \right)}} \left( t \right) = R_{1}^{{\left( {13} \right)}} \left( {\psi_{1}^{TB} \left( t \right)} \right)R_{2}^{{\left( {13} \right)}} \left( {\psi_{2}^{TB} \left( t \right)} \right)R_{3}^{{\left( {13} \right)}} \left( {\psi_{3}^{TB} \left( t \right)} \right)\). The desired top-plate attitude: \(R_{*d*}^{{\left( {13} \right)}} = I_{3}\) is expressed by zero Tait–Bryan angles: \(\psi_{1*d*}^{TB} \left( t \right) = \psi_{2*d*}^{TB} \left( t \right) = \psi_{3*d*}^{TB} \left( t \right) = 0\). This angular representation of a rotation matrix was explained in Appendix A to plot admissible workspace. For \(R^{{\left( {13} \right)}} \left( t \right)\) the corresponding Tait–Bryan angles \(\psi_{i}^{TB} \left( t \right), i = 1, 2, 3\) are computed by using Eq. (A14) applied to \(R^{{\left( {13} \right)}} \left( t \right)\) instead of \(R^{{\left( {13/0} \right)}}\)(t). (These angles are not used in the inverse kinematics computations for control but merely adopted to show \(R_{{}}^{{\left( {13} \right)}} \left( t \right)\) using three angular coordinates.)
Experimental results of a displacement in the \(x_{1}\)-direction, b displacement in the \(x_{2}\)-direction, c displacement in the \(x_{3}\)-direction, d Tait–Bryan angle \(\psi_{1}^{TB} \left( t \right)\), e Tait–Bryan angle \(\psi_{2}^{TB} \left( t \right)\), and f Tait–Bryan angle \(\psi_{3}^{TB} \left( t \right)\) of the base plate and controlled top plate
To quantitatively assess the controller performance, in Table 1, root mean square error (RMSE) and mean absolute error (MAE) of the translational displacements and Tait–Bryan angles of the top plate are shown as well as the rates of compensation against the motion of the base plate. It is observed from Figs. 9 and Table 1 that the base plate motion is successfully compensated in each component. In the part II-paper the results of IKC is compared with those of inverse dynamics control (IDC).
6 Concluding remarks
In this paper for a base-moving Stewart platform, utilizing body- and joint-attached, orthonormal coordinate frames, the configuration space is mathematically defined employing 4 × 4 frame connection matrices of the special Euclidian group, SE(3), which combines both SO(3) and \({\mathbb{R}}^{3}\). Configurational loop closure constraints are presented for a representative closed loop and solved analytically for both inverse and forward kinematics (see Appendix A). Next, velocities of each moving coordinate frames are computed. In the computations, to be consistent with the Lie algebra so(3) of SO(3), skew-symmetric angular velocity matrices are defined first from the flow of rotation matrices with time, from which angular velocity vectors in \({\mathbb{R}}^{3}\) are defined. Using body-attached moving frames whose connections are rigorously expressed by frame connection matrices, readers can systematically and unambiguously compute frame velocities (since vector bases of moving frames are explicitly shown).
Finally, to evaluate the performance of an inverse kinematic controller, experimental tests are presented on a scale model of the system. Further, in Appendix A, workspace analysis is presented for preliminary design of a Stewart platform. In the part II-paper, utilizing the velocities of body-attached coordinate frames, analytical equations of motion are derived, and their control applications are presented.
Change history
14 March 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11071-022-07320-x
References
Stewart, D.: A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 180(1–15), 371–385 (1965)
Fichter, E.F.: A Stewart platform based manipulator: general theory and practical construction. Int. J. Robot. Res. 5(2), 157–181 (1986)
Lebret, G., Liu, K., Lewis, F.L.: Dynamic analysis and control of a Stewart platform manipulator. J. Field Robot. 10(5), 629–655 (1993)
Dasgupta, B., Mruthyunjaya, T.: A Newton-Euler formulation for the inverse dynamics of the stewart platform manipulator. Mech. Mach. Theory 33(8), 1135–1152 (1998)
Lee, S.-H., Song, J.-B., Choi, W.-C., Hong, D.: Position control of a stewart platform using inverse dynamics control with approximate dynamics. Mechatronics 13, 605–619 (2003)
Becerra-Vergus, M. and Belo, E.: Dynamic modeling of a six degree-of-freedom flight simulator motion base. J. Comput. Nonlinear Dyn., 10(5), paper 051020, 13 pages (2015).
Ophaswongse, C., Murray, R. C., and Agrawal, S. K.: Wrench capability of a Stewart platform with series elastic actuators. J. Mech. Robot., 10(2), paper 021002, 8pages (2018).
Slavutin, M., Sheffer, A., Shai, O. and Reich, Y.: A Complete geometric singular characterization of the 6/6 Stewart platform. J. Mech. Robot., 10(4), paper 041011, 10 pages (2018).
Miunske, T., Pradipta, J. and Sawodny, O.: model predictive motion cueing algorithm for an overdetermined Stewart platform. J. Dyn. Syst. Measur. Control, 141(2), paper 021006, 9 pages (2019).
Gosh, M. and Dasmahapatra, S.: Kinematic modeling of Stewart platform. In Dawn, S., Balas, V., Esposito, A., and Gope, S. (eds) Intelligent Techniques and Applications in Science and Technology ICIMSAT 2019. Learning and Analysis in Intelligent Systems 12, Springer, Cham (2020).
Amir, S.L., Mehdi, T.M., Ahmad, K.: Trajectory tracking control of a pneumatically actuated 6-DOF Gough-Stewart parallel robot using backstepping-sliding mode controller and geometry-based quasi forward kinematic method. Robot. Comput. Integr. Manuf. 54, 96–114 (2018)
Xiaolin, D., Shijie, S., Wenbo, X., Zhangchao, H., Dawei, G.: Modal space neural network compensation control for Gough-Stewart robot with uncertain load. Neurocomputing 449, 245–257 (2021)
Ahmadi, S.S., Rahmani, A.: Nonlinear model predictive control of a Stewart platform based on improved dynamic model. Int. J. Theor. Appl. Mech. 5, 18–26 (2020)
Hu, S., Jing, X.: A 6-DOF Passive Vibration Isolator Based on Stewart Structure with X-shaped Legs. Nonlinear Dyn. 91(1), 157–185 (2018)
Min, W., Yingyi, H., Y, S., Jiheng, D., Huayan, P., Shujin, Y., Jinglei, Z., Yan P., Shaorong, X., Jun, L.: An adjustable low-frequency vibration isolation Stewart platform based on electromagnetic negative stiffness. Int. J. Mech. Sci., 181, paper 105714, 10 pages (2020).
Campos, A., Quintero, J., Saltarén, R., Ferre, M., and Aracil, R.: An Active helideck testbed for floating structures based on a Stewart-Gough platform. 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS (2008).
Niwa, S., Tanaka, Y., Goto, H., and Nomiyama, N.: Active vibration compensation for Catwalk by hydraulic parallel mechanism. In: Proceedings of The 10th JFPS International Symposium on Fluid Power 2017 FUKUOKA, 2D22 (2017).
Arnold, V.I.: Mathematical Methods of Classical Mechanics, 2nd edn. Springer-Verlag, New York (1989)
Holm, D.D.: Geometric Mechanics: Part II: Rotating, Translating, Rolling. Imperial College Press, London, UK (2008)
Murakami, H.: A moving frame method for multi- body dynamics. In: Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, IMECE2013–62833: pp. V04AT04A079; 12 pages. San Diego, CA, November 15–21 (2013).
Murakami, H.: A moving frame method for multi-body dynamics using SE(3). In: Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, IMECE2015–51192: pp. V04BT04A003; 19 pages. Houston, Texas, November 13–19 (2015).
Wittenburg, J.: Dynamics of Multibody Systems, Second Edition, Springer, Berlin, ISBN 978–3–540–73913–5 (2008).
Frankel, T.: The Geometry of Physics: An Introduction, 3rd edn. Cambridge University Press, New York (2012)
Asada, H., and Slotine, J.J.- E.: Robot Analysis and Control, Wiley, New York (1986).
Ball, R. S.: A Treatise on the Theory of Screws, Cambridge University Press (1900).
Brockett, R. W.: Robot Manipulators and the Product of Exponentials Formula. In: P. A. Fuhrman, editor, Mathematical Theory of Networks and Systems, pp. 120–129, Springer (1984).
Murray, R.M., Li, Z., Sastry, S.S.: A Mathematical Introduction to Robotic Manipulation. CRC Press, Boca Raton, FL (1994)
Murakami, H., Rios, O., and Impelluso T. J.: A Theoretical and Numerical Study of the Dzhanibekov and Tennis Racket Phenomena. ASME J. Appl. Mech., 83(11): 111006 (10 pages) (2016).
Leshchenko, D., Ershkov, S., Kozachenko, T.: Evolution of a heavy rigid body rotation under the action of unsteady restoring and perturbation torques. Nonlinear Dyn. 103(5), 1517–1528 (2021). https://doi.org/10.1007/S11071-020-06195-0
Collins, C.O., III., Blomquist, B., Persson, O., Lund, B., Rogers, W.E., Thomson, J., Wang, D., Smith, M., Doble, M., Wadhams, P., Kohout, A., Fairall, C., Graber, H.C.: Doppler correction of wave frequency spectra measured by underway vessels. J. Atmos. Ocean. Tech. 3(2), 429–436 (2017)
Ershkov, S.V., Shamin, R.V.: The dynamics of asteroid rotation, governed by YORP effect: the kinematic Ansatz. Acta Astronaut. 149, 47–54 (2018)
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Kinematics for design and workspace analyses
A base-moving Stewart platform installed on a floor in a moving ship or vehicle is designed to maintain a set of desired position and attitude even if the base plate translates and rotates due to the motion of a moving vehicle. Therefore, the workspace of the platform is described by its reachable ranges of the relative position, \(s_{C}^{(13/0)} \left( t \right) \in {\mathbb{R}}^{3}\) (= three-dimensional vector space), and the relative rotation, \(R^{(13/0)} \left( t \right) \in SO\left( 3 \right)\), with respect to the base plate. They are components of the relative frame connection matrix \(E^{{\left( {13/0} \right)}} \left( t \right)\) in Eqs. (4a) and (4b). For the Stewart platform to function properly, it is necessary to maintain enough clearance between the top plate and the base plate during their relative motion to prevent the top plate from touching the base plate.
1.1 Inverse kinematics for leg design
The preliminary design begins with choosing the dimensions of the base plate and the top plate. For the base plate in Fig. 5, the radius of the mid-circle, \(\hat{r}_{m}^{\left( 0 \right)}\), the truncation angle, \(\Delta \hat{\theta }^{\left( 0 \right)}\), and for the top plate in Fig. 4, \(\hat{r}_{m}^{{\left( {13} \right)}}\) and \(\Delta \hat{\theta }^{{\left( {13} \right)}}\) must be determined. Here, the truncation angles are assumed to be equal: \(\Delta \hat{\theta } = \Delta \hat{\theta }^{\left( 0 \right)} = \Delta \hat{\theta }^{{\left( {13} \right)}}\), where \(\Delta \hat{\theta } < \pi\)/3. In addition, in the reference configuration shown in Fig. 1, the initial elevation \(\hat{h}^{\left( 0 \right)}\) of the top plate from the base, must be selected. From those values, the initial configuration of the platform including the leg lengths are computed utilizing the loop closure constraints in Eqs. (20d) and (20e).
Next design step is, for a specified service environment, to select a set of essential positions and attitudes of the top plate relative to the base plate under service environments, which are crucial for the top plate to maintain the desired configuration to mitigate the motion of the base plate. Each of the essential relative frame-connection matrices between body-(13) frame and body-(0) frame are identified by “*” as:
For a specified \(E^{*(13/0)}\), finding the corresponding leg length, \(l^{\left( k \right)}\), and the UJ rotation angles, \(\phi_{1}^{\left( k \right)}\) and \(\phi_{2}^{\left( k \right)}\) as well as the rotation at the SJ, \(R_{{T_{k} SJ}}^{{\left( {SJ13/2k} \right)}}\) for leg-(k), \(k = 1, 2, \cdots , 6\), define a problem of inverse kinematics. This can be analytically solved using the loop closure constraints, Eqs. (20d) and (20e), which are expressed with respect to body-(0) vector basis \({\varvec{e}}^{\left( 0 \right)} \left( t \right)\).
First, to determine \(l^{\left( k \right)}\), \(\phi_{1}^{\left( k \right)}\) and \(\phi_{2}^{\left( k \right)}\), Eq. (20e) is expressed with respect to
which was defined in Eq. (10a). The resulting equation has unknowns on the left-hand side and the known matrices on the right as:
After expanding the left-hand side using Eqs. (10d), (11b), (A2a) and (A2b) for leg-(k) becomes
where the 3 × 1 column matrix \(w^{*\left( k \right)}\) represents the known right-hand side of Eqs. (A2a) and (A2b):
Using Eq. (40a), the first term on the right-hand side of Eq. (A3b) is written in vector form as:
As a result, the third row of Eq. (A3b) becomes observing that \({\mathbf{e}}_{{3 B_{k} }}^{\left( 0 \right)} \left( t \right) = {\mathbf{e}}_{3}^{\left( 0 \right)} \left( t \right)\) as:
The first term on the right-hand side expresses the projection of the position relative vector \({\varvec{e}}^{{*\left( {13} \right)}} \left( t \right)\hat{s}_{{T_{k} }}^{{\left( {13} \right)}}\) of the center of the kth spherical joint, SJ-(k), onto the unit normal vector \({\varvec{e}}_{3}^{\left( 0 \right)} \left( t \right)\) of the base plate, body-(0).
In (128), the minimum of \(w_{3}^{*\left( k \right)}\) for \(k = 1, \cdots , 6\) expresses the clearance between the top plate and the base plate, which must be positive to prevent the top-plate touching the base plate during their relative motion. Therefore, in what follows it is assumed that \(w_{3}^{*\left( k \right)} > 0\).
Equation (A3a) is solved analytically to give the inverse kinematics equations:
For each essential relative frame-connection matrix, \(E^{*(13/0)}\), of the top plate, for leg-(k), \(k = 1, 2, \cdots , 6\), one finds the maximum leg length \(l_{max}\), the minimum length \(l_{min}\) and maximum absolute values of \(\phi_{1}^{\left( k \right)}\) and \(\phi_{2}^{\left( k \right)}\), written as \(\left| {\phi_{1} } \right|_{max}\) and \(\left| {\phi_{2} } \right|_{max}\), respectively. From those values computed for selected, essential frame connection-matrices, one finds the design values: \(l_{max}^{*}\), \(l_{\min }^{*}\), \(\left| {\phi_{1}^{*} } \right|_{max}\) and \(\left| {\phi_{2}^{*} } \right|_{max}\). The necessary stroke of the actuated translational joint (ATJ) is defined as \(l_{max}^{*} - l_{min}^{*} .\)
Second, the relative rotation at each spherical joint is computed from Eq. (20c) incorporating \(\phi_{3}^{(2k/2k - 1)} = 0\) as:
Equations (A4) and (A5) with Eq. (A3b) are the analytical equations for inverse kinematics.
1.2 Initial leg configurations
The initial values of \(l^{\left( k \right)} \left( 0 \right), \phi_{1}^{\left( k \right)} \left( 0 \right)\), \(\phi_{2}^{\left( k \right)} \left( 0 \right)\) and \(R_{{T_{k} {\text{SJ}}}}^{{\left( {SJ13/2k} \right)}} \left( 0 \right)\) are required for all legs to define the initial configuration of the platform with an initial relative elevation, \(\hat{h}^{\left( 0 \right)}\), between the top and the base plates. Equations (A3a)–(A3d) and (A4) are written for t = 0 using \(R^{(13/0)} \left( 0 \right) = I_{3}\) and \(s_{C}^{{\left( {13/0} \right)}} \left( 0 \right) = e_{3} \hat{h}^{\left( 0 \right)}\). The resulting initial values are
where
whose components are computed explicitly using Eqs. (5b), (9b) and (10b) as:
Since \(w_{3}^{\left( k \right)} \left( 0 \right) = \hat{h}^{\left( 0 \right)} - \hat{h}_{SJ}^{{\left( {13} \right)}} - \hat{h}_{UJ}^{\left( 0 \right)} > 0\)., the substitution of Eq. (A6c) into Eq. (A6a) yields the following initial values:
Equations (A7a)–(A7c) indicate that initial leg lengths, \(l^{\left( k \right)} \left( 0 \right) \ne 0\), and the leg rotation angles of the cross axis pivoted by the leg yokes, \(\phi_{2}^{\left( k \right)} \left( 0 \right)\), are the same for all legs, while the rotation angles of the cross axis journaled to the base yoke, \(\phi_{1}^{\left( k \right)} \left( 0 \right)\), are alternating. These initial values are consistent with the reference configuration, shown in Fig. 1.
The initial relative rotation at each spherical joint is obtained from Eq. (A5) as:
Next, the equations for forward kinematics are presented.
1.3 Forward kinematics
In the forward kinematics, for a given “compatible set” of six leg configurations one finds a top-plate configuration relative to a base-plate configuration, i.e., \(R^{{\left( {13/0} \right)}}\) and \(s_{C}^{{\left( {13/0} \right)}}\). A compatible set of leg configurations indicates that they are consistent with the loop closure constraints. As a result, only leg-(1) configuration suffices to determine the top plate configuration. Let \(l^{\left( 1 \right)} , \phi_{1}^{\left( 1 \right)}\), \(\phi_{2}^{\left( 1 \right)}\) and \(R_{{T_{1} {\text{SJ}}}}^{{\left( {SJ13/2} \right)}}\) be prescribed. Then Eqs. (20d) and (20e) for k = 1, with the approximation of \(\phi_{3}^{{\left( {2k/2k - 1} \right)}} = 0, \) can be used to find \(R^{{\left( {13/0} \right)}}\) and \(s_{C}^{{\left( {13/0} \right)}}\) as:
The remaining task is to determine the compatible configurations for leg-(2), \(\cdots\), leg-(6). Equation (20e) with Eq. (A9b) gives
Equation (A10) takes the same form as Eq. (A3a) by expressing the known right-hand side of Eq. (A10) as \(w^{*}\). Then \(l^{\left( k \right)} , \phi_{1}^{\left( k \right)}\) and \(\phi_{2}^{\left( k \right)}\) are obtained as shown in Eq. (A4). The remaining \(R_{{T_{1} {\text{SJ}}}}^{{\left( {SJ13/2k} \right)}}\) can be easily computed from Eq. (20d).
1.4 Workspace of the Stewart platform
The workspace of the platform in Fig. 3 is a set of accessible configurations of the top plate relative to that of the base plate, which are expressed by the accessible frame-connection matrices, \(E^{(13/0)} \in SE\left( 3 \right)\) in Eqs. (4a), (4b). \(E^{(13/0)}\) may be interpreted as follows: \(R^{(13/0)} \in SO\left( 3 \right)\) is attached to each accessible \(s_{C}^{(13/0)} \in {\mathbb{R}}^{3}\) to show its accessible rotation. Therefore, the workspace \(W^{*}\) is expressed by the frame connection matrix \(E^{(13/0)}\) whose components satisfy Eq. (20e) as well as the leg constraints:
Although \(R^{(13/0)}\) has nine components, the columns express the components of three orthonormal coordinate vectors, as Eq. (4a) shows. This orthonormality of the columns yields six constraints. As a result, \(R^{(13/0)}\) is expressed “locally” by three angular coordinates, such as Euler angles and Tait–Bryan angles, explained in [22], as well as recently proposed wisdom angles [31].
Euler angles represent the rotation as a sequence of elementary rotations with the body-attached \(s_{3}\)-axis by \(\theta^{E}\), the \(s_{1}\)-axis by \(\phi^{E}\), and the \(s_{3}\)-axis by \(\psi^{E}\) as:
Euler angles fail to represent the rotation matrix at its critical point: \(\sin \phi^{E} = 0\), i.e.,\( \phi^{E} = 0\), where the inverse of Eq. (A12) does not exist, i.e., homeomorphism is lost. Since the critical point of Euler angles corresponds to the reference configuration where the top plate and the base plate are parallel to each other, Euler angels are not qualified to express \(R^{(13/0)}\). (It is noted here that the critical attitude is changed by adopting a difference cyclic order of the Euler angle representation, such as the rotations about the axes 2-3-2 and 1-2-1.)
Tait–Bryan angles \(\left( {\begin{array}{*{20}c} {\psi_{1}^{TB} } & {\psi_{2}^{TB} } & {\psi_{3}^{TB} } \\ \end{array} } \right)^{T}\) express each rotation as a sequence of elementary rotations:
which has critical points at \(\cos \psi_{2}^{TB} = 0\), i.e., \(\psi_{2}^{TB} = \pm \pi /2\). This critical point represents the configuration where the top plate becomes vertical to the base plate, which does not happen due the constraints on leg length in Eqs. (A4) and (A11). Therefore, Tait–Bryan angles are adopted to represents \(R^{{\left( {13/0} \right)}}\) for the platform.
The inverse relation to Eq. (A13) away from the critical points is
Using Tait–Bryan angles for the coordinates of \(R^{{\left( {13/0} \right)}}\) and \(\left( {\begin{array}{*{20}c} {s_{1C}^{(13/0)} } & {s_{2C}^{(13/0)} } & {s_{3C}^{{\left( {13/0} \right)}} } \\ \end{array} } \right)^{T}\) for the coordinates of \(s_{C}^{{\left( {13/0} \right)}}\), the workspace \(W^{*}\) of the platform is expressed by the six coordinates:
with the constraints, Eq. (A11). (Although Tait–Bryan angles \(\left( {\begin{array}{*{20}c} {\psi_{1}^{TB} } & {\psi_{2}^{TB} } & {\psi_{3}^{TB} } \\ \end{array} } \right)^{T}\) are expressed in a column matrix it is important to observe that they are not a vector.)
Recognizing the limitations of using three-dimensional plots to express the six-dimensional workspace, plots are only created for limited rotations with \({\varvec{e}}_{1}^{\left( 0 \right)}\), i.e., \(\psi_{2}^{TB} = \psi_{3}^{TB} = 0\) for the Stewart platform whose design values are listed in Table
2. The initial leg configurations are defined as follows: \(\phi_{1}^{\left( 1 \right)} \left( 0 \right) = \phi_{1}^{\left( 3 \right)} \left( 0 \right) = \phi_{1}^{\left( 5 \right)} \left( 0 \right) = - 13.1^\circ\), \(\phi_{1}^{\left( 2 \right)} \left( 0 \right) = \phi_{1}^{\left( 4 \right)} \left( 0 \right) = \phi_{1}^{\left( 6 \right)} \left( 0 \right) = 13.1^\circ\), \(\phi_{2}^{\left( k \right)} \left( 0 \right) = 14.1^\circ\) and \(d^{\left( k \right)} \left( 0 \right) = 0.05\) m for \(k = 1, 2, \cdots ,6\).
Figures 10a-c illustrate the plots of accessible \(s_{C}^{{\left( {13/0} \right)}}\) for \(\psi_{1}^{TB} = 0^\circ\), \(\psi_{1}^{TB} = 10^\circ\), and \(\psi_{1}^{TB} = 20^\circ\), respectively, for \(\psi_{2}^{TB} = \psi_{3}^{TB} = 0^\circ\). These figures help users confirm that the selected essential configurations of the top table, adopted for the initial design, are indeed accessible.
In computations, it is necessary to keep a desired top-plate configuration within the workspace. It is observed and analytically confirmed that the boundary of workspace has cusps where a different actuator begins to be actuated. To keep the top-plate configuration within the workspace, two computational methods are available: (i) radial return and (ii) normal return. In this paper, the radial return method is adopted since the normal return method experiences difficulties in computing normal directions near the cusps on the boundary. In the radial method if a trial desired top-plate configuration goes outside the workspace, the corrected compromised state is proportionally pulled back to the origin to return to the inside of the workspace, while staying as close as possible near the boundary.
Appendix B: Proof of Eq. (26b)
Equation (26b) in three dimensions is derived by utilizing the following three equations, which are expressed by adopting the summation convention for repeated indices from 1 to 3.
The first equation is the definition of the skew-symmetric angular velocity matrix:
where \(\in_{m n k}\) denotes the permutation symbol. Its value is one if the sequence (m, n, k) is an even permutation of (1, 2, 3), such as (2, 3, 1), (3, 1, 2); the value is \(- 1\) if the sequence is an odd permutation of (1, 2, 3), such as (2, 1, 3), (1, 3, 2), (3, 2, 1); and the value is zero for other cases, such as (1, 2, 2), (2, 3, 2), (1, 1, 1).
The second equation is the definition of rotation matrices, \(R R^{T} = I_{3}\), written in indicial form as:
where the Kronecker delta: \(\delta_{kp} = 1\) if \(k = p\) and \(\delta_{kp} = 0\) if \(k \ne p\).
The third equation is the definition of matrix determinant for a right-handed rotation matrix, whose determinant is one: \(\det R = 1\):
The \(\left( {i, j} \right)\) -element of the left-hand side of Eq. (26b) becomes, using Eqs. (B1)–(B3) in this order:
As a result, Eq. (26b) is proven for element \(\left( {i, j} \right)\):
For the readers who are familiar with the Lie group theory, the left-hand side of Eq. (26b) define the adjoint representation of \(R^{T} \in SO\left( 3 \right)\), written as \(Ad\left( {R^{T} } \right)\), which linearly transforms \(\overleftrightarrow {\mathop{\omega }} \in so\left( 3 \right)\) into another skew symmetric matrix in so(3) [23]. Identifying the components of skew symmetric matrices as vector components in \({\mathbb{R}}^{3} \) as shown in Eqs. (22b) and (23), Eq. (B5) states that for \(\omega \in {\mathbb{R}}^{3}\), \(Ad\left( {R^{T} } \right)\) becomes \(R^{T}\) in \({\mathbb{R}}^{3}\):
.
Readers are encouraged to learn a neat derivation of Eq. (26b) by Holm [7a], where Holm’s \(\widehat{\left( \right)}\)-operation is our \({\mathop {\left( \right)}\limits^{\longleftrightarrow}}\)-operation.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ono, T., Eto, R., Yamakawa, J. et al. Analysis and control of a Stewart platform as base motion compensators - Part I: Kinematics using moving frames. Nonlinear Dyn 107, 51–76 (2022). https://doi.org/10.1007/s11071-021-06767-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06767-8