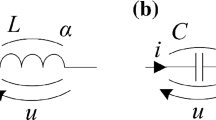Ferromagnetic core coil hysteresis modeling using fractional derivatives

Abstract

The modeling of a ferromagnetic core coil magnetic hysteresis has been considered. The measurement basis consisted of waveforms that have been recorded for various levels of the iron core saturation levels. The investigated models included classical cases as well as models including a nonlinear fractional coil. The possibilities of solutions for transient problems including such models have been recalled. The details of the estimation process have been described next, where each model evaluation made use of an original methodology dealing with periodic steady states. The influence of the model response on parameter changes has also been studied. Further on the parameter estimation procedure has been described, and the results for the various models have been presented.

1 Introduction

1.1 Ferromagnetic core coil modeling

The modeling of distinct circuit elements is important due to the need for simulations of real phenomena of electrical engineering in power systems and electronic circuits. This, in no small part, is due to the need of foresight of the events that can occur in a studied system.

An element category, which is challenging when it comes to modeling, comprises of iron-core coils and transformers. This is largely caused by the need to reflect magnetic hystereses, which is especially difficult during transient states or nonsinusoidal responses with a significant contribution of higher harmonics.

The subject of accurate modeling of the more difficult cases of attempts to resemble magnetic hystereses is still an open topic [1, 2]. Some of the most popular models are: the Jiles–Atherton model [3], the Preisach model [4] and the Chua model [5]. Over the years, there have been many propositions to modify these models in order to reflect the results of measurements made on iron-core coils more accurately [6, 7]. Unfortunately, the application of a significant number of models yields at least one of the following problems:

• a complex description, which leads to difficulties in implementations [8]; also—adaptability becomes a problem, e.g., when one wants to include the model in computations in a selected computational environment (e.g., in Matlab [9], Octave [10]),

• a large number of equations, which directly leads to longer computation times [11],

• the involvement of sophisticated functions, e.g., in models supporting anisotropy [12],

• problems in numerical stability, due to some nonlinearities difficult to handle for typical algorithms [13].

The paper is focused on the introduction of models, where the above listed problems do not appear.

Often models are built with the B–H relationship in mind, which is applicable in electromagnetic field analyses. This paper concerns another category applied in modeling, which is a circuit approach, from which one can reconstruct a $\psi$-i relationship. This approach is useful when considering an element as a whole (for practical uses), when characteristics of inductive devices (e.g., transformers, fluxgate sensors) are investigated, instead of considering the physical properties of a material [14]. Also, phenomenological models can be applied, where although artificial variables are introduced—the computations still yield voltage and current waveforms. The circuit element approach has an advantage that it can be directly confronted with measurements performed on the modeled element.

1.2 Application of fractional calculus

In the study—fractional derivatives have been applied. They are a part of the mathematical field of fractional calculus [15, 16], which includes definitions of both fractional derivatives and integrals.

Some important foundations as to the theoretical concepts of fractional calculus have been introduced in the nineteenth century [17,18,19,20]. However, the majority of interest around the field when practical applications are concerned have been noticed in recent years. Fractional calculus has been applied in studies devoted to:

• heat transfer process modeling [21,22,23,24,25],

• the study of biomedical signals [26, 27],

• analyses of control systems [28, 29], including several studies concerning the control of synchronous machines [30,31,32,33],

• electrical impedance spectroscopy [34,35,36]

• the design of fractional-order filters [37, 38]

• electric and magnetic field studies [39, 40],

• modeling of seismic mass transducers [41],

• continuum mechanics [42].

Most importantly fractional calculus has been applied with much success in problems associated with electrical engineering. In a significant amount, these are studies concerning the modeling of supercapacitors [43,44,45,46,47] and ferromagnetic core coils [48,49,50,51].

Among the various definitions of the elements of fractional calculus (i.e., fractional derivatives and integrals [52,53,54]) the Caputo fractional derivative of order $\alpha \in [0,1]$ has been considered:

$$\begin{aligned} _{t_{0}} ^{} \mathrm {D} _{t} ^{\mathrm {\alpha }} x(t) = \frac{1}{ \mathrm { \Gamma } (1-\alpha ) } \int _{ {t_{0}} } ^{ {t} } \frac{ x^{(1)} (\tau ) }{ (t-\tau )^\alpha } \mathrm {d}\tau , \end{aligned}$$

(1)

with $t_0$ being the initial time instance of an analysis, $x^{(1)}$ representing the first derivative of x(t) and $\mathrm {\Gamma }(\cdot )$ representing the gamma function:

$$\begin{aligned} \mathrm {\Gamma }(z) = \int _0^\infty x^{z-1} \mathrm {e}^{-x} \mathrm {d}x. \end{aligned}$$

(2)

2 Measurements

The studies in this paper make use of the results of measurements that have been accumulated throughout the last three years [48, 50, 55, 56]. The measurements have been performed initially with a digital interference and event recorder RZ1 (manufactured by the Kared Company [57]). Over the successive investigation trials, an original measurement tool built on an Arduino platform [50] has been developed.

Throughout the collection of recorded waveforms—the measurements of one selected coil have been chosen for further investigations. These comprise of periodic steady state voltage and current waveforms for various levels of the coil core saturation (exemplary cases in Fig. 1). More information on the measurements of the selected coil can be found in [55].

Fig. 1

Two sets of voltage and current waveforms recorded for: a a large core saturation, b a small core saturation

The flux linkage in a coil is defined as:

$$\begin{aligned} \varPsi (t) = \int _{t_0}^{t} u (t)\;\mathrm {d}t + \varPsi (t_0), \end{aligned}$$

(3)

where $t_0$ is the initial time instance of the analysis and u is the voltage across the coil. Because this quantity is not measured directly, the study applies the above formula to obtain the flux linkage values from the voltage waveforms. The realization of the above is performed numerically, through Newton–Cotes formulae [58]. The flux linkage and current waveform pairs allow to reconstruct the hysteresis loops. An example of the obtained hysteresis loops is depicted in Fig. 2.

Fig. 2

Exemplary hysteresis loops obtained for different supply voltage levels (resulting in large, medium and small core saturation levels)

3 Investigated models

Profound experience earned in numerous previous studies [48, 50, 55, 59,60,61,62] has allowed to narrow down the class of the considered models. A model, which is often considered up-to-date and one of the easiest in its implementation, is the classical model, comprising of a parallel connection between a resistor and a nonlinear coil [63, 64]. For simpler reference—this model is further on called the $RL_\mathrm {N}$ model. Also, one can slightly modify the model by introducing a nonlinear resistance (this, in turn, is further on called the $R_\mathrm {N}L_\mathrm {N}$ model) Both variants are presented in Fig. 3.

Fig. 3

Ferromagnetic core coil models applying classical circuit elements

The imperfection of the above-mentioned model variants in terms of the reflection of measurements (especially concerning the current waveforms [55, 60]), during a large saturation condition of the core has forced an upgrade of the model. The resulting model consists of a resistor and a nonlinear fractional coil (this model is called the $RL_\mathrm {N}^{\alpha }$ model). One can also consider its simpler version (which consists of a fractional, nonlinear coil alone—this is called the $L_\mathrm {N}^{\alpha }$ model) and an extension of the model, which introduces a nonlinear resistance (called the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model).

Fig. 4

Ferromagnetic core coil models applying a nonlinear fractional coil (symbol as proposed in [65])

The nonlinear fractional coil is an element, which is described by the differential equation:

$$\begin{aligned} _{t_0}^{} \mathrm {D} _{t} ^{\mathrm {\alpha }} \psi (t) = u(t), \end{aligned}$$

(4)

where u is the voltage across that element, while $\psi$ is an artificial variable (with the unit $\mathrm {Wb}\cdot \mathrm {s}^{\alpha -1}$). Along with the above equation, the $\psi$-i relationship needs to be defined through a nonlinear equation. The computed $\psi$ variable is only considered during a simulation process. The final flux linkage waveform for all of the models is defined through (3).

A further extension of the model can be made by including a fractional capacitor (Fig. 5). This is further on referred to as the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model.

Fig. 5

Ferromagnetic core coil model applying a nonlinear fractional coil and a fractional capacitor (the symbols for fractional elements as proposed in [65])

The fractional capacitor response is described through the fractional differential equation:

$$\begin{aligned} C_\beta \,\! \, _{t_0}^{} \mathrm {D} _{t} ^{\mathrm {\beta }} u(t) = i(t), \end{aligned}$$

(5)

with $C_\beta$ being an artificial parameter, with a unit of $\mathrm {F}\cdot \mathrm {s}^{\beta -1}$.

4 Solving problems with fractional derivatives

With the conventional elements appearing in a circuit problem, the solution tools that are available generally fall under solvers for DAE (differential algebraic equations). When fractional elements appear, the problems can be described by the following general system of FDAE (fractional differential algebraic equations):

$$\begin{aligned} \begin{aligned} {\mathbf {D}} _{t} ^{\varvec{\alpha }} \textit{\textbf{x}}(t)&= f(t, \textit{\textbf{x}}(t), \textit{\textbf{y}}(t)),\\ 0&= g(t, \textit{\textbf{x}}(t), \textit{\textbf{y}}(t)), \end{aligned} \end{aligned}$$

(6)

where $\textit{\textbf{x}}(t)$ contains the variables that appear under fractional derivatives (and the orders are put in the vector $\varvec{\alpha }$), while $\textit{\textbf{y}}(t)$ holds the remaining variables. ${\mathbf {D}} _{t} ^{\varvec{\alpha }} \textit{\textbf{x}}(t)$ denotes the vector of fractional derivatives, i.e., the k-th entry is the fractional derivative of $x_k(t)$ with the order being the k-th entry of $\varvec{\alpha }$ (that is $\alpha _k$). For such problems, the possibilities are much less numerous. For linear problems, one can apply some analytical solutions [66]; however, for a single nonlinear element appearing in the problem, these are no longer valid. Also, analytical solutions are only obtained for some specific source time functions (like unit step or sinusoidal functions [67]) and the most often considered system is one where all fractional derivatives are of the same order $\alpha$ [68] (the solution is then much simpler, but it is uncommon for such a system to show up in practice if more than one fractional element appears). There are various numerical methods that have been described in the literature that deal with FDAE [these are often considered in various general forms [69,70,71], not necessarily as in (6)]. However, the availability of computational tools that allow to solve FDAE is very low. Let us consider a problem where the following elements appear:

• autonomous voltage and current sources (described by any type of time functions) and controlled voltage or current sources,

• linear and nonlinear resistors,

• coils that are linear or nonlinear, which can also be regular coils or fractional coils,

• capacitors that are linear or nonlinear, which can be regular capacitors or fractional capacitors (hence, leaving the possibility of a nonlinear fractional capacitor).

For certain implementation conveniences—the following form can be applied for the FDAE [72, 73]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textit{\textbf{M}}_\mathrm {I} \textit{\textbf{y}} (t) + \textit{\textbf{M}}_\mathrm {II} \textit{\textbf{x}} (t) = \textit{\textbf{T}} \textit{\textbf{v}} (t) + \left[ \begin{array}{c} \textit{\textbf{0}}_{n_y - n_\mathrm {NL}} \\ \textit{\textbf{F}}_\mathrm {NL}(\textit{\textbf{w}}(t)) \end{array} \right] , \\ {\mathbf {D}} _t ^{ \varvec{\alpha } } \textit{\textbf{x}}(t) + \textit{\textbf{M}}_\mathrm {III} \textit{\textbf{y}} (t) + \textit{\textbf{M}}_\mathrm {IV} \textit{\textbf{x}} (t) = \textit{\textbf{0}}_{n_x}, \end{array}\right. } \end{aligned}$$

(7)

where

• $\textit{\textbf{x}}$ is the vector of variables under fractional derivatives (length of this vector: $n_x$),

• $\textit{\textbf{y}}$ is the vector for the remaining variables (its length: $n_y$),

• $\textit{\textbf{w}}$ joins the above two vectors:

  $$\begin{aligned} \textit{\textbf{w}}(t) = \left[ \begin{array}{ll} \textit{\textbf{y}}(t) \\ \textit{\textbf{x}}(t) \end{array} \right] , \end{aligned}$$

  (8)

• $\textit{\textbf{v}}(t)$ consists of the functions representing the time waveforms of the autonomous sources (the length of this vector is $n_v$),

• $\textit{\textbf{M}}_\mathrm {I}$ is an $n_y \times n_y$ matrix, $\textit{\textbf{M}}_\mathrm {II}$ is an $n_y \times n_x$ matrix, $\textit{\textbf{M}}_\mathrm {III}$ is an $n_x \times n_y$ matrix, $\textit{\textbf{M}}_\mathrm {IV}$ is an $n_x \times n_x$ matrix and $\textit{\textbf{T}}$ is an $n_y \times n_v$ matrix,

• the notation $\textit{\textbf{0}}_k$ is applied in general for the description of a vector of k zeros.

Additionally, the vector $\textit{\textbf{F}}_\mathrm {NL}(\textit{\textbf{w}}(t))$ is introduced (with the length $n_\mathrm {NL}$). In (7), it has been described more generally; however, it actually contains functions where each only depends on a single different variable. The only solvers that are available for such problems are the adaptive step size solvers [73, 74] based on the method called SubIval [75, 76] (this is an acronym for “the subinterval-based method for fractional derivative computations,” which first appeared in [77]) and constant step size solvers based on fractional linear multistep methods [78] and product integration rule methods [79, 80]. For periodic steady state problems (taking into account certain simplifications concerning the involvement of higher harmonics), one can apply the harmonic balance methodology [65], but this method is not available in a solver. When an analysis is required that includes one of the proposed models, it is best to apply one of the mentioned numerical solvers for transient problems. The estimation process alone in the case of this study does not require a transient solution to be computed in each model evaluation as it bases on periodic steady state solutions. The manner, in which a model evaluation is performed for selected parameter values, is described in Sect. 5. An example of how the $\textit{\textbf{w}}(t)$ vector is established and how the system described through (7) is formulated, when solving a circuit problem featuring the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model, is given in “Appendix A.”

5 Model response in the estimation process

This section explains how a single evaluation of a model is performed, i.e., how an output waveform is produced for a provided input waveform. As it has been mentioned before—the measurement basis of the modeling process comprises of the voltage and current waveforms (more accurately—the recorded signal sample pairs). In order to reduce the time of the estimation process—for a single period of the 50 Hz voltage source—the final amount of samples taken into account is equal to $n_\mathrm {pts} = 300$ for the estimation process (in single model evaluations). For final observations of the results (comparisons between model and measurement waveforms), $n_\mathrm {obs} = 2000$ time axis nodes are taken into account. The voltage samples selected for the estimation process are expressed as the vector $\textit{\textbf{u}}_\mathrm {meas}$, while the current samples are further on called $\textit{\textbf{i}}_\mathrm {meas}$.

When having access to the voltage and current on the coil itself – one can inspect the response of the model for an assumed input of a waveform reconstructed from the voltage or current samples. Then, the other quantity serves as the output of the model, which, when compared with measurements, allows to ascertain the accuracy. Because in each of the studied models the voltage is common for all elements—it is selected as the input quantity.

Because of the nonlinearities appearing in the models, a single evaluation could prove demanding (and, most of all, relatively time consuming) when considering that evaluation as a time-dependent problem. Hence, the periodic steady state is considered, which allows for a particular approach. It involves procedures, where the following operations appear:

• (A) a time frequency analysis for the input waveform, resulting in a vector of odd harmonics up to $h_\mathrm {max}$ (e.g., then the notation for the voltage harmonics is $\underline{\textit{\textbf{u}}}$),

• (B) a fractional differentiation or integration for the periodic steady state, which is in this approach performed on the complex valued representation; e.g., the fractional derivative of order $\alpha$ for a periodic waveform f(t) (expressed through a vector of harmonics $\underline{\textit{\textbf{f}}}$) and resulting in a waveform g(t) (expressed as the vector of harmonics $\underline{\textit{\textbf{g}}}$) is computed through the Hadamard product [65]:

  $$\begin{aligned} \underline{\textit{\textbf{g}}} = \underline{\textit{\textbf{s}}}_\alpha \circ \underline{\textit{\textbf{f}}}, \end{aligned}$$

  (9)

  where

  $$\begin{aligned} \underline{\textit{\textbf{s}}}_\alpha = [ \begin{array}{cccc} {j}_\alpha \omega _{1}^{\alpha }&{j}_\alpha \omega _{3}^{\alpha }&\ldots&{j}_\alpha \omega _{h_\mathrm {max}}^{\alpha } \end{array}]^\mathrm {T}, \end{aligned}$$

  (10)

  and:

  $$\begin{aligned} {j}_\alpha = \exp \left( {j}\frac{\pi }{2} \alpha \right) , \end{aligned}$$

  (11)

• (C) for a set of samples in a vector $\textit{\textbf{f}}$ (expressing a waveform f(t)), for a nonlinear dependency f–g—the evaluation of a set of samples $\textit{\textbf{g}}$ (expressing a waveform g(t)),

• (D) a reconstruction of the output waveform (expressed as a vector $\textit{\textbf{g}}$) from a vector of harmonics $\underline{\textit{\textbf{g}}}$.

The above operations are similar to what one can observed when solving a problem during the application of the harmonic balance methodology [65] mentioned in Sect. 4. For each of the elements of a model (connected in parallel), the voltage waveform is taken into account as the input and the current output for that element is evaluated. The final output of each model (depicted previously in Figs. 3, 4, 5) is then the sum of the currents. Figure 6 shows block diagrams for exemplary (most advanced) considered model elements.

Fig. 6

Block diagrams for exemplary model elements (“cplx” denotes the time frequency analysis described previously in item (A), “(t)” denotes the waveform reconstruction mentioned in item (D))

What should be emphasized when the model performance is assessed during a parameter estimation procedure is that the task for a model is to accurately resemble hystereses for each core saturation level while using one set of parameters. Hence, such an evaluation, as described in this section, is performed for the waveforms of each considered core saturation level. More on how the model performance is then examined (and on the method of obtaining the parameters) can be found in Sect. 7.

6 Susceptibility on parameter changes

Before a parameter estimation procedure is conducted—one can examine the influence of the particular parameters on the model output; where one can especially observe the resulting hysteresis (this can also be useful in an initial selection of the parameter values). The examples of this section are all given for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model with the following initial parameter values:

$$\begin{aligned} \begin{array}{l} \alpha = 0.9,\\ \beta = 0.5,\\ C_\beta = 10^{-4}\,\mathrm {F}\cdot \mathrm {s}^{\beta -1}. \end{array} \end{aligned}$$

The above initial parameter values have been selected empirically. They allowed the model to yield a hysteresis shape similar to one that could appear in practice (with $\beta$ and $C_\beta$ introducing only a slight influence).

The $\psi$-i relationship is described by the function:

$$\begin{aligned} \psi (i) = \psi _0 \arctan \left( \frac{i}{i_0}\right) , \end{aligned}$$

(12)

where the coefficient values:

$$\begin{aligned} \begin{array}{l} \psi _0 = 1.4\,\mathrm {Wb}\cdot \mathrm {s}^{\alpha -1},\\ i_0 = 1\,\mathrm {A} \end{array} \end{aligned}$$

are applied. This function has been selected initially, for the trials of this section. It is actually one that has been used in previous studies [59]. The function used in the parameter estimation procedure (later on) has a more general form (more on this in Sect. 7).

The nonlinear resistance, applied for the simulations of this section, is described by the following nonlinear u-i dependence:

$$\begin{aligned} i(u) = {\text {sgn}}(u) i_n \left| \frac{u}{u_n} \right| ^n, \end{aligned}$$

(13)

where initially:

$$\begin{aligned} \begin{array}{l} i_n = 0.01\,\mathrm {A},\\ u_n = 200\,\mathrm {V},\\ n = 1. \end{array} \end{aligned}$$

Similarly as in the case of the $\psi$-i relationship, this function has only been selected for the trials of this section, while a more general form is selected for the actual parameter estimation (Sect. 7).

For a studied susceptibility on a selected parameter (or set of parameters concerning one nonlinear function), only the selected one (or ones) are modified, while the other ones remain as given above. The influence of the $\psi$-i function changes on the model output is presented in Fig. 7.

Fig. 7

Influence of coefficient changes in an exemplary $\psi$-i function of a nonlinear fractional coil on the model output: (a) modifications of $\psi _0$, (b) modifications of $i_0$

The effects are much like those that could be observed when modifying a nonlinear function in an $RL_\mathrm {N}$ model, even though $\psi$-i does not directly represent the anhysteretic curve when $\alpha \ne 1$.

The influence of the modification of the nonlinear resistor u-i function on the model output is presented in Fig. 8.

Fig. 8

Influence of the changes of coefficients in an exemplary u-i function of a nonlinear resistor on the model output

What has been observed is that the above modifications allow to influence the width of the hysteresis either for a smaller range of the flux and current levels or for the entire range.

Next, the influence on the fractional derivative order (denoted by $\alpha$) applied in the nonlinear fractional coil has been studied. The results are depicted in Fig. 9.

Fig. 9

Influence of the fractional derivative order $\alpha$ (in a nonlinear fractional coil) on the model output (and a magnification of the result on the right)

A strong influence of the $\alpha$ parameter on the model output can be observed. What is interesting, in particular, is a deformation that one could not obtain when modifying the previously studied features of the model. From these trials, one can determine that values at around 0.9 and above might be adequate and that this value should not be lower than 0.8 (even in this case the hysteresis shape does not look like one observed for ferromagnetic core coils).

The modification of the fractional capacitor parameters is studied next. The influence of $\beta$ is presented in Fig. 10, while the influence of $C_\beta$ is depicted in Fig. 11.

Fig. 10

Influence of the pseudo-capacitance $C_\beta$ (in a fractional capacitor) on the model output

Fig. 11

Influence of the fractional derivative order $\beta$ (in a fractional capacitor) on the model output

Some of the resulting features are like no others that could be imposed when modifying the previous parameters. One can also observe some influences similar to those that have been noticed earlier (e.g., concerning the hysteresis width). However, a distinct feature that can be introduced is what could be interpreted as an opposite slope of the anhysteretic curve, e.g., similar to what can be observed when taking into account capacitances in transformer windings [81].

7 Parameter estimation procedure

The computations of the study have been performed in the GNU Octave [10] environment. The introduction of the measurement waveforms, their processing, the possibility of model evaluations and the implementation of all other necessary operations all required individual computational scripts to be written.

Obviously, the model type determines the amount of the estimated parameters. What is also important, in the case of appearing nonlinear elements, is the form in which the nonlinear function is considered. These could be formed, e.g., through pre-established nonlinear functions (as given in examples of Sect. 6 and in previous studies [59, 60]) or as it has been done in previous studies for the nonlinear coil [48, 50, 55], i.e., through $\psi$-i positive value pairs (with an assumption that the $\psi$-i relationship results in an odd function) with:

• the i values set up in some interval $[0, i_{\max }]$ and a given constant step $\mathrm {\Delta } i$ between the consecutive values,

• the $\psi$ values being the ones that are estimated,

• $n_{\psi \text {-}i}$ representing the amount of the values,

• for values between the established $\psi$-i value pairs—spline interpolation is used,

• for a negative value, the result for |i| is taken and then multiplied by $-1$.

The above has proven to work well [50, 55], but an even better approach has been established in order to assure that the $\psi$-i relationship results in a monotonically increasing function. Instead of the $\psi$ values—the estimated values can be given as $\mathrm {\Delta } \psi _k$ and for each $\psi _k$, $k = 1, 2, \ldots \; n_{\psi \text {-}i}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{lll} \psi _k = 0 &{}\mathrm {if}&{}k=1,\\ \psi _k = \psi _{k-1} + \left| \mathrm {\Delta }\psi _k\right| + \mathrm {\Delta }\psi _\mathrm {min} &{}\mathrm {if}&{}k\ne 1.\\ \end{array} \end{array}\right. } \end{aligned}$$

(14)

For this study, $\mathrm {\Delta }\psi _\mathrm {min} = 10^{-5}\,\mathrm {Wb}\cdot \mathrm {s}^{\alpha -1}$ has been assumed, along with $n_{\psi \text {-}i}= 15$, $i_{\max } = 1.5\,\mathrm {A}$ and $\mathrm {\Delta }i = \frac{i_{\max }}{n_{\psi \text {-}i}- 1}$. The same concept can be applied for a nonlinear resistor. However, here the u values are assumed from the start, while the $i_R$ values are estimated. The number of u-$i_R$ pairs is $n_{u \text {-}i_R}= 15$, $u_{\max } = 450\,\mathrm {V}$ and $\mathrm {\Delta }u = \frac{u_{\max }}{n_{u \text {-}i_R}- 1}$. Taking the above into account, as an example, a single set of parameters for the $RL_\mathrm {N}^{\alpha }$ model consists of the $\mathrm {\Delta }\psi _k$ values and R, $\alpha$ values, while for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model a set of parameters consists of $\alpha$, $\beta$, $C_\beta$ along with the $\mathrm {\Delta }\psi _k$ and $\mathrm {\Delta }i_k$ values.

The evaluation of each model involved the consideration of 6 sets of voltage and current waveform pairs and the computation of the output quantity (which is the current) according to what has been described in Sect. 5. The current output of the model is then expressed through samples that are put in a vector $\textit{\textbf{i}}$. These are compared with the measurement results of $\textit{\textbf{i}}_\mathrm {meas}$. The following value is computed for each considered set of the voltage–current sample pairs:

$$\begin{aligned} f_k = \frac{1 }{ n_\mathrm {pts} } \sum (\textit{\textbf{i}} - \textit{\textbf{i}}_\mathrm {meas})^2 \end{aligned}$$

(15)

where k is the number of the voltage–current waveform pair. In the estimation process, the $f_k$ values for all the considered sets are summed up. Then, the sum of these:

$$\begin{aligned} F = \sum _{k=1} ^{6} f_k \end{aligned}$$

(16)

is minimized. The estimation process for each model has made use of an algorithm, which consisted of series executions of the Nelder–Mead method (implemented in the nelder_mead_min function in the optimization package in Octave) followed by an application of the multidirectional search method (through the fmins function). Such hybrid optimization algorithms (combining two optimization methods) can be found in [82].

In order to possess an insight into the accuracy of the agreement of the waveforms one can observe the model and measurement waveforms and the resulting hystereses. Additionally, the following error value is defined:

$$\begin{aligned} \epsilon _k = \frac{ \sqrt{ \frac{1 }{ n_\mathrm {pts} } \sum (\textit{\textbf{i}} - \textit{\textbf{i}}_\mathrm {meas})^2 } }{ i_{\max } } \cdot 100\,\%, \end{aligned}$$

(17)

where $i_{\max }$ is the maximum of absolute values of the vector $\textit{\textbf{i}}_\mathrm {meas}$ and, as previously in the case of $f_k$, k is the number of the voltage–current waveform pair. Note that the above is evaluated for each set of the voltage–current sample pairs.

8 Modeling results

For each more advanced model, both strategies have been applied, where the initial parameters have been selected either through:

• parameter tweaking, where the values have been determined through observations of the model output (hysteresis, as in Sect. 6),

• a selection of parameters, which have been optimal for a less advanced model (e.g., the starting parameters for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model have been directly determined by the optimal parameters for the $RL_\mathrm {N}^{\alpha }$ model).

The estimation process for each model has been executed for both of the above starting parameter strategies, while the final results have been taken from the strategy that has produced the lower F value. A comparison of the objective function values for the considered models is presented in Table 1.

Table 1 Comparison of objective function values for the considered models (values rounded to 5 significant digits)

In a general comparison, one can observe:

• a slight improvement when adding a nonlinear resistance in the classical model (i.e., resulting in the $R_\mathrm {N}L_\mathrm {N}$ model),

• an unexpected advantage of the $L_\mathrm {N}^{\alpha }$ model in comparison with the $R_\mathrm {N}L_\mathrm {N}$ model,

• the most noticeable improvements (of the agreement between the measurements and simulation results) have been observed up to the application of the $RL_\mathrm {N}^{\alpha }$ model, while consecutive upgrades to $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ and $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ models have produced only slight improvements.

In this study, an important fact is that the model-measurement resemblance is fitted for various levels of the core saturation (with F actually presenting a measure of the total accuracy) for a single set of parameters. In order to determine the ability to reflect the measurements for each model for each of the core saturation levels separately—the $\epsilon _k$ values have been determined [defined by (17) in Sect. 7]. The results are presented in Table 2.

Table 2 Comparison of errors (in percentages) for the considered models (values rounded to the ten thousandth)

Additionally to the previous observations, what can be noticed is that for some improvements of the objective function value F there have been some reduced accuracies when it comes to the errors in the cases of distinct core saturation levels (e.g., for $\epsilon _6$ when upgrading to the $R_\mathrm {N}L_\mathrm {N}$ model). The classical models (without fractional elements) generally seem to fail in attempts to adequately resemble each considered set of measurements at the same time for one selected set of parameters. This can also be noticed when observing the model and measurement hysteresis comparisons for one of the classical models. As an example—the comparison for the $R_\mathrm {N}L_\mathrm {N}$ model is depicted in Fig. 12. An additional flaw of the integer-order models is the inability to accurately resemble the hysteresis for when the core becomes more saturated (magnification in Fig. 12). This can be especially observed above the saturation knee.

Fig. 12

Hystereses comparison ($R_\mathrm {N}L_\mathrm {N}$ model simulations versus measurements) for various iron core saturation levels

As mentioned before—an unexpected improvement in the accuracy has been observed when applying the $L_\mathrm {N}^{\alpha }$ model (consisting of just a nonlinear fractional coil—in this case the parameter $\alpha = 0.9664$). An improvement can be observed also when upgrading it to an $RL_\mathrm {N}^{\alpha }$ model (in this case $\alpha$ remained unchanged), where not only F is a smaller value but also all the $\epsilon _k$ values indicate a better result. When applying the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model instead, a slight improvement is observed in almost all cases (except $\epsilon _6$, though that value is very similar to its equivalent in the $RL_\mathrm {N}^{\alpha }$ model). A compilation of the hysteresis comparisons for the various iron core saturation levels for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model is presented in Fig. 13. One could also notice that the value of the $\alpha$ parameter has not changed.

The addition of a fractional capacitor to the model has also produced an insignificant improvement, which is why the hysteresis comparisons are not depicted in this paper. The parameter estimation procedure has yielded the fractional derivative orders $\alpha = 0.9662$ and $\beta = 0.7331$.

Fig. 13

Hystereses comparison ($R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model simulations versus measurements) for various iron core saturation levels

A very good resemblance can be observed when comparing the model results with the measurements, which can also be noticed when the current waveforms are compared (Fig. 14). As a reminder: the voltage waveforms are not compared as for each of the simulations the input for each model has been that voltage waveform.

Fig. 14

Comparison of current waveforms for various core saturation levels (for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model)

9 Summary and conclusions

The investigations of this paper concerned the modeling of a ferromagnetic core coil response, where an emphasis has been put on the reflection of the hysteresis. A circuit approach has been applied, meaning that the element is treated as a whole and the $\psi$-i relationship is taken into account. The measurement basis consisted of sets of voltage and current waveforms that have been gathered throughout the authors’ previous studies. The collections of recorded waveforms have allowed an insight to various levels of the core saturation levels (examples in Figs. 1, 2), where the flux linkage waveforms have been recreated from the voltage waveforms (this is described in Sect. 2, where (3) has been applied). From the above—six of the sets (each representing a different level of the core saturation) have been taken into account for further investigations.

The task for a model was to have the ability to accurately reflect the measurement waveforms (and, hence, the hystereses) for the various core saturation levels. Unlike other studies, where often only one or two scenarios are taken into account [3, 59] the study aimed at an ability of a model to reflect all the cases of the core saturation levels for a single set of parameters.

Experience gained in previous studies has allowed to extract six different circuit element-based models that could be useful in this study. These included classical circuit elements and elements applying fractional calculus (their detailed description has been given in Sect. 3, Figs. 3, 4 and 5):

• the classical model (often appearing in the literature) featuring a resistor and a nonlinear coil—this has been called the $RL_\mathrm {N}$ model,

• an extension of the classical model, replacing the linear resistance with one that is nonlinear (the $R_\mathrm {N}L_\mathrm {N}$ model),

• a simple (yet what has later turned out to be surprisingly accurate) model featuring a nonlinear fractional coil alone (the $L_\mathrm {N}^{\alpha }$ model),

• a model featuring a resistance and a nonlinear fractional coil (the $RL_\mathrm {N}^{\alpha }$ model),

• an extension of the above, which replaced the linear resistance with a nonlinear one (the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model),

• a further extension, adding a fractional capacitor (the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model).

The inclusion of fractional calculus-based elements adds a certain complexity to the mathematical form of the considered problems [which are then either considered in a general form given by (6) or, more specifically, by (7)]. The ability to solve such problems is addressed in Sect. 4.

The models generally all consisted of single elements connected in parallel, which allowed to apply a particular approach when each of the models has been evaluated in an estimation process. A single model evaluation (for a given set of parameters) involved the operations described in Sect. 5.

For a better familiarity on how each feature of the considered model influences their response (especially on the shape of the resulting hysteresis), a susceptibility analysis is performed and presented in Sect. 6. Further on, this has also been helpful when selecting a set of initial parameters for each of the models. The final general forms of the nonlinear functions (for nonlinear resistances and nonlinear coil $\psi$-i relationships) are discussed in Sect. 7 along with details on the estimation procedure and the form of the objective function [described by (15) and (16)]. Additionally, the reflection of the hysteresis for each core saturation level separately has also been considered, where the error given by (17) has been defined.

The modeling results are presented in Sect. 8. Both the final values of the objective function and the error values (for each considered core saturation level) have been addressed (Tables 1, 2). From the analysis in that section, the following can be concluded:

• the $R_\mathrm {N}L_\mathrm {N}$ model has introduced some slight improvements—the objective function value has improved in general; for some core saturation levels, one can observe a significant improvement (given by the $\epsilon _1$, $\epsilon _2$ and $\epsilon _3$ errors); however, the accuracy for the remaining ones has been decreased (especially for the lowest core saturation level, which could be observed through the $\epsilon _6$ error value),

• for the classical models, one can generally observe two flaws: the first is that they are not able to reflect all the hysteresis saturation scenarios at once for one set of parameters (although a very good agreement can be achieved for a single hysteresis—this has been shown in previous studies [59, 61]), while the second is the difficulty in properly resembling the hysteresis width above the saturation knee (example in Fig. 13),

• as mentioned in Sect. 8—a very interesting result can be observed when applying a model comprising of a nonlinear fractional coil alone (the $L_\mathrm {N}^{\alpha }$ model)—one can observe a significantly better result than for the models basing on classical circuit elements (both in terms of the $\epsilon _k$ error values and the objective function F),

• a still noticeable improvement can be observed when adding a linear resistor to the nonlinear fractional coil model (resulting in the $RL_\mathrm {N}^{\alpha }$ model),

• an insignificant improvement could be observed when the model is extended to the case of the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model—the error values have improved in five of the six cases (by an insignificant amount) and one case (described by $\epsilon _6$) suffered from a slight loss in accuracy; the objective function also suggested an insignificant improvement,

• the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model also introduced only slight improvements in the resemblance of the studied coil hystereses.

The $RL_\mathrm {N}^{\alpha }$ model, in some terms, could be considered as the optimal model for the studied coil because of the accuracy improvement in comparison with less advanced models. It is worthwhile to point out that this model only requires one additional parameter in comparison with the classical $RL_\mathrm {N}$ model (i.e., the parameter $\alpha$). Further additions to the model (a nonlinear resistance or a fractional capacitor) have not introduced significant improvements. However, one can already notice a very good agreement for the $R_\mathrm {N}L_\mathrm {N}^{\alpha }$ model, leaving not much space for further improvements. The hystereses (Fig. 13) and waveforms (Fig. 14) have been very accurately reflected, where in some cases the differences are almost indistinguishable. This suggests at a very useful application of this model in simulation practices on real objects (e.g., for ferroresonance analyses [55], even transient state simulations [48]).

The inclusion of the fractional capacitor has not introduced significant improvements for the reflection of the studied hystereses; however, the inclusion of this element allowed to introduce features that could not be achieved otherwise (discussed in Sect. 7, observed in Figs. 10 and 11). This can be useful when circumstances would lead to such features being observed (it can be pointed out that such cases are possible for real objects applying ferromagnetic cores [81]).

Future studies will be aimed at the design of models that could accurately resemble measurements not only obtained for various ferromagnetic core saturation levels, but also for scenarios, where very significant components of higher harmonics will be introduced on purpose.

A Example of FDAE formulation

This appendix explains how a system in the form of (7) is formulated for a circuit containing an exemplary model that has been considered in this paper.

The $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model has been selected for the example as it is the most advanced one that has been studied. The system will be formulated in a general manner, i.e., the voltage and all the selected currents (on nonlinear and inertial elements) along with node potentials will be included in the equations. The mentioned variables are marked as in Fig. 15.

Fig. 15

Variables of $\textit{\textbf{w}}(t)$ marked in the $R_\mathrm {N}L_\mathrm {N}^{\alpha }C_\beta$ model as a part of a circuit problem

Initially, only the equations will be formulated, which the model introduces, while further ones will be introduced depending on where the model is placed in a circuit. The $\textit{\textbf{x}}(t)$ vector consists of the variables under fractional derivatives, hence:

$$\begin{aligned} \textit{\textbf{x}}(t) = [\begin{array}{cc} \psi (t)&u(t) \end{array}]^\mathrm {T}, \end{aligned}$$

(18)

where the derivative orders are given by:

$$\begin{aligned} \varvec{\alpha } = [\begin{array}{cc} \alpha&\beta \end{array}]^\mathrm {T}, \end{aligned}$$

(19)

while:

$$\begin{aligned} \textit{\textbf{y}}(t) = [\begin{array}{ccccc} V_1(t)&V_2(t)&i_\mathrm {NL}(t)&i_\psi (t)&i_\beta (t) \end{array}]^\mathrm {T}. \end{aligned}$$

(20)

The source vector $\textit{\textbf{v}}(t)$ will be introduced later, when the placement of the model in the circuit will be determined. The potential difference introduces the equation:

$$\begin{aligned} V_1(t) - V_2(t) - u(t) = 0, \end{aligned}$$

(21)

which determines a row in the $\textit{\textbf{M}}_\mathrm {I}$ and $\textit{\textbf{M}}_\mathrm {II}$ matrices. For the purpose of this example, it is assumed that the equations start from $n_\mathrm {start}$, hence:

$$\begin{aligned} \begin{array}{l} M_{\mathrm {I}\;n_\mathrm {start}, 1} = 1,\\ M_{\mathrm {I}\;n_\mathrm {start}, 2} = -1,\\ M_{\mathrm {II}\;n_\mathrm {start}, 2} = -1. \end{array} \end{aligned}$$

(22)

The remaining equations that the model introduces are the nonlinear equations and the fractional differential equations. For the nonlinear equations, when implementations are considered [72, 73], it is convenient to introduce an auxiliary vector $\textit{\textbf{i}}_\mathrm {arg}$, whose entries denote the indices of the arguments of the functions appearing in $\textit{\textbf{F}}_\mathrm {NL}$, e.g., for $n_\mathrm {NL} = 3$ and:

$$\begin{aligned} \textit{\textbf{i}}_\mathrm {arg} = [\begin{array}{ccc} 4&7&1 \end{array}]^\mathrm {T} \end{aligned}$$

(23)

the vector $\textit{\textbf{F}}_\mathrm {NL}$ takes the form:

$$\begin{aligned} \textit{\textbf{F}}_\mathrm {NL} = [\begin{array}{ccc} f_1(w_4(t))&f_2(w_7(t))&f_3(w_1(t)) \end{array}]^\mathrm {T}. \end{aligned}$$

(24)

The nonlinear equations describe the u-$i_\mathrm {NL}$ and $\psi$-$i_\psi$ relationships. For a $u(i_\mathrm {NL})$ description:

$$\begin{aligned} u = f_u(i_\mathrm {NL}). \end{aligned}$$

(25)

The first entry in $\textit{\textbf{F}}_\mathrm {NL}$ is then the $f_u$ function, while:

$$\begin{aligned} i_{\mathrm {arg}\;1} = 3. \end{aligned}$$

(26)

According to the form given by (7), the nonlinear equations appear as the last $n_\mathrm {NL}$ algebraic equations. Assuming that the equations the model introduces appear starting from $n_\mathrm {NL start}$—the left-hand side in (25) introduces:

$$\begin{aligned} M_{\mathrm {II}\;n_\mathrm {NL start}, 2} = 1. \end{aligned}$$

(27)

For an $i_\mathrm {NL}(u)$ function:

$$\begin{aligned} i_\mathrm {NL} = f_i(u). \end{aligned}$$

(28)

where $f_i$ then appears as the first entry in $\textit{\textbf{F}}_\mathrm {NL}$, while:

$$\begin{aligned} i_{\mathrm {arg}\;1} = 7, \end{aligned}$$

(29)

and:

$$\begin{aligned} M_{\mathrm {I}\;n_\mathrm {NL start}, 3} = 1. \end{aligned}$$

(30)

Similarly for the $\psi$-i relationship—assuming that the nonlinear equation is:

$$\begin{aligned} \psi = f_\psi (i_\psi ). \end{aligned}$$

(31)

the second entry in $\textit{\textbf{F}}_\mathrm {NL}$ is then the $f_\psi$ function and:

$$\begin{aligned} i_{\mathrm {arg}\;2} = 4, \end{aligned}$$

(32)

with:

$$\begin{aligned} M_{\mathrm {II}\;n_\mathrm {NL start}+1, 1} = 1. \end{aligned}$$

(33)

On the other hand, for a nonlinear function:

$$\begin{aligned} i_\psi = f(\psi ), \end{aligned}$$

(34)

f appears as the second entry in $\textit{\textbf{F}}_\mathrm {NL}$ and:

$$\begin{aligned} i_{\mathrm {arg}\;2} = 6, \end{aligned}$$

(35)

with:

$$\begin{aligned} M_{\mathrm {I}\;n_\mathrm {NL start}+1, 4} = 1. \end{aligned}$$

(36)

The remaining equations are the fractional differential equations:

$$\begin{aligned} _{t_0}^{} \mathrm {D} _{t} ^{\mathrm {\alpha }} \psi (t) = u(t), \end{aligned}$$

(37)

and:

$$\begin{aligned} C_\beta \,\! \, _{t_0}^{} \mathrm {D} _{t} ^{\mathrm {\beta }} u(t) = i_\beta (t). \end{aligned}$$

(38)

Assuming that already $n_\mathrm {rem.}$ differential equations have been introduced, the following entries are added:

$$\begin{aligned} M_{\mathrm {IV}\;n_\mathrm {rem.} + 1, 2} = -1. \end{aligned}$$

(39)

and:

$$\begin{aligned} M_{\mathrm {III}\;n_\mathrm {rem.} + 2, 5} = -\frac{1}{C_\beta }. \end{aligned}$$

(40)

Further additions to the matrices and the $\textit{\textbf{F}}_\mathrm {NL}$ vector are introduced when the remaining part of the circuit is determined.

For a simple case of a circuit when only a voltage source, described by e(t), is connected to the terminals of the model, i.e., the $V_1$ and $V_2$ nodes, and directed at the $V_1$ node, no additional variables are introduced to $\textit{\textbf{x}}(t)$ and $\textit{\textbf{y}}(t)$, while $\textit{\textbf{v}}(t)$ becomes:

$$\begin{aligned} \textit{\textbf{v}}(t) = [e(t)], \end{aligned}$$

(41)

the additional equations are then:

$$\begin{aligned} V_1(t) = e(t), \end{aligned}$$

(42)

and

$$\begin{aligned} V_2(t) = 0, \end{aligned}$$

(43)

which introduce:

$$\begin{aligned} \begin{array}{l} M_{\mathrm {I}\;1, 1} = 1,\\ T_{1, 1} = 1 \end{array} \end{aligned}$$

(44)

and

$$\begin{aligned} M_{\mathrm {I}\;1, 2} = 1, \end{aligned}$$

(45)

, respectively. Additionally:

$$\begin{aligned} \begin{array}{l} n_\mathrm {start}= 3,\\ n_\mathrm {rem.} = 0,\\ n_\mathrm {NL start}= n_y - n_\mathrm {NL} + 1 = 4. \end{array} \end{aligned}$$

When all the necessary matrices, vectors and functions have been defined—the system can be solved through a solver basing on the SubIval method as mentioned in Sect. 4, e.g., the one that is available for GNU Octave and Matlab [73].