Displacement transmissibility of a Coulomb friction oscillator subject to joined base-wall motion

Abstract

This study investigates the displacement transmissibility of single-degree-of-freedom systems with a Coulomb friction contact between a mass and a fixed or oscillating wall. While forced vibration and base motion problems have been extensively investigated, little work has been conducted on the joined base-wall problem. Based on the work of Den Hartog (Trans Am Soc Mech Eng 53:107–115, 1930), analytical expressions of the displacement transmissibility are derived and validated numerically. The mass absolute motion was analysed in the joined base-wall motion case with a new technique, with results such as: (1) the development of a method for motion regime determination; (2) the existence of an inversion point in transmissibility curves, after which friction damping amplifies the mass response; (3) the gradual disappearing of the resonant peak when the ratio between friction and elastic forces is increased. Moreover, numerical analysis provides further insight into the frequency region where mass sticking occurs in the base motion problem.

1 Introduction

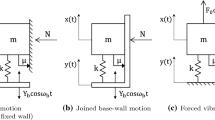
Developing a fundamental understanding of the role played by friction damping in structural dynamics is nowadays an important challenge for exploring suitable structural designs. Many engineering systems, such as aerospace and automotive vehicles, turbo-machines and buildings, are in fact characterised by the presence of frictional joints. As an important source of energy dissipation, friction may also be introduced in mechanical and civil structures to serve purposes such as isolation and vibration control. At an early stage of a design, the performance of a frictional contact under dynamic load is usually investigated by considering a single-degree-of-freedom (1-DoF) system subject to harmonic base excitation. This contribution is focused on the investigation of the main features of the dynamic response of such a model, both to base motion and to joined base-wall motion. The latter is of interest for many industrial applications, such as the dovetail root of a turbine blade; however, its response features are yet mostly unexplored.

Fig. 1

1-DoF mass-spring-viscous damper system under harmonic base motion (a) and its theoretical displacement transmissibility evaluated at different damping ratios (b)

The dynamic behaviour of a 1-DoF system under base motion is usually investigated with the displacement transmissibility, which is the ratio between the amplitudes of mass and base motions. This metric can be augmented by including the evaluation of phase shift between input and output displacements. In the viscous 1-DoF system shown in Fig. 1a, the base excitation is transmitted to the mass through a spring and a viscous dashpot in parallel. The response can be obtained as a superposition of the analytical forced responses to the elastic and the viscous forces [2]. The displacement transmissibility for different values of damping ratio is portrayed in Fig. 1b as a function of the ratio between forcing and natural frequencies. It is possible to observe that as the damping increases, the resonant peak is shifted to the left and for a frequency ratio below $\sqrt{2}$ the transmissibility is reduced; above this value, there is an inversion of the curves and so the damping amplifies the transmissibility. This behaviour needs to be accounted during the design stage.

In a 1-DoF system with a Coulomb friction contact, the problem is complicated by the nonlinearity of the equations which can lead to a periodic sticking during the mass vibration, defined as stick-slip behaviour (see e.g. [3, 4]). A general solution to the governing equation cannot been found in a closed form, and numerical techniques are usually employed [2]. Nonetheless, the base motion problem can be investigated as an equivalent forced vibration problem [1] that can be solved with alternative analytical approaches. These approaches are briefly reviewed in what follows. In 1930, Den Hartog proposed in [1] a method for the analysis of forced vibration with Coulomb friction; the author suggested a local solution for the steady sliding motion, allowing the description of quantities such as the amplitude of the mass motion or the phase shift between input load and response, and a condition for locating the transition between stick-slip and continuous motion. Only after many years, the same problem has been approached with different techniques, such as numerical integration in time domain [5], phase-plane methods [6], incremental harmonic balance [7], equivalent linearisation method [8] and others. In 2001, Hong and Liu [9] proposed a new approach aiming to improve Den Hartog’s solution. This includes the calculation of the conditions which lead to a purely sliding motion and a new estimation of the maximum velocity of the sliding mass and its time lag. Hong and Liu have shown that the same expressions as Den Hartog’s for the maximum displacement and its phase lag are recovered. Moreover, their analytical results were validated with a numerical solution [10].

The base motion problem has been addressed as a forced vibration problem in references [1, 6, 10, 11]. In particular, Den Hartog [1] proposed an extension of his theory to the classical base motion problem and also to the case where base and wall are jointed so that the wall is oscillating with the same harmonic motion imposed on the base. However, for the base motion case, some implications were not sufficiently discussed, including details about the stick-slip occurrence at high frequency ratios and the existence of an upper limit of the ratio between friction and spring force amplitudes allowing a continuous motion.

For the joined base-wall motion case, a series of results based on Den Hartog’s theory are represented for the first time. However, such results are referred exclusively to the relative mass-wall motion. The presented analysis goes much further, discussing the conditions for mass sticking and reaching a formulation holding for mass absolute motion, which allows the evaluation of both the displacement transmissibility and the phase shift between excitation and response.

A numerical approach based on the resolution of the governing equations was introduced in order to validate the analytical transmissibility curves. Furthermore, the numerical evidence allows the assessment of the analytical forecast about the transition between continuous and stick-slip motion. Being not based on Den Hartog’s assumptions, this technique is able to extend the transmissibility curves also to the stick-slip region. Particular attention is paid to the minimum number of parameters necessary to describe the problem both in an analytical and in a numerical approach, leading to a more suitable formulation of the equations.

The paper is organised as follows: Sect. 2 is dedicated to detailed review of Den Hartog’s theory on forced vibration; in Sect. 3, the analytical formulation of the base motion problem is discussed; Sect. 4 presents the results regarding the joined base-wall motion case; the numerical approach and the validation are introduced in Sect. 5.

2 Review of Den Hartog’s theory on forced vibrations

In reference [1], Den Hartog introduced an approach for the analysis of the forced vibration of a 1-DoF mass-spring system under harmonic load in the presence of a Coulomb friction contact between mass and a ground-fixed wall. The main outcomes from his work are the possibility to determine analytically the conditions for which the mass is sticking or slipping during the steady-state motion and the amplitude of mass displacement when such motion is continuous. The governing equations, as well as the main results, are discussed in this section.

Fig. 2

1-DoF mass-spring system with a friction contact under harmonic load

Let us consider a 1-DoF system composed by a mass m connected to ground through a spring whose stiffness is k (Fig. 2); be such mass rubbing against a ground-fixed wall in the presence of a compression load N, in such a way as to form a contact characterised by a friction coefficient $\mu$. A monoharmonic load, with amplitude $F_0$ and frequency $\omega _b$, is assumed to be applied directly to the mass. The general equation of motion of the system represented in Fig. 2 is:

$$\begin{aligned} m\ddot{x}+kx+\mu N\hbox {sgn}({\dot{x}})=F_0\cos \omega _b t \end{aligned}$$

(1)

Suppose that the steady-state condition has been reached, and the mass is vibrating with a steady and continuous periodic motion; no assumptions are made here regarding the harmonicity of this response. Mass motion is supposed to exhibit the same period as the force, so it is possible to consider a time interval $[0,2\pi /\omega _b]$ between a generic couple of subsequent maxima (Fig. 3) as completely representative of the steady-state motion. Further, it is reasonable to assume that a phase shift will be present in general between the applied force and the mass displacement. Due to the symmetric loading, the motion is assumed as symmetric with respect to the origin of the x-axis and the minimum condition will therefore occur when $t=\pi /\omega _b$. Being the motion assumed as continuous, ${\dot{x}}<0$ in all the internal points of the interval $[0,\pi /\omega _b]$, so Eq. (1) will be reduced to:

$$\begin{aligned} \ddot{x}+\omega _n^2\bigg (x-\dfrac{\mu N}{k}\bigg )=\dfrac{F_0}{m}\cos (\omega _bt+\phi ) \end{aligned}$$

(2)

Fig. 3

Steady-state continuous motion of a 1-DoF system with Coulomb friction

Equation (2) is linear and its boundary conditions can be written in terms of displacement and velocity at both the ends of the half period:

The maximum absolute displacement $x_0$ and the phase angle $\phi$ are both unknown. It must be underlined that such a phase angle is intended by Den Hartog as referred to the maxima of force and motion and the phase angle between their zeros will be different in general.

Introducing the frequency ratio:

$$\begin{aligned} r=\dfrac{\omega _b}{\omega _n} \end{aligned}$$

as the ratio between the driving and the natural frequencies of the excited system, the solution of Eq. (2) can be expressed as:

$$\begin{aligned} x(t)&=A_n\cos \omega _nt+B_n\sin \omega _nt \nonumber \\&\quad +\dfrac{F_0}{k}\dfrac{1}{1-r^2}\cos (\omega _b t+\phi )+\dfrac{\mu N}{k} \end{aligned}$$

(4)

where the constants $A_n$ and $B_n$ can be removed by imposing the conditions (3a):

$$\begin{aligned} x(t)&=x_0\cos \omega _nt+\dfrac{\mu N}{k}(1-\cos \omega _nt) \nonumber \\&\quad +\dfrac{F_0}{k}\dfrac{1}{1-r^2}\bigg [\cos \phi (\cos \omega _b t-\cos \omega _nt) \nonumber \\&\quad +\sin \phi (r\sin \omega _nt-\sin \omega _b t)\bigg ] \end{aligned}$$

(5)

The imposition of the conditions (3b) allows the finding of the unknown values of $x_0$ and $\phi$; substituting them in Eq. (5) and in its derivative:

where:

Hence:

Introducing the damping functionU(r) and the response functionV(r):

it is possible to write Eq. (8) as:

Substituting the results (10) in Eq. (5) and applying the condition (3b), it is finally possible to determine the amplitude of the mass motion:

$$\begin{aligned} x_0=\dfrac{F_0}{k}\sqrt{V^2-\bigg (\dfrac{\mu N}{F_0}\bigg )^2U^2} \end{aligned}$$

(11)

Equation (11) indicates as the ratio between the amplitude of mass vibration and its static displacement $F_0/k$ is not directly dependent on the applied force, but it is rather related to the ratio between friction and external force amplitudes; Den Hartog’s curves for such amplitude ratio are plotted in Fig. 4 at different values of the force ratio.

Fig. 4

Dimensionless amplitudes of vibration in a 1-DoF system with Coulomb friction

A fundamental issue of this approach is understanding when the solution (11) is valid. As the assumption of ${\dot{x}}<0$ was posed for all the internal points of the considered time interval, the solution x(t) must clearly respect this condition. Applying it to the derivative of Eq. (5), the condition obtained is:

$$\begin{aligned} x_0>\dfrac{\mu N}{k}\dfrac{S}{r^2} \end{aligned}$$

(12)

where:

$$\begin{aligned} S(r)=\max \limits _{0 \le t \le {\pi \over \omega _b}}\bigg [\dfrac{r\sin \omega _nt+Ur^2(\cos \omega _b t-\cos \omega _nt)}{\sin \omega _b t}\bigg ] \end{aligned}$$

From (11) and (12):

$$\begin{aligned} x_0>\dfrac{F_0}{k}\sqrt{\dfrac{V^2}{1+\bigg (\dfrac{Ur^2}{S}\bigg )^2}} \end{aligned}$$

(13)

so there is a unique limit condition for the validity of Eq. (11), independently of the ratio between friction and external force. The meaning of this condition (dotted in Fig. 4) is that, if ${\dot{x}}=0$ in any of the internal points of the time interval, a stop condition is occurring and the motion is no longer continuous. A particular behaviour is further highlighted in Fig. 4: only the curve corresponding to $\mu N/F_0=0.8$ shows a finite peak value at resonance, which is also shifted to the left ($r<1$). Den Hartog suggested that the lower value of force ratio for which a finite resonance is observed is:

$$\begin{aligned} \dfrac{\mu N}{F_0}=\dfrac{\pi }{4} \end{aligned}$$

(14)

The numerical simulation of the mass motion led in Sect. 5 allows to observe that this phenomenon is due to stick-slip occurrence at $r=1$. This means that Eq. (14) can be obtained by evaluating the force ratio at which the displacement transmissibility and boundary curves intersect for $r \rightarrow 1$. It can be shown that $S=1$ at resonance; from Eqs. (11) and (13):

$$\begin{aligned} \dfrac{\mu N}{F_0}= & {} \displaystyle {\lim _{r \rightarrow 1}}\bigg (-\dfrac{V}{U}\bigg ) \nonumber \\= & {} \displaystyle {\lim _{r \rightarrow 1}} \, \dfrac{r(1-\cos \pi /r)}{\sin \pi /r(r^2-1)}=\dfrac{\pi }{4} \end{aligned}$$

(15)

Fig. 5

Phase-angle diagram for a 1-DoF system with Coulomb friction

Den Hartog derives another limit condition for the non-stop motion from Eqs. (11) and (12); it can be written in terms of the ratio between friction and external forces:

$$\begin{aligned} \dfrac{\mu N}{F_0}<\sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg )^2+U^2}} \end{aligned}$$

(16)

Finally, a limit condition can be obtained also on the phase angle by using Eqs. (10), (11) and (16). The result from Den Hartog’s theory is plotted in Fig. 5.

3 Vibration transmission in base motion with fixed wall case

Den Hartog affirms that the approach introduced in Sect. 2 can be applied to the absolute motion of the mass excited from a harmonic base motion; the rubbing wall is supposed to be fixed. In this section, the main results deriving from this statement will be presented and discussed in terms of their impact on vibration transmission. Furthermore, a better understanding about the mass motion regime at high frequencies is carried out.

Fig. 6

1-DoF mass-spring system with friction contact under harmonic base excitation

Consider the 1-DoF system introduced in Fig. 2; be the mass excited from the monoharmonic motion of the base, rather than from an external force (Fig. 6). The equation of motion of such system can be written as:

$$\begin{aligned} m\ddot{x}+k(x-y)+\mu N \mathrm {sgn}({\dot{x}})=0 \end{aligned}$$

(17)

so, if the base motion is:

$$\begin{aligned} y(t)=Y_b\cos \omega _b t \end{aligned}$$

(18)

Eq. (17) becomes:

$$\begin{aligned} m\ddot{x}+kx+\mu N \mathrm {sgn}({\dot{x}})=kY_b\cos \omega _b t \end{aligned}$$

(19)

Comparing Eqs. (1) and (19), it is plain how the analytical results will be exactly the same, as observed in base motion problems for undamped systems [2], if $F_0=kY_b$, completely agreeing with Den Hartog’s observation. It is worth noting as this position is in no way introducing alterations in the response able to alter its accordance with Den Hartog’s assumptions. Therefore, the main results are obtained applying this trivial substitution and reported in Eqs. (20–23). The phase angle between force and displacement will be:

and the maximum amplitude of mass displacement will be:

$$\begin{aligned} x_0=Y_b\sqrt{V^2-\bigg (\dfrac{\mu N}{kY_b}\bigg )^2U^2} \end{aligned}$$

(21)

Fig. 7

Theoretical displacement transmissibility in a 1-DoF system under base motion with ground-fixed wall

The displacement transmissibility is defined as the ratio between the maximum response magnitude and input displacement magnitude at the input frequency [2]; it is usually plotted as a function of the frequency ratio. Therefore, here it is given exactly by the ratio $x_0/Y_b$ (Fig. 7):

$$\begin{aligned} \dfrac{|X|}{|Y|}=\sqrt{V^2-\bigg (\dfrac{\mu N}{kY}\bigg )^2U^2} \end{aligned}$$

(22)

The limit conditions for the non-stop motion have exactly the same formulation introduced in Sect. 2:

The most important implications of the presented results are:

• the possibility of a priori evaluation of the amplitude of the mass motion, if continuous;

• the possibility of forecasting the presence of mass sticking along the steady-state motion;

• being U, V and S functions of r, the above results depend only on two parameters, i.e. the frequency ratio itself and the force ratio between friction and spring force amplitudes:

  $$\begin{aligned} \dfrac{F_\mu }{F_k}=\dfrac{\mu N}{kY} \end{aligned}$$

This last property is particularly important for its impact on the design of friction dampers as it implies that the same result, in terms of steady-state motion, can be achieved with different set of parameters, as long as frequency and force ratios are unaltered; this property will be discussed extensively in Sect. 5.

Fig. 8

Transition force ratio value as a function of frequency ratio

The mass will indefinitely remain still if:

$$\begin{aligned} kY\le \mu N \end{aligned}$$

(24)

In this case, i.e. if the force ratio is at least equal to 1, the elastic force is never enough to overcome the friction force. When the condition (24) is not verified, the mass may exhibit both a continuous or a stick-slip motion but never be stationary.

In Fig. 7, it is not clear if the transmissibility curves always intersect the boundary line at high frequencies. A better way to analyse this problem is shown in Fig. 8, where the force ratio corresponding to the transition between continuous and stick-slip motion, described in condition (23b), is plotted as a function of the frequency ratio. It is possible to observe as the limit force ratio curve tends to an asymptotic value when $r \rightarrow +\infty$; this value is evaluated as:

$$\begin{aligned} \displaystyle {\lim _{r \rightarrow +\infty }}\sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg ) +U^2}}=\dfrac{2}{\sqrt{4+\pi ^2}}\cong 0.5370 \end{aligned}$$

(25)

It is therefore possible to affirm that regime transition at high frequencies will occur at a certain point only if the force ratio is higher than the above value.

Another important result which can be deducted from Fig. 8 is the existence of a maximum value of the transition force ratio, lower than 1, above which the continuous motion is not possible. Such value has been found to be:

$$\begin{aligned} \max \sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg )+U^2}}\cong 0.8265 \end{aligned}$$

(26)

and it is obtained at $r\cong 0.8490$. This is the last value of frequency ratio for which it is possible to observe a continuous motion while increasing the force ratio.

4 Vibration transmission in joined base-wall motion case

Another extension of Den Hartog’s theory is to vibration transmission when base and wall are moving together. Among his final annotations, Den Hartog [1] affirms:

If the rubbing wall be tied to the upper end of the spring and this end with the wall be subjected to the motion $y(t)=Y_b\cos \omega _b t$, the above solution (Sect. 2) holds for the relative motion between mass and wall, if only $F_0/k$ be replaced by $Y_br^2$.

This section discusses the implications of such statement in terms of the relative motion between mass and wall, presenting the results deriving from the suggested position. A more complete approach will be introduced with the goal of describing the mass absolute motion and, consequently, the actual displacement transmissibility and phase shift between excitation and response. The results show interesting similarities with viscously damped systems and also a more complex scenario in terms of possible motion regimes, due to the introduction of the frequency ratio in the above position.

Fig. 9

1-DoF mass-spring system with friction contact under harmonic joined base-wall excitation

Let us consider a 1-DoF system whose only difference with the system in Fig. 6 is that base and wall are jointed, therefore also the wall is subject to harmonic motion (Fig. 9). The equation of motion of such system differs from Eq. (17) only in terms of friction force: as the wall is moving, the relative velocity between the mass and the wall must be taken into account:

$$\begin{aligned} m\ddot{x}+k(x-y)+\mu N \mathrm {sgn}({\dot{x}}-{\dot{y}})=0 \end{aligned}$$

(27)

Introducing the new variable $z=x-y$ and substituting the expression of y(t), Eq. (27) becomes:

$$\begin{aligned} m\ddot{z}+kz+\mu N \mathrm {sgn}({\dot{z}})=m\omega _b^2Y_b\cos \omega _b t \end{aligned}$$

(28)

whence:

$$\begin{aligned} m\ddot{z}+kz+\mu N \mathrm {sgn}({\dot{z}})=kY_br^2\cos \omega _b t \end{aligned}$$

(29)

This equation is written in a coordinate system integral with base and wall in the form a forced vibration. The apparent external force acting on the mass is:

$$\begin{aligned} F(t)=kY_br^2\cos \omega _b t \end{aligned}$$

(30)

so, in agreement with Den Hartog’s statement, the solution holds for the relative mass-wall motion if the relation:

$$\begin{aligned} F_0=kY_br^2 \end{aligned}$$

(31)

is verified. Applying this condition to the solution (5), it yields:

$$\begin{aligned} z(t)&=z_0\cos \omega _nt+\dfrac{\mu N}{k}(1-\cos \omega _nt) \nonumber \\&\quad +\dfrac{Y_br^2}{1-r^2} \bigg [\cos \phi (\cos \omega _b t-\cos \omega _nt) \nonumber \\&\quad +\sin \phi (r\sin \omega _nt-\sin \omega _b t)\bigg ] \end{aligned}$$

(32)

where the values of $\phi$ and $z_0$ are obtained from the boundary conditions (3a–3b), expressed in terms of the variable z. So:

and:

$$\begin{aligned} z_0=Y_br^2\sqrt{V^2-\dfrac{1}{r^4}\bigg (\dfrac{\mu N}{kY_b}\bigg )^2U^2} \end{aligned}$$

(34)

The dimensionless amplitude of the relative motion between mass and wall is then represented as a function of the frequency ratio in Fig. 10; the limit of validity of Den Hartog’s theory for such motion can be derived from the condition ${\dot{z}}<0$, exactly as in Sect. 2, or more simply imposing the position (31) in Eq. (13):

$$\begin{aligned} \dfrac{|Z|}{|Y|}> r^2\sqrt{\dfrac{V^2}{1+\bigg (\dfrac{Ur^2}{S}\bigg )^2}} \end{aligned}$$

(35)

Fig. 10

Dimensionless amplitude of the relative motion between mass and wall

Fig. 11

Phase angle between excitation and relative mass-wall displacement

Observing Fig. 10, it is also clear as there will be no intersections between the amplitude curves and the boundary described by Eq. (35) at high frequencies, where Den Hartog’s assumptions will be therefore always verified. Figure 11 shows the phase angle between the excitation y(t) and the relative mass-wall motion z(t) as evaluated from Eq. (33). From now on, such angle will be indicated as $\phi _{yz}$ in order not to confuse it with the phase shift between base and mass motion.

Fig. 12

Steady-state continuous motion of a 1-DoF system under joined base-wall motion

If the relative mass-wall motion can be easily studied as an extension of Den Hartog’s theory, this is not true for the mass absolute motion. Even if a relation between $z_0$ and $x_0$ can be found as:

$$\begin{aligned} x_0&=z_0+y_0=z_0+Y_b\cos \phi _{yz} \nonumber \\&=z_0+\dfrac{z_0}{Vr^2}=z_0\dfrac{r^2+1-r^2}{r^2}=\dfrac{z_0}{r^2} \end{aligned}$$

(36)

it appears evident from Fig. 12 that $x_0$ is different from the maximum absolute value |X| assumed by x(t) in the time interval $[0, \pi /\omega _b]$. In order to evaluate the displacement transmissibility, it is necessary to know the amplitude of the motion x(t), i.e.:

$$\begin{aligned} |X|=\max \limits _{t\in [0, {\pi \over \omega _b}]}|x(t)| \end{aligned}$$

(37)

where:

$$\begin{aligned} x(t)=y(t)+z(t) \end{aligned}$$

(38)

By using Eqs. (18) and (32), x(t) can be written as:

$$\begin{aligned} x(t)&=x_0r^2\cos \omega _nt+\dfrac{\mu N}{k}(1-\cos \omega _nt) \nonumber \\&\quad +Y_b\cos (\omega t+\phi _{yz}) +\dfrac{Y_br^2}{1-r^2} \nonumber \\&\quad \bigg [\cos \phi _{yz}(\cos \omega _b t -\cos \omega _nt) \nonumber \\&\quad +\sin \phi _{yz}(r\sin \omega _nt-\sin \omega _b t)\bigg ] \end{aligned}$$

(39)

Fig. 13

Graphical identification of mass motion regime on frequency ratio–force ratio plane

The approach developed for the evaluation of the displacement transmissibility is based on a maximum problem rather than on a specific analytical expression. For this reason, it is not possible to impose a limit condition for the continuous motion in terms of this quantity, as done in Eqs. (13) and (23a). Nevertheless, it is possible to write it in terms of force ratio from Eq. (16):

$$\begin{aligned} \dfrac{F_\mu }{F_k}< r^2\sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg )^2+U^2}} \end{aligned}$$

(40)

As confirmed numerically in Sect. 5, if the force ratio is larger than such limit value, a relative stick-slip motion will occur between mass and wall. An important reflection must be made also on the condition for mass complete sticking: if Eq. (24) states that in the fixed wall case this is achieved for a unitary force ratio, independently of the frequency ratio, in the joined base-wall motion case mass motion is not possible when the amplitude of the apparent external force acting on the mass itself does not overcome the friction force amplitude:

$$\begin{aligned} kY_br^2\le \mu N \end{aligned}$$

(41)

whence:

$$\begin{aligned} r\le \sqrt{\dfrac{F_\mu }{F_k}} \end{aligned}$$

(42)

The relation (42) has two important implications:

• mass motion is possible also at force ratio values larger than 1, if the frequency ratio is high enough;

• mass may stick completely at low frequencies even if the force ratio is minor than 1.

Equations (40) and (42) result in three mass behaviours which can be identified for specific values of frequency and force ratios also via graphic approach as proposed in Fig. 13. The above conditions divide the frequency ratio–force ratio plane into three regions corresponding to as many motion regimes: it is particularly interesting to observe as there is no overlap between the two curves. Consequently, whatever the force ratio, there is always a range of frequencies for which it is possible to observe stick-slip motion; nevertheless, such range is notably narrower when the force ratio is around 0.5.

Fig. 14

Theoretical displacement transmissibility in a 1-DoF system under joined base-wall motion (a) and detail of the inversion (b)

The displacement transmissibility |X| / |Y| has been evaluated in the continuous motion region by determining numerically the maximum value of x(t) as described in Eqs. (37–39) and the resulting curves are portrayed in Fig. 14a at different force ratios. The limit condition, represented by Eq. (40), can be imposed during the evaluation of each transmissibility curve, in such a way to plot the value only when the motion is continuous. Particularly, the dotted line has been obtained reiterating the procedure for all the force ratios in the interval [0,1.5] and provides a graphical representation of the transition from stick-slip to continuous motion.

Furthermore, Fig. 14a shows as the condition (14) is valid also for the joined base-wall motion: all the resonant peaks obtained for high force ratios have a finite value and increasing such ratio it is notable as they get more and more smoothed and shifted at higher frequencies. When $r\gg 1$, transmissibility tends to zero, so the mass will have more and more narrow oscillations independently of wall motion till getting asymptotically stationary.

One of the most interesting elements highlighted in Fig. 14a is the presence of an inversion of the curves (in details in Fig. 14b), a phenomenon observable also in viscous systems subject to base motion: the vibration transmission becomes wider by effect of the damping. It is worth underlining the physical similitude between the motion here analysed and the well-known base motion problem applied to viscous 1-DoF systems (Fig. 1): in both these cases, the motion is transmitted not only through the spring but also through the damper (whatever dashpot or friction contact). Despite no resemblance being found between the analytical models employed for viscous and dry Coulomb damping, these similarities offer some interesting elements for a comparison:

• whereas the inversion always occurs at $r_{\mathrm{inv}}=\sqrt{2}$ in the presence of viscous damping, here the phenomenon appears to occur at very slightly higher frequencies and in a very narrow region $1.4<r_{\mathrm{inv}}<1.55$ rather than in a single point;

• transmissibility value at the inversion with Coulomb damping is not equal to 1 as in the viscous case but a bit lower.

It is opportune to point out that, although possible, transmissibility curves have not been plotted at force ratios higher than 1.4; the motivation of this choice resides in the impossibility to catch the inversion or any other phenomena of interest at larger values of such ratio, due to stick-slip occurrence (see Fig. 13).

A last challenge for achieving a full description of mass response to joined base-wall motion is the determination of the steady-state phase angle $\phi _{xy}$ between the excitation and the response. Whereas the phase angle $\phi _{yz}$ has already been obtained analytically from Eq. (33) and represented in Fig. 11, $\phi _{xy}$ must clearly be obtained numerically, as it is referred to x(t) and y(t) maxima.

Fig. 15

Phase angle between relative mass-wall displacement and absolute mass motion

Fig. 16

Phase angle between relative excitation and absolute mass motion

The first step is the numerical evaluation of the time instant $t_{xz}\in [0,\pi /\omega _b]$ where the maximum of |x(t)| is reached; this allows the calculation of the phase angle $\phi _{xz}$ between absolute and relative mass motions:

In Fig. 15, it is possible to see that $\phi _{xz}$, just as $\phi _{yz}$, always belongs to the interval $[0,180^{\circ }]$ (see Fig. 11): this means that both x(t) and y(t) peaks anticipate z(t) (which is the origin of the time coordinate system) and their observed absolute maximum value will be negative as a consequence. Also, $\phi _{yz}$ is always larger than $\phi _{xz}$ and so (as expected) the negative peak of x(t) will always follow the negative peak of y(t). Therefore, Fig. 12 is well representative of the problem in terms of peaks position and it is completely fair to evaluate $\phi _{xy}$ as:

$$\begin{aligned} \phi _{xy}=(\pi -\phi _{xz})-(\pi -\phi _{yz})=\phi _{yz}-\phi _{xz} \end{aligned}$$

(44)

The results are finally reported in Fig. 16.

5 Numerical validation and extension to stick-slip motion regime

A numerical model in MATLAB [12] has been employed for the validation of the theory presented in the previous sections. The code is based on the numerical resolution of the differential equations of motion of the 1-DoF systems introduced above; beyond the validation goal, this approach is able to provide results also outside the region of validity of Den Hartog’s theory, for the stick-slip motion, as no assumptions were made here regarding mass motion continuity.

5.1 Base motion with fixed wall case

The base motion problem introduced in Sect. 3 is governed by Eq. (19). Den Hartog’s approach reveals the dependency of the motion on two parameters, the frequency ratio and the force ratio: it is possible to demonstrate how this property can be extended also to the general solution, including transients and the possibility of a stick-slip behaviour.

Fig. 17

Numerical evaluation of displacement transmissibility in a mass-spring-fixed wall system (a) and detail of the curves outside the boundaries of the analytical forecast (b)

The equation of motion presents seven variables: t, m, k, $\mu$, N, $Y_b$ and $\omega _b$. Only three dimensions are required to describe such quantities: [kg], [m] and [s]. According to Buckingham’s theorem [13], it should be possible to identify at least four dimensionless groups in Eq. (19). Therefore, introducing, for instance, dimensionless time and position as:

it would be expected to obtain a dimensionless equation where only two other dimensionless parameters are present. Introducing the statement (45) in Eq. (19), it is possible to write:

$$\begin{aligned}&m\omega _n^2Y_b\dfrac{d^2 {\bar{x}}}{d \tau ^2}+kY_b{\bar{x}}+\mu N\mathrm {sgn}\bigg ({\omega _nY_b\dfrac{d {\bar{x}}}{d \tau }}\bigg ) \nonumber \\&\quad =kY_b\cos r\tau \end{aligned}$$

(46)

Dividing by $kY_b$ and removing any positive constants from the argument of the sgn function:

$$\begin{aligned} \dfrac{m\omega _n^2}{k}{\bar{x}}''+{\bar{x}}+\dfrac{\mu N}{kY_b}\mathrm {sgn}({\bar{x}}')=\cos r\tau \end{aligned}$$

(47)

therefore:

$$\begin{aligned} {\bar{x}}''+{\bar{x}}+\dfrac{F_\mu }{F_k}\mathrm {sgn}({\bar{x}}')=\cos r\tau \end{aligned}$$

(48)

Equation (48) is a dimensionless form of the governing equation of the problem, and it shows clearly the solution dependency on the above-mentioned ratios only, as well as on the dimensionless time. This result implies that it is possible to approach the transmissibility analysis for a stick-slip motion numerically still referring only to r and $F_\mu /F_k$, without the necessity to know all the other mentioned parameters.

In order to solve Eq. (48) in MATLAB with the ode45 function, it is required to write it as a system of first order differential equations [12]. This is achieved defining $x_1={\bar{x}}$, so that:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x_1}=x_2 \\ \dot{x_2}=\cos r\tau -x_1-\dfrac{F_\mu }{F_k}\mathrm {sgn}(x_2) \end{array} \right. \end{aligned}$$

(49)

Fig. 18

Comparison between analytical and numerical displacement transmissibility in a mass-spring-fixed wall system

Fig. 19

Examples of mass response in different motion regimes

The transmission parameters must be investigated only in the steady-state condition, so the first part of the response, which is dominated by the initial conditions, can be disregarded. As for the time interval, it is fundamental to impose a fixed time step during the simulation in order to obtain correct information in frequency domain; recalling that the sampling frequency is:

$$\begin{aligned} f_\mathrm{s}=\dfrac{1}{\mathrm{d}t} \end{aligned}$$

(50)

it will be necessary to keep it at least two times higher than the maximum frequency considered in the problem [14]. Introducing the dimensionless time, it is possible to refer directly to the dimensionless frequency ${\bar{f}}=f/f_n$; this quantity is exactly the frequency ratio r when $f=f_b$. Substituting $\tau$ and ${\bar{f}}$ in Eq. (50), the dimensionless sampling frequency is evaluated as:

$$\begin{aligned} {\bar{f}}_\mathrm{s}=\dfrac{2\pi }{\mathrm{d}\tau } \end{aligned}$$

(51)

The length of the time interval will affect the resolution of the frequency spectrum, and anyway, it has to be such not to lose information on the steady-state behaviour.

Analysing the frequency spectra of $x(\tau )$ and $y(\tau )$, it will be possible to obtain the displacement transmissibility as:

$$\begin{aligned} \dfrac{|X(r)|}{|Y(r)|} \end{aligned}$$

and to plot the response in all the range of interest in order to observe if other contributes are present at different frequencies. The code can, at last, be easily reiterated for all the values of frequency ratio in the chosen range $0\le r\le 5$.

The overall displacement transmissibility is portrayed in Fig. 17a at different force ratios, while Fig. 17b shows in detail the evolution of the transmissibility curves at low frequency ratios, where Den Hartog’s theory cannot be applied. An excellent agreement between theoretical and numerical transmissibilities is achieved in Fig. 18. Nevertheless, some minor discrepancies can be observed at the transition from stick-slip to continuous regime.

In Fig. 17a, b it is possible to observe a series of properties across the different curves, also outside the region of validity of Den Hartog’s theory, related to the different motion regimes represented in Fig. 19.

• The quasi-static motion is characterised by very low values of transmissibility, inversely proportionally to force ratio. This behaviour occurs during the multiple stops regime (Fig. 19a), where friction effect is very strong.

• In the two stops regime (Fig. 19b), the transmissibility is increased by friction, except in the case of very high force ratio ($F_\mu /F_k=0.8$). Further, this effect appears to end always at $r\cong 0.6$, where an inversion of the curves with $F_\mu /F_k<\pi /4$ can be observed.

• Even if Den Hartog’s forecast on regime transition is accurate in terms of r value, displacement transmissibility is higher than expected around the transition frequency and there is no real intersection between the numerical curves and the theoretical boundary condition.

• At higher driving frequencies, when the regime is plainly continuous (Fig. 19c), the theoretical results are extremely accurate.

• When the driving and the natural frequencies are very close, the beating phenomena will occur (Fig. 19d).

• While the resonant peak is infinite for $F_\mu /F_k<\pi /4$ and the response never reaches a steady-state condition, Fig. 19e shows how for high force ratios a stick-slip behaviour occurs also when the system is driven at resonance and a steady-state condition is reached after a few cycles. In this case, the peak value is finite and it appears at frequency ratios lower than 1, where the motion is still continuous and has a larger amplitude (Fig. 18d).

• At very high values of r stick-slip will occur again if the force ratio is high enough, as stated in Eq. (25).

Fig. 20

Numerical evaluation of displacement transmissibility in a mass-spring-moving wall system

5.2 Joined base-wall motion case

The approach introduced in Sect. 5.1 holds also for the joined base-wall motion problem. The governing equation for the relative mass-wall motion (29) can be expressed in the same form of Eq. (48) introducing the dimensionless time presented in Eq. (45) and the dimensionless relative position:

$$\begin{aligned} {\bar{z}}=\dfrac{z}{Y_b} \end{aligned}$$

(52)

Therefore, the final expression is:

$$\begin{aligned} {\bar{z}}''+{\bar{z}}+\dfrac{F_\mu }{F_k}\mathrm {sgn}({\bar{z}}')=r^2\cos r\tau \end{aligned}$$

(53)

while mass absolute motion can be obtained from:

$$\begin{aligned} {\bar{x}}={\bar{z}}+\cos r\tau \end{aligned}$$

(54)

By imposing $z_1={\bar{z}}$, the state-space representation of Eq. (53) is written as:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z_1}=z_2 \\ \dot{z_2}=r^2\cos r\tau -z_1-\dfrac{F_\mu }{F_k}\mathrm {sgn}(z_2) \end{array} \right. \end{aligned}$$

(55)

Fig. 21

Comparison between analytical and numerical displacement transmissibility in a mass-spring-moving wall system. Dark grey, light grey and white regions represent, respectively, the analytical forecast for sticking, stick-slip and sliding motion

Fig. 22

Numerical evidence of relative stick-slip motion between mass and wall ($r=0.95$, $F_\mu /F_k=0.8$)

The numerical transmissibilities, portrayed in Fig. 20 as functions of the frequency ratio, offer a very good agreement with the curves obtained in Sect. 4, as shown in Fig. 21. It is possible to appreciate also the agreement with the forecast on motion regime introduced in Fig. 13.

• At the beginning of each curve, where the mass is supposed to remain still on the wall, the transmissibility is always equal to 1, as there is no relative motion respect to wall (see Eq. 42).

• When the motion starts, a very narrow decrease of transmissibility can be observed unless the force ratio is very low as in Fig. 21. This means that the occurrence of the relative stick-slip motion between mass and wall, shown in Fig. 22, implies a reduction in amplitude in the mass absolute motion.

An interesting result can be observed in Fig. 21e, f. When the force ratio is very large, the resonant peak gradually decreases until it disappears. This type of behaviour is quite similar to the one observed for overdamped viscous systems. In this case, the peak disappears because, increasing the force ratio, complete sticking and stick-slip regimes occur at higher and higher frequency ratios until damping completely the original peak.

6 Concluding remarks

A new approach has been developed for the evaluation of the main properties of a 1-DoF system with Coulomb friction under harmonic (i) base excitation with ground-fixed wall; (ii) joined base-wall excitation.

Den Hartog’s theory on forced vibrations in the presence of Coulomb damping [1] was extended successfully to base motion with fixed wall case, allowing a better understanding of the problem and highlighting its impact also in friction dampers design; a few innovative results were presented in terms of stick-slip occurrence at high frequencies and maximum value of force ratio allowing a continuous mass motion at least at one value of frequency ratio.

Joined base-wall motion problem was dealt with extensively, extending Den Hartog’s theory to relative mass-wall motion and introducing a new analysis regarding mass absolute motion. The key results were: (i) the development of new understanding about the motion regimes and how they are supposed to occur depending on frequency and force ratios; (ii) the evaluation of the displacement transmissibility and a qualitative comparison with its evolution in viscous systems, particularly focused on the existence in both the cases of a inversion of the curves at high frequencies, where damping amplifies the transmission; (iii) a method for the evaluation of the phase shift between excitation and response.

The numerical resolution of the differential governing equations of these problems allowed: (i) the comparison between analytical and numerical displacement transmissibilities, which showed an excellent agreement between the two approaches; (ii) the validation of the theoretical boundary identifying stick-slip and continuous motion regions in the frequency ratio–force ratio plane; (iii) an interesting insight into transmissibility evolution in the stick-slip region. The development of an alternative formulation of the differential equations highlighted how mass motion can be described through only two parameters, the frequency ratio and the force ratio, independently of Den Hartog’s assumption. This means that also the stick-slip motion can be analysed relying only on these parameters and a complete description of the transmissibility can be achieved integrating the theoretical and the numerical approaches. Finally, the numerical curves allowed to observe the gradual disappearing of the resonant peak when the force ratio increases over $\pi /4$. The main goal of the numerical approach was to provide a validation for the proposed analytical results. Further validation of the presented results can be achieved with an experimental investigation; however, this is not the focus of this paper.

Overall, the presented results give information that can support the design of friction joints for several engineering structures. Experimental testing validating the results presented in this paper will be discussed in a separate publication.