1 Introduction

Mathieu equations describe parametrically driven oscillators. They have been investigated for decades using a variety of techniques like harmonic balance, Lindstedt–Poincare perturbation theory, multiple timescale techniques and Krylov–Bogoliubov amplitude and phase equations. An important feature of the Mathieu equation is that systems described by it show instability in a set of tongue-shaped regions in the parameter space spanned by the driving frequency and the amplitude of the drive. The tongues emanate from certain points on the frequency axis where the natural frequency is \(\frac{n}{2}\) times the driving frequency with \( n=1,2,3\ldots \) being the set of integers. The motion is strictly periodic only on the lines separating the stable from the unstable zones. In the stable zone, the motion is quasi-periodic in general. The techniques referred to above are used to study the boundaries where the motion is periodic. These techniques have been covered comprehensively in various texts and lecture notes (e.g. [1,2,3]). The study of coupled Mathieu equations became popular about three decades ago and can be found in the treatment of elastic pendula (two coupled degrees of freedom) [4], in the study of colliding particle beams in a two-dimensional accelerator [5] or in the description of two-mode dynamics of rotating rings with variable spin-speed [6]. The fact that the usual techniques for obtaining the boundaries of the single- variable Mathieu equation can be used to calculate the unstable zones of the coupled system was demonstrated clearly by Mahmoud [7].

More recently, a different perspective on this class of problems was discussed by Landa et al. [8]. While the usual emphasis had been on finding the instability zones and the periodic solutions on the boundary of the instability zones, these authors developed a technique for finding the classical as well as the quantum solutions in the region where the motion is bounded. One of the important problems addressed in this work is the one-dimensional quantum parametric oscillator which describes the motion of a single ion confined in a radio-frequency trap [9]. A comprehensive account of the existence of periodic orbits for a variety of generalised forms of the Mathieu equation was provided by Younesian et al. [10]. This included nonlinear Mathieu equations treated by harmonic balance and averaging [11], bifurcations in cubic Mathieu equations [12] and resonances in quasi-periodic Mathieu equations [13]. Another direction in which the Mathieu equation was extended was the introduction of time delay [14]. That the usual perturbative techniques associated with the Mathieu equation could be used for a nonlinear Mathieu equation with delay was established by Morrison and Rand [15]. Yet another extension of these driven systems has been the introduction of systems with fractional derivatives. The appropriateness of the usual perturbative techniques for exploring the regions of bounded motion has recently been established [16,17,18].

While the second-order (recently even fractional order) non-autonomous differential equations, which is the class to which the Mathieu equation belongs, have been studied from a formal mathematical standpoint as well as from the applicational viewpoint of perturbation theory, the higher-order equations have been, to the best of our knowledge, studied only from a formal perspective [19,20,21,22]. It turns out that the one-dimensional quantum parametric oscillator discussed above gives rise to an infinite set of higher-order Mathieu like equations. Our aim in this paper will be to explore the effectiveness of the usual perturbative techniques to study the unstable zones of these higher-order Mathieu-like equations. We will use known perturbative techniques to find the boundaries between the regions where the solution is bounded and where they are unbounded. It will turn out that the boundaries thus obtained will agree with the boundaries obtained numerically.

A combination of Heisenberg’s equation of motion and Ehrenfest’s theorem in quantum mechanics describes the time development of the expectation value of any operator \({\mathcal {O}}(x)\) under a given Hamiltonian \({\mathcal {H}}\). If \(\varPsi (x,t)\) is the wave function at any time t (we consider only one- dimensional space), then the expectation value is \(\langle {\mathcal {O}} \rangle =\int _{-\infty }^{\infty }\varPsi ^{*}(x,t){\mathcal {O}}(x) \varPsi (x,t)\hbox {d}x\) and Ehrenfest’s theorem states

$$\begin{aligned} i \hbar \dfrac{\hbox {d}}{\hbox {d}t}\langle {\mathcal {O}} \rangle =\langle [{\mathcal {O}},{\mathcal {H}}]\rangle \end{aligned}$$
(1)

where \(\langle [{\mathcal {O}},{\mathcal {H}}]\rangle \) is the commutator of \({\mathcal {O}}\) and \({\mathcal {H}}\). A quantum mechanical state is prescribed by \(\varPsi (x,t)\) which is a complex valued function generally written as \(\varPsi (x,t)=\sqrt{P(x,t)}e^{i \phi (x,t)}\), where \(P(x,t)=|\varPsi (x,t)|^2\) is the probability distribution associated with the state at any time t. Ehrenfest’s theorem has rarely been used except to study classical trajectories. However, it can provide useful information about various moments of the probability distribution and as such can yield information regarding the form of the distribution. A particularly interesting situation is the motion of a particle in a time-dependent harmonic trapping function represented by the potential \({\mathcal {V}}=\frac{1}{2} \mathrm{m}\omega ^2 x^2 (1 + \epsilon f(t))\) where f(t) is a periodic function with period \(T=\frac{2 \pi }{\varOmega }\). The Hamiltonian operator for the quantum parametric oscillator is [23]

$$\begin{aligned} {\mathcal {H}}=\frac{p^2}{2 m}+\frac{1}{2} \mathrm{m}\omega ^2 x^2 (1 + \epsilon f(t)) \end{aligned}$$
(2)

with \(f(t)=f(t+T)=f(t+\frac{2 \pi }{\varOmega })\). In the above, \(p=-i \hbar \frac{\hbox {d}}{\hbox {d}x}\) is the momentum operator. In this case, for an initial wave function which is Gaussian, the time development of \(\varPsi (x,t)\) can be found if the dynamics is in the part of \(\omega -\epsilon \) space where the classical motion is bounded [24,25,26,27]. For arbitrary initial wave functions, it is virtually impossible to arrive at the time development exactly. In this situation, Ehrenfest’s theorem is very useful since it provides exact equations for all the moments. Each moment gives rise to a non-autonomous dynamical [28] system, and this very physical problem gives rise to the whole set of interesting mathematical systems which are worth studying in their own right. In this work, we will focus on the mathematical aspects of the dynamical systems arising from Ehrenfest’s theorem for the moments.

The process of arriving at the equations of motion is straightforward. One needs to use Eq. (1) and carry out evaluation of \([{\mathcal {O}},{\mathcal {H}}]\) with the \({\mathcal {H}}\) of Eq. (2). As an example, we explicitly work out the first moment \(\langle x \rangle \) which represents the mean position of the quantum particle. From Eq. (1) and the basic commutation relation \([x,p]=i\hbar \), we see that

$$\begin{aligned} \dfrac{\hbox {d}}{\hbox {d}t}\left\langle x \right\rangle= & {} \frac{1}{i \hbar }\left\langle \left[ x,\frac{p^2}{2 m}+\frac{1}{2} \text {m}\omega ^2 x^2 \left( 1 + \epsilon f(t)\right) \right] \right\rangle \nonumber \\= & {} \frac{1}{i \hbar }\left\langle \left[ x,\frac{p^2}{2 m}\right] \right\rangle =\frac{\left\langle p \right\rangle }{m} \end{aligned}$$
(3)

and

$$\begin{aligned} \dfrac{\hbox {d}}{\hbox {d}t}\left\langle p \right\rangle= & {} \frac{1}{i \hbar }\left\langle \left[ p,\frac{p^2}{2 m}+\frac{1}{2} \text {m}\omega ^2 x^2 \left( 1 + \epsilon f(t)\right) \right] \right\rangle \nonumber \\= & {} \frac{1}{i \hbar }\frac{1}{2} \text {m}\omega ^2\left\langle \left[ p,x^2 \left( 1 + \epsilon f(t)\right) \right] \right\rangle \nonumber \\= & {} - \text {m}\omega ^2 \left\langle x \right\rangle \left( 1 + \epsilon f(t)\right) \end{aligned}$$
(4)

One move derivative of Eq. (3) and use of Eq. (4) leads to

$$\begin{aligned} \frac{\hbox {d}^2}{\hbox {d}t^2} \langle x \rangle + \omega ^2 (1 + \epsilon f(t))\langle x \rangle = 0 \end{aligned}$$
(5)

This is the dynamics of the mean position of the particle, and it follows the classical trajectory obtained from the Hamiltonian of Eq. (2).

If \(f(t)=\cos (\varOmega t)\), then we have the familiar Mathieu equation.

$$\begin{aligned} \frac{\hbox {d}^2}{\hbox {d}t^2} \langle x \rangle + \omega ^2 (1 + \epsilon \cos (\varOmega t))\langle x \rangle = 0 \end{aligned}$$
(6)

The dynamics of all moments \(\langle x^n \rangle \) have to be obtained by a process of repeated differentiation and use of Eq. (1). The moments \(\langle x^n \rangle \) are associated with different features of the probability distribution. In particular for \(n=2\),

$$\begin{aligned} V=\langle x^2 \rangle -\langle x \rangle ^2 \end{aligned}$$
(7)

is the variance. This is the most important moment as its nonzero value signals a complete departure from classical physics. For \(n=3\), we have

$$\begin{aligned} S=\left\langle (x -\left\langle x \right\rangle )^3\right\rangle , \end{aligned}$$
(8)

which is the skewness, and for \(n=4\)

$$\begin{aligned} K=\left\langle (x -\left\langle x \right\rangle )^4\right\rangle , \end{aligned}$$
(9)

which is the kurtosis of the distribution. We write down the equations of motion (the derivation of the dynamics of V is shown in “Appendix A”, the others follow in a similar manner)

$$\begin{aligned}&\frac{\hbox {d}^3}{\hbox {d}t^3} V +4\omega ^2(1 + \epsilon f(t))\frac{\hbox {d}}{\hbox {d}t} V + 2\omega ^2 \epsilon {\dot{f}}V=0 \end{aligned}$$
(10)
$$\begin{aligned}&\dfrac{\hbox {d}^4}{\hbox {d}t^4} S +10\omega ^2(1 + \epsilon f(t))\frac{\hbox {d}^2}{\hbox {d}t^2} S + 9\omega ^4(1 + \epsilon f(t))^2 S \nonumber \\&\quad +\, 10\omega ^2 \epsilon {\dot{f}} \frac{\hbox {d}}{\hbox {d}t}S+3\omega ^2 \epsilon \ddot{f} S=0 \end{aligned}$$
(11)

and

$$\begin{aligned}&\frac{\hbox {d}^5}{\hbox {d}t^5} K +20\omega ^2(1 + \epsilon f(t))\frac{\hbox {d}^3}{\hbox {d}t^3} K +24\omega ^2 \epsilon {\dot{f}} \frac{\hbox {d}^2}{\hbox {d}t^2}K\nonumber \\&\quad +\, 64\omega ^4(1 + \epsilon f(t))^2 \frac{\hbox {d}}{\hbox {d}t}K + 18\omega ^2 \epsilon \ddot{f} \frac{\hbox {d}}{\hbox {d}t} K\nonumber \\&\quad +\,64\omega ^4 \epsilon (1 + \epsilon f(t)) {\dot{f}} K+4\omega ^2 \epsilon \dddot{f} K=0 \end{aligned}$$
(12)

For the discussions in this paper, we will focus entirely on \(f(t)=\cos (\varOmega t)\).

The properties of Mathieu equation (Eq. 6) are well known [1,2,3]. We will recall them in Sect. 2 to carefully explain the perturbation theory technique that we will use and the numerical procedure that we will follow in the rest of the paper.

If we consider the dynamics of the variance V and redefine \(4\omega ^2\) as \({\bar{\omega }}^2\), then Eq. (10) becomes for \(f(t)=\cos (\varOmega t)\)

$$\begin{aligned}&\frac{\hbox {d}^3 V}{\hbox {d}t^3} +{\bar{\omega }}^2(1 + \epsilon \cos (\varOmega t) )\frac{\hbox {d}V}{\hbox {d}t}\nonumber \\&\quad -\, \frac{\epsilon {\bar{\omega }}^2}{2} \varOmega \sin (\varOmega t)V=0 \end{aligned}$$
(13)

We further simplify by redefining the combination \( \epsilon {\bar{\omega }}^2 \) as \({\bar{\epsilon }}\), so that

$$\begin{aligned}&\frac{\hbox {d}^3 V}{\hbox {d}t^3} +{\bar{\omega }}^2\frac{\hbox {d}V}{\hbox {d}t} +{\bar{\epsilon }} \cos (\varOmega t)\frac{\hbox {d}V}{\hbox {d}t}\nonumber \\&\quad -\frac{\bar{\epsilon }}{2} \varOmega \sin (\varOmega t)V=0 \end{aligned}$$
(14)

The above equation corresponds to the dynamical system with the structure \(X_{i}=A_{ij}(t)X_{j}\) with \(A_{ij}(t)=A_{ij}(t+\frac{2 \pi }{\varOmega })=A_{ij}(t+T)\).

Explicitly,

$$\begin{aligned} {\dot{V}}= & {} U \end{aligned}$$
(15a)
$$\begin{aligned} {\dot{U}}= & {} W \end{aligned}$$
(15b)
$$\begin{aligned} {\dot{W}}= & {} -{\bar{\omega }}^2 U - {\bar{\epsilon }} \cos (\varOmega t) U +\frac{{\bar{\epsilon }} }{2} \varOmega \sin (\varOmega t)V \end{aligned}$$
(15c)

The trace of the matrix \(A_{ij}(t)\) is clearly zero, and hence, the three Floquet multipliers \(\mu _1, \mu _2\) and \(\mu _3\) satisfy \(\mu _1 \mu _2 \mu _3=1\). Consequently, the periodic solutions can have the periods T, 2T and 3T. For a subharmonic response of period 3T (frequency \(\frac{\varOmega }{3}\)), we would have periodic solutions originating from \({\bar{\omega }}=\frac{\varOmega }{3},\frac{4 \varOmega }{3}\ldots ,\) etc. For a periodic response of period 2T, the solutions start at \({\bar{\omega }}=\frac{\varOmega }{2}, \frac{3 \varOmega }{2}\ldots ,\) etc and for a response of period T, the solutions start at \({\bar{\omega }}=\varOmega , 2\varOmega \ldots ,\) etc.

In a similar fashion, the equations of motion of S and K are in principle capable of showing periodicities T, 2T, 3T, 4T and T, 2T, 3T, 4T, 5T, respectively.

Using different perturbation techniques [2], we will study the properties of the dynamical systems shown in Eqs. (10)–(12). The techniques (harmonic balance and Krylov–Bogoliubov) will be geared to finding the periodic trajectories. In the case of Eq. (13) specifically, we obtain the following:

  • A) Harmonic balance shows that period 3T trajectories exist only on a curve emanating from \({\bar{\omega }}=\frac{\varOmega }{3}\) with no instability zones in the vicinity of \(\frac{\varOmega }{3}\).

  • B) A similar situation holds in the vicinity of \({\bar{\omega }}=\frac{\varOmega }{2}\), although the structure of Eq. (13) would have indicated otherwise.

  • C) In the vicinity of \({\bar{\omega }}=\varOmega \), the Krylov–Bogoliubov technique reveals the existence of two curves corresponding to the periodic orbits emanating from this point. In the region bounded by the two curves lies the instability zone where the solutions are unbounded. The boundaries, quite surprisingly, happen to be identical to that for Eq. (6) a result confirmed by our numerical studies.

For Eq. (11), the conclusions are qualitatively similar with the unstable zone emanating from \({\bar{\omega }}=\varOmega \) alone. For Eq. (12), however, we have instability zones emanating from \({\bar{\omega }}=\frac{\varOmega }{4},\frac{\varOmega }{2}~and~\varOmega \). In this case, the instability zone emanating from \({\bar{\omega }}=\varOmega \) is far wider than those for Eqs. (6), (10) and (11).

We briefly recapitulate the primary results of the Mathieu equation in Sect. 2. In Sect. 3, we deal with the dynamics of the variance in detail, and in Sect. 4, we study the skewness and the kurtosis. We conclude with a short summary in Sect. 5.

2 Properties of Mathieu equation

In this section, we review the properties of the Mathieu equation which is a second-order differential equation

$$\begin{aligned} {\ddot{X}}+\omega ^2 X + \epsilon \cos (\varOmega t) X=0. \end{aligned}$$
(16)

It has the dynamical system form \({\dot{X}}=Y~\text {and}~{\dot{Y}}=-(\omega ^2 +\epsilon \cos (\varOmega t)X)\). Since the dynamical system is traceless, the two Floquet multipliers \(\mu _{1,2}\) satisfy \(\mu _1 \mu _2 =1\). This means that the system can have responses of period T and 2T. Since \(T=\frac{\varOmega }{2\pi }\), harmonic balance indicates that period 2T solutions should emerge from \(\omega =\frac{\varOmega }{2}\) and period T solution should emerge from \(\omega =\varOmega \). We first explore the straightforward perturbative method for obtaining periodic solutions of period 2T, around \(\omega =\frac{\varOmega }{2}\). Accordingly, we write

$$\begin{aligned} \omega =\frac{\varOmega }{2}+\varDelta \omega (\epsilon )=\frac{\varOmega }{2}+\delta _1 \epsilon +\delta _2 \epsilon ^2 +\cdots \end{aligned}$$
(17)

and expand

$$\begin{aligned} X=X_0+X_1 \epsilon +X_2 \epsilon ^2 +\cdots \end{aligned}$$
(18)

Substituting into Eq. (16) and equating the coefficient of each power of \(\epsilon \) to zero, we have

$$\begin{aligned}&{\ddot{X}}_0 + \frac{\varOmega ^2}{4}X_0 =0 \end{aligned}$$
(19a)
$$\begin{aligned}&{\ddot{X}}_1 + \frac{\varOmega ^2}{4}X_1 =-\varOmega \delta _1 X_0 -\cos (\varOmega t)X_0 \end{aligned}$$
(19b)
$$\begin{aligned}&{\ddot{X}}_2 + \frac{\varOmega ^2}{4}X_2 =-\varOmega \delta _2 X_0 -\delta _1 ^2 X_0-\varOmega \delta _1 X_1\nonumber \\&-\cos (\varOmega t)X_0 \end{aligned}$$
(19c)

From Eq. (19a), \(X_0=A \cos (\frac{\varOmega }{2}t)+B\sin (\frac{\varOmega }{2}t)\) and inserting this solution in Eq. (19b),

$$\begin{aligned}&\!\!\!{\ddot{X}}_1 + \frac{\varOmega ^2}{4}X_1\! =\!-\varOmega \delta _1 \left( A \cos \left( \frac{\varOmega }{2}t\right) \!+\!B\sin \left( \frac{\varOmega }{2}t\right) \right) \nonumber \\&\qquad -\,\cos \left( \varOmega tx\right) \left( A \cos \left( \frac{\varOmega }{2}t\right) +B\sin \left( \frac{\varOmega }{2}t\right) \right) \nonumber \\&\quad =-\varOmega \delta _1 A \cos \left( \frac{\varOmega }{2}t\right) -\varOmega \delta _1 B \sin \left( \frac{\varOmega }{2}t\right) \nonumber \\&\qquad -\,\frac{A}{2}\left( \cos \left( \frac{3\varOmega }{2}t\right) +\cos \left( \frac{\varOmega }{2}t\right) \right) \nonumber \\&\qquad -\,\frac{B}{2}\left( \sin \left( \frac{3\varOmega }{2}t\right) -\sin \left( \frac{\varOmega }{2}t\right) \right) \end{aligned}$$
(20)

For \(X_1\) to be finite, we cannot have \(\cos (\frac{\varOmega t}{2})\) or \(\sin (\frac{\varOmega t}{2})\) terms on the right-hand side. These terms are known as secular terms and have to be removed order by order in perturbation theory. This requires \(B=0\) and \(\delta _1=-\frac{1}{2\varOmega }\) if the solutions are of the \(\cos (\frac{\varOmega t}{2})\) variety and \(A=0\) and \(\delta _1=+\frac{1}{2\varOmega }\) if the solutions are of the form \(\sin (\frac{\varOmega t}{2})\). Thus, the curves on which the solution is periodic are given by

$$\begin{aligned} X&=A \cos \left( \frac{\varOmega t}{2}\right) ~~~~~~ on~~ \omega =\frac{\varOmega }{2}-\frac{\epsilon }{2 \varOmega }+{\mathcal {O}}\left( \epsilon ^2\right) \end{aligned}$$
(21a)
$$\begin{aligned} X&=B \sin \left( \frac{\varOmega t}{2}\right) ~~~~~~ on~~ \omega =\frac{\varOmega }{2}+\frac{\epsilon }{2 \varOmega }+{\mathcal {O}}\left( \epsilon ^2\right) \end{aligned}$$
(21b)

That the solution is divergent between the two lines of periodicity above and quasi-periodic outside is shown by the technique of Krylov–Bogoliubov. It proceeds by writing the solution X(t) as

$$\begin{aligned} X(t)=A(t)\cos \left( \frac{\varOmega t}{2}\right) +B(t)\sin \left( \frac{\varOmega t}{2}\right) \end{aligned}$$
(22)

near the point \(\omega =\frac{\varOmega }{2}\). We will assume A(t) and B(t) to be slowly varying (so that \({\dot{A}}<<{\ddot{A}}\) and similarly for B) and find the dynamical systems for A and B. The fixed point will give the periodic solutions. Taking derivatives and keeping the relevant terms

$$\begin{aligned} {\dot{X}}(t)= & {} {\dot{A}}(t)\cos \left( \frac{\varOmega t}{2}\right) +{\dot{B}}(t)\sin \left( \frac{\varOmega t}{2}\right) \nonumber \\&+\frac{\varOmega }{2}B(t)\cos \left( \frac{\varOmega t}{2}\right) -\frac{\varOmega }{2}A(t)\sin \left( \frac{\varOmega t}{2}\right) \nonumber \\\end{aligned}$$
(23)
$$\begin{aligned} {\ddot{X}}(t)= & {} -\varOmega {\dot{A}}(t)\sin \left( \frac{\varOmega t}{2}\right) +\varOmega {\dot{B}}(t)\cos \left( \frac{\varOmega t}{2}\right) \nonumber \\&-\frac{\varOmega ^2}{4}\left( A(t)\cos \left( \frac{\varOmega t}{2}\right) +B(t)\sin \left( \frac{\varOmega t}{2}\right) \right) \nonumber \\ \end{aligned}$$
(24)

With \(\omega ^2 =\frac{\varOmega ^2}{4}+\varOmega \delta \) to the lowest order in \(\delta \), we insert Eqs. (22) and  (24) in Eq. (16) to write

$$\begin{aligned}&-\varOmega {\dot{A}}(t)\sin \left( \frac{\varOmega t}{2}\right) +\varOmega {\dot{B}}(t)\cos \left( \frac{\varOmega t}{2}\right) \nonumber \\&\quad +\,\delta \; \epsilon \; \varOmega \left( A(t)\cos \left( \frac{\varOmega t}{2}\right) +B(t)\sin \left( \frac{\varOmega t}{2}\right) \right) \nonumber \\&\quad +\,\epsilon \cos \left( \varOmega t\right) \left( A(t)\cos \left( \frac{\varOmega t}{2}\right) \right. \nonumber \\&\left. \quad +\, B(t)\sin \left( \frac{\varOmega t}{2}\right) \right) =0 \end{aligned}$$
(25)

Setting the coefficients of \(\cos (\frac{\varOmega t}{2})\) and \(\sin (\frac{\varOmega t}{2})\) to zero, we get

$$\begin{aligned} {\dot{A}}&=(\delta -\frac{\epsilon }{2 \varOmega }) B \end{aligned}$$
(26a)
$$\begin{aligned} {\dot{B}}&=-(\delta +\frac{\epsilon }{2 \varOmega }) A \end{aligned}$$
(26b)

leading to the solution

$$\begin{aligned} A(t)=C_1\; e^{i \left( \sqrt{\delta ^2 -\frac{\epsilon ^2}{4 \varOmega ^2}}\right) t}+C_2 e^{-i \left( \sqrt{\delta ^2 -\frac{\epsilon ^2}{4 \varOmega ^2}}\right) t} \end{aligned}$$
(27)
Fig. 1
figure 1

Zones of bounded and unbounded solutions for \(\langle x \rangle \). The red shaded regions show the unstable zones. The boundaries obtained around \(\omega = \frac{\varOmega }{2}\) from perturbation theory are shown by the blue dashed lines. (Color figure online)

Full size image

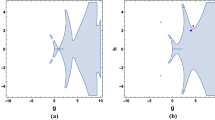
The answer reveals that the slow variation of A(t) comes from the fact the coefficient of t in the exponential is small. It also shows that if \(\delta ^2 >\frac{\epsilon ^2}{4 \varOmega ^2}\), the solutions are periodic with frequency \(\sqrt{\delta ^2 -\frac{\epsilon ^2}{4 \varOmega ^2}}\) and hence the solution for X(t) [as seen from Eq. (22)] is quasi-periodic. For \(\delta = \pm \frac{\epsilon }{2 \varOmega }\), the solution X(t) is periodic as A(t) and B(t) become constants. This agree exactly with the curves we found from the perturbation theory for periodic solutions. For \(\delta <|\frac{\epsilon }{2 \varOmega }|\) (the region bounded by the curves where the solution is periodic), X(t) diverges. Hence, we have a situation where quasi-periodic solutions are separated from diverging solutions by curves on which the solution is periodic. Searching for periodic solutions is a good strategy for finding zones where the solutions may diverge. It should be noted that the Krylov–Bogoliubov technique is extremely versatile as it gives a complete picture of what is going on, in the vicinity of the periodic solution. It should be noted that the multiple timescale technique (see Ref. [29]) yields identical answers. The numerically obtained picture of solutions of the Mathieu equation are shown in Fig. 1.

To solve the higher-order differential equations, we used the Runge–Kutta (RK) recursion formula. Higher-order differential equations can be represented by a set of first-order differential equations. Runge–Kutta algorithm has the form \( y_{i+1} = y_{i} + h \phi (x_i, y_i, h) \), to numerically solve the first-order differential equation, where \(\phi \) is an increment function of the approximation of f(x, y) in the interval of \(x_{i} \le x \le x_{i+1}\). We have used fourth-order RK formulas, where \(\phi \) is the weighted average of four derivative evaluations \(k_1, k_2, k_3\) and \(k_4\) on the interval \(x_{i} \le x \le x_{i+1} \), that is,

$$\begin{aligned} y_{i+1} = y_{i} + \dfrac{h}{6} (k_1 + 2 k_2 + 2 k _3 + k_4), \end{aligned}$$

where,

$$\begin{aligned} k_1= & {} f\left( x_i, y_i\right) ,\\ k_2= & {} f\left( x_i + \frac{h}{2}, y_i + \frac{h}{2}k_1\right) ,\\ k_3= & {} f\left( x_i + \frac{h}{2}, y_i + \frac{h}{2}k_2\right) ,\\ k_4= & {} f\left( x_i + h, y_i +h k_3\right) . \end{aligned}$$

We have used a step size of \(h = 0.01\). Smaller values of h do not change the computed boundaries.

With this introduction to the techniques to be used, we now turn to a fairly elaborate discussion of the third-order equation Eq. (14) satisfied by V(t). The derivation of the equation is given in “Appendix A”.

3 The properties of the third-order non-autonomous equation for the variance

The general discussions of Eqs. (10–12) from the mathematical point of view can be found in Refs. [19,20,21,22]. We begin by noting the fact that Eq. (13) can have periodic motion with periods 3T, 2T and T and by asking for the region in \(({\bar{\omega }}-\epsilon )\) space where the solution of period 3T should be obtained. This has to be the primary resonance near \({\bar{\omega }}=\frac{\varOmega }{3}\) and we write

$$\begin{aligned} {\bar{\omega }}=\frac{\varOmega }{3}+\varDelta {\bar{\omega }}(\epsilon )=\frac{\varOmega }{3}+\delta _1 \epsilon +\delta _2 \epsilon ^2+\cdots \end{aligned}$$
(28)

Perturbation theory is what we want to begin with and write

$$\begin{aligned} V=V_0+ \epsilon V_1 + \epsilon ^2 V_2+\cdots \end{aligned}$$
(29)

Substituting the expansion in Eq. (13), we have

$$\begin{aligned}&\left( \dddot{V}_0+ \epsilon \dddot{V}_1 + \epsilon ^2 \dddot{V}_2+..\right) +\left( \frac{\varOmega ^2}{9}+2\frac{\varOmega }{3}\delta _1 \epsilon \right. \nonumber \\&\left. +2\frac{\varOmega }{3}\delta _2 \epsilon ^2\right) \left( {\dot{V}}_0+ \epsilon {\dot{V}}_1 + \epsilon ^2 {\dot{V}}_2+..\right) +\epsilon \cos \left( \varOmega t\right) \nonumber \\&\left( {\dot{V}}_0+ \epsilon {\dot{V}}_1+..\right) - \frac{\epsilon \varOmega }{2} \sin \left( \varOmega t\right) \left( V_0+ \epsilon V_1+..\right) =0\nonumber \\ \end{aligned}$$
(30)

The analysis of the above equation up to \({\mathcal {O}}(\epsilon ^{2})\) is presented in “Appendix B”. We find that there is no zone of instability to \({\mathcal {O}}(\epsilon ^{2})\) and the periodic orbits appear on the curve \({\bar{\omega }} =- \dfrac{27 \epsilon ^2}{128 \varOmega ^3}\).

We now focus on the orbits of period 2T. A harmonic balance argument suggests that these will exist in the vicinity of \({\bar{\omega }}=\frac{\varOmega }{2}\). We write \({\bar{\omega }}=\frac{\varOmega }{2}+\delta \), where \(\delta \) is small and try a Krylov–Bogoliubov technique with the trial solution

$$\begin{aligned} V(t)= & {} A_1(t)\cos \left( \frac{\varOmega t}{2}\right) + B_1(t)\sin \left( \frac{\varOmega t}{2}\right) \nonumber \\&+\,A_2(t)\cos \left( \frac{3 \varOmega t}{2}\right) + B_2(t)\sin \left( \frac{3 \varOmega t}{2}\right) \nonumber \\ \end{aligned}$$
(31)

We provide the expressions for \({\dot{V}}\), \({\ddot{V}}\) and \(\dddot{V}\) in “Appendix B”.

From the coefficients of \(\sin (\frac{\varOmega t}{2}), \cos (\frac{\varOmega t}{2}),\sin (\frac{3\varOmega t}{2})\) and \(\cos (\frac{3\varOmega t}{2})\) in Eq. (B.10) of “Appendix B”,

$$\begin{aligned}&-\frac{\varOmega ^2}{2}{\dot{A}}_1+\frac{\delta \; \varOmega ^2 }{2} B_1+\frac{\epsilon \; \varOmega }{2} B_2=0 \end{aligned}$$
(32a)
$$\begin{aligned}&-\frac{\varOmega ^2}{2}{\dot{B}}_1-\frac{\delta \; \varOmega ^2 }{2} A_1 -\frac{\epsilon \; \varOmega }{2} A_2=0 \end{aligned}$$
(32b)
$$\begin{aligned}&-\frac{13\varOmega ^2}{2}{\dot{A}}_2-3\varOmega ^3 B_2+\frac{\epsilon \; \varOmega }{2} B_1=0\end{aligned}$$
(32c)
$$\begin{aligned}&-\frac{13\varOmega ^2}{2}{\dot{B}}_2 +3\varOmega ^3 A_2-\frac{\epsilon \; \varOmega }{2} A_1=0 \end{aligned}$$
(32d)

The eigenvalues \(\lambda \) of this set of equations are obtained from the condition

$$\begin{aligned} \begin{vmatrix} \lambda&-\delta&0&-\frac{\epsilon }{\varOmega } \\ \delta&\lambda&\frac{\epsilon }{\varOmega }&0 \\ 0&-\frac{\epsilon }{13\varOmega }&\lambda&\frac{6 \varOmega }{13} \\ \frac{13\epsilon }{\varOmega }&0&-\frac{6 \varOmega }{13}&\lambda \end{vmatrix} =0 \end{aligned}$$
(33)
Fig. 2
figure 2

Zones of bounded and unbounded solutions for \(\varDelta ^2\). The golden colour shaded regions show the unstable zones. The dashed line shows where periodic orbits occur according to perturbation theory. The difference from Fig. 1 lies in the extra periodic line originating at \(\omega = \frac{\varOmega }{4}\). (Color figure online)

Full size image

which gives the following quadratic equation in \(\lambda ^2\):

$$\begin{aligned}&\lambda ^4 +\lambda ^2 \left( \frac{36 \varOmega ^2}{169}+\delta ^2\right) +\frac{36 \varOmega ^2 \delta ^2}{169}\\&\quad +\frac{12 \epsilon ^2 \delta }{169 \varOmega }+\frac{\epsilon ^4}{169 \varOmega ^4}=0 \end{aligned}$$

The two roots for \(\lambda ^2\) are obtained as

$$\begin{aligned} \lambda ^2= & {} -\frac{1}{2}\left( \frac{36 \varOmega ^2}{169}+\delta ^2\right) \nonumber \\&\pm \, \sqrt{\frac{1}{4}\left( \frac{36 \varOmega ^2}{169}+\delta ^2\right) ^2 - \left( \frac{36 \varOmega ^2 \delta ^2}{169}+\frac{12 \epsilon ^2 \delta }{169 \varOmega }+\frac{\epsilon ^4}{169 \varOmega ^4}\right) }\nonumber \\ \end{aligned}$$
(34)

We note that neither of the roots can be positive, and hence, there is no instability zone around \({\bar{\omega }}=\frac{\varOmega }{2}\). The periodic orbit is obtained for \(\lambda =0\) which corresponds to \(\delta =-\frac{\epsilon ^2}{6 \varOmega ^3}\). This is interesting since the anticipated instability zone is not there. It can be traced to an accidental cancellation of terms in \(\cos (\frac{\varOmega t}{2})\) and \(\sin (\frac{\varOmega t}{2})\) coming from the third and fourth terms of Eq. (14).

We now try to find out the solutions of period T which are expected to occur near \({\bar{\omega }}=\varOmega \). Setting \({\bar{\omega }}=\varOmega +\delta \), we carry out the Krylov–Bogoliubov method with the ansatz,

$$\begin{aligned} V(t)= & {} \,A_0(t)+A_1(t)\cos (\varOmega t)+ B_1(t)\sin (\varOmega t)\nonumber \\&+\,A_2(t)\cos (2\varOmega t)+ B_2(t)\sin (2 \varOmega t) \end{aligned}$$
(35)

where \(A_0,A_1,B_1,A_2,B_2\) are all slowly varying function of time. Our calculation technique is exactly the same as detailed in the derivation of Eqs. (29)–(32d) and finally yields

$$\begin{aligned} {\dot{A}}_0= & {} -\frac{\epsilon \varOmega }{4}B_1\nonumber \\ {\dot{A}}_1= & {} \frac{2\delta }{\varOmega }B_1+\frac{3}{8}\epsilon \varOmega B_2\nonumber \\ {\dot{B}}_1= & {} -\frac{2\delta }{\varOmega }A_1-\frac{3}{8}\epsilon \varOmega A_2-\frac{\epsilon \varOmega }{4}A_0\nonumber \\ {\dot{A}}_2= & {} -\frac{6}{11}\varOmega B_2\nonumber \\ {\dot{B}}_2= & {} \frac{6}{11}\varOmega A_2 \end{aligned}$$
(36)

The eigenvalue \(\lambda \) satisfies a fifth-order equation which always has a zero eigenvalue. Of the four remaining eigenvalues, two are purely imaginary and the other two have the form \(\pm \sqrt{\frac{\epsilon ^2 \varOmega ^2}{16}-4\delta ^2}\), and hence, there is a zone of divergent solution bounded by \(\delta =\pm \frac{\epsilon }{8}\) exactly as for the Mathieu equation near \(\omega =\frac{\varOmega }{2}\).

We have solved Eq. (14) numerically using Runge–Kutta methods to obtained the instability zones as shown in Fig. 2. The instability zones agree exactly with those found in Fig. 1 for small values of \(\epsilon \). As seen from our calculation, the first instability zone appears at \({\bar{\omega }} = 2 \omega =\varOmega \) and its width is exactly the same as the instability zone in Fig. 1 around \(\omega =\frac{\varOmega }{2}\). This explains why the recent numerical work of Hashemloo et al. [27] finds that the width increases indefinitely only in the parameters zones where the mean position increases. We end this section by noting that the absence of an instability zone around \({\bar{\omega }}= \frac{\varOmega }{3} \)(which corresponds to \( \omega = \frac{\varOmega }{6} \)) is presumably due to the fact that in the absence of the periodic forcing, the system exhibits a zero mode. The absence of a zone around \( \omega = \frac{\varOmega }{4} \) is accidental because of the coefficients of f and \({\dot{f}}\) in Eq. (10) differing exactly by a factor of two.

4 The properties of the fourth- and fifth-order equations for the skewness and kurtosis

We begin our discussion with the skewnessS, rewriting Eq. (11) to \({\mathcal {O}}(\epsilon )\). This leads to

$$\begin{aligned}&\dfrac{\hbox {d}^4}{\hbox {d}t^4} S +10\omega ^2\frac{\hbox {d}^2}{\hbox {d}t^2} S + 9\omega ^4 S +10\omega ^2 \epsilon f(t)\frac{\hbox {d}^2}{\hbox {d}t^2} S \nonumber \\&\quad +\,18\omega ^4 \epsilon f(t)S+ 10\epsilon \omega ^2 {\dot{f}} \frac{\hbox {d}}{\hbox {d}t}S+3 \omega ^2 \epsilon \ddot{f} S=0 \nonumber \\ \end{aligned}$$
(37)

with \(f=\cos (\varOmega t)\). Writing this as a fourth-order dynamical system \({\dot{X}}_i=A_{ij}X_j\) with periodic coefficients, we find that \(M_{ij}\) is traceless and hence the solutions X(t) can have periodicities 4T, 3T, 2T and T. There are solutions with frequency \(\frac{\varOmega }{4},\frac{\varOmega }{3},\frac{\varOmega }{2}\) and \(\varOmega \). The difference between Eq. (37) and the system studied in Sects. 2 and 3 is that the unperturbed solution \(S_0\) of Eq. (37) [i.e. solution for \(\epsilon =0\)] is a two-frequency solution (this is a significant difference that can occur with the higher-order Mathieu equation)

$$\begin{aligned} S_0(t)= & {} A_1\cos (\omega t)+ B_1\sin (\omega t) +A_2\cos (3\omega t)\nonumber \\&\quad + B_2\sin (3 \omega t). \end{aligned}$$
(38)

The expected resonant response can happen when either \(\omega \) or \(3\omega \) matches \(\frac{\varOmega }{4},\frac{\varOmega }{3},\frac{\varOmega }{2}\) and \(\varOmega \). Harmonic balance indicates which matching would lead to dominant effect and inspection shows that the conditions \(\omega =\frac{\varOmega }{6}\) or \(\frac{\varOmega }{2}\) are the ones capable of producing response at \({\mathcal {O}}(\epsilon )\). The details of the calculations are presented in “Appendix C”. Here we simply report that there is no divergent region near \( \omega = \frac{\varOmega }{6} \), while in the vicinity of \( \omega = \frac{\varOmega }{2} \), we have the boundaries given by the curves shown in Eq. (C.8a).

Fig. 3
figure 3

Zones of bounded and unbounded solutions for skewness. The blue shaded regions show the unstable zones. The red dashed lines show the boundaries obtained from perturbation theory. (Color figure online)

Full size image

We show the instability zones obtained from our computational work and the boundaries obtained from perturbation theory in Fig. 3.

We now turn to the dynamics of the kurtosisK Eq. (12) and writing it as a dynamical system find that once again the matrix A is traceless and the possible time periods of the solution can be 5T, 4T, .., T with frequencies \(\frac{\varOmega }{5},\frac{\varOmega }{4},..,\varOmega \). Noting that the \(\epsilon =0\) system has a solution with frequencies \(2\omega \) and \(4\omega \), we find from a visual inspection of harmonic balance that at \({\mathcal {O}}(\epsilon )\), the possibilities are the matches at \(\omega =\frac{\varOmega }{8}\) and \(\omega =\frac{\varOmega }{4}\) and \(\omega =\frac{\varOmega }{2}\). We rewrite Eq. (12) in a more streamlined form by writing \(2\omega \) as \({\bar{\omega }}\) and \(\epsilon {\bar{\omega }}^2\) as \({\bar{\epsilon }}\). With there new redefinition, we have (keeping terms to \({\mathcal {O}}({\bar{\epsilon }})\) only as our calculations will be done to the order)

$$\begin{aligned}&\overset{.....}{K} +5{\bar{\omega }}^2\dddot{K} +4{\bar{\omega }}^4{\dot{K}}=-5{\bar{\epsilon }} \cos (\varOmega t)\dddot{K} \nonumber \\&-\,8{\bar{\omega }}^2{\bar{\epsilon }} \cos (\varOmega t){\dot{K}}+6 {\bar{\epsilon }} \varOmega \sin (\varOmega t) {\ddot{K}}\nonumber \\&+\, \frac{9}{2}{\bar{\epsilon }}\varOmega ^2 \cos (\varOmega t) {\dot{K}} +4{\bar{\omega }}^2{\bar{\epsilon }} \varOmega \sin (\varOmega t) K\nonumber \\&-\,\varOmega ^3 {\bar{\epsilon }} \sin (\varOmega t) K \end{aligned}$$
(39)

To explore \(\omega \) near \(\frac{\varOmega }{8}\), we need to set \({\bar{\omega }}=\frac{\varOmega }{4}+\delta \). Expanding \(\delta \) as \(\delta _1 {\bar{\epsilon }} +\delta _2 {\bar{\epsilon }} ^2\), we retain the first term alone and write Eq. (39) as

$$\begin{aligned}&\overset{.....}{K} +5\frac{\varOmega ^2}{16} \dddot{K} +4\left( \frac{\varOmega }{4}\right) ^4{\dot{K}} + \frac{5 \varOmega }{2} \delta _1 {\bar{\epsilon }} \dddot{K} + \frac{\varOmega ^3}{4} \delta _1 {\bar{\epsilon }} {\dot{K}}\nonumber \\&\quad =-5{\bar{\epsilon }} \cos (\varOmega t)\dddot{K} - \frac{\varOmega ^2}{2}{\bar{\epsilon }} \cos (\varOmega t){\dot{K}}\\&\qquad +\,6 {\bar{\epsilon }} \varOmega \sin (\varOmega t) {\ddot{K}} \nonumber \\&\qquad +\, \frac{9}{2}{\bar{\epsilon }} \varOmega ^2 \cos (\varOmega t) {\dot{K}} -\frac{3}{4}{\bar{\epsilon }} \varOmega ^3 \sin (\varOmega t) K \end{aligned}$$

At \({\mathcal {O}}(1)\)

$$\begin{aligned} \overset{.....}{K_0} +5\frac{\varOmega ^2}{16} \dddot{K}_0 +4\left( \frac{\varOmega }{4}\right) ^4{\dot{K}}_0 =0 \end{aligned}$$
(40)

with the solution

$$\begin{aligned} K_0= & {} A_0 + A_1 \cos (\frac{\varOmega }{4} t)+B_1 \sin (\frac{\varOmega }{4}t)\nonumber \\&+\,A_2 \cos (\frac{\varOmega }{2} t)+B_2 \sin (\frac{\varOmega }{2}t) \end{aligned}$$
(41)

At \({\mathcal {O}}({\bar{\epsilon }})\)

$$\begin{aligned}&\overset{.....}{K_1} +5\frac{\varOmega ^2}{16} \dddot{K}_1 +4\left( \frac{\varOmega }{4}\right) ^4{\dot{K}}= - \frac{5 \varOmega }{2} \delta _1 \dddot{K}_0 \nonumber \\&\quad - \frac{\varOmega ^3}{4} \delta _1 {\dot{K}}_0 -5 \cos (\varOmega t)\dddot{K}_0 +4 \varOmega ^2 \cos (\varOmega t){\dot{K}}_0\nonumber \\&\quad +\, 6 \varOmega \sin (\varOmega t) {\ddot{K}}_0 -\frac{3}{4}\varOmega ^3 \sin (\varOmega t) K_0 \end{aligned}$$
(42)

The relevant resonance-inducing terms on the r.h.s. of Eq. (41) are of the two varieties: one set proportional to \(A_1 \cos (\frac{\varOmega }{4})\) and \(B_1 \sin (\frac{\varOmega }{4})\) which have \(\delta _1\) as a prefactor and the other set proportional to \(A_2 \cos (\frac{\varOmega }{2})\) and \(B_2 \sin (\frac{\varOmega }{2})\) where coefficients contain terms with \(\delta _1\) and also without. Setting \(\delta _1 =0\) to remove resonance is not an option. Hence, the resonance is removed by setting \(A_1 = B_1 = 0\) and

$$\begin{aligned} \delta _1= & {} +\dfrac{1 }{\varOmega } \; \; \; \textit{ for the solution } A_2 \cos \left( \frac{\varOmega t}{2}\right) \nonumber \\= & {} -\dfrac{1}{ \varOmega } \; \; \;\textit{ for the solution } B_2 \sin \left( \frac{\varOmega t}{2}\right) \end{aligned}$$
(43)

This produces a zone starting at \(\omega = \frac{\varOmega }{8}\) where the solutions diverge in time. On the boundaries of this zone, the solution is periodic with a period 2T.

An identical calculation holds near \(\omega =\frac{\varOmega }{4}\), but now the width of the zone is exactly double that the zone around \(\omega =\frac{\varOmega }{8}\).

We finally consider the case \(\omega =\frac{\varOmega }{2}+\delta \). In this case, as for V(t), the perturbative technique used above does not work. With \(\omega =\frac{\varOmega }{2}+\delta \), we write Eq. (12) to the lowest order in \(\delta \) and \(\epsilon \) as

$$\begin{aligned}&\frac{\hbox {d}^5K}{\hbox {d}t^5} +5\varOmega ^2\frac{\hbox {d}^3K}{\hbox {d}t^3} + 4\varOmega ^4\frac{\hbox {d}K}{\hbox {d}t}\nonumber \\&\quad =-20\varOmega \delta \frac{\hbox {d}^3K}{\hbox {d}t^3}-32\varOmega ^3\delta \frac{\hbox {d}K}{\hbox {d}t}\nonumber \\&\qquad -5\epsilon \varOmega ^2 \cos (\varOmega t) \frac{\hbox {d}^3K}{\hbox {d}t^3}+6\epsilon \varOmega ^3 \sin (\varOmega t) \frac{\hbox {d}^2K}{\hbox {d}t^2}\nonumber \\&\qquad -\frac{7}{2}\epsilon \varOmega ^4\cos (\varOmega t) \frac{\hbox {d}K}{\hbox {d}t} +3\epsilon \varOmega ^5 \sin (\varOmega t) K \end{aligned}$$
(44)

We use the Krylov–Bogoliubov method with

$$\begin{aligned} K(t)= & {} A_0 (t) + A_1 (t)\cos (\omega t)+ B_1 (t) \sin (\omega t)\nonumber \\&+A_2 (t)\cos (2\omega t)+ B_2 (t)\sin (2 \omega t)\nonumber \\&+A_3 (t)\cos (3\omega t)+ B_3 (t)\sin (3 \omega t) \end{aligned}$$
(45)

where \(A_0, A_1, A_2, A_3, B_1, B_2, B_3 \) are slowly varying function of time. We had to include three harmonics in this case as opposed to the two harmonics in Eqs. (31) and (35) because the zeroth-order solution of Eq. (44) has the structure \(K = A_0 + A_1\cos (\omega t)+ B_1 \sin (\omega t)+A_2 \cos (2\omega t)+ B_2\sin (2 \omega t)\). At \({\mathcal {O}}(\epsilon )\), we consequently generate the \(\cos (3\omega t)\) and \( \sin (3 \omega t) \) terms which need to be in the Krylov–Bogoliubov method.

Straightforward algebra now leads to

$$\begin{aligned} {\dot{A}}_0= & {} -\frac{3\epsilon }{16}B_1\nonumber \\ {\dot{A}}_1= & {} 2\delta B_1 -\epsilon B_2\nonumber \\ {\dot{B}}_1= & {} -2\delta A_1+\epsilon A_2-\frac{\epsilon }{2}A_0\nonumber \\ {\dot{A}}_2= & {} 4 \delta B_2 + \frac{3 \epsilon }{32} B_1 +\frac{49}{32}\epsilon B_3\nonumber \\ {\dot{B}}_2= & {} -4 \delta A_2 - \frac{3 \epsilon }{32} A_1 - \frac{49}{32}\epsilon A_3\nonumber \\ {\dot{A}}_3= & {} -\frac{60}{137} B_3 + \frac{27}{274}\epsilon B_2\nonumber \\ {\dot{B}}_3= & {} \frac{60}{137} A_3 - \frac{27}{274}\epsilon A_2 \end{aligned}$$
(46)

As expected there is a zero mode, as there was for the variance. The other eigenvalues are \(\lambda = \pm i \frac{60}{137}+{\mathcal {O}}(\epsilon )\) and the remaining four obtained from the solution of

$$\begin{aligned} \lambda ^4 +\lambda ^2 \left( 20 \delta ^2- \frac{9 \epsilon ^2}{32}\right) +64 \delta ^4 +\frac{153 }{1024}\epsilon ^4=0 \end{aligned}$$
Fig. 4
figure 4

Zones of bounded and unbounded solutions for kurtosis. The green shaded regions show the unstable zones. The dashed lines show the calculated instability zones. For \(\omega = \frac{\varOmega }{2}\), it is discussed why the actual bounding can be somewhat wider. (Color figure online)

Full size image

For real value of \( \lambda ^2 \), one requires \(\left( 20 \delta ^2- \frac{9 \epsilon ^2}{32}\right) > 256 \delta ^4 +\frac{153 }{256}\epsilon ^4\). If \( \lambda ^2 \) is real, then clearly for \( \lambda ^2 \) to have a positive root(instability) \(20 \delta ^2 < \frac{9 \epsilon ^2}{32}\) which would mean \(\delta ^2 < \frac{9 \epsilon ^2}{640}\) which would imply the unstable zone is \( \delta < |\frac{3 }{8 \sqrt{10}}|\epsilon \) which is very close to \(\frac{\epsilon }{8}\). However, this is not the complete story since this is true only when \(\lambda ^2\) has real roots. If \(\lambda \) has complex roots with \(\lambda ^2\) having the structure \(\lambda ^2 = -\alpha \pm i \beta \), where \(\alpha \) is positive being in the stable zone \( \delta > |\frac{3 }{8 \sqrt{10}}|\epsilon \) then \(\lambda = \root 4 \of {\alpha ^2 + \beta ^2} e^{\pm i \theta /2}\) where \(\cos (\theta ) = \frac{\alpha }{\sqrt{\alpha ^2 + \beta ^2}}\) and \(\sin (\theta ) = \frac{\beta }{\sqrt{\alpha ^2 + \beta ^2}}\). A negative \(\cos (\theta )\) puts \(\theta \) in the range \(\frac{\pi }{2}\) to \(\frac{3\pi }{2}\) and \(\cos (\frac{\theta }{2})\) is in the range \(\frac{\pi }{4}\) to \(\frac{3\pi }{4}\). This implies \(\cos (\frac{\theta }{2})\) is positive for \(\frac{\pi }{2}< \theta <\frac{3\pi }{4}\) and this is what magnifies the instability zone around \(\omega = \frac{\varOmega }{2}\), way beyond what happens for \(\langle x \rangle , V\) and S. As can be seen from Fig. 4, our perturbative calculations are in accordance with the numerical data. It should be seen that at this order of Mathieu equation, the main feature of instabilities arising at lower frequencies than the second-order equation is clearly borne out as the accidental cancellation no longer happen. However, in this case as \(\epsilon \) increases, the region in parameter space where the kurtosis diverges becomes very large as seen from our numerical work and this makes the long time quantum dynamics in such systems of particular interest. The long time shape of the probability distribution needs to have a power law fall off in the regions where the kurtosis diverges.

5 Conclusions

Linear differential equations with periodic coefficients and of order greater than two are a rarity physical sciences. The quantum parametric oscillator provides a real physical system [24,25,26,27] where such equations make a natural appearance when the dynamics of higher moments is considered. Since description of the quantum state is in terms of probabilities one studies the dynamics of the mean value \(\langle x \rangle \) instead of the position of x itself. But the mean is not sufficient to picture the distribution and hence moments like the variance are essential. The fact that the moments follow Mathieu equations of higher order imply that while the mean may remain bounded, the fluctuation around the mean or the spread parameter kurtosis may diverge with time leading a drastic change in shape of the probability distribution. Hence, the quantum parametric oscillator provides the physical justification for investigating higher-order Mathieu equations.

The discussion on higher-order Mathieu-like equations have till now been restricted to mathematical analysis. We wanted to explore the practical issue of whether the perturbation techniques that work so well for finding the instability zones of the Mathieu equations would be equally useful for higher-order Mathieu equation. As seen from Figs. 2, 3 and 4, that is indeed the case. It will be noted that we never found any instability zone around lowest admissible frequency \(\omega = \frac{\varOmega }{6}\) in our study of the variance in Sect. 3. This we attribute to the existence of a zero mode in the system. The fact that there was no instability zone around \(\omega = \frac{\varOmega }{4}\) was due to an accidental cancellation. This did not occur for the kurtosis and instability zones can be seen emanating from \(\omega = \frac{\varOmega }{4}\) and \(\omega = \frac{\varOmega }{8}\) in Fig. 4. From a purely technical point of view, the fact that traditional technique like harmonic balance and Krylov–Bogoliubov provides results which could be verified in their zones of validity by numerical analysis indicates the robustness of these methods and should lead to interesting future investigations.