1 Introduction

It has been well known that neural energy expenditure caused by task stimulation usually accounts for only 5% of brain energy expenditure in the resting states, while in the past, most understanding of the brain stems from the study of this 5% of brain activities. As is well known, the structures of brain regions and their neural activity patterns are all different and neuroscientists often use the dynamic blood oxygen level-dependent (BOLD) signals measured by functional magnetic resonance imaging (fMRI) to look at brain activity as a whole to get global information of brain activity. But when the brain is activated, it is difficult to obtain an accurate understanding of the neural activities in the brain in various states because of the averaging distribution of blood flow in the brain as well as nonlinear coupling relationship between blood flow and oxygen consumption. At the same time, we cannot understand the interaction among neurons in the brain area with such a method [1, 2].

At present, there is not a new experimental technique to simultaneously integrate neuro-electrophysiological recording and fMRI data in a perfect way in the field of neuroscience, including optogenetics technology to be only a local observable technique. If the new technology is not available in a long period of time, we should have a new research method which can unify reductionism and holism in theory and accurately reproduce not only the neuro-electrophysiological records, but also the global information of the functional activities of the brain by using fMRI technology. In order to achieve this goal, it involves how to understand the nature of neuronal activity in the brain [3].

For this purpose, a novel theory of neural coding has been proposed in neuroscience researches [4,5,6,7,8,9,10,11,12,13], which provides a new perspective on how to understand the nature of neuronal activity. The core of this coding theory is that there is a unique correspondence between various neuronal membrane potentials and their neural energy expenditure, which makes it possible to convert the firing patterns of a variety of complex, highly nonlinear membrane potentials into new neural information processing methods that are processed in an energy’s firing pattern and have been named as neural energy coding [7,8,9,10,11,12,13]. According to such a coding theory, we found that neural energy coding can well integrate the reductionism and holism in the field of cognitive neuroscience and be used as the main basis for the study of global neural activity of brain functionality [11]. The reasons are as follows: (1) Neural energy model, as a model of global brain function, can be used to analyze and describe the various levels of phenomena in neuroscience experiments, so that the results at various levels are no longer mutually exclusive, mutually contradictory, and unrelated [14]. (2) Neural energy can describe the interaction of large-scale neurons in the entire brain (referring to the interaction of multiple brain regions), and except this, any conventional neural coding theory is impossible [15,16,17,18]. (3) Currently, it is difficult to obtain records from damage experiments of multiple brain regions at the same time. Although EEG and MEG can sample for neuronal activities from various regions of the brain, it is very difficult to estimate cortical interactions based on these extracranial signals [19]. The main obstacle is the lack of a theoretical tool to efficiently analyze cortex–cortex interactions in high-dimensional space, and there is also no conversion relationship between scalp EEG and cortical potential. However, neural energy provides an effective scheme for solving the above problems. (4) Since the energy is a scalar, whether it is a single or neuron population, or whether it is a network or a behavioral, as well as a linear or a nonlinear neural model, their dynamic responses can be used to describe patterns of energy coding by superposition of neural energy [4, 6,7,8,9,10,11,12]. Thus, global information about the inherent, intrinsic, and functional neural activities can be obtained, while it cannot be achieved by other traditional coding theories [15, 17,18,19,20,21].

The vast majority of the current studies on neural energy are to qualitatively analyze the energy expenditure of neural activities from the perspective of blood flow and through fMRI experimental techniques [22]. In our previous work, a novel neuron biophysical model named Wang–Zhang was proposed [8]. By modifying this model, we presented the energy function of a single neuron membrane potential and its computational method; thus, we found a new working mechanism of neuronal activity [6]. Our study indicates that neuron does not only consume energy in traditional sense, while it firstly absorbs energy from the blood flow and then consumes energy, so this important finding modifies the traditional point of view that neuron only consumes energy. Since this new finding allows us to explain the many neurophysiological phenomena that have so far failed to give a reasonable explanation, it is of important scientific significance [11]. After that, we proposed the coding of neural energy in structural network as well as energy distribution under different parameters [9, 10]. Recently, we applied this novel neural coding theory to the mental exploration, which took the spatial distribution of the power of the positional cells in hippocampus at the same time as a neural energy field to perform investigation. The results showed that almost the best path of exploration can be found as long as ten times of performing mental exploration. Compared with published studies, the method of neural energy field can greatly improve the efficiency of mental exploration [12].

This study is a part of our series of studies on the development of the global neural models of brain functions, as its objective is to bring up a novel neural coding theory that can be used to explore the global neural activities of the brain. In order to prove the validity of Wang–Zhang’s neuron biophysical model [6, 11], this study used the H–H model to calculate the energy characteristics of action potentials and membrane potentials. Since almost all previous studies focused on how neural energy will be changed by neural activities. However, the inverse question of this problem is whether the changes in neural energy would cause the changes in neuronal activities. The reverse question is whether neural energy can regulate the state of neural activities. Its scientific significance is that the evolution of neural energy at subthreshold state is directly related to the changes in the neural dark energy in the default mode network, so whether neural energy can modulate the state of neural activity as well as the study of the nature of consciousness has an important scientific significance [23, 24]. As far as our current literature is concerned, this problem has not attracted enough attention from neuroscientists, which is because the widely used H–H model is based on a basic assumption that the operation of the ion pump can ensure that the Nernst potential is constant [25]. In addition, modern experimental techniques are also difficult to directly detect the consumed energy in firing procedure of an action potential for a single neuron. Therefore, it is necessary to understand why the ion pump cannot guarantee a constant potential through computational model, that is, how the energy regulates neuronal activity when energy supply of neuron system is insufficient.

2 Models and results

The circuit model of H–H equation is shown in Fig. 1.

Fig. 1
figure 1

Circuit diagram of the H–H model

Full size image

Its differential equation is described as:

$$\begin{aligned} C_m \frac{\hbox {d}V_\mathrm{m} }{\hbox {d}t}= & {} g_\mathrm{l} (E_\mathrm{l} -V_\mathrm{m} )+g_\mathrm{Na} m^{3}h(E_\mathrm{Na} -V_\mathrm{m} )\nonumber \\&+\,g_\mathrm{k} n^{4}(E_\mathrm{l} -V_\mathrm{m} )+I \end{aligned}$$
(1)

of which, \(C_\mathrm{m}\) is membrane capacitance of neuronal cell membranes, \(V_\mathrm{m}\) is membrane potential, \(E_\mathrm{Na} \) and \(E_\mathrm{K} \) are Nernst potentials of sodium ions and potassium ions, respectively, while \(E_\mathrm{l} \) is potential when the leakage current is zero. In addition, \(\hat{{g}}_\mathrm{Na}\) and \(\hat{{g}}_\mathrm{K}\) are variable conductance of sodium ion channels and potassium channels, respectively, among them, \(\hat{{g}}_\mathrm{Na} =g_\mathrm{Na} m^{3}h\), and \(\hat{{g}}_\mathrm{K} =g_\mathrm{K} n^{4}\), while \(g_\mathrm{l}\) is leakage conductance. The variable conductance of the sodium and potassium channels is described by the following set of nonlinear differential equations:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{\hbox {d}n}{\hbox {d}t}=\sigma _n (1-n)-\beta _n n} \\ {\frac{\hbox {d}m}{\hbox {d}t}=\sigma _m (1-m)-\beta _m m} \\ {\frac{\hbox {d}h}{\hbox {d}t}=\sigma _h (1-h)-\beta _h h} \\ \end{array} }} \right. \end{aligned}$$
(2)

In which:

$$\begin{aligned} \alpha _n= & {} \frac{0.01(10+V_\mathrm{m} -V_\mathrm{r} )}{\exp [0.1(10+V_\mathrm{m} -V_\mathrm{r} )-1]} \\ \beta _n= & {} 0.125\exp \left( \frac{V_\mathrm{m} -V_\mathrm{r} }{80}\right) \\ \alpha _m= & {} \frac{0.1(25+V_\mathrm{m} -V_\mathrm{r} )}{\exp [0.1(25+V_\mathrm{m} -V_\mathrm{r} )-1]} \\ \beta _m= & {} 4\exp \left( \frac{V_\mathrm{m} -V_\mathrm{r} }{18}\right) \\ \alpha _h= & {} 0.07\exp \left( \frac{V_\mathrm{m} -V_\mathrm{r} }{20}\right) \\ \beta _h= & {} \frac{1}{\exp [0.1(30+V_\mathrm{m} -V_\mathrm{r} )+1]} \end{aligned}$$

\(V_\mathrm{r} \) is resting potential.

The procedure that neuron firing action potentials is as follows: (1) The postsynaptic neurons are stimulated by presynaptic neurons, and the permeability of sodium ions to the cell membrane increases, and then the sodium ions begin to flow inward, while the membrane potential approaches the threshold for preparation of depolarization (subthreshold activity). (2) The permeability of cell membrane to sodium ions further increases, and sodium ions flow inward largely, while the membrane potentials increase rapidly (sup-threshold activity). (3) The permeability of cell membrane to sodium ions is weakened, while the permeability to potassium ions increases, and potassium ions flow outward, as well as membrane potential begins to decrease after achieving the peak to perform repolarization. (4) The permeability of cell membrane to potassium ions further increases, and potassium ions flow outward until hyperpolarized. (5) Permeability of the membrane to potassium decreases, and membrane potential increases to the level of resting.

In the circuit model of the H–H equation, the total energy can be expressed as:

$$\begin{aligned} W_\mathrm{all} =C_\mathrm{m} \frac{\hbox {d}V_\mathrm{m} }{\hbox {d}t}V_\mathrm{m} +i_\mathrm{Na} E_\mathrm{Na} +i_\mathrm{K} E_\mathrm{K} +i_\mathrm{l} E_\mathrm{l} \end{aligned}$$

while

$$\begin{aligned} C_\mathrm{m} \frac{\hbox {d}V_\mathrm{m} }{\hbox {d}t}=I-i_\mathrm{Na} -i_\mathrm{K} -i_\mathrm{l} \end{aligned}$$

Thus

$$\begin{aligned} W_\mathrm{all}= & {} IV_\mathrm{m} +i_\mathrm{Na} (E_\mathrm{Na} -V_\mathrm{m} )+i_\mathrm{K} (E_\mathrm{K} -V_\mathrm{m} )\\&+\,i_\mathrm{l} (E_\mathrm{l} -V_\mathrm{m} ) \end{aligned}$$

That is

$$\begin{aligned} W_\mathrm{all}= & {} IV_\mathrm{m} +(i_\mathrm{Na} E_\mathrm{Na} +i_\mathrm{K} E_\mathrm{K} +i_\mathrm{l} E_\mathrm{l} )\\&-\,V_\mathrm{m} (i_\mathrm{Na} +i_\mathrm{K} +i_\mathrm{l} ) \end{aligned}$$

In which, \(IV_\mathrm{m} \) is the energy provided by the outside surroundings to the circuit system and \(i_\mathrm{Na} E_\mathrm{Na} +i_\mathrm{K} E_\mathrm{K} +i_\mathrm{l} E_\mathrm{l} \) is energy provided by the voltage source represented by the Nernst potential, while \(V_\mathrm{m} (i_\mathrm{Na} +i_\mathrm{K} +i_\mathrm{l} )\) is the energy in the potential differences between the inside and the outside membrane. However, in the course of the firing action potentials by neurons, if we do not consider the energy consumed by the changes in cell membrane permeability, the involved energy includes the energy provided by oxygen and glucose in the blood flow to neuron, the energy in the potential differences between the internal and external cell membranes, as well as the bioenergy consumed when the ion pump transports ions against the difference in concentration gradient (that is ATP). The increase in the glucose consumption produced by the excitement of the brain is mainly caused by the activation of sodium potassium ATP pump [26,27,28,29,30]. The former two describe the relationship between the subthreshold neurons and the bioenergy, while the ion diffusion through the ion channel along the ion concentration difference does not consume energy. However, from the dynamic point of view, in the course of the transformation of subthreshold neurons into functional neurons, the sum of these three types of energy is equal to the total energy in the circuit system of H–H model. The former two types of energy are corresponding to \(IV_\mathrm{m}\) and \(V_\mathrm{m} (i_\mathrm{Na} +i_\mathrm{K} +i_\mathrm{l} )\) in circuit, respectively; then, the energy \((i_\mathrm{Na} E_\mathrm{Na} +i_\mathrm{K} E_\mathrm{K} +i_\mathrm{l} E_\mathrm{l})\) provided by the Nernst potential is equal to the bioenergy consumed by the ion pump. Actually, in this process, the sodium–potassium pump continually transports ions against the ion concentration gradient, and thus directly consumes the bioenergy, which means that one ATP can pump out three sodium ions and pump in two potassium ions. This also confirms the existence of the ion pump that provides energy to neural activities by continuously transporting ions to provide a steady Nernst potential. Thereafter, we can calculate the power consumed by the ion pump through the power of voltage source represented by using the Nernst potential in the circuit diagram in Fig. 1; then, the energy consumed by neuronal activity is:

Fig. 2
figure 2

Action potential of neuron and corresponding power consumption based on H–H model

Full size image
$$\begin{aligned} P=\left| i_\mathrm{K} E_\mathrm{K} \right| +\left| i_\mathrm{l} E_\mathrm{l} \right| -\left| i_\mathrm{Na} E_\mathrm{Na} \right| \end{aligned}$$
(3)

The negative sign of the third term in Eq. (3) refers that in the circuit of Fig. 1, the direction of the voltage source \(E_\mathrm{Na} \) and the current \(i_\mathrm{Na} \) is opposite to\(E_\mathrm{K} \), \(E_\mathrm{l} \) as well as \(i_\mathrm{K} \), \(i_\mathrm{l} \) (sodium current is toward the cell, while the potassium current and leakage current are outward). For an action potential, neuronal energy expenditure can be calculated by the above equation (Fig. 2).

The parameter values in the calculation are shown in Table 1.

Table 1 The parameter values in the calculation
Full size table

It is noted that the calculated result of power is negative during a period when the neurons begin to fire action potentials. The explanation of this negative power is as follows: When resting, the permeability of cell membrane to potassium ions is 30 \(\times \) larger than that to sodium ions, so ion flow in the depolarization state is generally composed of sodium ion flow, with the direction from outside the membrane into the membrane; thus, the calculated result is negative. From the circuit point of view, the negative power produced by the voltage source that is represented by the Nernst potential reveals that other components of the circuit work to the voltage source, that is, the capacitor discharges in this stage to release the stored energy in the capacitor. The capacitance in the H–H model corresponds to the cell membrane of the neuron, while sodium ions enter the neuron by the role of the potential gradient caused by the potential gradient between the inside and the outside of the membrane. This can be regarded as the stored energy of cell membrane providing energy to the influx of sodium ions, which precisely corresponds to capacitor discharge. It can be seen from the above discussion that the motion of the ions completely corresponds to the circuit model. In addition, this phenomenon of negative power (Fig. 2) is well consistent with the calculated results (Fig. 3) of the Wang–Zhang’s neuron model [6, 11]. It should be emphasized that the H–H model is established at the molecular level and that our model is directly based on the neuron. Therefore, although there are some errors in the waveforms of their action potentials, the two models are exactly the same observed from the perspective of energy changes, which means there are components of negative power in the calculated results of neuronal energy in H–H model, reflecting that there is profound internal relationship between the two models. Compared with H–H model, another advantage of the Wang–Zhang’s model [6, 11] is that function of membrane potential and the energy function of the neuron can be obtained, while H–H model can only obtain the numerical solution.

Fig. 3
figure 3

Neuron firing action potential and its corresponding power consumption in the Wang–Zhang model

Full size image

The above computational results show that the ratio of positive and negative area of the neural energy reflects the increase in cerebral blood flow and oxygen consumption to be not matched [30]. Neurons are stimulated to cause significant increase in cerebral blood flow. However, there is an oxygen demand for depolarization (it is not oxygen consumption at the moment), mainly showing energy absorption or release of energy storage [6]. At the stage of the repolarization of the neuron, the storage of energy has been exhausted. At this time, the oxygen consumption of the neuron is greatly increased, showing the energy consumption.

Let us return to a basic assumption in the H–H model: Nernst potentials of potassium and sodium ions are constant due to the existence of the ion pump. In other words, the instantaneous power of the ion pump is not limited. In fact, from the observation results of fMRI blood flow, the energy supply of the nervous system has regional characteristics. For example, the blood flow of visual cortex will increase significantly under visual stimulation, which means not every neuron is fully provided with bioenergy in the blood flow (oxygen and glucose), but depending on the different tasks that are currently implemented, part of the bioenergy in the blood flow can reach the designated area of the cortex activation, while the blood flow of noneffector cells around the activation area also had a corresponding increase, and at this time, it does not meet the actual situation that the Nernst potential is constant. For this reason, the proportion of the increase in blood flow will be higher than the oxygen consumption rate. The relatively high proportion of the increase in blood flow is because the blood flow increases around nonfunctional cells but does not consume oxygen [26]. The question we are investigating is whether these changes in the supply of bioenergy carried by blood flow will cause changes in neuronal activities, in other words, how energy modulates neuronal activities. That is, when the energy supply of neurons is insufficient, how the Nernst potential will change, and whether the change will result in the neurons cannot firing action potential but only perform subthreshold activity.

Considering that sodium ion channels always precede potassium ion activity in the process of neuronal activities. At the same time, the Nernst potential of sodium ion (55 mV) is higher than the Nernst potential of potassium ion (− 72 mV). In the meanwhile, conductance of sodium ion is much greater than that of potassium ion [in formula (1) \(g_\mathrm{Na}=120\), \(g_\mathrm{k} =36\)]. Thus, sodium ion channels play a major role in the above-mentioned problems. For sodium ion channels, if a maximum power existed for sodium ion pump \(P_\mathrm{m} \), then

$$\begin{aligned} \hat{{g}}_\mathrm{Na} (E_\mathrm{Na} -v_\mathrm{m} )E_\mathrm{Na} \le p_\mathrm{m} \end{aligned}$$
(4)

In which

$$\begin{aligned} \hat{g}_\mathrm{Na} =g_\mathrm{Na} m^{3}h. \end{aligned}$$

Formula (4) is regarded as a quadratic inequality concerning \(E_\mathrm{Na} \); then, its solution is:

$$\begin{aligned}&\frac{1}{2}V_\mathrm{m} -\frac{1}{2}\sqrt{V_\mathrm{m} ^{2}+\frac{4}{\hat{{g}}_\mathrm{Na} }P_\mathrm{m} }\le E_\mathrm{Na} \le \frac{1}{2}V_\mathrm{m} \\&\quad +\,\frac{1}{2}\sqrt{V_\mathrm{m} ^{2}+\frac{4}{\hat{{g}}_\mathrm{Na} }P_\mathrm{m} } \end{aligned}$$

And because outside the membrane is greater than inside the membrane for the concentration gradient of sodium ions, the Nernst potential is constantly positive. At the same time, if the power of the sodium ion channel is less than the maximum power, the Nernst potential should be normal value of 55mV. Therefore, the Nernst potential of sodium ions can be calculated as follows:

$$\begin{aligned} E_\mathrm{Na} =\left\{ {{\begin{array}{lll} {\frac{1}{2}V_\mathrm{m} -\frac{1}{2}\sqrt{V_\mathrm{m}^2 +\frac{4}{\hat{{g}}_\mathrm{Na} }P_\mathrm{m} }}&{}\quad {\hbox {if}}&{}\quad {P_\mathrm{Na} >P_\mathrm{m} } \\ {55}&{}\quad {\hbox {if}}&{}\quad {P_\mathrm{Na} \le P_\mathrm{m} } \\ \end{array} }} \right. \end{aligned}$$
(5)

where \(P_\mathrm{Na} =E_\mathrm{Na} \hat{{g}}_\mathrm{Na} (E_\mathrm{Na} -V_\mathrm{m} )\)

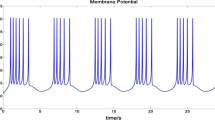
The adjusted H–H model can be obtained after formula (5) is substituted into formula (1). According to the above analysis, we control the energy supply of a single neuron to simulate whether energy supply can satisfy the differences in neuronal activities caused by the two situations when the neurons are intermittently stimulated. The results of the simulation are shown in Fig. 4. In the first 20 ms, the maximum power of the sodium ion pump is limited, so the situation of insufficient blood flow is simulated, and under this condition, the sodium ion pump fails to provide a stable Nernst potential \(E_\mathrm{Na} \). In the last 30 ms, the maximum power of the sodium channel is not limited, which simulates the situation of sufficient blood flow. From the results, we can see that the neuron is at subthreshold activity when there is insufficient energy supply. If the energy supply is not limited, it manifests as the firing of action potential at sup-threshold. It is worth noting that the stimulations of the neurons in these two phases are identical. This represents that insufficient energy supply limits the neuronal activities to subthreshold state. In short, neural energy can modulate neuronal activities. The local magnificent results for the first 20 ms are shown in Fig. 5.

Fig. 4
figure 4

Neuronal activity under different states of energy supply

Full size image
Fig. 5
figure 5

Neuronal activity under the states of insufficient energy supply (local)

Full size image

It can be seen from Fig. 5 that when the sodium ion pump cannot provide a stable Nernst potential, the activity of subthreshold membrane potential is based on energy expenditure. When the default mode network is coupled with the resting-state network, it is possible to explain why more than 90% of the energy expenditure is devoted to the inherent, intrinsic activity of the brain, whereas neural energy expenditure caused by task stimulation usually accounts for only 5% of the energy expenditure of brain under resting state [26, 32].

3 Open problems

It is emphasized that the calculation results of positive and negative powers in Figs. 2 and 3 are fully matched with experimental data [29]. These findings once again demonstrate that a new working mechanism of neuronal activity found previously is correct and effective, which were of great scientific significance for the discussion of the coupling properties between the default pattern network and the functional neuron network, the synchronous movement, as well as the proposal of the functional global neural model of the brain in the future.

As the ratio of the increase in blood flow to the increase in oxygen consumption is 5:1 [29], from the calculated results of positive and negative powers in Figs. 3 and 4, it just reflects that the ratio of energy expenditure to energy absorption of neurons is 5:1. The prerequisite is that the regulative relationship between neuronal activity and the increase in blood flow can be expressed through the relationship of bioenergy carried by neural activity and blood flow [6]. And the regular changes in energy absorption and consumption when a single neuron fires action potential provide a scientific explanation for clarifying the negative pulse phenomenon in dynamic BOLD signal [31, 32]. Thus, laws of energy metabolism in neurons can reflect the underlying mechanism of membrane potential changes, which combine the two neuronal models established at different levels and then give the intrinsic relationship between them; thus, it can be seen that H–H model is equivalent to the Wang–Zhang model, and also it is used to jointly reveal the nature of neuronal activity. Neuronal activity is essentially regulated by neural energy, which is closely related to neural energy regardless of how membrane potential changes.

Based on the neural energy model, we have been able to quantify the hemodynamic phenomena in the brain [36]. Also, we will give the neural energy encoding of the olfactory nervous system from the perspective of global brain function. More importantly, we can also demonstrate that the neural energy method can be used to quantify analysis the inverse relationship between the default mode network and the working memory network and supported by experimental data.

The biophysics model of the mth neuron in a coupled neuronal cluster can describe the basic characteristics of electronic activities of neuron population, under both subthreshold and sup-threshold conditions. However, we cannot get their activity laws from this biophysical model, because for a circuit system used to describe living cells (neurons), it is necessary to give a constraint on the membrane potential to be solved (since any circuitry is inanimate). For the theoretical basis that the spontaneous potential activity of neuronal clusters follows the rules of self-organization (according to the points of view by Professor Haken [35]), so, according to the results of Yale University neuroscientists’ experiment that the transmission of neural signals is tightly coupled with energy dissipation [36], we judge that the constraints given by this new biophysical model are likely to be the energy function of the circuit system. This is the biggest innovation in this study [8]. We know that for a known dynamical system, the kinetic energy and potential energy of the system can be written to get its Lagrange function. Nevertheless, in electronic model of neuron given by us, assuming that potential energy equals a constant (and power is the average energy), we can assume that the power dissipated in the electrical model could be regarded as the energy function of the dynamical system. Thus, we can derive the Lagrange function to get the Hamiltonian equation of motion. It serves as a constraint in the biophysical model and plays a key role in the complete description of the biophysics model. Whether such ideas are reasonable depends on whether the results of such an assumption are consistent with the results of neuro-electrophysiological experiments. Judging from our calculation results, they are completely consistent so that it fully confirms that our judgment is entirely correct, because this conclusion is based on the experimental results of neuro-electrophysiology.

4 Conclusion

  1. (1)

    This study calculated the energy expenditure of a single neuron from the perspective of ion channel and based on the classical H–H neuron model and compared with a novel neuro-biophysical model proposed recently [6], revealing that the overall change pattern of the two models was completely consistent with the experimental results of neuro-electrophysiology both in terms of membrane potential and energy expenditure. In particular, through the calculation of this study, H–H model also had a phenomena of negative power revealed by Wang–Zhang model [6]. Thus, it can be seen that these two neuron models are not only equivalent in nature, but also have a profound internal relationship.

  2. (2)

    The power consumed when the neurons fire action potentials has negative components. From a static point of view, this is because at the stage of depolarization that generates action potentials, the neurons absorb oxygenated hemoglobin from the cerebral blood flow. But the changes in stimulation and cerebral blood flow are dynamic, so neurons need to release the stored energy before absorbing oxygenated hemoglobin, manifesting as negative neural energy. The demand for oxygen consumption is beginning to increase at the moment. However, in the repolarization stage of the action potentials, oxygenated hemoglobin is converted into deoxyhemoglobin, and negative neural energy is converted into positive neural energy. In addition, energy absorption is converted into energy expenditure. This view can explain why there is a 31% of increase in the blood flow of the contralateral hemisphere while there is only a 6% of corresponding increase in oxygen consumption when neuronal population and neural networks are activated [22], that is, the ratio of the increase in blood flow to oxygen consumption is 5:1. The quantitative calculation results can scientifically explain the phenomenon of the negative pulse in the dynamic blood oxygen level-dependent (BOLD) signal [31].

  3. (3)

    Under insufficient energy supply, neurons will only manifest as subthreshold activity when stimulated, but cannot fire action potentials. In general, we are usually concerned about the imbalance distribution of neural energy caused by neural activities under stimulation. However, neural activities are also modulated and constrained by neural energy. The mechanism is that ion pump that lacks energy supply cannot provide constant Nernst potential for sodium ions, and in the early stage of the change in cell membrane permeability, it cannot provide continuous flow of sodium ions to reach the threshold potential [27, 28]. Thus, the electrophysiological activity of neurons is strictly constrained by energy levels in the brain. When energy supply of ion pump of the sodium ion channels is insufficient, the response of neurons is subthreshold activity to any form and intensity of stimulation. But only when the maximum power of sodium ion channels is not constrained, the neurons will be sup-threshold firing.

  4. (4)

    Under the same stimulation conditions, whether the neurons can transition from subthreshold activity to sup-threshold activity is depended on whether the neurons can be fully energized. The two states of energy supply (subthreshold and sup-threshold) determine whether the ion pump can provide stable Nernst potential for sodium ions. That is, from the perspective of energy, the Nernst potential of sodium ion closely connects the subthreshold and the sup-threshold activity.

As the membrane potential and the corresponding energy expenditure have a unique correspondence, the traditional membrane potential encoding can also be expressed by the neural energy coding [9,10,11,12,13,14]. This will provide a sufficient theoretical basis for future studies on perceptual cognition and the construction of global neural models for brain function, which is a new brain theory of neuro combined with holism and reductionism. Its scientific significance lies in the subthreshold neural energy is directly associated with dark energy of neurons in the default model of network [32, 33], while 90% of the brain energy (dark energy of the neural) as well as the inherent neural energy metabolism of the spontaneous activity when the brain is at resting state has not been deeply studied [26, 34]. Owing to that the nature of neural energy metabolism is intrinsic and inherent in case of the spontaneous activity, the contribution to the cognitive neuroscience is what we have not known.