Cubic–quintic nonlinear parametric resonance of a simply supported beam

Abstract

We investigated the cubic–quintic nonlinear response in a parametrically excited simply supported beam subjected to a spring force in the axial direction. Taking into account the cubic and quintic geometric nonlinearities of curvature of the beam, the governing equation of the parametrically excited beam was derived based on Hamilton’s principle. The fifth-order approximate solution was analytically obtained using the method of multiple scales; with this calculation, the third-order nonlinear normal mode was also obtained. Its associated amplitude revealed saddle-node bifurcation and a hysteresis in the frequency response curve, which could not be predicted using the third-order approximate solution for the governing equation that included only cubic nonlinearity. Experimental results taken using a simple apparatus qualitatively verify the theoretically predicted nonlinear features in the parametric resonance caused by the cubic–quintic geometric nonlinearity of the beam.

Appendices

Appendix A

The dimensionless linear damping coefficient $\mu$ was experimentally identified to be

$$\begin{aligned} \mu =\frac{\omega }{\pi }\ln \frac{v(t_n)}{v(t_{n+1})}, \end{aligned}$$

(55)

where $\omega$ is the dimensionless first natural frequency of the beam. Figure 10 shows the experimental free vibration of the beam.

Fig. 10

Experimental free vibration of the beam

Appendix B

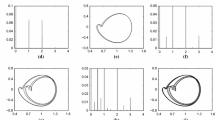
In the case of relative large response amplitude, the excitation displacement of Fig. 9a includes the unexpected the frequency component $2\varOmega =44.4$ Hz, which is different from the applied excitation frequency $\varOmega$. This is due to the limitation of power of the shaker. That can be explained in detail as follows: In the case of higher amplitude, the response frequency component as Fig. 9b in the original manuscript consists of a half the excitation frequency $\varOmega /2$ (11.1 Hz), and 1.5 times the excitation frequency $3\varOmega /2$ (33.3 Hz) which is not small. Because the axial displacement at $s=1$ is $\displaystyle {u(1)=-\frac{1}{2}\int _0^1{u'}^2ds}$ from Eq. (2) [18], the frequency component in the axial motion at $s=1$ includes the sum of these frequencies $\varOmega /2+3\varOmega /2=2\varOmega$. By this effect and the insufficient power of the shaker, the excitation displacement includes the unexpected frequency component $2\varOmega$ as shown in Fig. 9a.