Dynamic behavior of an electrostatic MEMS resonator with repulsive actuation

Abstract

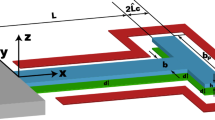
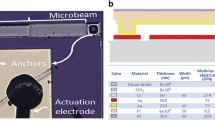
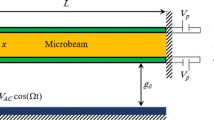
Static and dynamic analyses of an electrostatic microbeam under repulsive force actuation are presented. The repulsive force, created through a specific electrode configuration, generates a net electrostatic force on the beam pushing it away from the substrate. This allows large out-of-plane actuation and eliminates the pull-in instability. For example, a dynamic amplitude of 15 $\upmu$m was recorded for a 500-$\upmu$m-long cantilever at a DC voltage of 195 V and an AC voltage of 1 V, while the initial gap was only 2 $\upmu$m. This study includes mathematical modeling and simulations for a cantilever and a clamped–clamped beam, as well as experimental validation. The beam is modeled using Euler–Bernoulli beam theory and electromechanical coupling effects. Cantilever tip displacement, clamped–clamped midpoint deflection, and natural frequency shifts are reported. Governing equations are solved numerically using the shooting method, which provides a complete picture of the beam dynamics. The numerical results are verified with experimental data from fabricated beams using PolyMUMPs standard fabrication. Frequency response results reveal a mixed softening and hardening behavior and secondary resonances originating from quadratic and cubic nonlinearities in the governing equations. The analysis provides insight for applications in optical and gas sensors where a large signal-to-noise ratio and, sometimes, a wide frequency bandwidth are desired.

Appendix

1.1 Harmonic balance

In addition to the numerical shooting technique, an analytical method of harmonic balance was also used to verify the shooting method results. A steady-state solution is assumed in the form of a Fourier series. This is plugged into the governing differential equation and coefficients of the harmonic terms are equated. This results in a coupled set of algebraic equations that can be solved numerically [45]. The steady-state solution of Eq. (5) is assumed to be in the form

$$\begin{aligned} q(t)=a_0 + \sum _{j=1}^{N} a_j \sin (j \omega t) + b_j \cos (j \omega t) \end{aligned}$$

(12)

where $a_j$ and $b_j$ are constants, and N is the number of harmonics to be considered. For the cantilever, good convergence occurs at two harmonics and above. If the AC voltage is low enough that the frequency response looks approximately linear, one harmonic provides a good estimate of the solution. However, if the AC voltage is high enough to produce significant softening, at least two harmonics are necessary for an accurate solution in the region of the resonant peak. It should also be noted that only one mode is to be considered for the harmonic balance calculation.

Equation (12) is then plugged into Eq. (5), and the coefficients of the harmonic terms, as well as the remaining non-harmonic terms, are equated. The non-harmonic terms solve for the static solution of Eq. (5), while the harmonic terms determine the dynamic solution. This procedure is performed using Mathematica.

Because the forcing function is a 5th-order polynomial, the coupled algebraic equations for $a_j$ and $b_j$ are nonlinear and are difficult to solve analytically. Therefore, the Newton–Raphson method is employed. Once $a_j$ and $b_j$ are known, the maximum steady-state amplitude can be obtained by the relation shown in Eq. (13),

$$\begin{aligned} W= a_0 + \sum _{j=1}^n \sqrt{{a_j}^2 + {b_j}^2} \end{aligned}$$

(13)

Figure 16 shows the comparison between the shooting and harmonic balance methods (2 harmonics) for the case of $V_\mathrm{DC}$ = 195 V and $V_\mathrm{AC}$ = 1 V with largest softening behavior in Fig. 6. The two results are in close agreement. It is noted that the harmonic balance method also yields a similar softening behavior.

Fig. 16

Comparison between shooting method and harmonic balance (2 harmonics) for one mode at $V_\mathrm{DC}=195$ V and $V_\mathrm{AC}=1$ V

Next, this process is repeated for the clamped–clamped beam. Figure 17 depicts the comparison between the harmonic balance and shooting method results showing close agreement. For this case, only one harmonic is needed to show good agreement with the shooting method results.

Fig. 17

Frequency response at $V_\mathrm{DC}=50$ V and $V_\mathrm{AC}=10$ V with shooting method (1 mode). The black solid line represents the stable solution. Markers indicate results from harmonic balance method with one harmonic term