Skip to main content
SpringerLink
Log in

Elucidating the escape dynamics of the four hill potential

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

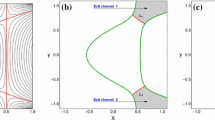
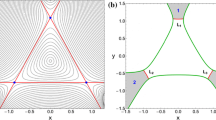
Abstract

The escape mechanism of the four hill potential is explored. A thorough numerical investigation takes place in several types of two-dimensional planes and also in a three-dimensional subspace of the entire four-dimensional phase space in order to distinguish between bounded (ordered and chaotic) and escaping orbits. The determination of the location of the basins of escape toward the different escape channels and their correlations with the corresponding escape time of the orbits is undoubtedly an issue of paramount importance. It was found that in all examined cases all initial conditions correspond to escaping orbits, while there is no numerical indication of stable bounded motion, apart from some isolated unstable periodic orbits. Furthermore, we monitor how the fractality evolves when the total orbital energy varies. The larger escape periods have been measured for orbits with initial conditions in the fractal basin boundaries, while the lowest escape rates belong to orbits with initial conditions inside the basins of escape. We hope that our numerical analysis will be useful for a further understanding of the escape dynamics of orbits in open Hamiltonian systems with two degrees of freedom.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. A sticky orbit is a special type of orbit which behaves as a regular one for long time intervals before it exhibits its true chaotic nature.

  2. The phenomenon of almost zero fractality, at the basin boundaries, at relatively high energy levels seems to be common in several types of Hamiltonian systems. For example, the same behavior is also observed in the Hénon-Heiles system but only for high enough values of the total orbital energy \((E > 2)\).

  3. The dimension of the complete phase space of a Hamiltonian system with N degrees of freedom is 2N. This phase space is foliated into \(2N-1\)-dimensional invariant leaves corresponding to the numerical values of the Hamiltonian. However, the dimension of the entire phase space always remains 2N, irrelevantly of any possible invariant foliation.

  4. The same phenomenon of the loss of the symmetry of a dynamical system due to the particular choice of the initial conditions of the orbits also applies for other types of Hamiltonian systems. For example, in the Hénon–Heiles system the \(2\pi /3\) symmetry is observable only in the configuration (x, y) space and only by using polar coordinates. On the other hand, for initial conditions of orbits in the \((y,\dot{y})\) phase space the three escape channels are no longer equiprobable (see, e.g., the series of papers on the Hénon-Heiles system by Sanjuán and collaborators).

References

  1. Aguirre, J., Vallego, J.C., Sanjuán, M.A.F.: Wada basins and chaotic invariant sets in the Hénon–Heiles system. Phys. Rev. E 64, 066208-1–066208-11 (2001)

    Article  Google Scholar 

  2. Aguirre, J., Viana, R.L., Sanjuán, M.A.F.: Fractal structures in nonlinear dynamics. Rev. Mod. Phys. 81, 333–386 (2009)

    Article  Google Scholar 

  3. Barrio, R., Blesa, F., Serrano, S.: Fractal structures in the Hénon–Heiles Hamiltonian. Europhys. Lett. 82, 10003 (2008)

    Article  Google Scholar 

  4. Barrio, R., Blesa, F., Serrano, S.: Bifurcations and safe regions in open Hamiltonians. New J. Phys. 11, 053004-1–053004-12 (2009)

    Article  Google Scholar 

  5. Benet, L., Trautman, D., Seligman, T.: Chaotic scattering in the restricted three-body problem. I. The Copenhagen Problem. Celest. Mech. Dyn. Astron. 66, 203–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  6. Benet, L., Seligman, T., Trautman, D.: Chaotic scattering in the restricted three-body problem II. Small mass parameters. Celest. Mech. Dyn. Astron. 71, 167–189 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bleher, S., Grebogi, C., Ott, E., Brown, R.: Fractal boundaries for exit in Hamiltonian dynamics. Phys. Rev. A 38, 930–938 (1988)

    Article  MathSciNet  Google Scholar 

  8. Bleher, S., Ott, E., Grebogi, C.: Routes to chaotic scattering. Phys. Rev. Lett. 63, 919–922 (1989)

    Article  Google Scholar 

  9. Bleher, S., Grebogi, C., Ott, E.: Bifurcation to chaotic scattering. Phys. D 46, 87–121 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  10. Churchill, R.C., et al.: In Casati, G., FordsComo, J. (eds.) Conference Proceedings on Stochastic Behavior in Classical and Quantum Hamiltonian Systems. Lecture Notes in Physics, Vol. 93, p 76. Springer, Berlin (1979)

  11. Contopoulos, G.: Asymptotic curves and escapes in Hamiltonian systems. Astron. Astrophys. 231, 41–55 (1990)

    MathSciNet  Google Scholar 

  12. Contopoulos, G.: Order and Chaos in Dynamical Astronomy. Springer, Berlin (2002)

    Book  MATH  Google Scholar 

  13. Contopoulos, G., Kaufmann, D.: Types of escapes in a simple Hamiltonian system. Astron. Astrophys. 253, 379–388 (1992)

    MathSciNet  MATH  Google Scholar 

  14. Contopoulos, G., Kandrup, H.E., Kaufmann, D.: Fractal properties of escape from a two-dimensional potential. Phys. D 64, 310–323 (1993)

    Article  MATH  Google Scholar 

  15. Contopoulos, G., Harsoula, M., Lukes-Gerakopoulos, G.: Periodic orbits and escapes in dynamical systems. Celest. Mech. Dyn. Astron. 113, 255–278 (2012)

    Article  MathSciNet  Google Scholar 

  16. Croustalloudi, M., Kalvouridis, T.: Attracting domains in ring-type N-body formations. Planet. Space Sci. 55, 53–69 (2007)

    Article  Google Scholar 

  17. Daza, A., Wagemakers, A., Georgeot, B., Guéry-Odelin, D., Sanjuán, M.A.F.: Basin entropy: a new tool to analyze uncertainty in dynamical systems. Sci. Rep. 6, 31416 (2016)

    Article  Google Scholar 

  18. de Moura, A.P.S., Letelier, P.S.: Fractal basins in Hénon-Heiles and other polynomial potentials. Phys. Lett. A 256, 362–368 (1999)

    Article  MathSciNet  Google Scholar 

  19. de Moura, A.P.S., Grebogi, C.: Countable and uncountable boundaries in chaotic scattering. Phys. Rev. E 66, 046214 (2002)

    Article  MathSciNet  Google Scholar 

  20. Drótos, G., Jung, C., Tél, T.: When is high-dimensional scattering chaos essentially two dimensional? Measuring the product structure of singularities. Phys. Rev. E 86, 056210 (2012)

    Article  Google Scholar 

  21. Drótos, G., Montoya, F.G., Jung, C., Tél, T.: Asymptotic observability of low-dimensional powder chaos in a three-degrees-of-freedom scattering system. Phys. Rev. E 90, 022906 (2014)

    Article  Google Scholar 

  22. Drótos, G., Jung, C.: The chaotic saddle of a three degrees of freedom scattering system reconstructed from cross section data. J. Phys. A 49, 235101 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ernst, A., Peters, T.: Fractal basins of escape and the formation of spiral arms in a galactic potential with a bar. Mon. Not. R. Astron. Soc. 443, 2579–2589 (2014)

    Article  Google Scholar 

  24. González, F., Drótos, G., Jung, C.: The decay of a normally hyperbolic invariant manifold to dust in a three degrees of freedom scattering system. J. Phys. A 47, 045101 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hénon, M.: Numerical exploration of the restricted problem, V. Astron. Astrophys. 1, 223–238 (1969)

    MATH  Google Scholar 

  26. Jung, C., Lipp, C., Seligman, T.H.: The inverse scattering problem for chaotic Hamiltonian systems. Ann. Phys. 275, 151–189 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  27. Jung, C., Mejia-Monasterio, C., Seligman, T.H.: Scattering one step from chaos. Phys. Lett. A 198, 306–314 (1995)

    Article  Google Scholar 

  28. Jung, C., Merlo, O., Seligman, T.H., Zapfe, W.P.K.: The chaotic set and the cross section for chaotic scattering in three degrees of freedom. New J. Phys. 12, 103021 (2010)

    Article  Google Scholar 

  29. Jung, C., Scholz, H.J.: Cantor set structure in the singularities of classical potential scattering. J. Phys. A 20, 3607–3617 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  30. Jung, C., Tél, T.: Dimension and escape rate of chaotic scattering from classical and semiclassical cross section data. J. Phys. A 24, 2793–2805 (1991)

    Article  Google Scholar 

  31. Kalvouridis, T.J.: On some new aspects of the photo-gravitational Copenhagen problem. Astrophys. Space Sci. 317, 107–117 (2008)

    Article  MATH  Google Scholar 

  32. Kalvouridis, T.J., Gousidou-Koutita, MCh.: Basins of attraction in the Copenhagen problem where the primaries are magnetic dipoles. Appl. Math. 3, 541–548 (2012)

    Article  Google Scholar 

  33. Kandrup, H.E., Siopis, C., Contopoulos, G., Dvorak, R.: Diffusion and scaling in escapes from two-degrees-of-freedom Hamiltonian systems. Chaos 9, 381–392 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kennedy, J., Yorke, J.A.: Basins of Wada. Phys. D 51, 213–225 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  35. Kumari, R., Kushvah, B.S.: Stability regions of equilibrium points in restricted four-body problem with oblateness effects. Astrophys. Space Sci. 349, 693–704 (2014)

    Article  Google Scholar 

  36. Lai, Y.-C., Tél, T.: Transient Chaos. Springer, New York (2011)

    Book  MATH  Google Scholar 

  37. Lyapunov, A.: Probléme general de las stabilité de mouvement. In: Annals of Mathematical Studies, vol. 17 (1949)

  38. Navarro, J.F., Henrard, J.: Spiral windows for escaping stars. Astron. Astrophys. 369, 1112–1121 (2001)

    Article  Google Scholar 

  39. Ott, E.: Chaos in Dynamical Systems. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  40. Poon, L., Campos, J., Ott, E., Grebogi, C.: Wada basins boundaries in chaotic scattering. Int. J. Bifurc. Chaos 6, 251–266 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  41. Press, H.P., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes in FORTRAN 77, 2nd edn. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  42. Schneider, J., Tél, T., Neufeld, Z.: Dynamics of leaking Hamiltonian systems. Phys. Rev. E 66, 066218 (2002)

    Article  MathSciNet  Google Scholar 

  43. Schneider, J., Tél, T.: Extracting flow structures from tracer data. Ocean Dyn. 53, 64–72 (2003)

    Article  Google Scholar 

  44. Seoane, J.M., Aguirre, J., Sanjuán, M.A.F., Lai, Y.C.: Basin topology in dissipative chaotic scattering. Chaos 16, 023101-1–023101-8 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  45. Seoane, J.M., Sanjuán, M.A.F., Lai, Y.C.: Fractal dimension in dissipative chaotic scattering. Phys. Rev. E 76, 016208-1–016208-6 (2007)

    Article  Google Scholar 

  46. Seoane, J., Sanjuán, M.A.F.: Exponential decay and scaling laws in noisy chaotic scattering. Phys. Lett. A 372, 110–116 (2008)

    Article  MATH  Google Scholar 

  47. Seoane, J., Sanjuán, M.A.F.: New developments in classical chaotic scattering. Rep. Prog. Phys. 76, 016001 (2013)

    Article  Google Scholar 

  48. Skokos, C.: Alignment indices: a new, simple method for determining the ordered or chaotic nature of orbits. J. Phys. A Math. Gen. 34, 10029–10043 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  49. Skokos, Ch., Antonopoulos, Ch., Bountis, T.C., Vrahatis, M.N.: Detecting order and chaos in Hamiltonian systems by the SALI method. J. Phys. A Math. Gen. 37, 6269–6284 (2004)

    Article  MathSciNet  Google Scholar 

  50. Sweet, D., Ott, E.: Fractal basin boundaries in higher-dimensional chaotic scattering. Phys. Lett. A 266, 134–139 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  51. Tuval, I., Schneider, J., Piro, O., Tél, T.: Opening up fractal structures of three-dimensional flows via leaking. Europhys. Lett. 65, 633–639 (2004)

    Article  Google Scholar 

  52. Waalkens, H., Burbanks, A., Wiggins, S.: A computational procedure to detect a new type of high-dimensional chaotic saddle and its application to the 3D Hill’s problem. J. Phys. A 37, L257–L265 (2004)

  53. Waalkens, H., Burbanks, A., Wiggins, S.: Escape from planetary neighbourhoods. MNRAS 361, 763–775 (2005)

    Article  Google Scholar 

  54. Wolfram, S.: The Mathematica Book. Wolfram Media, Champaign (2003)

    MATH  Google Scholar 

  55. Zotos, E.E.: A Hamiltonian system of three degrees of freedom with eight channels of escape: the great escape. Nonlinear Dyn. 76, 1301–1326 (2014)

    Article  Google Scholar 

  56. Zotos, E.E.: Escapes in Hamiltonian systems with multiple exit channels: part I. Nonlin. Dyn. 78, 1389–1420 (2014)

    Article  MathSciNet  Google Scholar 

  57. Zotos, E.E.: Revealing the escape mechanism of three-dimensional orbits in a tidally limited star cluster. MNRAS 446, 770–792 (2015)

    Article  Google Scholar 

  58. Zotos, E.E.: Escapes in Hamiltonian systems with multiple exit channels: part II. Nonlin. Dyn. 82, 357–398 (2015)

    Article  MathSciNet  Google Scholar 

  59. Zotos, E.E.: Fractal basin boundaries and escape dynamics in a multiwell potential. Nonlin. Dyn. 85, 1613–1633 (2016)

    Article  MathSciNet  Google Scholar 

  60. Zotos, E.E.: Fractal basins of attraction in the planar circular restricted three-body problem with oblateness and radiation pressure. Astrophys. Space Sci. 361, 181 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

I would like to gratefully and sincerely thank Dr. Christof Jung for all the illuminating discussions during this research. My warmest thanks also go to the two anonymous referees for the careful reading of the manuscript as well as for all the apt suggestions and comments which allowed us to improve both the quality and the clarity of the paper.

Funding The author states that he has not received any research grants.

Author information

Authors and Affiliations

  1. Department of Physics, School of Science, Aristotle University of Thessaloniki, 541 24, Thessaloniki, Greece

    Euaggelos E. Zotos

Authors
  1. Euaggelos E. Zotos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Euaggelos E. Zotos.

Ethics declarations

Conflict of interest

The author declares that he has no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zotos, E.E. Elucidating the escape dynamics of the four hill potential. Nonlinear Dyn 89, 135–151 (2017). https://doi.org/10.1007/s11071-017-3441-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3441-1

Keywords

Search

Navigation