Bifurcation analysis and solitary-like wave solutions for extended ${{\varvec{(2+1)}}}$-dimensional Konopelchenko–Dubrovsky equations

Abstract

In this paper, the bifurcation analysis as well as the sub-equation expansion method will be applied to study the extended $(2+1)$-dimensional Konopelchenko–Dubrovsky equations. The bifurcation analysis is first used to obtain the existence of traveling wave solutions. Then via the sub-equation expansion method, some new solitary-like wave solutions for each parameter condition are obtained.

Appendix A: some solutions of Eq. (3.3).

Case (1) Kink-shaped solitary-like wave solutions.

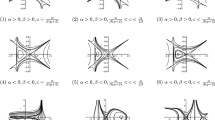
(I). If $d_0=\frac{{d_2}^2}{4d_4}, d_1=d_3=0, d_2 < 0, d_4>0$, then Eq. (3.3) has a kink-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{-\displaystyle \frac{{d_2 }}{{2d_4 }}} \mathrm{tanh}\left( \sqrt{-\displaystyle \frac{d_2}{2} } \xi \right) . \end{aligned} \end{aligned}$$

(5.1)

If $d_0=\displaystyle \frac{{d_2}^2}{4d_4}, d_1=d_3=0, d_2> 0, d_4 > 0$, then Eq. (3.3) has a kink-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, \epsilon \sqrt{ \displaystyle \frac{{d_2 }}{{2d_4 }}} \mathrm{tan}\left( \sqrt{\displaystyle \frac{d_2}{2} } \xi \right) . \end{aligned} \end{aligned}$$

(5.2)

If $d_0=d_1=0, d_3\ne 0, d_2 > 0, d_4 =c$, then Eq. (3.3) has a kink-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, -\displaystyle \frac{d_2}{d_3}\left[ 1+\epsilon \mathrm{tanh}\left( \sqrt{\displaystyle \frac{d_2}{2} } \xi \right) \right] . \end{aligned} \end{aligned}$$

(5.3)

If $d_0=d_1=0, d_3\ne 0, d_2 > 0, d_4 =c$, then Eq. (3.3) has a kink-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, -\displaystyle \frac{d_2}{d_3}\left[ 1+\epsilon \mathrm{coth}\left( \sqrt{\displaystyle \frac{d_2}{2} } \xi \right) \right] . \end{aligned} \end{aligned}$$

(5.4)

(II). Bell-shaped solitary-like wave solutions.

If $d_0=d_1=d_3=0, d_2 > 0, d_{4} < 0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\sqrt{ - \displaystyle \frac{{d_2 }}{{d_4 }}} \mathrm{sech}\left( \sqrt{d_2 } \xi \right) , \end{aligned} \end{aligned}$$

(5.5)

If $d_0=d_1=d_3=0, d_2 < 0, d_4 > 0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\sqrt{ - \displaystyle \frac{{d_2 }}{{d_4 }}} \mathrm{sec}\left( \sqrt{-d_2 } \xi \right) , \end{aligned} \end{aligned}$$

(5.6)

If $d_0>0,d_1=d_3=d_4=0, d_2 > 0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{ \displaystyle \frac{{d_0 }}{{d_2 }}} \mathrm{sinh}\left( \sqrt{d_2 } \xi \right) , \end{aligned} \end{aligned}$$

(5.7)

If $d_1\ne 0,d_0=d_3=d_4=0, d_2 > 0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, -\displaystyle \frac{d_1}{2d_2}+\displaystyle \frac{\epsilon d_1}{2d_2}\mathrm{sinh}\left( 2\sqrt{d_2 } \xi \right) , \end{aligned} \end{aligned}$$

(5.8)

If $d_0=d_1=d_4=0, d_2>0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, - \displaystyle \frac{{d_2 }}{{d_3 }}{\mathrm{sech}}^2 \left( \displaystyle \frac{{\sqrt{d_2 } }}{2}\xi \right) . \end{aligned} \end{aligned}$$

(5.9)

If $d_0=d_1=d_4=0,d_2<0$, then Eq. (3.3) has a bell-shaped solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,- \displaystyle \frac{{d_2 }}{{d_3 }}{\mathrm{sec}}^2 \left( \displaystyle \frac{{\sqrt{-d_2 } }}{2}\xi \right) . \end{aligned} \end{aligned}$$

(5.10)

(III). Solitary-like wave solutions (1).

If $d_1=d_3=d_4=0, d_0>0, d_2<0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{\displaystyle \frac{-d_0}{d_2}} {\mathrm{sin}}\left( \sqrt{-h_2}\xi \right) . \end{aligned} \end{aligned}$$

(5.11)

If $d_0=d_3=d_4=0, d_1\ne 0, d_2<0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,-\displaystyle \frac{d_1}{2d_2}+\displaystyle \frac{\epsilon d_1}{2d_2}\sin \left( \sqrt{-d_2}\xi \right) . \end{aligned} \end{aligned}$$

(5.12)

If $d_0=d_1=d_2=0, d_3\ne 0, d_4<0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{d_3}{2d_4}\exp {\displaystyle \frac{\epsilon d_3}{2\sqrt{-d_4}}}. \end{aligned} \end{aligned}$$

(5.13)

If $d_0=\displaystyle \frac{d^{2}_1}{4d_2}, d_1=c, d_2>0, d_3=d_4=0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,-\displaystyle \frac{d_1}{2d_2}+\exp \left( \epsilon \sqrt{d_2}\xi \right) . \end{aligned} \end{aligned}$$

(5.14)

If $d_0=c, d_1\ne 0, d_2=0, d_3=d_4=0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,-\displaystyle \frac{d_0}{d_1}+\displaystyle \frac{1}{4}d_1\xi ^{2}. \end{aligned} \end{aligned}$$

(5.15)

If $d_0>0, d_1=d_2=0, d_3=d_4=0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =\epsilon \sqrt{d_0}\xi . \end{aligned} \end{aligned}$$

(5.16)

(IV). Solitary-like wave solutions(2).

If $d_0=d_1=0, d_2> 0, d_3=c, d_{4}>0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, -\displaystyle \frac{{d_2 {\mathrm{sech}} ^2 \left( \displaystyle \frac{1}{2}\sqrt{ d_2 } \xi \right) }}{{2\epsilon \sqrt{ d_2 d_4 } \mathrm{tanh} \left( \displaystyle \frac{1}{2}\sqrt{ d_2 } \xi \right) +d_3 }}. \end{aligned} \end{aligned}$$

(5.17)

If $d_0=d_1=0, d_2> 0, d_3=c, d_{4}>0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, \displaystyle \frac{{d_2 {\mathrm{csch}} ^2 \left( \displaystyle \frac{1}{2}\sqrt{ d_2 } \xi \right) }}{{2\epsilon \sqrt{ d_2 d_4 } \mathrm{coth}\left( \displaystyle \frac{1}{2}\sqrt{ d_2 } \xi \right) +d_3 }}. \end{aligned} \end{aligned}$$

(5.18)

If $d_0=d_1=0, d_2 < 0, d_3=c, d_{4}>0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,-\displaystyle \frac{{d_2 {\mathrm{sec}}^2 \left( \displaystyle \frac{1}{2}\sqrt{- d_2 } \xi \right) }}{{2\epsilon \sqrt{ - d_2 d_4 } \mathrm{tan}(\displaystyle \frac{1}{2}\sqrt{ - d_2 } \xi ) +d_3 }}. \end{aligned} \end{aligned}$$

(5.19)

If $d_0=d_1=0, d_2 < 0, d_3=c, d_{4}>0$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\, -\displaystyle \frac{{d_2 {\mathrm{csc}}^2 \left( \displaystyle \frac{1}{2}\sqrt{- d_2 } \xi \right) }}{{2\epsilon \sqrt{ - d_2 d_4 } \cot \left( \displaystyle \frac{1}{2}\sqrt{ - d_2 } \xi \right) +d_3 }}. \end{aligned} \end{aligned}$$

(5.20)

If $d_0=d_1=0, d_2 > 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{2d_2 \mathrm{sech}\left( \sqrt{d_2 } \xi \right) }}{{\epsilon \sqrt{ d^{2}_{3}-4d_2 d_4 }-d_3\mathrm{sech} \left( \sqrt{d_2 } \xi \right) }}. \end{aligned} \end{aligned}$$

(5.21)

If $d_0=d_1=0, d_2 < 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{2d_2 \mathrm{csc}\left( \sqrt{-d_2 } \xi \right) }}{{\epsilon \sqrt{ d^{2}_{3}-4d_2 d_4 }-d_3\mathrm{csc} \left( \sqrt{-d_2 } \xi \right) }}. \end{aligned} \end{aligned}$$

(5.22)

If $d_0=d_1=0, d_2 < 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{2d_2 \mathrm{sec}\left( \sqrt{-d_2 } \xi \right) }}{{\epsilon \sqrt{ d^{2}_{3}-4d_2 d_4 }-d_3\mathrm{sec}(\sqrt{-d_2 } \xi )}}. \end{aligned} \end{aligned}$$

(5.23)

If $d_0=d_1=0, d_2 > 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{2d_2 \mathrm{csch}\left( \sqrt{d_2 } \xi \right) }}{{\epsilon \sqrt{ -d^{2}_{3}+4d_2 d_4 }-d_3\mathrm{csch}\left( \sqrt{d_2 } \xi \right) }}. \end{aligned} \end{aligned}$$

(5.24)

If $d_0=d_1=0, d_2 > 0, d_{3}\ne 0, d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{-d_2d_3 \mathrm{sech}^{2}\left( \displaystyle \frac{1}{2}\sqrt{d_2 } \xi \right) }}{d^{2}_{3}-d_2 d_4\left( 1+\epsilon \tanh \left( \displaystyle \frac{1}{2}\sqrt{d_2 }\xi \right) \right) ^2}. \end{aligned} \end{aligned}$$

(5.25)

If $d_0=d_1=0, d_2 > 0, d_{3}\ne 0, d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{d_2d_3 \mathrm{csch}^{2}\left( \displaystyle \frac{1}{2}\sqrt{d_2 } \xi \right) }}{d^{2}_{3}-d_2 d_4\left( 1+\epsilon \coth \left( \displaystyle \frac{1}{2}\sqrt{d_2 }\xi \right) \right) ^2}. \end{aligned} \end{aligned}$$

(5.26)

If $d_0=d_1=0, d_2 > 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{4d_2\mathrm{exp}\left( \epsilon \sqrt{d_2}\xi \right) }}{\left( \hbox {exp}\left( \epsilon \sqrt{d_2}\xi \right) ^{2}-d_{3}\right) ^{2}-4d_2 d_4}. \end{aligned} \end{aligned}$$

(5.27)

If $d_0=d_1=0, d_2 > 0, d_{3}=d_{4}=c$, then Eq. (3.3) has a solitary-like wave solution

$$\begin{aligned} \begin{aligned} \phi =&\,\displaystyle \frac{{\pm 4d_2\mathrm{exp}\left( \epsilon \sqrt{d_2}\xi \right) }}{1-4d_2 d_4exp\left( 2\epsilon \sqrt{d_2}\xi \right) }. \end{aligned} \end{aligned}$$

(5.28)

Case (2) Jacobi-like and Weierstrass-like doubly periodic solutions.

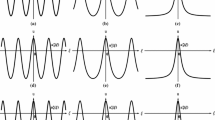
If $d_{1}=d_{3}=0, d_4 < 0, d_2 > 0, d_0= \displaystyle \frac{{d_2 ^2 m^2 (1 - m)^2}}{{d_4 (2m^2-1)^2 }}$, then Eq. (3.3) has a Jacobi-like and Weierstrass-like doubly periodic solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{\displaystyle \frac{{ - d_2 m^2 }}{{d_4 (2m^2 - 1)}}} \mathrm{cn}\left( \sqrt{\displaystyle \frac{{d_2 }}{{2m^2 - 1}}} \xi \right) , \end{aligned} \end{aligned}$$

(5.29)

If $d_{1}=d_{3}=0, d_4 < 0, d_2> 0, d_0= \displaystyle \frac{{d_2 ^2 (1 - m^2 )}}{{d_4 (2 - m^2)^2 }}$, then Eq. (3.3) has a Jacobi-like and Weierstrass-like doubly periodic solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{\displaystyle \frac{{ - d^2 }}{{d_4 (2 - m^2)}}} {\mathrm{dn}}\left( \sqrt{\displaystyle \frac{{d_2 }}{{2 - m^2}}} \xi \right) , \end{aligned} \end{aligned}$$

(5.30)

If $d_{1}=d_{3}=0, d_4> 0, d_2 < 0, d_0= \displaystyle \frac{{d_2 ^2 m^2 }}{{d_4 (m^2 + 1)^2}}$, then Eq. (3.3) has a Jacobi-like and Weierstrass-like doubly periodic solution

$$\begin{aligned} \begin{aligned} \phi =&\,\epsilon \sqrt{\displaystyle \frac{{ - d_2 m^2 }}{{d_4 (m^2 + 1)}}} \mathrm{sn}\left( \sqrt{-\displaystyle \frac{{d_2 }}{{m^2 + 1}}} \xi \right) , \end{aligned} \end{aligned}$$

(5.31)

where m is a modulus.

$$\begin{aligned} \begin{aligned} \phi = \wp \left( \displaystyle \frac{\sqrt{d_3}}{2}\xi , g_2, g_3\right) ,&d_2=0, d_3 > 0, \end{aligned} \end{aligned}$$

(5.32)

where $g_2=-4\displaystyle \frac{d_1}{d_3}$ and $g_3=-4\displaystyle \frac{d_0}{d_3}$.